期末应用题易错精选题(含解析)-2024-2025学年数学五年级下册苏教版
文档属性
| 名称 | 期末应用题易错精选题(含解析)-2024-2025学年数学五年级下册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 742.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 11:31:05 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
期末应用题易错精选题-2024-2025学年数学五年级下册苏教版
1.一块梯形麦地,面积是0.12公顷。它的上底与下底的和是80米,高是多少米?(用方程解)
2.今年爸爸的年龄是小明的3.2倍,妈妈的年龄是小明的2.6倍,已知爸爸比妈妈大9岁。今年小明多少岁?爸爸、妈妈呢?
3.为参加“最美教室”评比,各班准备绿植布置教室。五年级准备的绿植盆数是四年级的1.3倍,五年级送给四年级6盆绿植后,五、四年级的绿植盆数一样多。原来五年级和四年级各有多少盆绿植?(列方程解答)
4.已知三角形的面积是100平方厘米,它的底是25厘米,高是多少厘米?(列方程解答)
5.今年哥哥和弟弟的年龄和为35岁,哥哥比弟弟大3岁。今年哥哥和弟弟各多少岁?(列方程解答)
6.一列客车和一列货车从相距465千米的甲、乙两地同时出发,相向而行。客车每小时行90千米,货车每小时行65千米,几小时后两车相遇?
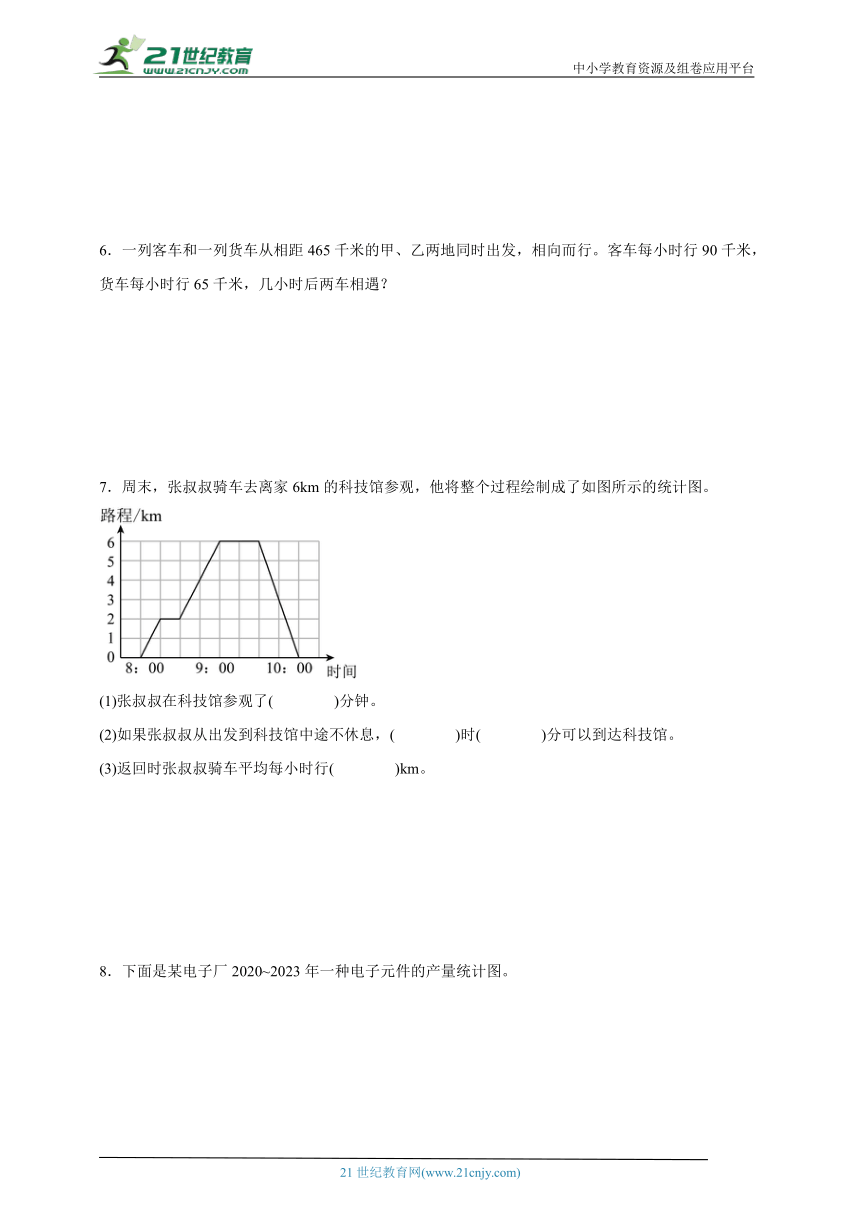
7.周末,张叔叔骑车去离家6km的科技馆参观,他将整个过程绘制成了如图所示的统计图。
(1)张叔叔在科技馆参观了( )分钟。
(2)如果张叔叔从出发到科技馆中途不休息,( )时( )分可以到达科技馆。
(3)返回时张叔叔骑车平均每小时行( )km。
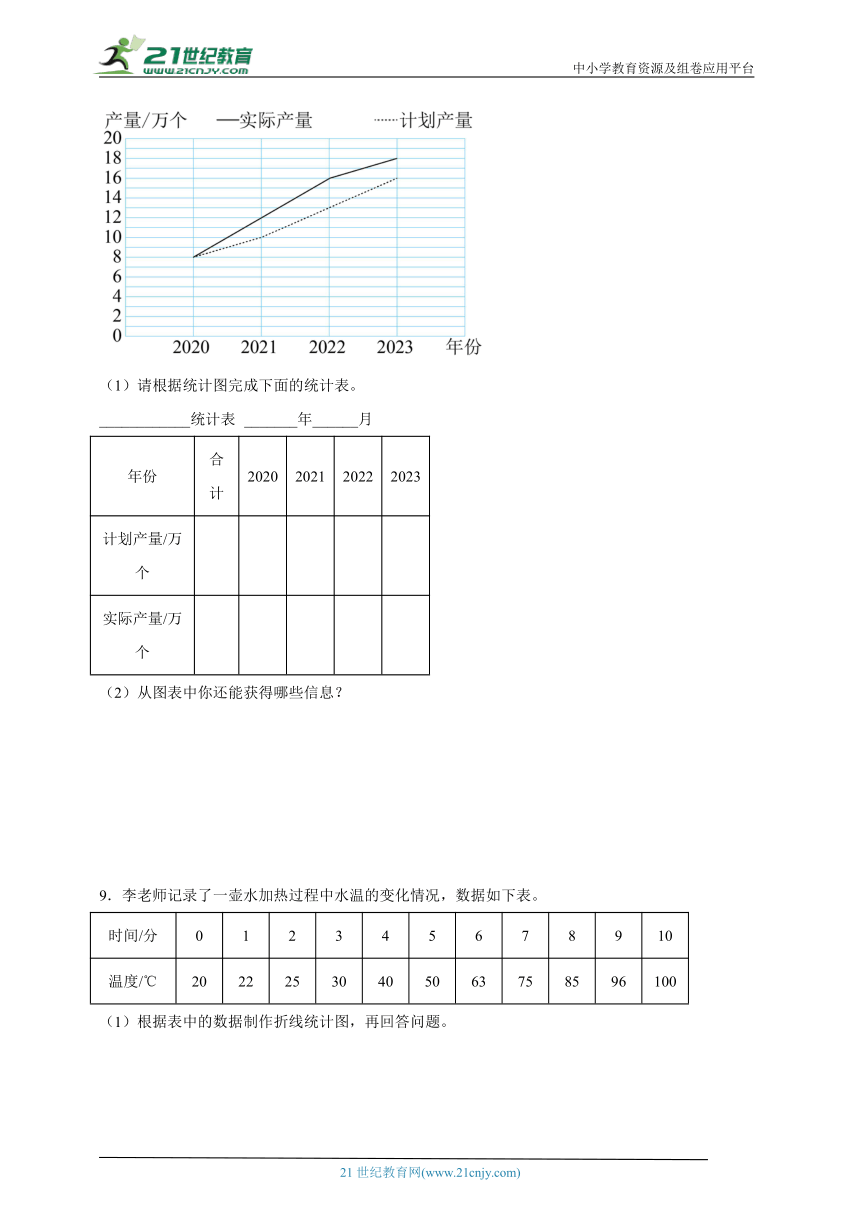
8.下面是某电子厂2020~2023年一种电子元件的产量统计图。
(1)请根据统计图完成下面的统计表。
____________统计表 _______年______月
年份 合计 2020 2021 2022 2023
计划产量/万个
实际产量/万个
(2)从图表中你还能获得哪些信息?
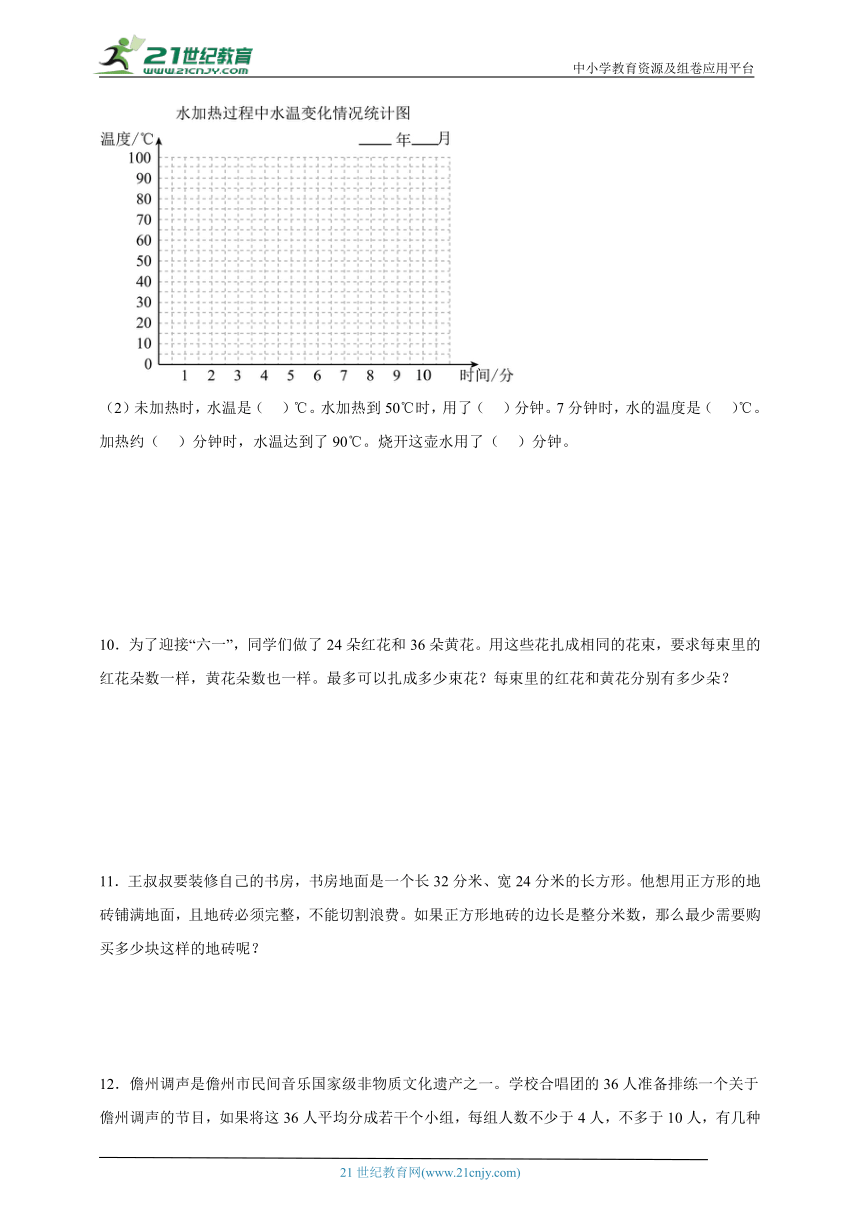
9.李老师记录了一壶水加热过程中水温的变化情况,数据如下表。
时间/分 0 1 2 3 4 5 6 7 8 9 10
温度/℃ 20 22 25 30 40 50 63 75 85 96 100
(1)根据表中的数据制作折线统计图,再回答问题。
(2)未加热时,水温是( )℃。水加热到50℃时,用了( )分钟。7分钟时,水的温度是( )℃。加热约( )分钟时,水温达到了90℃。烧开这壶水用了( )分钟。
10.为了迎接“六一”,同学们做了24朵红花和36朵黄花。用这些花扎成相同的花束,要求每束里的红花朵数一样,黄花朵数也一样。最多可以扎成多少束花?每束里的红花和黄花分别有多少朵?
11.王叔叔要装修自己的书房,书房地面是一个长32分米、宽24分米的长方形。他想用正方形的地砖铺满地面,且地砖必须完整,不能切割浪费。如果正方形地砖的边长是整分米数,那么最少需要购买多少块这样的地砖呢?
12.儋州调声是儋州市民间音乐国家级非物质文化遗产之一。学校合唱团的36人准备排练一个关于儋州调声的节目,如果将这36人平均分成若干个小组,每组人数不少于4人,不多于10人,有几种分法?(写出具体的分法)
13.王师傅5分钟加工7个零件,李师傅6分钟加工9个零件,杨师傅加工13个零件用了7分钟。谁的工作效率最高?
14.录人一份稿件,小李用了13分钟,比小王少用4分钟。小李用的时间是小王的几分之几?小王用的时间是小李的几分之几?
15.学校图书馆买来5箱图书,一共300本,平均分给12个班,每班分到多少本?每班分到几分之几箱?每班分得这些图书的几分之几?
16.小华调查了全班同学在三八妇女节送给妈妈的礼物:的同学送鲜花,的同学送贺卡,其余同学送的是自己画的画。送画的同学占全班同学的几分之几?
17.截至2022年6月,我国使用网络的人数约占全国人口的。不使用网络的人数约占全国人口的几分之几?
18.一台拖拉机耕一块地,上午耕了公顷,下午比上午多耕了公顷。下午耕地多少公顷?
19.如图,长方形中空白部分的周长是10.28分米,求涂色部分的面积。
20.如图,一个圆形池塘的周长是251.2米,池塘周围有一条4米宽的环形路。
(1)这个池塘的面积是多少平方米?
(2)环形路的占地面积是多少平方米?
21.如图,圆的周长是37.68分米,圆与长方形面积相等。
(1)长方形的长与宽各是多少分米?
(2)涂色部分的面积是多少平方分米?
22.王叔叔用18.84米长的篱笆靠墙围了一个半圆形菜园(如图),这个半圆形菜园的半径是多少米?
23.如图,如果正方形的面积是24平方厘米,那么圆的面积是多少平方厘米?
24.一堆钢管堆成一个近似的梯形,已知最上层有3根,最下层有20根,相邻两层之间相差1根。这堆钢管一共有多少根?
25.有大、小两筐水果,大筐水果的质量是小筐水果的1.6倍。如果从大筐中取出12千克水果放入小筐,两筐水果的质量就相等了。原来大、小两筐水果的质量各是多少千克?
《期末应用题易错精选题-2024-2025学年数学五年级下册苏教版》参考答案
1.30米
【分析】根据1公顷=10000平方米,把0.12公顷转化为以平方米为单位,设高是米,根据,列方程并求解即可。
【详解】解:设高是米。
0.12公顷=1200平方米
答:高是30米。
2.小明15岁;爸爸48岁;妈妈39岁
【分析】根据题意,设小明的年龄是x岁,那么爸爸的年龄是3.2x岁,妈妈的年龄是2.6x岁,用爸爸的年龄减去妈妈的年龄就等于9岁,据此列出方程求解即可解答。
【详解】解:设小明的年龄是x岁。
3.2x-2.6x=9
0.6x=9
0.6x÷0.6=9÷0.6
x=15
爸爸:3.2x=3.2×15=48(岁)
妈妈:2.6x=2.6×15=39(岁)
答:今年小明15岁,爸爸48岁,妈妈39岁。
3.五年级52盆;四年级40盆
【分析】根据“五年级准备的绿植盆数是四年级的1.3倍”,可以设原来四年级有盆绿植,则原来五年级有1.3盆绿植;根据“五年级送给四年级6盆绿植后,五、四年级的绿植盆数一样多”可得出等量关系:原来五年级绿植的盆数-6盆=原来四年级绿植的盆数+6盆,据此列出方程,并求解。
【详解】解:设原来四年级有盆绿植,则原来五年级有1.3盆绿植。
1.3-6=+6
1.3-6-=+6-
0.3-6=6
0.3-6+6=6+6
0.3=12
0.3÷0.3=12÷0.3
=40
原来五年级有:40×1.3=52(盆)
答:原来五年级有52盆绿植,四年级有40盆绿植。
4.8厘米
【分析】根据三角形面积公式:底×高÷2=三角形面积,设高是x厘米,列方程:25x÷2=100,解方程,即可解答。
【详解】解:设高是x厘米。
25x÷2=100
25x÷2×2=100×2
25x=200
25x÷25=200÷25
x=8
答:高是8厘米。
5.哥哥:19岁;弟弟16岁
【分析】设今年弟弟x岁,哥哥比弟弟大3岁,则哥哥是(x+3)岁;哥哥弟弟的年龄和为35岁,即今年哥哥年龄+今年弟弟年龄=35岁,列方程:x+x+3=35,解方程,即可解答。
【详解】解:设今年弟弟x岁,则今年哥哥(x+3)岁。
x+x+3=35
2x+3=35
2x+3-3=35-3
2x=32
2x÷2=32÷2
x=16
哥哥:16+3=19(岁)
答:今年哥哥19岁,弟弟16岁。
6.3小时
【分析】把相遇时间设为未知数,等量关系式:(客车的速度+货车的速度)×相遇时间=两车行驶的总路程,故设两车的相遇时间为x小时,据此列方程解答。
【详解】解:设x小时后两车相遇。
(90+65)x=465
155x=465
155x÷155=465÷155
x=3
答:3小时后两车相遇。
7.(1)30
(2) 8 45
(3)12
【分析】折线统计图中的横轴表示时间,1小时即60分钟平均分成4小格,那么每小格表示60÷4=15分钟。
(1)从图中可知,张叔叔在科技馆参观的时间是2小格,即参观了30分钟。
(2)从图中可知,张叔叔休息了15分钟,如果不休息那就提前了15分钟,用原来到达科技馆的时刻减去15分钟即可。
(3)返回时的路程是6km,时间是30分钟即0.5小时,根据速度=路程÷时间求出他的速度。
【详解】(1)60÷4=15(分钟)
15×2=30(分钟)
张叔叔在科技馆参观了30分钟。
(2)9时-15分钟=8时45分
如果张叔叔从出发到科技馆中途不休息,8时45分可以到达科技馆。
(3)30分钟=0.5小时
6÷0.5=12(km)
返回时张叔叔骑车平均每小时行12km。
8.(1)见详解
(2)2020年计划产量和实际产量相等(答案不唯一)
【分析】(1)由图可知,实线表示实际产量,虚线表示计划产量,2020、2021、2022、2023年的计划产量分别为8万个、10万个、13万个、16万个,实际产量分别为8万个、12万个、16万个、18万个;用算式8+10+13+16求得计划产量合计,用算式8+12+16+18求得实际产量合计。据此解答即可。
(2)从图表中,可以看到2020年计划产量和实际产量都是8万元,也就是计划产量和实际产量相等。(答案不唯一)
【详解】(1)8+10+13+16
=31+16
=47(万个)
8+12+16+18
=36+18
=54(万个)
所以:
某电子厂2020~2023年一种电子元件的产量统计表 2024年12月
年份 合计 2020 2021 2022 2023
计划产量/万个 47 8 10 13 16
实际产量/万个 54 8 12 16 18
(2)从图表中,我知道了2020年计划产量和实际产量相等。(答案不唯一)
9.(1)图见详解;
(2)20;5;75;8.5;10
【分析】先根据表中的数据绘成折线统计图,未加热时的水温就是0分钟时的水温;找出水温50℃时的时间,就是水加热到50℃,用的时间;找出7分钟时水的温度,就是7分钟时,水的温度;第8分钟时水温是85°,第9分钟时水温是96°,所以水温是90°时,时间一定在8分钟到9分钟之间,答案不唯一,合理即可;水开时的温度是100℃,找出此时的时间,就是烧开这壶水所用的时间,据此解题即可。
【详解】(1)水加热过程中水温变化情况统计图
2024年11月
(2)未加热时,水温是20℃。水加热到50℃时,用了5分钟。7分钟时,水的温度是75℃。加热约8.5分钟时(这个空答案不唯一,在八分钟和九分钟之间合理即可),水温达到了90℃。烧开这壶水用了10分钟。
10.红花2朵;黄花3朵
【分析】要使每束花里红花的朵数相同,黄花的朵数也相同,则扎成的花束的数量是24和36的公因数,最多扎的束数就是24和36的最大公因数。用质因数分解法可以求两个数的最大公因数,全部共有的质因数(公有质因数)相乘的积就是这两个数的最大公因数。
分别用24和36除以求得的最大公因数,即最多扎的束数,再用红花和黄花的朵数分别除以扎的束数即可求出每束花中红花和黄花各有多少朵。
【详解】24=2×2×2×3
36=2×2×3×3
所以24和36的最大公因数是:2×2×3=12;
24÷12=2(朵)
36÷12=3(朵)
答:最多可以扎成12束花,每束里的红花有2朵,黄花有3朵。
11.12块
【分析】地砖的边长取书房的长和宽的最大公因数时,才能保证地砖完整且数量最少。首先将32和24分解质因数,计算出它们的最大公因数即为方砖的边长;再用长方形地面的长和宽分别除以地砖边长,得到每行、每列能铺的地砖数;最后将每行和每列的地砖数相乘,得到铺满地面最少需要地砖的块数(总数量=每行数量×每列数量)。
【详解】32=2×2×2×2×2
24=2×2×2×3
32和24的最大公因数是2×2×2=8,所以正方形地砖的边长是8分米。
(32÷8)×(24÷8)
=4×3
=12(块)
答:最少需要购买12块这样的地砖。
12.3种;分法见详解
【分析】先把36写成两个因数的积,求出36的所以因数,根据每组人数不少于4人,不多于10人,其中大于或等于4而小于或等于10的因数就是一组的人数,再用36分别除以每组的人数确定有几种分法即可。
【详解】36=1×36=2×18=3×12=4×9=6×6,所以36的因数有1、2、3、4、6、9、12、18、36;
其中大于或等于4小于或等于10的因数有4、6、9;
36÷4=9(组)
36÷6=6(组)
36÷9=4(组)
答:有3种分法;分法为:每组4人,分9组;每组6人,分6组;每组9人,分4组。
13.杨师傅
【分析】根据题意,先用每人做零件的个数除以加工的时间,求出每分钟加工零件的个数,即是每人的工作效率;再根据分数大小比较的方法进行比较即可得解。
分数大小的比较:
分母相同时,分子越大,分数值就越大;
分子相同时,分母越大,分数值反而越小;
分子、分母都不相同时,利用分数的基本性质化成同分母或同分子的分数进行比较。
【详解】王师傅:(个)
李师傅:(个)
杨师傅:(个)
,,
答:杨师傅的工作效率最高。
14.;
【分析】已知小李用了13分钟,比小王少用4分钟,即小王比小李多用4分钟,用小李用的时间加上4,即是小王用的时间;
求小李用的时间是小王的几分之几,用小李用的时间除以小王用的时间即可;
求小王用的时间是小李的几分之几,用小王用的时间除以小李用的时间即可。
【详解】13+4=17(分钟)
13÷17=
17÷13=
答:小李用的时间是小王的,小王用的时间是小李的。
15.25本;箱;
【分析】根据平均分用除法计算,第一问用总本数除以班数,第二问用总箱数除以班数,第三问把图书总数看作单位“1”,根据分数的意义,把1平均分成12份,每份是。
【详解】(本)
(箱)
答:每班分到25本,每班分到箱,每班分得这些图书的。
16.
【分析】把全班同学的人数看作单位“1”,用单位“1”减去送鲜花的、送贺卡的同学所占的分率,求出送画的同学占全班同学的几分之几即可。
【详解】1--
=-
=-
=
答:送画的同学占全班同学的。
17.
【分析】把全国人口总人数看作单位“1”,我国使用网络的人数约占全国人口的,求不使用网络的人数约占全国人口的分率,用1-解答。
【详解】1-=
答:不使用网络的人数约占全国人口的。
18.公顷
【分析】下午耕地的公顷数=上午耕地的公顷数+多耕地的公顷数。异分母分数加法通分转化为同分母分数相加即可。
【详解】(公顷)
答:下午耕地公顷。
19.6.28平方分米
【分析】长方形中空白部分的周长相当于一个半圆的周长,根据半圆的周长=(π+2)r,已知长方形空白部分的周长,代入半圆的周长计算公式,计算出半径;涂色部分的面积=圆的面积÷2,根据圆的面积=πr2,代入数值计算,据此解答。
【详解】10.28÷(3.14+2)
=10.28÷5.14
=2(分米)
3.14×22÷2
=3.14×4÷2
=12.56÷2
=6.28(平方分米)
答:涂色部分的面积是6.28平方分米。
20.(1)5024平方米
(2)1055.04平方米
【分析】(1)根据圆的周长=2πr,代入数值计算出圆形池塘的半径;再根据圆的面积=πr2,代入数值计算,所得结果即为这个池塘的面积。
(2)求环形路的占地面积也就是求这个圆环的面积,根据圆环的面积=π×(R2-r2),已知外圆的半径=池塘的半径+4,代入相应数值计算,所得结果即为环形路的占地面积。
【详解】(1)池塘的半径:251.2÷3.14÷2=40(米)
3.14×402
=3.14×1600
=5024(平方米)
答:这个池塘的面积是5024平方米。
(2)外圆的半径为:40+4=44(米)
3.14×(442-402)
=3.14×(1936-1600)
=3.14×336
=1055.04(平方米)
答:环形路的占地面积是1055.04平方米。
21.(1)长:18.84分米;宽:6分米
(2)84.78平方分米
【分析】(1)根据圆的周长=2πr,代入数值计算出圆的半径,圆的半径与长方形的宽相等;再根据圆的面积=πr2,代入数值计算出圆的面积,且圆的面积与长方形的面积相等;最后用圆的面积除以圆的半径,所得结果即为长方形的长。
(2)涂色部分的面积等于长方形的面积减去四分之一圆的面积,结合(1)中计算出的数值,代入公式计算,据此解答。
【详解】(1)圆的半径:37.68÷3.14÷2=6(分米)
圆的半径与长方形的宽相等,因此长方形的宽为6分米。
圆的面积:3.14×62
=3.14×36
=113.04(平方分米)
长方形的长:113.04÷6=18.84(分米)
答:长方形的长是18.84分米,宽是6分米。
(2)113.04-113.04÷4
=113.04-28.26
=84.78(平方分米)
答:涂色部分的面积是84.78平方分米。
22.6米
【分析】因为王叔叔用18.84米长的篱笆靠墙围了个半圆形菜园,这里18.84米是半圆的弧长。
圆的周长公式为C=2r,那么半圆的弧长就是r,用半圆的弧长除以即可求出这个半圆形菜园的半径是多少米。
【详解】18.84÷3.14=6(米)
答:这个半圆形菜园的半径是6米。
23.18.84平方厘米
【分析】从图中可知,圆的直径等于正方形的边长。设圆的半径为r厘米,则圆的直径是2r厘米,根据“边长×边长=正方形的面积”,据此列出方程,并求出半径的平方即r2的值。根据圆的面积公式S=πr2,把r2的值代入圆的面积公式,求出这个圆的面积。
【详解】解:设圆的半径为r厘米。
(2r)×(2r)=24
4r2=24
r2=24÷4
r2=6
圆的面积:3.14×6=18.84(平方厘米)
答:圆的面积是18.84平方厘米。
24.207根
【分析】因为相邻两层之间相差1根,因此共(20-3+1)层,结合梯形面积公式,总根数=(最上层根数+最下层根数)×层数÷2,列式解答即可。
【详解】(3+20)×(20-3+1)÷2
=23×18÷2
=207(根)
答:这堆钢管一共有207根。
25.大筐质量是64千克,小筐质量是40千克。
【分析】这是一道典型的差倍问题,从大筐取出12千克放入小筐,两筐水果的质量就相等了,说明原本大筐的质量比小筐的质量多了24千克,特别注意这里大小两筐的质量差不是12千克。而大筐质量是小筐的1.6倍,把小筐的质量看作1份,则大筐就是1.6份,相差0.6份,结合相差的数量24千克,即可求出1份的质量,从而推出大小两筐分别的质量。
【详解】12×2=24(千克)
24÷(1.6-1)
=24÷0.6
=40(千克)
40+24=64(千克)
答:原来大筐的质量是64千克,小筐的质量是40千克。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末应用题易错精选题-2024-2025学年数学五年级下册苏教版
1.一块梯形麦地,面积是0.12公顷。它的上底与下底的和是80米,高是多少米?(用方程解)
2.今年爸爸的年龄是小明的3.2倍,妈妈的年龄是小明的2.6倍,已知爸爸比妈妈大9岁。今年小明多少岁?爸爸、妈妈呢?
3.为参加“最美教室”评比,各班准备绿植布置教室。五年级准备的绿植盆数是四年级的1.3倍,五年级送给四年级6盆绿植后,五、四年级的绿植盆数一样多。原来五年级和四年级各有多少盆绿植?(列方程解答)
4.已知三角形的面积是100平方厘米,它的底是25厘米,高是多少厘米?(列方程解答)
5.今年哥哥和弟弟的年龄和为35岁,哥哥比弟弟大3岁。今年哥哥和弟弟各多少岁?(列方程解答)
6.一列客车和一列货车从相距465千米的甲、乙两地同时出发,相向而行。客车每小时行90千米,货车每小时行65千米,几小时后两车相遇?
7.周末,张叔叔骑车去离家6km的科技馆参观,他将整个过程绘制成了如图所示的统计图。
(1)张叔叔在科技馆参观了( )分钟。
(2)如果张叔叔从出发到科技馆中途不休息,( )时( )分可以到达科技馆。
(3)返回时张叔叔骑车平均每小时行( )km。
8.下面是某电子厂2020~2023年一种电子元件的产量统计图。
(1)请根据统计图完成下面的统计表。
____________统计表 _______年______月
年份 合计 2020 2021 2022 2023
计划产量/万个
实际产量/万个
(2)从图表中你还能获得哪些信息?
9.李老师记录了一壶水加热过程中水温的变化情况,数据如下表。
时间/分 0 1 2 3 4 5 6 7 8 9 10
温度/℃ 20 22 25 30 40 50 63 75 85 96 100
(1)根据表中的数据制作折线统计图,再回答问题。
(2)未加热时,水温是( )℃。水加热到50℃时,用了( )分钟。7分钟时,水的温度是( )℃。加热约( )分钟时,水温达到了90℃。烧开这壶水用了( )分钟。
10.为了迎接“六一”,同学们做了24朵红花和36朵黄花。用这些花扎成相同的花束,要求每束里的红花朵数一样,黄花朵数也一样。最多可以扎成多少束花?每束里的红花和黄花分别有多少朵?
11.王叔叔要装修自己的书房,书房地面是一个长32分米、宽24分米的长方形。他想用正方形的地砖铺满地面,且地砖必须完整,不能切割浪费。如果正方形地砖的边长是整分米数,那么最少需要购买多少块这样的地砖呢?
12.儋州调声是儋州市民间音乐国家级非物质文化遗产之一。学校合唱团的36人准备排练一个关于儋州调声的节目,如果将这36人平均分成若干个小组,每组人数不少于4人,不多于10人,有几种分法?(写出具体的分法)
13.王师傅5分钟加工7个零件,李师傅6分钟加工9个零件,杨师傅加工13个零件用了7分钟。谁的工作效率最高?
14.录人一份稿件,小李用了13分钟,比小王少用4分钟。小李用的时间是小王的几分之几?小王用的时间是小李的几分之几?
15.学校图书馆买来5箱图书,一共300本,平均分给12个班,每班分到多少本?每班分到几分之几箱?每班分得这些图书的几分之几?
16.小华调查了全班同学在三八妇女节送给妈妈的礼物:的同学送鲜花,的同学送贺卡,其余同学送的是自己画的画。送画的同学占全班同学的几分之几?
17.截至2022年6月,我国使用网络的人数约占全国人口的。不使用网络的人数约占全国人口的几分之几?
18.一台拖拉机耕一块地,上午耕了公顷,下午比上午多耕了公顷。下午耕地多少公顷?
19.如图,长方形中空白部分的周长是10.28分米,求涂色部分的面积。
20.如图,一个圆形池塘的周长是251.2米,池塘周围有一条4米宽的环形路。
(1)这个池塘的面积是多少平方米?
(2)环形路的占地面积是多少平方米?
21.如图,圆的周长是37.68分米,圆与长方形面积相等。
(1)长方形的长与宽各是多少分米?
(2)涂色部分的面积是多少平方分米?
22.王叔叔用18.84米长的篱笆靠墙围了一个半圆形菜园(如图),这个半圆形菜园的半径是多少米?
23.如图,如果正方形的面积是24平方厘米,那么圆的面积是多少平方厘米?
24.一堆钢管堆成一个近似的梯形,已知最上层有3根,最下层有20根,相邻两层之间相差1根。这堆钢管一共有多少根?
25.有大、小两筐水果,大筐水果的质量是小筐水果的1.6倍。如果从大筐中取出12千克水果放入小筐,两筐水果的质量就相等了。原来大、小两筐水果的质量各是多少千克?
《期末应用题易错精选题-2024-2025学年数学五年级下册苏教版》参考答案
1.30米
【分析】根据1公顷=10000平方米,把0.12公顷转化为以平方米为单位,设高是米,根据,列方程并求解即可。
【详解】解:设高是米。
0.12公顷=1200平方米
答:高是30米。
2.小明15岁;爸爸48岁;妈妈39岁
【分析】根据题意,设小明的年龄是x岁,那么爸爸的年龄是3.2x岁,妈妈的年龄是2.6x岁,用爸爸的年龄减去妈妈的年龄就等于9岁,据此列出方程求解即可解答。
【详解】解:设小明的年龄是x岁。
3.2x-2.6x=9
0.6x=9
0.6x÷0.6=9÷0.6
x=15
爸爸:3.2x=3.2×15=48(岁)
妈妈:2.6x=2.6×15=39(岁)
答:今年小明15岁,爸爸48岁,妈妈39岁。
3.五年级52盆;四年级40盆
【分析】根据“五年级准备的绿植盆数是四年级的1.3倍”,可以设原来四年级有盆绿植,则原来五年级有1.3盆绿植;根据“五年级送给四年级6盆绿植后,五、四年级的绿植盆数一样多”可得出等量关系:原来五年级绿植的盆数-6盆=原来四年级绿植的盆数+6盆,据此列出方程,并求解。
【详解】解:设原来四年级有盆绿植,则原来五年级有1.3盆绿植。
1.3-6=+6
1.3-6-=+6-
0.3-6=6
0.3-6+6=6+6
0.3=12
0.3÷0.3=12÷0.3
=40
原来五年级有:40×1.3=52(盆)
答:原来五年级有52盆绿植,四年级有40盆绿植。
4.8厘米
【分析】根据三角形面积公式:底×高÷2=三角形面积,设高是x厘米,列方程:25x÷2=100,解方程,即可解答。
【详解】解:设高是x厘米。
25x÷2=100
25x÷2×2=100×2
25x=200
25x÷25=200÷25
x=8
答:高是8厘米。
5.哥哥:19岁;弟弟16岁
【分析】设今年弟弟x岁,哥哥比弟弟大3岁,则哥哥是(x+3)岁;哥哥弟弟的年龄和为35岁,即今年哥哥年龄+今年弟弟年龄=35岁,列方程:x+x+3=35,解方程,即可解答。
【详解】解:设今年弟弟x岁,则今年哥哥(x+3)岁。
x+x+3=35
2x+3=35
2x+3-3=35-3
2x=32
2x÷2=32÷2
x=16
哥哥:16+3=19(岁)
答:今年哥哥19岁,弟弟16岁。
6.3小时
【分析】把相遇时间设为未知数,等量关系式:(客车的速度+货车的速度)×相遇时间=两车行驶的总路程,故设两车的相遇时间为x小时,据此列方程解答。
【详解】解:设x小时后两车相遇。
(90+65)x=465
155x=465
155x÷155=465÷155
x=3
答:3小时后两车相遇。
7.(1)30
(2) 8 45
(3)12
【分析】折线统计图中的横轴表示时间,1小时即60分钟平均分成4小格,那么每小格表示60÷4=15分钟。
(1)从图中可知,张叔叔在科技馆参观的时间是2小格,即参观了30分钟。
(2)从图中可知,张叔叔休息了15分钟,如果不休息那就提前了15分钟,用原来到达科技馆的时刻减去15分钟即可。
(3)返回时的路程是6km,时间是30分钟即0.5小时,根据速度=路程÷时间求出他的速度。
【详解】(1)60÷4=15(分钟)
15×2=30(分钟)
张叔叔在科技馆参观了30分钟。
(2)9时-15分钟=8时45分
如果张叔叔从出发到科技馆中途不休息,8时45分可以到达科技馆。
(3)30分钟=0.5小时
6÷0.5=12(km)
返回时张叔叔骑车平均每小时行12km。
8.(1)见详解
(2)2020年计划产量和实际产量相等(答案不唯一)
【分析】(1)由图可知,实线表示实际产量,虚线表示计划产量,2020、2021、2022、2023年的计划产量分别为8万个、10万个、13万个、16万个,实际产量分别为8万个、12万个、16万个、18万个;用算式8+10+13+16求得计划产量合计,用算式8+12+16+18求得实际产量合计。据此解答即可。
(2)从图表中,可以看到2020年计划产量和实际产量都是8万元,也就是计划产量和实际产量相等。(答案不唯一)
【详解】(1)8+10+13+16
=31+16
=47(万个)
8+12+16+18
=36+18
=54(万个)
所以:
某电子厂2020~2023年一种电子元件的产量统计表 2024年12月
年份 合计 2020 2021 2022 2023
计划产量/万个 47 8 10 13 16
实际产量/万个 54 8 12 16 18
(2)从图表中,我知道了2020年计划产量和实际产量相等。(答案不唯一)
9.(1)图见详解;
(2)20;5;75;8.5;10
【分析】先根据表中的数据绘成折线统计图,未加热时的水温就是0分钟时的水温;找出水温50℃时的时间,就是水加热到50℃,用的时间;找出7分钟时水的温度,就是7分钟时,水的温度;第8分钟时水温是85°,第9分钟时水温是96°,所以水温是90°时,时间一定在8分钟到9分钟之间,答案不唯一,合理即可;水开时的温度是100℃,找出此时的时间,就是烧开这壶水所用的时间,据此解题即可。
【详解】(1)水加热过程中水温变化情况统计图
2024年11月
(2)未加热时,水温是20℃。水加热到50℃时,用了5分钟。7分钟时,水的温度是75℃。加热约8.5分钟时(这个空答案不唯一,在八分钟和九分钟之间合理即可),水温达到了90℃。烧开这壶水用了10分钟。
10.红花2朵;黄花3朵
【分析】要使每束花里红花的朵数相同,黄花的朵数也相同,则扎成的花束的数量是24和36的公因数,最多扎的束数就是24和36的最大公因数。用质因数分解法可以求两个数的最大公因数,全部共有的质因数(公有质因数)相乘的积就是这两个数的最大公因数。
分别用24和36除以求得的最大公因数,即最多扎的束数,再用红花和黄花的朵数分别除以扎的束数即可求出每束花中红花和黄花各有多少朵。
【详解】24=2×2×2×3
36=2×2×3×3
所以24和36的最大公因数是:2×2×3=12;
24÷12=2(朵)
36÷12=3(朵)
答:最多可以扎成12束花,每束里的红花有2朵,黄花有3朵。
11.12块
【分析】地砖的边长取书房的长和宽的最大公因数时,才能保证地砖完整且数量最少。首先将32和24分解质因数,计算出它们的最大公因数即为方砖的边长;再用长方形地面的长和宽分别除以地砖边长,得到每行、每列能铺的地砖数;最后将每行和每列的地砖数相乘,得到铺满地面最少需要地砖的块数(总数量=每行数量×每列数量)。
【详解】32=2×2×2×2×2
24=2×2×2×3
32和24的最大公因数是2×2×2=8,所以正方形地砖的边长是8分米。
(32÷8)×(24÷8)
=4×3
=12(块)
答:最少需要购买12块这样的地砖。
12.3种;分法见详解
【分析】先把36写成两个因数的积,求出36的所以因数,根据每组人数不少于4人,不多于10人,其中大于或等于4而小于或等于10的因数就是一组的人数,再用36分别除以每组的人数确定有几种分法即可。
【详解】36=1×36=2×18=3×12=4×9=6×6,所以36的因数有1、2、3、4、6、9、12、18、36;
其中大于或等于4小于或等于10的因数有4、6、9;
36÷4=9(组)
36÷6=6(组)
36÷9=4(组)
答:有3种分法;分法为:每组4人,分9组;每组6人,分6组;每组9人,分4组。
13.杨师傅
【分析】根据题意,先用每人做零件的个数除以加工的时间,求出每分钟加工零件的个数,即是每人的工作效率;再根据分数大小比较的方法进行比较即可得解。
分数大小的比较:
分母相同时,分子越大,分数值就越大;
分子相同时,分母越大,分数值反而越小;
分子、分母都不相同时,利用分数的基本性质化成同分母或同分子的分数进行比较。
【详解】王师傅:(个)
李师傅:(个)
杨师傅:(个)
,,
答:杨师傅的工作效率最高。
14.;
【分析】已知小李用了13分钟,比小王少用4分钟,即小王比小李多用4分钟,用小李用的时间加上4,即是小王用的时间;
求小李用的时间是小王的几分之几,用小李用的时间除以小王用的时间即可;
求小王用的时间是小李的几分之几,用小王用的时间除以小李用的时间即可。
【详解】13+4=17(分钟)
13÷17=
17÷13=
答:小李用的时间是小王的,小王用的时间是小李的。
15.25本;箱;
【分析】根据平均分用除法计算,第一问用总本数除以班数,第二问用总箱数除以班数,第三问把图书总数看作单位“1”,根据分数的意义,把1平均分成12份,每份是。
【详解】(本)
(箱)
答:每班分到25本,每班分到箱,每班分得这些图书的。
16.
【分析】把全班同学的人数看作单位“1”,用单位“1”减去送鲜花的、送贺卡的同学所占的分率,求出送画的同学占全班同学的几分之几即可。
【详解】1--
=-
=-
=
答:送画的同学占全班同学的。
17.
【分析】把全国人口总人数看作单位“1”,我国使用网络的人数约占全国人口的,求不使用网络的人数约占全国人口的分率,用1-解答。
【详解】1-=
答:不使用网络的人数约占全国人口的。
18.公顷
【分析】下午耕地的公顷数=上午耕地的公顷数+多耕地的公顷数。异分母分数加法通分转化为同分母分数相加即可。
【详解】(公顷)
答:下午耕地公顷。
19.6.28平方分米
【分析】长方形中空白部分的周长相当于一个半圆的周长,根据半圆的周长=(π+2)r,已知长方形空白部分的周长,代入半圆的周长计算公式,计算出半径;涂色部分的面积=圆的面积÷2,根据圆的面积=πr2,代入数值计算,据此解答。
【详解】10.28÷(3.14+2)
=10.28÷5.14
=2(分米)
3.14×22÷2
=3.14×4÷2
=12.56÷2
=6.28(平方分米)
答:涂色部分的面积是6.28平方分米。
20.(1)5024平方米
(2)1055.04平方米
【分析】(1)根据圆的周长=2πr,代入数值计算出圆形池塘的半径;再根据圆的面积=πr2,代入数值计算,所得结果即为这个池塘的面积。
(2)求环形路的占地面积也就是求这个圆环的面积,根据圆环的面积=π×(R2-r2),已知外圆的半径=池塘的半径+4,代入相应数值计算,所得结果即为环形路的占地面积。
【详解】(1)池塘的半径:251.2÷3.14÷2=40(米)
3.14×402
=3.14×1600
=5024(平方米)
答:这个池塘的面积是5024平方米。
(2)外圆的半径为:40+4=44(米)
3.14×(442-402)
=3.14×(1936-1600)
=3.14×336
=1055.04(平方米)
答:环形路的占地面积是1055.04平方米。
21.(1)长:18.84分米;宽:6分米
(2)84.78平方分米
【分析】(1)根据圆的周长=2πr,代入数值计算出圆的半径,圆的半径与长方形的宽相等;再根据圆的面积=πr2,代入数值计算出圆的面积,且圆的面积与长方形的面积相等;最后用圆的面积除以圆的半径,所得结果即为长方形的长。
(2)涂色部分的面积等于长方形的面积减去四分之一圆的面积,结合(1)中计算出的数值,代入公式计算,据此解答。
【详解】(1)圆的半径:37.68÷3.14÷2=6(分米)
圆的半径与长方形的宽相等,因此长方形的宽为6分米。
圆的面积:3.14×62
=3.14×36
=113.04(平方分米)
长方形的长:113.04÷6=18.84(分米)
答:长方形的长是18.84分米,宽是6分米。
(2)113.04-113.04÷4
=113.04-28.26
=84.78(平方分米)
答:涂色部分的面积是84.78平方分米。
22.6米
【分析】因为王叔叔用18.84米长的篱笆靠墙围了个半圆形菜园,这里18.84米是半圆的弧长。
圆的周长公式为C=2r,那么半圆的弧长就是r,用半圆的弧长除以即可求出这个半圆形菜园的半径是多少米。
【详解】18.84÷3.14=6(米)
答:这个半圆形菜园的半径是6米。
23.18.84平方厘米
【分析】从图中可知,圆的直径等于正方形的边长。设圆的半径为r厘米,则圆的直径是2r厘米,根据“边长×边长=正方形的面积”,据此列出方程,并求出半径的平方即r2的值。根据圆的面积公式S=πr2,把r2的值代入圆的面积公式,求出这个圆的面积。
【详解】解:设圆的半径为r厘米。
(2r)×(2r)=24
4r2=24
r2=24÷4
r2=6
圆的面积:3.14×6=18.84(平方厘米)
答:圆的面积是18.84平方厘米。
24.207根
【分析】因为相邻两层之间相差1根,因此共(20-3+1)层,结合梯形面积公式,总根数=(最上层根数+最下层根数)×层数÷2,列式解答即可。
【详解】(3+20)×(20-3+1)÷2
=23×18÷2
=207(根)
答:这堆钢管一共有207根。
25.大筐质量是64千克,小筐质量是40千克。
【分析】这是一道典型的差倍问题,从大筐取出12千克放入小筐,两筐水果的质量就相等了,说明原本大筐的质量比小筐的质量多了24千克,特别注意这里大小两筐的质量差不是12千克。而大筐质量是小筐的1.6倍,把小筐的质量看作1份,则大筐就是1.6份,相差0.6份,结合相差的数量24千克,即可求出1份的质量,从而推出大小两筐分别的质量。
【详解】12×2=24(千克)
24÷(1.6-1)
=24÷0.6
=40(千克)
40+24=64(千克)
答:原来大筐的质量是64千克,小筐的质量是40千克。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
