期末应用题易错精选题(含解析)-2024-2025学年数学六年级下册苏教版
文档属性
| 名称 | 期末应用题易错精选题(含解析)-2024-2025学年数学六年级下册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 966.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 11:31:41 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末应用题易错精选题-2024-2025学年数学六年级下册苏教版
1.学校为做好校内课后服务工作,针对学生兴趣爱好情况作了调查。被调查的学生按A(球类)、B(乐器类)、C(书法绘画类)、D(舞蹈类)四个类型进行统计,每个学生只选其中一类,然后绘制了如下两幅统计图:图1和图2。
(1)经检查图1是正确的,图2中A、B、C、D四类中有一类出现错误,有错误的是( )类,喜欢该类的学生应该有( )人。
(2)喜欢舞蹈类的人数在扇形统计图中所占圆心角度数为( )。
(3)喜欢B类的学生比喜欢D类的学生少( )%。
(4)如果从被调查的学生中随意抽取1名学生,那么这名学生喜欢( )类的可能性最大。
2.2021年5月11日,第七次全国人口普查结果公布,小丽通过查阅资料,了解到第七次全国人口普查的年龄构成情况,绘制成下面的统计图。
(1)参与第七次全国人口普查的人口总数是( )亿人。
(2)把上面两幅统计图补充完整。
(3)小丽从“百度百科”中查到:当一个国家或地区60岁及以上老年人口占人口总数的10%,或65岁及以上老年人口占人口总数的7%时,就意味着这个国家或地区的人口处于老龄化。参照这个标准,请你分析一下,我国人口目前是否达到“老龄化”?请说明理由。
3.一种饮料采用圆柱形易拉罐包装,从易拉罐外面量,底面直径是8厘米,高10厘米,易拉罐侧面印有“净含量350毫升”字样。请问生产商是否欺骗了消费者?
4.一种圆柱形通风管的底面直径是16厘米,每节通风管长1.5米。做20节这样的通风管,至少需要铁皮多少平方米?
5.操场上有一个圆锥形沙堆,量得底面周长是12.56米,高是1.8米。现在要将这堆沙铺在长6米、宽2米的长方体沙坑里,能铺多厚?
6.会议大厅里有10根底面直径是0.4米、高是5米的圆柱形柱子,现在要刷上油漆,刷油漆的面积一共是多少平方米?如果每平方米用油漆0.3千克,刷这些柱子要用油漆多少千克?
7.有一个底面直径是8厘米、高是17厘米的圆柱形容器,容器中装有一些水,水面距杯口2厘米。把一个铁块放入容器,铁块完全浸没在水中,同时有部分水溢出;当把铁块取出后,水面距杯口还有7厘米。求铁块的体积。
8.如图,一张长方形铁皮被分割成两个圆和一个长方形(涂色部分为余料),正好能围成一个圆柱,这个圆柱的体积是多少立方分米?
9.如图是一个粮仓,它由一个圆柱和一个圆锥组合而成。如果每立方米粮食的质量是0.6吨,这个粮仓最多能装多少吨粮食?
10.一名工人搬运1000只花瓶,规定每搬运一只花瓶得劳务费0.4元,如果打碎,不但得不到这只花瓶的劳务费,还要赔1.6元。这名工人运完后共得劳务费360元,他打碎了多少只花瓶?
11.同学们在美术课上学习制作中国结,制作一个小中国结需要7分米红绳,制作一个大中国结需要11分米红绳,一共做了20个中国结,共用去184分米红绳。请问同学们制作了多少个大中国结?
12.在比例尺是1∶2000000的地图上,量得甲、乙两地的距离是4.5厘米。在比例尺是1∶5000000的地图上,甲、乙两地的距离是多少厘米?
13.下图的比例尺是1∶200,根据条件计算出图形的实际面积是多少平方米。
14.在比例尺是1∶4000000的地图上,量得甲、乙两地相距2.5厘米。一辆汽车以50千米/时的速度从甲地开往乙地,多少小时可以到达?
15.在比例尺是1∶30000000的地图上,甲、乙两地之间的航空线长4.5厘米。在比例尺是1∶25000000的地图上,甲、乙两地之间的航空线长多少厘米?
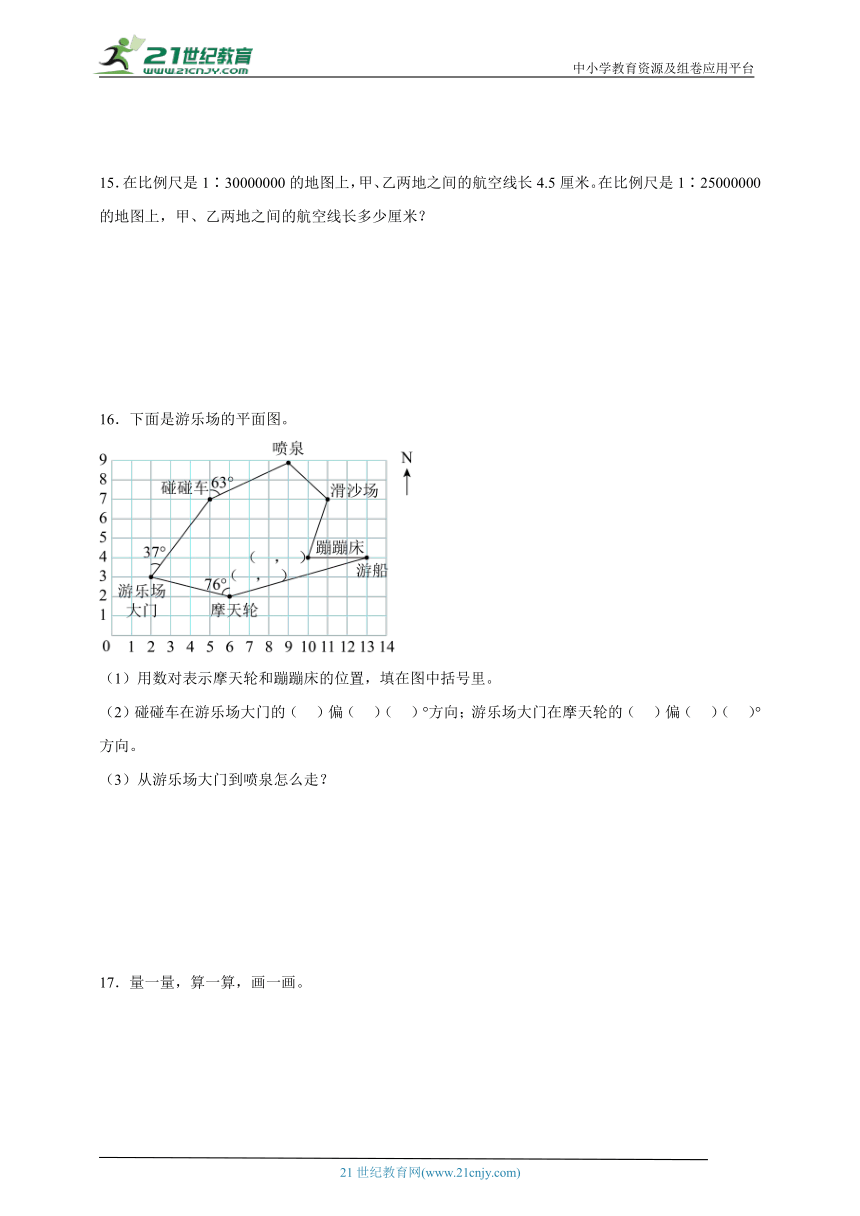
16.下面是游乐场的平面图。
(1)用数对表示摩天轮和蹦蹦床的位置,填在图中括号里。
(2)碰碰车在游乐场大门的( )偏( )( )°方向;游乐场大门在摩天轮的( )偏( )( )°方向。
(3)从游乐场大门到喷泉怎么走?
17.量一量,算一算,画一画。
(1)小明家在学校的什么方向多少米处?小红家呢?
(2)小刚家在学校的北偏东30°方向750米处,在图中表示出小刚家的位置。
(3)小芳家在学校的北偏西55°方向1250米处,在图中表示出小芳家的位置。
18.A、B两地相距240千米,如果要2小时到达,每小时应行多少千米?如果要3小时、4小时、5小时……到达呢?把下表填写完整。
行驶时间/时 2 3 4 5 6 8 …
每小时行驶的路程/千米 …
(1)相对应的两个数的乘积分别是多少?
(2)这个乘积表示什么意义?用数量关系式表示它与行驶时间和速度的关系。
(3)行驶时间和速度成反比例吗?为什么?
19.下表是某日张师傅加工零件的情况。
加工时间/时 1 2 3 4 5 6 7 8
加工数量/个 30 60 90 120 150 180 210 240
(1)根据表中数据,先在图中描出加工时间和加工数量的对应点,再把这些点依次连起来。
(2)张师傅加工零件的时间和加工零件的数量成正比例吗?说明理由。
(3)根据图像判断,张师傅3.5小时加工了多少个零件?6.5小时呢?
20.观察下面两个表格,并回答问题。
(1)卡车的载质量和需要卡车的数量如下表。
卡车载质量/吨 2 4 5 10 20
需要卡车数量/辆 50 25 20 10 5
(2)用同样的卡车运送物资的总质量和需要卡车的数量如下表。
物资总质量/吨 15 25 30 35 40
需要卡车数量/辆 3 5 6 7 8
根据表中信息,先分别用数量关系式表示每个表中两个相关联的量之间的关系,再判断哪两个量成正比例,哪两个量成反比例。
21.工程队每天铺设管道24米,照这样的效率,2天、3天、4天……能铺设管道多少米?
(1)把下表填写完整。
时间/天 1 2 3 4 5 6 …
长度/米 24 …
(2)根据表中数据,先在图中描出铺设管道的时间和长度相对应的点,再把它们依次连起来。
(3)铺设管道的时间和长度成什么比例?为什么?
(4)根据图像判断,8天能铺设多少米管道?铺设100米管道大约需要多少天?
《期末应用题易错精选题-2024-2025学年数学六年级下册苏教版》参考答案
1.(1)C;60
(2)90°
(3)40
(4)A
【分析】(1)由图1可知,C类比D类少,比B类多。而图2中,C类比B类和D类都多,则C类是错误的。由图1可知,A类有120人,占被调查的学生人数的40%,根据已知一个数的百分之几,求这个数,用120÷40%求出被调查的学生人数,再根据求一个数的百分之几,用乘法分别求出B、C、D的人数,再与图2中的人数进行比较,即可验证结论;
(2)圆心角的度数是360度,由图1可知,喜欢舞蹈类的人数占总人数的25%,把360度看作单位“1”,根据求一个数的百分之几是多少,用乘法解答;
(3)求喜欢B类的学生比喜欢D类的学生少百分之几,用两个百分率的差除以D类的百分率;列式:(25%-15%)÷25%计算即可。
(4)扇形统计图中哪种兴趣爱好所占的百分比最大,那么这名学生喜欢哪类的可能性最大;据此进行比较即可解答。
【详解】(1)120÷40%=300(人)
300×15%=45(人)
300×20%=60(人)
300×25%=75(人)
所以有错误的类是C类,喜欢该类的学生应该有60人。
(2)360×25%=90°
所以喜欢舞蹈类的人数在扇形统计图中所占圆心角度数为90°。
(3)(25%-15%)÷25%
=10%÷25%
=0.1÷0.25
=40%
所以喜欢B类的学生比喜欢D类的学生少40%。
(4)15%<20%<25%<40%
喜欢A类的学生占的百分率最大,所以这名学生喜欢A类的可能性最大。
2.(1)14;(2)见详解;(3)我国人口目前已经达到“老龄化”, 因为我国60岁及以上老年人口超过人口总数的10%,且65岁及以上老年人口超过人口总数的7%
【分析】(1)通过观察可知,60~64岁人口占总人口的5%,已知60~64岁人口有0.7亿人,把总人口看作单位“1”,根据百分数除法的意义,用0.7÷5%即可求出总人数。
(2)把总人口看作单位“1”,根据百分数乘法的意义,用总人口×65%即可求出15~59岁人口数量;再用总人数减去0~64岁人口数量,即可求出65岁及以上人口数量;然后根据求一个数是另一个数的百分之几,用一个数除以另一个数再乘100%,则分别用除法求出65岁及以上老年人口占人口总数的百分率以及0~14岁人口占人口总数的百分率,据此作图。
(3)通过计算可知,65岁及以上老年人口占人口总数的12%,60岁及以上老年人口占人口总数的(12%+5%),说明我国已经处于老龄化。
【详解】(1)0.7÷5%=14(亿人)
参与第七次全国人口普查的人口总数是14亿人。
(2)15~59岁人口数量:14×65%=9.1(亿人)
65岁以上人口数量:14-2.52-9.1-0.7=1.68(亿人)
65岁及以上老年人口占人口总数:1.68÷14×100%=12%
0~14岁人口占人口总数:2.52÷14×100%=18%
(3)12%+5%=17%
17%>10%
12%>7%
答:我国人口目前已经达到“老龄化”, 因为我国60岁及以上老年人口超过人口总数的10%,且65岁及以上老年人口超过人口总数的7%。
3.没有
【分析】已知圆柱形易拉罐从外面量的底面直径是8厘米,高10厘米,根据圆柱的体积(容积)公式V=πr2h,以及进率“1立方厘米=1毫升”,求出易拉罐的容积,再与净含量进行比较,得出结论。
【详解】3.14×(8÷2)2×10
=3.14×42×10
=3.14×16×10
=502.4(立方厘米)
502.4立方厘米=502.4毫升
502.4>350
答:生产商没有欺骗消费者。
4.15.072平方米
【分析】分析题目,先根据1米=100厘米把16厘米换算成以米为单位,圆柱形通风管只需要计算侧面积,圆柱的侧面积=πdh,据此求出做一个圆柱形通风管需要多少平方米的铁皮,再乘个数即可求出需要铁皮的总面积。
【详解】16厘米=0.16米
3.14×0.16×1.5
=0.5024×1.5
=0.7536(平方米)
0.7536×20=15.072(平方米)
答:至少需要铁皮15.072平方米。
5.0.628米
【分析】根据圆的周长公式:可知:底面半径=底面周长÷圆周率÷2,圆锥体积=底面积×高÷3,据此求出沙堆体积,铺的厚度相当于长方体的高,再根据长方体的高=体积÷长÷宽,列式解答即可。
【详解】3.14×(12.56÷3.14÷2)2×1.8÷3
=3.14×22×1.8÷3
=3.14×4×1.8÷3
=7.536(立方米)
7.536÷6÷2=0.628(米)
答:能铺0.628米厚。
6.62.8平方米;18.84千克
【分析】刷油漆的部分是圆柱形柱子的侧面积,根据圆柱侧面积=底面周长×高,求出1根柱子的侧面积,再乘10,是刷油漆的总面积,总面积×每平方米用油漆质量=要用的油漆总质量,据此列式解答。
【详解】3.14×0.4×5×10
=6.28×10
=62.8(平方米)
62.8×0.3=18.84(千克)
答:刷油漆的面积一共是62.8平方米,刷这些柱子要用油漆18.84千克。
7.351.68立方厘米
【分析】根据把一个铁块放入容器,铁块完全浸没在水中,同时有部分水溢出,可知当铁块铁块完全浸没在水中,水是满的,当把铁块取出后,水面距杯口还有7厘米,说明水面下降了7厘米,则下降部分的体积就是铁块的体积。下降部分是个圆柱体,根据圆柱的体积,把数据代入公式即可求解。
【详解】3.14×(8÷2)2×7
=3.14×42×7
=3.14×16×7
=351.68(立方厘米)
答:铁块的体积是351.68立方厘米。
8.100.48立方分米
【分析】根据题意,把一张长方形铁皮被分割成两个圆和一个长方形,那么这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高;
从图中可知,圆柱的高等于圆的直径的2倍,据此求出圆柱的高;再根据圆柱的体积公式V=πr2h,求出这个圆柱的体积。
【详解】圆柱的高:2×2×2=8(分米)
圆柱的体积:
3.14×22×8
=3.14×4×8
=100.48(立方分米)
答:这个圆柱的体积是100.48立方分米。
9.79.128吨
【分析】圆柱的体积=底面积×高,V=πr2h,圆锥的面积=底面积×高÷3,V=πr2h,代入数据计算出粮仓的体积,粮仓的体积乘每立方米粮食的质量,就是这个粮仓所装的粮食质量。
【详解】3.14×(6÷2)2×4+3.14×(6÷2)2×2×
=3.14×32×4+3.14×32×2×
=3.14×9×4+3.14×9×2×
=113.04+56.52×
=113.04+18.84
=131.88(立方米)
131.88×0.6=79.128(吨)
答:这个粮仓最多能装79.128吨粮食。
10.20只
【分析】根据题意,设他打碎了只花瓶,那么没打碎的花瓶有(1000-)只,每只可得劳务费0.4元;如果打碎,不但得不到这只花瓶的劳务费,还要赔1.6元,那么打碎只花瓶,要赔1.6元;
等量关系:搬运一只花瓶的劳务费×完好的花瓶数量-打碎一只花瓶要赔的钱数×打碎花瓶的数量=最终得到的劳务费,据此列出方程,并求解。
【详解】解:设他打碎了只花瓶。
0.4×(1000-)-1.6=360
400-0.4-1.6=360
400-(0.4+1.6)=360
400-2=360
400-2+2=360+2
360+2=400
360+2-360=400-360
2=40
2÷2=40÷2
=20
答:他打碎了20只花瓶。
11.11个
【分析】分析题目,设同学们制作了x个大中国结,则制作了(20-x)个小中国结,根据等量关系式:制作一个大中国结需要的红绳长度×制作的大中国结的个数+制作一个小中国结需要的红绳长度×制作的小中国结的个数=184列出方程11x+7(20-x)=184,进一步解出方程即可。
【详解】解:设同学们制作了x个大中国结,则制作了(20-x)个小中国结。
11x+7(20-x)=184
11x+140-7x=184
4x=184-140
4x=44
4x÷4=44÷4
x=11
答:同学们制作了11个大中国结。
12.1.8厘米
【分析】在比例尺1∶2000000中图上距离1厘米代表实际距离2000000厘米,也就是20千米;已知甲、乙两地的图上距离是4.5厘米,实际距离就是4.5个20千米,用乘法计算;在比例尺1∶5000000中图上距离1厘米代表实际距离5000000厘米,也就是50千米;甲、乙两地实际距离不变,仍是4.5×20=90千米,计算图上距离就是计算90里面有几个50,用除法计算。
【详解】2000000厘米=20千米
4.5×20=90(千米)
5000000厘米=50千米
90÷50=1.8(厘米)
答:甲、乙两地的距离是1.8厘米。
13.200平方米
【分析】先依据“实际距离=图上距离÷比例尺”求出这个图形长和宽的实际长度,进而利用长方形的面积公式=长×宽,求出这个图形的实际面积。
【详解】10÷
=10×200
=2000(厘米)
2000厘米=20米
5÷
=5×200
=1000(厘米)
1000厘米=10米
20×10=200(平方米)
答:图形的实际面积是200平方米。
14.2小时
【分析】先根据实际距离=图上距离÷比例尺,据此求出实际距离是多少厘米,再把厘米化为千米,然后根据路程÷速度=时间,据此解答即可。
【详解】2.5÷
=2.5×4000000
=10000000(厘米)
10000000厘米=100千米
100÷50=2(小时)
答:2小时可以到达。
15.5.4厘米
【分析】根据实际距离=图上距离÷比例尺,代入数据可求出甲、乙两地之间的实际距离,再根据图上距离=实际距离×比例尺,代入第二幅地图的比例尺即可得解。
【详解】(厘米)
(厘米)
答:甲、乙两地之间的航空线长5.4厘米。
16.(1)摩天轮(6,2);蹦蹦床(10,4)
(2)北;东;37;北;西;76
(3)见详解
【分析】(1)用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;据此用数对表示图上的摩天轮和蹦蹦床的位置。
(2)以图上的“上北下南,左西右东”确定方向,得出碰碰车与游乐场大门,以及游乐场大门与摩天轮的位置关系。
(3)从游乐场大门到喷泉,可以先从游乐场大门走到碰碰车,再走到喷泉。结合图上的方向和角度描述从游乐场大门到喷泉的路线。
【详解】(1)用数对表示摩天轮和蹦蹦床的位置,如下图:
(2)碰碰车在游乐场大门的(北)偏(东)(37)°方向;游乐场大门在摩天轮的(北)偏(西)(76)°方向。(答案不唯一)
(3)先从游乐场大门向北偏东37°方向走到碰碰车,再从碰碰车向北偏东63°方向走到喷泉。(答案不唯一)
17.(1)小明家在学校南偏东60°方向575米处;小红家在学校南偏西45°方向450米处。
(2)(3)见详解
【分析】(1)以东偏北30°为例,表示以正南正北坐标交点为顶点,以正东方向为一条边向北作一个30°的角,这个角的另一条边上就是东偏北30°方向,据此描述题目里的方向。测量出小明家、小红家到学校的图上距离,再依据比例尺算出实际距离,最后结合图中方角度确定方向和位置;
(2)先将实际距离换算为厘米,实际距离乘比例尺得到图上距离,然后根据给定的方向和角度在图中确定小刚家的位置;
(3)先将实际距离换算为厘米,实际距离乘比例尺得到图上距离,然后根据给定的方向和角度在图中确定小芳家的位置。
【详解】(1)小明家、小红家到学校的图上距离是2.3厘米、1.8厘米。(以实际测量数值为准)
(米)
小明家在学校南偏东60°方向575米处。
(米)
小红家在学校南偏西45°方向450米处。
(2)
(厘米)
如下图所示。
(3)
(厘米)
如下图所示。
18.表格见详解
(1)240
(2)路程;路程=速度×时间
(3)成反比例;原因见详解
【分析】根据每小时行驶的路程= A、B两地相距240千米÷行驶时间,据此完成表格即可;
(1)将相对应的两个数相乘分别求出它们的乘积即可;
(2)这个乘积表示路程,根据路程、速度和时间之间的关系解答即可;
(3)两个相关联的量,一个量变化,另一个量也随之变化,且它们乘积一定,则这两个量成反比例;若它们的比值一定,则这两个量成正比例。。
【详解】240÷2=120,240÷3=80,240÷4=60,240÷5=48,240÷6=40,240÷8=30
表格如下:
行驶时间/时 2 3 4 5 6 8 …
每小时行驶的路程/千米 120 80 60 48 40 30 …
(1)2×120=240,3×80=240,4×60=240,5×48=240,6×40=240,8×30=240
相对应的两个数的乘积都是240。
(2)这个乘积表示路程,路程=速度×时间;
(3)因为时间×速度=路程(一定),积一定,行驶时间和速度成反比例。
19.(1)见详解
(2)成正比。理由:张师傅加工零件的数量与加工零件的时间的比值是定值。
(3)105个零件;195个零件
【分析】(1)横轴表示时间,纵轴表示零件个数,据此描点连线。
(2)判断两个量是否成正比例,就看这两种量对应的数据的比值是否一定,如果一定,就成正比例。计算张师傅加工零件的数量与加工零件的时间的比值,看比值是否是定值。
(3)观察图像,得出张师傅3.5小时、6.5小时加工了多少个零件。
【详解】(1)如图所示
(2),即(定值),所以张师傅加工零件的数量与加工零件的时间成正比。
(3)由图像得到,张师傅3.5小时加工了105个零件,6.5小时加工了195个零件。
20.(1)卡车载质量×需要的卡车数量=总吨数(一定);卡车载质量和需要的卡车数量成反比例
(2)物资总质量÷需要卡车数量=卡车载质量(一定);物资总质量和需要卡车数量成正比例
【分析】两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果x÷y=k(一定),x和y成正比例关系;如果xy=k(一定),x和y成反比例关系,据此分析。
【详解】(1)2×50=100(吨)、4×25=100(吨)、5×20=100(吨)……
卡车载质量×需要的卡车数量=总吨数(一定)
(2)15÷3=5(吨)、25÷5=5(吨)、30÷6=5(吨)……
物资总质量÷需要卡车数量=卡车载质量(一定)
答:物资总质量和需要卡车数量成正比例,卡车载质量和需要的卡车数量成反比例。
21.(1)48;72;96;120;144
(2)见详解
(3)正比例;铺设长度÷对应天数=每天铺设长度(一定)
(4)192米;4天
【分析】(1)根据每天铺设长度×铺设天数=相应天数铺设长度,列式计算并填表即可;
(2)根据各数量的多少,在方格图的纵、横的交点上描出表示数量多少的点;把各点用线段顺次连接起来,标记数据即可;
(3)两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果x÷y=k(一定),x和y成正比例关系;如果xy=k(一定),x和y成反比例关系,据此分析;
(4)观察图像,找到横轴8天对应的长度和竖轴100米对应的大约天数即可。
【详解】(1)24×2=48(米)
24×3=72(米)
24×4=96(米)
24×5=120(米)
24×6=144(米)
时间/天 1 2 3 4 5 6 …
长度/米 24 48 72 96 120 144 …
(2)
(3)24÷1=24(米)、48÷2=24(天)、72÷3=24(天)……
答:铺设管道的时间和长度成正比例,因为铺设长度÷对应天数=每天铺设长度(一定)。
(4)根据图像判断,8天能铺设192米管道,铺设100米管道大约需要4天。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末应用题易错精选题-2024-2025学年数学六年级下册苏教版
1.学校为做好校内课后服务工作,针对学生兴趣爱好情况作了调查。被调查的学生按A(球类)、B(乐器类)、C(书法绘画类)、D(舞蹈类)四个类型进行统计,每个学生只选其中一类,然后绘制了如下两幅统计图:图1和图2。
(1)经检查图1是正确的,图2中A、B、C、D四类中有一类出现错误,有错误的是( )类,喜欢该类的学生应该有( )人。
(2)喜欢舞蹈类的人数在扇形统计图中所占圆心角度数为( )。
(3)喜欢B类的学生比喜欢D类的学生少( )%。
(4)如果从被调查的学生中随意抽取1名学生,那么这名学生喜欢( )类的可能性最大。
2.2021年5月11日,第七次全国人口普查结果公布,小丽通过查阅资料,了解到第七次全国人口普查的年龄构成情况,绘制成下面的统计图。
(1)参与第七次全国人口普查的人口总数是( )亿人。
(2)把上面两幅统计图补充完整。
(3)小丽从“百度百科”中查到:当一个国家或地区60岁及以上老年人口占人口总数的10%,或65岁及以上老年人口占人口总数的7%时,就意味着这个国家或地区的人口处于老龄化。参照这个标准,请你分析一下,我国人口目前是否达到“老龄化”?请说明理由。
3.一种饮料采用圆柱形易拉罐包装,从易拉罐外面量,底面直径是8厘米,高10厘米,易拉罐侧面印有“净含量350毫升”字样。请问生产商是否欺骗了消费者?
4.一种圆柱形通风管的底面直径是16厘米,每节通风管长1.5米。做20节这样的通风管,至少需要铁皮多少平方米?
5.操场上有一个圆锥形沙堆,量得底面周长是12.56米,高是1.8米。现在要将这堆沙铺在长6米、宽2米的长方体沙坑里,能铺多厚?
6.会议大厅里有10根底面直径是0.4米、高是5米的圆柱形柱子,现在要刷上油漆,刷油漆的面积一共是多少平方米?如果每平方米用油漆0.3千克,刷这些柱子要用油漆多少千克?
7.有一个底面直径是8厘米、高是17厘米的圆柱形容器,容器中装有一些水,水面距杯口2厘米。把一个铁块放入容器,铁块完全浸没在水中,同时有部分水溢出;当把铁块取出后,水面距杯口还有7厘米。求铁块的体积。
8.如图,一张长方形铁皮被分割成两个圆和一个长方形(涂色部分为余料),正好能围成一个圆柱,这个圆柱的体积是多少立方分米?
9.如图是一个粮仓,它由一个圆柱和一个圆锥组合而成。如果每立方米粮食的质量是0.6吨,这个粮仓最多能装多少吨粮食?
10.一名工人搬运1000只花瓶,规定每搬运一只花瓶得劳务费0.4元,如果打碎,不但得不到这只花瓶的劳务费,还要赔1.6元。这名工人运完后共得劳务费360元,他打碎了多少只花瓶?
11.同学们在美术课上学习制作中国结,制作一个小中国结需要7分米红绳,制作一个大中国结需要11分米红绳,一共做了20个中国结,共用去184分米红绳。请问同学们制作了多少个大中国结?
12.在比例尺是1∶2000000的地图上,量得甲、乙两地的距离是4.5厘米。在比例尺是1∶5000000的地图上,甲、乙两地的距离是多少厘米?
13.下图的比例尺是1∶200,根据条件计算出图形的实际面积是多少平方米。
14.在比例尺是1∶4000000的地图上,量得甲、乙两地相距2.5厘米。一辆汽车以50千米/时的速度从甲地开往乙地,多少小时可以到达?
15.在比例尺是1∶30000000的地图上,甲、乙两地之间的航空线长4.5厘米。在比例尺是1∶25000000的地图上,甲、乙两地之间的航空线长多少厘米?
16.下面是游乐场的平面图。
(1)用数对表示摩天轮和蹦蹦床的位置,填在图中括号里。
(2)碰碰车在游乐场大门的( )偏( )( )°方向;游乐场大门在摩天轮的( )偏( )( )°方向。
(3)从游乐场大门到喷泉怎么走?
17.量一量,算一算,画一画。
(1)小明家在学校的什么方向多少米处?小红家呢?
(2)小刚家在学校的北偏东30°方向750米处,在图中表示出小刚家的位置。
(3)小芳家在学校的北偏西55°方向1250米处,在图中表示出小芳家的位置。
18.A、B两地相距240千米,如果要2小时到达,每小时应行多少千米?如果要3小时、4小时、5小时……到达呢?把下表填写完整。
行驶时间/时 2 3 4 5 6 8 …
每小时行驶的路程/千米 …
(1)相对应的两个数的乘积分别是多少?
(2)这个乘积表示什么意义?用数量关系式表示它与行驶时间和速度的关系。
(3)行驶时间和速度成反比例吗?为什么?
19.下表是某日张师傅加工零件的情况。
加工时间/时 1 2 3 4 5 6 7 8
加工数量/个 30 60 90 120 150 180 210 240
(1)根据表中数据,先在图中描出加工时间和加工数量的对应点,再把这些点依次连起来。
(2)张师傅加工零件的时间和加工零件的数量成正比例吗?说明理由。
(3)根据图像判断,张师傅3.5小时加工了多少个零件?6.5小时呢?
20.观察下面两个表格,并回答问题。
(1)卡车的载质量和需要卡车的数量如下表。
卡车载质量/吨 2 4 5 10 20
需要卡车数量/辆 50 25 20 10 5
(2)用同样的卡车运送物资的总质量和需要卡车的数量如下表。
物资总质量/吨 15 25 30 35 40
需要卡车数量/辆 3 5 6 7 8
根据表中信息,先分别用数量关系式表示每个表中两个相关联的量之间的关系,再判断哪两个量成正比例,哪两个量成反比例。
21.工程队每天铺设管道24米,照这样的效率,2天、3天、4天……能铺设管道多少米?
(1)把下表填写完整。
时间/天 1 2 3 4 5 6 …
长度/米 24 …
(2)根据表中数据,先在图中描出铺设管道的时间和长度相对应的点,再把它们依次连起来。
(3)铺设管道的时间和长度成什么比例?为什么?
(4)根据图像判断,8天能铺设多少米管道?铺设100米管道大约需要多少天?
《期末应用题易错精选题-2024-2025学年数学六年级下册苏教版》参考答案
1.(1)C;60
(2)90°
(3)40
(4)A
【分析】(1)由图1可知,C类比D类少,比B类多。而图2中,C类比B类和D类都多,则C类是错误的。由图1可知,A类有120人,占被调查的学生人数的40%,根据已知一个数的百分之几,求这个数,用120÷40%求出被调查的学生人数,再根据求一个数的百分之几,用乘法分别求出B、C、D的人数,再与图2中的人数进行比较,即可验证结论;
(2)圆心角的度数是360度,由图1可知,喜欢舞蹈类的人数占总人数的25%,把360度看作单位“1”,根据求一个数的百分之几是多少,用乘法解答;
(3)求喜欢B类的学生比喜欢D类的学生少百分之几,用两个百分率的差除以D类的百分率;列式:(25%-15%)÷25%计算即可。
(4)扇形统计图中哪种兴趣爱好所占的百分比最大,那么这名学生喜欢哪类的可能性最大;据此进行比较即可解答。
【详解】(1)120÷40%=300(人)
300×15%=45(人)
300×20%=60(人)
300×25%=75(人)
所以有错误的类是C类,喜欢该类的学生应该有60人。
(2)360×25%=90°
所以喜欢舞蹈类的人数在扇形统计图中所占圆心角度数为90°。
(3)(25%-15%)÷25%
=10%÷25%
=0.1÷0.25
=40%
所以喜欢B类的学生比喜欢D类的学生少40%。
(4)15%<20%<25%<40%
喜欢A类的学生占的百分率最大,所以这名学生喜欢A类的可能性最大。
2.(1)14;(2)见详解;(3)我国人口目前已经达到“老龄化”, 因为我国60岁及以上老年人口超过人口总数的10%,且65岁及以上老年人口超过人口总数的7%
【分析】(1)通过观察可知,60~64岁人口占总人口的5%,已知60~64岁人口有0.7亿人,把总人口看作单位“1”,根据百分数除法的意义,用0.7÷5%即可求出总人数。
(2)把总人口看作单位“1”,根据百分数乘法的意义,用总人口×65%即可求出15~59岁人口数量;再用总人数减去0~64岁人口数量,即可求出65岁及以上人口数量;然后根据求一个数是另一个数的百分之几,用一个数除以另一个数再乘100%,则分别用除法求出65岁及以上老年人口占人口总数的百分率以及0~14岁人口占人口总数的百分率,据此作图。
(3)通过计算可知,65岁及以上老年人口占人口总数的12%,60岁及以上老年人口占人口总数的(12%+5%),说明我国已经处于老龄化。
【详解】(1)0.7÷5%=14(亿人)
参与第七次全国人口普查的人口总数是14亿人。
(2)15~59岁人口数量:14×65%=9.1(亿人)
65岁以上人口数量:14-2.52-9.1-0.7=1.68(亿人)
65岁及以上老年人口占人口总数:1.68÷14×100%=12%
0~14岁人口占人口总数:2.52÷14×100%=18%
(3)12%+5%=17%
17%>10%
12%>7%
答:我国人口目前已经达到“老龄化”, 因为我国60岁及以上老年人口超过人口总数的10%,且65岁及以上老年人口超过人口总数的7%。
3.没有
【分析】已知圆柱形易拉罐从外面量的底面直径是8厘米,高10厘米,根据圆柱的体积(容积)公式V=πr2h,以及进率“1立方厘米=1毫升”,求出易拉罐的容积,再与净含量进行比较,得出结论。
【详解】3.14×(8÷2)2×10
=3.14×42×10
=3.14×16×10
=502.4(立方厘米)
502.4立方厘米=502.4毫升
502.4>350
答:生产商没有欺骗消费者。
4.15.072平方米
【分析】分析题目,先根据1米=100厘米把16厘米换算成以米为单位,圆柱形通风管只需要计算侧面积,圆柱的侧面积=πdh,据此求出做一个圆柱形通风管需要多少平方米的铁皮,再乘个数即可求出需要铁皮的总面积。
【详解】16厘米=0.16米
3.14×0.16×1.5
=0.5024×1.5
=0.7536(平方米)
0.7536×20=15.072(平方米)
答:至少需要铁皮15.072平方米。
5.0.628米
【分析】根据圆的周长公式:可知:底面半径=底面周长÷圆周率÷2,圆锥体积=底面积×高÷3,据此求出沙堆体积,铺的厚度相当于长方体的高,再根据长方体的高=体积÷长÷宽,列式解答即可。
【详解】3.14×(12.56÷3.14÷2)2×1.8÷3
=3.14×22×1.8÷3
=3.14×4×1.8÷3
=7.536(立方米)
7.536÷6÷2=0.628(米)
答:能铺0.628米厚。
6.62.8平方米;18.84千克
【分析】刷油漆的部分是圆柱形柱子的侧面积,根据圆柱侧面积=底面周长×高,求出1根柱子的侧面积,再乘10,是刷油漆的总面积,总面积×每平方米用油漆质量=要用的油漆总质量,据此列式解答。
【详解】3.14×0.4×5×10
=6.28×10
=62.8(平方米)
62.8×0.3=18.84(千克)
答:刷油漆的面积一共是62.8平方米,刷这些柱子要用油漆18.84千克。
7.351.68立方厘米
【分析】根据把一个铁块放入容器,铁块完全浸没在水中,同时有部分水溢出,可知当铁块铁块完全浸没在水中,水是满的,当把铁块取出后,水面距杯口还有7厘米,说明水面下降了7厘米,则下降部分的体积就是铁块的体积。下降部分是个圆柱体,根据圆柱的体积,把数据代入公式即可求解。
【详解】3.14×(8÷2)2×7
=3.14×42×7
=3.14×16×7
=351.68(立方厘米)
答:铁块的体积是351.68立方厘米。
8.100.48立方分米
【分析】根据题意,把一张长方形铁皮被分割成两个圆和一个长方形,那么这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高;
从图中可知,圆柱的高等于圆的直径的2倍,据此求出圆柱的高;再根据圆柱的体积公式V=πr2h,求出这个圆柱的体积。
【详解】圆柱的高:2×2×2=8(分米)
圆柱的体积:
3.14×22×8
=3.14×4×8
=100.48(立方分米)
答:这个圆柱的体积是100.48立方分米。
9.79.128吨
【分析】圆柱的体积=底面积×高,V=πr2h,圆锥的面积=底面积×高÷3,V=πr2h,代入数据计算出粮仓的体积,粮仓的体积乘每立方米粮食的质量,就是这个粮仓所装的粮食质量。
【详解】3.14×(6÷2)2×4+3.14×(6÷2)2×2×
=3.14×32×4+3.14×32×2×
=3.14×9×4+3.14×9×2×
=113.04+56.52×
=113.04+18.84
=131.88(立方米)
131.88×0.6=79.128(吨)
答:这个粮仓最多能装79.128吨粮食。
10.20只
【分析】根据题意,设他打碎了只花瓶,那么没打碎的花瓶有(1000-)只,每只可得劳务费0.4元;如果打碎,不但得不到这只花瓶的劳务费,还要赔1.6元,那么打碎只花瓶,要赔1.6元;
等量关系:搬运一只花瓶的劳务费×完好的花瓶数量-打碎一只花瓶要赔的钱数×打碎花瓶的数量=最终得到的劳务费,据此列出方程,并求解。
【详解】解:设他打碎了只花瓶。
0.4×(1000-)-1.6=360
400-0.4-1.6=360
400-(0.4+1.6)=360
400-2=360
400-2+2=360+2
360+2=400
360+2-360=400-360
2=40
2÷2=40÷2
=20
答:他打碎了20只花瓶。
11.11个
【分析】分析题目,设同学们制作了x个大中国结,则制作了(20-x)个小中国结,根据等量关系式:制作一个大中国结需要的红绳长度×制作的大中国结的个数+制作一个小中国结需要的红绳长度×制作的小中国结的个数=184列出方程11x+7(20-x)=184,进一步解出方程即可。
【详解】解:设同学们制作了x个大中国结,则制作了(20-x)个小中国结。
11x+7(20-x)=184
11x+140-7x=184
4x=184-140
4x=44
4x÷4=44÷4
x=11
答:同学们制作了11个大中国结。
12.1.8厘米
【分析】在比例尺1∶2000000中图上距离1厘米代表实际距离2000000厘米,也就是20千米;已知甲、乙两地的图上距离是4.5厘米,实际距离就是4.5个20千米,用乘法计算;在比例尺1∶5000000中图上距离1厘米代表实际距离5000000厘米,也就是50千米;甲、乙两地实际距离不变,仍是4.5×20=90千米,计算图上距离就是计算90里面有几个50,用除法计算。
【详解】2000000厘米=20千米
4.5×20=90(千米)
5000000厘米=50千米
90÷50=1.8(厘米)
答:甲、乙两地的距离是1.8厘米。
13.200平方米
【分析】先依据“实际距离=图上距离÷比例尺”求出这个图形长和宽的实际长度,进而利用长方形的面积公式=长×宽,求出这个图形的实际面积。
【详解】10÷
=10×200
=2000(厘米)
2000厘米=20米
5÷
=5×200
=1000(厘米)
1000厘米=10米
20×10=200(平方米)
答:图形的实际面积是200平方米。
14.2小时
【分析】先根据实际距离=图上距离÷比例尺,据此求出实际距离是多少厘米,再把厘米化为千米,然后根据路程÷速度=时间,据此解答即可。
【详解】2.5÷
=2.5×4000000
=10000000(厘米)
10000000厘米=100千米
100÷50=2(小时)
答:2小时可以到达。
15.5.4厘米
【分析】根据实际距离=图上距离÷比例尺,代入数据可求出甲、乙两地之间的实际距离,再根据图上距离=实际距离×比例尺,代入第二幅地图的比例尺即可得解。
【详解】(厘米)
(厘米)
答:甲、乙两地之间的航空线长5.4厘米。
16.(1)摩天轮(6,2);蹦蹦床(10,4)
(2)北;东;37;北;西;76
(3)见详解
【分析】(1)用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;据此用数对表示图上的摩天轮和蹦蹦床的位置。
(2)以图上的“上北下南,左西右东”确定方向,得出碰碰车与游乐场大门,以及游乐场大门与摩天轮的位置关系。
(3)从游乐场大门到喷泉,可以先从游乐场大门走到碰碰车,再走到喷泉。结合图上的方向和角度描述从游乐场大门到喷泉的路线。
【详解】(1)用数对表示摩天轮和蹦蹦床的位置,如下图:
(2)碰碰车在游乐场大门的(北)偏(东)(37)°方向;游乐场大门在摩天轮的(北)偏(西)(76)°方向。(答案不唯一)
(3)先从游乐场大门向北偏东37°方向走到碰碰车,再从碰碰车向北偏东63°方向走到喷泉。(答案不唯一)
17.(1)小明家在学校南偏东60°方向575米处;小红家在学校南偏西45°方向450米处。
(2)(3)见详解
【分析】(1)以东偏北30°为例,表示以正南正北坐标交点为顶点,以正东方向为一条边向北作一个30°的角,这个角的另一条边上就是东偏北30°方向,据此描述题目里的方向。测量出小明家、小红家到学校的图上距离,再依据比例尺算出实际距离,最后结合图中方角度确定方向和位置;
(2)先将实际距离换算为厘米,实际距离乘比例尺得到图上距离,然后根据给定的方向和角度在图中确定小刚家的位置;
(3)先将实际距离换算为厘米,实际距离乘比例尺得到图上距离,然后根据给定的方向和角度在图中确定小芳家的位置。
【详解】(1)小明家、小红家到学校的图上距离是2.3厘米、1.8厘米。(以实际测量数值为准)
(米)
小明家在学校南偏东60°方向575米处。
(米)
小红家在学校南偏西45°方向450米处。
(2)
(厘米)
如下图所示。
(3)
(厘米)
如下图所示。
18.表格见详解
(1)240
(2)路程;路程=速度×时间
(3)成反比例;原因见详解
【分析】根据每小时行驶的路程= A、B两地相距240千米÷行驶时间,据此完成表格即可;
(1)将相对应的两个数相乘分别求出它们的乘积即可;
(2)这个乘积表示路程,根据路程、速度和时间之间的关系解答即可;
(3)两个相关联的量,一个量变化,另一个量也随之变化,且它们乘积一定,则这两个量成反比例;若它们的比值一定,则这两个量成正比例。。
【详解】240÷2=120,240÷3=80,240÷4=60,240÷5=48,240÷6=40,240÷8=30
表格如下:
行驶时间/时 2 3 4 5 6 8 …
每小时行驶的路程/千米 120 80 60 48 40 30 …
(1)2×120=240,3×80=240,4×60=240,5×48=240,6×40=240,8×30=240
相对应的两个数的乘积都是240。
(2)这个乘积表示路程,路程=速度×时间;
(3)因为时间×速度=路程(一定),积一定,行驶时间和速度成反比例。
19.(1)见详解
(2)成正比。理由:张师傅加工零件的数量与加工零件的时间的比值是定值。
(3)105个零件;195个零件
【分析】(1)横轴表示时间,纵轴表示零件个数,据此描点连线。
(2)判断两个量是否成正比例,就看这两种量对应的数据的比值是否一定,如果一定,就成正比例。计算张师傅加工零件的数量与加工零件的时间的比值,看比值是否是定值。
(3)观察图像,得出张师傅3.5小时、6.5小时加工了多少个零件。
【详解】(1)如图所示
(2),即(定值),所以张师傅加工零件的数量与加工零件的时间成正比。
(3)由图像得到,张师傅3.5小时加工了105个零件,6.5小时加工了195个零件。
20.(1)卡车载质量×需要的卡车数量=总吨数(一定);卡车载质量和需要的卡车数量成反比例
(2)物资总质量÷需要卡车数量=卡车载质量(一定);物资总质量和需要卡车数量成正比例
【分析】两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果x÷y=k(一定),x和y成正比例关系;如果xy=k(一定),x和y成反比例关系,据此分析。
【详解】(1)2×50=100(吨)、4×25=100(吨)、5×20=100(吨)……
卡车载质量×需要的卡车数量=总吨数(一定)
(2)15÷3=5(吨)、25÷5=5(吨)、30÷6=5(吨)……
物资总质量÷需要卡车数量=卡车载质量(一定)
答:物资总质量和需要卡车数量成正比例,卡车载质量和需要的卡车数量成反比例。
21.(1)48;72;96;120;144
(2)见详解
(3)正比例;铺设长度÷对应天数=每天铺设长度(一定)
(4)192米;4天
【分析】(1)根据每天铺设长度×铺设天数=相应天数铺设长度,列式计算并填表即可;
(2)根据各数量的多少,在方格图的纵、横的交点上描出表示数量多少的点;把各点用线段顺次连接起来,标记数据即可;
(3)两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果x÷y=k(一定),x和y成正比例关系;如果xy=k(一定),x和y成反比例关系,据此分析;
(4)观察图像,找到横轴8天对应的长度和竖轴100米对应的大约天数即可。
【详解】(1)24×2=48(米)
24×3=72(米)
24×4=96(米)
24×5=120(米)
24×6=144(米)
时间/天 1 2 3 4 5 6 …
长度/米 24 48 72 96 120 144 …
(2)
(3)24÷1=24(米)、48÷2=24(天)、72÷3=24(天)……
答:铺设管道的时间和长度成正比例,因为铺设长度÷对应天数=每天铺设长度(一定)。
(4)根据图像判断,8天能铺设192米管道,铺设100米管道大约需要4天。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
