3.6.1直线和圆的位置关系课件(共20张PPT) 北师大版 九年级(下册)
文档属性
| 名称 | 3.6.1直线和圆的位置关系课件(共20张PPT) 北师大版 九年级(下册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 23.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 15:24:27 | ||
图片预览





文档简介
(共20张PPT)
第三章
3.6.1 直线和圆的位置关系
复习回顾
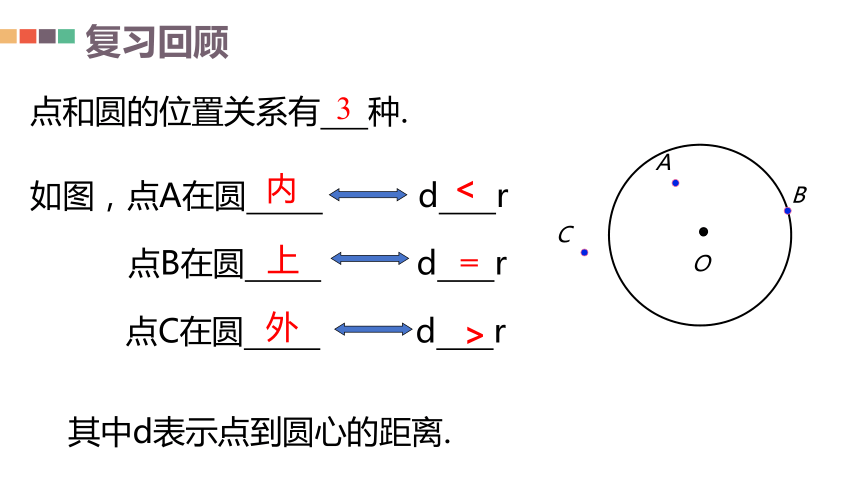
点和圆的位置关系有 种.
A
B
C
O
3
如图,点A在圆 d r
内
<
点B在圆 d r
上
=
点C在圆 d r
外
>
其中d表示点到圆心的距离.
情境引入
“日出江花红胜火,春来江水绿如蓝,能不忆江南?”
学习目标
1.了解直线和圆的三种位置关系.
2.掌握切线的概念.
3.探索切线与过切点的半径之间的关系.
探究活动1
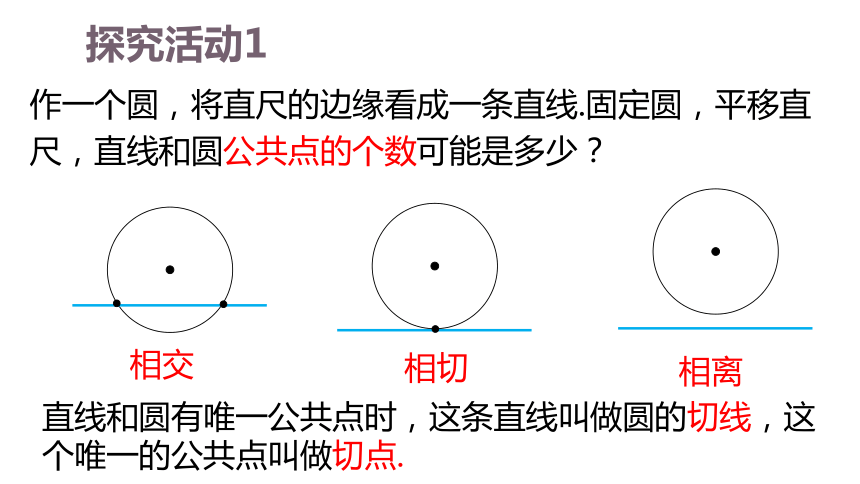
作一个圆,将直尺的边缘看成一条直线.固定圆,平移直尺,直线和圆公共点的个数可能是多少?
相离
相交
相切
直线和圆有唯一公共点时,这条直线叫做圆的切线,这个唯一的公共点叫做切点.
巩固练习
判断图中直线与圆的位置关系.
探究活动2
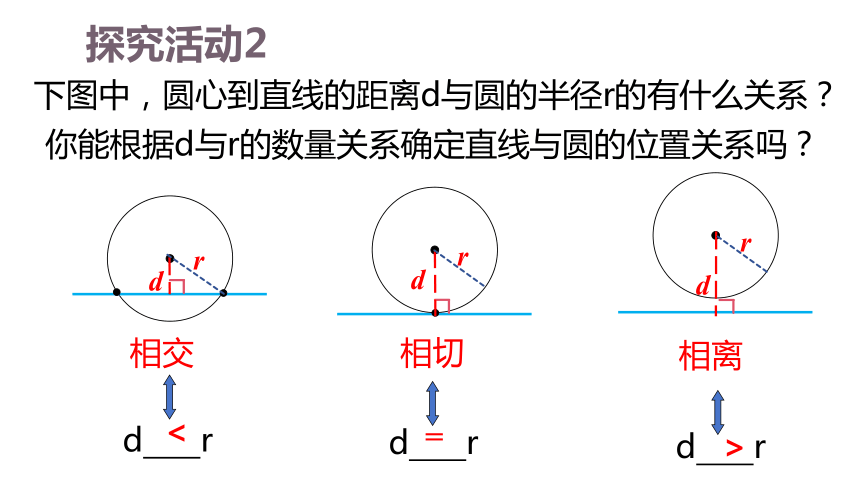
下图中,圆心到直线的距离d与圆的半径r的有什么关系?
相交
相切
相离
你能根据d与r的数量关系确定直线与圆的位置关系吗?
d r
d r
d r
<
=
>
d
r
r
r
d
d
知识小结
判断直线和圆的位置关系的方法有 种.
(1)根据图形中直线和圆的 个数来判断.
(2)根据 到 的距离d与半径r的数量关系来判断.
两
数形结合
公共点
圆心
直线
巩固练习
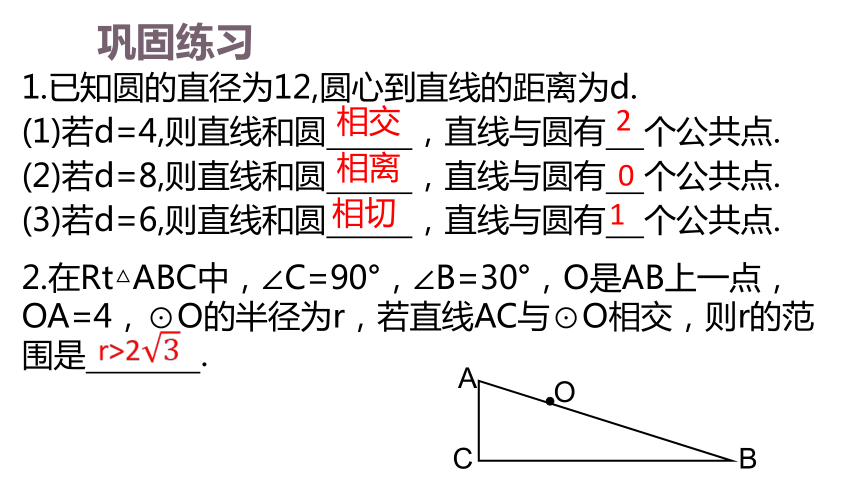
1.已知圆的直径为12,圆心到直线的距离为d.
(1)若d=4,则直线和圆 ,直线与圆有 个公共点.
(2)若d=8,则直线和圆 ,直线与圆有 个公共点.
(3)若d=6,则直线和圆 ,直线与圆有 个公共点.
相交
2
相切
1
相离
0
2.在Rt△ABC中,∠C=90°,∠B=30°,O是AB上一点,OA=4,⊙O的半径为r,若直线AC与⊙O相交,则r的范围是 .
C
B
A
O
r>2
探究活动3
(1)这三个图形是轴对称图形吗?如果是,请在课本P89,图3-22中画出他们的对称轴.
相离
相交
相切
l
l
l
探究活动3
(2)如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系 说说你的理由.
C
D
B
●O
A
解:AB⊥CD,理由如下:
∵该图是轴对称图形,AB所在的直线是对称轴
∴沿AB对折图形时,∠BAD=∠BAC
又∵∠BAD+∠BAC=180°
∴∠BAD=∠BAC=90°
∴AB⊥CD
A
C
O
切线的性质
圆的切线 .
D
垂直于过切点的半径
几何语言:
∵CD与⊙O相切于点A,
∴CD⊥OA.
例题精讲
如图,已知Rt△ABC的斜边AB=8 cm,AC=4 cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
例题精讲
如图,已知Rt△ABC的斜边AB=8 cm,AC=4 cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
(2)以点C为圆心,分别以2 cm和4 cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
自我检测
1.如图,PA是⊙O的切线,切点为A,PO的延长线交⊙O于点B,若∠P=40°,则∠B的度数为 .
2.如图,在平面直角坐标系中,半径为2的圆P的圆心P的坐标为(﹣3,0),将圆P沿x轴的正方向平移,使得圆P与y轴相切,则平移的距离为 .
第1题图
第2题图
链接中考
(2022·陕西)如图,AB是⊙O的直径,AM是⊙O的切线,AC、CD是⊙O的弦,且CD⊥AB,垂足为E,连接BD并延长,交AM于点P.
(1)求证:∠CAB=∠APB;
链接中考
(2)若⊙O的半径r=5,AC=8,求线段PD的长.
课堂小结
本节课的学习目标你都实现了吗?
1.了解直线和圆的三种位置关系.
2.掌握切线的概念.
3.探索切线与过切点的半径之间的关系.
方法总结
无切点时,过圆心作垂直
有切点时,连半径得垂直
常用辅助线:
第三章
3.6.1 直线和圆的位置关系
复习回顾
点和圆的位置关系有 种.
A
B
C
O
3
如图,点A在圆 d r
内
<
点B在圆 d r
上
=
点C在圆 d r
外
>
其中d表示点到圆心的距离.
情境引入
“日出江花红胜火,春来江水绿如蓝,能不忆江南?”
学习目标
1.了解直线和圆的三种位置关系.
2.掌握切线的概念.
3.探索切线与过切点的半径之间的关系.
探究活动1
作一个圆,将直尺的边缘看成一条直线.固定圆,平移直尺,直线和圆公共点的个数可能是多少?
相离
相交
相切
直线和圆有唯一公共点时,这条直线叫做圆的切线,这个唯一的公共点叫做切点.
巩固练习
判断图中直线与圆的位置关系.
探究活动2
下图中,圆心到直线的距离d与圆的半径r的有什么关系?
相交
相切
相离
你能根据d与r的数量关系确定直线与圆的位置关系吗?
d r
d r
d r
<
=
>
d
r
r
r
d
d
知识小结
判断直线和圆的位置关系的方法有 种.
(1)根据图形中直线和圆的 个数来判断.
(2)根据 到 的距离d与半径r的数量关系来判断.
两
数形结合
公共点
圆心
直线
巩固练习
1.已知圆的直径为12,圆心到直线的距离为d.
(1)若d=4,则直线和圆 ,直线与圆有 个公共点.
(2)若d=8,则直线和圆 ,直线与圆有 个公共点.
(3)若d=6,则直线和圆 ,直线与圆有 个公共点.
相交
2
相切
1
相离
0
2.在Rt△ABC中,∠C=90°,∠B=30°,O是AB上一点,OA=4,⊙O的半径为r,若直线AC与⊙O相交,则r的范围是 .
C
B
A
O
r>2
探究活动3
(1)这三个图形是轴对称图形吗?如果是,请在课本P89,图3-22中画出他们的对称轴.
相离
相交
相切
l
l
l
探究活动3
(2)如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系 说说你的理由.
C
D
B
●O
A
解:AB⊥CD,理由如下:
∵该图是轴对称图形,AB所在的直线是对称轴
∴沿AB对折图形时,∠BAD=∠BAC
又∵∠BAD+∠BAC=180°
∴∠BAD=∠BAC=90°
∴AB⊥CD
A
C
O
切线的性质
圆的切线 .
D
垂直于过切点的半径
几何语言:
∵CD与⊙O相切于点A,
∴CD⊥OA.
例题精讲
如图,已知Rt△ABC的斜边AB=8 cm,AC=4 cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
例题精讲
如图,已知Rt△ABC的斜边AB=8 cm,AC=4 cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
(2)以点C为圆心,分别以2 cm和4 cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
自我检测
1.如图,PA是⊙O的切线,切点为A,PO的延长线交⊙O于点B,若∠P=40°,则∠B的度数为 .
2.如图,在平面直角坐标系中,半径为2的圆P的圆心P的坐标为(﹣3,0),将圆P沿x轴的正方向平移,使得圆P与y轴相切,则平移的距离为 .
第1题图
第2题图
链接中考
(2022·陕西)如图,AB是⊙O的直径,AM是⊙O的切线,AC、CD是⊙O的弦,且CD⊥AB,垂足为E,连接BD并延长,交AM于点P.
(1)求证:∠CAB=∠APB;
链接中考
(2)若⊙O的半径r=5,AC=8,求线段PD的长.
课堂小结
本节课的学习目标你都实现了吗?
1.了解直线和圆的三种位置关系.
2.掌握切线的概念.
3.探索切线与过切点的半径之间的关系.
方法总结
无切点时,过圆心作垂直
有切点时,连半径得垂直
常用辅助线:
