期末重难点检测卷-2024-2025学年数学五年级下册人教版(含解析)
文档属性
| 名称 | 期末重难点检测卷-2024-2025学年数学五年级下册人教版(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 656.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末重难点检测卷-2024-2025学年数学五年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面大长方形的面积都是2m2,用阴影部分表示,正确的是( )。
A.①②④ B.①② C.①④ D.②③
2.小维用相同的小正方体搭立体图形(如图),如果拿掉一个小正方体,从正面、上面和左面看到的形状都是,拿掉的是( )。
A.①号 B.②号 C.③号 D.④号
3.整数、小数和分数的加减法运算都是计数单位相同才能直接相加减,下面算式中的“2”和“3”能直接相加减的是( )。
A.43+25 B.0.73-0.21 C. D.
4.一个由64个小正方体拼成的大正方体,在它的表面涂上红色,其中两面涂色的小正方体有( )个。
A.8 B.16 C.24 D.32
5.有9袋白糖,其中8袋每袋500克,另1袋不是500克,但不知道比500克重还是轻,用天平称,至少( )次就能保证把它找出来。
A.2 B.3 C.4 D.5
6.在、、、、、中,不能化成有限小数的分数有( )个。
A.2 B.3 C.4 D.5
7.96是16和12的( )。
A.公因数 B.公倍数 C.最大公因数 D.最小公倍数
8.一个长方体的长a厘米,宽b厘米,高c厘米。如果它的高增加4厘米,那么表面积比原来增加( )平方厘米。
A. B. C.8ab D.
二、填空题
9.在括号内填上适当的质数。
16=( )+( ) 24=( )+( )
10.===9÷( )=( )(填小数)。
11.涂色部分占整个图形的,写成小数是( )。
12.如图,一个长方体长8厘米、高4厘米,涂色的两个面的面积之和是60平方厘米,这个长方体的体积是( )立方厘米。
13.要围成一个底面周长是28cm、高是5cm的长方体框架,至少需要( )cm的铁丝。
14.a与b都是一位数,且都是质数,如果a+b=12,那么a与b的最大公因数是( ),最小公倍数是( )。
15.一块长方体木块刚好截成两个一样的小正方体,表面积之和增加了18平方分米,原来长方体的表面积是( )平方分米。
16.从0、2、4、5四张数字中选出三个,组成一个既是2和3的倍数,又有因数5的数,可以是( )或( )。
三、计算题
17.直接写出得数。
40×1.2= 25×0.4= = 29÷18=
2.4×0.5= 1.25×80= 3.6÷0.06= 1÷3=
18.计算。
19.解方程。
9x-18=36 1.6x+2.9x=13.5
20.求下面图形的体积是多少?(单位cm)
四、解答题
21.“3.14数学节”时,红星小学的同学们为了做海报,要将一张长24厘米,宽18厘米的画纸,裁成大小一样且尽可能大的正方形,要求不能有剩余,裁得的正方形画纸边长最长是多少厘米?可以裁出多少个这样的正方形画纸?(写出主要思考过程,再在下边的长方形中画图验证)
22.一辆货车和一辆轿车同时从A、B两地出发,相向而行。当货车行了全程的时,轿车行了全程的,这时货车、轿车间的距离占全程的几分之几?
23.如图,是一个棱长为3分米的正方体募捐箱,上面留有一个长1分米,宽3厘米的长方形入口,这个募捐箱的表面积是多少?
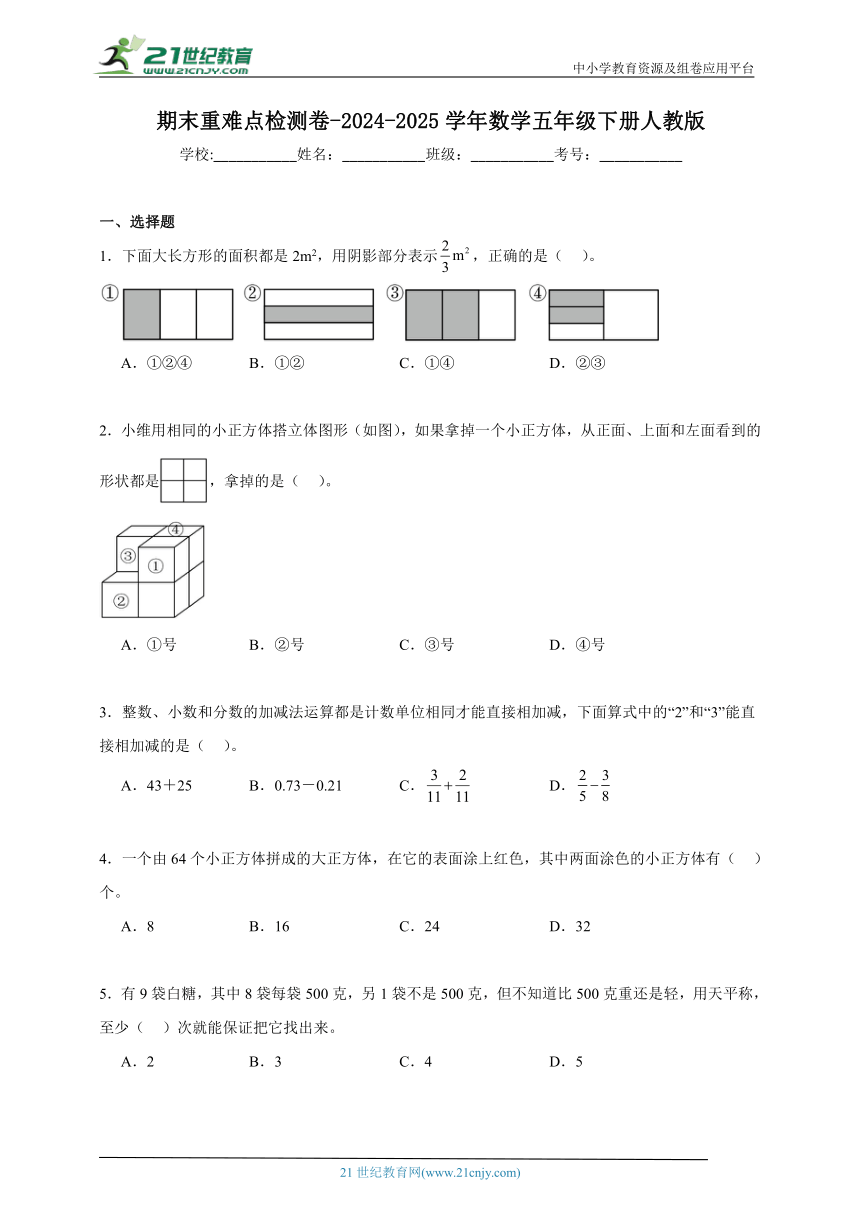
24.学校要开运动会了,同一个班的彬彬和亮亮努力训练,备战运动会的100米短跑。下面是他们每周训练成绩统计图。
(1)观察统计图,说说彬彬和亮亮的100米短跑训练效果。
(2)提一个数学问题并解答。
(3)每个项目每班一人参加比赛。如果你是班主任,你会选择谁参加?请说明理由。
25.修路队修一段路,第一天修了千米,第一天比第二天多修了千米,两天共修路多少千米?
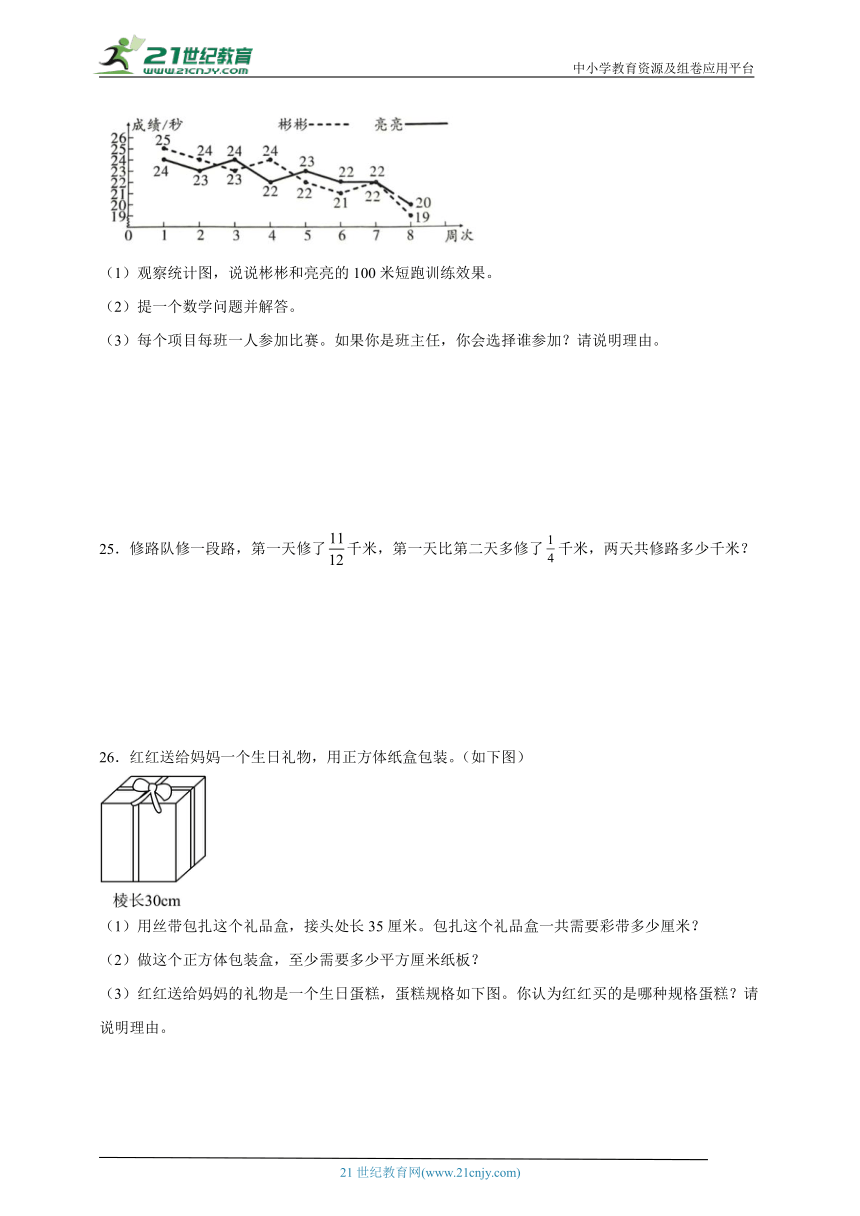
26.红红送给妈妈一个生日礼物,用正方体纸盒包装。(如下图)
(1)用丝带包扎这个礼品盒,接头处长35厘米。包扎这个礼品盒一共需要彩带多少厘米?
(2)做这个正方体包装盒,至少需要多少平方厘米纸板?
(3)红红送给妈妈的礼物是一个生日蛋糕,蛋糕规格如下图。你认为红红买的是哪种规格蛋糕?请说明理由。
《期末重难点检测卷-2024-2025学年数学五年级下册人教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 A D C C B B B B
1.A
【分析】可求出m2占2m2的几分之几,根据求一个数占另一个数的几分之几用除法计算,再结合分数的意义进行选择。
【详解】
图形①②④都表示阴影部分占大长方形的,图形④表示阴影部分不是占大长方形的。
故答案为:A
2.D
【分析】
根据题意,分别拿掉①号、②号、③号和④号,再从正面、上面和左面看到的观察形状,确定是即可。
【详解】
A.拿掉①号,正面和上面是,但是左面是;
B.拿掉②号,正面和左面是,但是上面是;
C.拿掉③号,上面和左面看是,但是正面是;
D.拿掉④号,从正面、上面和左面看到的形状都是。
故答案为:D
3.C
【分析】根据整数、小数和分数的加减法运算都是计数单位相同才能直接相加减,逐项分析各个选项中的“2”和“3”的计数单位是否相同,进而解答。
【详解】A.43+25;43的“3”在个位,25的“2”在十位,不能直接相加;
B.0.73-0.21;0.73的“3”在百分位上,0.21的“2”在十分位上,不能直接相减;
C.+;分母相同,可以直接相加;
D.-;分母不同,不能直接相减。
算式中的“2”和“3”能直接相加减的是+。
故答案为:C
4.C
【分析】假设小正方体的棱长是1厘米,由64个小正方体拼成一个大正方体,64=4×4×4,大正方体的棱长是4厘米;正方体有8个顶点,12条棱,6个面;三面涂色的小正方体位于大正方体的顶点上,即有8个三面涂色的小正方体;两面涂色的在每条棱上(除去顶点的小正方体),有(4-2)×12个,每个面中间会有4个小正方体是一面涂色的,一面涂色的共有4×6个,据此解答。
【详解】(4-2)×12
=2×12
=24(个)
一个由64个小正方体拼成的大正方体,在它的表面涂上红色,其中两面涂色的小正方体有24个。
故答案为:C
5.B
【分析】用天平找次品时,如果待测物品有3个或3个以上,首先要把待测物品分成3份,能平均分的要平均分,不能平均分的要使多的那份的个数与少的那份的个数相差最少,这样可以保证找出次品需要称量的次数最少;依此解答。
【详解】先将这9袋白糖分成(3袋+ 3袋+3袋)三组,取(3袋+ 3袋)这两组分别放入天平称量,即可找出有次品的一组。
若天平平衡,则可确定次品在未取的3袋白糖组中;再将剩下的3袋分成(1袋+1袋+1袋),取(1袋+1袋)放在天平的两端,若天平平衡,则次品就是剩余的那袋;若天平不平衡,正品就是剩余的1袋,将有可能是次品的两袋分别与正品的1袋称量,即可找出次品。
若天平不平衡,则剩余的3袋就是正品,则将其他两组的3袋分别与正品中的3袋放天平的两边,此时即可找出次品组;再将次品组的3袋分成2袋+1袋,并取其中的2袋、正品中的2袋分别放天平的两边,如果天平平衡,则剩下的1袋就是次品;如果天平不平衡,则将次品分成1袋+1袋,并分别与正品的1袋进行称量,即可找出次品。由此可知,用天平称,至少3次就能保证把它找出来。
故答案为:B
6.B
【分析】有限小数是指小数部分的位数是有限的。一个最简分数,如果分母中只含有质因数2和5,这个分数就能化成有限小数,据此解答。
【详解】的分母只含有质因数2,所以可以化成有限小数;
的分母只含有质因数5,所以可以化成有限小数
的分母只含有质因数3,所以不可以化成有限小数;
的分母含有质因数2和5,所以可以化成有限小数;
的分母含有质因数2和3,所以不可以化成有限小数;
的分母含有质因数2和3,所以不可以化成有限小数。
不能化成有限小数的分数:、、,共3个。
故答案为:B
7.B
【分析】公因数:两个数公共的因数。最大公因数:两个数公因数中最大的。
公倍数:两个数公有的倍数。最小公倍数:两个数公倍数中最小的。
可利用列举法,将两个数的因数和倍数一一列举,从而找出公因数和最大公因数,公倍数和最小公倍数。求最大公因数和最小公倍数时,也可以将这两个数分别分解质因数,公有质因数的乘积是这两个数的最大公因数,公有质因数和独有质因数的乘积是这两个数的最小公倍数。
据此,先找出16和12的公因数、公倍数、最大公因数和最小公倍数,再判断96是什么即可。
【详解】A.16的因数有1、2、4、8、16,12的因数有1、2、3、4、6、12,那么16和12的公因数有1、2、4;
B.16的倍数有16、32、48、64、80、96……,12的倍数有12、24、36、48、60、72、84、96……,所以16和12的公倍数有48、96……;
C.根据A选项的分析可知,16和12的最大公因数是4;
D.根据B选项的分析可知,16和12的最小公倍数是48;
所以,96是16和12的公倍数。
故答案为:B
8.B
【分析】长方体的高增加4厘米后,增加的表面积实际上是一个长方体长a厘米,宽b厘米,高为4厘米的四个侧面的面积,即两个长为a厘米,宽为4厘米的长方形和两个长为b厘米,宽为4厘米的长方形,根据长方形的面积=长×宽,代入数据计算,即可求出表面积增加了多少平方厘米,据此解答。
【详解】由分析得:
a×4×2+b×4×2=(8a+8b)平方厘米
即表面积比原来增加(8a+8b)平方厘米。
故答案为:B
9. 3/5 13/11 5/7/11 19/17/13
【分析】质数是指只能被1和它本身整除的数,在24以内的质数有:2、3、5、7、11、13、17、19、23。据此可计算得出答案。
【详解】16=3+13,16=5+11;24=5+19,24=7+17,24=11+13。
10.36;15;7.5;1.2
【分析】根据分数的基本性质,将的分子和分母同时乘6,可得=;将的分子和分母同时乘3,可得=;根据分数与除法的关系,可得=18÷15,根据商不变性质,将18÷15的被除数和除数同时除以2,可得18÷15=9÷7.5;分数化成小数:用分子除以分母,按照除数是整数的小数除法进行计算,据此可得=1.2。
【详解】===9÷7.5=1.2
11.;0.5
【分析】根据分数的意义,把整个图形看作单位“1”,平均分成4份,每份用分数表示为;涂色部分占其中的2份,用分数表示为,化简后是;再把分数化成小数,用分子除以分母即可。
【详解】=
=1÷2=0.5
涂色部分占整个图形的,写成小数是0.5。
12.160
【分析】因为涂色的两个面一个是长方体的左面(宽×高),一个是底面(长×宽),这两个面面积之和是60平方厘米,而长是8厘米,高是4厘米。我们可以先算出长和高的和:8+4=12(厘米)。然后用两个面的面积和除长和高的和,就可以得到长方体的宽,即60÷12=5(厘米),最后根据长方体体积公式V=长×宽×高求出体积。
【详解】长和高的和为:8+4=12(厘米)
长方体的宽为:60÷12=5(厘米)
长方体体积为:
8×5×4
=40×4
=160(立方厘米)
这个长方体的体积是160立方厘米。
13.76
【分析】求铁丝长度相当于求长方体棱长总和,长方体上下两个面完全一样,上下两个面共8条棱,铁丝长度=底面周长×2+高×4,据此列式计算。
【详解】28×2+5×4
=56+20
=76(cm)
至少需要76cm的铁丝。
14. 1 35
【分析】根据题意,a与b都是一位数,且都是质数,由a+b=12,可知5+7=12,由此确定a、b的值,且a与b是互质数;
根据“当两个数是互质数时,它们的最大公因数是1,最小公倍数是两数的乘积”,求出a与b的最大公因数和最小公倍数。
【详解】5+7=12,5、7都是一位数,且都是质数;
所以a=5,b=7或a=7,b=5;
5和7的最大公因数是1,最小公倍数是5×7=35;
那么a与b的最大公因数是1,最小公倍数是35。
15.90
【分析】根据题意可知,一刀增加2个面,已知表面积之和增加了18平方分米,说明2个正方形面的面积是18平方分米,用18÷2即可求出1个正方形面的面积,再根据正方体的表面积=棱长×棱长×6,求出1个小正方体的表面积,进而求出2个小正方体的表面积,然后减去18平方分米即可。
【详解】18÷2=9(平方分米)
9×6×2
=54×2
=108(平方分米)
108-18=90(平方分米)
原来长方体的表面积是90平方分米。
16. 240 420
【分析】从0、2、4、5四张数字中选出三个组成一个三位数,这个三位数是2和5的倍数,那么这个三位数的个位一定是0;同时又是3的倍数,则这个三位数的各位上的数字之和是3的倍数;据此得出这个三位数。
【详解】从0、2、4、5四张数字中选出三个,组成一个既是2和3的倍数,又有因数5的数,可以是240或420。(答案不唯一)
17.48;10;216;;
1.2;100;60;;
【详解】略
18.2;1;
【分析】(1)利用加法交换律和结合律进行简便计算;
(2)利用减法的性质进行简便计算;
(3)先算小括号里的减法,再算括号外的减法。
【详解】
19.x=6;x=3;x=
【分析】9x-18=36,根据等式的性质1,方程两边同时加上18,再根据等式的性质2,方程两边同时除以9即可;
1.6x+2.9x=13.5,先化简方程左边含有x的算式,即求出1.6+2.9的和,再根据等式的性质2,方程两边同时除以1.6+2.9的和即可;
x-(+)=,先计算出+的和,再根据等式的性质1,方程两边同时加上(+)的和即可。
【详解】9x-18=36
解:9x-18+18=36+18
9x=54
9x÷9=54÷9
x=6
1.6x+2.9x=13.5
解:4.5x=13.5
4.5x÷4.5=13.5÷4.5
x=3
x-(+)=
解:x-(+)=
x-=
x-+=+
x=+
x=
20.232cm3
【分析】求图形的体积,用长8cm,宽5cm,高6cm的长方体体积减去棱长为2cm的正方体体积;根据长方体和体积=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数值计算分别计算出长方体的体积和正方体的体积,再相减即可解答。
【详解】8×5×6-2×2×2
=40×6-4×2
=240-8
=232(cm3)
图形的体积是232cm3。
21.6厘米;12个
图见详解
【分析】(1)根据题意,求裁的正方形边长尽可能大,就是求24和18的最大公因数,根据求最大公因数的方法:两个数的公有质因数的连乘积,据此求出正方形的边长;再分别求出长方形画纸的长边、宽边含有的小正方形画纸的块数,再把两个数相乘即可求出可以需要的小正方形画纸的块数。
【详解】24=2×2×2×3
18=2×3×3
24和18的最大公因数是2×3=6;裁得的正方形的边长是6厘米。
(24÷6)×(18÷6)
=4×3
=12(个)
如图:
答:裁得的正方形画纸边长最长是6厘米,可以裁出12个这样的正方形画纸。
22.
【分析】把A、B两地的距离看做单位“1”,当货车行了全程的,轿车行了全程的时,因为与的和大于1,说明货车与轿车相遇后分别继续向前行驶,那么货车、轿车间的距离等于全程的与全程的的和再减去1,据此解答。
【详解】+-1
=+-1
=-1
=
答:这时货车、轿车间的距离占全程的。
23.53.7平方分米
【分析】这个募捐箱的表面积等于正方体的表面积减去长1分米,宽3厘米的长方形的面积,根据正方体的表面积=棱长×棱长×6,长方形的面积=长×宽,代入数据解答即可。
【详解】3×3×6=54(平方分米)
3厘米=0.3分米
1×0.3=0.3(平方分米)
54-0.3=53.7(平方分米)
答:这个募捐箱的表面积是53.7平方分米。
24.(1)经过训练,他们所用的时间整体来看在逐渐减少,说明跑步速度有很大提升。
(2)提问:彬彬第几周进步最大?第八周进步最大。(答案不唯一)
(3)我会选择彬彬参赛,因为经过训练,彬彬的进步更大一些。(答案不唯一)
【分析】(1)根据统计图可得,彬彬和亮亮所用时间的整体趋势都是在逐渐减少的,用时缩短了,速度就提高了,所以训练效果较好。
(2)根据折线统计图的特点,线段越陡变化速度越快,可提问彬彬第几周进步最大。
(3)可根据二人训练前后的进步情况进行选择,答案不唯一,合理即可。
【详解】(1)经过训练,他们所用的时间整体来看在逐渐减少,说明跑步速度有很大提升。
(2)提问:彬彬第几周进步最大?(答案不唯一)
第二周:25-24=1(秒)
第三周:24-23=1(秒)
第五周:24-22=2(秒)
第六周:22-21=1(秒)
第八周:22-19=3(秒)
3>2>1
答:彬彬第八周进步最大。
(3)我会选择彬彬参赛,因为经过训练,彬彬的进步更大一些。(答案不唯一)
25.千米
【分析】根据题意,第二天修的千米数=第一天修的千米数-,则两天一共修的千米数=第一天修的千米数+第二天修的千米数。
【详解】
=
=(千米)
答:两天共修路千米。
26.(1)275厘米
(2)5400平方厘米
(30)A;理由见详解
【分析】(1)根据题意,用丝带包扎棱长为30厘米的正方体礼品盒,观察图形可知,包扎这个礼品盒至少需要丝带的长度=8条棱长+打结用的长度,据此解答。
(2)求做这个正方体包装盒,至少需要纸板的面积,就是求正方体的表面积;根据正方体的表面积公式S=6a2,代入数据计算求解。
(3)蛋糕的长、宽、高要比正方体包装盒的棱长小,才能放进去;把A、B两种蛋糕的长、宽、高与正方体的棱长进行比较,据此解答。
【详解】(1)30×8+35
=240+35
=275(厘米)
答:包扎这个礼品盒一共需要彩带275厘米。
(2)30×30×6
=900×6
=5400(平方厘米)
答:至少需要5400平方厘米纸板。
(3)A:20<30,25<30,26<30;
B:30=30,32>30,5<30;
答:红红买的是A规格蛋糕。因为蛋糕需放进盒子里,所以蛋糕的长、宽、高要比正方体纸盒的棱长小,A规格蛋糕符合要求,而B规格蛋糕中32>30,不能放进盒子里。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末重难点检测卷-2024-2025学年数学五年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面大长方形的面积都是2m2,用阴影部分表示,正确的是( )。
A.①②④ B.①② C.①④ D.②③
2.小维用相同的小正方体搭立体图形(如图),如果拿掉一个小正方体,从正面、上面和左面看到的形状都是,拿掉的是( )。
A.①号 B.②号 C.③号 D.④号
3.整数、小数和分数的加减法运算都是计数单位相同才能直接相加减,下面算式中的“2”和“3”能直接相加减的是( )。
A.43+25 B.0.73-0.21 C. D.
4.一个由64个小正方体拼成的大正方体,在它的表面涂上红色,其中两面涂色的小正方体有( )个。
A.8 B.16 C.24 D.32
5.有9袋白糖,其中8袋每袋500克,另1袋不是500克,但不知道比500克重还是轻,用天平称,至少( )次就能保证把它找出来。
A.2 B.3 C.4 D.5
6.在、、、、、中,不能化成有限小数的分数有( )个。
A.2 B.3 C.4 D.5
7.96是16和12的( )。
A.公因数 B.公倍数 C.最大公因数 D.最小公倍数
8.一个长方体的长a厘米,宽b厘米,高c厘米。如果它的高增加4厘米,那么表面积比原来增加( )平方厘米。
A. B. C.8ab D.
二、填空题
9.在括号内填上适当的质数。
16=( )+( ) 24=( )+( )
10.===9÷( )=( )(填小数)。
11.涂色部分占整个图形的,写成小数是( )。
12.如图,一个长方体长8厘米、高4厘米,涂色的两个面的面积之和是60平方厘米,这个长方体的体积是( )立方厘米。
13.要围成一个底面周长是28cm、高是5cm的长方体框架,至少需要( )cm的铁丝。
14.a与b都是一位数,且都是质数,如果a+b=12,那么a与b的最大公因数是( ),最小公倍数是( )。
15.一块长方体木块刚好截成两个一样的小正方体,表面积之和增加了18平方分米,原来长方体的表面积是( )平方分米。
16.从0、2、4、5四张数字中选出三个,组成一个既是2和3的倍数,又有因数5的数,可以是( )或( )。
三、计算题
17.直接写出得数。
40×1.2= 25×0.4= = 29÷18=
2.4×0.5= 1.25×80= 3.6÷0.06= 1÷3=
18.计算。
19.解方程。
9x-18=36 1.6x+2.9x=13.5
20.求下面图形的体积是多少?(单位cm)
四、解答题
21.“3.14数学节”时,红星小学的同学们为了做海报,要将一张长24厘米,宽18厘米的画纸,裁成大小一样且尽可能大的正方形,要求不能有剩余,裁得的正方形画纸边长最长是多少厘米?可以裁出多少个这样的正方形画纸?(写出主要思考过程,再在下边的长方形中画图验证)
22.一辆货车和一辆轿车同时从A、B两地出发,相向而行。当货车行了全程的时,轿车行了全程的,这时货车、轿车间的距离占全程的几分之几?
23.如图,是一个棱长为3分米的正方体募捐箱,上面留有一个长1分米,宽3厘米的长方形入口,这个募捐箱的表面积是多少?
24.学校要开运动会了,同一个班的彬彬和亮亮努力训练,备战运动会的100米短跑。下面是他们每周训练成绩统计图。
(1)观察统计图,说说彬彬和亮亮的100米短跑训练效果。
(2)提一个数学问题并解答。
(3)每个项目每班一人参加比赛。如果你是班主任,你会选择谁参加?请说明理由。
25.修路队修一段路,第一天修了千米,第一天比第二天多修了千米,两天共修路多少千米?
26.红红送给妈妈一个生日礼物,用正方体纸盒包装。(如下图)
(1)用丝带包扎这个礼品盒,接头处长35厘米。包扎这个礼品盒一共需要彩带多少厘米?
(2)做这个正方体包装盒,至少需要多少平方厘米纸板?
(3)红红送给妈妈的礼物是一个生日蛋糕,蛋糕规格如下图。你认为红红买的是哪种规格蛋糕?请说明理由。
《期末重难点检测卷-2024-2025学年数学五年级下册人教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 A D C C B B B B
1.A
【分析】可求出m2占2m2的几分之几,根据求一个数占另一个数的几分之几用除法计算,再结合分数的意义进行选择。
【详解】
图形①②④都表示阴影部分占大长方形的,图形④表示阴影部分不是占大长方形的。
故答案为:A
2.D
【分析】
根据题意,分别拿掉①号、②号、③号和④号,再从正面、上面和左面看到的观察形状,确定是即可。
【详解】
A.拿掉①号,正面和上面是,但是左面是;
B.拿掉②号,正面和左面是,但是上面是;
C.拿掉③号,上面和左面看是,但是正面是;
D.拿掉④号,从正面、上面和左面看到的形状都是。
故答案为:D
3.C
【分析】根据整数、小数和分数的加减法运算都是计数单位相同才能直接相加减,逐项分析各个选项中的“2”和“3”的计数单位是否相同,进而解答。
【详解】A.43+25;43的“3”在个位,25的“2”在十位,不能直接相加;
B.0.73-0.21;0.73的“3”在百分位上,0.21的“2”在十分位上,不能直接相减;
C.+;分母相同,可以直接相加;
D.-;分母不同,不能直接相减。
算式中的“2”和“3”能直接相加减的是+。
故答案为:C
4.C
【分析】假设小正方体的棱长是1厘米,由64个小正方体拼成一个大正方体,64=4×4×4,大正方体的棱长是4厘米;正方体有8个顶点,12条棱,6个面;三面涂色的小正方体位于大正方体的顶点上,即有8个三面涂色的小正方体;两面涂色的在每条棱上(除去顶点的小正方体),有(4-2)×12个,每个面中间会有4个小正方体是一面涂色的,一面涂色的共有4×6个,据此解答。
【详解】(4-2)×12
=2×12
=24(个)
一个由64个小正方体拼成的大正方体,在它的表面涂上红色,其中两面涂色的小正方体有24个。
故答案为:C
5.B
【分析】用天平找次品时,如果待测物品有3个或3个以上,首先要把待测物品分成3份,能平均分的要平均分,不能平均分的要使多的那份的个数与少的那份的个数相差最少,这样可以保证找出次品需要称量的次数最少;依此解答。
【详解】先将这9袋白糖分成(3袋+ 3袋+3袋)三组,取(3袋+ 3袋)这两组分别放入天平称量,即可找出有次品的一组。
若天平平衡,则可确定次品在未取的3袋白糖组中;再将剩下的3袋分成(1袋+1袋+1袋),取(1袋+1袋)放在天平的两端,若天平平衡,则次品就是剩余的那袋;若天平不平衡,正品就是剩余的1袋,将有可能是次品的两袋分别与正品的1袋称量,即可找出次品。
若天平不平衡,则剩余的3袋就是正品,则将其他两组的3袋分别与正品中的3袋放天平的两边,此时即可找出次品组;再将次品组的3袋分成2袋+1袋,并取其中的2袋、正品中的2袋分别放天平的两边,如果天平平衡,则剩下的1袋就是次品;如果天平不平衡,则将次品分成1袋+1袋,并分别与正品的1袋进行称量,即可找出次品。由此可知,用天平称,至少3次就能保证把它找出来。
故答案为:B
6.B
【分析】有限小数是指小数部分的位数是有限的。一个最简分数,如果分母中只含有质因数2和5,这个分数就能化成有限小数,据此解答。
【详解】的分母只含有质因数2,所以可以化成有限小数;
的分母只含有质因数5,所以可以化成有限小数
的分母只含有质因数3,所以不可以化成有限小数;
的分母含有质因数2和5,所以可以化成有限小数;
的分母含有质因数2和3,所以不可以化成有限小数;
的分母含有质因数2和3,所以不可以化成有限小数。
不能化成有限小数的分数:、、,共3个。
故答案为:B
7.B
【分析】公因数:两个数公共的因数。最大公因数:两个数公因数中最大的。
公倍数:两个数公有的倍数。最小公倍数:两个数公倍数中最小的。
可利用列举法,将两个数的因数和倍数一一列举,从而找出公因数和最大公因数,公倍数和最小公倍数。求最大公因数和最小公倍数时,也可以将这两个数分别分解质因数,公有质因数的乘积是这两个数的最大公因数,公有质因数和独有质因数的乘积是这两个数的最小公倍数。
据此,先找出16和12的公因数、公倍数、最大公因数和最小公倍数,再判断96是什么即可。
【详解】A.16的因数有1、2、4、8、16,12的因数有1、2、3、4、6、12,那么16和12的公因数有1、2、4;
B.16的倍数有16、32、48、64、80、96……,12的倍数有12、24、36、48、60、72、84、96……,所以16和12的公倍数有48、96……;
C.根据A选项的分析可知,16和12的最大公因数是4;
D.根据B选项的分析可知,16和12的最小公倍数是48;
所以,96是16和12的公倍数。
故答案为:B
8.B
【分析】长方体的高增加4厘米后,增加的表面积实际上是一个长方体长a厘米,宽b厘米,高为4厘米的四个侧面的面积,即两个长为a厘米,宽为4厘米的长方形和两个长为b厘米,宽为4厘米的长方形,根据长方形的面积=长×宽,代入数据计算,即可求出表面积增加了多少平方厘米,据此解答。
【详解】由分析得:
a×4×2+b×4×2=(8a+8b)平方厘米
即表面积比原来增加(8a+8b)平方厘米。
故答案为:B
9. 3/5 13/11 5/7/11 19/17/13
【分析】质数是指只能被1和它本身整除的数,在24以内的质数有:2、3、5、7、11、13、17、19、23。据此可计算得出答案。
【详解】16=3+13,16=5+11;24=5+19,24=7+17,24=11+13。
10.36;15;7.5;1.2
【分析】根据分数的基本性质,将的分子和分母同时乘6,可得=;将的分子和分母同时乘3,可得=;根据分数与除法的关系,可得=18÷15,根据商不变性质,将18÷15的被除数和除数同时除以2,可得18÷15=9÷7.5;分数化成小数:用分子除以分母,按照除数是整数的小数除法进行计算,据此可得=1.2。
【详解】===9÷7.5=1.2
11.;0.5
【分析】根据分数的意义,把整个图形看作单位“1”,平均分成4份,每份用分数表示为;涂色部分占其中的2份,用分数表示为,化简后是;再把分数化成小数,用分子除以分母即可。
【详解】=
=1÷2=0.5
涂色部分占整个图形的,写成小数是0.5。
12.160
【分析】因为涂色的两个面一个是长方体的左面(宽×高),一个是底面(长×宽),这两个面面积之和是60平方厘米,而长是8厘米,高是4厘米。我们可以先算出长和高的和:8+4=12(厘米)。然后用两个面的面积和除长和高的和,就可以得到长方体的宽,即60÷12=5(厘米),最后根据长方体体积公式V=长×宽×高求出体积。
【详解】长和高的和为:8+4=12(厘米)
长方体的宽为:60÷12=5(厘米)
长方体体积为:
8×5×4
=40×4
=160(立方厘米)
这个长方体的体积是160立方厘米。
13.76
【分析】求铁丝长度相当于求长方体棱长总和,长方体上下两个面完全一样,上下两个面共8条棱,铁丝长度=底面周长×2+高×4,据此列式计算。
【详解】28×2+5×4
=56+20
=76(cm)
至少需要76cm的铁丝。
14. 1 35
【分析】根据题意,a与b都是一位数,且都是质数,由a+b=12,可知5+7=12,由此确定a、b的值,且a与b是互质数;
根据“当两个数是互质数时,它们的最大公因数是1,最小公倍数是两数的乘积”,求出a与b的最大公因数和最小公倍数。
【详解】5+7=12,5、7都是一位数,且都是质数;
所以a=5,b=7或a=7,b=5;
5和7的最大公因数是1,最小公倍数是5×7=35;
那么a与b的最大公因数是1,最小公倍数是35。
15.90
【分析】根据题意可知,一刀增加2个面,已知表面积之和增加了18平方分米,说明2个正方形面的面积是18平方分米,用18÷2即可求出1个正方形面的面积,再根据正方体的表面积=棱长×棱长×6,求出1个小正方体的表面积,进而求出2个小正方体的表面积,然后减去18平方分米即可。
【详解】18÷2=9(平方分米)
9×6×2
=54×2
=108(平方分米)
108-18=90(平方分米)
原来长方体的表面积是90平方分米。
16. 240 420
【分析】从0、2、4、5四张数字中选出三个组成一个三位数,这个三位数是2和5的倍数,那么这个三位数的个位一定是0;同时又是3的倍数,则这个三位数的各位上的数字之和是3的倍数;据此得出这个三位数。
【详解】从0、2、4、5四张数字中选出三个,组成一个既是2和3的倍数,又有因数5的数,可以是240或420。(答案不唯一)
17.48;10;216;;
1.2;100;60;;
【详解】略
18.2;1;
【分析】(1)利用加法交换律和结合律进行简便计算;
(2)利用减法的性质进行简便计算;
(3)先算小括号里的减法,再算括号外的减法。
【详解】
19.x=6;x=3;x=
【分析】9x-18=36,根据等式的性质1,方程两边同时加上18,再根据等式的性质2,方程两边同时除以9即可;
1.6x+2.9x=13.5,先化简方程左边含有x的算式,即求出1.6+2.9的和,再根据等式的性质2,方程两边同时除以1.6+2.9的和即可;
x-(+)=,先计算出+的和,再根据等式的性质1,方程两边同时加上(+)的和即可。
【详解】9x-18=36
解:9x-18+18=36+18
9x=54
9x÷9=54÷9
x=6
1.6x+2.9x=13.5
解:4.5x=13.5
4.5x÷4.5=13.5÷4.5
x=3
x-(+)=
解:x-(+)=
x-=
x-+=+
x=+
x=
20.232cm3
【分析】求图形的体积,用长8cm,宽5cm,高6cm的长方体体积减去棱长为2cm的正方体体积;根据长方体和体积=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数值计算分别计算出长方体的体积和正方体的体积,再相减即可解答。
【详解】8×5×6-2×2×2
=40×6-4×2
=240-8
=232(cm3)
图形的体积是232cm3。
21.6厘米;12个
图见详解
【分析】(1)根据题意,求裁的正方形边长尽可能大,就是求24和18的最大公因数,根据求最大公因数的方法:两个数的公有质因数的连乘积,据此求出正方形的边长;再分别求出长方形画纸的长边、宽边含有的小正方形画纸的块数,再把两个数相乘即可求出可以需要的小正方形画纸的块数。
【详解】24=2×2×2×3
18=2×3×3
24和18的最大公因数是2×3=6;裁得的正方形的边长是6厘米。
(24÷6)×(18÷6)
=4×3
=12(个)
如图:
答:裁得的正方形画纸边长最长是6厘米,可以裁出12个这样的正方形画纸。
22.
【分析】把A、B两地的距离看做单位“1”,当货车行了全程的,轿车行了全程的时,因为与的和大于1,说明货车与轿车相遇后分别继续向前行驶,那么货车、轿车间的距离等于全程的与全程的的和再减去1,据此解答。
【详解】+-1
=+-1
=-1
=
答:这时货车、轿车间的距离占全程的。
23.53.7平方分米
【分析】这个募捐箱的表面积等于正方体的表面积减去长1分米,宽3厘米的长方形的面积,根据正方体的表面积=棱长×棱长×6,长方形的面积=长×宽,代入数据解答即可。
【详解】3×3×6=54(平方分米)
3厘米=0.3分米
1×0.3=0.3(平方分米)
54-0.3=53.7(平方分米)
答:这个募捐箱的表面积是53.7平方分米。
24.(1)经过训练,他们所用的时间整体来看在逐渐减少,说明跑步速度有很大提升。
(2)提问:彬彬第几周进步最大?第八周进步最大。(答案不唯一)
(3)我会选择彬彬参赛,因为经过训练,彬彬的进步更大一些。(答案不唯一)
【分析】(1)根据统计图可得,彬彬和亮亮所用时间的整体趋势都是在逐渐减少的,用时缩短了,速度就提高了,所以训练效果较好。
(2)根据折线统计图的特点,线段越陡变化速度越快,可提问彬彬第几周进步最大。
(3)可根据二人训练前后的进步情况进行选择,答案不唯一,合理即可。
【详解】(1)经过训练,他们所用的时间整体来看在逐渐减少,说明跑步速度有很大提升。
(2)提问:彬彬第几周进步最大?(答案不唯一)
第二周:25-24=1(秒)
第三周:24-23=1(秒)
第五周:24-22=2(秒)
第六周:22-21=1(秒)
第八周:22-19=3(秒)
3>2>1
答:彬彬第八周进步最大。
(3)我会选择彬彬参赛,因为经过训练,彬彬的进步更大一些。(答案不唯一)
25.千米
【分析】根据题意,第二天修的千米数=第一天修的千米数-,则两天一共修的千米数=第一天修的千米数+第二天修的千米数。
【详解】
=
=(千米)
答:两天共修路千米。
26.(1)275厘米
(2)5400平方厘米
(30)A;理由见详解
【分析】(1)根据题意,用丝带包扎棱长为30厘米的正方体礼品盒,观察图形可知,包扎这个礼品盒至少需要丝带的长度=8条棱长+打结用的长度,据此解答。
(2)求做这个正方体包装盒,至少需要纸板的面积,就是求正方体的表面积;根据正方体的表面积公式S=6a2,代入数据计算求解。
(3)蛋糕的长、宽、高要比正方体包装盒的棱长小,才能放进去;把A、B两种蛋糕的长、宽、高与正方体的棱长进行比较,据此解答。
【详解】(1)30×8+35
=240+35
=275(厘米)
答:包扎这个礼品盒一共需要彩带275厘米。
(2)30×30×6
=900×6
=5400(平方厘米)
答:至少需要5400平方厘米纸板。
(3)A:20<30,25<30,26<30;
B:30=30,32>30,5<30;
答:红红买的是A规格蛋糕。因为蛋糕需放进盒子里,所以蛋糕的长、宽、高要比正方体纸盒的棱长小,A规格蛋糕符合要求,而B规格蛋糕中32>30,不能放进盒子里。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
