北师大版六年级上册数学总复习——圆(二) 课件(共32张PPT)
文档属性
| 名称 | 北师大版六年级上册数学总复习——圆(二) 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 13:02:14 | ||
图片预览











文档简介
(共32张PPT)
1、一个半圆的半径是12厘米,它的周长是多少厘米?
3.14×82 ÷2= 100.48(平方厘米)
41.12÷5.14 = 8(厘米)
答:它的面积是100.48平方厘米。
复习:
2、一个半圆的周长是41.12厘米,它的面积是多少平方厘米?
2×3.14×12÷2 = 37.68(厘米)
37.68+12×2 = 61.68(厘米)
或:5.14×12= 61.68(厘米)
答:它的周长是61.68厘米。
总复习
圆(二)
小学 / 数学 / 北师大版 / 六年级上册
一、圆的特征
1、圆:一条曲线围成的封闭图形
2、圆(本质特征):圆上各点到定点的距离(半径)都相等
二、圆的画法
直径d
半径r
圆心 O
知识整理:
三、圆各部分的名称
圆的相关概念:圆心,半径,直径
圆心:固定的一点叫做圆心,通常用字母“O”来表示
半径:圆心到圆上任意一点的距离叫半径,通常用字母“r”表示
直径:通过圆心并且两端都在圆上的线段,叫做直径,直径通常用字母“d”表示
知识整理:
圆心的位置确定圆的位置;圆的半径决定了圆的大小
知识整理:
轴对称图形:如果一个图形沿着一条直线对折后两边完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴
对称轴两侧相对的点到对称轴的距离相等
圆是轴对称图形
1、 找圆心的方法:把圆对折,再对折,两条折痕的交点就是圆心。
2、 圆的轴对称性
圆是轴对称图形,直径所在的直线是圆的对称轴。圆有无数条对称轴。
正方形有4条对称轴,等边三角形有三条对称轴。
知识整理:
如下图,将一个圆沿直径切割成若干份后拼成一个近似的长方形,周长增加12厘米,原来圆形的面积是多少平方厘米?
半径:12÷2=6(厘米)
面积: 3.14×62
=3.14×36
=113.04(平方厘米)
答:原来圆形的面积是113.04平方厘米。
典型分析:
如下图,将一个圆沿直径切割成若干份后拼成一个近似的长方形,周长增加20厘米,原来圆形的面积是多少平方厘米?
半径:20÷2=10(厘米)
面积: 3.14×102
=3.14×100
=314(平方厘米)
答:原来圆形的面积是314平方厘米。
练一练:
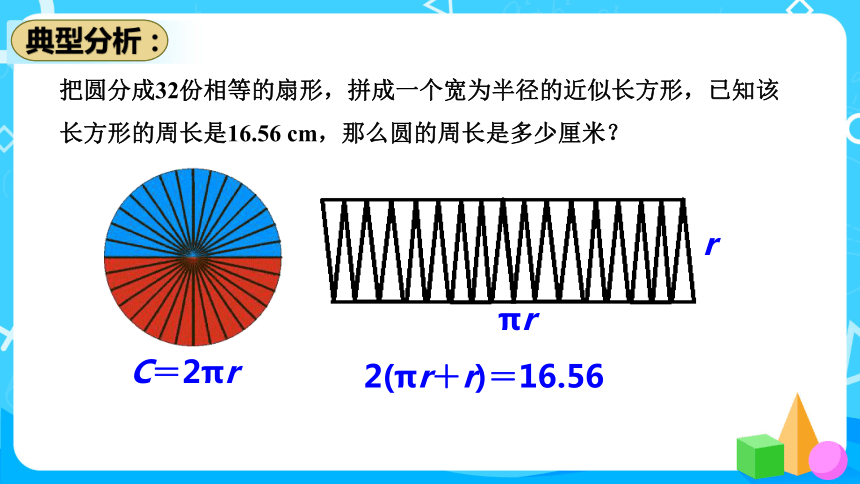
把圆分成32份相等的扇形,拼成一个宽为半径的近似长方形,已知该
长方形的周长是16.56 cm,那么圆的周长是多少厘米?
r
πr
2(πr+r)=16.56
C=2πr
典型分析:
解:设圆的半径为r cm。
把圆分成32份相等的扇形,拼成一个宽为半径的近似长方形,已知该
长方形的周长是16.56 cm,那么圆的周长是多少厘米?
2(3.14r+r)=16.56
2×3.14×2=12.56(cm)
答:那么圆的周长是12.56厘米。
典型分析:
6.28r+2r=16.56
8.28r= 16.56
r= 2
一根铁丝长37.68米,在一根圆形木棒上正好绕200圈,木棒横截面的半径是多少厘米?木棒横截面的面积是多少?
37.68÷200=0.1884(米)
0.1884米=18.84厘米
18.84÷3.14=6(厘米)
答:木棒横截面的半径是3厘米。
6÷2=3(厘米)
3.14×32=28.26(平方厘米)
答:木棒横截面的面积是28.26平方厘米。
典型分析:
把4个直径是10 cm的圆柱形酒精瓶子捆扎在一起,截面如图所示,
捆扎一圈需要绳子多少厘米?(接头处不计)
3.14×10+10×4=71.4(cm)
典型分析:
3.14×20÷2=31.4(cm)
如图,等边三角形空白部分是三个相同的扇形,等边三角形的边长
是20 cm。阴影部分的周长是多少厘米?
圆周长的一半
转化
典型分析:
剪拼
3.14×12+12×2=61.68(cm)
2.求阴影部分的周长。
阴影部分的周长
=直径12cm的圆周长+正方形的2个边长
典型分析:
设数
如图,甲、乙两只小虫同时从A点出发,分别沿两条不同的路线爬向B点。
若甲、乙两只小虫的速度相同,甲、乙两只小虫谁先爬到B点?
d1
d2
d3
d1+d2=d3
甲的路程:(πd3)÷2
乙的路程: (πd1+πd2)÷2= π (d1+d2)÷2
甲的路程=乙的路程
甲、乙两只小虫同时爬到B点
典型分析:
解:设中半圆的直径是4 cm,小半圆的直径是2 cm,
则大半圆的直径是4+2=6(cm)
如图,甲、乙两只小虫同时从A点出发,分别沿两条不同的路线爬向B点。
若甲、乙两只小虫的速度相同,甲、乙两只小虫谁先爬到B点?
甲所爬的路程:3.14×6÷2=9.42(cm)
乙所爬的路程:3.14×4÷2+3.14×2÷2=9.42(cm)
9.42=9.42
甲、乙两只小虫同时爬到B点。
典型分析:
逆推
一个半圆形的周长是20.56 cm,它的半径是多少厘米?
20.56÷(3.14+2)=4(cm)
πr+2r = 半圆形的周长
r(π+2) = 半圆形的周长
r =半圆形的周长÷(π+2)
典型分析:
求下图中阴影部分的周长和面积。(单位:dm)
周长: 3.14×4÷2+3.14×(4+1+1)÷2+1×2
=6.28+9.42+2
=17.7(dm)
面积:4÷2=2(dm) 2+1=3(dm)
3.14×(32-22)÷2=7.85(dm2)
典型分析:
下图中的阴影部分的面积是20平方厘米,图中圆环的面积是多少?
阴影部分的是大正方形面积减去小正方形面积。
大正方形边长是圆环的大半径。
小正方形边长是圆环的小半径。
R2-r =20
S环=π(R2-r )
3.14×20=62.8(平方厘米)
典型分析:
如图,阴影部分的面积是90 cm2,环形的面积是多少平方厘米?
设大圆的半径为R cm,小圆的半径为r cm。
R2÷2-r2÷2=90 R2-r2=180
3.14×180=565.2(cm2)
典型分析:
1、下图中大圆的周长是37.68厘米,环宽是2厘米,求圆环的面积。
2、下图中阴影部分的面积是12平方厘米,求圆环的面积。
课堂练习:
37.68÷3.14÷2=6(厘米)
6-2=4(厘米)
3.14×(6 -4 )
=3.14×20
=62.8(平方厘米)
3.14×12=37.68(平方厘米)
选择题
1.广场有一个直径为8m的圆形喷水池,喷水池周边有一条2m宽的小路,这条小路的面积是( )平方米。
A.50.24 B. 12.56 C.65.94 D.62.8
2.在同一个圆中,周长是直径的( )倍。
A.3 B.3.14 C.π D.2π
D
C
综合练习:
3.如图,从点A到点B有甲、乙、丙三条路线,每条路线都是由一个或两个半圆组成的。比较这三条路线的长度,你认为( )。
选择题
A.甲最长 B.乙最长
C.丙最长 D.三条路线长度相等
4.在正方形里画一个最大的圆,圆的周长是正方形周长的( )。
D
D
设圆的直径是d,则正方形的边长是d。
C圆=πd
C正=4d
πd÷4d=
综合练习:
5.推导圆面积公式时,把一个圆分成若干等份,拼成一个平行四边形,这个平行四边形的周长是( )。
A.2πr B.πr+r C.2πr+2r D.πr+2r
6.一个挂钟的时针长5厘米,分针长8厘米,从12时到6时,时针针尖走过的距离是( )厘米。
A.10π B.16π C.5π D.8π
C
A
综合练习:
7.下列图形中,空白部分与阴影部分的周长相等,但面积不相等的图形是( )。
8.下列各图,没有运用“转化”方法的是( )。
B
B
综合练习:
判断题
1.一个圆的周长总是它直径的3.14倍。( )
2.把一个圆平均分成两个半圆,每个半圆的周长是原来整圆周长的一半。( )
3.圆的直径增加1m,则周长增加πm.( )
4.两个圆的半径之比是2:3,它们的周长的比也是2:3。( )
5.半径是4厘米的半圆,它的周长是16.56厘米。( )。
×
×
√
√
×
综合练习:
判断题
1.圆的周长比正方形的周长大,则圆的面积也比正方形的面积大。( )
2.妙想用三根同样长的铁丝分别围成长方形、正方形和圆,长方形的面积最大。( )
3.如图中正方形的面积是10cm2,则圆的面积是31.4cm2。( )
4.用两根长都是18.84cm的铁丝分别围成一个圆和一个正方形,它们的面积相等(铁丝均无剩余)。( )
5.圆中过圆心的线段叫做直径。( )
√
×
√
×
×
综合练习:
判断。
(1)半径为2厘米的圆,它的周长和面积相等。 ( )
(2)两个圆的周长相等,面积也一定相等。 ( )
(3)圆的半径越长,圆面积就越大。 ( )
(4)圆的半径扩大3倍,它的面积扩大6倍。 ( )
(5)两个圆的半径比是3∶4,则面积比是9∶16。( )
×
√
√
×
√
综合练习:
如图,一个长方形的院子,院外长满了青草,在长方形的院墙的墙角处栓着一只羊,如果绳子长8米,这只羊吃草的面积最多是多少平方米?
3.14×8 ×=150.72(平方米)
8-6=2(米)
3.14×2 ×=3.14(平方米)
150.72+3.14=153.86(平方米)
答:这只羊吃草的面积最多是153.86平方米。
课堂练习:
一个运动场如下图,两端是半圆形,中间是长方形。已知长方形的长是100米,圆的半径是32米。这个运动场的面积是多少平方米?
3.14×32 =3215.36(平方米)
3215.36+6400=9615.36(平方米)
100×(32×2)=6400(平方米)
答:这个运动场的面积是9615.36平方米。
课堂练习:
下图中黄色部分的直径是10米,大圆的直径是18米,绿色部分的面积是多少?
18÷2=9(米)
3.14×(9 -5 )
10÷2=5(米)
=3.14×56
=175.84(平方米)
课堂练习:
布置作业:
练习册:78页
1、一个半圆的半径是12厘米,它的周长是多少厘米?
3.14×82 ÷2= 100.48(平方厘米)
41.12÷5.14 = 8(厘米)
答:它的面积是100.48平方厘米。
复习:
2、一个半圆的周长是41.12厘米,它的面积是多少平方厘米?
2×3.14×12÷2 = 37.68(厘米)
37.68+12×2 = 61.68(厘米)
或:5.14×12= 61.68(厘米)
答:它的周长是61.68厘米。
总复习
圆(二)
小学 / 数学 / 北师大版 / 六年级上册
一、圆的特征
1、圆:一条曲线围成的封闭图形
2、圆(本质特征):圆上各点到定点的距离(半径)都相等
二、圆的画法
直径d
半径r
圆心 O
知识整理:
三、圆各部分的名称
圆的相关概念:圆心,半径,直径
圆心:固定的一点叫做圆心,通常用字母“O”来表示
半径:圆心到圆上任意一点的距离叫半径,通常用字母“r”表示
直径:通过圆心并且两端都在圆上的线段,叫做直径,直径通常用字母“d”表示
知识整理:
圆心的位置确定圆的位置;圆的半径决定了圆的大小
知识整理:
轴对称图形:如果一个图形沿着一条直线对折后两边完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴
对称轴两侧相对的点到对称轴的距离相等
圆是轴对称图形
1、 找圆心的方法:把圆对折,再对折,两条折痕的交点就是圆心。
2、 圆的轴对称性
圆是轴对称图形,直径所在的直线是圆的对称轴。圆有无数条对称轴。
正方形有4条对称轴,等边三角形有三条对称轴。
知识整理:
如下图,将一个圆沿直径切割成若干份后拼成一个近似的长方形,周长增加12厘米,原来圆形的面积是多少平方厘米?
半径:12÷2=6(厘米)
面积: 3.14×62
=3.14×36
=113.04(平方厘米)
答:原来圆形的面积是113.04平方厘米。
典型分析:
如下图,将一个圆沿直径切割成若干份后拼成一个近似的长方形,周长增加20厘米,原来圆形的面积是多少平方厘米?
半径:20÷2=10(厘米)
面积: 3.14×102
=3.14×100
=314(平方厘米)
答:原来圆形的面积是314平方厘米。
练一练:
把圆分成32份相等的扇形,拼成一个宽为半径的近似长方形,已知该
长方形的周长是16.56 cm,那么圆的周长是多少厘米?
r
πr
2(πr+r)=16.56
C=2πr
典型分析:
解:设圆的半径为r cm。
把圆分成32份相等的扇形,拼成一个宽为半径的近似长方形,已知该
长方形的周长是16.56 cm,那么圆的周长是多少厘米?
2(3.14r+r)=16.56
2×3.14×2=12.56(cm)
答:那么圆的周长是12.56厘米。
典型分析:
6.28r+2r=16.56
8.28r= 16.56
r= 2
一根铁丝长37.68米,在一根圆形木棒上正好绕200圈,木棒横截面的半径是多少厘米?木棒横截面的面积是多少?
37.68÷200=0.1884(米)
0.1884米=18.84厘米
18.84÷3.14=6(厘米)
答:木棒横截面的半径是3厘米。
6÷2=3(厘米)
3.14×32=28.26(平方厘米)
答:木棒横截面的面积是28.26平方厘米。
典型分析:
把4个直径是10 cm的圆柱形酒精瓶子捆扎在一起,截面如图所示,
捆扎一圈需要绳子多少厘米?(接头处不计)
3.14×10+10×4=71.4(cm)
典型分析:
3.14×20÷2=31.4(cm)
如图,等边三角形空白部分是三个相同的扇形,等边三角形的边长
是20 cm。阴影部分的周长是多少厘米?
圆周长的一半
转化
典型分析:
剪拼
3.14×12+12×2=61.68(cm)
2.求阴影部分的周长。
阴影部分的周长
=直径12cm的圆周长+正方形的2个边长
典型分析:
设数
如图,甲、乙两只小虫同时从A点出发,分别沿两条不同的路线爬向B点。
若甲、乙两只小虫的速度相同,甲、乙两只小虫谁先爬到B点?
d1
d2
d3
d1+d2=d3
甲的路程:(πd3)÷2
乙的路程: (πd1+πd2)÷2= π (d1+d2)÷2
甲的路程=乙的路程
甲、乙两只小虫同时爬到B点
典型分析:
解:设中半圆的直径是4 cm,小半圆的直径是2 cm,
则大半圆的直径是4+2=6(cm)
如图,甲、乙两只小虫同时从A点出发,分别沿两条不同的路线爬向B点。
若甲、乙两只小虫的速度相同,甲、乙两只小虫谁先爬到B点?
甲所爬的路程:3.14×6÷2=9.42(cm)
乙所爬的路程:3.14×4÷2+3.14×2÷2=9.42(cm)
9.42=9.42
甲、乙两只小虫同时爬到B点。
典型分析:
逆推
一个半圆形的周长是20.56 cm,它的半径是多少厘米?
20.56÷(3.14+2)=4(cm)
πr+2r = 半圆形的周长
r(π+2) = 半圆形的周长
r =半圆形的周长÷(π+2)
典型分析:
求下图中阴影部分的周长和面积。(单位:dm)
周长: 3.14×4÷2+3.14×(4+1+1)÷2+1×2
=6.28+9.42+2
=17.7(dm)
面积:4÷2=2(dm) 2+1=3(dm)
3.14×(32-22)÷2=7.85(dm2)
典型分析:
下图中的阴影部分的面积是20平方厘米,图中圆环的面积是多少?
阴影部分的是大正方形面积减去小正方形面积。
大正方形边长是圆环的大半径。
小正方形边长是圆环的小半径。
R2-r =20
S环=π(R2-r )
3.14×20=62.8(平方厘米)
典型分析:
如图,阴影部分的面积是90 cm2,环形的面积是多少平方厘米?
设大圆的半径为R cm,小圆的半径为r cm。
R2÷2-r2÷2=90 R2-r2=180
3.14×180=565.2(cm2)
典型分析:
1、下图中大圆的周长是37.68厘米,环宽是2厘米,求圆环的面积。
2、下图中阴影部分的面积是12平方厘米,求圆环的面积。
课堂练习:
37.68÷3.14÷2=6(厘米)
6-2=4(厘米)
3.14×(6 -4 )
=3.14×20
=62.8(平方厘米)
3.14×12=37.68(平方厘米)
选择题
1.广场有一个直径为8m的圆形喷水池,喷水池周边有一条2m宽的小路,这条小路的面积是( )平方米。
A.50.24 B. 12.56 C.65.94 D.62.8
2.在同一个圆中,周长是直径的( )倍。
A.3 B.3.14 C.π D.2π
D
C
综合练习:
3.如图,从点A到点B有甲、乙、丙三条路线,每条路线都是由一个或两个半圆组成的。比较这三条路线的长度,你认为( )。
选择题
A.甲最长 B.乙最长
C.丙最长 D.三条路线长度相等
4.在正方形里画一个最大的圆,圆的周长是正方形周长的( )。
D
D
设圆的直径是d,则正方形的边长是d。
C圆=πd
C正=4d
πd÷4d=
综合练习:
5.推导圆面积公式时,把一个圆分成若干等份,拼成一个平行四边形,这个平行四边形的周长是( )。
A.2πr B.πr+r C.2πr+2r D.πr+2r
6.一个挂钟的时针长5厘米,分针长8厘米,从12时到6时,时针针尖走过的距离是( )厘米。
A.10π B.16π C.5π D.8π
C
A
综合练习:
7.下列图形中,空白部分与阴影部分的周长相等,但面积不相等的图形是( )。
8.下列各图,没有运用“转化”方法的是( )。
B
B
综合练习:
判断题
1.一个圆的周长总是它直径的3.14倍。( )
2.把一个圆平均分成两个半圆,每个半圆的周长是原来整圆周长的一半。( )
3.圆的直径增加1m,则周长增加πm.( )
4.两个圆的半径之比是2:3,它们的周长的比也是2:3。( )
5.半径是4厘米的半圆,它的周长是16.56厘米。( )。
×
×
√
√
×
综合练习:
判断题
1.圆的周长比正方形的周长大,则圆的面积也比正方形的面积大。( )
2.妙想用三根同样长的铁丝分别围成长方形、正方形和圆,长方形的面积最大。( )
3.如图中正方形的面积是10cm2,则圆的面积是31.4cm2。( )
4.用两根长都是18.84cm的铁丝分别围成一个圆和一个正方形,它们的面积相等(铁丝均无剩余)。( )
5.圆中过圆心的线段叫做直径。( )
√
×
√
×
×
综合练习:
判断。
(1)半径为2厘米的圆,它的周长和面积相等。 ( )
(2)两个圆的周长相等,面积也一定相等。 ( )
(3)圆的半径越长,圆面积就越大。 ( )
(4)圆的半径扩大3倍,它的面积扩大6倍。 ( )
(5)两个圆的半径比是3∶4,则面积比是9∶16。( )
×
√
√
×
√
综合练习:
如图,一个长方形的院子,院外长满了青草,在长方形的院墙的墙角处栓着一只羊,如果绳子长8米,这只羊吃草的面积最多是多少平方米?
3.14×8 ×=150.72(平方米)
8-6=2(米)
3.14×2 ×=3.14(平方米)
150.72+3.14=153.86(平方米)
答:这只羊吃草的面积最多是153.86平方米。
课堂练习:
一个运动场如下图,两端是半圆形,中间是长方形。已知长方形的长是100米,圆的半径是32米。这个运动场的面积是多少平方米?
3.14×32 =3215.36(平方米)
3215.36+6400=9615.36(平方米)
100×(32×2)=6400(平方米)
答:这个运动场的面积是9615.36平方米。
课堂练习:
下图中黄色部分的直径是10米,大圆的直径是18米,绿色部分的面积是多少?
18÷2=9(米)
3.14×(9 -5 )
10÷2=5(米)
=3.14×56
=175.84(平方米)
课堂练习:
布置作业:
练习册:78页
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
