2025年山东省潍坊市中考数学五模试卷(含答案)
文档属性
| 名称 | 2025年山东省潍坊市中考数学五模试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 156.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 17:55:03 | ||
图片预览




文档简介
2025年山东省潍坊市中考数学五模试卷
一、选择题:本题共6小题,每小题4分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各数中,是负数的是( )
A. B. C. D.
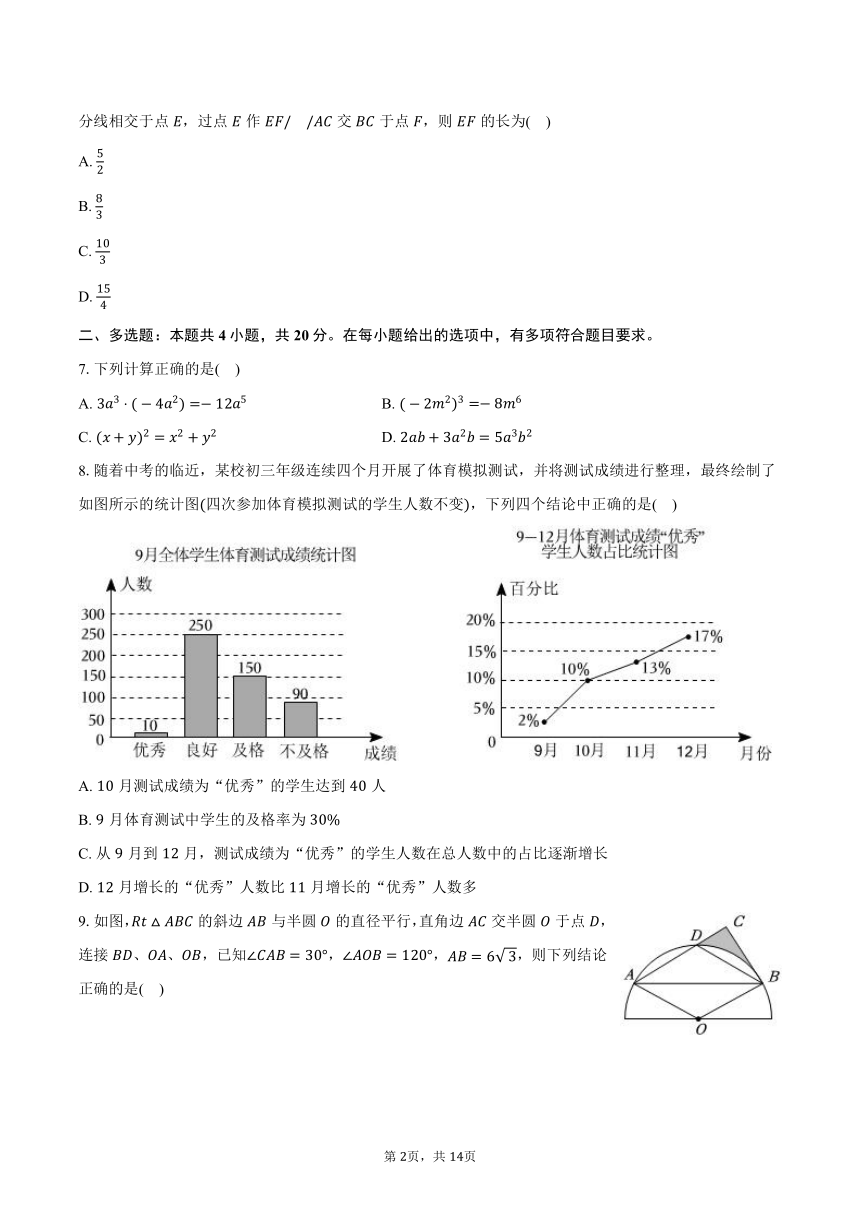
2.如图,将矩形纸片沿虚线按箭头方向向右对折,再将对折后的纸片沿虚线向下对折,然后剪下一个小三角形,再把纸片打开,打开后的展开图为( )
A. B. C. D.
3.在平面直角坐标系中,将抛物线:为常数,且沿轴向上平移个单位,得到抛物线,则抛物线的顶点一定在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4.九章算术中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到里远的城市,所需时间比规定时间多天;若改为快马派送,则所需时间比规定时间少天,已知快马的速度是慢马的倍,求规定时间.设规定时间为天,则下列分式方程正确的是( )
A. B.
C. D.
5.如图,的边经过点且与相交于点,,与相切于点若,则的度数为( )
A.
B.
C.
D.
6.如图,在中,,,,、的平分线相交于点,过点作交于点,则的长为( )
A.
B.
C.
D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
7.下列计算正确的是( )
A. B.
C. D.
8.随着中考的临近,某校初三年级连续四个月开展了体育模拟测试,并将测试成绩进行整理,最终绘制了如图所示的统计图四次参加体育模拟测试的学生人数不变,下列四个结论中正确的是( )
A. 月测试成绩为“优秀”的学生达到人
B. 月体育测试中学生的及格率为
C. 从月到月,测试成绩为“优秀”的学生人数在总人数中的占比逐渐增长
D. 月增长的“优秀”人数比月增长的“优秀”人数多
9.如图,的斜边与半圆的直径平行,直角边交半圆于点,连接、、,已知,,,则下列结论正确的是( )
A. 与半圆相切 B. 四边形为菱形
C. 的弧长为 D. 阴影区域的面积为
10.如图,为矩形的边上一点,动点,同时从点出发,点沿折线运动到点时停止,点沿运动到点时停止,它们运动的速度都是设,同时出发秒时,的面积为已知与的函数关系图象如图曲线为抛物线的一部分,下列结论正确的是( )
A. B. 点的坐标为
C. 当时,的面积为 D. 当时,与相似
三、填空题:本题共4小题,每小题4分,共16分。
11.清代诗人袁枚创作了一首诗苔:“白日不到处,青春恰自来苔花如米小,也学牡丹开”歌颂了苔在恶劣环境下仍有自己的生命意向若苔花的花粉粒直径约为米,用科学记数法表示为______.
12.当 ______时,解分式方程会出现增根.
13.如图,在平面直角坐标系中,点是轴上一动点,点是直线上一动点,,,,则的最大值是______.
14.仿照下列式子的规律填空:
第个等式:;
第个等式:;
第个等式:;
第个等式:;
第个等式:______.
四、解答题:本题共8小题,共90分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
计算:;
解不等式组:.
16.本小题分
阅读理解材料:已知实数,满足,,且.
根据材料求的值.
由题知,是方程的两个不相等的实数根,
根据一元二次方程根与系数的关系得,,
.
解决以下问题:
方程的两个实数根为,,则 ______, ______.
已知实数,满足,,且,求的值.
已知实数,满足,,且,求的值.
17.本小题分
某校为了有效提升学生综合素质,同时减轻学生课业负担,决定在全校开展丰富多彩的学生课外活动,经研究确定课外活动类型为体育、社会实践、文化艺术、科技创新和读书共五类项目,并在组织活动前进行了初步调查,调查要求在以上五类项目中只能选一项最感兴趣的一项,现随机抽查了名学生,并将其结果绘制成如下不完整的统计图,请解答下列问题:
直接写出 ______,“社会实践”在扇形统计图中扇形圆心角的度数为______;
补全条形统计图;
已知该校共有名学生,请你估计该校最喜欢读书活动的学生数;
根据统计图中的数据,请你针对课外活动提出一条合理化建议.
18.本小题分
定义:在四边形中,若有一个角是直角,且从这个直角顶点引出的对角线把对角分成的两个角中,有一个是直角,我们称这样的四边形为“双垂四边形”.
如图,在“双垂四边形”中,若,则 ______;
如图,在“双垂四边形”中,,,为线段上一点,,且,求的长.
19.本小题分
如图,是的弦,是的切线,过点作于点,交于点,作直径交于点,连接.
求证:;
若半径长为,,求的长.
20.本小题分
如图,小华想测量银川承天寺塔的高度,他在处仰望塔顶,测得仰角是,再往塔的方向前进米至处,测得仰角为,那么该塔约有多高?小华的身高忽略不计,,结果精确到米
21.本小题分
综合与探究
已知反比例函数点和点在该反比例函数的图象上点在点的左侧,过点分别作轴、轴的垂线,垂足分别为、;过点分别作轴、轴的垂线,垂足分别为,;与相交于点,连接,.
如图,若点的横坐标是,点的横坐标是,则点的坐标为______,点的坐标为______.
如图,点是反比例函数图象上任意一点,,则,若,试判断与的数量关系和位置关系,并说明理由.
若点的横坐标是点的横坐标的倍,直接写出的值用含的代数式表示.
22.本小题分
如图,在平面直角坐标系中,二次函数的图象记为与轴交于点,,与轴交于点,二次函数的图象记为经过点,直线与两个图象,分别交于点,,与轴交于点.
求,的值.
当点在线段上时,求的最大值.
设点,到直线的距离分别为,当时,对应的值有______个;当时,对应的值有______个;当时,对应的值有______个;当时,对应的值有______个
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【解析】原式
.
,
解不等式得,,
解不等式得,,
所以不等式组的解集为:.
16.【解析】方程的两个实数根为,,
,;
故答案为:,;
,,且,
、可看作方程的两根,
,,
,
;
,
,
,
,
即,
、可看作方程的两根,
,,
.
17.【解析】,
,
故答案为:,;
选择“社会实践”的学生人数为人,
补全条形统计图如下:
人,
答:估计该校最喜欢读书活动的学生数有人;
由图表可知,参加科技创新的人数较少,我认为学校要加强科技创新的宣传,并提供相应条件,促进科技创新活动的开展.建议有积极意义即可.
18.【解析】,
,
,
故答案为:;
同理可得,,
,,
,
,
又,
,
≌,
.
19.【解析】证明:如图,连接,
是的切线,
,
,
,
,
由圆周角定理得:,,
;
如图,连接,
是的直径,
,
,
,
,
,
,
,
,
,
在中,,
,,
在中,,即,
解得:负值舍去,
,,
∽,
,即,
解得:.
20.【解析】设米,
,,
米,
,,
米,
米,
,
,
米,
答:该塔约有米.
21.【解析】点的横坐标为,
,
,
把代入得:,
,
过点分别作轴、轴的垂线,垂足分别为、;过点分别作轴、轴的垂线,垂足分别为,;与相交于点,
.
故答案为:,;
点是反比例函数图象上任意一点,,,
,,,,
,,
,
,
,,
,
,;
设点,则,,,
,
,
.
22.【解析】二次函数,
令,可得或,
即,,
把,代入中,可得
,解得,
故的值为,的值为;
由知的表达式为,
设,则,,
故,
即的最大值为;
作于点,于点,设交于点,如图所示,
由待定系数法可知直线的表达式为,
,
,
,,
,,
,
,,
即,
进而可得,
当时,
即,故,
当时,,
那么由图可知当时或时,共种情况满足题意,
故对应的值有个;
当时,即,这与相矛盾,故不成立,对应的值有个;
当时,由可知,,
故,
,即,
解得或或或,
故对应的值有个;
当时,
恒成立,
对应的值有无数个.
故答案为:,,,无数.
第11页,共14页
一、选择题:本题共6小题,每小题4分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各数中,是负数的是( )
A. B. C. D.
2.如图,将矩形纸片沿虚线按箭头方向向右对折,再将对折后的纸片沿虚线向下对折,然后剪下一个小三角形,再把纸片打开,打开后的展开图为( )
A. B. C. D.
3.在平面直角坐标系中,将抛物线:为常数,且沿轴向上平移个单位,得到抛物线,则抛物线的顶点一定在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4.九章算术中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到里远的城市,所需时间比规定时间多天;若改为快马派送,则所需时间比规定时间少天,已知快马的速度是慢马的倍,求规定时间.设规定时间为天,则下列分式方程正确的是( )
A. B.
C. D.
5.如图,的边经过点且与相交于点,,与相切于点若,则的度数为( )
A.
B.
C.
D.
6.如图,在中,,,,、的平分线相交于点,过点作交于点,则的长为( )
A.
B.
C.
D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
7.下列计算正确的是( )
A. B.
C. D.
8.随着中考的临近,某校初三年级连续四个月开展了体育模拟测试,并将测试成绩进行整理,最终绘制了如图所示的统计图四次参加体育模拟测试的学生人数不变,下列四个结论中正确的是( )
A. 月测试成绩为“优秀”的学生达到人
B. 月体育测试中学生的及格率为
C. 从月到月,测试成绩为“优秀”的学生人数在总人数中的占比逐渐增长
D. 月增长的“优秀”人数比月增长的“优秀”人数多
9.如图,的斜边与半圆的直径平行,直角边交半圆于点,连接、、,已知,,,则下列结论正确的是( )
A. 与半圆相切 B. 四边形为菱形
C. 的弧长为 D. 阴影区域的面积为
10.如图,为矩形的边上一点,动点,同时从点出发,点沿折线运动到点时停止,点沿运动到点时停止,它们运动的速度都是设,同时出发秒时,的面积为已知与的函数关系图象如图曲线为抛物线的一部分,下列结论正确的是( )
A. B. 点的坐标为
C. 当时,的面积为 D. 当时,与相似
三、填空题:本题共4小题,每小题4分,共16分。
11.清代诗人袁枚创作了一首诗苔:“白日不到处,青春恰自来苔花如米小,也学牡丹开”歌颂了苔在恶劣环境下仍有自己的生命意向若苔花的花粉粒直径约为米,用科学记数法表示为______.
12.当 ______时,解分式方程会出现增根.
13.如图,在平面直角坐标系中,点是轴上一动点,点是直线上一动点,,,,则的最大值是______.
14.仿照下列式子的规律填空:
第个等式:;
第个等式:;
第个等式:;
第个等式:;
第个等式:______.
四、解答题:本题共8小题,共90分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
计算:;
解不等式组:.
16.本小题分
阅读理解材料:已知实数,满足,,且.
根据材料求的值.
由题知,是方程的两个不相等的实数根,
根据一元二次方程根与系数的关系得,,
.
解决以下问题:
方程的两个实数根为,,则 ______, ______.
已知实数,满足,,且,求的值.
已知实数,满足,,且,求的值.
17.本小题分
某校为了有效提升学生综合素质,同时减轻学生课业负担,决定在全校开展丰富多彩的学生课外活动,经研究确定课外活动类型为体育、社会实践、文化艺术、科技创新和读书共五类项目,并在组织活动前进行了初步调查,调查要求在以上五类项目中只能选一项最感兴趣的一项,现随机抽查了名学生,并将其结果绘制成如下不完整的统计图,请解答下列问题:
直接写出 ______,“社会实践”在扇形统计图中扇形圆心角的度数为______;
补全条形统计图;
已知该校共有名学生,请你估计该校最喜欢读书活动的学生数;
根据统计图中的数据,请你针对课外活动提出一条合理化建议.
18.本小题分
定义:在四边形中,若有一个角是直角,且从这个直角顶点引出的对角线把对角分成的两个角中,有一个是直角,我们称这样的四边形为“双垂四边形”.
如图,在“双垂四边形”中,若,则 ______;
如图,在“双垂四边形”中,,,为线段上一点,,且,求的长.
19.本小题分
如图,是的弦,是的切线,过点作于点,交于点,作直径交于点,连接.
求证:;
若半径长为,,求的长.
20.本小题分
如图,小华想测量银川承天寺塔的高度,他在处仰望塔顶,测得仰角是,再往塔的方向前进米至处,测得仰角为,那么该塔约有多高?小华的身高忽略不计,,结果精确到米
21.本小题分
综合与探究
已知反比例函数点和点在该反比例函数的图象上点在点的左侧,过点分别作轴、轴的垂线,垂足分别为、;过点分别作轴、轴的垂线,垂足分别为,;与相交于点,连接,.
如图,若点的横坐标是,点的横坐标是,则点的坐标为______,点的坐标为______.
如图,点是反比例函数图象上任意一点,,则,若,试判断与的数量关系和位置关系,并说明理由.
若点的横坐标是点的横坐标的倍,直接写出的值用含的代数式表示.
22.本小题分
如图,在平面直角坐标系中,二次函数的图象记为与轴交于点,,与轴交于点,二次函数的图象记为经过点,直线与两个图象,分别交于点,,与轴交于点.
求,的值.
当点在线段上时,求的最大值.
设点,到直线的距离分别为,当时,对应的值有______个;当时,对应的值有______个;当时,对应的值有______个;当时,对应的值有______个
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【解析】原式
.
,
解不等式得,,
解不等式得,,
所以不等式组的解集为:.
16.【解析】方程的两个实数根为,,
,;
故答案为:,;
,,且,
、可看作方程的两根,
,,
,
;
,
,
,
,
即,
、可看作方程的两根,
,,
.
17.【解析】,
,
故答案为:,;
选择“社会实践”的学生人数为人,
补全条形统计图如下:
人,
答:估计该校最喜欢读书活动的学生数有人;
由图表可知,参加科技创新的人数较少,我认为学校要加强科技创新的宣传,并提供相应条件,促进科技创新活动的开展.建议有积极意义即可.
18.【解析】,
,
,
故答案为:;
同理可得,,
,,
,
,
又,
,
≌,
.
19.【解析】证明:如图,连接,
是的切线,
,
,
,
,
由圆周角定理得:,,
;
如图,连接,
是的直径,
,
,
,
,
,
,
,
,
,
在中,,
,,
在中,,即,
解得:负值舍去,
,,
∽,
,即,
解得:.
20.【解析】设米,
,,
米,
,,
米,
米,
,
,
米,
答:该塔约有米.
21.【解析】点的横坐标为,
,
,
把代入得:,
,
过点分别作轴、轴的垂线,垂足分别为、;过点分别作轴、轴的垂线,垂足分别为,;与相交于点,
.
故答案为:,;
点是反比例函数图象上任意一点,,,
,,,,
,,
,
,
,,
,
,;
设点,则,,,
,
,
.
22.【解析】二次函数,
令,可得或,
即,,
把,代入中,可得
,解得,
故的值为,的值为;
由知的表达式为,
设,则,,
故,
即的最大值为;
作于点,于点,设交于点,如图所示,
由待定系数法可知直线的表达式为,
,
,
,,
,,
,
,,
即,
进而可得,
当时,
即,故,
当时,,
那么由图可知当时或时,共种情况满足题意,
故对应的值有个;
当时,即,这与相矛盾,故不成立,对应的值有个;
当时,由可知,,
故,
,即,
解得或或或,
故对应的值有个;
当时,
恒成立,
对应的值有无数个.
故答案为:,,,无数.
第11页,共14页
同课章节目录
