2025年浙江省初中中考数学适应性试卷(含答案)
文档属性
| 名称 | 2025年浙江省初中中考数学适应性试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 84.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 20:24:45 | ||
图片预览



文档简介
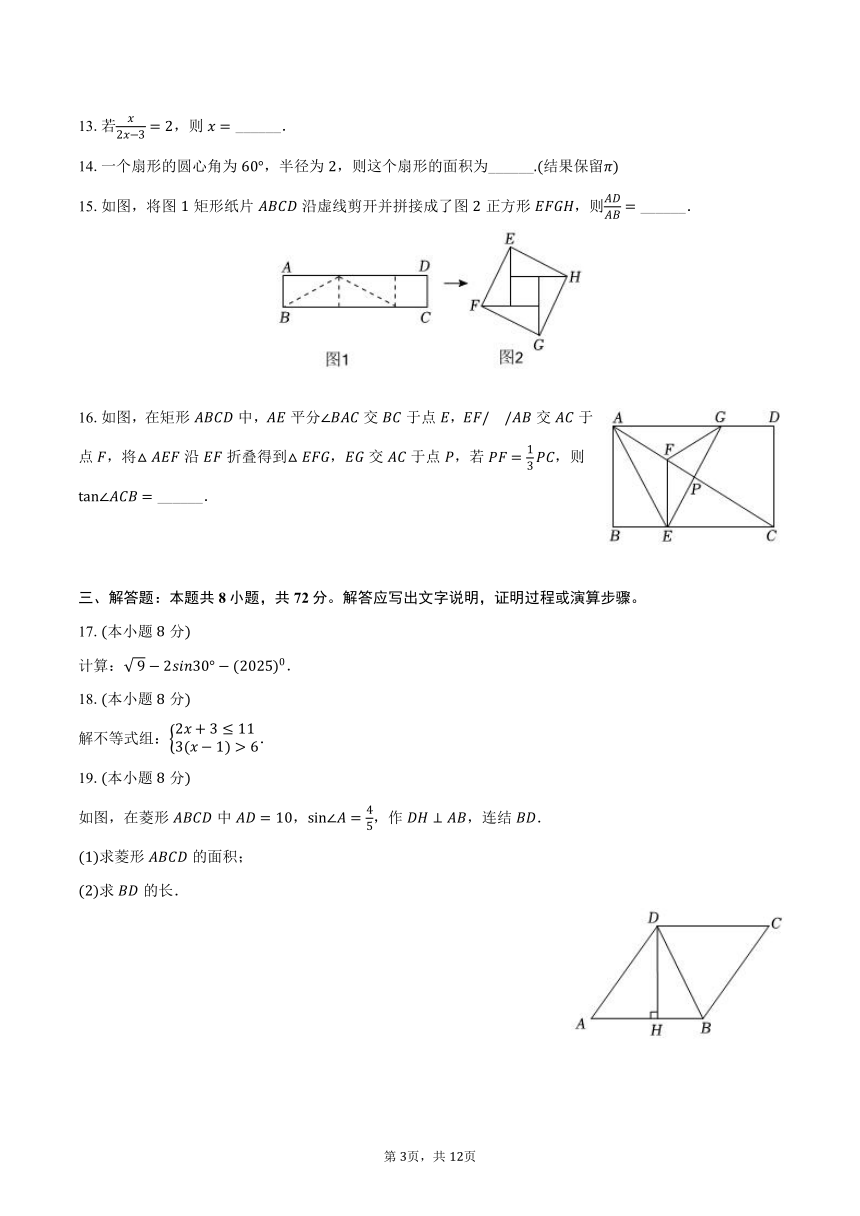
2025年浙江省初中中考数学适应性试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.有,,,四个数,其中最小的数是( )
A. B. C. D.
2.下列计算正确的是( )
A. B. C. D.
3.如图,由个棱长均为的立方体组成的几何体,它的左视图为( )
A. B. C. D.
4.年浙江省总产值为亿元,数用科学记数法可表示为( )
A. B. C. D.
5.如图,,若,则为( )
A. B. C. D.
6.如图所示网格中,线段是由线段位似放大而成,则位似中心是( )
A.
B.
C.
D.
7.某公司招聘技术人员,需对应聘者进行测试,测试项目包括基础知识、操作能力、创新能力,并规定上述三项成绩依次按,,的比例计入总成绩某应聘者的测试成绩统计如下:
项目 基础知识 操作能力 创新能力
成绩
则此应聘者的总成绩是( )
A. B. C. D.
8.端午节是我国的传统佳节,民间历来有吃粽子的习俗端午节期间,某商店对一款粽子推出优惠活动,决定每个粽子打八折,打折后元买到的粽子数量比打折前多了个,设粽子的原价为元个,可列出方程( )
A. B.
C. D.
9.如图,矩形的面积为,点的坐标为,轴,轴,若反比例函数的图象过点、,则的值为( )
A.
B.
C.
D.
10.如图,在等腰中,,,点是斜边的中点,点在上,连结,作于点,连结,则点从点向点移动过程中点不与、重合,角度的大小为( )
A. 由小变大
B. 由大变小
C. 不变
D. 不能确定
二、填空题:本题共6小题,每小题3分,共18分。
11.因式分解: .
12.一个游戏转盘如图所示,红色扇形的圆心角为,让转盘自由转动,当转盘停止时,指针落在红色区域的概率是______.
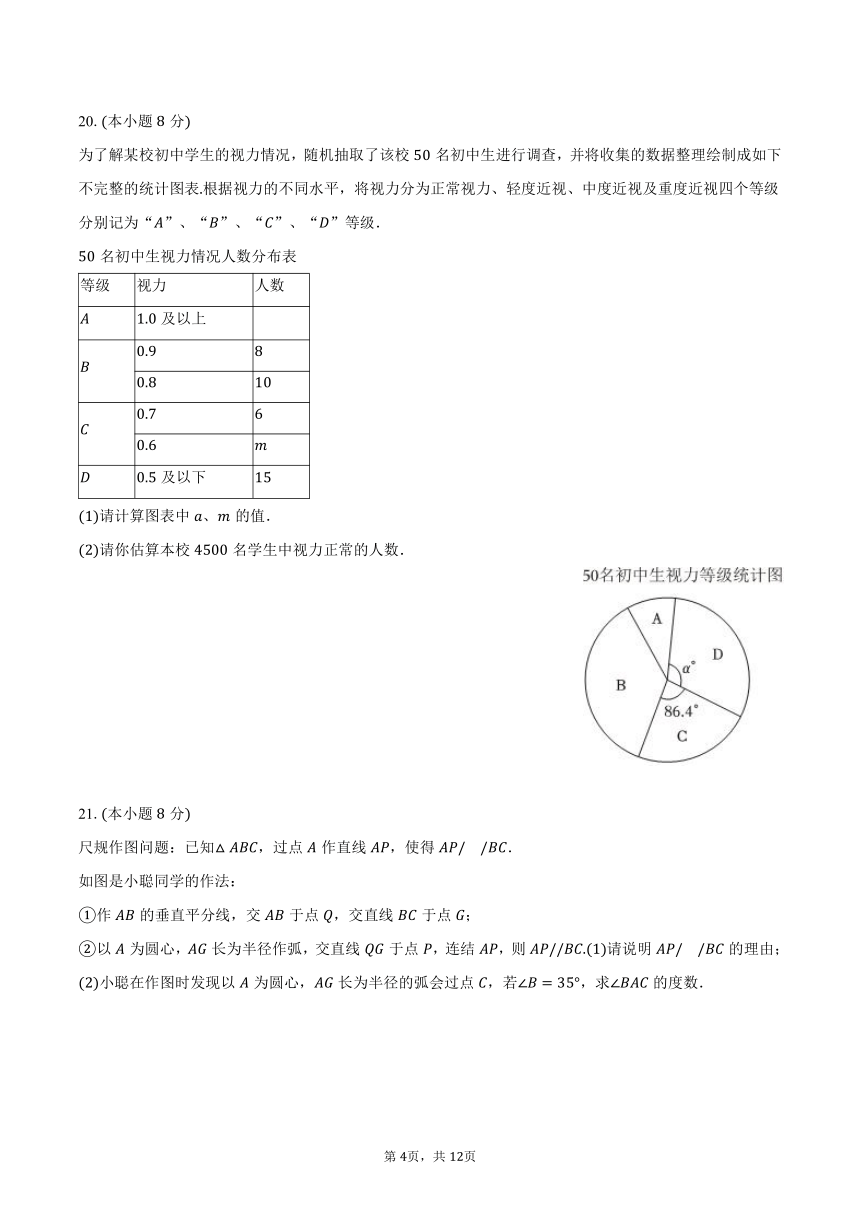
13.若,则 ______.
14.一个扇形的圆心角为,半径为,则这个扇形的面积为______结果保留
15.如图,将图矩形纸片沿虚线剪开并拼接成了图正方形,则 ______.
16.如图,在矩形中,平分交于点,交于点,将沿折叠得到,交于点,若,则 ______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:.
18.本小题分
解不等式组:.
19.本小题分
如图,在菱形中,,作,连结.
求菱形的面积;
求的长.
20.本小题分
为了解某校初中学生的视力情况,随机抽取了该校名初中生进行调查,并将收集的数据整理绘制成如下不完整的统计图表根据视力的不同水平,将视力分为正常视力、轻度近视、中度近视及重度近视四个等级分别记为“”、“”、“”、“”等级.
名初中生视力情况人数分布表
等级 视力 人数
及以上
及以下
请计算图表中、的值.
请你估算本校名学生中视力正常的人数.
21.本小题分
尺规作图问题:已知,过点作直线,使得.
如图是小聪同学的作法:
作的垂直平分线,交于点,交直线于点;
以为圆心,长为半径作弧,交直线于点,连结,则请说明的理由;
小聪在作图时发现以为圆心,长为半径的弧会过点,若,求的度数.
22.本小题分
某工厂员工生产一款零件,员工的日工资结算方案如下:
方案一:基本工资每天元,每生产一个零件加计元.
方案二:当生产数量不超过个时,发基本工资每天元,每超过一个加计元.
如图所示是日工资元关于生产数量个的函数图象.
求时,方案二的日工资元关于生产数量个的函数表达式;
甲员工发现他选择方案一所得的工资比选择方案二所得的工资高,求甲员工生产的零件个数的范围;
乙员工发现他选择方案一所得的工资比选择方案二所得的工资少元,则乙员工生产了多少个零件?
23.本小题分
已知二次函数.
若二次函数经过点,
求二次函数解析式;
当时,求的取值范围;
若,点、、在二次函数图象上,请比较,,的大小.
24.本小题分
已知四边形内接于,对角线与交于点.
如图,若为直径,点是中点,,.
求证:∽;
求的长;
如图,若,,且、不过点,、分别为、的中点,连结、、、,试猜想四边形的形状,并证明你的猜想.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【解析】解:原式
.
18.【答案】.
【解析】解:,
解不等式得,,
解不等式得,,
不等式组的解集为:
19.【解析】四边形是菱形,
,
,,
,
,
菱形的面积;
在中,,,
,
,
.
20.【解析】,
,
等级的人数为人,
;
人,
答:估算本校名学生中视力正常的人数有人.
21.【解析】证明:是线段的垂直平分线,
,,
,
,
,
,
;
解:,
,
,
,
,
,
.
22.【解析】根据题意得:当时,方案二的日工资元关于生产数量个的函数表达式为,
即,
当时,方案二的日工资元关于生产数量个的函数表达式为;
根据题意得:方案一的日工资元关于生产数量个的函数表达式为;
当时,方案二的日工资元关于生产数量个的函数表达式为.
当时,,
解得:,
;
当时,,
解得:,
.
综上所述,甲员工生产的零件个数的范围为;
当时,,
解得:;
当时,,
解得:.
答:乙员工生产了个或个零件.
23.【解析】把代入,
,
解得,
二次函数的解析式的解析式为;
,
时,有最小值为,
当时,,
当时,,
当时,的取值范围为;
二次函数图象的对称轴为直线,
,
点到直线的距离最大,点到直线的距离最小,
.
24.【解析】证明:为直径,
,
点是中点,
,
,,
为等腰直角三角形,
,
,
,
∽;
解:,,
∽,
,
,
,
为等腰直角三角形,
.
,
,
,
,
;
四边形是菱形.理由:
延长,交于点,如图,
,
,
,
,
、分别为、的中点,
,,
.
,、分别为、的中点,
是斜边上的中线,是斜边上的中线,
,,
,,
,
.
,
.
,
,
,
,
,
同理:,
四边形是平行四边形,
,
四边形是菱形.
第7页,共12页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.有,,,四个数,其中最小的数是( )
A. B. C. D.
2.下列计算正确的是( )
A. B. C. D.
3.如图,由个棱长均为的立方体组成的几何体,它的左视图为( )
A. B. C. D.
4.年浙江省总产值为亿元,数用科学记数法可表示为( )
A. B. C. D.
5.如图,,若,则为( )
A. B. C. D.
6.如图所示网格中,线段是由线段位似放大而成,则位似中心是( )
A.
B.
C.
D.
7.某公司招聘技术人员,需对应聘者进行测试,测试项目包括基础知识、操作能力、创新能力,并规定上述三项成绩依次按,,的比例计入总成绩某应聘者的测试成绩统计如下:
项目 基础知识 操作能力 创新能力
成绩
则此应聘者的总成绩是( )
A. B. C. D.
8.端午节是我国的传统佳节,民间历来有吃粽子的习俗端午节期间,某商店对一款粽子推出优惠活动,决定每个粽子打八折,打折后元买到的粽子数量比打折前多了个,设粽子的原价为元个,可列出方程( )
A. B.
C. D.
9.如图,矩形的面积为,点的坐标为,轴,轴,若反比例函数的图象过点、,则的值为( )
A.
B.
C.
D.
10.如图,在等腰中,,,点是斜边的中点,点在上,连结,作于点,连结,则点从点向点移动过程中点不与、重合,角度的大小为( )
A. 由小变大
B. 由大变小
C. 不变
D. 不能确定
二、填空题:本题共6小题,每小题3分,共18分。
11.因式分解: .
12.一个游戏转盘如图所示,红色扇形的圆心角为,让转盘自由转动,当转盘停止时,指针落在红色区域的概率是______.
13.若,则 ______.
14.一个扇形的圆心角为,半径为,则这个扇形的面积为______结果保留
15.如图,将图矩形纸片沿虚线剪开并拼接成了图正方形,则 ______.
16.如图,在矩形中,平分交于点,交于点,将沿折叠得到,交于点,若,则 ______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:.
18.本小题分
解不等式组:.
19.本小题分
如图,在菱形中,,作,连结.
求菱形的面积;
求的长.
20.本小题分
为了解某校初中学生的视力情况,随机抽取了该校名初中生进行调查,并将收集的数据整理绘制成如下不完整的统计图表根据视力的不同水平,将视力分为正常视力、轻度近视、中度近视及重度近视四个等级分别记为“”、“”、“”、“”等级.
名初中生视力情况人数分布表
等级 视力 人数
及以上
及以下
请计算图表中、的值.
请你估算本校名学生中视力正常的人数.
21.本小题分
尺规作图问题:已知,过点作直线,使得.
如图是小聪同学的作法:
作的垂直平分线,交于点,交直线于点;
以为圆心,长为半径作弧,交直线于点,连结,则请说明的理由;
小聪在作图时发现以为圆心,长为半径的弧会过点,若,求的度数.
22.本小题分
某工厂员工生产一款零件,员工的日工资结算方案如下:
方案一:基本工资每天元,每生产一个零件加计元.
方案二:当生产数量不超过个时,发基本工资每天元,每超过一个加计元.
如图所示是日工资元关于生产数量个的函数图象.
求时,方案二的日工资元关于生产数量个的函数表达式;
甲员工发现他选择方案一所得的工资比选择方案二所得的工资高,求甲员工生产的零件个数的范围;
乙员工发现他选择方案一所得的工资比选择方案二所得的工资少元,则乙员工生产了多少个零件?
23.本小题分
已知二次函数.
若二次函数经过点,
求二次函数解析式;
当时,求的取值范围;
若,点、、在二次函数图象上,请比较,,的大小.
24.本小题分
已知四边形内接于,对角线与交于点.
如图,若为直径,点是中点,,.
求证:∽;
求的长;
如图,若,,且、不过点,、分别为、的中点,连结、、、,试猜想四边形的形状,并证明你的猜想.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【解析】解:原式
.
18.【答案】.
【解析】解:,
解不等式得,,
解不等式得,,
不等式组的解集为:
19.【解析】四边形是菱形,
,
,,
,
,
菱形的面积;
在中,,,
,
,
.
20.【解析】,
,
等级的人数为人,
;
人,
答:估算本校名学生中视力正常的人数有人.
21.【解析】证明:是线段的垂直平分线,
,,
,
,
,
,
;
解:,
,
,
,
,
,
.
22.【解析】根据题意得:当时,方案二的日工资元关于生产数量个的函数表达式为,
即,
当时,方案二的日工资元关于生产数量个的函数表达式为;
根据题意得:方案一的日工资元关于生产数量个的函数表达式为;
当时,方案二的日工资元关于生产数量个的函数表达式为.
当时,,
解得:,
;
当时,,
解得:,
.
综上所述,甲员工生产的零件个数的范围为;
当时,,
解得:;
当时,,
解得:.
答:乙员工生产了个或个零件.
23.【解析】把代入,
,
解得,
二次函数的解析式的解析式为;
,
时,有最小值为,
当时,,
当时,,
当时,的取值范围为;
二次函数图象的对称轴为直线,
,
点到直线的距离最大,点到直线的距离最小,
.
24.【解析】证明:为直径,
,
点是中点,
,
,,
为等腰直角三角形,
,
,
,
∽;
解:,,
∽,
,
,
,
为等腰直角三角形,
.
,
,
,
,
;
四边形是菱形.理由:
延长,交于点,如图,
,
,
,
,
、分别为、的中点,
,,
.
,、分别为、的中点,
是斜边上的中线,是斜边上的中线,
,,
,,
,
.
,
.
,
,
,
,
,
同理:,
四边形是平行四边形,
,
四边形是菱形.
第7页,共12页
同课章节目录
