2025年辽宁省初中学业水平模拟考试(三)数学试卷(PDF版,含答案)
文档属性
| 名称 | 2025年辽宁省初中学业水平模拟考试(三)数学试卷(PDF版,含答案) |

|
|
| 格式 | |||
| 文件大小 | 489.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 20:35:13 | ||
图片预览



文档简介
2025年辽宁省初中学业水平模拟考试(三)
数学试卷
(本试卷共 23 小题满分 120 分考试时长 120 分钟)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.答选择题时,选出每小题答案后,用 2B 铅笔把答题卡对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.答非选择题时,将答案写在答题卡上.写在本试卷上
无效.
3.考试结束后,将本试卷和答题卡一并交回.
y ax bx c b , 4ac b
2
参考公式:抛物线 的顶点坐标是
2a 4a
第一部分 选择题(共30分)
一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符
合题目要求的)
1.负数的概念最早出现在我国古代著名的数学专著《九章算术》中.下列算式中,运算结果为负数的是( )
A. 22 B.| 2| C. 2 D. ( 2)2
2.米斗是我国古代粮仓、粮栈、米行等必备的用具,是称量粮食的量器,如图 1是一种无盈米斗,其示图(不
计厚度)如图 2所示,则其俯视图是( )
(图1) (图2)
A. B. C. D.
3.“嫦娥六号”返回器携带来自月背的月球样品安全着陆,历时 53天,38万公里的太空往返之旅,数据 380000
用科学记数法表示为( )
A.38 104 B.0.38 105 C.3.8 104 D.3.8 105
4.在平面直角坐标系中,点 P 1,2 关于坐标原点的对称点 P 的坐标为( )
A. 1, 2 B. 1,2 C. 1, 2 D. 1,2
5 x 2.将分式方程 3化为整式方程,正确的是( )
x 2 2 x
A. x 2 3 B. x 2 3 C. x 2 3 x 2 D. x 2 3 x 2
6.在一个不透明袋子中有红球和黑球共 10个球,这些球除颜色外无其他差别.从袋子中随机取出一个球是红
3
球的概率是 ,则袋子中红球的个数是( )
5
A.2 B.4 C.6 D.8
7.如图,菱形 ABCD的对角线 AC,BD交于点 O,若 1 65 29 ,则 2为( )
A.34 29 B.34 31 C. 24 31 D.25 31
k
8.如图,正比例函数 y1 k1x的图象与反比例函数 y 22 的图象相交于 A、B两点,其中 A点的横坐标为 3,x
当 y1 y2 时,x的取值范围是( )
A. x 3或 x 3 B. x 3或0 x 3 C. 3 x 0或0 x 3 D. 3 x 0或 x 3
9.如图,△ABC与△DEF 是以点 O为位似中心的位似图形,若△ABC与△DEF 的面积比为 4 :9,则
OB :OE的值为( )
A.4 :9 B.3:1 C. 2 :1 D.2 :3
10.如图,将抛物线C1 : y x 1
2 2 2平移到抛物线C2 : y x 2 1,点 P m,n1 ,Q m,n2 分别
在抛物线C ,C 上.下列结论:①无论 m取何值,都有 n2 0;②若点 P平移后的对应点为 P ,则PP 3 2;
③当 3 m 1时,线段 PQ的长随着 m的增大而减小.其中正确的结论为( )
A.①②③ B.①② C.①③ D.②③
第二部分 非选择题(共90分)
二、填空题(本题共 5 小题,每小题 3 分,共 15 分)
11.x的 2倍与 3的差为正数,用不等式表示为______.
12.古代建筑中的榫卯结构精妙绝伦,体现了古人的智慧.如图,这是一种古代建筑构件“榫头”的示意图,
其中两直角边长分别为6cm和8cm,斜面(阴影部分)为长方形,其中长方形的一边长为3cm,则此长方形
2
的面积为______cm .
13.在登山过程中,海拔每升高1km,气温下降6℃,某登山大本营所在的位置的气温是12℃,登山队员从
大本营出发登山,当海拔升高 xkm时( x 0),所在位置的气温是 y℃,则 y与 x的函数表达式是______.
14.《九章算术》第六章“均输”中有这样一个问题:今有空车日行八十里,重车日行六十里;今载太仓粟输
上林,五日三返,问太仓去上林几何 译文如下:有人用车把米从太仓运到上林,空车时每天行驶 80里,装米
时每天行驶 60里,载货去,空车返回,5天往返 3次问太仓到上林的距离是______里.
15.如图,在平面直角坐标系中,正方形OABC的顶点 C,A分别在 x轴,y轴上,其中点 A 0,4 ,点 D为
OA的中点,连接 BD.点 P为OC边上一点,连接DP,先以点 P为圆心,DP长为半径作弧,交 BD于点
1
E,再分别以点D,E为圆心,大于 DE的长为半径作弧,两弧交于点F,作射线 PF 交DE于点G.若DG DO,
2
则点 P的坐标为______.
三、解答题(本题共 8 小题,共 75 分,解答应写出文字说明、演算步骤或推理过程)
1 1
16.(10 分)(1)(5分)计算: 2 3
( 4) ( 8) 12 | 3 1|;
a 12 5 2a 3( )( 分)计算: 1 .
a 2 a2 4
17.(8分)某苹果园种植一种优质苹果,随着果树的成长,该苹果园的总产量从 2022年的 30吨增加到 2024
年的 43.2吨.
(1)求这个苹果园总产量平均每年增产的百分率;
(2)若平均每年增产的百分率率不变,2025年该苹果园的总产量能突破 50吨吗 请说明理由.
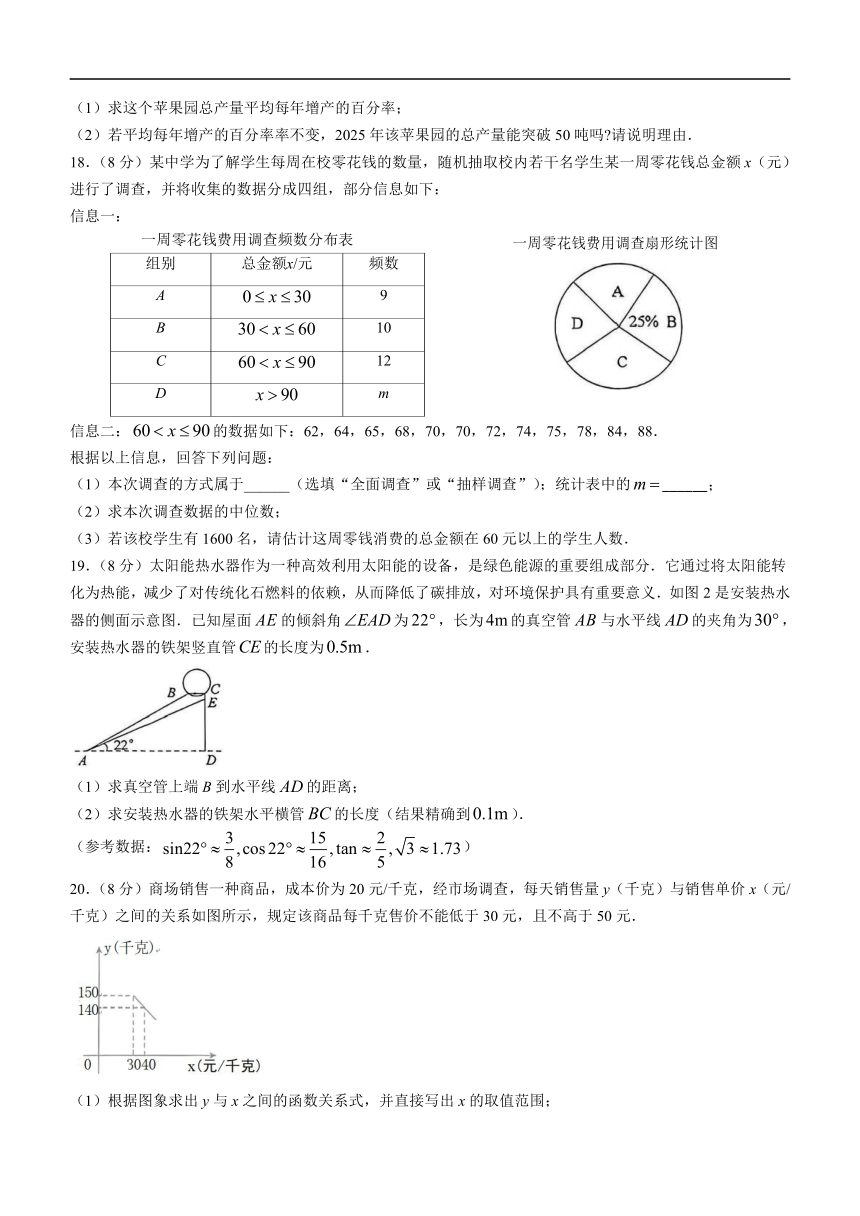
18.(8分)某中学为了解学生每周在校零花钱的数量,随机抽取校内若干名学生某一周零花钱总金额 x(元)
进行了调查,并将收集的数据分成四组,部分信息如下:
信息一:
一周零花钱费用调查频数分布表 一周零花钱费用调查扇形统计图
组别 总金额x/元 频数
A 0 x 30 9
B 30 x 60 10
C 60 x 90 12
D x 90 m
信息二:60 x 90的数据如下:62,64,65,68,70,70,72,74,75,78,84,88.
根据以上信息,回答下列问题:
(1)本次调查的方式属于______(选填“全面调查”或“抽样调查”);统计表中的m ______;
(2)求本次调查数据的中位数;
(3)若该校学生有 1600名,请估计这周零钱消费的总金额在 60元以上的学生人数.
19.(8分)太阳能热水器作为一种高效利用太阳能的设备,是绿色能源的重要组成部分.它通过将太阳能转
化为热能,减少了对传统化石燃料的依赖,从而降低了碳排放,对环境保护具有重要意义.如图 2是安装热水
器的侧面示意图.已知屋面 AE的倾斜角 EAD为 22 ,长为 4m的真空管 AB与水平线 AD的夹角为30 ,
安装热水器的铁架竖直管CE的长度为0.5m.
(1)求真空管上端 B到水平线 AD的距离;
(2)求安装热水器的铁架水平横管 BC的长度(结果精确到0.1m).
3
(参考数据: sin22 , cos 22 15 2 , tan , 3 1.73)
8 16 5
20.(8分)商场销售一种商品,成本价为 20元/千克,经市场调查,每天销售量 y(千克)与销售单价 x(元/
千克)之间的关系如图所示,规定该商品每千克售价不能低于 30元,且不高于 50元.
(1)根据图象求出 y与 x之间的函数关系式,并直接写出 x的取值范围;
(2)商场销售该商品每天的利润能否达到 4000元 如果能,求出每千克的售价;如果不能,请说明理由.
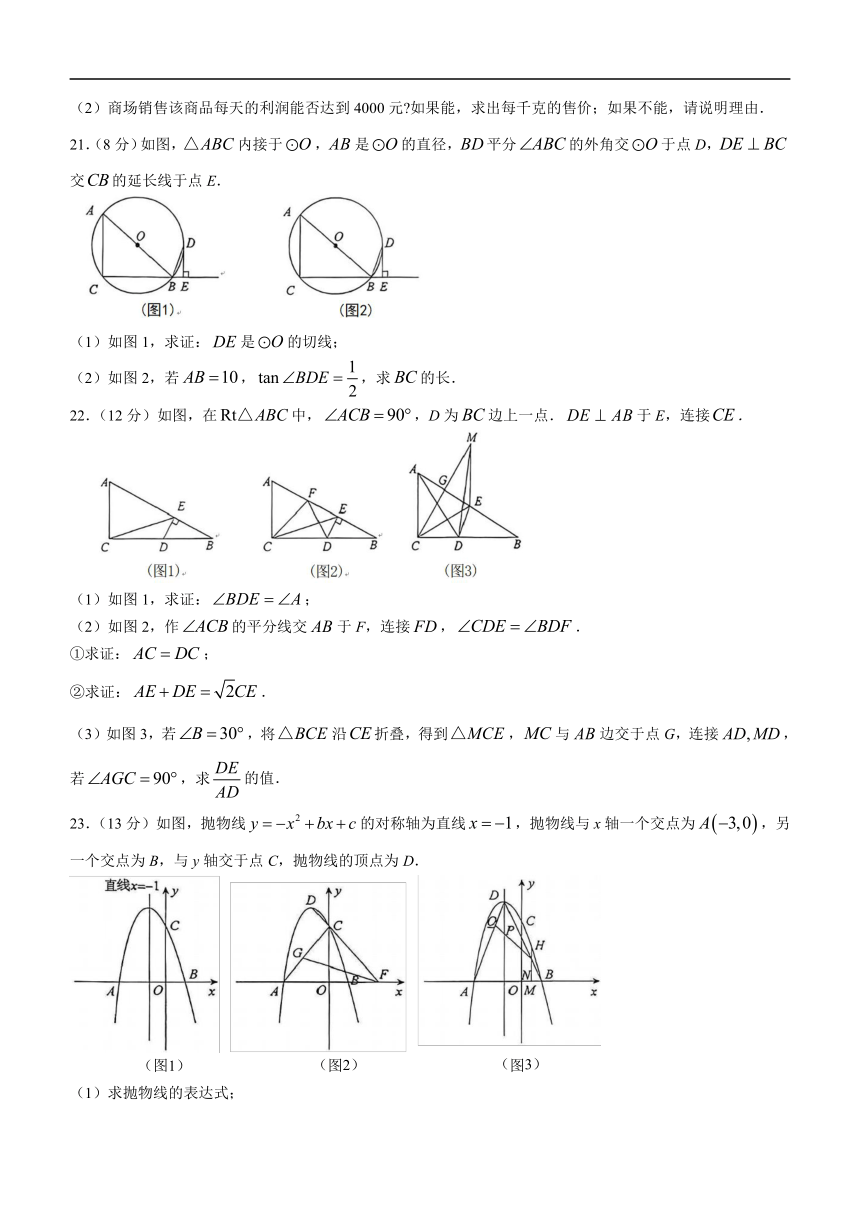
21.(8分)如图,△ABC内接于 O,AB是 O的直径,BD平分 ABC的外角交 O于点 D,DE BC
交CB的延长线于点 E.
(1)如图 1,求证:DE是 O的切线;
(2)如图 2,若 AB 10, tan BDE 1 ,求 BC的长.
2
22.(12分)如图,在Rt△ABC中, ACB 90 ,D为 BC边上一点.DE AB于 E,连接CE.
(1)如图 1,求证: BDE A;
(2)如图 2,作 ACB的平分线交 AB于 F,连接 FD, CDE BDF.
①求证: AC DC;
②求证: AE DE 2CE.
(3)如图 3,若 B 30 ,将△BCE 沿CE折叠,得到△MCE,MC与 AB边交于点 G,连接 AD,MD,
若 AGC 90 DE,求 的值.
AD
23 13 y x2.( 分)如图,抛物线 bx c的对称轴为直线 x 1,抛物线与 x轴一个交点为 A 3,0 ,另
一个交点为 B,与 y轴交于点 C,抛物线的顶点为 D.
(图1) (图2) (图3)
(1)求抛物线的表达式;
(2)如图 1,点 E在抛物线的对称轴上, BEC 90 ,求点 E的坐标;
(3)如图 2,连接 AC,DC,延长DC交 x轴于点 F,点 G在线段 AC上,连接 FG,将线段FG绕点 F逆
时针旋转90 得到线段 FG ,当点G 在抛物线上时,求点G 的坐标;
(4)如图 3,点 H在第一象限的抛物线上,过 H作HM x轴于 M,交 BD于点 N,点 Q在线段 AD上,
连接 NQ,满足 ABD DNQ 45 ,NQ与抛物线的对称轴交于点 P.
①求 DPQ的度数;
②若 BN DQ,求点 H的坐标.
2025 年辽宁省初中学业水平模拟考试数学(三)
一、选择题(本题共 10 小题,每小题 3 分,共 30 分)
1.A 2.B 3.D 4.A 5.D 6.C 7.C 8.B 9.D 10.A
二、填空题(本题共 5 小题,每小题 3 分,共 15 分)
11.2x 3 0 12.30 13. y 6x 12 x 0 40014. 15. 5 1,07
三、解答题(本题共 8 小题,共 75 分)
16.(1)解:原式 3 ( 2) 2 3 3 1································································4分
2 3;············································································································5分
a 1 a 2 (a 2)(a 2)
(2)解:原式
····························································8分
a 2 a 2 2a 3
2a 3 (a 2)(a 2)
····························································································9分
a 2 2a 3
a 2.···············································································································10分
17.解:(1)设这个苹果园总产量平均每年增产的百分率是 x,
根据题意得:30(1 x)2 43.2 ,···········································································2分
解得: x1 0.2 20%, x2 2.2(不符合题意,舍去).·············································4分
答:这个苹果园总产量平均每年增产的百分率是 20%;···············································5分
(2)2025年该苹果园的总产量能突破 50吨.···························································6分
理由: 43.2 (1 20%) 51.84吨,·····································································7分
51.84 50, 2025年该苹果园的总产量能突破 50吨.··········································8分
18.解:(1)抽样调查;························································································1分
9;·····················································································································2分
(2) 共调查了10 25% 40人,将这 40个数据从小到大排列,第 20,21两个数据为 C组的 62,64,
························································································································3分
62 64
中位数为 63元,·················································································4分
2
答:这组数据的中位数为 63元;·············································································5分
(3)1600 12 9 840(名),···········································································7分
40
答:估计一周零钱消费的总金额在 60元以上的学生人数大约为 840名.··························8分
19.解:(1)如图,过 B作BF AD于 F, AFB DFB 90 ,························1分
AB 4 m, BAD 30 1 , BF AB 2m,······················································2分
2
答:点 B到 AD的距离为 2m;··············································································3分
(2)在Rt△ABF 中, AFB 90 , BAF 30 , cos BAF AF ,
AB
AF AB cos BAF 4 cos30 2 3m ,······················································4分
BF AD,CD AD,BC∥FD, BFD CDF BCD 90 ,
四边形 BFDC是矩形, CD BF 2m,BC FD,············································5分
CE 0.5m, DE CD CE 2 0.5 1.5m,
在Rt△ADE DE中, ADE 90 , DAE 22 , tan DAE ,
AD
AD DE DE 1.5 3.75m,·························································6分
tan EAD tan 22 2
5
BC DF AD AF 3.75 2 3 3.75 2 1.73 0.29 0.3m .·································7分
答: BC的长度约为0.3m.····························································································8分
20.解:(1)设每天销售量 y(千克)与销售单价 x(元/千克)之间的关系为 y kx b k 0 ,将点
150 30k b30,150 , 40,140 分别代入得: ,····························································1分
140 40k b
k 1
解得: ,········································································································3分
b 180
y x 180(30 x 50);·······················································································4分
(2)商场销售该商品每天的利润不能达到 4000元,···························································5分
设商场销售该商品每天利润心元,根据题意得,
w (x 20)( x 180) x 2 200x 3600 (x 100) 2 6400 ,·····································6分
1 0,抛物线开口向下,抛物线对称轴为直线 x 100,
30 x 50时,在对称轴左侧,w随 x的增大而增大,
当 x 50时,w最大,最大值为 3900元,······································································7分
3900 4000,∴商场销售该商品每天的利润不能达到 4000元.·········································8分
21.解:(1)证明:如图 1,连接OD. OD OB, OBD ODB.································1分
BD平分 ABC的外角, OBD EBD. ODB EBD. OD∥BE.···················2分
DE CB交CB的延长线于 E. BED 90 , ODE 90 .
OD DE. OD为 O半径. DE是 O的切线;····················································3分
(2)如图 2,连接OD, AD,过 O作OF BC于 F. AB是 O的直径.
ADB 90 . ADB DEB, ABD DBE.
△DBE∽△ABD, AD DE .·················································································4分
BD BE
在Rt△BDE中, tan BDE BE 1 AD 2.设 BD a, AD 2a.
DE 2 BD
2
根据勾股定理得. AB AD BD2 5a. AB 10. a 2 5.·································5分
BD 2 5 .在Rt△BDE中,DE 2BE ,根据勾股定理得,
BD BE 2 DE 2 5BE . 5BE 2 5. BE 2,DE 4 .·································6分
OF BC, OFB 90 . OFB DEF ODE 90 . 四边形ODEF 为矩
形. OF DE 4.
在Rt△OBF OB 1中, AB 5 2,根据勾股定理得 BF OB OF 2 52 42 3.······7分
2
OF BC. BC 2BF 6.·················································································8分
22.解:(1)证明: DE AB于 E, BED 90 , B BDE 90 ,···················1分
ACB 90 A B 90 , BDE A;························································2分
(2)①证明: CDE BDF , CDE EDF BDF EDF ,
即 BDE CDF. BDE A, A CDF .·····················································3分
CF 平分 ACB. ACF DCF .又 CF CF.
△ACF≌△DCF(AAS), AC DC;·····································································4分
②证明:如图 1,过 C作CM CE交 ED延长线于 M. ECM 90 ,
ACB 90 , ACE DCM 90 DCE.······················································5分
BDE CDM , BDE A. A CDM ,又 AC DC.
△ACE≌△DCM (ASA). CE CM , AE DM ,·····················································6分
△ECM 是等腰直角三角形. EM 2CE. EM DM DE,
AE DE 2CE.·······························································································7分
(3)如图 2,连接 AM .
ACB 90 , B 30 , BAC 60 , AB 2AC,
设 AC a 2,则 AB 2a,根据勾股定理得,BC AB AC2 3a.
AGC 90 , ACG 90 60 30 . △BCE沿CE翻折得到△MCE,
BCE MCE 90 30 30 .······························································8分
2
ACE ACG MCE 60 , ACE CAE 60 , △ACE是等边三角形.
AE AC CE a, BE AB AE 2a a a.··········································9分
在Rt△BDE 3中, B 30 , DE a,BD 2 3 a.
3 3
CD BC BD 3a 2 3 a 3 a,
3 3
3 a
tan CAD CD 3 2 3 3 , CAD 30 , AD 2CD a .··················10分
AC a 3 3
在Rt△BCG中, BC 2CG, 翻折, BC MC. MC 2CG.
AGC 90 , AG MC, AM AC a, MAB CAB 60 .····················11分
CAD 30 , BAD CAB CAD 60 30 30 .
MAD MAB BAD 60 30 90 .
在Rt△MAD中,根据勾股定理得,
2 21
MD AM 2 AD 2 2 3 21 DM 7 a 2 a3
a . 3 .···················12分
3 AD 2 3 2
3
b
1 b 2
23.解:(1 2)根据题意得 2 ( 1) ,解得 , y x 2x 3;··················2分
c 3 9 3b c 0
(2)如图 1,过 C作CM 直线 x 1于 M. CME 90 ,
BEC BNE 90 . CEM BEN BEN EBN 90 .
CEM EBN .································································································3分
CME BNE, △CME∽△ENB.
CM ME
. A( 3,0).抛物线对称轴为直线 x 1. B(1,0).
EN BN
BN 2, C(0,3), OC MN 3. CM 1 3 EN 1. .
EN 2
EN 2 3EN 2 0,EN 2或EN 1, E1( 1,1)或 E2 ( 1,2);····································5分
(3)当 x 1时, y 1 2 3 4, D( 1,4). C(0,3).∴直线CD的解析式为 y x 3,
F (3,0). OA OF. CO AF. CA CF .
OA OC, CAO 45 . AFC 45 .·································································6分
如图 2,过 F作 FM AF 交 AC延长线于 M,连接 AG .则 FM FA, M 45 .
MFA GFG 90 , MFG AFG ,又 FG FG ,
△MFG≌△AFG (SAS). FAG 45 , AG ∥FC.·············································7分
设直线 AG 的解析式为 y x n,代入 A( 3,0). n 3.∴直线 AG 的解析式为 y x 3.联立
y x 3 x1 3 x2 2
.解得 . .
y x
2 2x 3 y
1 0 y2 5
G (2, 5);·········································································································8分
(4)① HM x轴, HM∥PD. MNB BDP.设 MNB BDP .
ABD 90 MNB 90 . ABD BNQ 45 , DNQ ABD 45 90 45
45 . DPQ DNQ BDP 45 45 ;·······································9分
②如图 3.过 Q作QJ DP于 J,过 N作 NI DP于 I,设DP交 AB于 R.
AD BD,DR AB. ADR BDR BNM .又 BN DQ.
△BNM≌△QDJ (AAS). BM QJ ,MN DJ .····················································10分
设H t, t 2 2t 3 BM QJ 1 t, AR 2 1 .DR 4 2
DQ 1
. DJ MN 2 2t.···············································································11分
DJ 2
DPQ BPR 45 . PJ QJ 1 t,NI MR PI t 1,
RI MN 2 2t, DR DJ PJ PI RI 4.
2 2t 1 t t 1 1 2 2t 4. t .····································································12分
2
x 1
2
y 1 1 7 1 7 当 时,
2
2 3 . H , .···················································13分
2 2 4 2 4
数学试卷
(本试卷共 23 小题满分 120 分考试时长 120 分钟)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.答选择题时,选出每小题答案后,用 2B 铅笔把答题卡对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.答非选择题时,将答案写在答题卡上.写在本试卷上
无效.
3.考试结束后,将本试卷和答题卡一并交回.
y ax bx c b , 4ac b
2
参考公式:抛物线 的顶点坐标是
2a 4a
第一部分 选择题(共30分)
一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符
合题目要求的)
1.负数的概念最早出现在我国古代著名的数学专著《九章算术》中.下列算式中,运算结果为负数的是( )
A. 22 B.| 2| C. 2 D. ( 2)2
2.米斗是我国古代粮仓、粮栈、米行等必备的用具,是称量粮食的量器,如图 1是一种无盈米斗,其示图(不
计厚度)如图 2所示,则其俯视图是( )
(图1) (图2)
A. B. C. D.
3.“嫦娥六号”返回器携带来自月背的月球样品安全着陆,历时 53天,38万公里的太空往返之旅,数据 380000
用科学记数法表示为( )
A.38 104 B.0.38 105 C.3.8 104 D.3.8 105
4.在平面直角坐标系中,点 P 1,2 关于坐标原点的对称点 P 的坐标为( )
A. 1, 2 B. 1,2 C. 1, 2 D. 1,2
5 x 2.将分式方程 3化为整式方程,正确的是( )
x 2 2 x
A. x 2 3 B. x 2 3 C. x 2 3 x 2 D. x 2 3 x 2
6.在一个不透明袋子中有红球和黑球共 10个球,这些球除颜色外无其他差别.从袋子中随机取出一个球是红
3
球的概率是 ,则袋子中红球的个数是( )
5
A.2 B.4 C.6 D.8
7.如图,菱形 ABCD的对角线 AC,BD交于点 O,若 1 65 29 ,则 2为( )
A.34 29 B.34 31 C. 24 31 D.25 31
k
8.如图,正比例函数 y1 k1x的图象与反比例函数 y 22 的图象相交于 A、B两点,其中 A点的横坐标为 3,x
当 y1 y2 时,x的取值范围是( )
A. x 3或 x 3 B. x 3或0 x 3 C. 3 x 0或0 x 3 D. 3 x 0或 x 3
9.如图,△ABC与△DEF 是以点 O为位似中心的位似图形,若△ABC与△DEF 的面积比为 4 :9,则
OB :OE的值为( )
A.4 :9 B.3:1 C. 2 :1 D.2 :3
10.如图,将抛物线C1 : y x 1
2 2 2平移到抛物线C2 : y x 2 1,点 P m,n1 ,Q m,n2 分别
在抛物线C ,C 上.下列结论:①无论 m取何值,都有 n2 0;②若点 P平移后的对应点为 P ,则PP 3 2;
③当 3 m 1时,线段 PQ的长随着 m的增大而减小.其中正确的结论为( )
A.①②③ B.①② C.①③ D.②③
第二部分 非选择题(共90分)
二、填空题(本题共 5 小题,每小题 3 分,共 15 分)
11.x的 2倍与 3的差为正数,用不等式表示为______.
12.古代建筑中的榫卯结构精妙绝伦,体现了古人的智慧.如图,这是一种古代建筑构件“榫头”的示意图,
其中两直角边长分别为6cm和8cm,斜面(阴影部分)为长方形,其中长方形的一边长为3cm,则此长方形
2
的面积为______cm .
13.在登山过程中,海拔每升高1km,气温下降6℃,某登山大本营所在的位置的气温是12℃,登山队员从
大本营出发登山,当海拔升高 xkm时( x 0),所在位置的气温是 y℃,则 y与 x的函数表达式是______.
14.《九章算术》第六章“均输”中有这样一个问题:今有空车日行八十里,重车日行六十里;今载太仓粟输
上林,五日三返,问太仓去上林几何 译文如下:有人用车把米从太仓运到上林,空车时每天行驶 80里,装米
时每天行驶 60里,载货去,空车返回,5天往返 3次问太仓到上林的距离是______里.
15.如图,在平面直角坐标系中,正方形OABC的顶点 C,A分别在 x轴,y轴上,其中点 A 0,4 ,点 D为
OA的中点,连接 BD.点 P为OC边上一点,连接DP,先以点 P为圆心,DP长为半径作弧,交 BD于点
1
E,再分别以点D,E为圆心,大于 DE的长为半径作弧,两弧交于点F,作射线 PF 交DE于点G.若DG DO,
2
则点 P的坐标为______.
三、解答题(本题共 8 小题,共 75 分,解答应写出文字说明、演算步骤或推理过程)
1 1
16.(10 分)(1)(5分)计算: 2 3
( 4) ( 8) 12 | 3 1|;
a 12 5 2a 3( )( 分)计算: 1 .
a 2 a2 4
17.(8分)某苹果园种植一种优质苹果,随着果树的成长,该苹果园的总产量从 2022年的 30吨增加到 2024
年的 43.2吨.
(1)求这个苹果园总产量平均每年增产的百分率;
(2)若平均每年增产的百分率率不变,2025年该苹果园的总产量能突破 50吨吗 请说明理由.
18.(8分)某中学为了解学生每周在校零花钱的数量,随机抽取校内若干名学生某一周零花钱总金额 x(元)
进行了调查,并将收集的数据分成四组,部分信息如下:
信息一:
一周零花钱费用调查频数分布表 一周零花钱费用调查扇形统计图
组别 总金额x/元 频数
A 0 x 30 9
B 30 x 60 10
C 60 x 90 12
D x 90 m
信息二:60 x 90的数据如下:62,64,65,68,70,70,72,74,75,78,84,88.
根据以上信息,回答下列问题:
(1)本次调查的方式属于______(选填“全面调查”或“抽样调查”);统计表中的m ______;
(2)求本次调查数据的中位数;
(3)若该校学生有 1600名,请估计这周零钱消费的总金额在 60元以上的学生人数.
19.(8分)太阳能热水器作为一种高效利用太阳能的设备,是绿色能源的重要组成部分.它通过将太阳能转
化为热能,减少了对传统化石燃料的依赖,从而降低了碳排放,对环境保护具有重要意义.如图 2是安装热水
器的侧面示意图.已知屋面 AE的倾斜角 EAD为 22 ,长为 4m的真空管 AB与水平线 AD的夹角为30 ,
安装热水器的铁架竖直管CE的长度为0.5m.
(1)求真空管上端 B到水平线 AD的距离;
(2)求安装热水器的铁架水平横管 BC的长度(结果精确到0.1m).
3
(参考数据: sin22 , cos 22 15 2 , tan , 3 1.73)
8 16 5
20.(8分)商场销售一种商品,成本价为 20元/千克,经市场调查,每天销售量 y(千克)与销售单价 x(元/
千克)之间的关系如图所示,规定该商品每千克售价不能低于 30元,且不高于 50元.
(1)根据图象求出 y与 x之间的函数关系式,并直接写出 x的取值范围;
(2)商场销售该商品每天的利润能否达到 4000元 如果能,求出每千克的售价;如果不能,请说明理由.
21.(8分)如图,△ABC内接于 O,AB是 O的直径,BD平分 ABC的外角交 O于点 D,DE BC
交CB的延长线于点 E.
(1)如图 1,求证:DE是 O的切线;
(2)如图 2,若 AB 10, tan BDE 1 ,求 BC的长.
2
22.(12分)如图,在Rt△ABC中, ACB 90 ,D为 BC边上一点.DE AB于 E,连接CE.
(1)如图 1,求证: BDE A;
(2)如图 2,作 ACB的平分线交 AB于 F,连接 FD, CDE BDF.
①求证: AC DC;
②求证: AE DE 2CE.
(3)如图 3,若 B 30 ,将△BCE 沿CE折叠,得到△MCE,MC与 AB边交于点 G,连接 AD,MD,
若 AGC 90 DE,求 的值.
AD
23 13 y x2.( 分)如图,抛物线 bx c的对称轴为直线 x 1,抛物线与 x轴一个交点为 A 3,0 ,另
一个交点为 B,与 y轴交于点 C,抛物线的顶点为 D.
(图1) (图2) (图3)
(1)求抛物线的表达式;
(2)如图 1,点 E在抛物线的对称轴上, BEC 90 ,求点 E的坐标;
(3)如图 2,连接 AC,DC,延长DC交 x轴于点 F,点 G在线段 AC上,连接 FG,将线段FG绕点 F逆
时针旋转90 得到线段 FG ,当点G 在抛物线上时,求点G 的坐标;
(4)如图 3,点 H在第一象限的抛物线上,过 H作HM x轴于 M,交 BD于点 N,点 Q在线段 AD上,
连接 NQ,满足 ABD DNQ 45 ,NQ与抛物线的对称轴交于点 P.
①求 DPQ的度数;
②若 BN DQ,求点 H的坐标.
2025 年辽宁省初中学业水平模拟考试数学(三)
一、选择题(本题共 10 小题,每小题 3 分,共 30 分)
1.A 2.B 3.D 4.A 5.D 6.C 7.C 8.B 9.D 10.A
二、填空题(本题共 5 小题,每小题 3 分,共 15 分)
11.2x 3 0 12.30 13. y 6x 12 x 0 40014. 15. 5 1,07
三、解答题(本题共 8 小题,共 75 分)
16.(1)解:原式 3 ( 2) 2 3 3 1································································4分
2 3;············································································································5分
a 1 a 2 (a 2)(a 2)
(2)解:原式
····························································8分
a 2 a 2 2a 3
2a 3 (a 2)(a 2)
····························································································9分
a 2 2a 3
a 2.···············································································································10分
17.解:(1)设这个苹果园总产量平均每年增产的百分率是 x,
根据题意得:30(1 x)2 43.2 ,···········································································2分
解得: x1 0.2 20%, x2 2.2(不符合题意,舍去).·············································4分
答:这个苹果园总产量平均每年增产的百分率是 20%;···············································5分
(2)2025年该苹果园的总产量能突破 50吨.···························································6分
理由: 43.2 (1 20%) 51.84吨,·····································································7分
51.84 50, 2025年该苹果园的总产量能突破 50吨.··········································8分
18.解:(1)抽样调查;························································································1分
9;·····················································································································2分
(2) 共调查了10 25% 40人,将这 40个数据从小到大排列,第 20,21两个数据为 C组的 62,64,
························································································································3分
62 64
中位数为 63元,·················································································4分
2
答:这组数据的中位数为 63元;·············································································5分
(3)1600 12 9 840(名),···········································································7分
40
答:估计一周零钱消费的总金额在 60元以上的学生人数大约为 840名.··························8分
19.解:(1)如图,过 B作BF AD于 F, AFB DFB 90 ,························1分
AB 4 m, BAD 30 1 , BF AB 2m,······················································2分
2
答:点 B到 AD的距离为 2m;··············································································3分
(2)在Rt△ABF 中, AFB 90 , BAF 30 , cos BAF AF ,
AB
AF AB cos BAF 4 cos30 2 3m ,······················································4分
BF AD,CD AD,BC∥FD, BFD CDF BCD 90 ,
四边形 BFDC是矩形, CD BF 2m,BC FD,············································5分
CE 0.5m, DE CD CE 2 0.5 1.5m,
在Rt△ADE DE中, ADE 90 , DAE 22 , tan DAE ,
AD
AD DE DE 1.5 3.75m,·························································6分
tan EAD tan 22 2
5
BC DF AD AF 3.75 2 3 3.75 2 1.73 0.29 0.3m .·································7分
答: BC的长度约为0.3m.····························································································8分
20.解:(1)设每天销售量 y(千克)与销售单价 x(元/千克)之间的关系为 y kx b k 0 ,将点
150 30k b30,150 , 40,140 分别代入得: ,····························································1分
140 40k b
k 1
解得: ,········································································································3分
b 180
y x 180(30 x 50);·······················································································4分
(2)商场销售该商品每天的利润不能达到 4000元,···························································5分
设商场销售该商品每天利润心元,根据题意得,
w (x 20)( x 180) x 2 200x 3600 (x 100) 2 6400 ,·····································6分
1 0,抛物线开口向下,抛物线对称轴为直线 x 100,
30 x 50时,在对称轴左侧,w随 x的增大而增大,
当 x 50时,w最大,最大值为 3900元,······································································7分
3900 4000,∴商场销售该商品每天的利润不能达到 4000元.·········································8分
21.解:(1)证明:如图 1,连接OD. OD OB, OBD ODB.································1分
BD平分 ABC的外角, OBD EBD. ODB EBD. OD∥BE.···················2分
DE CB交CB的延长线于 E. BED 90 , ODE 90 .
OD DE. OD为 O半径. DE是 O的切线;····················································3分
(2)如图 2,连接OD, AD,过 O作OF BC于 F. AB是 O的直径.
ADB 90 . ADB DEB, ABD DBE.
△DBE∽△ABD, AD DE .·················································································4分
BD BE
在Rt△BDE中, tan BDE BE 1 AD 2.设 BD a, AD 2a.
DE 2 BD
2
根据勾股定理得. AB AD BD2 5a. AB 10. a 2 5.·································5分
BD 2 5 .在Rt△BDE中,DE 2BE ,根据勾股定理得,
BD BE 2 DE 2 5BE . 5BE 2 5. BE 2,DE 4 .·································6分
OF BC, OFB 90 . OFB DEF ODE 90 . 四边形ODEF 为矩
形. OF DE 4.
在Rt△OBF OB 1中, AB 5 2,根据勾股定理得 BF OB OF 2 52 42 3.······7分
2
OF BC. BC 2BF 6.·················································································8分
22.解:(1)证明: DE AB于 E, BED 90 , B BDE 90 ,···················1分
ACB 90 A B 90 , BDE A;························································2分
(2)①证明: CDE BDF , CDE EDF BDF EDF ,
即 BDE CDF. BDE A, A CDF .·····················································3分
CF 平分 ACB. ACF DCF .又 CF CF.
△ACF≌△DCF(AAS), AC DC;·····································································4分
②证明:如图 1,过 C作CM CE交 ED延长线于 M. ECM 90 ,
ACB 90 , ACE DCM 90 DCE.······················································5分
BDE CDM , BDE A. A CDM ,又 AC DC.
△ACE≌△DCM (ASA). CE CM , AE DM ,·····················································6分
△ECM 是等腰直角三角形. EM 2CE. EM DM DE,
AE DE 2CE.·······························································································7分
(3)如图 2,连接 AM .
ACB 90 , B 30 , BAC 60 , AB 2AC,
设 AC a 2,则 AB 2a,根据勾股定理得,BC AB AC2 3a.
AGC 90 , ACG 90 60 30 . △BCE沿CE翻折得到△MCE,
BCE MCE 90 30 30 .······························································8分
2
ACE ACG MCE 60 , ACE CAE 60 , △ACE是等边三角形.
AE AC CE a, BE AB AE 2a a a.··········································9分
在Rt△BDE 3中, B 30 , DE a,BD 2 3 a.
3 3
CD BC BD 3a 2 3 a 3 a,
3 3
3 a
tan CAD CD 3 2 3 3 , CAD 30 , AD 2CD a .··················10分
AC a 3 3
在Rt△BCG中, BC 2CG, 翻折, BC MC. MC 2CG.
AGC 90 , AG MC, AM AC a, MAB CAB 60 .····················11分
CAD 30 , BAD CAB CAD 60 30 30 .
MAD MAB BAD 60 30 90 .
在Rt△MAD中,根据勾股定理得,
2 21
MD AM 2 AD 2 2 3 21 DM 7 a 2 a3
a . 3 .···················12分
3 AD 2 3 2
3
b
1 b 2
23.解:(1 2)根据题意得 2 ( 1) ,解得 , y x 2x 3;··················2分
c 3 9 3b c 0
(2)如图 1,过 C作CM 直线 x 1于 M. CME 90 ,
BEC BNE 90 . CEM BEN BEN EBN 90 .
CEM EBN .································································································3分
CME BNE, △CME∽△ENB.
CM ME
. A( 3,0).抛物线对称轴为直线 x 1. B(1,0).
EN BN
BN 2, C(0,3), OC MN 3. CM 1 3 EN 1. .
EN 2
EN 2 3EN 2 0,EN 2或EN 1, E1( 1,1)或 E2 ( 1,2);····································5分
(3)当 x 1时, y 1 2 3 4, D( 1,4). C(0,3).∴直线CD的解析式为 y x 3,
F (3,0). OA OF. CO AF. CA CF .
OA OC, CAO 45 . AFC 45 .·································································6分
如图 2,过 F作 FM AF 交 AC延长线于 M,连接 AG .则 FM FA, M 45 .
MFA GFG 90 , MFG AFG ,又 FG FG ,
△MFG≌△AFG (SAS). FAG 45 , AG ∥FC.·············································7分
设直线 AG 的解析式为 y x n,代入 A( 3,0). n 3.∴直线 AG 的解析式为 y x 3.联立
y x 3 x1 3 x2 2
.解得 . .
y x
2 2x 3 y
1 0 y2 5
G (2, 5);·········································································································8分
(4)① HM x轴, HM∥PD. MNB BDP.设 MNB BDP .
ABD 90 MNB 90 . ABD BNQ 45 , DNQ ABD 45 90 45
45 . DPQ DNQ BDP 45 45 ;·······································9分
②如图 3.过 Q作QJ DP于 J,过 N作 NI DP于 I,设DP交 AB于 R.
AD BD,DR AB. ADR BDR BNM .又 BN DQ.
△BNM≌△QDJ (AAS). BM QJ ,MN DJ .····················································10分
设H t, t 2 2t 3 BM QJ 1 t, AR 2 1 .DR 4 2
DQ 1
. DJ MN 2 2t.···············································································11分
DJ 2
DPQ BPR 45 . PJ QJ 1 t,NI MR PI t 1,
RI MN 2 2t, DR DJ PJ PI RI 4.
2 2t 1 t t 1 1 2 2t 4. t .····································································12分
2
x 1
2
y 1 1 7 1 7 当 时,
2
2 3 . H , .···················································13分
2 2 4 2 4
同课章节目录
