2025年数学小升初高频易错考点专题训练:立体图形(含解析)
文档属性
| 名称 | 2025年数学小升初高频易错考点专题训练:立体图形(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 402.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 09:02:59 | ||
图片预览




文档简介
登录二一教育在线组卷平台 助您教考全无忧
2025年数学小升初高频易错考点专题训练:立体图形
一、单选题
1.一个正方体的表面展开图如下图所示,那么原正方体中与“1”所在面相对的面所标的字是( )。
A.2 B.4 C.5 D.6
2. 用同样的小正方体拼成一个较大的正方体,至少需要( )个小正方体。
A.4 B.8 C.10
3.把一个圆柱体削成一个最大的圆锥体,削去部分是圆柱体的( )。
A. B. C.
4.下面哪个图,不能折成正方体。( )
A. B. C.
5.圆柱的任意一条高和底面上相对应的一条半径所组成的角是( )。
A.锐角 B.直角 C.钝角
6.图中呈现的是一瓶已经喝了一些的果汁和一个圆锥形玻璃杯,如果瓶中的果汁倒入这种圆锥形玻璃杯,最多可以倒满( )。(容器厚度忽略不计)
A.2杯 B.3杯 C.4杯 D.6杯
7.把一个圆柱制成一个最大的圆锥,削去部分的体积是圆柱体积的( )
A.3倍 B.2倍 C. D.
8.一个长方体火柴盒长5厘米、宽4厘米、高1.5厘米。做这样一个火柴盒外盒要用硬纸板多少平方厘米?列式为( )
A.5×4×2+4×1.5×2 B.(4×1.5+5×1.5)×2+5×4
C.5×4×2+5×1.5 D.(4+1.5)×2×5
9.一个圆柱的底面直径是10厘米,高是4分米,它的侧面积是( )平方厘米。
A.400 B.12.56 C.125.6 D.1256
10.一块长方体木料的长是5cm,宽是4cm,高是3cm。把它锯成一个最大的正方体后,剩下木料的体积(不计损耗)是( )cm3。
A.2 B.33 C.18 D.30
二、判断题
11.如果圆柱的底面半径扩大4倍,高不变,则它的体积扩大16倍。 ( )
12.一个正方体的棱长扩大3倍,它的表面积就扩大6倍。
13.一个圆锥的底面半径扩大到原来的3倍,高不变,它的体积就扩大到原来的9倍。
( )
14.表面积相等的两个圆柱,它们的体积一定相等。( )
15.一个正方体和一个圆柱体的底面积和高都相等,它们的体积也一定相等。( )
16.如果一个正方体的棱长扩大到原来的4倍,它的体积就扩大到原来的64倍。( )
三、填空题
17.该图 可以折叠成长方体
18.一个长方体,长5厘米,宽4厘米,高3厘米,它的表面积是 平方厘米,体积是 立方厘米.
19.方方想把包好的粽子放进盒子里送给奶奶,她用厚卡纸制作了一个漂亮的正方体包装盒,这个包装盒的棱长为20cm。做一个这样的包装盒至少需要 cm2的厚卡纸,这个包装盒的容积是 cm3。(卡纸的厚度忽略不计)
20. 一个棱长6分米的正方体削成一个最大的圆柱体,这个圆柱的底面积是 平方分米,体积是 立方分米。
21.如图是一个正方体的展开图.写有数字“1”的面和写有 的面是相对的。
22.一顶帽子上面是圆柱形,用黄色布料做;帽檐部分是圆环,用紫色布料做(如下图)。制作这顶帽子至少需要 cm2的黄色布料。(单位:cm)
23.从一个长为8厘米、宽为7厘米,高为6厘米的长方体中截下一个最大的正方体,剩下的几何体的体积是 立方厘米。
24.把体积是28.26m 圆柱削成一个最大的圆锥,削去部分的体积是 m 。
25.要砌一条长6米,高2米,厚24厘米的墙,如果用长24厘米,宽12厘米,厚6厘米的砖来砌,至少需要 块。
26.直角三角形ABC,AC=4厘米,AB=5厘米,BC=3厘米,如果以直角边为轴旋转一周得到一个 形,它的体积最大是 立方厘米.
四、计算题
27.求下面图形的表面积和体积:(注:圆锥只求体积)
(1)
(2)
五、解答题
28.在一个棱长为4厘米的正方体的上面、前面、右面的正中位置分别挖一个边长为1厘米的正方形小孔,并打通到对面。求打孔后剩下部分的体积。
29.“造纸术”是我国“四大发明”之一。《天工开物》中记载了造纸的具体流程:取材→蒸煮→入帘→压纸→烘干。
(1)在“入帘”环节要把煮烂的木浆倒入纸槽。一个从里面量长12 dm、宽10 dm、高5dm的长方体纸槽最多能容纳 L木浆。
(2)宣纸烘干后,为了在运输过程中宣纸不受损坏,工匠制作了专用的木箱来装宣纸。如果一个长方体木箱长6 dm、宽5dm、高6dm,那么制作这个木箱至少需要多少平方分米的木板?
30.一个圆柱形水桶的底面半径是4 cm。把一块铁块从水桶中取出后,水桶里的水面下降了1.5cm。这块铁块的体积是多少立方厘米?(铁块上的水忽略不计)
31.一圆锥形谷堆底部周长为9米,高为4米,经过一夜发现谷堆在重力作用下底部的周长变为12米。若谷堆的容量不变,那么此时谷堆的高为多少?
32.用12个棱长1cm的小正方体搭一个长方体,什么时候搭成的长方体表面积最小
(1)先列表试一试,算一算。
长/cm 12
宽/cm 1
高/cm 1
棱长之和/cm 56
表面积/cm2 50
(2)长方体在体积相等的情况下,什么时候表面积最小
(3)如果要包装24个小正方体,你会选择哪种外包装方案 为什么
六、解决问题
33.一个长方体和一个正方体的棱长总和相等。已知长方体的长是4cm、宽是3cm、高是5cm。
(1)正方体的棱长是多少厘米?
(2)正方体的表面积是多少平方厘米?
(3)正方体的体积是多少立方厘米?
34.有一个长方体容器,底面长30厘米,宽20厘米,高10厘米,里面的水深6厘米(最大面为底面),如果把这个容器盖紧(不漏水),再朝左竖起来(最小面为底面),里面的水深是多少厘米?
35.求圆锥的体积
七、图形计算
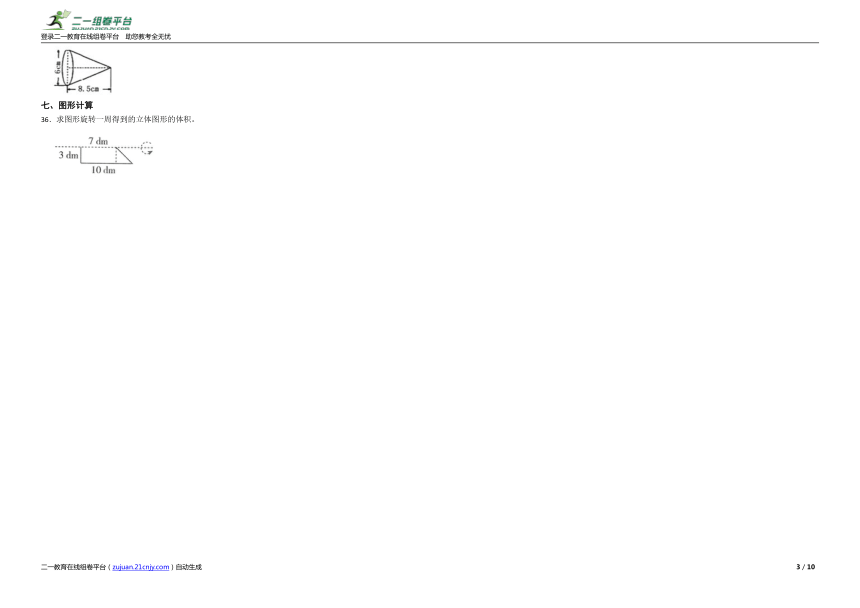
36.求图形旋转一周得到的立体图形的体积。
答案解析部分
1.【答案】C
【解析】【解答】解:“1”与“5”相间,所以与“1”所在面相对的面所标的字是“5”,C选项正确;
故答案为:C。
【分析】根据正方体表面展开图相对面的性质:相间的两个正方形是相对面;观察展开图,“1”和“5”相间,所以“1”的相对面是“5”;“2”和“4”相间,是一组相对面;“3”和“6”相间,是一组相对面,由此可得出正确答案为C。
2.【答案】B
【解析】【解答】解:2×2×2=8(个),至少需要8个小正方体。
故答案为:B。
【分析】用同样大小的正方体拼成一个较大的正方体,每条棱上至少需要2个小正方体,所以拼成这个大正方体至少需要的小正方体是8个。
3.【答案】B
4.【答案】B
【解析】【解答】解:第二个图形不能折成正方体。
故答案为:B。
【分析】
5.【答案】B
【解析】【解答】解:圆柱的任意一条高和底面上相对应的一条半径所组成的角是直角。
故答案为:B。
【分析】圆柱两个底面之间的距离就是圆柱的高。圆柱的任意一条高都垂直与底面,当然也垂直于对应的半径。
6.【答案】D
【解析】【解答】解:3×2=6(杯)
故答案为:D。
【分析】果汁瓶的底面直径和圆锥形玻璃杯杯口的直径相等,瓶中果汁的高度是2h,圆锥形玻璃杯中能装饮料的高度为h;等底等高的情况下,圆柱的体积是圆锥体积的3倍;据此计算出可以倒的杯数。
7.【答案】C
【解析】【解答】解: 把一个圆柱制成一个最大的圆锥,削去部分的体积是圆柱体积的。
故答案为:C。
【分析】 把一个圆柱制成一个最大的圆锥,圆锥的体积是圆柱体积的,则削去部分的体积是圆柱体积的。
8.【答案】D
【解析】【解答】解:5×4×2+5×1.5×2=(4+1.5)×5×2。
故答案为:D。
【分析】做这样一个火柴盒外盒要用硬纸板的面积=长×宽×2+长×高×2=(宽+高) ×长×2。
9.【答案】D
【解析】【解答】解:4分米=40厘米
3.14×10×40
=31.4×40
=1256(平方厘米)
故答案为:D。
【分析】圆柱的侧面积=底面周长×高;其中,底面周长=π×直径。
10.【答案】B
【解析】【解答】解:5×4×3-3×3×3
=20×3-9×3
=60-27
=33(立方厘米)
故答案为:B。
【分析】把长方体锯成一个最大的正方体,正方体的棱长与长方体长、宽、高中最小的数据相等; 剩下木料的体积=长方体的体积-正方体的体积;其中,长方体的体积=长×宽×高;正方体的体积=棱长×棱长×棱长。
11.【答案】正确
【解析】【解答】解:如果圆柱的底面半径扩大4倍,高不变,则它的体积扩大4×4=16倍。
故答案为:正确。
【分析】圆柱的体积=πr2h,当底面半径扩大4倍,高不变时,现在圆柱的体积=π(r×4)2h=16πr2h=原来圆柱的体积×16。
12.【答案】错误
【解析】【解答】解:一个正方体的棱长扩大3倍,它的表面积就扩大9倍,原题说法错误。
故答案为:错误。
【分析】正方体的棱长扩大多少倍,正方体的表面积扩大棱长扩大倍数的平方倍.
13.【答案】正确
【解析】【解答】解:半径扩大到原来的3倍, 底面的面积扩大到原来的9倍,高不变,所以体积也扩大到原来的9倍。
故答案为:正确
【分析】圆锥体积公式为:其中,为底面半径,为高。代入变化后的半径计算新体积
当半径变为,高不变时,新体积为:因此,体积确实扩大到原来的9倍。
14.【答案】错误
【解析】【解答】解:表面积相等的两个圆柱,它们的体积不一定相等。原题说法错误。
故答案为:错误。
【分析】表面积相等的两个圆柱,圆柱的底面积和高都不一定相等,所以体积不一定相等。
15.【答案】正确
【解析】【解答】解:正方体是特殊的长方体,所以一个正方体和一个圆柱体的底面积和高都相等,它们的体积也一定相等。
故答案为:正确。
【分析】由于圆柱的体积计算公式,是把圆柱体切拼成近似的长方体,由长方体的体积公式推导出圆柱体的体积公式,都是体积=底面积×高,所以它们的体积也一定相等。
16.【答案】正确
【解析】【解答】解:4×4×4
=16×4
=64
故答案为:正确。
【分析】正方体的体积=棱长×棱长×棱长,正方体的棱长扩大到原来的4倍,它的体积就扩大到原来的64倍。
17.【答案】能
【解析】【分析】通过观察,符合长方体展开图
18.【答案】94;60
【解析】【解答】表面积:
(5×4+5×3+4×3)×2
=(20+15+12)×2
=47×2
=94(平方厘米)
体积:
5×4×3
=20×3
=60(立方厘米)
故答案为:94;60.
【分析】已知长方体的长、宽、高,求长方体的表面积,用公式:长方体的表面积=(长×宽+长×高+宽×高)×2,求长方体的体积,用公式:长方体的体积=长×宽×高,据此列式解答.
19.【答案】2400;8000
【解析】【解答】解:20×20×6
=400×6
=2400(cm2)
20×20×20
=400×20
=8000(cm3)。
故答案为:2400;8000。
【分析】做一个这样的包装盒至少需要厚卡纸的面积=正方体包装盒的棱长×棱长×6,这个包装盒的容积=棱长×棱长×棱长。
20.【答案】28.26;169.56
【解析】【解答】解: 正方体削成一个最大的圆柱体,圆柱的底面直径是6分米,高是6分米,
圆柱的底面半径:6÷2=3(分米)
底面积:3.14×3×3=28.26(平方分米)
体积:28.26×6=169.56(立方分米)
故答案为:28.26;169.56。
【分析】π×底面半径的平方=圆柱的底面积,圆柱的底面积×高=圆柱的体积。
21.【答案】字母“A”
【解析】【解答】解:3和“B”是相对的面,“2”和“C”是相对的面,那么“1”和“A”是相对的面。
故答案为:字母“A”。
【分析】以“A”为正方体的底面将其围成正方体,那么3和“B”是正方体左右的两个面,“2”和“C”是正方体前后的两个面,“1”是正方体上面的面,据此解答。
22.【答案】942
【解析】【解答】解:20÷2=10(厘米)
3.14×20×10+3.14×102
=62.8×10+3.14×100
=628+314
=942(平方厘米)。
故答案为:942。
【分析】制作这顶帽子至少需要黄色布料的面积=圆柱的底面直径×π×高+π×圆柱底面半径2。
23.【答案】120
【解析】【解答】解:(立方厘米)
故答案为:120。
【分析】最大的立方体棱长为6,用长方体体积减去正方体体积即可。
24.【答案】18.84
【解析】【解答】解:28.26×=18.84(m3)
故答案为:18.84。
【分析】把一格圆柱的体积削成最大的圆锥,圆锥的体积是圆柱体积的,则削去部分的体积就是圆柱体积的,由此计算即可。
25.【答案】1667
【解析】【解答】解:24厘米=0.24米,12厘米=0.12米,6厘米=0.06米
6×2×0.24÷(0.24×0.12×0.06)
=2.88÷0.001728
≈1667(块)
故答案为:1667
【分析】用墙的体积除以一块砖的体积即可求出需要的块数,注意统一单位.
26.【答案】圆锥;50.24
【解析】【解答】解:以直角边为轴旋转一周得到一个圆锥形,体积最大是:
3.14×4 ×3×
=3.14×16
=50.24(立方厘米)
故答案为:圆锥;50.24。
【分析】以直角三角形的一条直角边为轴旋转一周会得到一个圆锥,圆锥的高是做轴的直角边,另一条直角边是底面半径,要使圆锥的体积最大,就要使底面积最大,所以底面半径是4厘米,高是3厘米时的体积是最大的。
27.【答案】(1)解:表面积:
32×3.14×2+3×2×3.14×4
=18×3.14+24×3.14
=42×3.14
=131.88(平方厘米)
体积:
32×3.14×4
=36×3.14
=113.04(立方厘米)
(2)解:体积:
(6÷2)2×3.14×6÷3
=18×3.14
=56.52(立方厘米)
【解析】【分析】(1)圆柱的表面积=底面积×2+侧面积,底面积=π×半径×半径,侧面积=π×直径×高;圆柱的体积=底面积×高;
(2)圆锥的体积=底面积×高÷3。
28.【答案】4×4×4-(1×1×4×3-1×1×2)= 54(立方厘米)
【解析】【分析】求部分体积问题,一般情况下是用总体积一部分体积=所求体积,有的时候体积有重叠,把重叠的部分减掉,即可求出正确的体积
29.【答案】(1)600
(2)解:(6×5+6×6+6×5)×2
=(30+36+30)×2
=96×2
= 192(dm3)
答:制作这个木箱至少需要192平方分米的木板。
【解析】【解答】解:(1)12×10×5
=120×5
=600(L)
故答案为:(1)600。
【分析】(1)长方体的容积=长×宽×高;
(2)长方体表面积=(长×宽+长×高+宽×高)×2;代数据计算即可。
30.【答案】解:3.14×42×1.5
=3.14×16×1.5
=50.24×1.5
=75.36(立方厘米);
答:这块铁块的体积是75.36立方厘米。
【解析】【分析】圆柱的底面是圆形,根据圆的面积公式S=πr2,求出圆柱的底面积;水桶里的水面下降了1.5cm,说明铁块的体积等于水面下降的体积,水面下降的体积等于圆柱的底面积乘水面下降的高度。
31.【答案】解:÷()=81×4÷144=2.25米
答:高为2.25米
【解析】【分析】解:谷堆底部半径=,体积为
周长变为12米,半径=,体积为。
两式相除得到现在的高=81×4÷144=2.25米
圆锥体积公式=底面积×高,根据题意代入求解即可。
32.【答案】(1)解:
长/cm 12 6 4 3
宽/cm 1 2 3 2
高/cm 1 1 1 2
棱长之和/cm 56 36 32 28
表面积/cm2 50 40 38 32
(2)解:在长为3厘米,宽为2厘米,高为2厘米的时候表面积最小。
(3)解:如果要包装24个小正方体,我会选择排成长为4厘米,宽为3厘米,高为2厘米的长方体,因为这样排列表面积最小,最省包装纸,降低包装成本。
【解析】【分析】(1)长方体的棱长总和=(长+宽+高)×4,长方体的表面积=(长×宽+长×高+宽×高)×2;
(2)计算后比较大下可知:在长为3厘米,宽为2厘米,高为2厘米的时候表面积最小;
(3)选择包装的长方体的表面积越小,成本就越少。
33.【答案】(1)解:(4+3+5)×4
=12×4
=48(厘米)
48÷12=4(厘米)
答:正方体的棱长是4厘米。
(2)解:4×4×6=96(平方厘米)
答:正方体的表面积是96平方厘米。
(3)解:4×4×4=64(立方厘米)
答:正方体的体积是64立方厘米。
【解析】【分析】(1)(长+宽+高)×4=长方体的棱长和;长方体的棱长和=正方体的棱长和,正方体的棱长和÷12=正方体的棱长;
(2)正方体的棱长×棱长×6=正方体的表面积;
(3)正方体的棱长×棱长×棱长=正方体的体积。
34.【答案】解:(30×20×6)÷(20×10)
=3600÷200
=18(cm)
答:里面的水深是18厘米。
【解析】【分析】水的体积是不变的。先根据原来的放置方法用长乘宽乘水的深度求出水的体积,然后用水的体积除以竖起来后的底面积即可求出此时的水深。
35.【答案】解:(6÷2) ×3.14×8.5×
=9×3.14×8.5×
=28.26×8.5×
=240.21×
=80.07(cm )
答:体积是80.07cm 。
【解析】【分析】圆锥的体积=(底面直径÷2)2×π×h×,据此代入数值作答即可。
36.【答案】解:3.14×32×10-3.14×32×(10-7)×
=3.14×90-3.14×9
=3.14×81
=254.34(dm3);
答:立体图形的体积是254.34dm3。
【解析】【分析】由题图可知,旋转一周得到的立体图形是一个底面半径为3dm、高为10dm的圆柱减去一个底面半径为3dm,高为10-7=3dm的圆锥,圆柱体积=πr2h,圆锥的体积=πr2h,据此求解。
试题分析部分
1、试卷总体分布分析
总分:136分
分值分布 客观题(占比) 56.0(41.2%)
主观题(占比) 80.0(58.8%)
题量分布 客观题(占比) 25(69.4%)
主观题(占比) 11(30.6%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
填空题 10(27.8%) 28.0(20.6%)
解答题 5(13.9%) 36.0(26.5%)
图形计算 1(2.8%) 5.0(3.7%)
计算题 1(2.8%) 10.0(7.4%)
解决问题 3(8.3%) 25.0(18.4%)
单选题 10(27.8%) 20.0(14.7%)
判断题 6(16.7%) 12.0(8.8%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (63.9%)
2 容易 (27.8%)
3 困难 (8.3%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 正方体的展开图 6.0(4.4%) 1,4,21
2 圆柱的侧面积、表面积 4.0(2.9%) 9,22
3 圆锥的特征 5.0(3.7%) 31
4 正方体的特征 2.0(1.5%) 2
5 正方体的体积 26.0(19.1%) 10,16,23,28,33
6 圆柱与圆锥体积的关系 8.0(5.9%) 3,6,7,24
7 长方体的表面积 27.0(19.9%) 8,18,29,32
8 长方体、正方体的容积 10.0(7.4%) 19,29
9 长方体的体积 15.0(11.0%) 10,18,23,25,34
10 圆锥的体积(容积) 31.0(22.8%) 13,26,27,31,35,36
11 正方体的表面积 6.0(4.4%) 12,19
12 圆柱的体积(容积) 30.0(22.1%) 11,14,15,20,27,30,36
13 长方体的展开图 2.0(1.5%) 17
14 圆柱的特征 2.0(1.5%) 5
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
2025年数学小升初高频易错考点专题训练:立体图形
一、单选题
1.一个正方体的表面展开图如下图所示,那么原正方体中与“1”所在面相对的面所标的字是( )。
A.2 B.4 C.5 D.6
2. 用同样的小正方体拼成一个较大的正方体,至少需要( )个小正方体。
A.4 B.8 C.10
3.把一个圆柱体削成一个最大的圆锥体,削去部分是圆柱体的( )。
A. B. C.
4.下面哪个图,不能折成正方体。( )
A. B. C.
5.圆柱的任意一条高和底面上相对应的一条半径所组成的角是( )。
A.锐角 B.直角 C.钝角
6.图中呈现的是一瓶已经喝了一些的果汁和一个圆锥形玻璃杯,如果瓶中的果汁倒入这种圆锥形玻璃杯,最多可以倒满( )。(容器厚度忽略不计)
A.2杯 B.3杯 C.4杯 D.6杯
7.把一个圆柱制成一个最大的圆锥,削去部分的体积是圆柱体积的( )
A.3倍 B.2倍 C. D.
8.一个长方体火柴盒长5厘米、宽4厘米、高1.5厘米。做这样一个火柴盒外盒要用硬纸板多少平方厘米?列式为( )
A.5×4×2+4×1.5×2 B.(4×1.5+5×1.5)×2+5×4
C.5×4×2+5×1.5 D.(4+1.5)×2×5
9.一个圆柱的底面直径是10厘米,高是4分米,它的侧面积是( )平方厘米。
A.400 B.12.56 C.125.6 D.1256
10.一块长方体木料的长是5cm,宽是4cm,高是3cm。把它锯成一个最大的正方体后,剩下木料的体积(不计损耗)是( )cm3。
A.2 B.33 C.18 D.30
二、判断题
11.如果圆柱的底面半径扩大4倍,高不变,则它的体积扩大16倍。 ( )
12.一个正方体的棱长扩大3倍,它的表面积就扩大6倍。
13.一个圆锥的底面半径扩大到原来的3倍,高不变,它的体积就扩大到原来的9倍。
( )
14.表面积相等的两个圆柱,它们的体积一定相等。( )
15.一个正方体和一个圆柱体的底面积和高都相等,它们的体积也一定相等。( )
16.如果一个正方体的棱长扩大到原来的4倍,它的体积就扩大到原来的64倍。( )
三、填空题
17.该图 可以折叠成长方体
18.一个长方体,长5厘米,宽4厘米,高3厘米,它的表面积是 平方厘米,体积是 立方厘米.
19.方方想把包好的粽子放进盒子里送给奶奶,她用厚卡纸制作了一个漂亮的正方体包装盒,这个包装盒的棱长为20cm。做一个这样的包装盒至少需要 cm2的厚卡纸,这个包装盒的容积是 cm3。(卡纸的厚度忽略不计)
20. 一个棱长6分米的正方体削成一个最大的圆柱体,这个圆柱的底面积是 平方分米,体积是 立方分米。
21.如图是一个正方体的展开图.写有数字“1”的面和写有 的面是相对的。
22.一顶帽子上面是圆柱形,用黄色布料做;帽檐部分是圆环,用紫色布料做(如下图)。制作这顶帽子至少需要 cm2的黄色布料。(单位:cm)
23.从一个长为8厘米、宽为7厘米,高为6厘米的长方体中截下一个最大的正方体,剩下的几何体的体积是 立方厘米。
24.把体积是28.26m 圆柱削成一个最大的圆锥,削去部分的体积是 m 。
25.要砌一条长6米,高2米,厚24厘米的墙,如果用长24厘米,宽12厘米,厚6厘米的砖来砌,至少需要 块。
26.直角三角形ABC,AC=4厘米,AB=5厘米,BC=3厘米,如果以直角边为轴旋转一周得到一个 形,它的体积最大是 立方厘米.
四、计算题
27.求下面图形的表面积和体积:(注:圆锥只求体积)
(1)
(2)
五、解答题
28.在一个棱长为4厘米的正方体的上面、前面、右面的正中位置分别挖一个边长为1厘米的正方形小孔,并打通到对面。求打孔后剩下部分的体积。
29.“造纸术”是我国“四大发明”之一。《天工开物》中记载了造纸的具体流程:取材→蒸煮→入帘→压纸→烘干。
(1)在“入帘”环节要把煮烂的木浆倒入纸槽。一个从里面量长12 dm、宽10 dm、高5dm的长方体纸槽最多能容纳 L木浆。
(2)宣纸烘干后,为了在运输过程中宣纸不受损坏,工匠制作了专用的木箱来装宣纸。如果一个长方体木箱长6 dm、宽5dm、高6dm,那么制作这个木箱至少需要多少平方分米的木板?
30.一个圆柱形水桶的底面半径是4 cm。把一块铁块从水桶中取出后,水桶里的水面下降了1.5cm。这块铁块的体积是多少立方厘米?(铁块上的水忽略不计)
31.一圆锥形谷堆底部周长为9米,高为4米,经过一夜发现谷堆在重力作用下底部的周长变为12米。若谷堆的容量不变,那么此时谷堆的高为多少?
32.用12个棱长1cm的小正方体搭一个长方体,什么时候搭成的长方体表面积最小
(1)先列表试一试,算一算。
长/cm 12
宽/cm 1
高/cm 1
棱长之和/cm 56
表面积/cm2 50
(2)长方体在体积相等的情况下,什么时候表面积最小
(3)如果要包装24个小正方体,你会选择哪种外包装方案 为什么
六、解决问题
33.一个长方体和一个正方体的棱长总和相等。已知长方体的长是4cm、宽是3cm、高是5cm。
(1)正方体的棱长是多少厘米?
(2)正方体的表面积是多少平方厘米?
(3)正方体的体积是多少立方厘米?
34.有一个长方体容器,底面长30厘米,宽20厘米,高10厘米,里面的水深6厘米(最大面为底面),如果把这个容器盖紧(不漏水),再朝左竖起来(最小面为底面),里面的水深是多少厘米?
35.求圆锥的体积
七、图形计算
36.求图形旋转一周得到的立体图形的体积。
答案解析部分
1.【答案】C
【解析】【解答】解:“1”与“5”相间,所以与“1”所在面相对的面所标的字是“5”,C选项正确;
故答案为:C。
【分析】根据正方体表面展开图相对面的性质:相间的两个正方形是相对面;观察展开图,“1”和“5”相间,所以“1”的相对面是“5”;“2”和“4”相间,是一组相对面;“3”和“6”相间,是一组相对面,由此可得出正确答案为C。
2.【答案】B
【解析】【解答】解:2×2×2=8(个),至少需要8个小正方体。
故答案为:B。
【分析】用同样大小的正方体拼成一个较大的正方体,每条棱上至少需要2个小正方体,所以拼成这个大正方体至少需要的小正方体是8个。
3.【答案】B
4.【答案】B
【解析】【解答】解:第二个图形不能折成正方体。
故答案为:B。
【分析】
5.【答案】B
【解析】【解答】解:圆柱的任意一条高和底面上相对应的一条半径所组成的角是直角。
故答案为:B。
【分析】圆柱两个底面之间的距离就是圆柱的高。圆柱的任意一条高都垂直与底面,当然也垂直于对应的半径。
6.【答案】D
【解析】【解答】解:3×2=6(杯)
故答案为:D。
【分析】果汁瓶的底面直径和圆锥形玻璃杯杯口的直径相等,瓶中果汁的高度是2h,圆锥形玻璃杯中能装饮料的高度为h;等底等高的情况下,圆柱的体积是圆锥体积的3倍;据此计算出可以倒的杯数。
7.【答案】C
【解析】【解答】解: 把一个圆柱制成一个最大的圆锥,削去部分的体积是圆柱体积的。
故答案为:C。
【分析】 把一个圆柱制成一个最大的圆锥,圆锥的体积是圆柱体积的,则削去部分的体积是圆柱体积的。
8.【答案】D
【解析】【解答】解:5×4×2+5×1.5×2=(4+1.5)×5×2。
故答案为:D。
【分析】做这样一个火柴盒外盒要用硬纸板的面积=长×宽×2+长×高×2=(宽+高) ×长×2。
9.【答案】D
【解析】【解答】解:4分米=40厘米
3.14×10×40
=31.4×40
=1256(平方厘米)
故答案为:D。
【分析】圆柱的侧面积=底面周长×高;其中,底面周长=π×直径。
10.【答案】B
【解析】【解答】解:5×4×3-3×3×3
=20×3-9×3
=60-27
=33(立方厘米)
故答案为:B。
【分析】把长方体锯成一个最大的正方体,正方体的棱长与长方体长、宽、高中最小的数据相等; 剩下木料的体积=长方体的体积-正方体的体积;其中,长方体的体积=长×宽×高;正方体的体积=棱长×棱长×棱长。
11.【答案】正确
【解析】【解答】解:如果圆柱的底面半径扩大4倍,高不变,则它的体积扩大4×4=16倍。
故答案为:正确。
【分析】圆柱的体积=πr2h,当底面半径扩大4倍,高不变时,现在圆柱的体积=π(r×4)2h=16πr2h=原来圆柱的体积×16。
12.【答案】错误
【解析】【解答】解:一个正方体的棱长扩大3倍,它的表面积就扩大9倍,原题说法错误。
故答案为:错误。
【分析】正方体的棱长扩大多少倍,正方体的表面积扩大棱长扩大倍数的平方倍.
13.【答案】正确
【解析】【解答】解:半径扩大到原来的3倍, 底面的面积扩大到原来的9倍,高不变,所以体积也扩大到原来的9倍。
故答案为:正确
【分析】圆锥体积公式为:其中,为底面半径,为高。代入变化后的半径计算新体积
当半径变为,高不变时,新体积为:因此,体积确实扩大到原来的9倍。
14.【答案】错误
【解析】【解答】解:表面积相等的两个圆柱,它们的体积不一定相等。原题说法错误。
故答案为:错误。
【分析】表面积相等的两个圆柱,圆柱的底面积和高都不一定相等,所以体积不一定相等。
15.【答案】正确
【解析】【解答】解:正方体是特殊的长方体,所以一个正方体和一个圆柱体的底面积和高都相等,它们的体积也一定相等。
故答案为:正确。
【分析】由于圆柱的体积计算公式,是把圆柱体切拼成近似的长方体,由长方体的体积公式推导出圆柱体的体积公式,都是体积=底面积×高,所以它们的体积也一定相等。
16.【答案】正确
【解析】【解答】解:4×4×4
=16×4
=64
故答案为:正确。
【分析】正方体的体积=棱长×棱长×棱长,正方体的棱长扩大到原来的4倍,它的体积就扩大到原来的64倍。
17.【答案】能
【解析】【分析】通过观察,符合长方体展开图
18.【答案】94;60
【解析】【解答】表面积:
(5×4+5×3+4×3)×2
=(20+15+12)×2
=47×2
=94(平方厘米)
体积:
5×4×3
=20×3
=60(立方厘米)
故答案为:94;60.
【分析】已知长方体的长、宽、高,求长方体的表面积,用公式:长方体的表面积=(长×宽+长×高+宽×高)×2,求长方体的体积,用公式:长方体的体积=长×宽×高,据此列式解答.
19.【答案】2400;8000
【解析】【解答】解:20×20×6
=400×6
=2400(cm2)
20×20×20
=400×20
=8000(cm3)。
故答案为:2400;8000。
【分析】做一个这样的包装盒至少需要厚卡纸的面积=正方体包装盒的棱长×棱长×6,这个包装盒的容积=棱长×棱长×棱长。
20.【答案】28.26;169.56
【解析】【解答】解: 正方体削成一个最大的圆柱体,圆柱的底面直径是6分米,高是6分米,
圆柱的底面半径:6÷2=3(分米)
底面积:3.14×3×3=28.26(平方分米)
体积:28.26×6=169.56(立方分米)
故答案为:28.26;169.56。
【分析】π×底面半径的平方=圆柱的底面积,圆柱的底面积×高=圆柱的体积。
21.【答案】字母“A”
【解析】【解答】解:3和“B”是相对的面,“2”和“C”是相对的面,那么“1”和“A”是相对的面。
故答案为:字母“A”。
【分析】以“A”为正方体的底面将其围成正方体,那么3和“B”是正方体左右的两个面,“2”和“C”是正方体前后的两个面,“1”是正方体上面的面,据此解答。
22.【答案】942
【解析】【解答】解:20÷2=10(厘米)
3.14×20×10+3.14×102
=62.8×10+3.14×100
=628+314
=942(平方厘米)。
故答案为:942。
【分析】制作这顶帽子至少需要黄色布料的面积=圆柱的底面直径×π×高+π×圆柱底面半径2。
23.【答案】120
【解析】【解答】解:(立方厘米)
故答案为:120。
【分析】最大的立方体棱长为6,用长方体体积减去正方体体积即可。
24.【答案】18.84
【解析】【解答】解:28.26×=18.84(m3)
故答案为:18.84。
【分析】把一格圆柱的体积削成最大的圆锥,圆锥的体积是圆柱体积的,则削去部分的体积就是圆柱体积的,由此计算即可。
25.【答案】1667
【解析】【解答】解:24厘米=0.24米,12厘米=0.12米,6厘米=0.06米
6×2×0.24÷(0.24×0.12×0.06)
=2.88÷0.001728
≈1667(块)
故答案为:1667
【分析】用墙的体积除以一块砖的体积即可求出需要的块数,注意统一单位.
26.【答案】圆锥;50.24
【解析】【解答】解:以直角边为轴旋转一周得到一个圆锥形,体积最大是:
3.14×4 ×3×
=3.14×16
=50.24(立方厘米)
故答案为:圆锥;50.24。
【分析】以直角三角形的一条直角边为轴旋转一周会得到一个圆锥,圆锥的高是做轴的直角边,另一条直角边是底面半径,要使圆锥的体积最大,就要使底面积最大,所以底面半径是4厘米,高是3厘米时的体积是最大的。
27.【答案】(1)解:表面积:
32×3.14×2+3×2×3.14×4
=18×3.14+24×3.14
=42×3.14
=131.88(平方厘米)
体积:
32×3.14×4
=36×3.14
=113.04(立方厘米)
(2)解:体积:
(6÷2)2×3.14×6÷3
=18×3.14
=56.52(立方厘米)
【解析】【分析】(1)圆柱的表面积=底面积×2+侧面积,底面积=π×半径×半径,侧面积=π×直径×高;圆柱的体积=底面积×高;
(2)圆锥的体积=底面积×高÷3。
28.【答案】4×4×4-(1×1×4×3-1×1×2)= 54(立方厘米)
【解析】【分析】求部分体积问题,一般情况下是用总体积一部分体积=所求体积,有的时候体积有重叠,把重叠的部分减掉,即可求出正确的体积
29.【答案】(1)600
(2)解:(6×5+6×6+6×5)×2
=(30+36+30)×2
=96×2
= 192(dm3)
答:制作这个木箱至少需要192平方分米的木板。
【解析】【解答】解:(1)12×10×5
=120×5
=600(L)
故答案为:(1)600。
【分析】(1)长方体的容积=长×宽×高;
(2)长方体表面积=(长×宽+长×高+宽×高)×2;代数据计算即可。
30.【答案】解:3.14×42×1.5
=3.14×16×1.5
=50.24×1.5
=75.36(立方厘米);
答:这块铁块的体积是75.36立方厘米。
【解析】【分析】圆柱的底面是圆形,根据圆的面积公式S=πr2,求出圆柱的底面积;水桶里的水面下降了1.5cm,说明铁块的体积等于水面下降的体积,水面下降的体积等于圆柱的底面积乘水面下降的高度。
31.【答案】解:÷()=81×4÷144=2.25米
答:高为2.25米
【解析】【分析】解:谷堆底部半径=,体积为
周长变为12米,半径=,体积为。
两式相除得到现在的高=81×4÷144=2.25米
圆锥体积公式=底面积×高,根据题意代入求解即可。
32.【答案】(1)解:
长/cm 12 6 4 3
宽/cm 1 2 3 2
高/cm 1 1 1 2
棱长之和/cm 56 36 32 28
表面积/cm2 50 40 38 32
(2)解:在长为3厘米,宽为2厘米,高为2厘米的时候表面积最小。
(3)解:如果要包装24个小正方体,我会选择排成长为4厘米,宽为3厘米,高为2厘米的长方体,因为这样排列表面积最小,最省包装纸,降低包装成本。
【解析】【分析】(1)长方体的棱长总和=(长+宽+高)×4,长方体的表面积=(长×宽+长×高+宽×高)×2;
(2)计算后比较大下可知:在长为3厘米,宽为2厘米,高为2厘米的时候表面积最小;
(3)选择包装的长方体的表面积越小,成本就越少。
33.【答案】(1)解:(4+3+5)×4
=12×4
=48(厘米)
48÷12=4(厘米)
答:正方体的棱长是4厘米。
(2)解:4×4×6=96(平方厘米)
答:正方体的表面积是96平方厘米。
(3)解:4×4×4=64(立方厘米)
答:正方体的体积是64立方厘米。
【解析】【分析】(1)(长+宽+高)×4=长方体的棱长和;长方体的棱长和=正方体的棱长和,正方体的棱长和÷12=正方体的棱长;
(2)正方体的棱长×棱长×6=正方体的表面积;
(3)正方体的棱长×棱长×棱长=正方体的体积。
34.【答案】解:(30×20×6)÷(20×10)
=3600÷200
=18(cm)
答:里面的水深是18厘米。
【解析】【分析】水的体积是不变的。先根据原来的放置方法用长乘宽乘水的深度求出水的体积,然后用水的体积除以竖起来后的底面积即可求出此时的水深。
35.【答案】解:(6÷2) ×3.14×8.5×
=9×3.14×8.5×
=28.26×8.5×
=240.21×
=80.07(cm )
答:体积是80.07cm 。
【解析】【分析】圆锥的体积=(底面直径÷2)2×π×h×,据此代入数值作答即可。
36.【答案】解:3.14×32×10-3.14×32×(10-7)×
=3.14×90-3.14×9
=3.14×81
=254.34(dm3);
答:立体图形的体积是254.34dm3。
【解析】【分析】由题图可知,旋转一周得到的立体图形是一个底面半径为3dm、高为10dm的圆柱减去一个底面半径为3dm,高为10-7=3dm的圆锥,圆柱体积=πr2h,圆锥的体积=πr2h,据此求解。
试题分析部分
1、试卷总体分布分析
总分:136分
分值分布 客观题(占比) 56.0(41.2%)
主观题(占比) 80.0(58.8%)
题量分布 客观题(占比) 25(69.4%)
主观题(占比) 11(30.6%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
填空题 10(27.8%) 28.0(20.6%)
解答题 5(13.9%) 36.0(26.5%)
图形计算 1(2.8%) 5.0(3.7%)
计算题 1(2.8%) 10.0(7.4%)
解决问题 3(8.3%) 25.0(18.4%)
单选题 10(27.8%) 20.0(14.7%)
判断题 6(16.7%) 12.0(8.8%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (63.9%)
2 容易 (27.8%)
3 困难 (8.3%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 正方体的展开图 6.0(4.4%) 1,4,21
2 圆柱的侧面积、表面积 4.0(2.9%) 9,22
3 圆锥的特征 5.0(3.7%) 31
4 正方体的特征 2.0(1.5%) 2
5 正方体的体积 26.0(19.1%) 10,16,23,28,33
6 圆柱与圆锥体积的关系 8.0(5.9%) 3,6,7,24
7 长方体的表面积 27.0(19.9%) 8,18,29,32
8 长方体、正方体的容积 10.0(7.4%) 19,29
9 长方体的体积 15.0(11.0%) 10,18,23,25,34
10 圆锥的体积(容积) 31.0(22.8%) 13,26,27,31,35,36
11 正方体的表面积 6.0(4.4%) 12,19
12 圆柱的体积(容积) 30.0(22.1%) 11,14,15,20,27,30,36
13 长方体的展开图 2.0(1.5%) 17
14 圆柱的特征 2.0(1.5%) 5
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
同课章节目录
