2024-2025学年期末考前冲刺预测卷(含解析)五年级下册数学(人教版)
文档属性
| 名称 | 2024-2025学年期末考前冲刺预测卷(含解析)五年级下册数学(人教版) |  | |
| 格式 | docx | ||
| 文件大小 | 447.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 08:40:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年五年级下册数学期末考前冲刺预测卷(人教版)
一、填空题
1.如图,按照这样的规律摆下去,第5幅图减少( )个面。
2.有20张卡片,上面分别写有数字1~20,从中任意摸一张。
(1)摸到3的倍数比摸到5的倍数的可能性( )。
(2)( )(填“经常”“偶尔”“不可能”或“一定”)摸到23的因数。
(3)如果按摸到的数是几位数分类(位数相同的为一类),会有( )种不同的结果。
(4)要提高摸到质数的可能性,可以再增加一张卡片,这张卡片上可以写数字( )(20以上,100以下)。
3.一场“1分钟跳绳”比赛活动,每个人可跳5次,取平均个数作最后成绩。小劳前4次分别跳了147个、149个、150个、154个。
(1)如果要清楚表现小芳4次跳绳成绩变化趋势,可将其成绩绘制成( )统计图,小芳4次跳绳成绩变化整体呈( )趋势。
(2)小芳4次的平均成绩是( )个。
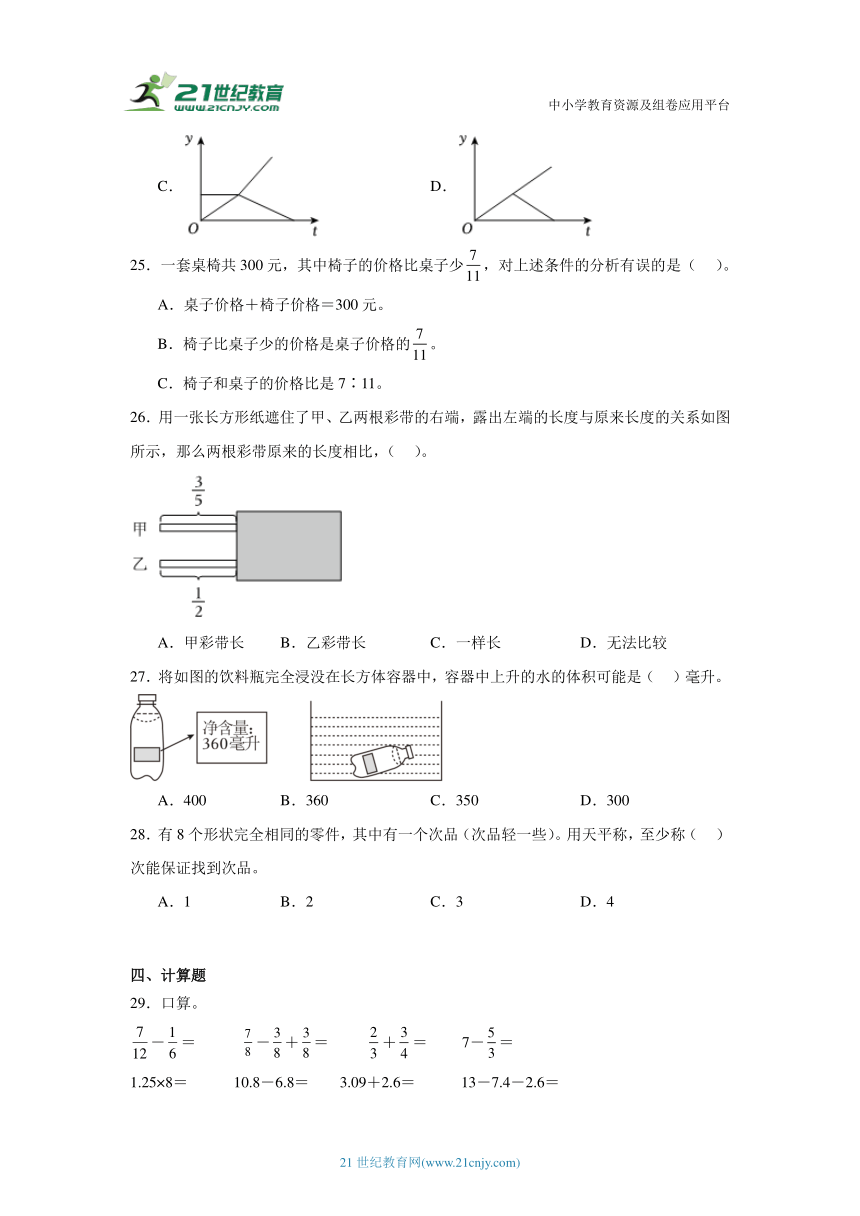
(3)“152个及以上”为优秀,小芳最后一次至少要跳( )个才能达到优秀水平。
4.神舟十号飞船于2013年6月11日17时从酒泉卫星发射中心发射,6月26日8时,神舟十号载人飞船返回舱在内蒙古中部预定区域安全着陆。神十在太空飞行共( )天( )时,合( )天。
5.小明去6千米远的公园玩,请根据折线图回答问题。
(1)小明在公园玩了( )分钟。
(2)如果一直走,不休息,能在( )时( )分到达公园。
(3)返回时,小明骑自行车的速度是每小时( )千米。
6.要反映大埔、五华、丰顺、平远四个县6月份的降水量,可以选用( )统计图,要反映广东省2024年1~6月份降水量的变化情况应选用( )统计图。
7.一个立体图形,从上面看是,从左面看是,要搭这样的立体图形,最少需要( )个小正方体,最多能用( )个小正方体。
8.把一个长、宽、高分别为12厘米、6厘米、3厘米的长方体切成同样大小的正方体,切成的正方体棱长最大是( )厘米,最多可切成( )个。
9.的分数单位是 ,再减去 个这样的分数单位就变成了最小的合数。
10.一个九位数,最高位上是最大的一位数,千万位上是2和3的最小公倍数,十万位上是最小的合数,其余各位上都是0,这个数写作 ,省略亿后面的尾数约是 。
11.张天悦在一个无盖的长方体玻璃容器中摆了若干个体积为1cm3的小正方体(如图)。制作这个容器需要 cm2的玻璃,它的体积是 cm3。
12.用如图所示的硬纸板做成一个无盖的长方体纸盒(单位:cm),这个纸盒的底面积是( )cm2,容积是( )cm3。(纸板厚度忽略不计)
二、判断题
13.一个数的倍数一定大于这个数的因数。( )
14.棱长为6cm的正方体表面积和体积相等。( )
15.一个长方形绕它的中心点至少要旋转90°才能与原长方形重合。( )
16.一个图形经过旋转后,形状和大小都不会变化。( )
17.把一根绳子剪成两段,第一段长m,第二段占全长的,第二段比第一段长。( )
18.一个正方体骰子的六个面上分别写着数字1~6,把它抛向空中,落下后朝上的点数是合数的可能性是。( )
三、选择题
19.下列数中,( )组的数字能组成一个三位数,它既是2的倍数,又是3的倍数,还是5的倍数。
A.2、3、5 B.0、2、3 C.0、5、8 D.0、5、7
20.投掷一枚硬币5次,有4次正面朝上,1次正面朝下,那么第6次投掷正面朝上的可能性是( )。
A. B. C.
21.如图是由4个同样的小正方体摆成的几何体,从左面看到的图形是( )。
A. B. C. D.
22.用8个边长是1分米的小正方体拼成一个大正方体,任意拿走一个小正方体后,表面积( )。
A.减少6平方分米 B.减少3平方分米 C.不变
23.红光小学鼓号队有31人,暑假期间有一个紧急演出,李老师需要尽快通知到每个队员。如果用打电话的方式,每分钟通知1人,每个同学接到电话后又打给其它同学,同时李老师也在不停的打,要通知全体队员至少需要_____分钟才能通知到所有人。( )
A.7 B.6 C.5 D.4
24.某期刊专栏登出一同学回忆父亲的诗:“同辞家门赴车站,别时叮咛嘱万千。学子满载信心去,老父怀抱希望还。”如果用纵轴y表示离家的距离,横轴t表示离家的时间,那么图象与上述诗意大致吻合的是( )。
A. B.
C. D.
25.一套桌椅共300元,其中椅子的价格比桌子少,对上述条件的分析有误的是( )。
A.桌子价格+椅子价格=300元。
B.椅子比桌子少的价格是桌子价格的。
C.椅子和桌子的价格比是7∶11。
26.用一张长方形纸遮住了甲、乙两根彩带的右端,露出左端的长度与原来长度的关系如图所示,那么两根彩带原来的长度相比,( )。
A.甲彩带长 B.乙彩带长 C.一样长 D.无法比较
27.将如图的饮料瓶完全浸没在长方体容器中,容器中上升的水的体积可能是( )毫升。
A.400 B.360 C.350 D.300
28.有8个形状完全相同的零件,其中有一个次品(次品轻一些)。用天平称,至少称( )次能保证找到次品。
A.1 B.2 C.3 D.4
四、计算题
29.口算。
-= -+= += 7-=
1.25×8= 10.8-6.8= 3.09+2.6= 13-7.4-2.6=
30.简便计算。
(1) (2)
(4)
31.解方程。
3(2-4)=9 12.3-7.5=57.6 2+23×4=134
32.细心算一算,求出下列图形的表面积和体积。(单位:)
五、作图题
33.操作。
(1)画出将圆A先向右平移2格,再向上平移2格后的图形B,平移后圆心的位置用数对表示是( )。
(2)过C点作直线O的平行线。
(3)先以P点为顶点画一个等腰三角形D,再画出将等腰三角形绕P点逆时针方向旋转90°后的图形E。
六、解答题
34.一个长方体形状的水池,长60米,宽30米,池中原来水深1.5米。如果用水泵向外排水,每分钟排2.5立方米,要求在15小时内把水池中的水排完,可能吗?
35.老师用泥巴做了一个长方体.如果把这个长方体的长增加2厘米,体积就增加40立方厘米;如果宽增加3厘米,体积就增加90立方厘米;如果高增加4厘米,体积就增加96立方厘米.求原来长方体的表面积是多少?
36.学校要把43根跳绳发给六年级正在上体育课的三个班,一班有64人,二班有56人,三班有52人,如果按人数分配发放,三个班各应领到多少跳绳?
37.冬天的一个早晨,李明和他爸爸踏着雪一前一后沿着一个圆形跑道从同一起点朝同一方向跑步锻炼,爸爸每步50厘米,李明每步30厘米,雪地上脚印时有重合,一圈跑下来,一共留下了1680个脚印,这个跑道一圈是多少米?
38.一间教室,长8米,宽6米,高3.5米.新学期粉刷教室的四壁,扣除门窗总面积20平方米,如果每平方米用涂料2.4千克,粉刷这间教室需涂料多少千克?(得数保留整数)
39.加工某种零件,需要三道工序.第一道工序的工人,每人每天可以完成48个;第二道工序的工人,每人每天可以完成32个;第三道工序的工人,每人每天可以完成28个.问三道工序至少各有多少工人搭配才算合理?
40.用一个底面是边长8厘米的正方形,高为17厘米的长方体容器,测量一个球形铁块的体积,容器中装的水距杯口还有2厘米。当铁块放入容器中,有部分水溢出,当把铁块取出后,水面下降5厘米,求铁球的体积。
41.学校甬路旁栽一行小树,从第一棵到最后一棵的距离是80米,原来每隔2米植一棵树,现小树长大,改为每5米植一棵树。如果两端不移动,中间有几棵树不用移动?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.8
【分析】观察规律:通过观察图形,发现每增加一幅图,减少面的数量存在一定规律。从第2幅图开始,相比前一幅图,每次增加的减少面数量是固定的。
总结规律表达式:经过分析可知,减少面的数量与图形的幅数存在这样的关系:减少面的数量=2×(图的幅数-1)。这里的2是每增加一幅图,减少面增加的数量(图的幅数-1)是因为从第2幅图才开始呈现这样的规律增加。
计算第5幅图减少面的数量:将图的幅数5代入上述规律表达式,即2×(5-1),按照先算括号内再算乘法的运算顺序进行计算。
【解析】2×(5-1)
=2×4
=8(个)
第5幅图减少8个面。
2.(1)大
(2)偶尔
(3)2
(4)23
【分析】(1)在1到20这些数中,判断3的倍数:根据倍数的定义,能被3整除的数就是3的倍数20÷3=6……2,所以3的倍数有3、6、9、12、15、18,共6个。判断5的倍数:能被5整除的数是5的倍数,20÷5=4,5的倍数有5、10、15、20,共4个。可能性大小比较:在总数相同的情况下,哪种数的数量越多,摸到的可能性就越大。因为6>4,所以摸到3的倍数比摸到5的倍数的可能性大。
(2)找23的因数:根据因数的定义,两个正整数相乘,这两个数都叫做积的因数23=1×23,所以23的因数是1和23 。判断摸到情况:在1到20中,只有1是23的因数,所以不是每次都能摸到23的因数,只是有时候能摸到,这种情况是偶尔能摸到。
(3)观察数的位数:在1到20中,1到9这9个数是一位数,10到20这11个数是两位数。分类结果:按照位数相同为一类来分,就有一位数和两位数这2种不同的结果。
(4)明确质数定义:质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数,选择合适数字:在20以上100以下有很多质数,比如23、29、31等。增加写有这些质数(如23)的卡片,质数在所有卡片中的数量占比就会增加根据可能性大小与数量有关,数是越多可能性越大,就能提高摸到质数的可能性。
【解析】(1)20÷3=6……2,3的倍数有6个;20÷5=4,5的倍数有4个。因为6> 4所以摸到3的倍数比摸到5的倍数的可能性大。
(2)23的因数是1和23 ,1到20中只有1是23的因数,所以是偶尔摸到23的因数。
(3)1到9是一位数,10到20是两位数,按位数分类有2种不同结果。
(4)20以上100以下质数如23,增加写有23的卡片可提高摸到质数可能性。(答案不唯一)
3.(1) 折线 上升
(2)150
(3)160
【分析】(1)要清楚地表示出小芳4次跳绳变化趋势,可选用折线统计图,不仅能表示数量,还能表示次数的变化趋势,小芳4次的成绩都是逐渐升高,据此得出答案。
(2)小芳平均成绩=4次成绩之和÷4,可计算得到平均数。
(3)先用及格线152乘5次得到总的跳绳次数,再减去4次跳绳个数之和得到答案。
【解析】(1)如果要清楚表现小芳4次跳绳成绩变化趋势,可将其成绩绘制成折线统计图,小芳4次跳绳成绩变化整体呈上升趋势。
(2)(147+149+150+154)÷4
=600÷4
=150(个)
即小芳4次的平均成绩是150个。
(3)152×5-(147+149+150+154)
=760-600
=160(个)
即小芳最后一次至少要跳160个才能达到优秀水平。
4.14 15
【分析】根据经过时间=结束时间-开始时间,求出经过时间,再根据1天=24小时进行换算,即可解答。
【解析】6月26日8时-6月11日17时=14天15小时
15÷24=(天)
14天15小时= 天
所以,神十在太空飞行共14天15时,合 天。
5.(1)30
(2) 8 50
(3)12
【分析】(1)根据图片可知小明9时到9时30分,距离没有发生变化,可以推测出这段时间小明一直在公园。用9时30分减去9时即可求出在公园的时间。
(2)根据图片可知,小明在从家到公园的途中,在8时20分到8时30分休息了10分钟。如果不休息,那么9时到达公园的时间可以提前10分钟,用9时减去10分即可。
(3)根据图片可知,小明9时30分从家出发,10时到家,一共用了30分钟,即0.5小时。用路程6千米除以时间0.5小时即可求出小明的速度。
【解析】(1)9时30分-9时=30分
所以小明在公园玩了30分钟。
(2)8时30分 8时20分=10分
9时-10分=8时50分
所以如果一直走,能在8时50分到达公园。
(3)10时-9时30分=30分
30分=0.5时
6÷0.5=12(千米/时)
所以返回时,小明骑自行车的速度是每小时12千米。
6.条形 折线
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;由此根据情况选择即可。
【解析】要反映大埔、五华、丰顺、平远四个县6月份的降水量,可以选用条形统计图,要反映广东省2024年1~6月份降水量的变化情况应选用折线统计图。
7.6 9
【分析】
根据观察物体的方法,一个立体图形,从上面看是,可知底层有5个小正方体,从左面看是,可知有2层,上层至少有1个小正方体,最多有4个小正方体,据此解答即可。
【解析】5+1=6(个)
5+4=9(个)
所以一个立体图形,从上面看是,从左面看是,要搭这样的立体图形,最少需要6个小正方体,最多能用9个小正方体。
8.3 8
【分析】要切成同样大小的正方体,正方体棱长需是长方体长、宽、高的公因数,12、6、3的公因数有1、3 ,所以最大公因数是3,即切成的正方体棱长最大是3厘米;
分别计算长方体长、宽、高方向能切出的正方体个数:长方体长12厘米,12÷3=4,长的方向可切出4个;宽6厘米,6÷3=2,宽的方向可切出2个;高3厘米,3÷3=1,高的方向可切出1个; 最后将三个方向个数相乘,4×2×1=8,最多可切成8个。
【解析】12=2×2×3
6=2×3
12、6、3的最大公因数是3,所以小正方体的棱长最大就是3厘米;
(12÷3)×(6÷3)×(3÷3)
=4×2×1
=8×1
=8(个)
所以最多可切成8个。
9. 29
【分析】将带分数化为假分数,分数单位由分母决定,分母是9,其分数单位就是;
明确最小合数是4 ,化为同分母分数,用减去得,里的个数就是要减去的个数。
【解析】==,分母是9,所以分数单位就是;
最小的合数是4,4=;
=,因此再减去29个这样的分数单位就变成了最小的合数。
10.960400000 10亿
【分析】最大的一位数是9,2和3的最小公倍数是2×3=6,最小的合数是4。据此先写出这个数。省略亿位后面的尾数,看千万位的大小,千万位是6,需向前进一;将亿位后面的数去掉,并在数的末尾添上一个亿字。
【解析】亿位上是9,千万位上是6,十万位上是4,其余各位上都是0,这个数写作:960400000,960400000≈10亿。
所以这个数写作960400000,省略亿后面的尾数约是10亿。
11.96 90
【分析】已知在长方体玻璃容器中摆了若干个体积为1cm3的小正方体,根据正方体的体积公式V=a3,可知体积为1立方厘米的小正方体的棱长是1cm;从图中可以看出,长方体玻璃容器的长摆了6个小正方体,则长是6cm;宽摆了5个小正方体,则宽是5cm;高摆了3个小正方体,则高是3cm;因为长方形的玻璃容器时无盖的,所以长方形容器的表面积=长×宽+长×高×2+宽×高×2,代入数据计算,求出这个玻璃容器的表面积;根据长方体的体积(容积)=长×宽×高,代入数据计算,求出这个玻璃容器的容积。
【解析】因为1×1×1=1(cm3),所以小正方体棱长为1cm,
长方体玻璃容器的长为:1×6=6(cm)
长方体玻璃容器的宽为:1×5=5(cm)
长方体玻璃容器的高为:1×3=3(cm)
6×5+6×3×2+5×3×2
=30+36+30
=96(cm2)
6×5×3
=30×3
=90(cm3)
所以制作这个容器需要96cm2的玻璃,它的体积是90cm3。
12.224 1344
【分析】根据长方体的展开图知,这个长方体的长是16cm,高是6cm,宽是(20-6=14)cm,根据长方体的底面积=长×宽,体积(容积)=底面积×高,把数据代入公式解答即可。
【解析】20-6=14(cm)
16×14=224(cm2)
224×6=1344(cm3)
这个纸盒的底面积是224cm2,容积是1344cm3。
13.×
【分析】一个数的倍数的个数是无限的,最小的是它本身,没有最大的倍数。一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。可举例说明。
【解析】一个数的最小倍数等于这个数的最大因数,如7既是7的倍数也是7的因数,所以原题说法错误。
故答案为:×
14.×
【分析】正方体的表面积是指正方体的6个面的总面积。正方体的体积是指正方体所占空间的大小。因为表面积和体积不是同类量,所以无法进行比较,据此判断。
【解析】正方体的表面积和体积不是同类量,所以无法进行比较。
原题说法错误。
故答案为:×
15.×
【分析】长方形有两条对称轴,对称轴交点如图所示,长方形至少绕其对称轴的交点顺时针(或逆时针)旋转180°,才能与原图形重合,据此解答。
【解析】根据分析可知,一个长方形绕它的中心点至少要旋转180°才能与原长方形重合。
原题干说法错误。
故答案为:×
16.√
【分析】旋转是指在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。
旋转的特征:图形旋转后,形状和大小都没有发生变化,只是位置发生了变化。
【解析】根据旋转的意义及特征可知,一个图形经过旋转后,形状和大小都不会变化。
原题说法正确。
故答案为:√
17.√
【分析】分析题目,把绳子的总长度看作单位“1”,第二段占全长的,则第一段占全长的(1-),据此比较对应的分率即可确定哪段长。
【解析】1-=
因为>,所以第二段比第一段长,原说法正确。
故答案为:√
18.×
【分析】把它抛向空中,落下后每个数字都可能朝上,即有6种可能的结果,在1~6中,合数有4和6。以这6种可能的结果为单位“1”,根据求一个数是另一个数的几分之几,用除法计算,用2÷6即可求出落下后朝上的点数是合数的可能性的大小。
【解析】在1~6中,合数有4和6。
2÷6=
落下后朝上的点数是合数的可能性是,原题说法错误。
故答案为:×。
19.D
【分析】2的倍数特征:个位上是0、2、4、6、8的数。
5的倍数特征:个位上是0或5的数。
2、5的倍数特征:个位上是0的数。
3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【解析】A.2+3+5=10,10不是3的倍数,且2、3、5中没有0,所以2、3、5组成的三位数既不是2、5的倍数,又不是3的倍数。
B.0+2+3=5,5不是3的倍数,0、2、3中的0放在个位,所以0、2、3组成的三位数可以是2、5的倍数,但不是3的倍数。
C.0+5+8=13,13不是3的倍数,0、5、8中的0放在个位,所以0、5、8组成的三位数可以是2、5的倍数,但不是3的倍数。
D.0+5+7=12,12是3的倍数,0、5、7中的0放在个位,所以0、5、7组成的三位数既是2、5的倍数,又是3的倍数。
故答案为:D
20.C
【分析】可能性大小,就是事情出现的概率,可能性等于所求情况数占总情况数的几分之几,硬币有两面,每一面的出现的可能性都是。
【解析】硬币有两面,每一面出现的可能性都是:1÷2=
所以第6次投掷正面朝上的可能性是。
故答案为:C
21.B
【分析】明确观察物体的方法,先确定有几列或几行,每列或每行有几个,形状是怎样的。从左面看,能看到两层小正方形,底下第一层两个小正方形,第二层一个小正方形靠左。
【解析】A.从正面看是;
B.从左面看是;
C.从上面看是;
D.不是的三视图。
故答案为:B
22.C
【分析】根据题意,用8个同样大小的小正方体拼成的,因为每个小正方体都在顶点处,每个小正方体都外露3个面,如果任意拿走1个小正方体,就会外露相同的3个面,所以它的表面积与原来相比不变。
【解析】据分析可知,用8个边长是1分米的小正方体拼成一个大正方体,任意拿走一个小正方体后,表面积不变。
故答案为:C
23.C
【分析】打电话通知队员时,每分钟通知1人,并且在下一分钟知道演出消息的人再分别通知1人,以此类推就是最快的通知方式。下一分钟知道消息的人数(包含老师)是这分钟的2倍。据此通过例举的方式,解题即可。
【解析】第一分钟通知到1个队员;
第二分钟最多可通知到1+2=3(个)队员;
第三分钟最多可通知到3+4=7(个)队员;
第四分钟最多可通知到7+8=15(个)队员;
第五分钟最多可通知到15+16=31(个)队员。
所以,要通知全体队员至少需要5分钟才能通知到所有人。
故答案为:C
24.B
【分析】同辞家门赴车站,两人同时从家出发,两条折线重合呈上升趋势;别时叮咛嘱万千,在车站停留,两条折线重合平缓无变化;学子满载信心去,老父怀抱希望还,表示这位同学的折线又呈上升趋势,表示父亲的折线呈下降趋势回到起点,据此分析。
【解析】A.没有表示出在车站停留,排除;
B.图象与诗意大致吻合;
C.没有表示出两人同时从家出发,也没有表示出在车站停留,排除;
D.没有表示出在车站停留,排除。
图象与上述诗意大致吻合的是。
故答案为:B
25.C
【分析】一套桌椅共300元,即桌子和椅子一共300元;其中椅子的价格比桌子少,是把桌子的价格看成单位“1”,平均分成11份,椅子价格比桌子价格少这样的7份;据此分析选项。
【解析】A.已知一套桌椅共300元,一套桌椅包含桌子和椅子,所以桌子价格+椅子价格=300元 ,该选项分析正确;
B.“椅子的价格比桌子少”,这里是把桌子价格看作单位“1”,所以椅子比桌子少的价格是桌子价格的 ,该选项分析正确。
C.椅子的价格比桌子少,把桌子价格看作11份,那么椅子比桌子少7份,椅子价格就是11-7=4份,所以椅子和桌子的价格比是4∶11,而不是7∶11,该选项分析错误。
故答案为:C
26.B
【分析】根据题意可知,甲的等于乙的,根据两个非0的因数相乘的积相等,一个因数越大,另一个因数越小进行解答即可。
【解析】甲×=乙×
=
=
>
所以甲<乙,即乙彩带长。
故答案为:B
27.A
【分析】由题目和图可知,矿泉水瓶中的水的体积为360毫升,因为矿泉水瓶中水并未装满,则当矿泉水瓶完全浸没在长方体容器时,此时上升水的体积就是矿泉水瓶的体积,则上升的水的体积一定大于360毫升。
【解析】由分析可知,矿泉水瓶中的水的体积为360毫升,因为矿泉水瓶中水并未装满,则当矿泉水完全浸没在长方体容器时,上升的水的体积一定大于360毫升。
故答案为:A
28.B
【分析】把8个零件分成(3,3,2)三组,把两个3个一组的放在天平上称,如天平平衡,则次品在2个的一组中,把这2个零件分成(1,1),放在天平上称,上跷的是次品;如不平衡,则把上跷的一组3个零件分成(1,1,1),任意两个放在天平上称,如平衡,没称的是次品,如不平衡,上跷的是次品。据此解答。
【解析】第一次称量:把8个零件分成3组:3、3、2,先在天平两边分别放3个零件,会有两种情况出现:
情况一:左右平衡,则次品在剩下的2个中,即可进行第二次称量;把剩下的2个,放在天平的两边一边1个,
则托盘上升一边为次品;
情况二:若左右不平衡,则次品在托盘上升的一边3个中,由此即可进行第二次称量,从上升一边的3个拿出2个,放在天平的两边一边1个,若天平平衡,则剩下1个是次品;若天平不平衡,则托盘上升一边为次品。
综上所述,至少需要称2次,才能找到次品。
故答案为:B
29.;;;;
10;4;5.69;3
【解析】略
30.(1)1;(2)192
(3);(4)1
【分析】(1),交换中间减数和加数的位置,添括号,括号前边是减号,添上括号,括号里的加号变减号,转化成,同时算出小括号里的加法和减法,最后算括号外的减法;
(2),逆用乘法分配律,先算(56.4+43.6),再与1.92相乘;
(3),根据减法的性质,将后两个数先加起来再计算;
(4),观察这个分数,先看分子中2013×2014,将2013拆成(2012+1),根据乘法分配律,小括号里的数分别与2014相乘,再相加,最终得,即分子转化成,分子是,与分母相同,约分后得1。
【解析】(1)
(2)
(3)
(4)
31.(1);(2);(3)
【分析】(1)先把方程化简成,再根据等式的基本性质,方程两边先同时加上12,再同时除以6求解;
(2)先把方程化简成,再根据等式的基本性质,方程两边同时除以4.8求解;
(3)先把方程化简成,再根据等式的基本性质,方程两边先同时减去92,再同时除以2求解。
【解析】(1)
解:
(2)
解:
(3)
解:
32.图1:表面积:216dm2;体积:204dm3
图2:表面积:79dm2;体积:41dm3
【分析】图1;正方体挖去一个长方体,减少3个面的面积,又增加3个面的面积,所以表面积=棱长是6dm正方体的表面积;根据正方体的表面积公式:表面积=棱长×棱长×6,代入数据,求出表面积;
体积=棱长是6dm的正方体的体积-长是2dm,宽是2dm,高是3dm长方体的体积,根据正方体体积公式:体积=棱长×棱长×棱长,长方体体积公式:体积=长×宽×高,代入数据,即可解答。
图2:表面积=长是4dm,宽是4dm,高是2dm的长方体的表面积+长是3dm,宽是2dm,高是1.5dm的长方体的侧面积,根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,长方体侧面积公式:侧面积=(长×高+宽×高)×2,代入数据,即可解答。
体积=长是4dm,宽是4dm,高是2dm的长方体的体积+长是3dm,宽是2dm,高是1.5dm的长方体的体积,根据长方体体积公式:体积=长×宽×高,代入数据,即可解答。
【解析】图1:表面积:
6×6×6
=36×6
=216(dm2)
体积:6×6×6-2×2×3
=36×6-4×3
=216-12
=204(dm3)
表面积是216dm2;体积是204dm3。
图2:表面积:
(4×4+4×2+4×2)×2+(3×1.5+2×1.5)×2
=(16+8+8)×2+(4.5+3)×2
=(24+8)×2+7.5×2
=32×2+7.5×2
=64+15
=79(dm2)
体积:
4×4×2+3×2×1.5
=16×2+6×1.5
=32+9
=41(dm3)
表面积是79dm2,体积是41dm3。
33.(1)图见详解;(4,5)
(2)(3)见详解
【分析】(1)根据平移的特征,将圆A的圆心先向右平移2格,再向上平移2格后画出平移后的圆。数对的表示方法:(列数,行数),数对的第一个数表示列,第二个数表示行,找出平移后的圆心在方格中对应的列数和行数,再用数对表示出来。
(2)根据画平行线的步骤“一贴、二靠、三推、四画”,把三角板的一条直角边与已知直线O重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和C点重合,过C点沿三角板的直角边画直线即可。
(3)等腰三角形是有两条边相等的三角形。先以点P为顶点画一个等腰三角形,然后根据旋转的特征,将三角形绕点P逆时针旋转90°,点P的位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
【解析】(1)画出将圆A先向右平移2格,再向上平移2格后的图形B,平移后圆心的位置用数对表示是(4,5)。
(1)(2)(3)如图:
34.不可能
【分析】先求出长方体形状的水池的水的体积,根据每分钟排2.5立方米,求出排出水用的时间,用的时间和15小时比较,小于15小时,就够,否则不够。据此解答即可。
【解析】长方体形状的水池的水的体积:
60×30×1.5
=1800×1.5
=2700(立方米)
2700÷2.5=1080(分钟)
1080分钟=18小时
因为18小时>15小时
所以15小时不够,不能把水池中的水排完。
答:要求在15小时内把水池中的水排完,不可能
35.148平方厘米
【解析】解决本题的关键是理解体积增加的部分是如何得到的.比如:把长方体的长增加2厘米,长方体的体积就会增加一个“以长方体的宽×高为底面积,2厘米为高的”小长方体的体积,即宽×高×2=40,所以可以得出:宽×高=20(平方厘米);同理可得:长×高=90÷3=30(平方厘米),长×宽=96÷4=24(平方厘米),这时再计算原来长方体的表面积就很简单了.
由题意可知,宽×高=40÷2=20(平方厘米)
长×高=90÷3=30(平方厘米)
长×宽=96÷4=24(平方厘米)
所以,2×(长×宽+长×高+宽×高) =2×(20+30+24) =148(平方厘米)
答:原来长方体的表面积是148平方厘米.
36.一班分到16根,二班分到14根,三班分到13根.
【解析】试题分析:首先求得三个班的总份数,再求得三个班各占总数的几分之几,最后求得三个班各应领到的跳绳,列式解答即可.
解:64+56+52=172(人)
43×=16(根)
43×=14(根)
43×=13(根);
答:一班分到16根,二班分到14根,三班分到13根.
【点评】此题主要考查按比例分配应用题的特点:已知两个数的比(三个数的比),两个数的和(三个数的和),求这两个数(三个数),用按比例分配解答.
37.这个跑道一圈长360米
【解析】试题分析:因他们的起点和走的方向完全相同,也就是一前一后的走,脚印一定有重合的,即重合在两人步子长度的公倍数上,所以先求出他们步长的最小公倍数,再求出他们脚印重合时的步数,然后再据总步数及最小公倍数即能求出这条路的长度,也就是环形跑道长
解答:解:50=5×5×2,30=2×3×5
50和30的最小公倍数是:2×3×5×5=150,
第一次两人脚印重合时,爸爸走的步数:150÷5=3(步),小明走的步数:150÷3=5(步),
即爸爸3步与小明5步时脚印重合一次,此时有3+5﹣1=7个脚印,距离是150厘米,
总共有1680个脚印,应重合的次数:1680÷7=240(次)
所以这条路长是240×150=36000(厘米)
36000厘米=360米;
答:这个跑道一圈长360米.
点评:完成本题首先要明确两人的脚印是有重合的,重合在两人步子长度的公倍数上,通过求他们步子长度的最小公倍数即能求出两人脚印重合时脚印数的循环规律.
38.粉刷这间教室需涂料303千克
【解析】试题分析:求需要粉刷的面积,就是用教室顶棚的面积加上四面墙壁的面积减去门窗的面积,长、宽、高已知,利用长方体的表面积公式即可求解;用需要粉刷的面积乘每平方米需要的涂料的量,就是一共需要的涂料的量.
解答:解:8×6+8×3.5×2+6×3.5×2﹣20
=48+56+42﹣20
=146﹣20
=126(平方米);
126×2.4=302.4≈303(千克);
答:粉刷这间教室需涂料303千克.
点评:解答有关长方体计算的实际问题,一定要搞清所求的是什么,再进一步选择合理的计算方法进行计算解答问题.
39.第一、二、三道工序至少需要工人分别为14人、21人、24人
【分析】先求出48,32和24的最小公倍数,然后用这个最小公倍数分别除以48,32,28即可.
【解析】要想搭配合理,那么每道工序完成的零件个数应该相等,
因为:[48,32,28]=672,所以:
第一道工序至少需要工人672÷48=14(人)
第二道工序至少需要工人672÷32=21(人)
第三道工序至少需要工人672÷28=24(人)
答:第一、二、三道工序至少需要工人分别为14人、21人、24人.
40.320立方厘米
【分析】由题意可知,当球形铁块放入容器中,有部分水溢出;长方体容器中下降(5﹣2)厘米的水的体积加上2厘米高的水的体积(溢出的水的体积)就等于这个球形铁块的体积;也就是说,球形铁块的体积,就相当于5厘米高的水的体积,根据长方体的体积公式V=Sh,列式解答。
【解析】8×8×5
=64×5
=320(立方厘米)。
答:铁球的体积是320立方厘米。
41.7棵
【分析】此题属于植树问题,两端不移动,要求中间有几棵树不用移动,只要求出在80以内2和5的公倍数即可解答,即是2和5的公倍数的米数是不动的。
【解析】80以内的2和5的公倍数有:10;20;30;40;50;60;70;
即10米、20米、30米、40米、50米、60米、70米处的7棵树不用动;
答:中间有7棵树不动。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年五年级下册数学期末考前冲刺预测卷(人教版)
一、填空题
1.如图,按照这样的规律摆下去,第5幅图减少( )个面。
2.有20张卡片,上面分别写有数字1~20,从中任意摸一张。
(1)摸到3的倍数比摸到5的倍数的可能性( )。
(2)( )(填“经常”“偶尔”“不可能”或“一定”)摸到23的因数。
(3)如果按摸到的数是几位数分类(位数相同的为一类),会有( )种不同的结果。
(4)要提高摸到质数的可能性,可以再增加一张卡片,这张卡片上可以写数字( )(20以上,100以下)。
3.一场“1分钟跳绳”比赛活动,每个人可跳5次,取平均个数作最后成绩。小劳前4次分别跳了147个、149个、150个、154个。
(1)如果要清楚表现小芳4次跳绳成绩变化趋势,可将其成绩绘制成( )统计图,小芳4次跳绳成绩变化整体呈( )趋势。
(2)小芳4次的平均成绩是( )个。
(3)“152个及以上”为优秀,小芳最后一次至少要跳( )个才能达到优秀水平。
4.神舟十号飞船于2013年6月11日17时从酒泉卫星发射中心发射,6月26日8时,神舟十号载人飞船返回舱在内蒙古中部预定区域安全着陆。神十在太空飞行共( )天( )时,合( )天。
5.小明去6千米远的公园玩,请根据折线图回答问题。
(1)小明在公园玩了( )分钟。
(2)如果一直走,不休息,能在( )时( )分到达公园。
(3)返回时,小明骑自行车的速度是每小时( )千米。
6.要反映大埔、五华、丰顺、平远四个县6月份的降水量,可以选用( )统计图,要反映广东省2024年1~6月份降水量的变化情况应选用( )统计图。
7.一个立体图形,从上面看是,从左面看是,要搭这样的立体图形,最少需要( )个小正方体,最多能用( )个小正方体。
8.把一个长、宽、高分别为12厘米、6厘米、3厘米的长方体切成同样大小的正方体,切成的正方体棱长最大是( )厘米,最多可切成( )个。
9.的分数单位是 ,再减去 个这样的分数单位就变成了最小的合数。
10.一个九位数,最高位上是最大的一位数,千万位上是2和3的最小公倍数,十万位上是最小的合数,其余各位上都是0,这个数写作 ,省略亿后面的尾数约是 。
11.张天悦在一个无盖的长方体玻璃容器中摆了若干个体积为1cm3的小正方体(如图)。制作这个容器需要 cm2的玻璃,它的体积是 cm3。
12.用如图所示的硬纸板做成一个无盖的长方体纸盒(单位:cm),这个纸盒的底面积是( )cm2,容积是( )cm3。(纸板厚度忽略不计)
二、判断题
13.一个数的倍数一定大于这个数的因数。( )
14.棱长为6cm的正方体表面积和体积相等。( )
15.一个长方形绕它的中心点至少要旋转90°才能与原长方形重合。( )
16.一个图形经过旋转后,形状和大小都不会变化。( )
17.把一根绳子剪成两段,第一段长m,第二段占全长的,第二段比第一段长。( )
18.一个正方体骰子的六个面上分别写着数字1~6,把它抛向空中,落下后朝上的点数是合数的可能性是。( )
三、选择题
19.下列数中,( )组的数字能组成一个三位数,它既是2的倍数,又是3的倍数,还是5的倍数。
A.2、3、5 B.0、2、3 C.0、5、8 D.0、5、7
20.投掷一枚硬币5次,有4次正面朝上,1次正面朝下,那么第6次投掷正面朝上的可能性是( )。
A. B. C.
21.如图是由4个同样的小正方体摆成的几何体,从左面看到的图形是( )。
A. B. C. D.
22.用8个边长是1分米的小正方体拼成一个大正方体,任意拿走一个小正方体后,表面积( )。
A.减少6平方分米 B.减少3平方分米 C.不变
23.红光小学鼓号队有31人,暑假期间有一个紧急演出,李老师需要尽快通知到每个队员。如果用打电话的方式,每分钟通知1人,每个同学接到电话后又打给其它同学,同时李老师也在不停的打,要通知全体队员至少需要_____分钟才能通知到所有人。( )
A.7 B.6 C.5 D.4
24.某期刊专栏登出一同学回忆父亲的诗:“同辞家门赴车站,别时叮咛嘱万千。学子满载信心去,老父怀抱希望还。”如果用纵轴y表示离家的距离,横轴t表示离家的时间,那么图象与上述诗意大致吻合的是( )。
A. B.
C. D.
25.一套桌椅共300元,其中椅子的价格比桌子少,对上述条件的分析有误的是( )。
A.桌子价格+椅子价格=300元。
B.椅子比桌子少的价格是桌子价格的。
C.椅子和桌子的价格比是7∶11。
26.用一张长方形纸遮住了甲、乙两根彩带的右端,露出左端的长度与原来长度的关系如图所示,那么两根彩带原来的长度相比,( )。
A.甲彩带长 B.乙彩带长 C.一样长 D.无法比较
27.将如图的饮料瓶完全浸没在长方体容器中,容器中上升的水的体积可能是( )毫升。
A.400 B.360 C.350 D.300
28.有8个形状完全相同的零件,其中有一个次品(次品轻一些)。用天平称,至少称( )次能保证找到次品。
A.1 B.2 C.3 D.4
四、计算题
29.口算。
-= -+= += 7-=
1.25×8= 10.8-6.8= 3.09+2.6= 13-7.4-2.6=
30.简便计算。
(1) (2)
(4)
31.解方程。
3(2-4)=9 12.3-7.5=57.6 2+23×4=134
32.细心算一算,求出下列图形的表面积和体积。(单位:)
五、作图题
33.操作。
(1)画出将圆A先向右平移2格,再向上平移2格后的图形B,平移后圆心的位置用数对表示是( )。
(2)过C点作直线O的平行线。
(3)先以P点为顶点画一个等腰三角形D,再画出将等腰三角形绕P点逆时针方向旋转90°后的图形E。
六、解答题
34.一个长方体形状的水池,长60米,宽30米,池中原来水深1.5米。如果用水泵向外排水,每分钟排2.5立方米,要求在15小时内把水池中的水排完,可能吗?
35.老师用泥巴做了一个长方体.如果把这个长方体的长增加2厘米,体积就增加40立方厘米;如果宽增加3厘米,体积就增加90立方厘米;如果高增加4厘米,体积就增加96立方厘米.求原来长方体的表面积是多少?
36.学校要把43根跳绳发给六年级正在上体育课的三个班,一班有64人,二班有56人,三班有52人,如果按人数分配发放,三个班各应领到多少跳绳?
37.冬天的一个早晨,李明和他爸爸踏着雪一前一后沿着一个圆形跑道从同一起点朝同一方向跑步锻炼,爸爸每步50厘米,李明每步30厘米,雪地上脚印时有重合,一圈跑下来,一共留下了1680个脚印,这个跑道一圈是多少米?
38.一间教室,长8米,宽6米,高3.5米.新学期粉刷教室的四壁,扣除门窗总面积20平方米,如果每平方米用涂料2.4千克,粉刷这间教室需涂料多少千克?(得数保留整数)
39.加工某种零件,需要三道工序.第一道工序的工人,每人每天可以完成48个;第二道工序的工人,每人每天可以完成32个;第三道工序的工人,每人每天可以完成28个.问三道工序至少各有多少工人搭配才算合理?
40.用一个底面是边长8厘米的正方形,高为17厘米的长方体容器,测量一个球形铁块的体积,容器中装的水距杯口还有2厘米。当铁块放入容器中,有部分水溢出,当把铁块取出后,水面下降5厘米,求铁球的体积。
41.学校甬路旁栽一行小树,从第一棵到最后一棵的距离是80米,原来每隔2米植一棵树,现小树长大,改为每5米植一棵树。如果两端不移动,中间有几棵树不用移动?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.8
【分析】观察规律:通过观察图形,发现每增加一幅图,减少面的数量存在一定规律。从第2幅图开始,相比前一幅图,每次增加的减少面数量是固定的。
总结规律表达式:经过分析可知,减少面的数量与图形的幅数存在这样的关系:减少面的数量=2×(图的幅数-1)。这里的2是每增加一幅图,减少面增加的数量(图的幅数-1)是因为从第2幅图才开始呈现这样的规律增加。
计算第5幅图减少面的数量:将图的幅数5代入上述规律表达式,即2×(5-1),按照先算括号内再算乘法的运算顺序进行计算。
【解析】2×(5-1)
=2×4
=8(个)
第5幅图减少8个面。
2.(1)大
(2)偶尔
(3)2
(4)23
【分析】(1)在1到20这些数中,判断3的倍数:根据倍数的定义,能被3整除的数就是3的倍数20÷3=6……2,所以3的倍数有3、6、9、12、15、18,共6个。判断5的倍数:能被5整除的数是5的倍数,20÷5=4,5的倍数有5、10、15、20,共4个。可能性大小比较:在总数相同的情况下,哪种数的数量越多,摸到的可能性就越大。因为6>4,所以摸到3的倍数比摸到5的倍数的可能性大。
(2)找23的因数:根据因数的定义,两个正整数相乘,这两个数都叫做积的因数23=1×23,所以23的因数是1和23 。判断摸到情况:在1到20中,只有1是23的因数,所以不是每次都能摸到23的因数,只是有时候能摸到,这种情况是偶尔能摸到。
(3)观察数的位数:在1到20中,1到9这9个数是一位数,10到20这11个数是两位数。分类结果:按照位数相同为一类来分,就有一位数和两位数这2种不同的结果。
(4)明确质数定义:质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数,选择合适数字:在20以上100以下有很多质数,比如23、29、31等。增加写有这些质数(如23)的卡片,质数在所有卡片中的数量占比就会增加根据可能性大小与数量有关,数是越多可能性越大,就能提高摸到质数的可能性。
【解析】(1)20÷3=6……2,3的倍数有6个;20÷5=4,5的倍数有4个。因为6> 4所以摸到3的倍数比摸到5的倍数的可能性大。
(2)23的因数是1和23 ,1到20中只有1是23的因数,所以是偶尔摸到23的因数。
(3)1到9是一位数,10到20是两位数,按位数分类有2种不同结果。
(4)20以上100以下质数如23,增加写有23的卡片可提高摸到质数可能性。(答案不唯一)
3.(1) 折线 上升
(2)150
(3)160
【分析】(1)要清楚地表示出小芳4次跳绳变化趋势,可选用折线统计图,不仅能表示数量,还能表示次数的变化趋势,小芳4次的成绩都是逐渐升高,据此得出答案。
(2)小芳平均成绩=4次成绩之和÷4,可计算得到平均数。
(3)先用及格线152乘5次得到总的跳绳次数,再减去4次跳绳个数之和得到答案。
【解析】(1)如果要清楚表现小芳4次跳绳成绩变化趋势,可将其成绩绘制成折线统计图,小芳4次跳绳成绩变化整体呈上升趋势。
(2)(147+149+150+154)÷4
=600÷4
=150(个)
即小芳4次的平均成绩是150个。
(3)152×5-(147+149+150+154)
=760-600
=160(个)
即小芳最后一次至少要跳160个才能达到优秀水平。
4.14 15
【分析】根据经过时间=结束时间-开始时间,求出经过时间,再根据1天=24小时进行换算,即可解答。
【解析】6月26日8时-6月11日17时=14天15小时
15÷24=(天)
14天15小时= 天
所以,神十在太空飞行共14天15时,合 天。
5.(1)30
(2) 8 50
(3)12
【分析】(1)根据图片可知小明9时到9时30分,距离没有发生变化,可以推测出这段时间小明一直在公园。用9时30分减去9时即可求出在公园的时间。
(2)根据图片可知,小明在从家到公园的途中,在8时20分到8时30分休息了10分钟。如果不休息,那么9时到达公园的时间可以提前10分钟,用9时减去10分即可。
(3)根据图片可知,小明9时30分从家出发,10时到家,一共用了30分钟,即0.5小时。用路程6千米除以时间0.5小时即可求出小明的速度。
【解析】(1)9时30分-9时=30分
所以小明在公园玩了30分钟。
(2)8时30分 8时20分=10分
9时-10分=8时50分
所以如果一直走,能在8时50分到达公园。
(3)10时-9时30分=30分
30分=0.5时
6÷0.5=12(千米/时)
所以返回时,小明骑自行车的速度是每小时12千米。
6.条形 折线
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;由此根据情况选择即可。
【解析】要反映大埔、五华、丰顺、平远四个县6月份的降水量,可以选用条形统计图,要反映广东省2024年1~6月份降水量的变化情况应选用折线统计图。
7.6 9
【分析】
根据观察物体的方法,一个立体图形,从上面看是,可知底层有5个小正方体,从左面看是,可知有2层,上层至少有1个小正方体,最多有4个小正方体,据此解答即可。
【解析】5+1=6(个)
5+4=9(个)
所以一个立体图形,从上面看是,从左面看是,要搭这样的立体图形,最少需要6个小正方体,最多能用9个小正方体。
8.3 8
【分析】要切成同样大小的正方体,正方体棱长需是长方体长、宽、高的公因数,12、6、3的公因数有1、3 ,所以最大公因数是3,即切成的正方体棱长最大是3厘米;
分别计算长方体长、宽、高方向能切出的正方体个数:长方体长12厘米,12÷3=4,长的方向可切出4个;宽6厘米,6÷3=2,宽的方向可切出2个;高3厘米,3÷3=1,高的方向可切出1个; 最后将三个方向个数相乘,4×2×1=8,最多可切成8个。
【解析】12=2×2×3
6=2×3
12、6、3的最大公因数是3,所以小正方体的棱长最大就是3厘米;
(12÷3)×(6÷3)×(3÷3)
=4×2×1
=8×1
=8(个)
所以最多可切成8个。
9. 29
【分析】将带分数化为假分数,分数单位由分母决定,分母是9,其分数单位就是;
明确最小合数是4 ,化为同分母分数,用减去得,里的个数就是要减去的个数。
【解析】==,分母是9,所以分数单位就是;
最小的合数是4,4=;
=,因此再减去29个这样的分数单位就变成了最小的合数。
10.960400000 10亿
【分析】最大的一位数是9,2和3的最小公倍数是2×3=6,最小的合数是4。据此先写出这个数。省略亿位后面的尾数,看千万位的大小,千万位是6,需向前进一;将亿位后面的数去掉,并在数的末尾添上一个亿字。
【解析】亿位上是9,千万位上是6,十万位上是4,其余各位上都是0,这个数写作:960400000,960400000≈10亿。
所以这个数写作960400000,省略亿后面的尾数约是10亿。
11.96 90
【分析】已知在长方体玻璃容器中摆了若干个体积为1cm3的小正方体,根据正方体的体积公式V=a3,可知体积为1立方厘米的小正方体的棱长是1cm;从图中可以看出,长方体玻璃容器的长摆了6个小正方体,则长是6cm;宽摆了5个小正方体,则宽是5cm;高摆了3个小正方体,则高是3cm;因为长方形的玻璃容器时无盖的,所以长方形容器的表面积=长×宽+长×高×2+宽×高×2,代入数据计算,求出这个玻璃容器的表面积;根据长方体的体积(容积)=长×宽×高,代入数据计算,求出这个玻璃容器的容积。
【解析】因为1×1×1=1(cm3),所以小正方体棱长为1cm,
长方体玻璃容器的长为:1×6=6(cm)
长方体玻璃容器的宽为:1×5=5(cm)
长方体玻璃容器的高为:1×3=3(cm)
6×5+6×3×2+5×3×2
=30+36+30
=96(cm2)
6×5×3
=30×3
=90(cm3)
所以制作这个容器需要96cm2的玻璃,它的体积是90cm3。
12.224 1344
【分析】根据长方体的展开图知,这个长方体的长是16cm,高是6cm,宽是(20-6=14)cm,根据长方体的底面积=长×宽,体积(容积)=底面积×高,把数据代入公式解答即可。
【解析】20-6=14(cm)
16×14=224(cm2)
224×6=1344(cm3)
这个纸盒的底面积是224cm2,容积是1344cm3。
13.×
【分析】一个数的倍数的个数是无限的,最小的是它本身,没有最大的倍数。一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。可举例说明。
【解析】一个数的最小倍数等于这个数的最大因数,如7既是7的倍数也是7的因数,所以原题说法错误。
故答案为:×
14.×
【分析】正方体的表面积是指正方体的6个面的总面积。正方体的体积是指正方体所占空间的大小。因为表面积和体积不是同类量,所以无法进行比较,据此判断。
【解析】正方体的表面积和体积不是同类量,所以无法进行比较。
原题说法错误。
故答案为:×
15.×
【分析】长方形有两条对称轴,对称轴交点如图所示,长方形至少绕其对称轴的交点顺时针(或逆时针)旋转180°,才能与原图形重合,据此解答。
【解析】根据分析可知,一个长方形绕它的中心点至少要旋转180°才能与原长方形重合。
原题干说法错误。
故答案为:×
16.√
【分析】旋转是指在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。
旋转的特征:图形旋转后,形状和大小都没有发生变化,只是位置发生了变化。
【解析】根据旋转的意义及特征可知,一个图形经过旋转后,形状和大小都不会变化。
原题说法正确。
故答案为:√
17.√
【分析】分析题目,把绳子的总长度看作单位“1”,第二段占全长的,则第一段占全长的(1-),据此比较对应的分率即可确定哪段长。
【解析】1-=
因为>,所以第二段比第一段长,原说法正确。
故答案为:√
18.×
【分析】把它抛向空中,落下后每个数字都可能朝上,即有6种可能的结果,在1~6中,合数有4和6。以这6种可能的结果为单位“1”,根据求一个数是另一个数的几分之几,用除法计算,用2÷6即可求出落下后朝上的点数是合数的可能性的大小。
【解析】在1~6中,合数有4和6。
2÷6=
落下后朝上的点数是合数的可能性是,原题说法错误。
故答案为:×。
19.D
【分析】2的倍数特征:个位上是0、2、4、6、8的数。
5的倍数特征:个位上是0或5的数。
2、5的倍数特征:个位上是0的数。
3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【解析】A.2+3+5=10,10不是3的倍数,且2、3、5中没有0,所以2、3、5组成的三位数既不是2、5的倍数,又不是3的倍数。
B.0+2+3=5,5不是3的倍数,0、2、3中的0放在个位,所以0、2、3组成的三位数可以是2、5的倍数,但不是3的倍数。
C.0+5+8=13,13不是3的倍数,0、5、8中的0放在个位,所以0、5、8组成的三位数可以是2、5的倍数,但不是3的倍数。
D.0+5+7=12,12是3的倍数,0、5、7中的0放在个位,所以0、5、7组成的三位数既是2、5的倍数,又是3的倍数。
故答案为:D
20.C
【分析】可能性大小,就是事情出现的概率,可能性等于所求情况数占总情况数的几分之几,硬币有两面,每一面的出现的可能性都是。
【解析】硬币有两面,每一面出现的可能性都是:1÷2=
所以第6次投掷正面朝上的可能性是。
故答案为:C
21.B
【分析】明确观察物体的方法,先确定有几列或几行,每列或每行有几个,形状是怎样的。从左面看,能看到两层小正方形,底下第一层两个小正方形,第二层一个小正方形靠左。
【解析】A.从正面看是;
B.从左面看是;
C.从上面看是;
D.不是的三视图。
故答案为:B
22.C
【分析】根据题意,用8个同样大小的小正方体拼成的,因为每个小正方体都在顶点处,每个小正方体都外露3个面,如果任意拿走1个小正方体,就会外露相同的3个面,所以它的表面积与原来相比不变。
【解析】据分析可知,用8个边长是1分米的小正方体拼成一个大正方体,任意拿走一个小正方体后,表面积不变。
故答案为:C
23.C
【分析】打电话通知队员时,每分钟通知1人,并且在下一分钟知道演出消息的人再分别通知1人,以此类推就是最快的通知方式。下一分钟知道消息的人数(包含老师)是这分钟的2倍。据此通过例举的方式,解题即可。
【解析】第一分钟通知到1个队员;
第二分钟最多可通知到1+2=3(个)队员;
第三分钟最多可通知到3+4=7(个)队员;
第四分钟最多可通知到7+8=15(个)队员;
第五分钟最多可通知到15+16=31(个)队员。
所以,要通知全体队员至少需要5分钟才能通知到所有人。
故答案为:C
24.B
【分析】同辞家门赴车站,两人同时从家出发,两条折线重合呈上升趋势;别时叮咛嘱万千,在车站停留,两条折线重合平缓无变化;学子满载信心去,老父怀抱希望还,表示这位同学的折线又呈上升趋势,表示父亲的折线呈下降趋势回到起点,据此分析。
【解析】A.没有表示出在车站停留,排除;
B.图象与诗意大致吻合;
C.没有表示出两人同时从家出发,也没有表示出在车站停留,排除;
D.没有表示出在车站停留,排除。
图象与上述诗意大致吻合的是。
故答案为:B
25.C
【分析】一套桌椅共300元,即桌子和椅子一共300元;其中椅子的价格比桌子少,是把桌子的价格看成单位“1”,平均分成11份,椅子价格比桌子价格少这样的7份;据此分析选项。
【解析】A.已知一套桌椅共300元,一套桌椅包含桌子和椅子,所以桌子价格+椅子价格=300元 ,该选项分析正确;
B.“椅子的价格比桌子少”,这里是把桌子价格看作单位“1”,所以椅子比桌子少的价格是桌子价格的 ,该选项分析正确。
C.椅子的价格比桌子少,把桌子价格看作11份,那么椅子比桌子少7份,椅子价格就是11-7=4份,所以椅子和桌子的价格比是4∶11,而不是7∶11,该选项分析错误。
故答案为:C
26.B
【分析】根据题意可知,甲的等于乙的,根据两个非0的因数相乘的积相等,一个因数越大,另一个因数越小进行解答即可。
【解析】甲×=乙×
=
=
>
所以甲<乙,即乙彩带长。
故答案为:B
27.A
【分析】由题目和图可知,矿泉水瓶中的水的体积为360毫升,因为矿泉水瓶中水并未装满,则当矿泉水瓶完全浸没在长方体容器时,此时上升水的体积就是矿泉水瓶的体积,则上升的水的体积一定大于360毫升。
【解析】由分析可知,矿泉水瓶中的水的体积为360毫升,因为矿泉水瓶中水并未装满,则当矿泉水完全浸没在长方体容器时,上升的水的体积一定大于360毫升。
故答案为:A
28.B
【分析】把8个零件分成(3,3,2)三组,把两个3个一组的放在天平上称,如天平平衡,则次品在2个的一组中,把这2个零件分成(1,1),放在天平上称,上跷的是次品;如不平衡,则把上跷的一组3个零件分成(1,1,1),任意两个放在天平上称,如平衡,没称的是次品,如不平衡,上跷的是次品。据此解答。
【解析】第一次称量:把8个零件分成3组:3、3、2,先在天平两边分别放3个零件,会有两种情况出现:
情况一:左右平衡,则次品在剩下的2个中,即可进行第二次称量;把剩下的2个,放在天平的两边一边1个,
则托盘上升一边为次品;
情况二:若左右不平衡,则次品在托盘上升的一边3个中,由此即可进行第二次称量,从上升一边的3个拿出2个,放在天平的两边一边1个,若天平平衡,则剩下1个是次品;若天平不平衡,则托盘上升一边为次品。
综上所述,至少需要称2次,才能找到次品。
故答案为:B
29.;;;;
10;4;5.69;3
【解析】略
30.(1)1;(2)192
(3);(4)1
【分析】(1),交换中间减数和加数的位置,添括号,括号前边是减号,添上括号,括号里的加号变减号,转化成,同时算出小括号里的加法和减法,最后算括号外的减法;
(2),逆用乘法分配律,先算(56.4+43.6),再与1.92相乘;
(3),根据减法的性质,将后两个数先加起来再计算;
(4),观察这个分数,先看分子中2013×2014,将2013拆成(2012+1),根据乘法分配律,小括号里的数分别与2014相乘,再相加,最终得,即分子转化成,分子是,与分母相同,约分后得1。
【解析】(1)
(2)
(3)
(4)
31.(1);(2);(3)
【分析】(1)先把方程化简成,再根据等式的基本性质,方程两边先同时加上12,再同时除以6求解;
(2)先把方程化简成,再根据等式的基本性质,方程两边同时除以4.8求解;
(3)先把方程化简成,再根据等式的基本性质,方程两边先同时减去92,再同时除以2求解。
【解析】(1)
解:
(2)
解:
(3)
解:
32.图1:表面积:216dm2;体积:204dm3
图2:表面积:79dm2;体积:41dm3
【分析】图1;正方体挖去一个长方体,减少3个面的面积,又增加3个面的面积,所以表面积=棱长是6dm正方体的表面积;根据正方体的表面积公式:表面积=棱长×棱长×6,代入数据,求出表面积;
体积=棱长是6dm的正方体的体积-长是2dm,宽是2dm,高是3dm长方体的体积,根据正方体体积公式:体积=棱长×棱长×棱长,长方体体积公式:体积=长×宽×高,代入数据,即可解答。
图2:表面积=长是4dm,宽是4dm,高是2dm的长方体的表面积+长是3dm,宽是2dm,高是1.5dm的长方体的侧面积,根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,长方体侧面积公式:侧面积=(长×高+宽×高)×2,代入数据,即可解答。
体积=长是4dm,宽是4dm,高是2dm的长方体的体积+长是3dm,宽是2dm,高是1.5dm的长方体的体积,根据长方体体积公式:体积=长×宽×高,代入数据,即可解答。
【解析】图1:表面积:
6×6×6
=36×6
=216(dm2)
体积:6×6×6-2×2×3
=36×6-4×3
=216-12
=204(dm3)
表面积是216dm2;体积是204dm3。
图2:表面积:
(4×4+4×2+4×2)×2+(3×1.5+2×1.5)×2
=(16+8+8)×2+(4.5+3)×2
=(24+8)×2+7.5×2
=32×2+7.5×2
=64+15
=79(dm2)
体积:
4×4×2+3×2×1.5
=16×2+6×1.5
=32+9
=41(dm3)
表面积是79dm2,体积是41dm3。
33.(1)图见详解;(4,5)
(2)(3)见详解
【分析】(1)根据平移的特征,将圆A的圆心先向右平移2格,再向上平移2格后画出平移后的圆。数对的表示方法:(列数,行数),数对的第一个数表示列,第二个数表示行,找出平移后的圆心在方格中对应的列数和行数,再用数对表示出来。
(2)根据画平行线的步骤“一贴、二靠、三推、四画”,把三角板的一条直角边与已知直线O重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和C点重合,过C点沿三角板的直角边画直线即可。
(3)等腰三角形是有两条边相等的三角形。先以点P为顶点画一个等腰三角形,然后根据旋转的特征,将三角形绕点P逆时针旋转90°,点P的位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
【解析】(1)画出将圆A先向右平移2格,再向上平移2格后的图形B,平移后圆心的位置用数对表示是(4,5)。
(1)(2)(3)如图:
34.不可能
【分析】先求出长方体形状的水池的水的体积,根据每分钟排2.5立方米,求出排出水用的时间,用的时间和15小时比较,小于15小时,就够,否则不够。据此解答即可。
【解析】长方体形状的水池的水的体积:
60×30×1.5
=1800×1.5
=2700(立方米)
2700÷2.5=1080(分钟)
1080分钟=18小时
因为18小时>15小时
所以15小时不够,不能把水池中的水排完。
答:要求在15小时内把水池中的水排完,不可能
35.148平方厘米
【解析】解决本题的关键是理解体积增加的部分是如何得到的.比如:把长方体的长增加2厘米,长方体的体积就会增加一个“以长方体的宽×高为底面积,2厘米为高的”小长方体的体积,即宽×高×2=40,所以可以得出:宽×高=20(平方厘米);同理可得:长×高=90÷3=30(平方厘米),长×宽=96÷4=24(平方厘米),这时再计算原来长方体的表面积就很简单了.
由题意可知,宽×高=40÷2=20(平方厘米)
长×高=90÷3=30(平方厘米)
长×宽=96÷4=24(平方厘米)
所以,2×(长×宽+长×高+宽×高) =2×(20+30+24) =148(平方厘米)
答:原来长方体的表面积是148平方厘米.
36.一班分到16根,二班分到14根,三班分到13根.
【解析】试题分析:首先求得三个班的总份数,再求得三个班各占总数的几分之几,最后求得三个班各应领到的跳绳,列式解答即可.
解:64+56+52=172(人)
43×=16(根)
43×=14(根)
43×=13(根);
答:一班分到16根,二班分到14根,三班分到13根.
【点评】此题主要考查按比例分配应用题的特点:已知两个数的比(三个数的比),两个数的和(三个数的和),求这两个数(三个数),用按比例分配解答.
37.这个跑道一圈长360米
【解析】试题分析:因他们的起点和走的方向完全相同,也就是一前一后的走,脚印一定有重合的,即重合在两人步子长度的公倍数上,所以先求出他们步长的最小公倍数,再求出他们脚印重合时的步数,然后再据总步数及最小公倍数即能求出这条路的长度,也就是环形跑道长
解答:解:50=5×5×2,30=2×3×5
50和30的最小公倍数是:2×3×5×5=150,
第一次两人脚印重合时,爸爸走的步数:150÷5=3(步),小明走的步数:150÷3=5(步),
即爸爸3步与小明5步时脚印重合一次,此时有3+5﹣1=7个脚印,距离是150厘米,
总共有1680个脚印,应重合的次数:1680÷7=240(次)
所以这条路长是240×150=36000(厘米)
36000厘米=360米;
答:这个跑道一圈长360米.
点评:完成本题首先要明确两人的脚印是有重合的,重合在两人步子长度的公倍数上,通过求他们步子长度的最小公倍数即能求出两人脚印重合时脚印数的循环规律.
38.粉刷这间教室需涂料303千克
【解析】试题分析:求需要粉刷的面积,就是用教室顶棚的面积加上四面墙壁的面积减去门窗的面积,长、宽、高已知,利用长方体的表面积公式即可求解;用需要粉刷的面积乘每平方米需要的涂料的量,就是一共需要的涂料的量.
解答:解:8×6+8×3.5×2+6×3.5×2﹣20
=48+56+42﹣20
=146﹣20
=126(平方米);
126×2.4=302.4≈303(千克);
答:粉刷这间教室需涂料303千克.
点评:解答有关长方体计算的实际问题,一定要搞清所求的是什么,再进一步选择合理的计算方法进行计算解答问题.
39.第一、二、三道工序至少需要工人分别为14人、21人、24人
【分析】先求出48,32和24的最小公倍数,然后用这个最小公倍数分别除以48,32,28即可.
【解析】要想搭配合理,那么每道工序完成的零件个数应该相等,
因为:[48,32,28]=672,所以:
第一道工序至少需要工人672÷48=14(人)
第二道工序至少需要工人672÷32=21(人)
第三道工序至少需要工人672÷28=24(人)
答:第一、二、三道工序至少需要工人分别为14人、21人、24人.
40.320立方厘米
【分析】由题意可知,当球形铁块放入容器中,有部分水溢出;长方体容器中下降(5﹣2)厘米的水的体积加上2厘米高的水的体积(溢出的水的体积)就等于这个球形铁块的体积;也就是说,球形铁块的体积,就相当于5厘米高的水的体积,根据长方体的体积公式V=Sh,列式解答。
【解析】8×8×5
=64×5
=320(立方厘米)。
答:铁球的体积是320立方厘米。
41.7棵
【分析】此题属于植树问题,两端不移动,要求中间有几棵树不用移动,只要求出在80以内2和5的公倍数即可解答,即是2和5的公倍数的米数是不动的。
【解析】80以内的2和5的公倍数有:10;20;30;40;50;60;70;
即10米、20米、30米、40米、50米、60米、70米处的7棵树不用动;
答:中间有7棵树不动。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
