2024-2025学年小升初重点校分班考考前冲刺预测卷(含解析)六年级下册数学(人教版)
文档属性
| 名称 | 2024-2025学年小升初重点校分班考考前冲刺预测卷(含解析)六年级下册数学(人教版) |  | |
| 格式 | docx | ||
| 文件大小 | 330.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 08:44:39 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年六年级下册数学小升初重点校分班考考前冲刺预测卷
一、填空题
1.把一个底面半径是4cm的圆柱切拼成一个近似的长方体(如图),其表面积增加了48cm2,圆柱的高是( )cm,圆柱的体积是( )cm3。
2.“大美南阳是一个值得三顾的地方”。六年级学生举办了“自己心目中的大美南阳——绘画比赛”。乐乐画了一幅图,用6cm的线段表示实际900m。这幅图的比例尺是( )。
3.妈妈将20000元存入银行,定期2年,年利率2.15%,那么2年后可得利息和本金( )元。
4.圆柱的高一定,圆柱的体积和底面积成( )比例,圆柱的侧面积一定,底面周长和高成( )比例。
5.以学校大门为起点,向东走即为正,向西走即为负。王老师从学校大门出发,走了﹢50米,接着又走了﹣60米,这时王老师一共走了( )米,他现在学校大门( )(填“东”或“西”)( )米处。
6.张谦老师编写了一本《数学童话》,得到稿费4800元。按规定,一次稿费超过800元的部分,应该以14%的税率纳税。张老师应该缴纳税款( )元,他实际得到稿费( )元。
7.如果把一个正方体6个面分别涂上红、黄两种颜色,那么至少有( )个面颜色是相同的。
8.盒子里有2个红球,5个绿球和4个黄球,这些球除了颜色不同以外其他完全相同,从中至少摸出( )个球,才能保证其中有一个绿球。
9.下面是张叔叔的一张存单,存款到期时一共可以取出 元。
某银行(定期)储蓄存单账号123456
币种:人民币 金额(大写)玖千元 小写: 9000元
存入日期 存期 年利率 起息日 到期日
2024年6月5日 3年 2.75% 2024年6月5日 2027年6月5日
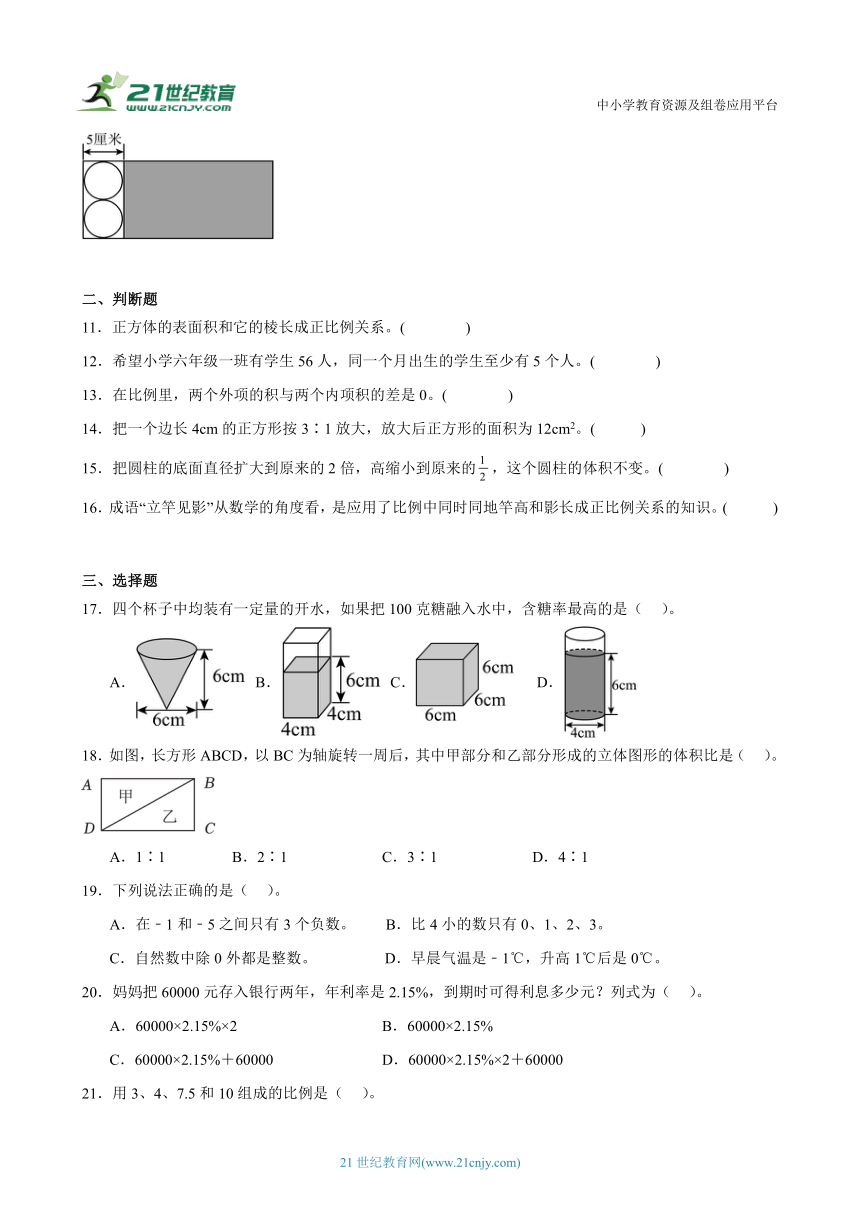
10.如图,若一块长方形卡纸剪下图中的涂色部分正好可以围成一个圆柱,则这个圆柱的底面周长是( )厘米,高是( )厘米。(π取3.14)
二、判断题
11.正方体的表面积和它的棱长成正比例关系。( )
12.希望小学六年级一班有学生56人,同一个月出生的学生至少有5个人。( )
13.在比例里,两个外项的积与两个内项积的差是0。( )
14.把一个边长4cm的正方形按3∶1放大,放大后正方形的面积为12cm2。( )
15.把圆柱的底面直径扩大到原来的2倍,高缩小到原来的,这个圆柱的体积不变。( )
16.成语“立竿见影”从数学的角度看,是应用了比例中同时同地竿高和影长成正比例关系的知识。( )
三、选择题
17.四个杯子中均装有一定量的开水,如果把100克糖融入水中,含糖率最高的是( )。
A. B. C. D.
18.如图,长方形ABCD,以BC为轴旋转一周后,其中甲部分和乙部分形成的立体图形的体积比是( )。
A.1∶1 B.2∶1 C.3∶1 D.4∶1
19.下列说法正确的是( )。
A.在﹣1和﹣5之间只有3个负数。 B.比4小的数只有0、1、2、3。
C.自然数中除0外都是整数。 D.早晨气温是﹣1℃,升高1℃后是0℃。
20.妈妈把60000元存入银行两年,年利率是2.15%,到期时可得利息多少元?列式为( )。
A.60000×2.15%×2 B.60000×2.15%
C.60000×2.15%+60000 D.60000×2.15%×2+60000
21.用3、4、7.5和10组成的比例是( )。
A.3∶10=7.5∶4 B.7.5∶4=3∶10 C.10∶7.5=4∶3
22.运动会上,在5分钟投篮比赛中,六(2)班的10名同学共投中了83个,总有一名队员至少投中( )个球。
A.7 B.8 C.9 D.10
23.小北准备用下面的长方形硬纸板做成一个无盖笔筒的侧面,他可以选用( )作底面。(单位:厘米,接缝处忽略不计)
A.①②④ B.②③④ C.①②③ D.①③④
24.根据我们的实际生活经验,下面该用负数表示的是( )。
A.亏损500元 B.收入300元 C.降低100元
25.笑笑在商场打七折的时候,花42元钱买了一个文具盒,便宜了多少元?下面算式正确的是( )。
A.42×70% B.42÷70%-42
C.42×(1-70%) D.42÷(1-70%)-42
26.口袋里有9个红球、4个白球、1个黑球,球除颜色外完全相同,每次从中摸一个球不放回,至少要摸出( )个球,才能保证取到的球里有两个颜色相同。
A.2 B.5 C.10 D.4
四、计算题
27.直接写出得数.
28.下面各题,怎样算简便就怎样算。
+++ 18×25%+×40+42×0.25 9.7÷1.25÷0.8
29.解比例。
1.8∶5.4=x∶2.4
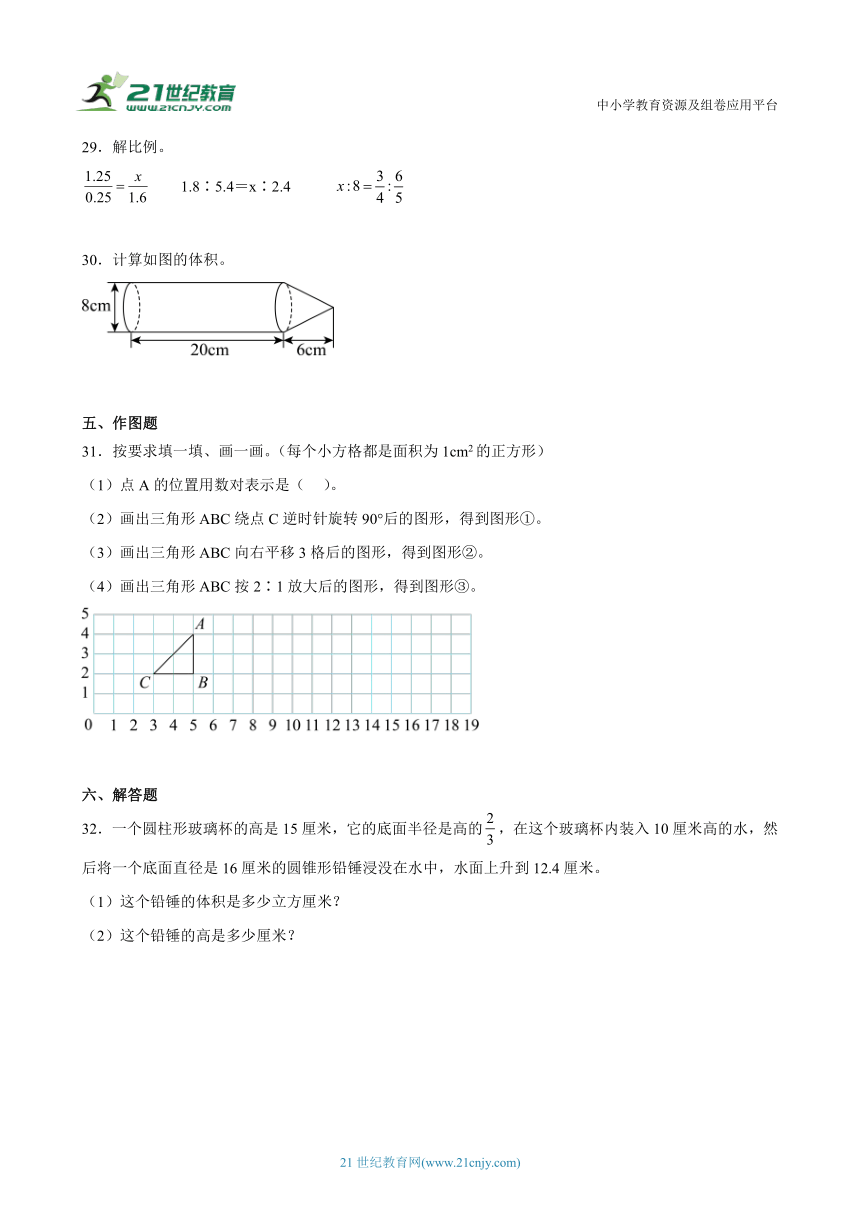
30.计算如图的体积。
五、作图题
31.按要求填一填、画一画。(每个小方格都是面积为1cm2的正方形)
(1)点A的位置用数对表示是( )。
(2)画出三角形ABC绕点C逆时针旋转90°后的图形,得到图形①。
(3)画出三角形ABC向右平移3格后的图形,得到图形②。
(4)画出三角形ABC按2∶1放大后的图形,得到图形③。
六、解答题
32.一个圆柱形玻璃杯的高是15厘米,它的底面半径是高的,在这个玻璃杯内装入10厘米高的水,然后将一个底面直径是16厘米的圆锥形铅锤浸没在水中,水面上升到12.4厘米。
(1)这个铅锤的体积是多少立方厘米?
(2)这个铅锤的高是多少厘米?
33.张希家要买一套总价120万元的住房,如果一次性付清房款可以享受九五折优惠。买这套房子要按照实际房价的1.5%缴纳契税,如果张希家一次性付清房款,要缴纳契税多少万元?
34.李华一家四口打算去北京游玩三天,李华家所在城市与北京之间的高铁车票和机票价格如下:
交通工具 票价 说明
火车 714元 身高1.2~1.5米的儿童半票
飞机 1200元 未满12周岁半价票
(1)李华身高1.48米,年龄未满12周岁,如果她与爸爸、妈妈和奶奶去北京旅游往返都乘火车,交通费至少要准备多少钱?
(2)如果单程乘坐飞机(成人机票打八折,儿童机票半价),那么单程至少要准备多少钱?
35.在比例尺是1∶5000000的地图上,量得A、B两座城市的距离是18厘米,一列高铁以每小时200千米的速度从A城开往B城,多少小时能够抵达?
36.为切实加强体育锻炼,提高学生身体素质,希望小学准备购买60根跳绳发到各班,现有甲、乙、丙三个商店可供选择,三个商店同品牌跳绳单价都是7元,但各个商店的优惠方法不同:
甲商店:买10根跳绳免费赠送2根,不足10根不赠送。
乙商店:每根跳绳按八五折优惠。
丙商店:购物每满200元减40元。
为了节省费用,希望小学应在哪个商店购买?
37.一个圆柱形的玻璃缸装有一些水,底面内直径为6厘米,高为12厘米。把一个圆锥形铅锤放入玻璃缸中(全部浸没),水面上升了0.5厘米,铅锤的高为2厘米,这个铅锤的底面积是多少平方厘米?
38.南昌西站到北京西站之间的高速铁路大约长1404千米。一趟高铁列车早上7:20从南昌西站出发匀速行驶,10:50途经郑州东站,13:20到达北京西站(途中经停时间忽略不计)。南昌西站到郑州东站的高速铁路大约有多长?(用比例解)
39.学校体育器材室准备购买200个足球,每个足球价格为60元。特步体育专卖店一律八八折出售,李宁专卖店“买八送一”,安踏专卖店满5000元减680元。请你帮学校算一算,到哪家店购买合算?
40.在一幅比例尺为1∶12000000的地图上,量得AB两地的图上距离为4.5厘米。甲乙两车同时从A、B两地相对开出,经过3小时相遇,甲、乙两车的速度比为5∶7。甲乙两车的速度分别是多少?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.6 301.44
【分析】根据题意,把一个圆柱切拼成一个近似的长方体,增加的表面积等于2个长方形的面积,长方形的长是圆柱的高,宽是圆柱的底面半径;用增加的表面积除以2,求出一个面的面积,再除以底面半径,即可求出圆柱的高;
根据圆柱的体积公式V=πr2h,代入数据计算,求出圆柱的体积。
【解析】圆柱的高:
48÷2÷4
=24÷4
=6(cm)
圆柱的体积:
3.14×42×6
=3.14×16×6
=301.44(cm3)
圆柱的高是6cm,圆柱的体积是301.44cm3。
2.1∶15000/
【分析】已知乐乐画了一幅图,用6cm的线段表示实际900m,根据“比例尺=图上距离∶实际距离”以及进率“1m=100cm”,求出这幅图的比例尺。
【解析】6cm∶900m
=6cm∶(900×100)cm
=6∶90000
=(6÷6)∶(90000÷6)
=1∶15000
这幅图的比例尺是1∶15000。
3.20860
【分析】先根据“利息=本金×利率×存期”求出到期时可得到的利息,再加上本金,即是到期时可取回的钱数。
【解析】20000×2.15%×2+20000
=20000×0.0215×2+20000
=860+20000
=20860(元)
那么2年后可得利息和本金20860元。
4.正 反
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解析】圆柱的体积÷底面积=高(一定),商一定,所以圆柱的体积和底面积成正比例;
圆柱的底面周长×高=圆柱的侧面积(一定),乘积一定,所以底面周长和高成反比例。
5.110 西 10
【分析】正数、负数表示两种相反意义的量。以学校大门为起点,向东走即为正,向西走即为负。
王老师从学校大门出发,走了﹢50米,即向东走了50米;接着又走了﹣60米,即向西走了60米;把两次走的距离相加,即是王老师一共走的路程;因为向西走的距离超过向东走的距离,那么此时的位置在起点的西边(60-50)米。
【解析】50+60=110(米)
60-50=10(米)
这时王老师一共走了110米,他现在学校大门西10米处。
6.560 4240
【分析】本题考查百分数的应用,税率问题。首先要确定需要纳税的部分:稿费超过800元的部分才纳税,张老师的稿费是4800元,超过800元的部分是4800-800=4000元,然后根据“税款=应纳税部分×税率”计算出应缴纳的税款,最后用总的稿费减去缴纳的税款,就是实际得到的稿费。
【解析】4800-800=4000(元)
4000×14%=560(元)
张老师应该缴纳税款560元。
4800-560=4240(元)
所以张老师实际得到稿费4240元。
7.3
【分析】分析题目,正方体一共有6个面,每个面都只有红色和黄色两种选择,题目要求至少有多少个面的颜色是相同的,所以需要考虑最不利的情况,即两种颜色的面各占一半,据此解答。
【解析】6÷2=3(个)
如果把一个正方体6个面分别涂上红、黄两种颜色,那么至少有3个面颜色是相同的。
8.7
【分析】要保证摸出绿球,要考虑最差结果,一直把其它球摸完才摸到绿球,也就是先把红球和黄球全部摸出,然后再摸一个球就一定是绿球。据此列式解答。
【解析】2+4+1
=6+1
=7(个)
所以从中至少摸出7个球,才能保证其中有一个绿球。
9.9742.5
【分析】从题意可知:本金是9000元,存期3年,年利率是2.75%。根据利息=本金×时间×利率,代入数据计算,求出利息,再加上本金,就是到期时一共可以取出的钱。
【解析】9000×2.75%×3+9000
=247.5×3+9000
=742.5+9000
=9742.5(元)
存款到期时一共可以取出9742.5元。
10.15.7 10
【分析】看图可知,圆柱底面直径=5厘米,根据圆的周长=圆周率×直径,求出底面周长;高=底面直径×2。
【解析】3.14×5=15.7(厘米)
5×2=10(厘米)
这个圆柱的底面周长是15.7厘米,高是10厘米。
11.×
【分析】判断两个相关联的量呈正比例或反比例时,要看两个变量的比值或乘积是否为定值,正方体的表面积=棱长×棱长×6,据此解答。
【解析】正方体的表面积=棱长×棱长×6,表达式变形可得:正方体的表面积÷棱长=棱长×6。表面积与棱长比值不一定,所以正方体的表面积和它的棱长不成正比例。
故答案为:×
12.√
【分析】一年有12个月,把12个月看作12个“抽屉”,56个学生看作56个“苹果”,用56除以12,求出商和余数,再用商加上1即可解答。
【解析】56÷12=4(人)……8(人)
4+1=5(人)
所以同一个月出生的学生至少有5个人,故原题说法正确。
故答案为:√
13.√
【分析】在比例里,两个外项之积等于两个内项之积,这是比例的基本性质,由此即可解决问题。
【解析】根据比例的基本性质可得:在比例里两内项的积等于两外项的积。
例如:3∶4=9∶12,4×9=36,3×12=36,36-36=0
即在比例里,两个外项的积与两个内项的积的差是0。
故答案为:√
14.×
【分析】根据题意,将正方形按3∶1放大,即放大后的正方形边上是原来边长的3倍,据此计算出放大后正方形的边长,再根据正方形的面积=边长×边长,计算出面积即可判断。
【解析】4×3=12(cm)
12×12=144(cm2)
即放大后正方形的面积为144cm2,即原说法错误。
故答案为:×
15.×
【分析】圆柱的体积V=πr2h,假设圆柱体原来的底面直径为2,直径扩大到原来的2倍后直径为4,假设原来的高为2,高缩小到原来的后高为1,根据圆柱的体积公式,算出原来圆柱的体积和变化后圆柱的体积,再进行比较即可。
【解析】假设圆柱体原来的底面直径为2,高为2。
变化前圆柱的体积:
3.14×(2÷2)2×2
=3.14×12×2
=3.14×1×2
=6.28
变化后圆柱的直径为2×2=4,变化后圆柱的高为2×=1。
变化后圆柱的体积:
3.14×(4÷2)2×1
=3.14×22×1
=3.14×4×1
=12.56
12.56÷6.28=2
把圆柱的底面直径扩大到原来的2倍,高缩小到原来的,这个圆柱的体积扩大到原来的2倍。
故答案为:×
16.√
【分析】同时同地物体的长度和它的影子的长度的比值一定,即物体的长度和它的影子的长度成正比例,据此解答。
【解析】成语“立竿见影”从数学的角度看,是应用了比例中同时同地竿高和影长成正比例关系的知识。说法正确。
故答案为:√
17.A
【分析】根据圆锥的体积公式:V=πr2h,长方体的体积公式:V=abh,正方体的体积公式:V=a3,圆柱的体积公式:V=πr2h,把数据代入公式求出四杯水的体积,然后进行比较,水的体积少的则含糖率就高。据此解答。
【解析】×3.14×(6÷2)2×6
=×3.14×32×6
=3.14×9×6
=56.52(立方厘米)
4×4×6
=16×6
=96(立方厘米)
6×6×6=216(立方厘米)
3.14×(4÷2)2×6
=3.14×22×6
=3.14×4×6
=75.36(立方厘米)
56.52<75.36<96<216
含糖率最高的是A。
故答案为:A
18.B
【分析】长方形绕着BC边旋转一周,形成一个圆柱,而三角形BCD(也就是乙部分)绕着BC边旋转一周,形成一个圆锥,甲部分形成的立体图形就是整个圆柱里面去掉乙部分形成的圆锥;分析题意可知形成的圆柱和圆锥等底等高,如果圆柱体积是3份,那么乙部分形成的立体图形圆锥体积就是1份,则甲部分形成的立体图形体积就是3-1=2份。
【解析】由分析可知:甲部分形成的立体图形的体积是2份,乙部分形成的立体图形的体积是1份,所以甲部分和乙部分形成的立体图形的体积比是2∶1。
故答案为:B
19.D
【分析】A.两个负数之间不仅有负整数也有负小数;
B.比4小的数不仅有整数,还有小数;
C.根据整数的认识解答;
D.根据对温度的认识解答。
【解析】A.在﹣1和﹣5之间有无数个负数,原题说法错误;
B.比4小的数有无数个,原题说法错误;
C.0和正整数统称为自然数,整数包括正整数、0和负整数,所以说0也是整数,即自然数都是整数,原题说法错误;
D.在温度计中0℃在﹣1℃的上面一格,所以早晨气温是﹣1℃,升高1℃后是0℃。原题说法正确。
故答案为:D
20.A
【分析】已知本金60000元,存期2年,年利率2.15%,求利息,根据“利息=本金×年利率×存期”,代入数据即可计算出利息。
【解析】60000×2.15%×2
=60000×0.0215×2
=1290×2
=2580(元)
所以计算到期时可得利息列式为60000×2.15%×2,结果是2580元。
故答案为:A
21.C
【分析】根据比例的基本性质,分别求出三个选项中比例的两个外项的积和两个内项的积,看积是否相等,如果相等,即可组成比例;不相等,就不能组成比例。
比例的基本性质:在比例里,两个外项的积等于两个内项的积。
【解析】A.3×4=12,10×7.5=75,12≠75,所以3∶10≠7.5∶4;
B.7.5×10=75,4×3=12,75≠12,所以7.5∶4≠3∶10;
C.10×3=30,7.5×4=30,30=30,所以10∶7.5=4∶3。
所以,用3、4、7.5和10组成的比例是10∶7.5=4∶3。
故答案为:C
22.C
【分析】根据题意,将投中的83个球平均分给10名队员,每名队员投中8个球,还剩下3个球,这3个球,无论分给哪名队员,总有一名队员至少抽中(8+1)个球。
【解析】83÷10=8(个)……3(个)
8+1=9(个)
总有一名队员至少投中9个球。
故答案为:C
23.B
【分析】由于做无盖笔筒的侧面,那么底面周长应该等于这个侧面的长或者是宽,根据圆的周长公式:周长=π×半径×2;正方形周长公式:周长=边长×4;分别求出各个底面的周长;再和长方形的长或宽进行比较,进而解答。
【解析】①3.14×(4×2)
=3.14×8
=25.12(厘米)
底面周长是25.12厘米;
②3.14×4=12.56(厘米)
底面周长是12.56厘米;
③3.14×4=12.56(厘米)
底面周长是12.56厘米;
④3.14×(3×2)
=3.14×6
=18.84(厘米)
底面周长是18.84厘米。
小北准备用下面的长方形硬纸板做成一个无盖笔筒的侧面,他可以选用②③④作底面。
故答案为:B
24.A
【分析】正负数表示一组相反意义的量,据此结合实际生经验,逐项分析。
【解析】A.不赚不亏记为0,亏损500元,相对于盈利,亏损应记为负数﹣500元。符合题意。
B.支出和收入表示相反意义的量,收入300元属于正向增加,用正数表示﹢300元。不符合题意。
C.降低100元需结合具体情境。若表示变化量(如成本减少100元),应记为负数(﹣100元);但若仅描述减少的数值(如“降低了100元”),通常直接使用正数表示减少的幅度。本题未明确为变化量,不强制用负数。不符合题意。
故答案为:A
25.B
【分析】原价×折扣=现价,用42元除以折扣求出原价,再用原价减去现价42元就是便宜的钱数,据此解答。
【解析】A.42×70%,用现价乘折扣70%没有实际意义,不符合题意;
B.42÷70%-42,先用42÷70%求出原价,再减去42元就是便宜的钱数,符合题意;
C.42×(1-70%),用现价乘现价比原价便宜的百分率,得不到便宜的金额,不符合题意;
D.42÷(1-70%)-42,用现价除以现价比原价便宜的百分率,不能得出原价,得不到便宜的金额,不符合题意。
故答案为:B
26.D
【分析】分析题目,要保证取到两个颜色的球,则最不利的情况是3种颜色的球各取了1个,最后再取1个一定能保证有2个球的颜色相同,据此解答。
【解析】3+1=4(个)
至少要摸出4个球,才能保证取到的球里有两个颜色相同。
故答案为:D
27.2018;384;0.8;0.75;
10.33;0.96;7;0.64;
;11
【解析】略
28.2;25;9.7
【分析】题1:根据加法交换律和结合律进行简算;
题2:先把25%、和0.25转化成相同的形式,再根据乘法分配律进行简算;
题3:根据除法的性质进行简算。
【解析】+++
=(+)+(+)
=1+1
=2
18×25%+×40+42×0.25
=18×0.25+0.25×40+42×0.25
=0.25×(18+40+42)
=0.25×100
=25
9.7÷1.25÷0.8
=9.7÷(1.25×0.8)
=9.7÷1
=9.7
29.x=8;x=0.8;x=5
【分析】(1)根据比例的性质化简,再根据等式的基本性质,方程两边同时除以0.25求解;
(2)根据比例的性质化简,再根据等式的基本性质,方程两边同时除以5.4求解;
(3)根据比例的性质化简,再根据等式的基本性质,方程两边同时除以求解。
【解析】(1)
解:0.25x=1.25×1.6
0.25x=2
0.25x÷0.25=2÷0.25
x=8
(2)1.8∶5.4=x∶2.4
解:5.4x=1.8×2.4
5.4x=4.32
5.4x÷5.4=4.32÷5.4
x=0.8
(3)x∶8=∶
解:x=8×
x=6
x÷=6÷
x=6×
x=5
30.1105.28立方厘米
【分析】观察图形可知,该组合体由一个国柱和一个圆锥组成。要计算其体积,需分别计算圆柱体积和圆锥体积,再将二者相加。计算圆柱体积时,根据圆柱体积公式V=πr2h(其中r是底面半径,h是高),已知底面直径为8厘米,可先求出半径,再结合圆柱的高20厘米来计算体积。计算圆锥体积时,依据圆锥体积公式V锥=π2h,同样根据已知条件求出半径,再结合圆锥的高6厘米计算体积。最后把圆柱体积和圆锥体积相加,得到组合体的体积。
【解析】计算底面半径:r=8÷2=4(厘米)
计算圆柱体积:
V柱=3.14×42×20
=3.14×16×20
=50.24×20
=1004.8(立方厘米)
计算圆锥体积:
V锥=×3.14×42×6
=×3.14×16×6
=×50.24×6
=×301.44
=100.48(立方厘米)
计算组合体体积:
V=V锥+V柱
=1004.8+100.48
=1105.28(立方厘米)
即图形的体积是1105.28立方厘米。
31.(1)(5,4)
(2)(3)(4)见详解
【分析】(1)数对的表示方法:(列数,行数),数对的第一个数表示列,第二个数表示行,找出点A在方格中对应的列数和行数,再用数对表示出来。
(2)根据旋转的特征,三角形ABC绕点C逆时针旋转90°,点C的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)根据平移的特征,把三角形ABC的各顶点向右平移3格,依次连接各顶点,即可得到平移后的图形。
(4)把三角形ABC按照2∶1放大,就是将三角形ABC的底和高放大到原来的2倍,放大后图形与原图形对应边长的比是2∶1,形状没有发生变化。
【解析】(1)点A的位置用数对表示是(5,4)。
(2)(3)(4)见下图
32.(1)753.6立方厘米;(2)11.25厘米
【分析】(1)求铅锤体积首先确定圆柱玻璃杯底面半径:已知圆柱形玻璃杯的高是15厘米,它的底面半径是高的,所以底面半径为15×=10厘米。
然后根据排水法原理:圆锥放入圆柱玻璃杯中,水面上升的体积就是圆锥的体积。水面从10厘米上升到12.4厘米,上升了12.4-10=2.4厘米。利用圆柱体积公式V=πr2h(r是底面半径,h是高),可算出上升的水的体积,也就是铅锤的体积。
(2)已知圆锥体积公式为V=πr2h(V是体积,r是底面半径,h是高),由(1)已求得圆锥体积,且已知圆锥底面直径是16厘米,可算出底面半径。将圆锥体积公式变形为h=3V÷(πr2),据此代入已知数据来计算圆锥的高即可。
【解析】(1)15×=10(厘米)
3.14×102×(12.4-10)
=3.14×100×2.4
=314×2.4
=753.6(立方厘米)
答:这个铅锤的体积是753.6立方厘米。
(2)753.6×3÷[3.14×(16÷2)2]
=2260.8÷[3.14×64]
=2260.8÷200.96
=11.25(厘米)
答:这个铅锤的高是11.25厘米。
33.1.71万元
【分析】把这套住房的总价看作单位“1”,一次性付清房款可以享受九五折优惠,即实际房价是总价的95%,根据求一个数的百分之几是多少,用乘法计算,求出实际房价;又已知还要按照实际房价的1.5%缴纳契税,把实际房价看作单位“1”,单位“1”已知,用实际房价乘1.5%,即可求出要缴纳契税的金额。
【解析】120×95%×1.5%
=114×1.5%
=1.71(万元)
答:要缴纳契税1.71万元。
34.(1)4998元
(2)3480元
【分析】(1)因为李华身高1.48米,在1.2-1.5米之间,年龄未满12周岁,所以李华乘火车是半票,爸爸、妈妈和奶奶是全票;用火车的票价乘3求出3个成年人的总票价,再加上火车票价的一半求出单程总票价,再乘2就是乘火车往返的交通费。
(2)单程乘坐飞机(成人机票打八折,儿童机票半价),打八折就是按原票价的80%收费,先用1200乘3求出3个成年人在不打折的情况下需要的飞机票钱数,再乘80%,求出三个成年人的飞机票价,再加上飞机票的一半就是么单程至少要准备的钱数。
【解析】(1)(714×3+714÷2)×2
=(2142+357)×2
=2499×2
=4998(元)
答:交通费至少要准备4998元。
(2)1200×3×80%+1200÷2
=3600×80%+600
=2880+600
=3480(元)
答:单程至少要准备3480元。
35.4.5小时
【分析】根据实际距离=图上距离÷比例尺,代入数值计算出A、B两座城市之间的实际距离;再根据时间=路程÷速度,代入相应数值计算,所得结果即为多少小时能够抵达。
【解析】18÷
=18×5000000
=90000000(厘米)
90000000厘米=900千米
900÷200=4.5(小时)
答:4.5小时能够抵达。
36.丙商店
【分析】甲商店:买10根跳绳免费赠送2根,把(10+2)根跳绳看作一组,60根跳绳一共有5组,每组需要付10根跳绳的钱数,根据“总价=单价×数量”求出需要付的总钱数;
乙商店:八五折即现价占原价的85%,每根跳绳的实际价格=每根跳绳原来的价格×85%,最后乘希望小学购买跳绳的数量求出需要付的总钱数;
丙商店:先根据“总价=单价×数量”求出需要付的总钱数,即420元,420元里面有两个200元,需要减去2×40=80元,实际需要付的钱数=原来需要付的总钱数-满减的钱数,最后比较大小选择需付钱数最少的商店,据此解答。
【解析】甲商店:60÷(10+2)
=60÷12
=5(组)
5×10×7
=50×7
=350(元)
乙商店:八五折=85%
7×85%×60=357(元)
丙商店:60×7=420(元)
420÷200=2(个)……20(元)
420-2×40
=420-80
=340(元)
因为340元<350元<357元,所以在丙商店购买最划算。
答:为了节省费用,希望小学应在丙商店购买。
37.21.195平方厘米
【分析】根据题意可知,把圆锥形铅锤放入圆柱形玻璃缸中(完全浸没,水未溢出),上升部分水的体积就等于这个铅锤的体积,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:V=Sh那么S=3V÷h,把数据代入公式解答。
【解析】3.14×(6÷2)2×0.5÷÷2
=3.14×32×0.5×3÷2
=3.14×9×0.5×3÷2
=14.13×3÷2
=42.39÷2
=21.195(平方厘米)
答:这个铅锤的底面积是21.195平方厘米。
38.819千米
【分析】根据经过时间=到达时间-出发时间,可分别求出高铁列车从南昌西站到北京西站及从南昌西站到郑州东站的时间,又根据,当速度一定时,路程与时间成正比例,设南昌西站到郑州东站的高速铁路大约有x千米,由题意可知等量关系式是:南昌西站到北京西站的路程∶南昌西站到北京西站的时间=昌西站到郑州东站的路程∶昌西站到郑州东站的时间,据此列比例并求解即可。
【解析】10时50分-7时20分=3时30分,3时30分=3.5时,13时20分-7时20分=6时
解:设南昌西站到郑州东站的高速铁路大约有x千米,由题意得:
1404∶6=x∶3.5
6x=4914
6x÷6=4914÷6
x=819
答:南昌西站到郑州东站的高速铁路大约有819千米。
39.特步体育专卖店
【分析】特步体育专卖店:一律八八折出售;把原价看作单位“1”,现价是原价的88%,单位“1”已知,用原价乘88%,求出一个足球的价格,再乘200,即可求出在特步体育专卖店购买200个足球需付的钱数;
李宁专卖店:“买八送一”;把“买8个送1个”看作一组,先用除法求出200里有几组余几个,用每组买的个数乘组数,再加上余数,求出实际需买足球的个数;然后根据“单价×数量=总价”,求出在李宁专卖店购买200个足球所需的钱数;
安踏专卖店:满5000元减680元;先根据“总价=单价×数量”求出以原价购买200个足球需要的钱数;再用除法求出总价里面有几个5000元,就减去几个680元,即是在安踏专卖店购买200个足球所需的钱数;
最后比较三家专卖店购买200个足球需付的钱数,得出在哪家店购买合算。
【解析】特步体育专卖店:
60×88%×200
=60×0.88×200
=52.8×200
=10560(元)
李宁专卖店:
8+1=9(个)
200÷9=22(组) 2(个)
实际购买数量:
22×8+2
=176+2
=178(个)
实际需付:
60×178=10680(元)
安踏专卖店:
200×60=12000(元)
12000÷5000=2(个) 2000(元)
12000-680×2
=12000-1360
=10640(元)
10560<10640<10680
答:到特步体育专卖店购买合算。
40.甲车的速度是75千米/时,乙车的速度是105千米/时
【分析】根据比例尺意义,图上距离1厘米代表实际距离12000000厘米,也就是120千米,已知A、B两地的图上距离为4.5厘米,所以用4.5×120计算出A、B两地的实际距离;
已知两车相遇时间与A、B两地实际距离,依据行程问题中“速度和=路程÷相遇时间”能求出甲乙两车速度和;
已知甲乙两车的速度比,把速度和按此比例分配,先确定总份数,再分别算出甲、乙速度占速度和的比例,最后用速度和乘对应比例得到甲乙两车各自速度。
【解析】12000000厘米=120千米
4.5×120=540(千米)
540÷3=180(千米/时)
180×
=180×
=15×5
=75(千米/时)
180×
=180×
=15×7
=105(千米/时)
答:甲车的速度是75千米/时,乙车的速度是105千米/时。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年六年级下册数学小升初重点校分班考考前冲刺预测卷
一、填空题
1.把一个底面半径是4cm的圆柱切拼成一个近似的长方体(如图),其表面积增加了48cm2,圆柱的高是( )cm,圆柱的体积是( )cm3。
2.“大美南阳是一个值得三顾的地方”。六年级学生举办了“自己心目中的大美南阳——绘画比赛”。乐乐画了一幅图,用6cm的线段表示实际900m。这幅图的比例尺是( )。
3.妈妈将20000元存入银行,定期2年,年利率2.15%,那么2年后可得利息和本金( )元。
4.圆柱的高一定,圆柱的体积和底面积成( )比例,圆柱的侧面积一定,底面周长和高成( )比例。
5.以学校大门为起点,向东走即为正,向西走即为负。王老师从学校大门出发,走了﹢50米,接着又走了﹣60米,这时王老师一共走了( )米,他现在学校大门( )(填“东”或“西”)( )米处。
6.张谦老师编写了一本《数学童话》,得到稿费4800元。按规定,一次稿费超过800元的部分,应该以14%的税率纳税。张老师应该缴纳税款( )元,他实际得到稿费( )元。
7.如果把一个正方体6个面分别涂上红、黄两种颜色,那么至少有( )个面颜色是相同的。
8.盒子里有2个红球,5个绿球和4个黄球,这些球除了颜色不同以外其他完全相同,从中至少摸出( )个球,才能保证其中有一个绿球。
9.下面是张叔叔的一张存单,存款到期时一共可以取出 元。
某银行(定期)储蓄存单账号123456
币种:人民币 金额(大写)玖千元 小写: 9000元
存入日期 存期 年利率 起息日 到期日
2024年6月5日 3年 2.75% 2024年6月5日 2027年6月5日
10.如图,若一块长方形卡纸剪下图中的涂色部分正好可以围成一个圆柱,则这个圆柱的底面周长是( )厘米,高是( )厘米。(π取3.14)
二、判断题
11.正方体的表面积和它的棱长成正比例关系。( )
12.希望小学六年级一班有学生56人,同一个月出生的学生至少有5个人。( )
13.在比例里,两个外项的积与两个内项积的差是0。( )
14.把一个边长4cm的正方形按3∶1放大,放大后正方形的面积为12cm2。( )
15.把圆柱的底面直径扩大到原来的2倍,高缩小到原来的,这个圆柱的体积不变。( )
16.成语“立竿见影”从数学的角度看,是应用了比例中同时同地竿高和影长成正比例关系的知识。( )
三、选择题
17.四个杯子中均装有一定量的开水,如果把100克糖融入水中,含糖率最高的是( )。
A. B. C. D.
18.如图,长方形ABCD,以BC为轴旋转一周后,其中甲部分和乙部分形成的立体图形的体积比是( )。
A.1∶1 B.2∶1 C.3∶1 D.4∶1
19.下列说法正确的是( )。
A.在﹣1和﹣5之间只有3个负数。 B.比4小的数只有0、1、2、3。
C.自然数中除0外都是整数。 D.早晨气温是﹣1℃,升高1℃后是0℃。
20.妈妈把60000元存入银行两年,年利率是2.15%,到期时可得利息多少元?列式为( )。
A.60000×2.15%×2 B.60000×2.15%
C.60000×2.15%+60000 D.60000×2.15%×2+60000
21.用3、4、7.5和10组成的比例是( )。
A.3∶10=7.5∶4 B.7.5∶4=3∶10 C.10∶7.5=4∶3
22.运动会上,在5分钟投篮比赛中,六(2)班的10名同学共投中了83个,总有一名队员至少投中( )个球。
A.7 B.8 C.9 D.10
23.小北准备用下面的长方形硬纸板做成一个无盖笔筒的侧面,他可以选用( )作底面。(单位:厘米,接缝处忽略不计)
A.①②④ B.②③④ C.①②③ D.①③④
24.根据我们的实际生活经验,下面该用负数表示的是( )。
A.亏损500元 B.收入300元 C.降低100元
25.笑笑在商场打七折的时候,花42元钱买了一个文具盒,便宜了多少元?下面算式正确的是( )。
A.42×70% B.42÷70%-42
C.42×(1-70%) D.42÷(1-70%)-42
26.口袋里有9个红球、4个白球、1个黑球,球除颜色外完全相同,每次从中摸一个球不放回,至少要摸出( )个球,才能保证取到的球里有两个颜色相同。
A.2 B.5 C.10 D.4
四、计算题
27.直接写出得数.
28.下面各题,怎样算简便就怎样算。
+++ 18×25%+×40+42×0.25 9.7÷1.25÷0.8
29.解比例。
1.8∶5.4=x∶2.4
30.计算如图的体积。
五、作图题
31.按要求填一填、画一画。(每个小方格都是面积为1cm2的正方形)
(1)点A的位置用数对表示是( )。
(2)画出三角形ABC绕点C逆时针旋转90°后的图形,得到图形①。
(3)画出三角形ABC向右平移3格后的图形,得到图形②。
(4)画出三角形ABC按2∶1放大后的图形,得到图形③。
六、解答题
32.一个圆柱形玻璃杯的高是15厘米,它的底面半径是高的,在这个玻璃杯内装入10厘米高的水,然后将一个底面直径是16厘米的圆锥形铅锤浸没在水中,水面上升到12.4厘米。
(1)这个铅锤的体积是多少立方厘米?
(2)这个铅锤的高是多少厘米?
33.张希家要买一套总价120万元的住房,如果一次性付清房款可以享受九五折优惠。买这套房子要按照实际房价的1.5%缴纳契税,如果张希家一次性付清房款,要缴纳契税多少万元?
34.李华一家四口打算去北京游玩三天,李华家所在城市与北京之间的高铁车票和机票价格如下:
交通工具 票价 说明
火车 714元 身高1.2~1.5米的儿童半票
飞机 1200元 未满12周岁半价票
(1)李华身高1.48米,年龄未满12周岁,如果她与爸爸、妈妈和奶奶去北京旅游往返都乘火车,交通费至少要准备多少钱?
(2)如果单程乘坐飞机(成人机票打八折,儿童机票半价),那么单程至少要准备多少钱?
35.在比例尺是1∶5000000的地图上,量得A、B两座城市的距离是18厘米,一列高铁以每小时200千米的速度从A城开往B城,多少小时能够抵达?
36.为切实加强体育锻炼,提高学生身体素质,希望小学准备购买60根跳绳发到各班,现有甲、乙、丙三个商店可供选择,三个商店同品牌跳绳单价都是7元,但各个商店的优惠方法不同:
甲商店:买10根跳绳免费赠送2根,不足10根不赠送。
乙商店:每根跳绳按八五折优惠。
丙商店:购物每满200元减40元。
为了节省费用,希望小学应在哪个商店购买?
37.一个圆柱形的玻璃缸装有一些水,底面内直径为6厘米,高为12厘米。把一个圆锥形铅锤放入玻璃缸中(全部浸没),水面上升了0.5厘米,铅锤的高为2厘米,这个铅锤的底面积是多少平方厘米?
38.南昌西站到北京西站之间的高速铁路大约长1404千米。一趟高铁列车早上7:20从南昌西站出发匀速行驶,10:50途经郑州东站,13:20到达北京西站(途中经停时间忽略不计)。南昌西站到郑州东站的高速铁路大约有多长?(用比例解)
39.学校体育器材室准备购买200个足球,每个足球价格为60元。特步体育专卖店一律八八折出售,李宁专卖店“买八送一”,安踏专卖店满5000元减680元。请你帮学校算一算,到哪家店购买合算?
40.在一幅比例尺为1∶12000000的地图上,量得AB两地的图上距离为4.5厘米。甲乙两车同时从A、B两地相对开出,经过3小时相遇,甲、乙两车的速度比为5∶7。甲乙两车的速度分别是多少?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.6 301.44
【分析】根据题意,把一个圆柱切拼成一个近似的长方体,增加的表面积等于2个长方形的面积,长方形的长是圆柱的高,宽是圆柱的底面半径;用增加的表面积除以2,求出一个面的面积,再除以底面半径,即可求出圆柱的高;
根据圆柱的体积公式V=πr2h,代入数据计算,求出圆柱的体积。
【解析】圆柱的高:
48÷2÷4
=24÷4
=6(cm)
圆柱的体积:
3.14×42×6
=3.14×16×6
=301.44(cm3)
圆柱的高是6cm,圆柱的体积是301.44cm3。
2.1∶15000/
【分析】已知乐乐画了一幅图,用6cm的线段表示实际900m,根据“比例尺=图上距离∶实际距离”以及进率“1m=100cm”,求出这幅图的比例尺。
【解析】6cm∶900m
=6cm∶(900×100)cm
=6∶90000
=(6÷6)∶(90000÷6)
=1∶15000
这幅图的比例尺是1∶15000。
3.20860
【分析】先根据“利息=本金×利率×存期”求出到期时可得到的利息,再加上本金,即是到期时可取回的钱数。
【解析】20000×2.15%×2+20000
=20000×0.0215×2+20000
=860+20000
=20860(元)
那么2年后可得利息和本金20860元。
4.正 反
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解析】圆柱的体积÷底面积=高(一定),商一定,所以圆柱的体积和底面积成正比例;
圆柱的底面周长×高=圆柱的侧面积(一定),乘积一定,所以底面周长和高成反比例。
5.110 西 10
【分析】正数、负数表示两种相反意义的量。以学校大门为起点,向东走即为正,向西走即为负。
王老师从学校大门出发,走了﹢50米,即向东走了50米;接着又走了﹣60米,即向西走了60米;把两次走的距离相加,即是王老师一共走的路程;因为向西走的距离超过向东走的距离,那么此时的位置在起点的西边(60-50)米。
【解析】50+60=110(米)
60-50=10(米)
这时王老师一共走了110米,他现在学校大门西10米处。
6.560 4240
【分析】本题考查百分数的应用,税率问题。首先要确定需要纳税的部分:稿费超过800元的部分才纳税,张老师的稿费是4800元,超过800元的部分是4800-800=4000元,然后根据“税款=应纳税部分×税率”计算出应缴纳的税款,最后用总的稿费减去缴纳的税款,就是实际得到的稿费。
【解析】4800-800=4000(元)
4000×14%=560(元)
张老师应该缴纳税款560元。
4800-560=4240(元)
所以张老师实际得到稿费4240元。
7.3
【分析】分析题目,正方体一共有6个面,每个面都只有红色和黄色两种选择,题目要求至少有多少个面的颜色是相同的,所以需要考虑最不利的情况,即两种颜色的面各占一半,据此解答。
【解析】6÷2=3(个)
如果把一个正方体6个面分别涂上红、黄两种颜色,那么至少有3个面颜色是相同的。
8.7
【分析】要保证摸出绿球,要考虑最差结果,一直把其它球摸完才摸到绿球,也就是先把红球和黄球全部摸出,然后再摸一个球就一定是绿球。据此列式解答。
【解析】2+4+1
=6+1
=7(个)
所以从中至少摸出7个球,才能保证其中有一个绿球。
9.9742.5
【分析】从题意可知:本金是9000元,存期3年,年利率是2.75%。根据利息=本金×时间×利率,代入数据计算,求出利息,再加上本金,就是到期时一共可以取出的钱。
【解析】9000×2.75%×3+9000
=247.5×3+9000
=742.5+9000
=9742.5(元)
存款到期时一共可以取出9742.5元。
10.15.7 10
【分析】看图可知,圆柱底面直径=5厘米,根据圆的周长=圆周率×直径,求出底面周长;高=底面直径×2。
【解析】3.14×5=15.7(厘米)
5×2=10(厘米)
这个圆柱的底面周长是15.7厘米,高是10厘米。
11.×
【分析】判断两个相关联的量呈正比例或反比例时,要看两个变量的比值或乘积是否为定值,正方体的表面积=棱长×棱长×6,据此解答。
【解析】正方体的表面积=棱长×棱长×6,表达式变形可得:正方体的表面积÷棱长=棱长×6。表面积与棱长比值不一定,所以正方体的表面积和它的棱长不成正比例。
故答案为:×
12.√
【分析】一年有12个月,把12个月看作12个“抽屉”,56个学生看作56个“苹果”,用56除以12,求出商和余数,再用商加上1即可解答。
【解析】56÷12=4(人)……8(人)
4+1=5(人)
所以同一个月出生的学生至少有5个人,故原题说法正确。
故答案为:√
13.√
【分析】在比例里,两个外项之积等于两个内项之积,这是比例的基本性质,由此即可解决问题。
【解析】根据比例的基本性质可得:在比例里两内项的积等于两外项的积。
例如:3∶4=9∶12,4×9=36,3×12=36,36-36=0
即在比例里,两个外项的积与两个内项的积的差是0。
故答案为:√
14.×
【分析】根据题意,将正方形按3∶1放大,即放大后的正方形边上是原来边长的3倍,据此计算出放大后正方形的边长,再根据正方形的面积=边长×边长,计算出面积即可判断。
【解析】4×3=12(cm)
12×12=144(cm2)
即放大后正方形的面积为144cm2,即原说法错误。
故答案为:×
15.×
【分析】圆柱的体积V=πr2h,假设圆柱体原来的底面直径为2,直径扩大到原来的2倍后直径为4,假设原来的高为2,高缩小到原来的后高为1,根据圆柱的体积公式,算出原来圆柱的体积和变化后圆柱的体积,再进行比较即可。
【解析】假设圆柱体原来的底面直径为2,高为2。
变化前圆柱的体积:
3.14×(2÷2)2×2
=3.14×12×2
=3.14×1×2
=6.28
变化后圆柱的直径为2×2=4,变化后圆柱的高为2×=1。
变化后圆柱的体积:
3.14×(4÷2)2×1
=3.14×22×1
=3.14×4×1
=12.56
12.56÷6.28=2
把圆柱的底面直径扩大到原来的2倍,高缩小到原来的,这个圆柱的体积扩大到原来的2倍。
故答案为:×
16.√
【分析】同时同地物体的长度和它的影子的长度的比值一定,即物体的长度和它的影子的长度成正比例,据此解答。
【解析】成语“立竿见影”从数学的角度看,是应用了比例中同时同地竿高和影长成正比例关系的知识。说法正确。
故答案为:√
17.A
【分析】根据圆锥的体积公式:V=πr2h,长方体的体积公式:V=abh,正方体的体积公式:V=a3,圆柱的体积公式:V=πr2h,把数据代入公式求出四杯水的体积,然后进行比较,水的体积少的则含糖率就高。据此解答。
【解析】×3.14×(6÷2)2×6
=×3.14×32×6
=3.14×9×6
=56.52(立方厘米)
4×4×6
=16×6
=96(立方厘米)
6×6×6=216(立方厘米)
3.14×(4÷2)2×6
=3.14×22×6
=3.14×4×6
=75.36(立方厘米)
56.52<75.36<96<216
含糖率最高的是A。
故答案为:A
18.B
【分析】长方形绕着BC边旋转一周,形成一个圆柱,而三角形BCD(也就是乙部分)绕着BC边旋转一周,形成一个圆锥,甲部分形成的立体图形就是整个圆柱里面去掉乙部分形成的圆锥;分析题意可知形成的圆柱和圆锥等底等高,如果圆柱体积是3份,那么乙部分形成的立体图形圆锥体积就是1份,则甲部分形成的立体图形体积就是3-1=2份。
【解析】由分析可知:甲部分形成的立体图形的体积是2份,乙部分形成的立体图形的体积是1份,所以甲部分和乙部分形成的立体图形的体积比是2∶1。
故答案为:B
19.D
【分析】A.两个负数之间不仅有负整数也有负小数;
B.比4小的数不仅有整数,还有小数;
C.根据整数的认识解答;
D.根据对温度的认识解答。
【解析】A.在﹣1和﹣5之间有无数个负数,原题说法错误;
B.比4小的数有无数个,原题说法错误;
C.0和正整数统称为自然数,整数包括正整数、0和负整数,所以说0也是整数,即自然数都是整数,原题说法错误;
D.在温度计中0℃在﹣1℃的上面一格,所以早晨气温是﹣1℃,升高1℃后是0℃。原题说法正确。
故答案为:D
20.A
【分析】已知本金60000元,存期2年,年利率2.15%,求利息,根据“利息=本金×年利率×存期”,代入数据即可计算出利息。
【解析】60000×2.15%×2
=60000×0.0215×2
=1290×2
=2580(元)
所以计算到期时可得利息列式为60000×2.15%×2,结果是2580元。
故答案为:A
21.C
【分析】根据比例的基本性质,分别求出三个选项中比例的两个外项的积和两个内项的积,看积是否相等,如果相等,即可组成比例;不相等,就不能组成比例。
比例的基本性质:在比例里,两个外项的积等于两个内项的积。
【解析】A.3×4=12,10×7.5=75,12≠75,所以3∶10≠7.5∶4;
B.7.5×10=75,4×3=12,75≠12,所以7.5∶4≠3∶10;
C.10×3=30,7.5×4=30,30=30,所以10∶7.5=4∶3。
所以,用3、4、7.5和10组成的比例是10∶7.5=4∶3。
故答案为:C
22.C
【分析】根据题意,将投中的83个球平均分给10名队员,每名队员投中8个球,还剩下3个球,这3个球,无论分给哪名队员,总有一名队员至少抽中(8+1)个球。
【解析】83÷10=8(个)……3(个)
8+1=9(个)
总有一名队员至少投中9个球。
故答案为:C
23.B
【分析】由于做无盖笔筒的侧面,那么底面周长应该等于这个侧面的长或者是宽,根据圆的周长公式:周长=π×半径×2;正方形周长公式:周长=边长×4;分别求出各个底面的周长;再和长方形的长或宽进行比较,进而解答。
【解析】①3.14×(4×2)
=3.14×8
=25.12(厘米)
底面周长是25.12厘米;
②3.14×4=12.56(厘米)
底面周长是12.56厘米;
③3.14×4=12.56(厘米)
底面周长是12.56厘米;
④3.14×(3×2)
=3.14×6
=18.84(厘米)
底面周长是18.84厘米。
小北准备用下面的长方形硬纸板做成一个无盖笔筒的侧面,他可以选用②③④作底面。
故答案为:B
24.A
【分析】正负数表示一组相反意义的量,据此结合实际生经验,逐项分析。
【解析】A.不赚不亏记为0,亏损500元,相对于盈利,亏损应记为负数﹣500元。符合题意。
B.支出和收入表示相反意义的量,收入300元属于正向增加,用正数表示﹢300元。不符合题意。
C.降低100元需结合具体情境。若表示变化量(如成本减少100元),应记为负数(﹣100元);但若仅描述减少的数值(如“降低了100元”),通常直接使用正数表示减少的幅度。本题未明确为变化量,不强制用负数。不符合题意。
故答案为:A
25.B
【分析】原价×折扣=现价,用42元除以折扣求出原价,再用原价减去现价42元就是便宜的钱数,据此解答。
【解析】A.42×70%,用现价乘折扣70%没有实际意义,不符合题意;
B.42÷70%-42,先用42÷70%求出原价,再减去42元就是便宜的钱数,符合题意;
C.42×(1-70%),用现价乘现价比原价便宜的百分率,得不到便宜的金额,不符合题意;
D.42÷(1-70%)-42,用现价除以现价比原价便宜的百分率,不能得出原价,得不到便宜的金额,不符合题意。
故答案为:B
26.D
【分析】分析题目,要保证取到两个颜色的球,则最不利的情况是3种颜色的球各取了1个,最后再取1个一定能保证有2个球的颜色相同,据此解答。
【解析】3+1=4(个)
至少要摸出4个球,才能保证取到的球里有两个颜色相同。
故答案为:D
27.2018;384;0.8;0.75;
10.33;0.96;7;0.64;
;11
【解析】略
28.2;25;9.7
【分析】题1:根据加法交换律和结合律进行简算;
题2:先把25%、和0.25转化成相同的形式,再根据乘法分配律进行简算;
题3:根据除法的性质进行简算。
【解析】+++
=(+)+(+)
=1+1
=2
18×25%+×40+42×0.25
=18×0.25+0.25×40+42×0.25
=0.25×(18+40+42)
=0.25×100
=25
9.7÷1.25÷0.8
=9.7÷(1.25×0.8)
=9.7÷1
=9.7
29.x=8;x=0.8;x=5
【分析】(1)根据比例的性质化简,再根据等式的基本性质,方程两边同时除以0.25求解;
(2)根据比例的性质化简,再根据等式的基本性质,方程两边同时除以5.4求解;
(3)根据比例的性质化简,再根据等式的基本性质,方程两边同时除以求解。
【解析】(1)
解:0.25x=1.25×1.6
0.25x=2
0.25x÷0.25=2÷0.25
x=8
(2)1.8∶5.4=x∶2.4
解:5.4x=1.8×2.4
5.4x=4.32
5.4x÷5.4=4.32÷5.4
x=0.8
(3)x∶8=∶
解:x=8×
x=6
x÷=6÷
x=6×
x=5
30.1105.28立方厘米
【分析】观察图形可知,该组合体由一个国柱和一个圆锥组成。要计算其体积,需分别计算圆柱体积和圆锥体积,再将二者相加。计算圆柱体积时,根据圆柱体积公式V=πr2h(其中r是底面半径,h是高),已知底面直径为8厘米,可先求出半径,再结合圆柱的高20厘米来计算体积。计算圆锥体积时,依据圆锥体积公式V锥=π2h,同样根据已知条件求出半径,再结合圆锥的高6厘米计算体积。最后把圆柱体积和圆锥体积相加,得到组合体的体积。
【解析】计算底面半径:r=8÷2=4(厘米)
计算圆柱体积:
V柱=3.14×42×20
=3.14×16×20
=50.24×20
=1004.8(立方厘米)
计算圆锥体积:
V锥=×3.14×42×6
=×3.14×16×6
=×50.24×6
=×301.44
=100.48(立方厘米)
计算组合体体积:
V=V锥+V柱
=1004.8+100.48
=1105.28(立方厘米)
即图形的体积是1105.28立方厘米。
31.(1)(5,4)
(2)(3)(4)见详解
【分析】(1)数对的表示方法:(列数,行数),数对的第一个数表示列,第二个数表示行,找出点A在方格中对应的列数和行数,再用数对表示出来。
(2)根据旋转的特征,三角形ABC绕点C逆时针旋转90°,点C的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)根据平移的特征,把三角形ABC的各顶点向右平移3格,依次连接各顶点,即可得到平移后的图形。
(4)把三角形ABC按照2∶1放大,就是将三角形ABC的底和高放大到原来的2倍,放大后图形与原图形对应边长的比是2∶1,形状没有发生变化。
【解析】(1)点A的位置用数对表示是(5,4)。
(2)(3)(4)见下图
32.(1)753.6立方厘米;(2)11.25厘米
【分析】(1)求铅锤体积首先确定圆柱玻璃杯底面半径:已知圆柱形玻璃杯的高是15厘米,它的底面半径是高的,所以底面半径为15×=10厘米。
然后根据排水法原理:圆锥放入圆柱玻璃杯中,水面上升的体积就是圆锥的体积。水面从10厘米上升到12.4厘米,上升了12.4-10=2.4厘米。利用圆柱体积公式V=πr2h(r是底面半径,h是高),可算出上升的水的体积,也就是铅锤的体积。
(2)已知圆锥体积公式为V=πr2h(V是体积,r是底面半径,h是高),由(1)已求得圆锥体积,且已知圆锥底面直径是16厘米,可算出底面半径。将圆锥体积公式变形为h=3V÷(πr2),据此代入已知数据来计算圆锥的高即可。
【解析】(1)15×=10(厘米)
3.14×102×(12.4-10)
=3.14×100×2.4
=314×2.4
=753.6(立方厘米)
答:这个铅锤的体积是753.6立方厘米。
(2)753.6×3÷[3.14×(16÷2)2]
=2260.8÷[3.14×64]
=2260.8÷200.96
=11.25(厘米)
答:这个铅锤的高是11.25厘米。
33.1.71万元
【分析】把这套住房的总价看作单位“1”,一次性付清房款可以享受九五折优惠,即实际房价是总价的95%,根据求一个数的百分之几是多少,用乘法计算,求出实际房价;又已知还要按照实际房价的1.5%缴纳契税,把实际房价看作单位“1”,单位“1”已知,用实际房价乘1.5%,即可求出要缴纳契税的金额。
【解析】120×95%×1.5%
=114×1.5%
=1.71(万元)
答:要缴纳契税1.71万元。
34.(1)4998元
(2)3480元
【分析】(1)因为李华身高1.48米,在1.2-1.5米之间,年龄未满12周岁,所以李华乘火车是半票,爸爸、妈妈和奶奶是全票;用火车的票价乘3求出3个成年人的总票价,再加上火车票价的一半求出单程总票价,再乘2就是乘火车往返的交通费。
(2)单程乘坐飞机(成人机票打八折,儿童机票半价),打八折就是按原票价的80%收费,先用1200乘3求出3个成年人在不打折的情况下需要的飞机票钱数,再乘80%,求出三个成年人的飞机票价,再加上飞机票的一半就是么单程至少要准备的钱数。
【解析】(1)(714×3+714÷2)×2
=(2142+357)×2
=2499×2
=4998(元)
答:交通费至少要准备4998元。
(2)1200×3×80%+1200÷2
=3600×80%+600
=2880+600
=3480(元)
答:单程至少要准备3480元。
35.4.5小时
【分析】根据实际距离=图上距离÷比例尺,代入数值计算出A、B两座城市之间的实际距离;再根据时间=路程÷速度,代入相应数值计算,所得结果即为多少小时能够抵达。
【解析】18÷
=18×5000000
=90000000(厘米)
90000000厘米=900千米
900÷200=4.5(小时)
答:4.5小时能够抵达。
36.丙商店
【分析】甲商店:买10根跳绳免费赠送2根,把(10+2)根跳绳看作一组,60根跳绳一共有5组,每组需要付10根跳绳的钱数,根据“总价=单价×数量”求出需要付的总钱数;
乙商店:八五折即现价占原价的85%,每根跳绳的实际价格=每根跳绳原来的价格×85%,最后乘希望小学购买跳绳的数量求出需要付的总钱数;
丙商店:先根据“总价=单价×数量”求出需要付的总钱数,即420元,420元里面有两个200元,需要减去2×40=80元,实际需要付的钱数=原来需要付的总钱数-满减的钱数,最后比较大小选择需付钱数最少的商店,据此解答。
【解析】甲商店:60÷(10+2)
=60÷12
=5(组)
5×10×7
=50×7
=350(元)
乙商店:八五折=85%
7×85%×60=357(元)
丙商店:60×7=420(元)
420÷200=2(个)……20(元)
420-2×40
=420-80
=340(元)
因为340元<350元<357元,所以在丙商店购买最划算。
答:为了节省费用,希望小学应在丙商店购买。
37.21.195平方厘米
【分析】根据题意可知,把圆锥形铅锤放入圆柱形玻璃缸中(完全浸没,水未溢出),上升部分水的体积就等于这个铅锤的体积,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:V=Sh那么S=3V÷h,把数据代入公式解答。
【解析】3.14×(6÷2)2×0.5÷÷2
=3.14×32×0.5×3÷2
=3.14×9×0.5×3÷2
=14.13×3÷2
=42.39÷2
=21.195(平方厘米)
答:这个铅锤的底面积是21.195平方厘米。
38.819千米
【分析】根据经过时间=到达时间-出发时间,可分别求出高铁列车从南昌西站到北京西站及从南昌西站到郑州东站的时间,又根据,当速度一定时,路程与时间成正比例,设南昌西站到郑州东站的高速铁路大约有x千米,由题意可知等量关系式是:南昌西站到北京西站的路程∶南昌西站到北京西站的时间=昌西站到郑州东站的路程∶昌西站到郑州东站的时间,据此列比例并求解即可。
【解析】10时50分-7时20分=3时30分,3时30分=3.5时,13时20分-7时20分=6时
解:设南昌西站到郑州东站的高速铁路大约有x千米,由题意得:
1404∶6=x∶3.5
6x=4914
6x÷6=4914÷6
x=819
答:南昌西站到郑州东站的高速铁路大约有819千米。
39.特步体育专卖店
【分析】特步体育专卖店:一律八八折出售;把原价看作单位“1”,现价是原价的88%,单位“1”已知,用原价乘88%,求出一个足球的价格,再乘200,即可求出在特步体育专卖店购买200个足球需付的钱数;
李宁专卖店:“买八送一”;把“买8个送1个”看作一组,先用除法求出200里有几组余几个,用每组买的个数乘组数,再加上余数,求出实际需买足球的个数;然后根据“单价×数量=总价”,求出在李宁专卖店购买200个足球所需的钱数;
安踏专卖店:满5000元减680元;先根据“总价=单价×数量”求出以原价购买200个足球需要的钱数;再用除法求出总价里面有几个5000元,就减去几个680元,即是在安踏专卖店购买200个足球所需的钱数;
最后比较三家专卖店购买200个足球需付的钱数,得出在哪家店购买合算。
【解析】特步体育专卖店:
60×88%×200
=60×0.88×200
=52.8×200
=10560(元)
李宁专卖店:
8+1=9(个)
200÷9=22(组) 2(个)
实际购买数量:
22×8+2
=176+2
=178(个)
实际需付:
60×178=10680(元)
安踏专卖店:
200×60=12000(元)
12000÷5000=2(个) 2000(元)
12000-680×2
=12000-1360
=10640(元)
10560<10640<10680
答:到特步体育专卖店购买合算。
40.甲车的速度是75千米/时,乙车的速度是105千米/时
【分析】根据比例尺意义,图上距离1厘米代表实际距离12000000厘米,也就是120千米,已知A、B两地的图上距离为4.5厘米,所以用4.5×120计算出A、B两地的实际距离;
已知两车相遇时间与A、B两地实际距离,依据行程问题中“速度和=路程÷相遇时间”能求出甲乙两车速度和;
已知甲乙两车的速度比,把速度和按此比例分配,先确定总份数,再分别算出甲、乙速度占速度和的比例,最后用速度和乘对应比例得到甲乙两车各自速度。
【解析】12000000厘米=120千米
4.5×120=540(千米)
540÷3=180(千米/时)
180×
=180×
=15×5
=75(千米/时)
180×
=180×
=15×7
=105(千米/时)
答:甲车的速度是75千米/时,乙车的速度是105千米/时。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
