2.3.1乘方(第二课时) 课件(共21张PPT) 人教版七年级上册数学
文档属性
| 名称 | 2.3.1乘方(第二课时) 课件(共21张PPT) 人教版七年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 556.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 06:15:00 | ||
图片预览







文档简介
(共21张PPT)
2.3 有理数的乘方
2.3.1 乘方
第2课时 有理数的混合运算
1.了解有理数混合运算的意义,掌握有理数的混合运算法则及运算顺序.
2.熟练地进行有理数的加、减、乘、除、乘方的运算,并在运算过程中合理使用运算律.
学习目标
情境导入
前面我们学习了有理数的加、减、乘、除和乘方运算,对各种运算的法则、运算律和运算技巧已经比较熟悉,如果遇到有理数的混合运算,你有信心进行准确的计算吗?下图是小玲和小亮的对话,你同意小亮的说法吗?
壹
新知探究
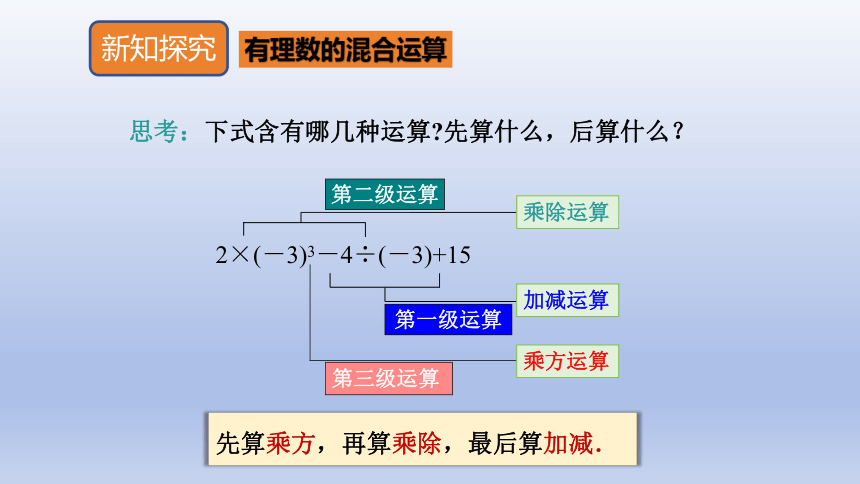
思考:下式含有哪几种运算 先算什么,后算什么?
乘方运算
第一级运算
第三级运算
乘除运算
第二级运算
2×(-3)3-4÷(-3)+15
加减运算
先算乘方,再算乘除,最后算加减.
有理数的混合运算
归纳小结
做有理数的混合运算时,应注意以下运算顺序:
1.先乘方,再乘除,最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,
按小括号、 中括号、大括号依次进行.
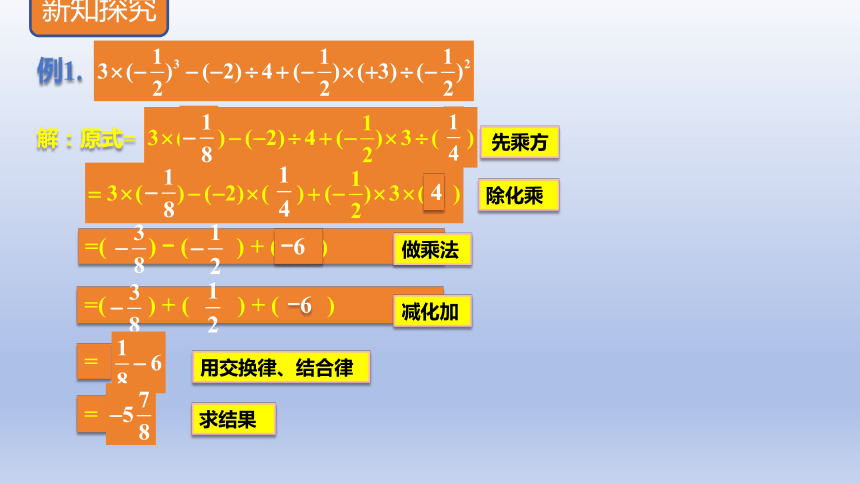
=( ) + ( ) + ( )
=( ) - ( ) + ( )
-6
解:原式=
例1.
4
-6
=
=
先乘方
除化乘
做乘法
用交换律、结合律
求结果
减化加
新知探究
例1 计算:
(1)2×(–3)3–4×(–3)+15; (2)(–2)3+(–3)×[(–4)2+2]–(–3)2÷(–2).
解:(1)原式=2×(–27)–(–12)+15
= –54+12+15
= –27
= –8+(–3)×18–(–4.5)
(2)原式= –8+(–3)×(16+2)–9÷(–2)
= –8–54+4.5
= –57.5
典例精析
例2 计算: .
解法一:
原式=
解法二:
原式=
= –11
= –6+(–5)
= –11
观察下面三行数:
–2, 4, –8, 16, –32, 64,…; ①
0, 6, –6, 18, –30, 66,…; ②
–1, 2, –4, 8, –16, 32,…. ③
(1)第①行数按什么规律排列?
解:(1)第①行数是
新知二 数字规律探究
分析:观察①,发现各数均为2的倍数.联系数的乘方,从符号和绝对值两方面考虑,可发现排列的规律.
合作探究
(2)第②③行数与第①行数分别有什么关系?
解:(2)第②行数是第①行相应的数加2,即
第③行数是第①行相应的数除以2,即
(3)取每行数的第10个数,计算这三个数的和.
解:(3)每行数中的第10个数的和是:
=1024+1026+512
=1024+(1024+2)+1024 0.5
=2562
智能点拨
观察下列三行数,你能提出哪些问题?
-2,4,-8,16,-32,64,… ①
0,6,-6,18,-30,66,… ②
-1,2,-4,8,-16,32,… ③
第②行
第③行
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
解:
(1)
(2)
智能点拨
观察下列三行数,你能提出哪些问题?
-2,4,-8,16,-32,64,…①
0,6,-6,18,-30,66,…②
-1,2,-4,8,-16,32,… ③
(3)取每行数的第10个数,计算这三个数的和.
解:
(3)
1.根据规律填空;
(1)1,4,9,16,25,36,______,______,...
(2)0,3,8,15,24,_______,_______,...
2.观察下列按规律排列的等式:0+1=12,2×1+2=22,3×2+3=32,4×3+4=42,...
请猜想第10个等式应为____________________,
请猜想第n个等式应为___________________。
49
64
35
48
10×9+10=102
n×(n-1)+n=n2
练一练
练一练
3.观察下列各式:
猜想:
若n是正整数,那么
例题
例4
探索规律:=3,个位数字是3;=9,个位数字是9; =27,个位数字是7;=81,个位数字是1;=243,个位数字是3; =729,个位数字是9……那么的个位数字是, 的个位数字是.
解析:由题意可知,对于3的幂,个位数字只出现3,9,7,1这四个数,且按这一顺序每4个一循环,因此,欲求, 的个位数字是多少,关键看共有几个循环,余数是几.因为7÷4=1……3,所以的个位数字是7,而2017÷4=504 …… 1,故的个位数字是3.
7
3
课堂检测
1.直接写出结果:
① -17+8=_____,② 3-6=_____,③(-3)×(- )=_____,
④ 2÷(-)=_____,⑤ -(-3)3=_____,⑥ =_____.
2.若a2=a,则a=________.
3.如果=2,=3,那么a2b=_______.
-9
-3
-4
27
0或1
±12
4.计算.
解:
解:
课堂检测
拓展训练
1.(1)计算:①2-1=___;②22-2-1=___; ③23-22-2-1=___; ④24-23-22-2-1 =___; ⑤25-24-23-22-2-1=___.
(2)根据上面的计算结果猜想:
22020-22019-22018-…-22-2-1的值为____;
2n-2n-l-2n-2-.….-22-2-1的值为____.
(3)根据上面猜想的结论,求213-212-211-210-29-28-27-26的值.
1
1
1
1
1
1
1
解:由猜想的结论得:213-212-211-210-29-28-27-26-25-24-23-22-2-1=1
所以,213-212-211-210-29-28-27-26
=1+1+2+22+23+24+25
=1+2+4+8+16+32
=64
2.已知m=b1+b2+b3+b4+···+b1000,当b=-1时,
求m5的值.
解:当b=-1时,
m=b1+b2+b3+b4+···+b1000
=(-1)1+(-1)2+(-1)3+(-1)4+···+(-1)1000
=-1+1-1+1-1···-1+1
=0.
所以m5=05=0.
拓展训练
有理数的加、减、乘、除、乘方混合运算的顺序:
1.先乘方,再乘除,最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号、中括
号、大括号依次进行.
课堂小结
2.3 有理数的乘方
2.3.1 乘方
第2课时 有理数的混合运算
1.了解有理数混合运算的意义,掌握有理数的混合运算法则及运算顺序.
2.熟练地进行有理数的加、减、乘、除、乘方的运算,并在运算过程中合理使用运算律.
学习目标
情境导入
前面我们学习了有理数的加、减、乘、除和乘方运算,对各种运算的法则、运算律和运算技巧已经比较熟悉,如果遇到有理数的混合运算,你有信心进行准确的计算吗?下图是小玲和小亮的对话,你同意小亮的说法吗?
壹
新知探究
思考:下式含有哪几种运算 先算什么,后算什么?
乘方运算
第一级运算
第三级运算
乘除运算
第二级运算
2×(-3)3-4÷(-3)+15
加减运算
先算乘方,再算乘除,最后算加减.
有理数的混合运算
归纳小结
做有理数的混合运算时,应注意以下运算顺序:
1.先乘方,再乘除,最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,
按小括号、 中括号、大括号依次进行.
=( ) + ( ) + ( )
=( ) - ( ) + ( )
-6
解:原式=
例1.
4
-6
=
=
先乘方
除化乘
做乘法
用交换律、结合律
求结果
减化加
新知探究
例1 计算:
(1)2×(–3)3–4×(–3)+15; (2)(–2)3+(–3)×[(–4)2+2]–(–3)2÷(–2).
解:(1)原式=2×(–27)–(–12)+15
= –54+12+15
= –27
= –8+(–3)×18–(–4.5)
(2)原式= –8+(–3)×(16+2)–9÷(–2)
= –8–54+4.5
= –57.5
典例精析
例2 计算: .
解法一:
原式=
解法二:
原式=
= –11
= –6+(–5)
= –11
观察下面三行数:
–2, 4, –8, 16, –32, 64,…; ①
0, 6, –6, 18, –30, 66,…; ②
–1, 2, –4, 8, –16, 32,…. ③
(1)第①行数按什么规律排列?
解:(1)第①行数是
新知二 数字规律探究
分析:观察①,发现各数均为2的倍数.联系数的乘方,从符号和绝对值两方面考虑,可发现排列的规律.
合作探究
(2)第②③行数与第①行数分别有什么关系?
解:(2)第②行数是第①行相应的数加2,即
第③行数是第①行相应的数除以2,即
(3)取每行数的第10个数,计算这三个数的和.
解:(3)每行数中的第10个数的和是:
=1024+1026+512
=1024+(1024+2)+1024 0.5
=2562
智能点拨
观察下列三行数,你能提出哪些问题?
-2,4,-8,16,-32,64,… ①
0,6,-6,18,-30,66,… ②
-1,2,-4,8,-16,32,… ③
第②行
第③行
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
解:
(1)
(2)
智能点拨
观察下列三行数,你能提出哪些问题?
-2,4,-8,16,-32,64,…①
0,6,-6,18,-30,66,…②
-1,2,-4,8,-16,32,… ③
(3)取每行数的第10个数,计算这三个数的和.
解:
(3)
1.根据规律填空;
(1)1,4,9,16,25,36,______,______,...
(2)0,3,8,15,24,_______,_______,...
2.观察下列按规律排列的等式:0+1=12,2×1+2=22,3×2+3=32,4×3+4=42,...
请猜想第10个等式应为____________________,
请猜想第n个等式应为___________________。
49
64
35
48
10×9+10=102
n×(n-1)+n=n2
练一练
练一练
3.观察下列各式:
猜想:
若n是正整数,那么
例题
例4
探索规律:=3,个位数字是3;=9,个位数字是9; =27,个位数字是7;=81,个位数字是1;=243,个位数字是3; =729,个位数字是9……那么的个位数字是, 的个位数字是.
解析:由题意可知,对于3的幂,个位数字只出现3,9,7,1这四个数,且按这一顺序每4个一循环,因此,欲求, 的个位数字是多少,关键看共有几个循环,余数是几.因为7÷4=1……3,所以的个位数字是7,而2017÷4=504 …… 1,故的个位数字是3.
7
3
课堂检测
1.直接写出结果:
① -17+8=_____,② 3-6=_____,③(-3)×(- )=_____,
④ 2÷(-)=_____,⑤ -(-3)3=_____,⑥ =_____.
2.若a2=a,则a=________.
3.如果=2,=3,那么a2b=_______.
-9
-3
-4
27
0或1
±12
4.计算.
解:
解:
课堂检测
拓展训练
1.(1)计算:①2-1=___;②22-2-1=___; ③23-22-2-1=___; ④24-23-22-2-1 =___; ⑤25-24-23-22-2-1=___.
(2)根据上面的计算结果猜想:
22020-22019-22018-…-22-2-1的值为____;
2n-2n-l-2n-2-.….-22-2-1的值为____.
(3)根据上面猜想的结论,求213-212-211-210-29-28-27-26的值.
1
1
1
1
1
1
1
解:由猜想的结论得:213-212-211-210-29-28-27-26-25-24-23-22-2-1=1
所以,213-212-211-210-29-28-27-26
=1+1+2+22+23+24+25
=1+2+4+8+16+32
=64
2.已知m=b1+b2+b3+b4+···+b1000,当b=-1时,
求m5的值.
解:当b=-1时,
m=b1+b2+b3+b4+···+b1000
=(-1)1+(-1)2+(-1)3+(-1)4+···+(-1)1000
=-1+1-1+1-1···-1+1
=0.
所以m5=05=0.
拓展训练
有理数的加、减、乘、除、乘方混合运算的顺序:
1.先乘方,再乘除,最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号、中括
号、大括号依次进行.
课堂小结
同课章节目录
