2025年福建省厦门六中中考数学模拟试卷(6月份)(含答案)
文档属性
| 名称 | 2025年福建省厦门六中中考数学模拟试卷(6月份)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 154.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 23:06:35 | ||
图片预览




文档简介
2025年福建省厦门六中中考数学模拟试卷(6月份)
一、选择题:本题共8小题,每小题4分,共32分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下面四个古典园林中的花窗图案,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.下列运算正确的是( )
A. B. C. D.
3.体积为的立方体的棱长是( )
A. 的平方根 B. 的算术平方根 C. 的立方 D. 的立方根
4.如图,将半圆绕直径所在的虚线旋转一周,得到的立体图形是( )
A. B. C. D.
5.如图,将沿方向平移到,若,,则平移距离为( )
A. B. C. D.
6.如图,是一个可折叠衣架,是地平线,当,时,就可以确定点、、在同一直线上,这样判定的依据是( )
A. 过直线外一点有且只有一条直线与这条直线平行
B. 内错角相等,两直线平行
C. 两点确定一条直线
D. 平行于同一直线的两直线平行
7.如图,在中,,的垂直平分线交于点若,则的度数是( )
A. B. C. D.
8.抛物线经过点、、则下列说法正确的是( )
A. 顶点可能在第一象限 B. 若,则顶点在第三象限
C. 顶点不可能在第二象限 D. 若,则顶点在第四象限
二、填空题:本题共8小题,每小题4分,共32分。
9.的相反数是______.
10.单项式的次数是______.
11.已知的边长两边长为和,第三边偶数,则第三边的值为______.
12.某校生物学兴趣小组,在相同条件下做黄豆的发芽试验,记录结果如下:
每批粒数
发芽的粒数
发芽的频率
则估计黄豆发芽的概率是______结果精确到.
13.如图,在平面直角坐标系中,菱形的顶点在轴正半轴上,边在轴上,若点的坐标为,点的坐标为,则点的坐标为______.
14.如图是某高速公路在转向处设计的一段圆曲线即圆弧,机动车转弯时从曲线起点行驶至终点,过点,的两条切线相交于点,机动车在从点到点行驶过程中转角为若这段圆弧的半径,,则图中危险区阴影部分的面积为______.
15.已知实数、、,满足,若,异号,则的取值范围为______.
16.如图,已知点,,是轴上位于点上方的一点,平分,平分,直线交于点若反比例函数的图象经过点,则的值为______.
三、解答题:本题共9小题,共86分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:.
18.本小题分
如图,将平行四边形的对角线向两个方向延长至点和点,使,求证:四边形是平行四边形.
19.本小题分
先化简,再求值:,其中.
20.本小题分
年,欧起全球热潮,其发布的开源大模型堪称“低成本,高效率”的典范,为世界贡献了“中国智慧”已知某公司拥有甲、乙两个数据中心,甲数据中心通过应用,使其数据迁移速度提升至乙数据中心的倍,且甲数据中心迁移数据比乙数据中心迁移数据所需时间少小时.
分别求甲、乙两个数据中心的数据迁移速度单位:小时;
现公司要求甲、乙两个数据中心协同完成一项紧急任务,共用小时至少完成的数据迁移,且同一时间只能一个数据中心工作,试问:不考虑其他因素,甲数据中心至少需要工作多少小时?
21.本小题分
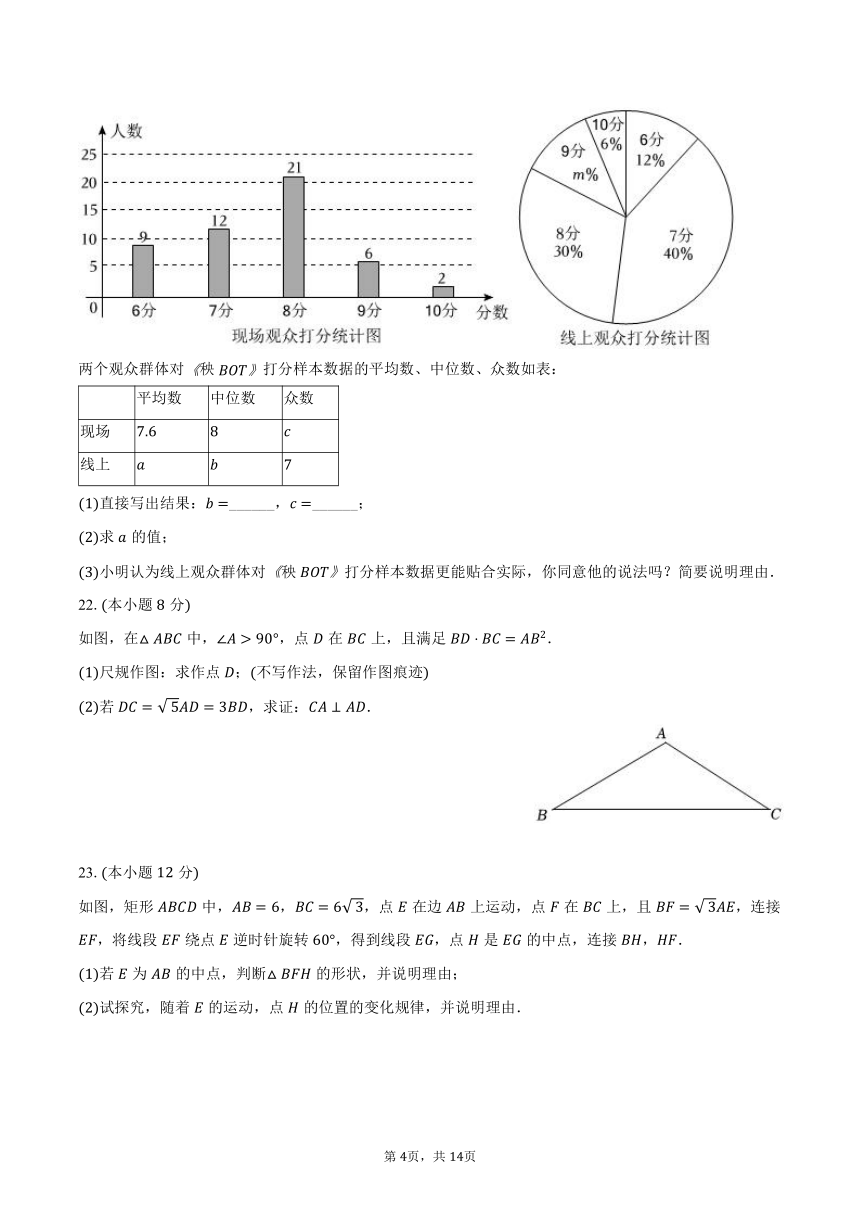
年春晚节目秧以机器人表演传统秧歌为主题,广受好评演出结束后,节目组随机抽取了名现场观众进行评分,同时统计出名线上观众评分满分分并根据得分绘制了以下不完整的统计图:
两个观众群体对秧打分样本数据的平均数、中位数、众数如表:
平均数 中位数 众数
现场
线上
直接写出结果:______,______;
求的值;
小明认为线上观众群体对秧打分样本数据更能贴合实际,你同意他的说法吗?简要说明理由.
22.本小题分
如图,在中,,点在上,且满足.
尺规作图:求作点;不写作法,保留作图痕迹
若,求证:.
23.本小题分
如图,矩形中,,,点在边上运动,点在上,且,连接,将线段绕点逆时针旋转,得到线段,点是的中点,连接,.
若为的中点,判断的形状,并说明理由;
试探究,随着的运动,点的位置的变化规律,并说明理由.
24.本小题分
太阳光线与地面的夹角叫做太阳高度角冬至是北半球各地白昼时间最短、黑夜最长的一天;夏至是北半球各地黑夜时间最短、白昼最长的一天设冬至这天正午时刻太阳高度角为,夏至这天正午时刻太阳高度角为.
厂家设计了可伸缩抛物线型遮阳棚,其侧面示意图如图所示曲线为遮阳棚,为遮阳棚安装在窗户上方的支架,,线段的长度称为遮阳棚的跨度已知遮阳棚所在的抛物线与抛物线的形状相同.
如图,为小明家的朝南窗户,测得,,窗户的高度为米为能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内,在安装遮阳棚时,需根据实际计算遮阳棚的跨度的长.
求小明家所需的遮阳棚的跨度;
春节前期,小明想在遮阳棚顶部挂一盏高为米的灯笼如图如图,灯笼与窗户的水平距离为米,灯笼的底端点与窗户的上沿点的铅垂高度为米,灯笼顶端点与悬挂点点的距离为米若,,求的最大值.
25.本小题分
已知内接于,为直径,在延长线上取一点,使得,连结,在下方,作,连结交于点,连结.
如图,若.
求证:是的切线;
若,求的值;
如图,若,时,试探究与的数量关系,并说明理由.
答案和解析
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】.
【解析】解:原式
.
18.【答案】证明:连接、,设与交于点.
四边形是平行四边形,,,
又,.
四边形是平行四边形.
19.【答案】,.
【解析】解:原式
,
当时,原式.
20.【解析】解:设乙数据中心的数据迁移速度为小时,则甲数据中心的数据迁移速度为小时,
由题意得:,
解得:,
经检验,是原方程的解,且符合题意,
,
答:甲数据中心的数据迁移速度为小时,乙数据中心的数据迁移速度为小时;
设甲数据中心工作小时,则乙数据中心工作小时,
由题意得:,
解得:,
答:甲数据中心至少需要工作小时.
21.【解析】线上观众打分为分的占,分的占,
线上打分的中位数分;
现场评分的众数为分,故,
故答案为:,;
现场打分的平均数分;
同意,因为线上观众群体对秧打分样本数据样本容量大,更能体现实际情况.
22.【解析】解:如图,点即为所求作;
理由:,,
∽,
,
,
即点即为所求作;
∽,
,
设,
,
,,
,
,
,
,
,
,
解得,
,
.
23.【解析】为等边三角形,理由如下:
四边形是矩形,
,
连接,
线段绕点逆时针旋转,
,,
为等边三角形,
,,
是的中点,
,,
在中,,
为的中点,
,
,
在中,,
,
,
在中,,
为等边三角形;
的位置不变;
,,
取中点,则,连接,
、、、四点共圆,
,
,
,
,,
,
∽,
,
,
,
,,
,
在中,,
在中,,
,
和都在的同侧,
,,三点共线,
的位置不变.
24.【解析】由题意,过点作垂线交于点,交于点,如图:
,
,
,
,
,
,
,
,
,
,即,
小明家所需的遮阳棚的跨度长为;
由题意,点坐标为,
将点坐标为代入得,,
令,
,
当时,取最小值,最小值为;当时,取大值,最大值为,
的取值范围,即,
,
当时,.
的最大值为米.
25.【解析】证明:为直径,
,
,,
,
在和中,
,
≌;
,
是的切线;
解:连结,
由知,≌,
,,
,
设,,
,,
,
,
,
;
解:,
理由:取优弧的中点,连结、,
,,
,
,
,
,
,
,
,
在和中,
,
≌,
,
,
设,,
,
,
,
,
,
,
,
,
.
第14页,共14页
一、选择题:本题共8小题,每小题4分,共32分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下面四个古典园林中的花窗图案,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.下列运算正确的是( )
A. B. C. D.
3.体积为的立方体的棱长是( )
A. 的平方根 B. 的算术平方根 C. 的立方 D. 的立方根
4.如图,将半圆绕直径所在的虚线旋转一周,得到的立体图形是( )
A. B. C. D.
5.如图,将沿方向平移到,若,,则平移距离为( )
A. B. C. D.
6.如图,是一个可折叠衣架,是地平线,当,时,就可以确定点、、在同一直线上,这样判定的依据是( )
A. 过直线外一点有且只有一条直线与这条直线平行
B. 内错角相等,两直线平行
C. 两点确定一条直线
D. 平行于同一直线的两直线平行
7.如图,在中,,的垂直平分线交于点若,则的度数是( )
A. B. C. D.
8.抛物线经过点、、则下列说法正确的是( )
A. 顶点可能在第一象限 B. 若,则顶点在第三象限
C. 顶点不可能在第二象限 D. 若,则顶点在第四象限
二、填空题:本题共8小题,每小题4分,共32分。
9.的相反数是______.
10.单项式的次数是______.
11.已知的边长两边长为和,第三边偶数,则第三边的值为______.
12.某校生物学兴趣小组,在相同条件下做黄豆的发芽试验,记录结果如下:
每批粒数
发芽的粒数
发芽的频率
则估计黄豆发芽的概率是______结果精确到.
13.如图,在平面直角坐标系中,菱形的顶点在轴正半轴上,边在轴上,若点的坐标为,点的坐标为,则点的坐标为______.
14.如图是某高速公路在转向处设计的一段圆曲线即圆弧,机动车转弯时从曲线起点行驶至终点,过点,的两条切线相交于点,机动车在从点到点行驶过程中转角为若这段圆弧的半径,,则图中危险区阴影部分的面积为______.
15.已知实数、、,满足,若,异号,则的取值范围为______.
16.如图,已知点,,是轴上位于点上方的一点,平分,平分,直线交于点若反比例函数的图象经过点,则的值为______.
三、解答题:本题共9小题,共86分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:.
18.本小题分
如图,将平行四边形的对角线向两个方向延长至点和点,使,求证:四边形是平行四边形.
19.本小题分
先化简,再求值:,其中.
20.本小题分
年,欧起全球热潮,其发布的开源大模型堪称“低成本,高效率”的典范,为世界贡献了“中国智慧”已知某公司拥有甲、乙两个数据中心,甲数据中心通过应用,使其数据迁移速度提升至乙数据中心的倍,且甲数据中心迁移数据比乙数据中心迁移数据所需时间少小时.
分别求甲、乙两个数据中心的数据迁移速度单位:小时;
现公司要求甲、乙两个数据中心协同完成一项紧急任务,共用小时至少完成的数据迁移,且同一时间只能一个数据中心工作,试问:不考虑其他因素,甲数据中心至少需要工作多少小时?
21.本小题分
年春晚节目秧以机器人表演传统秧歌为主题,广受好评演出结束后,节目组随机抽取了名现场观众进行评分,同时统计出名线上观众评分满分分并根据得分绘制了以下不完整的统计图:
两个观众群体对秧打分样本数据的平均数、中位数、众数如表:
平均数 中位数 众数
现场
线上
直接写出结果:______,______;
求的值;
小明认为线上观众群体对秧打分样本数据更能贴合实际,你同意他的说法吗?简要说明理由.
22.本小题分
如图,在中,,点在上,且满足.
尺规作图:求作点;不写作法,保留作图痕迹
若,求证:.
23.本小题分
如图,矩形中,,,点在边上运动,点在上,且,连接,将线段绕点逆时针旋转,得到线段,点是的中点,连接,.
若为的中点,判断的形状,并说明理由;
试探究,随着的运动,点的位置的变化规律,并说明理由.
24.本小题分
太阳光线与地面的夹角叫做太阳高度角冬至是北半球各地白昼时间最短、黑夜最长的一天;夏至是北半球各地黑夜时间最短、白昼最长的一天设冬至这天正午时刻太阳高度角为,夏至这天正午时刻太阳高度角为.
厂家设计了可伸缩抛物线型遮阳棚,其侧面示意图如图所示曲线为遮阳棚,为遮阳棚安装在窗户上方的支架,,线段的长度称为遮阳棚的跨度已知遮阳棚所在的抛物线与抛物线的形状相同.
如图,为小明家的朝南窗户,测得,,窗户的高度为米为能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内,在安装遮阳棚时,需根据实际计算遮阳棚的跨度的长.
求小明家所需的遮阳棚的跨度;
春节前期,小明想在遮阳棚顶部挂一盏高为米的灯笼如图如图,灯笼与窗户的水平距离为米,灯笼的底端点与窗户的上沿点的铅垂高度为米,灯笼顶端点与悬挂点点的距离为米若,,求的最大值.
25.本小题分
已知内接于,为直径,在延长线上取一点,使得,连结,在下方,作,连结交于点,连结.
如图,若.
求证:是的切线;
若,求的值;
如图,若,时,试探究与的数量关系,并说明理由.
答案和解析
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】.
【解析】解:原式
.
18.【答案】证明:连接、,设与交于点.
四边形是平行四边形,,,
又,.
四边形是平行四边形.
19.【答案】,.
【解析】解:原式
,
当时,原式.
20.【解析】解:设乙数据中心的数据迁移速度为小时,则甲数据中心的数据迁移速度为小时,
由题意得:,
解得:,
经检验,是原方程的解,且符合题意,
,
答:甲数据中心的数据迁移速度为小时,乙数据中心的数据迁移速度为小时;
设甲数据中心工作小时,则乙数据中心工作小时,
由题意得:,
解得:,
答:甲数据中心至少需要工作小时.
21.【解析】线上观众打分为分的占,分的占,
线上打分的中位数分;
现场评分的众数为分,故,
故答案为:,;
现场打分的平均数分;
同意,因为线上观众群体对秧打分样本数据样本容量大,更能体现实际情况.
22.【解析】解:如图,点即为所求作;
理由:,,
∽,
,
,
即点即为所求作;
∽,
,
设,
,
,,
,
,
,
,
,
,
解得,
,
.
23.【解析】为等边三角形,理由如下:
四边形是矩形,
,
连接,
线段绕点逆时针旋转,
,,
为等边三角形,
,,
是的中点,
,,
在中,,
为的中点,
,
,
在中,,
,
,
在中,,
为等边三角形;
的位置不变;
,,
取中点,则,连接,
、、、四点共圆,
,
,
,
,,
,
∽,
,
,
,
,,
,
在中,,
在中,,
,
和都在的同侧,
,,三点共线,
的位置不变.
24.【解析】由题意,过点作垂线交于点,交于点,如图:
,
,
,
,
,
,
,
,
,
,即,
小明家所需的遮阳棚的跨度长为;
由题意,点坐标为,
将点坐标为代入得,,
令,
,
当时,取最小值,最小值为;当时,取大值,最大值为,
的取值范围,即,
,
当时,.
的最大值为米.
25.【解析】证明:为直径,
,
,,
,
在和中,
,
≌;
,
是的切线;
解:连结,
由知,≌,
,,
,
设,,
,,
,
,
,
;
解:,
理由:取优弧的中点,连结、,
,,
,
,
,
,
,
,
,
在和中,
,
≌,
,
,
设,,
,
,
,
,
,
,
,
,
.
第14页,共14页
同课章节目录
