苏教版六年级下册数学期末提分押题卷(含答案)
文档属性
| 名称 | 苏教版六年级下册数学期末提分押题卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 860.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 00:00:00 | ||
图片预览




文档简介
登录二一教育在线组卷平台 助您教考全无忧
苏教版六年级下册数学期末提分押题卷
一、单选题
1.原价为每瓶8元的某种果汁正在搞促销活动,甲商店每瓶降价20%,乙商店“买四送一”丙商店每瓶打七五折出售,小明要买12瓶果汁,从( )商店买便宜。
A.甲 B.乙 C.丙 D.不确定
2.将左边的图形绕虚线旋转一周后会得到的立体图形是( )。
A. B. C. D.
3.在新冠疫情流行期间,采用( )既能反映每天病患的人数,又能反映疫情变化的情况和趋势。
A.条形统计图 B.折线统计图 C.扇形统计图 D.三种都可以
4.成数表示( )。
A.一个数是另一个数的百分之几 B.一个数是另一个数的几倍
C.一个数是另一个数的十分之几 D.一个数是另一个数的几分之几
5.如果收入10元记作“+10",那么“-6”表示( )。
A.支出4元 B.收入4元 C.支出6元 D.收入6元
6.下列说法不正确的是( )。
A.因为圆周长C=πd,所以π与d成反比例。
B.梯形面积一定,上、下底的和与高成反比例。
C.长方形的周长一定,它的长和宽不成比例。
D.实际距离一定,图上距离和比例尺成正比例。
7.奇奇爸爸上班的时间是早上8:48,他有以下4种交通工具可以选择。若爸爸8∶25从家出发,他选择( )才不会迟到。
①骑电动车:20分钟 ②坐公交车:半小时 ③坐地铁:15分钟 ④开车:13分钟
A.①②④ B.①③④ C.②③④
8. 盒子里放 8 个球,应该放( ),摸到白球的可能性比黄球的可能性大。
A.6 个红球
B.3 个白球和 3 个黄球
C.4 个白球和 2 个黄球
9.一次乒乓球比赛, 共有 512 名乒乓球运动员参加比赛。比赛采用淘汰制赛法,两个人赛一场, 失败者被淘汰, 将不再参加比赛; 获胜者进入下轮比赛, 如此进行下去, 直到决赛出第一名为止, 这次比赛一共要进行 ( ) 场。
A.1024 B.511 C.256 D.174
10.一个圆柱体杯中盛满18升水,把一个与它等底等高的铁圆锥倒插入杯底,拿出圆锥后,圆柱形杯中还有( )水。
A.12升 B.9升 C.15升 D.9升
二、判断题
11.判断对错.
周长相等的两个圆,面积一定相等.
12.一个圆柱的侧面展开图是正方形,那么这个圆柱的底面直径和高相等。( )
13.把一块长方体橡皮泥捏成正方体后,体积和表面积都没有变化。( )
14.扇形统计图可以直观的表示部分数量与总数之间的关系。( )
15.一个棱长是6厘米的正方体,它的表面积和体积相等。( )
16.因为速度×时间=路程,所以速度和时间成反比例.
17.等底等高的长方体和圆柱体,长方体的体积是圆柱的3倍( )
18.一个长、宽、高分别是7厘米、5厘米、3厘米的长方体,体积是105平方厘米。
19.有12枚金币,其中1枚是假的(假金币重一些),如果借助天平,至少需要称3次才能保证将假金币找出来。( )
20.一个正方体的棱长扩大到原来的5倍,它的表面积和体积都扩大到原来的25倍。( )
三、填空题
21.某市出租车收费标准:前3千米内(含3 千米)收费13元,超过3千米的部分,每千米2.4元,不足1千米的按照 1 千米计算。若出租车走了5.4千米,需要支付 元。
22.小梅星期六作息时间情况如下图.
根据扇形统计图,把下表填写完整.
23.把线段比例尺改写为数值比例尺是 ,比例尺1:60000表示实际距离是图上距离的 倍。
24.4个棱长为5dm的正方体木箱放在墙角处(如图),有 个面露在外面,露在外面的面积是 dm2。
25.如图,在一张边长10cm的正方形纸上剪下一个最大的圆,这个圆的面积是 cm2,剩余部分的面积是 cm2。
26.一个长方体长10厘米、宽8厘米、高6厘米,把它切成两个相同的小长方体,表面积最多增加 平方厘米。
27.把圆规两脚张开4厘米,画出的圆的面积是 平方厘米。如果想画出周长31.4厘米的圆,圆规两脚应张开 厘米。
28.狐狸和黄鼠狼进行跳跃比赛,狐狸每次跳米,黄鼠狼每次跳米。它们每秒跳一次。比赛途中,从起点开始每隔米设有一个陷阱。当它们之中有一个掉进陷阱时,另一个跳了 米。
29.淘气的储蓄罐里有5角和1元的硬币,一共12枚,共有8.5元,5角硬币有 枚,1元硬币有 枚。
30.笑笑发现同学用了水后没有关水龙头,不断地流水。为了养成同学们良好的用水习惯,笑笑做了关于水龙头流水的实验记录。如图表示的是流出水的体积和时间的关系。
(1)从图中可知,流出水的体积和时间成 比例关系。
(2)照这样计算,50分钟流水 L,要流出180L水,需要 分钟。
四、解答题
31.一个长方体盒子,从里面量得长是24cm,宽是16cm,高是12cm,若要在里面放入棱长相同的小正方体且没有剩余空间,则小正方体的棱长最长是多少cm 一共可以放几个这样的小正方体
32.“丝绸之路”是古代连接中西方的商道。传统的丝绸之路起自我国古代都城长安,以罗马为终点,在一幅比例尺为1:7000000的地图上约长92cm,传统的丝绸之路实际全长约多少千米?
33.用一只平底锅煎蛋饼,每次能同时放两块蛋饼,如果煎一块蛋饼需要6分钟(正反两面各需3分钟) ,那么,要煎30块蛋饼至少需要多少分钟?
34.轩轩调查了台州近3年三月各种天气的情况,并将统计结果进行了整理。
(1)根据已知信息,把统计表和统计图补充完整。(百分号前保留一位小数)
(2)奶奶说:“台州三月多阴雨天。”你认为正确吗 结合扇形统计图中的数据,说明理由。
(3)家住北京的李泰,他还会说北京的三月多阴雨天吗 你会怎么去验证这句话呢
35.一个底面积为48平方分米的容器中装有水,如果把等底等高的一个圆柱形和一个圆锥形铁块全部沉没于水中,水面上升10分米,那么这块圆柱形铁块的体积是多少立方分米?
五、作图题
36.
(1)画出纸条绕点A顺时针旋转90°后的纸条。
(2)画出铅笔绕点O逆时针旋转90°后的铅笔。
六、解决问题
37.一个无盖的圆柱形铁皮水桶,底面周长是12.56分米,高是5分米,做这个水桶至少需多少平方分米的铁皮?
38.垃圾分类有利于改善城乡环境,保障人体健康,维护生态安全。垃圾的种类有可回收物、厨余垃圾、有害垃圾和其他垃圾。同学们对一个小区一周产生的垃圾构成情况进行了调查,请你根据统计图完成下面的问题。
(1)这个小区一周共产生 吨垃圾。
(2)算出这个小区一周共产生 吨可回收物,再将条形统计图补充完整。
(3)这个小区一周产生的其他垃圾比可回收物少 %
(4)厨余垃圾经过生物技术就地处理堆肥,其中30%可转化成有机肥料。这个小区一周产生的厨余垃圾经过生物技术处理后,可以生产多少吨有机肥料?
39.小华和乐乐相约一起去书店各买同一本字典,到了书店才发现小华的钱还差3.5元,乐乐的钱还差4.5元。两人的钱合起来共28元,一本字典多少元?
40.某县去年秋粮食产量为2.8万吨,前年比去年少三成。前年秋粮食产量是多少万吨?
41.兰兰一家周末去必胜客西餐厅吃饭,美团上有该餐厅的代金券如下图。到店后兰兰还得知消费满200元可享受九折优惠,但两种优惠方式不能同时使用。兰兰一家周末在西餐厅总共消费320元,这两种优惠方式哪一种更优惠?请通过计算说明。
七、口算与估算
42. 直接写出得数。
0.54×10= 0.4×2.5=
8.5×0.02= 8×(3-1.75)=
0.7×101= 0.9-0.9×0.9=
八、竖式计算
43.列竖式计算,带*的要验算。
0.28×0.08= *3.45×8.6=
8.06×6.2= *63.5×0.14=
九、图形计算
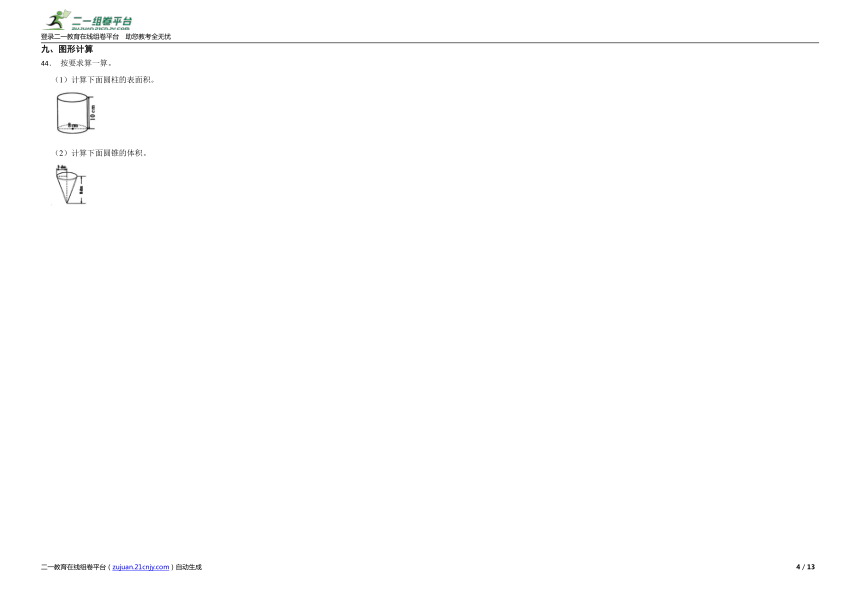
44. 按要求算一算。
(1)计算下面圆柱的表面积。
(2)计算下面圆锥的体积。
答案解析部分
1.【答案】C
【解析】【解答】甲:8×(1-20%)×12=76.8元;
乙:8×10=80元;
丙:8×75%×12=72元;
72<76.8<80
故答案为:C
【分析】总价=单价×数量。甲商店每瓶降价20%,就是按原价的80%售卖,则每瓶单价为8×(1-20%),再乘数量12,结果为76.8元;乙商店买四送一,就是买四袋可以送一袋,那么要12袋我们可以只花10袋的钱,直接8×10=80元;丙商店每瓶打七五折,就是按原价的75%售卖,则每瓶单价为8×75%,总价为8×0.75×12=72元,最后比较数的大小即可得出答案。
2.【答案】C
【解析】【解答】解:将这个图形绕虚线旋转一周后会得到的立体图形是圆锥。
故答案为:C。
【分析】这个图形是三角形,绕着一条直角边旋转一周后会得到一个圆锥。
3.【答案】B
【解析】【解答】解:在新冠疫情流行期间,采用折线统计图既能反映每天病患的人数,又能反映疫情变化的情况和趋势。
故答案为:B。
【分析】条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况;扇形统计图能反应各个部分占总体的百分之几。
4.【答案】C
【解析】【解答】解:成数表示一个数是另一个数的十分之几。
故答案为:C。
【分析】成数表示一个数是另一个数的十分之几,俗称“几成”;“几成”就是十分之几,也就是百分之几十。
5.【答案】C
【解析】【解答】解:如果收入10元记作“+10",那么“-6”表示支出6元。
故答案为:C。
【分析】正数和负数表示具有相反意义的量,收入记作正数,则支出记作负数。
6.【答案】A
【解析】【解答】解:A、圆周长C=πd,C÷d=π(一定),C与d成正比例。所以说法错误;
B、(上底+下底)×高÷2=梯形面积(一定), 上、下底的和与高成反比例 。正确;
C、(长+宽)×2=长方形周长(一定), 它的长和宽不成比。正确;
D、图上距离÷比例尺=实际距离(一定),图上距离和比例尺成正比例。 正确。
故答案为:A。
【分析】两种相关联的量,它们的商一定时成正比例,它们的积一定时成反比例,否则不成比例。
7.【答案】B
【解析】【解答】解:①8时25分+20分=8时45分,不会迟到;②8时25分+30分=8时55分,会迟到;③8时25分+15分=8时40分,不会迟到;④8时25分+13分=8 时38分,不会迟到。所以选择①③④。
故答案为:B。
【分析】用爸爸出发的时间加上使用每种交通工具用的时间,只需要不超过8:48即可。
8.【答案】C
【解析】【解答】解:A:摸到白球和黄球的可能性都为0
B:摸到白球和黄球的可能性相等
C:4>2,摸到白球的可能性比黄球的可能性大
故答案为:C。
【分析】根据“在一个盒子中,球的数量越多,摸到的可能性越大”,进行判断即可。
9.【答案】B
【解析】【解答】
解:∵每淘汰1名选手就要有一场比赛,
∴只剩最后第一名,需要淘汰512-1=511名,
∴这次乒乓球比赛一共要比赛511场.
故答案为:B.
【分析】 根据淘汰赛的规则,每淘汰1名选手就有一场比赛,最后只剩第一名1人,用总人数减去1即可得到比赛场数.
10.【答案】A
【解析】【解答】解:18×=12(升)
故答案为:A。
【分析】 一个与圆柱等底等高的铁圆锥的体积是圆柱体积的,拿出圆锥后,圆柱形杯中还有的水。
11.【答案】正确
【解析】【解答】根据圆的周长公式:C=2πr,可以得出两个圆周长相等,则它们的半径就相等;
再根据圆的面积公式:S=πr2,半径相等则面积就相等.
故答案为:正确
【分析】圆的周长=圆周率×直径=圆周率×半径×2;圆的面积=圆周率×半径×半径.
12.【答案】错误
【解析】【解答】解:一个圆柱的侧面展开图是正方形,那么这个圆柱的底面周长和高相等。
故答案为:错误。
【分析】当圆柱的底面周长和高相等时,就得到一个正方形,正方形的边长相当于圆柱的底面周长和高。
13.【答案】错误
【解析】【解答】解:把一块长方体橡皮泥捏成正方体后,体积没有变化,表面积可能变化,原题干说法错误。
故答案为:错误。
【分析】把一块长方体橡皮泥捏成正方体后,体积没有变化,还是原来橡皮泥的体积。
14.【答案】正确
【解析】【解答】解:扇形统计图可以直观的表示部分数量与总数之间的关系。
故答案为:正确。
【分析】根据扇形统计图的特征作答即可。
15.【答案】错误
【解析】【解答】解:一个棱长是6厘米的正方体,它的表面积=6×6×6=216(平方厘米),它的体积=6×6×6=216(立方厘米),虽然数值相同,但单位不同,所以它的表面积和它的体积不相等,故“一个棱长是6厘米的正方体,它的表面积和体积相等”这个说法是错误的。
故答案为:错误。
【分析】正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,据此代入数据解答即可,注意:单位不同则不相等。
16.【答案】错误
【解析】【解答】解:题中没有说明路程一定时,速度和时间不一定成反比例,原题说法错误.
故答案为:错误
【分析】如果路程一定,那么速度和时间的乘积一定,速度和时间成反比例.
17.【答案】错误
【解析】【解答】等底等高的长方体和圆柱体,长方体的体积等于圆柱体体积,原题说法错误.
故答案为:错误.
【分析】 因为长方体和圆柱体的体积公式都是:V=Sh,所以等底等高的长方体和圆柱体,长方体的体积等于圆柱体体积,据此判断.
18.【答案】错误
【解析】【解答】7×5×3
=35×3
=105(立方厘米)
原题说法错误.
故答案为:错误.
【分析】已知长方体的长、宽、高,求长方体的体积,用长×宽×高=长方体体积,据此列式解答,体积用体积单位.
19.【答案】正确
20.【答案】错误
21.【答案】20.2
【解析】【解答】解:5.4千米按6千米收费,6千米分为3千米+3千米
13+2.4×3=13+7.2=20.2(元)
需要支付20.2元
故答案为:20.2。
【分析】前3千米的收费+超出3千米部分的收费=一共需要支付的钱数。
22.【答案】2.4,10%;2.4;3.6,15%;9.6,40%
【解析】【解答】总时间:6÷25%=24(时);
看电视:24×10%=2.4(小时),占10%;
吃饭:24×10%=2.4(小时);
活动:24×15%=3.6(小时);
睡眠:24×40%=9.6(小时).
故答案为:2.4,10%;2.4;3.6,15%;9.6,40%
【分析】用课外班的时间除以所占的百分比求出总时间;用总时间分别乘每项任务所占的百分率即可求出每项任务的时间并填表即可.
23.【答案】1:5000;60000
【解析】【解答】解:50米=5000厘米,把线段比例尺改写为数值比例尺是1:5000;比例尺1:60000表示图上距离:实际距离=1:60000,那么实际距离就是图上距离的60000倍。
故答案为:1:5000;60000。
【分析】从线段比例尺 可以看出,图上1厘米表示实际距离50米,根据比例尺=图上距离:实际距离即可解答;第二问求实际距离是图上距离的多少倍,反过来用比的后项除以比的前项即可解答。
24.【答案】9;225
【解析】【解答】解:有9个面露在外面;
5×5×9
=25×9
=225(平方分米)。
故答案为:9;225。
【分析】有9个面露在外面;露在外面的面积=正方体的棱长×棱长×露在外面的面的个数。
25.【答案】78.5;21.5
【解析】【解答】解:10÷2=5(cm)
52×3.14=78.5(cm2)
10×10-78.5
=100-78.5
=21.5(cm2)
故答案为:78.5;21.5。
【分析】圆的直径=边长,半径=直径÷2,yu8an的面积=π×半径2;剩余部分面积=正方形面积-圆的面积。
26.【答案】160
【解析】【解答】解:10×8×2
=80×2
=160(平方厘米)。
故答案为:160。
【分析】最多增加的表面积=最大的面的长×宽×2。
27.【答案】50.24;5
28.【答案】7
【解析】【解答】 解:狐狸的速度是:=(米),
黄鼠狼的速度是=(米),
陷阱的距离是(米);
分子15,28的最小公倍数是420;
10和28的最小公倍数是140;
当黄鼠狼跳米时,掉入陷阱,此时各跳了14次,狐狸这时跳了7米。
×14=7(米)
故答案为:7。
【分析】先把狐狸的速度、黄鼠狼的速度、陷阱的距离分别化成分母是30的分数;再根据分子分别找出15,28以及10和28的最小公倍数,进而求解。
29.【答案】7;5
【解析】【解答】解:5角=0.5元
5角硬币有:(12×1-8.5)÷(1-0.5)
=3.5÷0.5
=7(枚);
1元硬币有:12-7=5(枚)。
故答案为:7;5。
【分析】5角=0.5元,假设全部是1元硬币,则一共有(12×1)元,比实际一共多了(12×1-8.5)元;1元硬币比5角硬币多(1-0.5)元;用假设比实际一共多的除以每枚多的即可求出5角硬币的数量;再用总数量减去5角硬币的数量即可求出1元硬币的数量。
30.【答案】(1)正
(2)100;90
【解析】【解答】解:(1)10÷5=2(L),20÷10=2(L),30÷15=2(L),40÷20=2(L),50÷25=2(L),即体积÷时间=每分钟流出水的体积(一定),商一定,所以流出水的体积和时间成正比例关系;
(2)50×2=100(L),180÷2=90(分钟)。
故答案为:(1)正;(2)100;90。
【分析】(1)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系,用y/x=k( k一定)来表示;
(2)根据第(1)题结论可知每分钟流出水的体积是2L,因此,流水时间×每分钟流出水的体积=50分钟总的流出水的体积,流出水的体积÷每分钟流出水的体积=需要的时间。
31.【答案】解:[24,16,12]=4
(24÷4)×(16÷4)×(12÷4)
=6×4×3
=72(个)
答:小正方体的棱长最长是4cm,一共可以放72个这样的小正方体。
【解析】【分析】24,16,12的最大公约数是小正方体最长的棱长,长能放的个数×宽能放的个数×高能放的个数=一共可以放小正方体的个数。
32.【答案】解:92÷ = 644000000(厘米)
644000000厘米= 6440千米
答:传统的丝绸之路实际全长约6440千米。
【解析】【分析】根据实际距离=图上距离÷比例尺求出丝绸之路的实际全长,注意厘米与千米之间单位的换算。
33.【答案】30÷3×9=90(分)
【解析】【分析】为了节约时间,可在第一次煎蛋饼时,把两块蛋饼放入锅内,3分钟后,把其中的一块取出,放入第三块蛋饼,锅中没拿出的那块煎另外一面,3分钟后,把两面都煎了的蛋饼(熟了)取出,再放入原来取出的只煎了一面的蛋饼,锅中放入的第三块蛋饼煎另一面,3分钟后,3块蛋饼都熟了,共需9分钟,因此,30块蛋饼煎熟的时间为30÷3×9=90(分)。
34.【答案】(1)统计表:17.2%,32.3%,50.5%
(2)正确。在扇形统计图中,阴雨天占的比例最大。
(3)(答案不唯一)不会。调查北京近3年三月各种天气的情况,根据统计结果判断即可。
【解析】【分析】
(1) 先求三年三月总天数,再算各类天气总天数,用 “部分量 ÷ 总量 ×100%” 得占比,用于完善图表。
(2) 依据扇形统计图中阴雨天占比最大,判断 “台州三月多阴雨天” 说法正确。
(3) 不能依台州情况判断北京,需调查北京近 3 年三月天气数据来验证说法。
35.【答案】解:48×10÷(1+ )
=480÷
=360(立方分米)
答:这块圆柱形铁块的体积是360立方分米。
【解析】【分析】由题意可知,圆柱和圆锥的总体积等于上升部分水的体积,利用“的底面积×高”求出容器中水的体积,当圆柱和圆锥等底等高时,圆柱的体积是圆锥的3倍,圆锥的体积是圆柱体积的,圆柱的体积=圆柱和圆锥的总体积÷(1+),据此解答。
36.【答案】(1)
(2)
【解析】【解答】(1)
(2)
【分析】画旋转图形的方法:把图形的每个点与旋转中心连接,再量出题目要求旋转的角度,最后依次连接,据此按要求作图。
37.【答案】解:12.56÷3.14÷2
=4÷2
=2(分米)
3.14×22+12.56×2
=12.56+25.12
=37.68(平方分米)
答:做这个水桶至少需75.36平方分米的铁皮。
【解析】【分析】要求需多少平方分米的铁皮就是求无盖圆柱的表面积:
先根据d=C÷π求出底面直径,再根据r=d÷2求出半径,从而求出底面积;
根据S侧面积=C×h,求出圆柱侧面积;
最后S无盖圆柱=S底面积+S侧面积。
38.【答案】(1)40
(2)10;
(3)36
(4)解:22×30%=6.6(吨)
答:可以生产6.6吨有机肥料。
【解析】【解答】解:(1)22÷55%=40(吨);
(2)40×25%=10(吨),
(3)(25%-16%)÷25%
=9%÷25%
=36%
故答案为:(1)40;
(2)10;
;
(3)36。
【分析】(1)厨余垃圾是22吨,共占垃圾总量的55%,根据分数除法的意义求出垃圾总量;
(2)用垃圾总量乘25%即可求出可回收物的质量,在统计图中相应的位置画出相应长度的长条;
(3)可回收物占的百分率减去其他垃圾占的百分率,再除以可回收物占的百分率即可求出少百分之几;
(4)用厨余垃圾质量乘30%即可求出可以生产有机肥料的质量。
39.【答案】解:(3.5+4.5+28)÷2
=36÷2
=18(元)
答:一本字典18元。
【解析】【分析】两人合起的钱+小华还差的钱+乐乐还差的钱=2本字典的钱数,2本字典的钱数÷2=1本字典的钱数。
40.【答案】解:2.8×(1-30%)
=2.8×70%
=1.96(万吨)
答:前年秋粮食产量是1.96万吨。
【解析】【分析】几成就是百分之几十;
前年秋粮食产量=去年秋粮食产量×(1-前年比去年少百分之几),据此作答即可。
41.【答案】解:打折:320×90%=288(元)
用代金券:320-(100-78)×2
=320-22×2
=320-44
=276(元)
276<288,所以用代金券更优惠。
答:使用代金券消费更优惠。
【解析】【分析】打折应付金额=原价×90%;每桌限用2张代金券,所以用代金券应付金额=原价-(100-78)×2,据此分别计算出两种优惠方式应付的钱,再比较即可。
42.【答案】解:
0.54×10=5.4 0.4×2.5=1
8.5×0.02=0.17 8×(3-1.75)=10
0.7×101=70.7 0.9-0.9×0.9=0.09
【解析】【分析】这道题主要考察的是小数乘法和小数减法的运算规则,需要根据小数乘法和减法的计算法则对每个算式进行准确计算,特别是对于含有括号和混合运算的算式,需要按照运算顺序先进行括号内的计算,再进行乘法和减法运算。
43.【答案】解:(1)0.28×0.08
=
(2)8.06×6.2
=
(3)3.45×8.6
=
验算:
(4)63.5×0.14
验算:
【解析】【分析】本题运用小数乘法的竖式的计算方法进行计算即可.
44.【答案】(1)解:S=3.14×(8÷2)2×2+3.14×8×10
=3.14×16×2+3.14×80
=100.48+251.2
=351.68(cm2)
(2)解:S=×3.14×32×8
=×3.14×72
=3.14×24
=75.36(cm3)
【解析】【分析】(1)圆柱体的表面积=2πr2+2πrh,据此代入数值计算;
(2)圆锥的体积=πr2h,据此代入数值计算。
试题分析部分
1、试卷总体分布分析
总分:164分
分值分布 客观题(占比) 66.0(40.2%)
主观题(占比) 98.0(59.8%)
题量分布 客观题(占比) 28(63.6%)
主观题(占比) 16(36.4%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
填空题 10(22.7%) 31.0(18.9%)
解答题 5(11.4%) 35.0(21.3%)
作图题 1(2.3%) 10.0(6.1%)
竖式计算 1(2.3%) 5.0(3.0%)
图形计算 1(2.3%) 10.0(6.1%)
解决问题 5(11.4%) 28.0(17.1%)
口算与估算 1(2.3%) 5.0(3.0%)
单选题 10(22.7%) 20.0(12.2%)
判断题 10(22.7%) 20.0(12.2%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (68.2%)
2 容易 (31.8%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 百分数的应用--折扣 7.0(4.3%) 1,41
2 体育比赛问题 2.0(1.2%) 9
3 扇形统计图的特点及绘制 17.0(10.4%) 14,34
4 作旋转后的图形 10.0(6.1%) 36
5 圆柱的侧面积、表面积 15.0(9.1%) 37,44
6 圆的周长 4.0(2.4%) 27
7 圆锥的特征 2.0(1.2%) 2
8 正方体的体积 4.0(2.4%) 15,20
9 小数除法混合运算 5.0(3.0%) 39
10 正、负数的意义与应用 2.0(1.2%) 5
11 统计图的选择 2.0(1.2%) 3
12 长方体的表面积 2.0(1.2%) 26
13 鸡兔同笼问题 4.0(2.4%) 29
14 圆柱与圆锥体积的关系 5.0(3.0%) 35
15 可能性的大小 2.0(1.2%) 8
16 最优策略:找次品问题 2.0(1.2%) 19
17 小数乘小数的小数乘法 5.0(3.0%) 42
18 成反比例的量及其意义 4.0(2.4%) 6,16
19 比例尺的认识 4.0(2.4%) 23
20 圆的面积 10.0(6.1%) 11,25,27
21 分段计费问题 2.0(1.2%) 21
22 统计图、统计表的综合应用 17.0(10.4%) 22,34
23 圆柱的体积(容积) 7.0(4.3%) 17,35
24 立方体的切拼 2.0(1.2%) 26
25 从扇形统计图获取信息 23.0(14.0%) 34,38
26 数列中的规律 2.0(1.2%) 9
27 百分数的其他应用 15.0(9.1%) 34
28 圆柱的展开图 2.0(1.2%) 12
29 组合体露在外面的面 4.0(2.4%) 24
30 小数的四则混合运算 4.0(2.4%) 29
31 单价、数量、总价的关系及应用 2.0(1.2%) 1
32 优化策略:烙饼问题 5.0(3.0%) 33
33 小数乘整数的小数乘法 5.0(3.0%) 42
34 百分数的应用--成数 7.0(4.3%) 4,40
35 24时计时法时间计算 2.0(1.2%) 7
36 最大公因数的应用 5.0(3.0%) 31
37 长方体的体积 4.0(2.4%) 17,18
38 成正比例的量及其意义 3.0(1.8%) 30
39 小数乘法混合运算 12.0(7.3%) 21,42,43
40 水中浸物模型 5.0(3.0%) 35
41 圆锥的体积(容积) 12.0(7.3%) 10,44
42 正方体的表面积 4.0(2.4%) 15,20
43 体积的等积变形 2.0(1.2%) 13
44 最小公倍数的应用 2.0(1.2%) 28
45 应用比例尺求图上距离或实际距离 5.0(3.0%) 32
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
苏教版六年级下册数学期末提分押题卷
一、单选题
1.原价为每瓶8元的某种果汁正在搞促销活动,甲商店每瓶降价20%,乙商店“买四送一”丙商店每瓶打七五折出售,小明要买12瓶果汁,从( )商店买便宜。
A.甲 B.乙 C.丙 D.不确定
2.将左边的图形绕虚线旋转一周后会得到的立体图形是( )。
A. B. C. D.
3.在新冠疫情流行期间,采用( )既能反映每天病患的人数,又能反映疫情变化的情况和趋势。
A.条形统计图 B.折线统计图 C.扇形统计图 D.三种都可以
4.成数表示( )。
A.一个数是另一个数的百分之几 B.一个数是另一个数的几倍
C.一个数是另一个数的十分之几 D.一个数是另一个数的几分之几
5.如果收入10元记作“+10",那么“-6”表示( )。
A.支出4元 B.收入4元 C.支出6元 D.收入6元
6.下列说法不正确的是( )。
A.因为圆周长C=πd,所以π与d成反比例。
B.梯形面积一定,上、下底的和与高成反比例。
C.长方形的周长一定,它的长和宽不成比例。
D.实际距离一定,图上距离和比例尺成正比例。
7.奇奇爸爸上班的时间是早上8:48,他有以下4种交通工具可以选择。若爸爸8∶25从家出发,他选择( )才不会迟到。
①骑电动车:20分钟 ②坐公交车:半小时 ③坐地铁:15分钟 ④开车:13分钟
A.①②④ B.①③④ C.②③④
8. 盒子里放 8 个球,应该放( ),摸到白球的可能性比黄球的可能性大。
A.6 个红球
B.3 个白球和 3 个黄球
C.4 个白球和 2 个黄球
9.一次乒乓球比赛, 共有 512 名乒乓球运动员参加比赛。比赛采用淘汰制赛法,两个人赛一场, 失败者被淘汰, 将不再参加比赛; 获胜者进入下轮比赛, 如此进行下去, 直到决赛出第一名为止, 这次比赛一共要进行 ( ) 场。
A.1024 B.511 C.256 D.174
10.一个圆柱体杯中盛满18升水,把一个与它等底等高的铁圆锥倒插入杯底,拿出圆锥后,圆柱形杯中还有( )水。
A.12升 B.9升 C.15升 D.9升
二、判断题
11.判断对错.
周长相等的两个圆,面积一定相等.
12.一个圆柱的侧面展开图是正方形,那么这个圆柱的底面直径和高相等。( )
13.把一块长方体橡皮泥捏成正方体后,体积和表面积都没有变化。( )
14.扇形统计图可以直观的表示部分数量与总数之间的关系。( )
15.一个棱长是6厘米的正方体,它的表面积和体积相等。( )
16.因为速度×时间=路程,所以速度和时间成反比例.
17.等底等高的长方体和圆柱体,长方体的体积是圆柱的3倍( )
18.一个长、宽、高分别是7厘米、5厘米、3厘米的长方体,体积是105平方厘米。
19.有12枚金币,其中1枚是假的(假金币重一些),如果借助天平,至少需要称3次才能保证将假金币找出来。( )
20.一个正方体的棱长扩大到原来的5倍,它的表面积和体积都扩大到原来的25倍。( )
三、填空题
21.某市出租车收费标准:前3千米内(含3 千米)收费13元,超过3千米的部分,每千米2.4元,不足1千米的按照 1 千米计算。若出租车走了5.4千米,需要支付 元。
22.小梅星期六作息时间情况如下图.
根据扇形统计图,把下表填写完整.
23.把线段比例尺改写为数值比例尺是 ,比例尺1:60000表示实际距离是图上距离的 倍。
24.4个棱长为5dm的正方体木箱放在墙角处(如图),有 个面露在外面,露在外面的面积是 dm2。
25.如图,在一张边长10cm的正方形纸上剪下一个最大的圆,这个圆的面积是 cm2,剩余部分的面积是 cm2。
26.一个长方体长10厘米、宽8厘米、高6厘米,把它切成两个相同的小长方体,表面积最多增加 平方厘米。
27.把圆规两脚张开4厘米,画出的圆的面积是 平方厘米。如果想画出周长31.4厘米的圆,圆规两脚应张开 厘米。
28.狐狸和黄鼠狼进行跳跃比赛,狐狸每次跳米,黄鼠狼每次跳米。它们每秒跳一次。比赛途中,从起点开始每隔米设有一个陷阱。当它们之中有一个掉进陷阱时,另一个跳了 米。
29.淘气的储蓄罐里有5角和1元的硬币,一共12枚,共有8.5元,5角硬币有 枚,1元硬币有 枚。
30.笑笑发现同学用了水后没有关水龙头,不断地流水。为了养成同学们良好的用水习惯,笑笑做了关于水龙头流水的实验记录。如图表示的是流出水的体积和时间的关系。
(1)从图中可知,流出水的体积和时间成 比例关系。
(2)照这样计算,50分钟流水 L,要流出180L水,需要 分钟。
四、解答题
31.一个长方体盒子,从里面量得长是24cm,宽是16cm,高是12cm,若要在里面放入棱长相同的小正方体且没有剩余空间,则小正方体的棱长最长是多少cm 一共可以放几个这样的小正方体
32.“丝绸之路”是古代连接中西方的商道。传统的丝绸之路起自我国古代都城长安,以罗马为终点,在一幅比例尺为1:7000000的地图上约长92cm,传统的丝绸之路实际全长约多少千米?
33.用一只平底锅煎蛋饼,每次能同时放两块蛋饼,如果煎一块蛋饼需要6分钟(正反两面各需3分钟) ,那么,要煎30块蛋饼至少需要多少分钟?
34.轩轩调查了台州近3年三月各种天气的情况,并将统计结果进行了整理。
(1)根据已知信息,把统计表和统计图补充完整。(百分号前保留一位小数)
(2)奶奶说:“台州三月多阴雨天。”你认为正确吗 结合扇形统计图中的数据,说明理由。
(3)家住北京的李泰,他还会说北京的三月多阴雨天吗 你会怎么去验证这句话呢
35.一个底面积为48平方分米的容器中装有水,如果把等底等高的一个圆柱形和一个圆锥形铁块全部沉没于水中,水面上升10分米,那么这块圆柱形铁块的体积是多少立方分米?
五、作图题
36.
(1)画出纸条绕点A顺时针旋转90°后的纸条。
(2)画出铅笔绕点O逆时针旋转90°后的铅笔。
六、解决问题
37.一个无盖的圆柱形铁皮水桶,底面周长是12.56分米,高是5分米,做这个水桶至少需多少平方分米的铁皮?
38.垃圾分类有利于改善城乡环境,保障人体健康,维护生态安全。垃圾的种类有可回收物、厨余垃圾、有害垃圾和其他垃圾。同学们对一个小区一周产生的垃圾构成情况进行了调查,请你根据统计图完成下面的问题。
(1)这个小区一周共产生 吨垃圾。
(2)算出这个小区一周共产生 吨可回收物,再将条形统计图补充完整。
(3)这个小区一周产生的其他垃圾比可回收物少 %
(4)厨余垃圾经过生物技术就地处理堆肥,其中30%可转化成有机肥料。这个小区一周产生的厨余垃圾经过生物技术处理后,可以生产多少吨有机肥料?
39.小华和乐乐相约一起去书店各买同一本字典,到了书店才发现小华的钱还差3.5元,乐乐的钱还差4.5元。两人的钱合起来共28元,一本字典多少元?
40.某县去年秋粮食产量为2.8万吨,前年比去年少三成。前年秋粮食产量是多少万吨?
41.兰兰一家周末去必胜客西餐厅吃饭,美团上有该餐厅的代金券如下图。到店后兰兰还得知消费满200元可享受九折优惠,但两种优惠方式不能同时使用。兰兰一家周末在西餐厅总共消费320元,这两种优惠方式哪一种更优惠?请通过计算说明。
七、口算与估算
42. 直接写出得数。
0.54×10= 0.4×2.5=
8.5×0.02= 8×(3-1.75)=
0.7×101= 0.9-0.9×0.9=
八、竖式计算
43.列竖式计算,带*的要验算。
0.28×0.08= *3.45×8.6=
8.06×6.2= *63.5×0.14=
九、图形计算
44. 按要求算一算。
(1)计算下面圆柱的表面积。
(2)计算下面圆锥的体积。
答案解析部分
1.【答案】C
【解析】【解答】甲:8×(1-20%)×12=76.8元;
乙:8×10=80元;
丙:8×75%×12=72元;
72<76.8<80
故答案为:C
【分析】总价=单价×数量。甲商店每瓶降价20%,就是按原价的80%售卖,则每瓶单价为8×(1-20%),再乘数量12,结果为76.8元;乙商店买四送一,就是买四袋可以送一袋,那么要12袋我们可以只花10袋的钱,直接8×10=80元;丙商店每瓶打七五折,就是按原价的75%售卖,则每瓶单价为8×75%,总价为8×0.75×12=72元,最后比较数的大小即可得出答案。
2.【答案】C
【解析】【解答】解:将这个图形绕虚线旋转一周后会得到的立体图形是圆锥。
故答案为:C。
【分析】这个图形是三角形,绕着一条直角边旋转一周后会得到一个圆锥。
3.【答案】B
【解析】【解答】解:在新冠疫情流行期间,采用折线统计图既能反映每天病患的人数,又能反映疫情变化的情况和趋势。
故答案为:B。
【分析】条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况;扇形统计图能反应各个部分占总体的百分之几。
4.【答案】C
【解析】【解答】解:成数表示一个数是另一个数的十分之几。
故答案为:C。
【分析】成数表示一个数是另一个数的十分之几,俗称“几成”;“几成”就是十分之几,也就是百分之几十。
5.【答案】C
【解析】【解答】解:如果收入10元记作“+10",那么“-6”表示支出6元。
故答案为:C。
【分析】正数和负数表示具有相反意义的量,收入记作正数,则支出记作负数。
6.【答案】A
【解析】【解答】解:A、圆周长C=πd,C÷d=π(一定),C与d成正比例。所以说法错误;
B、(上底+下底)×高÷2=梯形面积(一定), 上、下底的和与高成反比例 。正确;
C、(长+宽)×2=长方形周长(一定), 它的长和宽不成比。正确;
D、图上距离÷比例尺=实际距离(一定),图上距离和比例尺成正比例。 正确。
故答案为:A。
【分析】两种相关联的量,它们的商一定时成正比例,它们的积一定时成反比例,否则不成比例。
7.【答案】B
【解析】【解答】解:①8时25分+20分=8时45分,不会迟到;②8时25分+30分=8时55分,会迟到;③8时25分+15分=8时40分,不会迟到;④8时25分+13分=8 时38分,不会迟到。所以选择①③④。
故答案为:B。
【分析】用爸爸出发的时间加上使用每种交通工具用的时间,只需要不超过8:48即可。
8.【答案】C
【解析】【解答】解:A:摸到白球和黄球的可能性都为0
B:摸到白球和黄球的可能性相等
C:4>2,摸到白球的可能性比黄球的可能性大
故答案为:C。
【分析】根据“在一个盒子中,球的数量越多,摸到的可能性越大”,进行判断即可。
9.【答案】B
【解析】【解答】
解:∵每淘汰1名选手就要有一场比赛,
∴只剩最后第一名,需要淘汰512-1=511名,
∴这次乒乓球比赛一共要比赛511场.
故答案为:B.
【分析】 根据淘汰赛的规则,每淘汰1名选手就有一场比赛,最后只剩第一名1人,用总人数减去1即可得到比赛场数.
10.【答案】A
【解析】【解答】解:18×=12(升)
故答案为:A。
【分析】 一个与圆柱等底等高的铁圆锥的体积是圆柱体积的,拿出圆锥后,圆柱形杯中还有的水。
11.【答案】正确
【解析】【解答】根据圆的周长公式:C=2πr,可以得出两个圆周长相等,则它们的半径就相等;
再根据圆的面积公式:S=πr2,半径相等则面积就相等.
故答案为:正确
【分析】圆的周长=圆周率×直径=圆周率×半径×2;圆的面积=圆周率×半径×半径.
12.【答案】错误
【解析】【解答】解:一个圆柱的侧面展开图是正方形,那么这个圆柱的底面周长和高相等。
故答案为:错误。
【分析】当圆柱的底面周长和高相等时,就得到一个正方形,正方形的边长相当于圆柱的底面周长和高。
13.【答案】错误
【解析】【解答】解:把一块长方体橡皮泥捏成正方体后,体积没有变化,表面积可能变化,原题干说法错误。
故答案为:错误。
【分析】把一块长方体橡皮泥捏成正方体后,体积没有变化,还是原来橡皮泥的体积。
14.【答案】正确
【解析】【解答】解:扇形统计图可以直观的表示部分数量与总数之间的关系。
故答案为:正确。
【分析】根据扇形统计图的特征作答即可。
15.【答案】错误
【解析】【解答】解:一个棱长是6厘米的正方体,它的表面积=6×6×6=216(平方厘米),它的体积=6×6×6=216(立方厘米),虽然数值相同,但单位不同,所以它的表面积和它的体积不相等,故“一个棱长是6厘米的正方体,它的表面积和体积相等”这个说法是错误的。
故答案为:错误。
【分析】正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,据此代入数据解答即可,注意:单位不同则不相等。
16.【答案】错误
【解析】【解答】解:题中没有说明路程一定时,速度和时间不一定成反比例,原题说法错误.
故答案为:错误
【分析】如果路程一定,那么速度和时间的乘积一定,速度和时间成反比例.
17.【答案】错误
【解析】【解答】等底等高的长方体和圆柱体,长方体的体积等于圆柱体体积,原题说法错误.
故答案为:错误.
【分析】 因为长方体和圆柱体的体积公式都是:V=Sh,所以等底等高的长方体和圆柱体,长方体的体积等于圆柱体体积,据此判断.
18.【答案】错误
【解析】【解答】7×5×3
=35×3
=105(立方厘米)
原题说法错误.
故答案为:错误.
【分析】已知长方体的长、宽、高,求长方体的体积,用长×宽×高=长方体体积,据此列式解答,体积用体积单位.
19.【答案】正确
20.【答案】错误
21.【答案】20.2
【解析】【解答】解:5.4千米按6千米收费,6千米分为3千米+3千米
13+2.4×3=13+7.2=20.2(元)
需要支付20.2元
故答案为:20.2。
【分析】前3千米的收费+超出3千米部分的收费=一共需要支付的钱数。
22.【答案】2.4,10%;2.4;3.6,15%;9.6,40%
【解析】【解答】总时间:6÷25%=24(时);
看电视:24×10%=2.4(小时),占10%;
吃饭:24×10%=2.4(小时);
活动:24×15%=3.6(小时);
睡眠:24×40%=9.6(小时).
故答案为:2.4,10%;2.4;3.6,15%;9.6,40%
【分析】用课外班的时间除以所占的百分比求出总时间;用总时间分别乘每项任务所占的百分率即可求出每项任务的时间并填表即可.
23.【答案】1:5000;60000
【解析】【解答】解:50米=5000厘米,把线段比例尺改写为数值比例尺是1:5000;比例尺1:60000表示图上距离:实际距离=1:60000,那么实际距离就是图上距离的60000倍。
故答案为:1:5000;60000。
【分析】从线段比例尺 可以看出,图上1厘米表示实际距离50米,根据比例尺=图上距离:实际距离即可解答;第二问求实际距离是图上距离的多少倍,反过来用比的后项除以比的前项即可解答。
24.【答案】9;225
【解析】【解答】解:有9个面露在外面;
5×5×9
=25×9
=225(平方分米)。
故答案为:9;225。
【分析】有9个面露在外面;露在外面的面积=正方体的棱长×棱长×露在外面的面的个数。
25.【答案】78.5;21.5
【解析】【解答】解:10÷2=5(cm)
52×3.14=78.5(cm2)
10×10-78.5
=100-78.5
=21.5(cm2)
故答案为:78.5;21.5。
【分析】圆的直径=边长,半径=直径÷2,yu8an的面积=π×半径2;剩余部分面积=正方形面积-圆的面积。
26.【答案】160
【解析】【解答】解:10×8×2
=80×2
=160(平方厘米)。
故答案为:160。
【分析】最多增加的表面积=最大的面的长×宽×2。
27.【答案】50.24;5
28.【答案】7
【解析】【解答】 解:狐狸的速度是:=(米),
黄鼠狼的速度是=(米),
陷阱的距离是(米);
分子15,28的最小公倍数是420;
10和28的最小公倍数是140;
当黄鼠狼跳米时,掉入陷阱,此时各跳了14次,狐狸这时跳了7米。
×14=7(米)
故答案为:7。
【分析】先把狐狸的速度、黄鼠狼的速度、陷阱的距离分别化成分母是30的分数;再根据分子分别找出15,28以及10和28的最小公倍数,进而求解。
29.【答案】7;5
【解析】【解答】解:5角=0.5元
5角硬币有:(12×1-8.5)÷(1-0.5)
=3.5÷0.5
=7(枚);
1元硬币有:12-7=5(枚)。
故答案为:7;5。
【分析】5角=0.5元,假设全部是1元硬币,则一共有(12×1)元,比实际一共多了(12×1-8.5)元;1元硬币比5角硬币多(1-0.5)元;用假设比实际一共多的除以每枚多的即可求出5角硬币的数量;再用总数量减去5角硬币的数量即可求出1元硬币的数量。
30.【答案】(1)正
(2)100;90
【解析】【解答】解:(1)10÷5=2(L),20÷10=2(L),30÷15=2(L),40÷20=2(L),50÷25=2(L),即体积÷时间=每分钟流出水的体积(一定),商一定,所以流出水的体积和时间成正比例关系;
(2)50×2=100(L),180÷2=90(分钟)。
故答案为:(1)正;(2)100;90。
【分析】(1)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系,用y/x=k( k一定)来表示;
(2)根据第(1)题结论可知每分钟流出水的体积是2L,因此,流水时间×每分钟流出水的体积=50分钟总的流出水的体积,流出水的体积÷每分钟流出水的体积=需要的时间。
31.【答案】解:[24,16,12]=4
(24÷4)×(16÷4)×(12÷4)
=6×4×3
=72(个)
答:小正方体的棱长最长是4cm,一共可以放72个这样的小正方体。
【解析】【分析】24,16,12的最大公约数是小正方体最长的棱长,长能放的个数×宽能放的个数×高能放的个数=一共可以放小正方体的个数。
32.【答案】解:92÷ = 644000000(厘米)
644000000厘米= 6440千米
答:传统的丝绸之路实际全长约6440千米。
【解析】【分析】根据实际距离=图上距离÷比例尺求出丝绸之路的实际全长,注意厘米与千米之间单位的换算。
33.【答案】30÷3×9=90(分)
【解析】【分析】为了节约时间,可在第一次煎蛋饼时,把两块蛋饼放入锅内,3分钟后,把其中的一块取出,放入第三块蛋饼,锅中没拿出的那块煎另外一面,3分钟后,把两面都煎了的蛋饼(熟了)取出,再放入原来取出的只煎了一面的蛋饼,锅中放入的第三块蛋饼煎另一面,3分钟后,3块蛋饼都熟了,共需9分钟,因此,30块蛋饼煎熟的时间为30÷3×9=90(分)。
34.【答案】(1)统计表:17.2%,32.3%,50.5%
(2)正确。在扇形统计图中,阴雨天占的比例最大。
(3)(答案不唯一)不会。调查北京近3年三月各种天气的情况,根据统计结果判断即可。
【解析】【分析】
(1) 先求三年三月总天数,再算各类天气总天数,用 “部分量 ÷ 总量 ×100%” 得占比,用于完善图表。
(2) 依据扇形统计图中阴雨天占比最大,判断 “台州三月多阴雨天” 说法正确。
(3) 不能依台州情况判断北京,需调查北京近 3 年三月天气数据来验证说法。
35.【答案】解:48×10÷(1+ )
=480÷
=360(立方分米)
答:这块圆柱形铁块的体积是360立方分米。
【解析】【分析】由题意可知,圆柱和圆锥的总体积等于上升部分水的体积,利用“的底面积×高”求出容器中水的体积,当圆柱和圆锥等底等高时,圆柱的体积是圆锥的3倍,圆锥的体积是圆柱体积的,圆柱的体积=圆柱和圆锥的总体积÷(1+),据此解答。
36.【答案】(1)
(2)
【解析】【解答】(1)
(2)
【分析】画旋转图形的方法:把图形的每个点与旋转中心连接,再量出题目要求旋转的角度,最后依次连接,据此按要求作图。
37.【答案】解:12.56÷3.14÷2
=4÷2
=2(分米)
3.14×22+12.56×2
=12.56+25.12
=37.68(平方分米)
答:做这个水桶至少需75.36平方分米的铁皮。
【解析】【分析】要求需多少平方分米的铁皮就是求无盖圆柱的表面积:
先根据d=C÷π求出底面直径,再根据r=d÷2求出半径,从而求出底面积;
根据S侧面积=C×h,求出圆柱侧面积;
最后S无盖圆柱=S底面积+S侧面积。
38.【答案】(1)40
(2)10;
(3)36
(4)解:22×30%=6.6(吨)
答:可以生产6.6吨有机肥料。
【解析】【解答】解:(1)22÷55%=40(吨);
(2)40×25%=10(吨),
(3)(25%-16%)÷25%
=9%÷25%
=36%
故答案为:(1)40;
(2)10;
;
(3)36。
【分析】(1)厨余垃圾是22吨,共占垃圾总量的55%,根据分数除法的意义求出垃圾总量;
(2)用垃圾总量乘25%即可求出可回收物的质量,在统计图中相应的位置画出相应长度的长条;
(3)可回收物占的百分率减去其他垃圾占的百分率,再除以可回收物占的百分率即可求出少百分之几;
(4)用厨余垃圾质量乘30%即可求出可以生产有机肥料的质量。
39.【答案】解:(3.5+4.5+28)÷2
=36÷2
=18(元)
答:一本字典18元。
【解析】【分析】两人合起的钱+小华还差的钱+乐乐还差的钱=2本字典的钱数,2本字典的钱数÷2=1本字典的钱数。
40.【答案】解:2.8×(1-30%)
=2.8×70%
=1.96(万吨)
答:前年秋粮食产量是1.96万吨。
【解析】【分析】几成就是百分之几十;
前年秋粮食产量=去年秋粮食产量×(1-前年比去年少百分之几),据此作答即可。
41.【答案】解:打折:320×90%=288(元)
用代金券:320-(100-78)×2
=320-22×2
=320-44
=276(元)
276<288,所以用代金券更优惠。
答:使用代金券消费更优惠。
【解析】【分析】打折应付金额=原价×90%;每桌限用2张代金券,所以用代金券应付金额=原价-(100-78)×2,据此分别计算出两种优惠方式应付的钱,再比较即可。
42.【答案】解:
0.54×10=5.4 0.4×2.5=1
8.5×0.02=0.17 8×(3-1.75)=10
0.7×101=70.7 0.9-0.9×0.9=0.09
【解析】【分析】这道题主要考察的是小数乘法和小数减法的运算规则,需要根据小数乘法和减法的计算法则对每个算式进行准确计算,特别是对于含有括号和混合运算的算式,需要按照运算顺序先进行括号内的计算,再进行乘法和减法运算。
43.【答案】解:(1)0.28×0.08
=
(2)8.06×6.2
=
(3)3.45×8.6
=
验算:
(4)63.5×0.14
验算:
【解析】【分析】本题运用小数乘法的竖式的计算方法进行计算即可.
44.【答案】(1)解:S=3.14×(8÷2)2×2+3.14×8×10
=3.14×16×2+3.14×80
=100.48+251.2
=351.68(cm2)
(2)解:S=×3.14×32×8
=×3.14×72
=3.14×24
=75.36(cm3)
【解析】【分析】(1)圆柱体的表面积=2πr2+2πrh,据此代入数值计算;
(2)圆锥的体积=πr2h,据此代入数值计算。
试题分析部分
1、试卷总体分布分析
总分:164分
分值分布 客观题(占比) 66.0(40.2%)
主观题(占比) 98.0(59.8%)
题量分布 客观题(占比) 28(63.6%)
主观题(占比) 16(36.4%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
填空题 10(22.7%) 31.0(18.9%)
解答题 5(11.4%) 35.0(21.3%)
作图题 1(2.3%) 10.0(6.1%)
竖式计算 1(2.3%) 5.0(3.0%)
图形计算 1(2.3%) 10.0(6.1%)
解决问题 5(11.4%) 28.0(17.1%)
口算与估算 1(2.3%) 5.0(3.0%)
单选题 10(22.7%) 20.0(12.2%)
判断题 10(22.7%) 20.0(12.2%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (68.2%)
2 容易 (31.8%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 百分数的应用--折扣 7.0(4.3%) 1,41
2 体育比赛问题 2.0(1.2%) 9
3 扇形统计图的特点及绘制 17.0(10.4%) 14,34
4 作旋转后的图形 10.0(6.1%) 36
5 圆柱的侧面积、表面积 15.0(9.1%) 37,44
6 圆的周长 4.0(2.4%) 27
7 圆锥的特征 2.0(1.2%) 2
8 正方体的体积 4.0(2.4%) 15,20
9 小数除法混合运算 5.0(3.0%) 39
10 正、负数的意义与应用 2.0(1.2%) 5
11 统计图的选择 2.0(1.2%) 3
12 长方体的表面积 2.0(1.2%) 26
13 鸡兔同笼问题 4.0(2.4%) 29
14 圆柱与圆锥体积的关系 5.0(3.0%) 35
15 可能性的大小 2.0(1.2%) 8
16 最优策略:找次品问题 2.0(1.2%) 19
17 小数乘小数的小数乘法 5.0(3.0%) 42
18 成反比例的量及其意义 4.0(2.4%) 6,16
19 比例尺的认识 4.0(2.4%) 23
20 圆的面积 10.0(6.1%) 11,25,27
21 分段计费问题 2.0(1.2%) 21
22 统计图、统计表的综合应用 17.0(10.4%) 22,34
23 圆柱的体积(容积) 7.0(4.3%) 17,35
24 立方体的切拼 2.0(1.2%) 26
25 从扇形统计图获取信息 23.0(14.0%) 34,38
26 数列中的规律 2.0(1.2%) 9
27 百分数的其他应用 15.0(9.1%) 34
28 圆柱的展开图 2.0(1.2%) 12
29 组合体露在外面的面 4.0(2.4%) 24
30 小数的四则混合运算 4.0(2.4%) 29
31 单价、数量、总价的关系及应用 2.0(1.2%) 1
32 优化策略:烙饼问题 5.0(3.0%) 33
33 小数乘整数的小数乘法 5.0(3.0%) 42
34 百分数的应用--成数 7.0(4.3%) 4,40
35 24时计时法时间计算 2.0(1.2%) 7
36 最大公因数的应用 5.0(3.0%) 31
37 长方体的体积 4.0(2.4%) 17,18
38 成正比例的量及其意义 3.0(1.8%) 30
39 小数乘法混合运算 12.0(7.3%) 21,42,43
40 水中浸物模型 5.0(3.0%) 35
41 圆锥的体积(容积) 12.0(7.3%) 10,44
42 正方体的表面积 4.0(2.4%) 15,20
43 体积的等积变形 2.0(1.2%) 13
44 最小公倍数的应用 2.0(1.2%) 28
45 应用比例尺求图上距离或实际距离 5.0(3.0%) 32
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
同课章节目录
