2.3空间直角坐标系
图片预览





文档简介
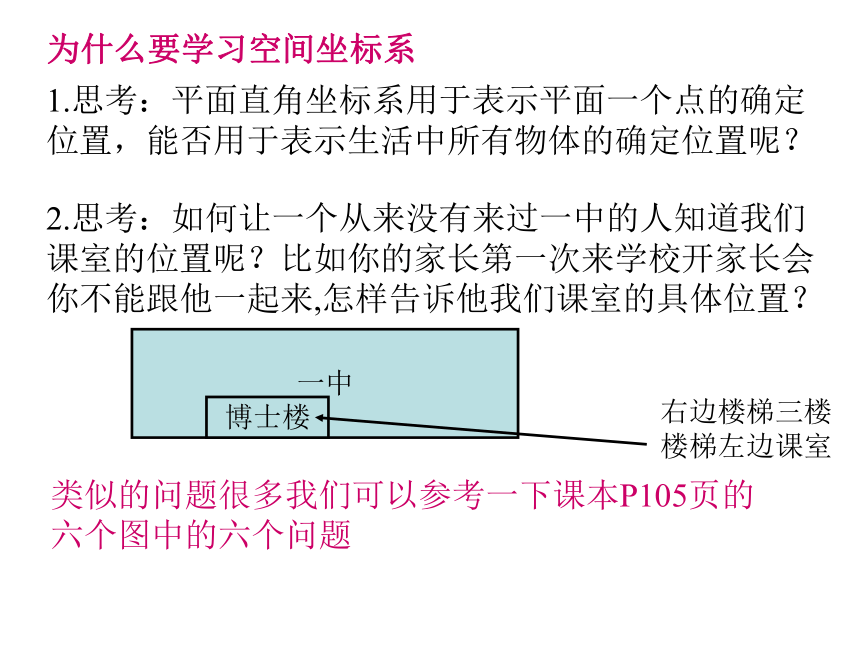
课件25张PPT。 空间直角坐标系为什么要学习空间坐标系1.思考:平面直角坐标系用于表示平面一个点的确定
位置,能否用于表示生活中所有物体的确定位置呢?2.思考:如何让一个从来没有来过一中的人知道我们
课室的位置呢?比如你的家长第一次来学校开家长会
你不能跟他一起来,怎样告诉他我们课室的具体位置?类似的问题很多我们可以参考一下课本P105页的
六个图中的六个问题一中博士楼右边楼梯三楼
楼梯左边课室 三个坐标轴的正方向符合右手系.一、空间直角坐标系 从空间某一点O引三条互相垂直的射线Ox、Oy、Oz.
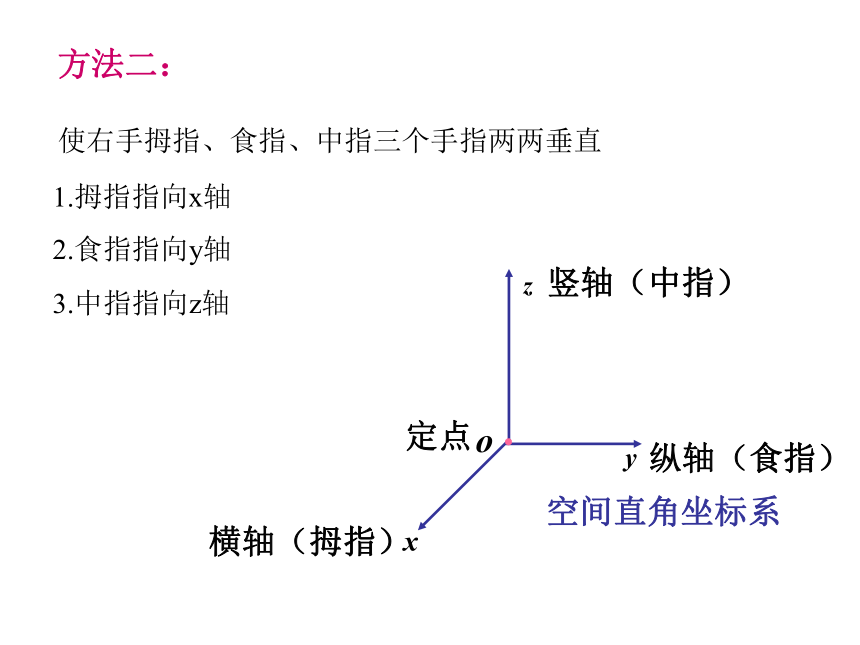
并取定长度单位和方向,就建立了空间直角坐标系 .其中O 点称为坐标原点,数轴Ox, Oy, Oz称为坐标轴,每两个坐标轴所在的平面Oxy、Oyz、Ozx叫做坐标平面.方法一:方法二:横轴(拇指)纵轴(食指)竖轴(中指)定点空间直角坐标系使右手拇指、食指、中指三个手指两两垂直1.拇指指向x轴2.食指指向y轴3.中指指向z轴试一试:分别一黑板中指定的长方体中底面的一个顶点为原点
建立适当的空间直角坐标系使得整个长方体都在直角
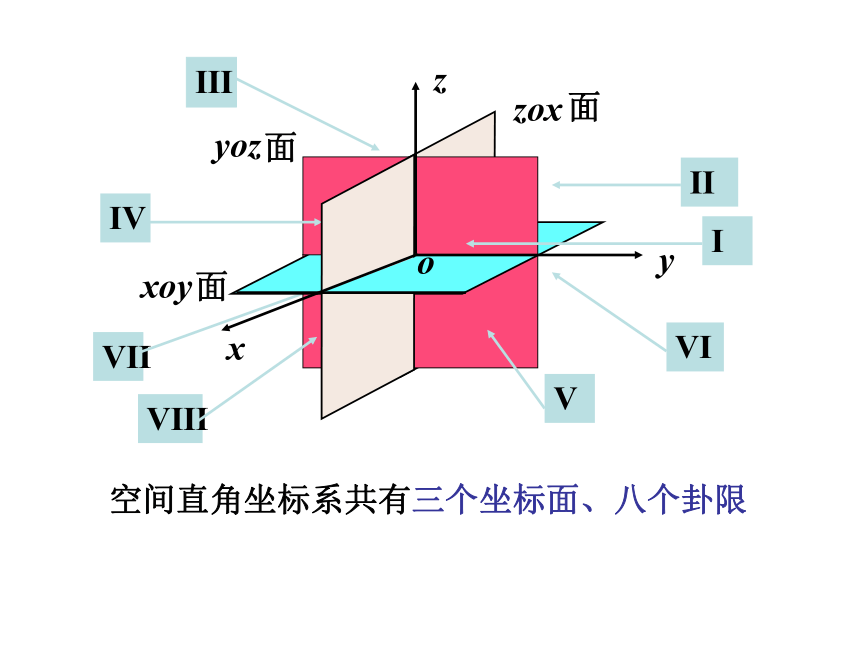
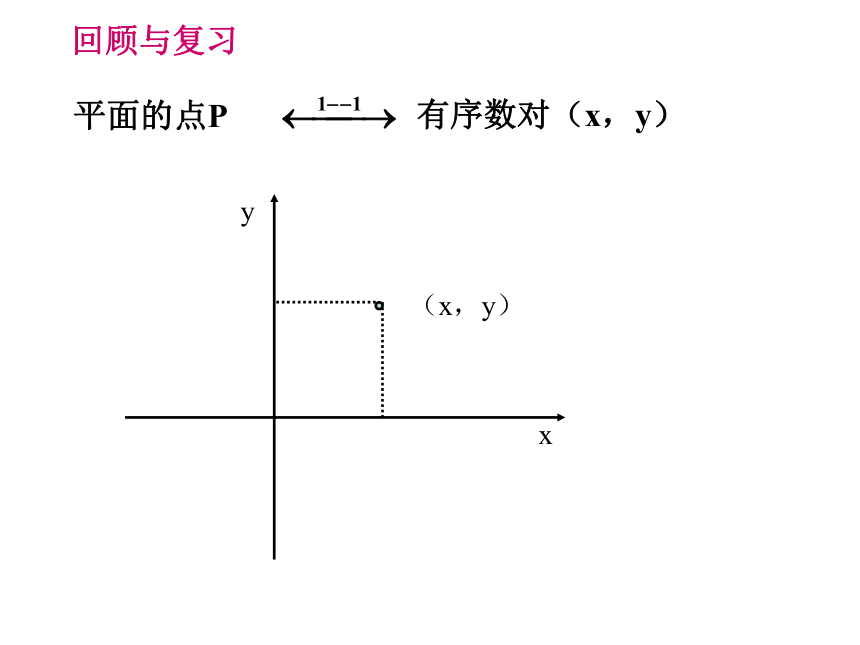
坐标系的正方向上。面面面空间直角坐标系共有三个坐标面、八个卦限平面的点P
有序数对(x,y)(x,y)xy回顾与复习空间的点P
有序数组特殊点的表示:x轴上的点坐标平面xoy上的点A,y轴上的点z轴上的点原点坐标平面yoz上的点B,坐标平面xoz上的点B,非特殊点P(x,y,z)试一试:分别一黑板中给定的长方体长、宽、高并建立好的
空间直角坐标系上指出指定各点的坐标。回顾与复习长方体的对角线公式已知长方体的长、宽、高分别为a,b,c则长方体的对角线长二、空间两点间的距离COM(x,y,z)xyz特殊地:若两点分别为二、空间两点间的距离特殊地:若两点分别为解例4所以点P的坐标为(9,0,0)或(-1,0,0)。解例5在xoy平面内的直线x+y=1上确定一点M,使M到
点N(6,5,1)的距离最小。由已知,可设M(x,1-x,0),则解原结论成立.补充解设P点坐标为所求点为补充思考P109练习 4在空间直角坐标系中,给定点M(1,-2,3),
求它分别关于坐标平面、坐标轴和原点的对称
点的坐标.M(1)关于坐标平
面xoz对称的点M’(1,2,3)M’123思考P109练习 4在空间直角坐标系中,给定点M(1,-2,3),
求它分别关于坐标平面、坐标轴和原点的对称
点的坐标。M(2)关于z轴对称的点M’(-1,2,3)M’123思考P109练习 4在空间直角坐标系中,给定点M(1,-2,3),
求它分别关于坐标平面、坐标轴和原点的对称
点的坐标。M(3)关于原点对称的点M’(-1,2,-3)M’123思考P109练习 4在空间直角坐标系中,给定点M(1,-2,3),
求它分别关于坐标平面、坐标轴和原点的对称
点的坐标。M123用前面的方法
把M点关于其
它坐标平面和
坐标轴对称的
点的坐标求出
来。空间直角坐标系 空间两点间距离公式(注意它与平面直角坐标系的区别)(轴、面、卦限)五、小结思考题在空间直角坐标系中,指出下列各点在哪个卦限?思考题解答A:Ⅳ; B:Ⅴ; C:Ⅷ; D:Ⅲ; 1、下列各点所在卦限分别是:
一、填空题练习题练习题答案
位置,能否用于表示生活中所有物体的确定位置呢?2.思考:如何让一个从来没有来过一中的人知道我们
课室的位置呢?比如你的家长第一次来学校开家长会
你不能跟他一起来,怎样告诉他我们课室的具体位置?类似的问题很多我们可以参考一下课本P105页的
六个图中的六个问题一中博士楼右边楼梯三楼
楼梯左边课室 三个坐标轴的正方向符合右手系.一、空间直角坐标系 从空间某一点O引三条互相垂直的射线Ox、Oy、Oz.
并取定长度单位和方向,就建立了空间直角坐标系 .其中O 点称为坐标原点,数轴Ox, Oy, Oz称为坐标轴,每两个坐标轴所在的平面Oxy、Oyz、Ozx叫做坐标平面.方法一:方法二:横轴(拇指)纵轴(食指)竖轴(中指)定点空间直角坐标系使右手拇指、食指、中指三个手指两两垂直1.拇指指向x轴2.食指指向y轴3.中指指向z轴试一试:分别一黑板中指定的长方体中底面的一个顶点为原点
建立适当的空间直角坐标系使得整个长方体都在直角
坐标系的正方向上。面面面空间直角坐标系共有三个坐标面、八个卦限平面的点P
有序数对(x,y)(x,y)xy回顾与复习空间的点P
有序数组特殊点的表示:x轴上的点坐标平面xoy上的点A,y轴上的点z轴上的点原点坐标平面yoz上的点B,坐标平面xoz上的点B,非特殊点P(x,y,z)试一试:分别一黑板中给定的长方体长、宽、高并建立好的
空间直角坐标系上指出指定各点的坐标。回顾与复习长方体的对角线公式已知长方体的长、宽、高分别为a,b,c则长方体的对角线长二、空间两点间的距离COM(x,y,z)xyz特殊地:若两点分别为二、空间两点间的距离特殊地:若两点分别为解例4所以点P的坐标为(9,0,0)或(-1,0,0)。解例5在xoy平面内的直线x+y=1上确定一点M,使M到
点N(6,5,1)的距离最小。由已知,可设M(x,1-x,0),则解原结论成立.补充解设P点坐标为所求点为补充思考P109练习 4在空间直角坐标系中,给定点M(1,-2,3),
求它分别关于坐标平面、坐标轴和原点的对称
点的坐标.M(1)关于坐标平
面xoz对称的点M’(1,2,3)M’123思考P109练习 4在空间直角坐标系中,给定点M(1,-2,3),
求它分别关于坐标平面、坐标轴和原点的对称
点的坐标。M(2)关于z轴对称的点M’(-1,2,3)M’123思考P109练习 4在空间直角坐标系中,给定点M(1,-2,3),
求它分别关于坐标平面、坐标轴和原点的对称
点的坐标。M(3)关于原点对称的点M’(-1,2,-3)M’123思考P109练习 4在空间直角坐标系中,给定点M(1,-2,3),
求它分别关于坐标平面、坐标轴和原点的对称
点的坐标。M123用前面的方法
把M点关于其
它坐标平面和
坐标轴对称的
点的坐标求出
来。空间直角坐标系 空间两点间距离公式(注意它与平面直角坐标系的区别)(轴、面、卦限)五、小结思考题在空间直角坐标系中,指出下列各点在哪个卦限?思考题解答A:Ⅳ; B:Ⅴ; C:Ⅷ; D:Ⅲ; 1、下列各点所在卦限分别是:
一、填空题练习题练习题答案
