广东省2025年七年级下册数学期末考试模拟卷(含答案)
文档属性
| 名称 | 广东省2025年七年级下册数学期末考试模拟卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 532.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 06:54:17 | ||
图片预览



文档简介
广东省(北师大版)2025年七年级下册数学期末考试模拟卷
满分120分 时间120分钟
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共30分)
1.下列成语描述的事件为必然事件的是( )
A.空中楼阁 B.水中捞月 C.日出东方 D.刻舟求剑
2.冠状病毒的一个变种是非典型肺炎的病原体,球形冠状病毒的直径是米,则这种冠状病毒的直径用科学记数法表示为( )
A.米 B.米 C.米 D.米
3.下列每组数分别是三根小木棒的长度,将它们首尾顺次相接,能摆成三角形的是( )
A.3,4,7 B.6,8,15 C.5,12,13 D.5,5,11
4.在圆的面积计算公式中,对于变量和常量的说法正确的是( )
A.2是常量,S、、R是变量 B.2,是常量,S、R是变量
C.2,S,是常量,R是变量 D.2,,R是常量,S是变量
5.下列计算正确的是( ).
A. B.
C. D.
6.如图,点E在的延长线上,下列条件中不能判定的是( )
A. B. C. D.
7.如图,是的角平分线,于点E,,,,则的长是( )
A.3 B.4 C.6 D.5
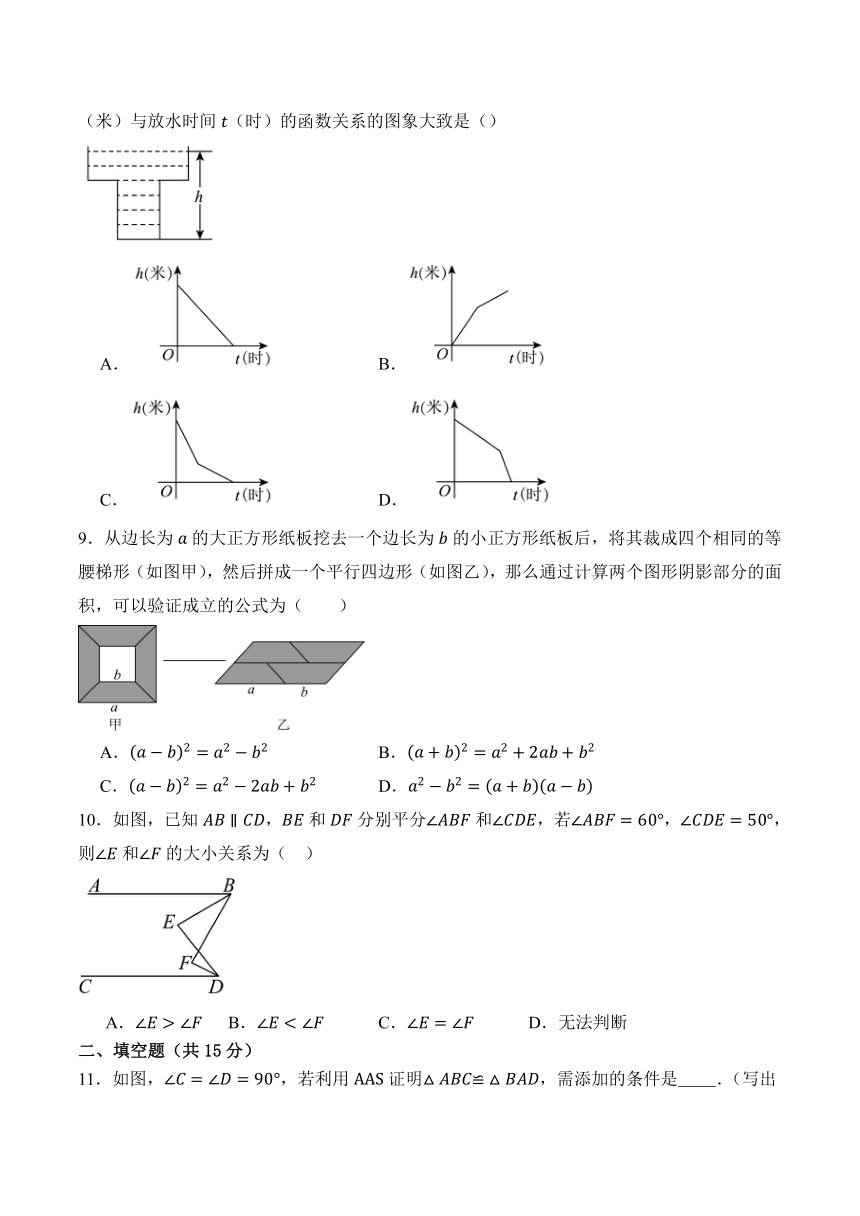
8.图是某蓄水池横截面的示意图,现将满池的水匀速全部放出.能刻画蓄水池中水的高度(米)与放水时间(时)的函数关系的图象大致是()
A. B.
C. D.
9.从边长为的大正方形纸板挖去一个边长为的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙),那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )
A. B.
C. D.
10.如图,已知,和分别平分和,若,,则和的大小关系为( )
A. B. C. D.无法判断
二、填空题(共15分)
11.如图,,若利用证明,需添加的条件是 .(写出一种即可)
12.一个长方形的一条边长为,另一条边长为,它的面积为,则S与x之间的关系式为 .
13.已知,则 .(用含的代数式表示)
14.如图①,“二八大杠”传统老式自行车承载了一代人的回忆,图②是它的几何示意图.已知,,当时,的度数为 .
15.如图,等腰三角形的底边长为6,面积是36,腰的垂直平分线分别交,边于,点.若点为边的中点,点为线段上一动点,则周长的最小值为 .
三、解答题(共75分)
16.(本题7分)如图已知,,,与互补.试判断与的位置关系,并说明理由.
17.(本题7分)计算:
(1);
(2).
18.(本题7分)一个不透明的袋中装有24个白球和若干个红球,它们除颜色外其他均相同.已知将袋中球摇匀后,从中任意摸出一个球是白球的概率是.
(1)求袋中总共有多少个球;
(2)从袋中取走10个球(其中没有红球)并将袋中球摇匀后,求从剩余的球中任意摸出一个球是红球的概率.
19.(本题9分)用无刻度直尺和圆规作图(不写作法,保留作图痕迹).
(1)如图①,作的平分线,交于点D;
(2)如图②,作一条直线l,使得点A关于l的对称点为点P.
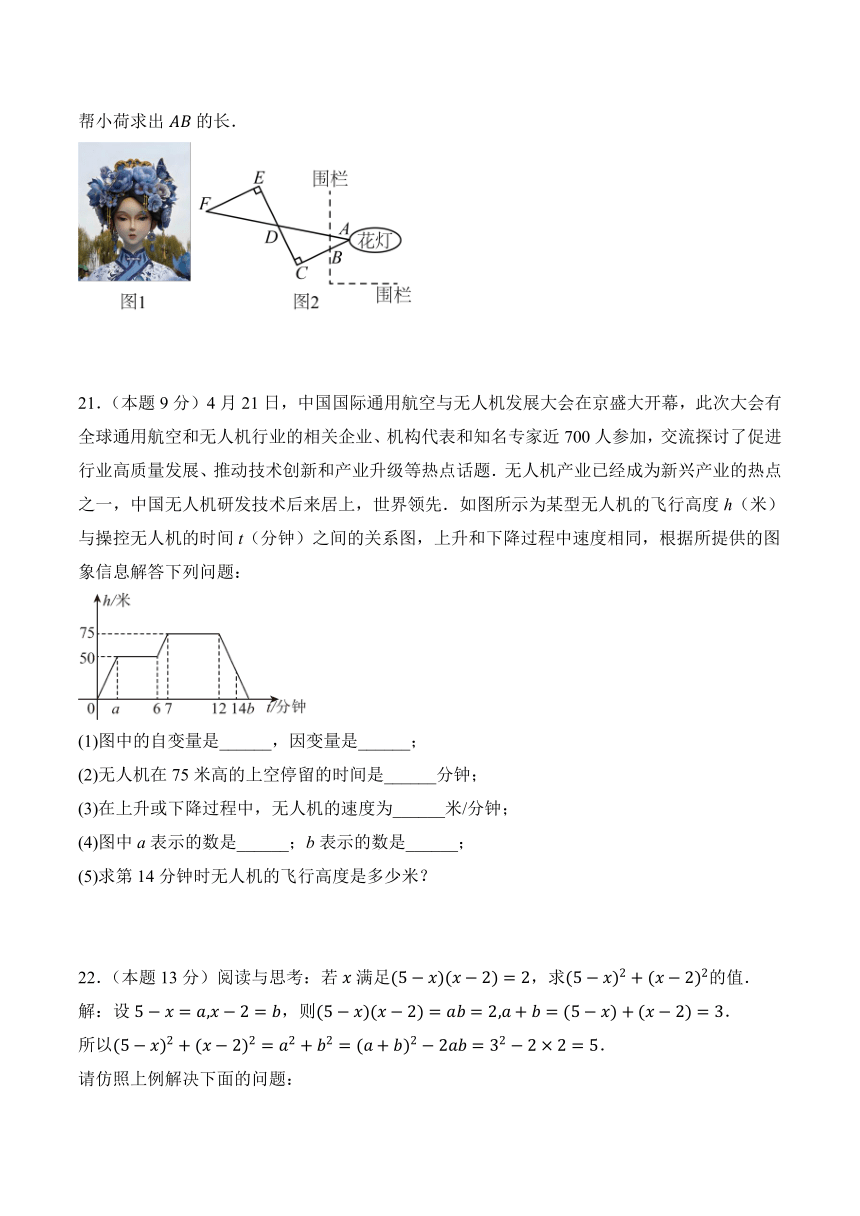
20.(本题9分)数学兴趣小组来到大明湖畔与美丽的花灯合影.如图2,小荷和小柳在花灯围栏旁的点B处拍了一张照片.小荷设计了一个方案测量花灯的边缘点A与点B的距离.小荷先沿方向走2.5米至点C,又沿着与垂直的方向走了3米至点D,并放置了一个标记物,接着往前再走相同的距离至点E,最后从点E处向左沿着与垂直的方向走了一定距离至点F.此时,她看到标记物正好遮住了花灯边缘的点A处,经过测量,米,请你帮小荷求出的长.
21.(本题9分)4月21日,中国国际通用航空与无人机发展大会在京盛大开幕,此次大会有全球通用航空和无人机行业的相关企业、机构代表和知名专家近700人参加,交流探讨了促进行业高质量发展、推动技术创新和产业升级等热点话题.无人机产业已经成为新兴产业的热点之一,中国无人机研发技术后来居上,世界领先.如图所示为某型无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系图,上升和下降过程中速度相同,根据所提供的图象信息解答下列问题:
(1)图中的自变量是______,因变量是______;
(2)无人机在75米高的上空停留的时间是______分钟;
(3)在上升或下降过程中,无人机的速度为______米/分钟;
(4)图中a表示的数是______;b表示的数是______;
(5)求第14分钟时无人机的飞行高度是多少米?
22.(本题13分)阅读与思考:若满足,求的值.
解:设,则 .
所以.
请仿照上例解决下面的问题:
(1)若满足,求的值;
(2)若满足,求的值;
(3)如图,点C是线段上的一点,以为边向两边作正方形,设,两正方形的面积和,求图中阴影部分的面积.
23.(本题14分)【问题背景】
“一线三垂直”模型是“一线三等角”模型的特殊情况,即三个等角的度数为,且三组边相互垂直,所以称为“一线三垂直”模型.当模型中有一组对应边长相等时,模型中必定存在全等三角形.
【问题解决】
(1)如图,在等腰直角中,,,过点作直线,于点,于点,则,与之间满足的数量关系是________;
如图,在等腰直角中,,,过点作直线,过点作于点,过点作于点,,,则的长为________.
【方法应用】
(2)如图,在中,,,.求的面积.
【拓展迁移】
(3)如图,在中,,,,以为直角边向右侧作一个等腰直角三角形,连接,请直接写出的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C B D B A D D B
二、填空题
11.(答案不唯一)
【分析】本题主要考查了三角形全等的判定,熟练掌握三角形全等的判定方法,是解题的关键.利用可得出,(答案不唯一)进而证明,即可得出答案.
【详解】解:在和中,
,
,
利用证明,需添加的条件是(答案不唯一).
故答案为:(答案不唯一).
12.
【分析】本题考查了函数,由长方形的面积列出函数,即可求解;理解长方形的面积与边长之间的关系是解题的关键.
【详解】解:由题意得
,
故答案为:.
13.
【分析】本题考查了同底数幂的乘法逆运算,根据同底数幂的乘法逆运算法则即可求解.
【详解】解:∵,
∴.
故答案为:.
14.
【分析】本题考查了平行线的性质.根据,可得,根据,可得,由此可得的度数,再根据即可得解.
【详解】解:∵,
,
,
,
,
,
故答案为:.
15.15
【分析】本题考查的是轴对称最短路线问题,连接,由于是等腰三角形,点是边的中点,故,再根据三角形的面积公式求出的长,再根据是线段的垂直平分线可知,点关于直线的对称点为点,故的长为的最小值,由此即可得出结论.熟知等腰三角形三线合一的性质是解答此题的关键.
【详解】解:连接,
是等腰三角形,点是边的中点,
,
,解得,
是线段的垂直平分线,
点关于直线的对称点为点,
的长为的最小值,
的周长最短.
故答案为:15.
三、解答题
16.;理由见解析
【分析】本题考查了平行线的判定和性质,掌握平行线的判定和性质是解题的关键.根据得出,则,进而推出,则,根据平行线的性质及垂直的定义即可得出结论.
【详解】解:,理由如下:
,
,
,
与互补,
,
,
,
,
.
17.(1)9
(2)
【分析】本题主要考查了零指数幂,负整数指数幂,积的乘方计算,单项式乘以单项式,熟知相关计算法则是解题的关键.
(1)先计算零指数幂,负整数整数幂和乘方,再计算加减法即可得到答案;
(2)先计算积的乘方,再计算单项式乘以单项式,最后合并同类项即可得到答案.
【详解】(1)解:
;
(2)解:
.
18.(1)袋中总共有个球;
(2)
【分析】要考查了概率公式的应用,熟练掌握概率公式(是总结果数,是事件发生的结果数 )是解题的关键.
(1)根据概率公式,已知白球数量和摸出白球的概率,设总球数为未知数,列方程求解.
(2)先算出红球数量,再算出取走个白球后剩余球总数和剩余红球数,最后用概率公式计算.
【详解】(1)解:设袋中总共有个球
白球有个,摸出白球的概率是,
∴
即,解得
袋中总共有个球
(2)解:由(1)知总球数个,白球个,则红球有个
取走个白球后,剩余球总数为个,红球数量不变仍为个
∴从剩余球中摸出红球的概率
19.(1)见解析
(2)见解析
【分析】本题考查了尺规作图——作一个角的平分线,尺规作图——作线段的垂直平分线,轴对称图形,解题关键是正确作出图形.
(1)利用尺规角平分线;
(2)依据对称点的连线被对称轴垂直平分进行作图即可.
【详解】(1)解:如图,射线即为所求.
(2)如图,直线l即为所求.
20.的长为米.
【分析】本题考查了全等三角形的判定和性质.利用证明,即可求解.
【详解】解:由题意得米,米,米,,
点在同一直线上,
在和中,,
∴,
∴米,
∴米,
答:的长为米.
21.(1)操控无人机的时间t,无人机的飞行高度h
(2)5
(3)25
(4)2,15
(5)第14分钟时无人机的飞行高度是25米
【分析】本题考查用图象表示变量之间的关系,解题的关键是看懂图象中数据,结合路程速度时间进行计算.
(1)根据数量变化关系直接判断即可得到答案;
(2)根据图象直接计算即可得到答案;
(3)根据分钟图象数据求解即可得到答案;
(4)根据(3)中的速度代入行程公式即可得到答案;
(5)根据行程公式求出下降路程,进而即可得到答案.
【详解】(1)解:由题意可得,
∵无人机高度随时间变化而变化,
∴自变量是操控无人机的时间(或t),因变量是无人机的飞行高度(或h),
故答案为:操控无人机的时间t,无人机的飞行高度h;
(2)解:由图象可得,
分钟无人机在米高的上空停留,
∴无人机在米高的上空停留的时间是:分钟,
故答案为:5;
(3)解:由分钟图象可得,
无人机的速度为:(米/分钟),
故答案为:;
(4)解:由(3)可得,
,,
解得:,,
故答案为:2,;
(5)解:由(3)可得,
,
∴第分钟时无人机的飞行高度是:(米),
答:第分钟时无人机的飞行高度是米.
22.(1)
(2)
(3)3
【分析】本题考查了完全平方公式的几何背景,利用完全平方公式变形后求解,熟练掌握完全平方公式并灵活运用是解题的关键.
(1)设,,先求得,再根据求得,再用,表示出,借助完全平方公式求解即可;
(2)设,,先求出,再根据,得到,利用完全平方公式求出即可;
(3)设,,先根据,,求得,,从而可求得,再求得图中阴影部分的面积.
【详解】(1)设,,
∴,
∵,
∴,
∴
,
∴的值为;
(2)设,,
∴,
∵,
∴,
∵,
∴,
∴,
∴;
(3)设,,则,,,
∵,,
∴,,
∴,
∴.
即阴影部分的面积为3.
23.(1) ;;(2);(3)或
【分析】本题考查了全等三角形的判定与性质,等腰三角形的性质,熟练掌握分类讨论的思想是解答本题的关键.
(1)根据,得到,结合,得到,,从而得到,即可得到,即可得到答案;
同理证明即可得到答案;
(2)作,交于点,证明即可得到答案;
(3)分,两种情况讨论,根据等腰直角三角形结合(1)的结论求解即可得到答案.
【详解】解:(1) ,,
,
,
,,
,
在和中,
,
,
,,
,
故答案为:;
,,
,
,
,,
,
在和中,
,
,
,,
,,
,
故答案为:;
(2)在中,,,,如图,作,交于点,
,,,
,
在和中,
,
,
,
;
(3)以为直角边向右侧作一个等腰直角三角形,,如图,作高线,过点作于,
,,,
,,
由(1)得:,
,
;
以为直角边向右侧作一个等腰直角三角形,,如图,作高线,过点作于,
,,,
,,
由(1)得:,
,
;
综上所述,的面积为或.
满分120分 时间120分钟
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共30分)
1.下列成语描述的事件为必然事件的是( )
A.空中楼阁 B.水中捞月 C.日出东方 D.刻舟求剑
2.冠状病毒的一个变种是非典型肺炎的病原体,球形冠状病毒的直径是米,则这种冠状病毒的直径用科学记数法表示为( )
A.米 B.米 C.米 D.米
3.下列每组数分别是三根小木棒的长度,将它们首尾顺次相接,能摆成三角形的是( )
A.3,4,7 B.6,8,15 C.5,12,13 D.5,5,11
4.在圆的面积计算公式中,对于变量和常量的说法正确的是( )
A.2是常量,S、、R是变量 B.2,是常量,S、R是变量
C.2,S,是常量,R是变量 D.2,,R是常量,S是变量
5.下列计算正确的是( ).
A. B.
C. D.
6.如图,点E在的延长线上,下列条件中不能判定的是( )
A. B. C. D.
7.如图,是的角平分线,于点E,,,,则的长是( )
A.3 B.4 C.6 D.5
8.图是某蓄水池横截面的示意图,现将满池的水匀速全部放出.能刻画蓄水池中水的高度(米)与放水时间(时)的函数关系的图象大致是()
A. B.
C. D.
9.从边长为的大正方形纸板挖去一个边长为的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙),那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )
A. B.
C. D.
10.如图,已知,和分别平分和,若,,则和的大小关系为( )
A. B. C. D.无法判断
二、填空题(共15分)
11.如图,,若利用证明,需添加的条件是 .(写出一种即可)
12.一个长方形的一条边长为,另一条边长为,它的面积为,则S与x之间的关系式为 .
13.已知,则 .(用含的代数式表示)
14.如图①,“二八大杠”传统老式自行车承载了一代人的回忆,图②是它的几何示意图.已知,,当时,的度数为 .
15.如图,等腰三角形的底边长为6,面积是36,腰的垂直平分线分别交,边于,点.若点为边的中点,点为线段上一动点,则周长的最小值为 .
三、解答题(共75分)
16.(本题7分)如图已知,,,与互补.试判断与的位置关系,并说明理由.
17.(本题7分)计算:
(1);
(2).
18.(本题7分)一个不透明的袋中装有24个白球和若干个红球,它们除颜色外其他均相同.已知将袋中球摇匀后,从中任意摸出一个球是白球的概率是.
(1)求袋中总共有多少个球;
(2)从袋中取走10个球(其中没有红球)并将袋中球摇匀后,求从剩余的球中任意摸出一个球是红球的概率.
19.(本题9分)用无刻度直尺和圆规作图(不写作法,保留作图痕迹).
(1)如图①,作的平分线,交于点D;
(2)如图②,作一条直线l,使得点A关于l的对称点为点P.
20.(本题9分)数学兴趣小组来到大明湖畔与美丽的花灯合影.如图2,小荷和小柳在花灯围栏旁的点B处拍了一张照片.小荷设计了一个方案测量花灯的边缘点A与点B的距离.小荷先沿方向走2.5米至点C,又沿着与垂直的方向走了3米至点D,并放置了一个标记物,接着往前再走相同的距离至点E,最后从点E处向左沿着与垂直的方向走了一定距离至点F.此时,她看到标记物正好遮住了花灯边缘的点A处,经过测量,米,请你帮小荷求出的长.
21.(本题9分)4月21日,中国国际通用航空与无人机发展大会在京盛大开幕,此次大会有全球通用航空和无人机行业的相关企业、机构代表和知名专家近700人参加,交流探讨了促进行业高质量发展、推动技术创新和产业升级等热点话题.无人机产业已经成为新兴产业的热点之一,中国无人机研发技术后来居上,世界领先.如图所示为某型无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系图,上升和下降过程中速度相同,根据所提供的图象信息解答下列问题:
(1)图中的自变量是______,因变量是______;
(2)无人机在75米高的上空停留的时间是______分钟;
(3)在上升或下降过程中,无人机的速度为______米/分钟;
(4)图中a表示的数是______;b表示的数是______;
(5)求第14分钟时无人机的飞行高度是多少米?
22.(本题13分)阅读与思考:若满足,求的值.
解:设,则 .
所以.
请仿照上例解决下面的问题:
(1)若满足,求的值;
(2)若满足,求的值;
(3)如图,点C是线段上的一点,以为边向两边作正方形,设,两正方形的面积和,求图中阴影部分的面积.
23.(本题14分)【问题背景】
“一线三垂直”模型是“一线三等角”模型的特殊情况,即三个等角的度数为,且三组边相互垂直,所以称为“一线三垂直”模型.当模型中有一组对应边长相等时,模型中必定存在全等三角形.
【问题解决】
(1)如图,在等腰直角中,,,过点作直线,于点,于点,则,与之间满足的数量关系是________;
如图,在等腰直角中,,,过点作直线,过点作于点,过点作于点,,,则的长为________.
【方法应用】
(2)如图,在中,,,.求的面积.
【拓展迁移】
(3)如图,在中,,,,以为直角边向右侧作一个等腰直角三角形,连接,请直接写出的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C B D B A D D B
二、填空题
11.(答案不唯一)
【分析】本题主要考查了三角形全等的判定,熟练掌握三角形全等的判定方法,是解题的关键.利用可得出,(答案不唯一)进而证明,即可得出答案.
【详解】解:在和中,
,
,
利用证明,需添加的条件是(答案不唯一).
故答案为:(答案不唯一).
12.
【分析】本题考查了函数,由长方形的面积列出函数,即可求解;理解长方形的面积与边长之间的关系是解题的关键.
【详解】解:由题意得
,
故答案为:.
13.
【分析】本题考查了同底数幂的乘法逆运算,根据同底数幂的乘法逆运算法则即可求解.
【详解】解:∵,
∴.
故答案为:.
14.
【分析】本题考查了平行线的性质.根据,可得,根据,可得,由此可得的度数,再根据即可得解.
【详解】解:∵,
,
,
,
,
,
故答案为:.
15.15
【分析】本题考查的是轴对称最短路线问题,连接,由于是等腰三角形,点是边的中点,故,再根据三角形的面积公式求出的长,再根据是线段的垂直平分线可知,点关于直线的对称点为点,故的长为的最小值,由此即可得出结论.熟知等腰三角形三线合一的性质是解答此题的关键.
【详解】解:连接,
是等腰三角形,点是边的中点,
,
,解得,
是线段的垂直平分线,
点关于直线的对称点为点,
的长为的最小值,
的周长最短.
故答案为:15.
三、解答题
16.;理由见解析
【分析】本题考查了平行线的判定和性质,掌握平行线的判定和性质是解题的关键.根据得出,则,进而推出,则,根据平行线的性质及垂直的定义即可得出结论.
【详解】解:,理由如下:
,
,
,
与互补,
,
,
,
,
.
17.(1)9
(2)
【分析】本题主要考查了零指数幂,负整数指数幂,积的乘方计算,单项式乘以单项式,熟知相关计算法则是解题的关键.
(1)先计算零指数幂,负整数整数幂和乘方,再计算加减法即可得到答案;
(2)先计算积的乘方,再计算单项式乘以单项式,最后合并同类项即可得到答案.
【详解】(1)解:
;
(2)解:
.
18.(1)袋中总共有个球;
(2)
【分析】要考查了概率公式的应用,熟练掌握概率公式(是总结果数,是事件发生的结果数 )是解题的关键.
(1)根据概率公式,已知白球数量和摸出白球的概率,设总球数为未知数,列方程求解.
(2)先算出红球数量,再算出取走个白球后剩余球总数和剩余红球数,最后用概率公式计算.
【详解】(1)解:设袋中总共有个球
白球有个,摸出白球的概率是,
∴
即,解得
袋中总共有个球
(2)解:由(1)知总球数个,白球个,则红球有个
取走个白球后,剩余球总数为个,红球数量不变仍为个
∴从剩余球中摸出红球的概率
19.(1)见解析
(2)见解析
【分析】本题考查了尺规作图——作一个角的平分线,尺规作图——作线段的垂直平分线,轴对称图形,解题关键是正确作出图形.
(1)利用尺规角平分线;
(2)依据对称点的连线被对称轴垂直平分进行作图即可.
【详解】(1)解:如图,射线即为所求.
(2)如图,直线l即为所求.
20.的长为米.
【分析】本题考查了全等三角形的判定和性质.利用证明,即可求解.
【详解】解:由题意得米,米,米,,
点在同一直线上,
在和中,,
∴,
∴米,
∴米,
答:的长为米.
21.(1)操控无人机的时间t,无人机的飞行高度h
(2)5
(3)25
(4)2,15
(5)第14分钟时无人机的飞行高度是25米
【分析】本题考查用图象表示变量之间的关系,解题的关键是看懂图象中数据,结合路程速度时间进行计算.
(1)根据数量变化关系直接判断即可得到答案;
(2)根据图象直接计算即可得到答案;
(3)根据分钟图象数据求解即可得到答案;
(4)根据(3)中的速度代入行程公式即可得到答案;
(5)根据行程公式求出下降路程,进而即可得到答案.
【详解】(1)解:由题意可得,
∵无人机高度随时间变化而变化,
∴自变量是操控无人机的时间(或t),因变量是无人机的飞行高度(或h),
故答案为:操控无人机的时间t,无人机的飞行高度h;
(2)解:由图象可得,
分钟无人机在米高的上空停留,
∴无人机在米高的上空停留的时间是:分钟,
故答案为:5;
(3)解:由分钟图象可得,
无人机的速度为:(米/分钟),
故答案为:;
(4)解:由(3)可得,
,,
解得:,,
故答案为:2,;
(5)解:由(3)可得,
,
∴第分钟时无人机的飞行高度是:(米),
答:第分钟时无人机的飞行高度是米.
22.(1)
(2)
(3)3
【分析】本题考查了完全平方公式的几何背景,利用完全平方公式变形后求解,熟练掌握完全平方公式并灵活运用是解题的关键.
(1)设,,先求得,再根据求得,再用,表示出,借助完全平方公式求解即可;
(2)设,,先求出,再根据,得到,利用完全平方公式求出即可;
(3)设,,先根据,,求得,,从而可求得,再求得图中阴影部分的面积.
【详解】(1)设,,
∴,
∵,
∴,
∴
,
∴的值为;
(2)设,,
∴,
∵,
∴,
∵,
∴,
∴,
∴;
(3)设,,则,,,
∵,,
∴,,
∴,
∴.
即阴影部分的面积为3.
23.(1) ;;(2);(3)或
【分析】本题考查了全等三角形的判定与性质,等腰三角形的性质,熟练掌握分类讨论的思想是解答本题的关键.
(1)根据,得到,结合,得到,,从而得到,即可得到,即可得到答案;
同理证明即可得到答案;
(2)作,交于点,证明即可得到答案;
(3)分,两种情况讨论,根据等腰直角三角形结合(1)的结论求解即可得到答案.
【详解】解:(1) ,,
,
,
,,
,
在和中,
,
,
,,
,
故答案为:;
,,
,
,
,,
,
在和中,
,
,
,,
,,
,
故答案为:;
(2)在中,,,,如图,作,交于点,
,,,
,
在和中,
,
,
,
;
(3)以为直角边向右侧作一个等腰直角三角形,,如图,作高线,过点作于,
,,,
,,
由(1)得:,
,
;
以为直角边向右侧作一个等腰直角三角形,,如图,作高线,过点作于,
,,,
,,
由(1)得:,
,
;
综上所述,的面积为或.
同课章节目录
