人教版数学七下课件5.2 平行线及其判定(共20张PPT)
文档属性
| 名称 | 人教版数学七下课件5.2 平行线及其判定(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 537.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-28 10:59:49 | ||
图片预览



文档简介
课件20张PPT。5.2 平行线及其判定
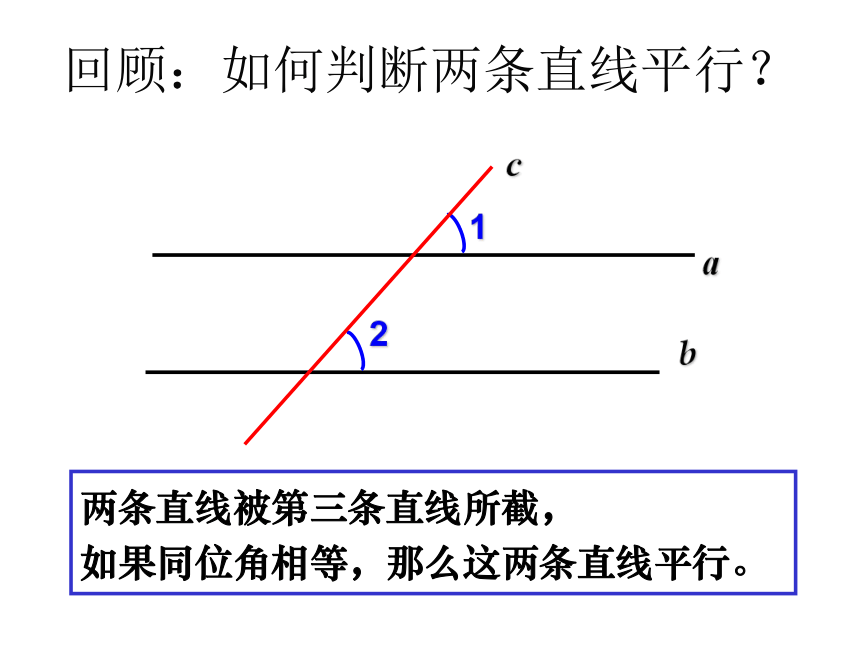
人教版七年级下册回顾:如何判断两条直线平行?两条直线被第三条直线所截,
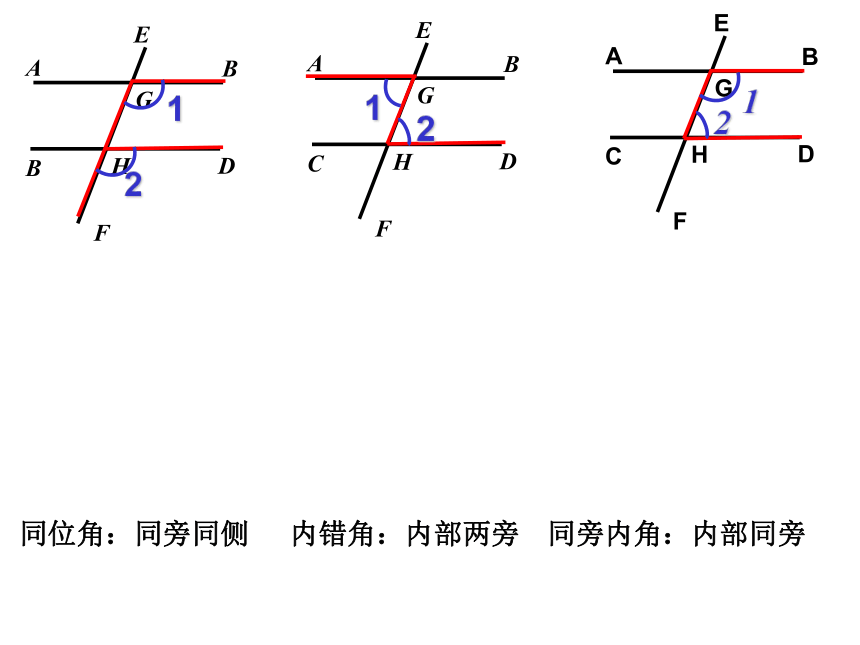
如果同位角相等,那么这两条直线平行。同位角:同旁同侧内错角:内部两旁同旁内角:内部同旁BD21E已知∠1= ∠2,
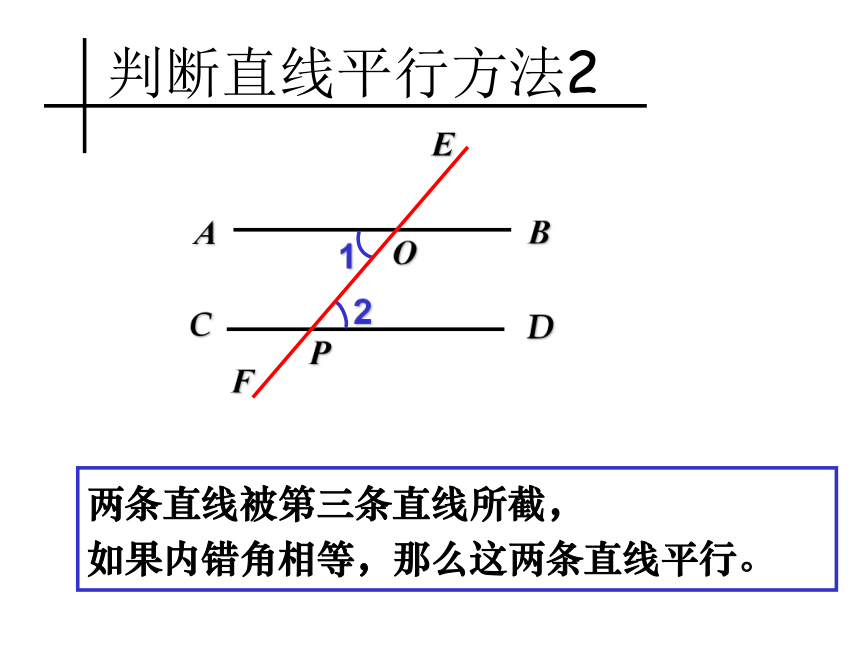
你能得出AB ∥CD吗?ACFOP因为 ∠1=∠2所以 ∠2=∠3 ∠1=∠3(对顶角相等)(等量代换)从而AB∥CD. (同位角相等,两直线平行)∠1和∠2是内错角 思考1答: AB ∥CD,理由如下:BD21E判断直线平行方法2ACFOP两条直线被第三条直线所截,
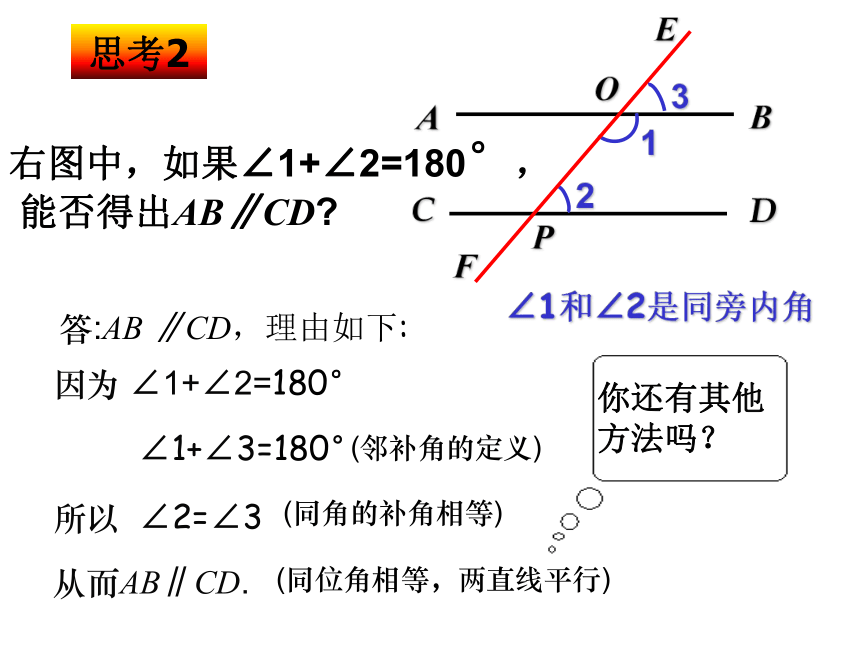
如果内错角相等,那么这两条直线平行。右图中,如果∠1+∠2=180°,
能否得出AB∥CD?思考2BD21EACFOP∠1和∠2是同旁内角 因为 ∠1+∠2=180°所以 ∠2=∠3 ∠1+∠3=180°(邻补角的定义)(同角的补角相等)从而AB∥CD. (同位角相等,两直线平行)你还有其他
方法吗?答:AB ∥CD,理由如下:右图中,如果∠1+∠2=180°,
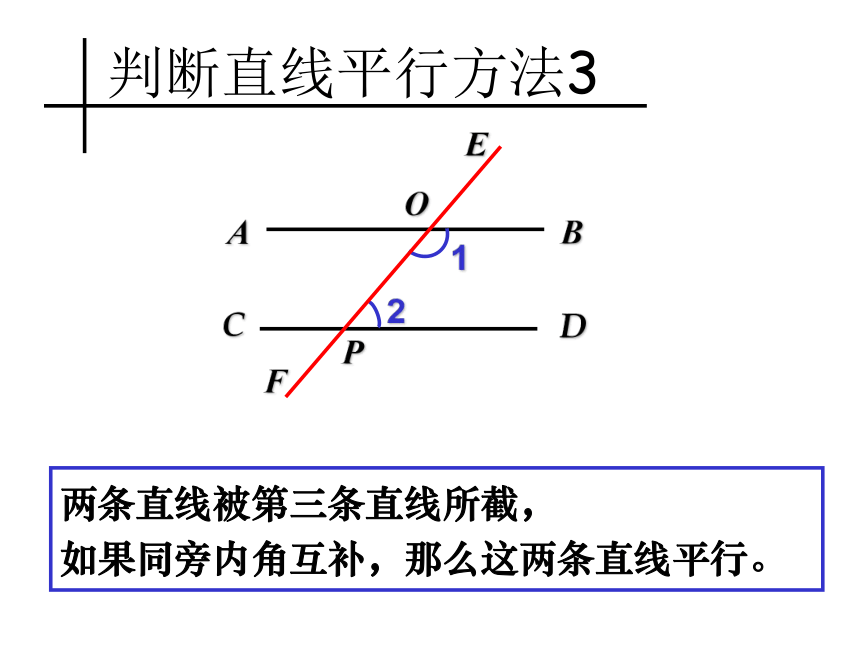
能得出AB∥CD吗?BD21EACFOP∠1和∠2是同旁内角 因为 ∠1+∠2=180°所以 ∠2=∠3 ∠1+∠3=180°(邻补角的定义)(同角的补角相等)从而AB∥CD. (内错角相等,两直线平行)理由:判断直线平行方法3两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行。BD21EACFOP
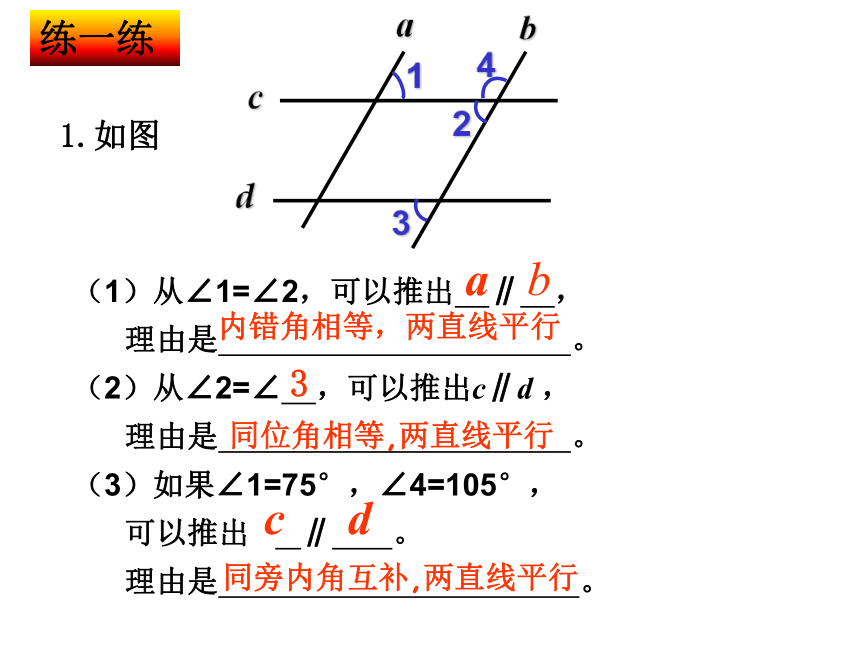
(1)从∠1=∠2,可以推出 ∥ ,
理由是 。
(2)从∠2=∠ ,可以推出c∥d ,
理由是 。
(3)如果∠1=75°,∠4=105°,
可以推出 ∥ 。
理由是 。练一练ba内错角相等,两直线平行同位角相等,两直线平行3cd42cd31ab同旁内角互补,两直线平行1.如图从∠1=∠4,可以推出 ∥ ,
理由是 。(3)从∠ABC +∠ =180,可以推出AB∥CD ,
理由是 。(2)从∠ =∠ ,可以推出AD∥BC,
理由是 。(4)从∠5=∠ ,可以推出AB∥CD,
理由是 。练一练AB内错角相等,两直线平行CDBCD同旁内角互补,两直线平行23内错角相等,两直线平行ABC同位角相等,两直线平行2.如图3.两条直线垂直于同一条直线,这两条
直线平行吗?为什么?答:垂直于同一条直线的两条直线平行.练一练因为 b⊥a所以 ∠2=90° (垂直的定义)从而b∥c. (同位角相等,两直线平行)所以 ∠1=90° (垂直的定义)因为 c ⊥a所以 ∠1=∠2(等量代换)解法1:理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)abc12解法2:理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)abc12解法3:结论如果两条直线都垂直于同一条直线,
那么这两条直线平行。bca有一块木板,身边只有直尺和量角器,我们怎样才能知道它上下边缘是否平行?试一试12方案1:45° 45° 45°1245°方案2:135° 45°方案3:收获通过这节课的学习,
你有哪些收获?议一议1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.如果两条直线都与第三条直线垂直,
那么这两条直线也互相平行.判定两条直线是否平行的方法有:小结
人教版七年级下册回顾:如何判断两条直线平行?两条直线被第三条直线所截,
如果同位角相等,那么这两条直线平行。同位角:同旁同侧内错角:内部两旁同旁内角:内部同旁BD21E已知∠1= ∠2,
你能得出AB ∥CD吗?ACFOP因为 ∠1=∠2所以 ∠2=∠3 ∠1=∠3(对顶角相等)(等量代换)从而AB∥CD. (同位角相等,两直线平行)∠1和∠2是内错角 思考1答: AB ∥CD,理由如下:BD21E判断直线平行方法2ACFOP两条直线被第三条直线所截,
如果内错角相等,那么这两条直线平行。右图中,如果∠1+∠2=180°,
能否得出AB∥CD?思考2BD21EACFOP∠1和∠2是同旁内角 因为 ∠1+∠2=180°所以 ∠2=∠3 ∠1+∠3=180°(邻补角的定义)(同角的补角相等)从而AB∥CD. (同位角相等,两直线平行)你还有其他
方法吗?答:AB ∥CD,理由如下:右图中,如果∠1+∠2=180°,
能得出AB∥CD吗?BD21EACFOP∠1和∠2是同旁内角 因为 ∠1+∠2=180°所以 ∠2=∠3 ∠1+∠3=180°(邻补角的定义)(同角的补角相等)从而AB∥CD. (内错角相等,两直线平行)理由:判断直线平行方法3两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行。BD21EACFOP
(1)从∠1=∠2,可以推出 ∥ ,
理由是 。
(2)从∠2=∠ ,可以推出c∥d ,
理由是 。
(3)如果∠1=75°,∠4=105°,
可以推出 ∥ 。
理由是 。练一练ba内错角相等,两直线平行同位角相等,两直线平行3cd42cd31ab同旁内角互补,两直线平行1.如图从∠1=∠4,可以推出 ∥ ,
理由是 。(3)从∠ABC +∠ =180,可以推出AB∥CD ,
理由是 。(2)从∠ =∠ ,可以推出AD∥BC,
理由是 。(4)从∠5=∠ ,可以推出AB∥CD,
理由是 。练一练AB内错角相等,两直线平行CDBCD同旁内角互补,两直线平行23内错角相等,两直线平行ABC同位角相等,两直线平行2.如图3.两条直线垂直于同一条直线,这两条
直线平行吗?为什么?答:垂直于同一条直线的两条直线平行.练一练因为 b⊥a所以 ∠2=90° (垂直的定义)从而b∥c. (同位角相等,两直线平行)所以 ∠1=90° (垂直的定义)因为 c ⊥a所以 ∠1=∠2(等量代换)解法1:理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)abc12解法2:理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)abc12解法3:结论如果两条直线都垂直于同一条直线,
那么这两条直线平行。bca有一块木板,身边只有直尺和量角器,我们怎样才能知道它上下边缘是否平行?试一试12方案1:45° 45° 45°1245°方案2:135° 45°方案3:收获通过这节课的学习,
你有哪些收获?议一议1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.如果两条直线都与第三条直线垂直,
那么这两条直线也互相平行.判定两条直线是否平行的方法有:小结
