11.1 不等式(第3课时)课件(共23张PPT)人教版数学七年级下册
文档属性
| 名称 | 11.1 不等式(第3课时)课件(共23张PPT)人教版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 10:43:28 | ||
图片预览








文档简介
(共23张PPT)
11.1 不等式(第3课时)
数学人教版(204)七年级下册
不等式有哪些性质?你能分别用文字语言和符号语言表示吗?
不等式的性质 1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
符号语言:如果 a>b,那么 a±c>b±c.
不等式的性质 2:不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质 3:不等式两边乘(或除以)同一个负数,不等号的方向改变.
符号语言:如果 a>b,c>0,那么 ac>bc ;
符号语言:如果 a>b,c<0,那么 ac<bc .
利用不等式的性质解下列不等式,并在数轴上表示解集:
(1)x-7>26; (2)3x<2x+1;
(3) x>50; (4)-4x>3.
问题
分析:解不等式,就是要借助不等式的性质使不等式逐步化为 x>m或 x< m ( m 为常数)的形式.
解:(1)根据不等式的性质 1,不等式两边加 7,不等号的方向不变,所以
(1)x-7>26;
x-7+7>26+7,
x>33.
0
33
这个不等式的解集在数轴上的表示如图所示.
解:(2)根据不等式的性质 1,不等式两边减 2x,不等号的方向不变,所以
(2)3x<2x+1;
3x-2x<2x+1-2x,
x<1.
0
1
这个不等式的解集在数轴上的表示如图所示.
(3) x>50;
x>75.
解:(3)根据不等式的性质 2,不等式两边乘 ,不等号的方向不变,所以
× x> ×50,
0
75
这个不等式的解集在数轴上的表示如图所示.
0
,
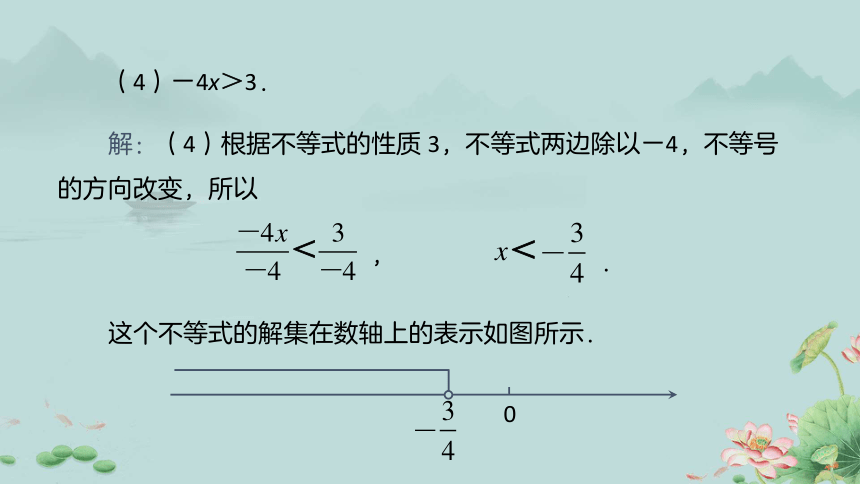
解:(4)根据不等式的性质 3,不等式两边除以-4,不等号的方向改变,所以
(4)-4x>3.
这个不等式的解集在数轴上的表示如图所示.
.
利用不等式的性质 1 可简化为“移项”;利用不等式的性质 2 或性质 3 就是把未知数的系数化为 1,要注意不等式两边乘(或除以)同一个负数时,不等号要改变方向,常数项的符号也要改变.
总结
问题
(1)一辆轿车在一条规定车速不低于 60 km/h,且不高于 100 km/h的高速公路上行驶,如何用式子来表示轿车在该高速公路上行驶的路程 s(单位:km)与行驶时间 x(单位:h)之间的关系呢?
根据路程与速度、时间之间的关系可得:s≥60x,且 s≤100x.
问题
(2)铁路部门对随身携带的行李有如下规定:每件行李的长、宽、高之和不得超过 160 cm.设行李的长、宽、高分别为 a cm,b cm,c cm,请你列出行李的长、宽、高满足的关系式.
根据题意可得:a+b+c≤160,且 a+b+c>0.
新知
观察式子:s≥60x,s≤100x,a+b+c≤160.它们有什么共同特点?
像 a≥b 或 a≤b 这样的式子,也经常用来表示两个数量的大小关系,它们也是不等式.
符号“≥”读作“大于或等于”,也可以说是“不小于”;符号“≤”读作“小于或等于”,也可以说是“不大于”.
思考
符号“≥”与“>”的含义有什么区别?“≤”与“<”呢?
x≥a 表示 x>a 或者 x=a;x≤a 表示 x<a 或者 x=a.“≥”和“≤”分别比“>”和“<”多了一层等于的含义.
a≥b 或 a≤b 形式的不等式,具有与前面所说的不等式的性质类似的性质.
如果 a≥b,那么
(2)ac≥bc(c>0);
(3)ac≤bc(c<0).
(1)a+c≥b+c,a-c≥b-c;
总结
思考
如何在数轴上表示 x<-1与 x≥3?
-2
-1
0
1
2
3
4
5
6
在数轴上表示不等式的解集时,无等号的画空心圆圈,有等号的画实心圆点.
在应用数轴表示不等式的解集时,要注意两个“确定”:一是确定“边界点”,二是确定“方向”.
(1)确定“边界点”:若边界点是不等式的解,则用实心圆点;若边界点不是不等式的解,则用空心圆圈.
(2)确定“方向”:对表示数 m 的边界点而言,x>m 或 x≥m 向右画,x<m 或 x≤m 向左画.
总结
问题
如图,一个长方体形状的鱼缸长 10 dm,宽 3.5 dm,高 7 dm.若鱼缸内已有水的高度为 1 dm,现准备向鱼缸内继续注水.用 V(单位:dm3)表示新注入水的体积,写出 V 的取值范围并在数轴上表示.
解:因为“已有水的体积+新注入水的体积V≤鱼缸的容积”,所以
10×3.5×1+V≤10×3.5×7,
解得 V≤210.
又由于新注入水的体积V 不能是负数,所以V 的取值范围是
0 ≤V≤210.
在数轴上表示 V 的取值范围如图所示.
在表示 0 和 210的点上画实心圆点,表示取值范围包含这两个点所对应的数.
0
210
例1 用不等式的性质解下列不等式,并在数轴上表示解集:
(1)x+5≥12; (2)-3x≤1-4x.
解:(1)根据不等式的性质 1,不等式两边减 5,不等号的方向不变,所以
x+5-5≥12-5,
x≥7.
0
7
这个不等式的解集在数轴上的表示如图所示.
例1 用不等式的性质解下列不等式,并在数轴上表示解集:
(1)x+5≥12; (2)-3x≤1-4x.
解:(2)根据不等式的性质 1,不等式两边加 4x,不等号的方向不变,所以
-3x+4x≤1-4x+4x ,
x≤1.
0
1
这个不等式的解集在数轴上的表示如图所示.
(1)在运用不等式的性质将不等式变形时,首先要注意每一步变形的依据,然后由不等式的性质判断不等号的方向是否改变.
(2)在数轴上表示不等式的解集,定边界点时,要注意是实心圆点还是空心圆圈.
总结
例2 某品牌服装 2022 年 1 月份的售价是每件 a 元,3 月份的售价上涨 10%,6 月份又比 3 月份下降 10%.
(1)用含有 a 的式子分别表示该品牌服装 3 月份和 6 月份的售价;
(2)几月份去购买该品牌服装最便宜?为什么?
解:(1)该品牌服装 3 月份的售价为每件(1+10%)a=1.1a(元),
6 月份的售价为每件(1-10%)×1.1a=0.99a(元);
(2)6 月份去购买该品牌服装最便宜.
因为 0.99<1<1.1,且 a>0,所以 0.99a<a<1.1a.
所以 6 月份去购买该品牌服装最便宜.
不等式在实际问题中的简单应用
利用不等式的性质解不等式
含“≤”“≥”的不等式
不等式的性质的应用
11.1 不等式(第3课时)
数学人教版(204)七年级下册
不等式有哪些性质?你能分别用文字语言和符号语言表示吗?
不等式的性质 1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
符号语言:如果 a>b,那么 a±c>b±c.
不等式的性质 2:不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质 3:不等式两边乘(或除以)同一个负数,不等号的方向改变.
符号语言:如果 a>b,c>0,那么 ac>bc ;
符号语言:如果 a>b,c<0,那么 ac<bc .
利用不等式的性质解下列不等式,并在数轴上表示解集:
(1)x-7>26; (2)3x<2x+1;
(3) x>50; (4)-4x>3.
问题
分析:解不等式,就是要借助不等式的性质使不等式逐步化为 x>m或 x< m ( m 为常数)的形式.
解:(1)根据不等式的性质 1,不等式两边加 7,不等号的方向不变,所以
(1)x-7>26;
x-7+7>26+7,
x>33.
0
33
这个不等式的解集在数轴上的表示如图所示.
解:(2)根据不等式的性质 1,不等式两边减 2x,不等号的方向不变,所以
(2)3x<2x+1;
3x-2x<2x+1-2x,
x<1.
0
1
这个不等式的解集在数轴上的表示如图所示.
(3) x>50;
x>75.
解:(3)根据不等式的性质 2,不等式两边乘 ,不等号的方向不变,所以
× x> ×50,
0
75
这个不等式的解集在数轴上的表示如图所示.
0
,
解:(4)根据不等式的性质 3,不等式两边除以-4,不等号的方向改变,所以
(4)-4x>3.
这个不等式的解集在数轴上的表示如图所示.
.
利用不等式的性质 1 可简化为“移项”;利用不等式的性质 2 或性质 3 就是把未知数的系数化为 1,要注意不等式两边乘(或除以)同一个负数时,不等号要改变方向,常数项的符号也要改变.
总结
问题
(1)一辆轿车在一条规定车速不低于 60 km/h,且不高于 100 km/h的高速公路上行驶,如何用式子来表示轿车在该高速公路上行驶的路程 s(单位:km)与行驶时间 x(单位:h)之间的关系呢?
根据路程与速度、时间之间的关系可得:s≥60x,且 s≤100x.
问题
(2)铁路部门对随身携带的行李有如下规定:每件行李的长、宽、高之和不得超过 160 cm.设行李的长、宽、高分别为 a cm,b cm,c cm,请你列出行李的长、宽、高满足的关系式.
根据题意可得:a+b+c≤160,且 a+b+c>0.
新知
观察式子:s≥60x,s≤100x,a+b+c≤160.它们有什么共同特点?
像 a≥b 或 a≤b 这样的式子,也经常用来表示两个数量的大小关系,它们也是不等式.
符号“≥”读作“大于或等于”,也可以说是“不小于”;符号“≤”读作“小于或等于”,也可以说是“不大于”.
思考
符号“≥”与“>”的含义有什么区别?“≤”与“<”呢?
x≥a 表示 x>a 或者 x=a;x≤a 表示 x<a 或者 x=a.“≥”和“≤”分别比“>”和“<”多了一层等于的含义.
a≥b 或 a≤b 形式的不等式,具有与前面所说的不等式的性质类似的性质.
如果 a≥b,那么
(2)ac≥bc(c>0);
(3)ac≤bc(c<0).
(1)a+c≥b+c,a-c≥b-c;
总结
思考
如何在数轴上表示 x<-1与 x≥3?
-2
-1
0
1
2
3
4
5
6
在数轴上表示不等式的解集时,无等号的画空心圆圈,有等号的画实心圆点.
在应用数轴表示不等式的解集时,要注意两个“确定”:一是确定“边界点”,二是确定“方向”.
(1)确定“边界点”:若边界点是不等式的解,则用实心圆点;若边界点不是不等式的解,则用空心圆圈.
(2)确定“方向”:对表示数 m 的边界点而言,x>m 或 x≥m 向右画,x<m 或 x≤m 向左画.
总结
问题
如图,一个长方体形状的鱼缸长 10 dm,宽 3.5 dm,高 7 dm.若鱼缸内已有水的高度为 1 dm,现准备向鱼缸内继续注水.用 V(单位:dm3)表示新注入水的体积,写出 V 的取值范围并在数轴上表示.
解:因为“已有水的体积+新注入水的体积V≤鱼缸的容积”,所以
10×3.5×1+V≤10×3.5×7,
解得 V≤210.
又由于新注入水的体积V 不能是负数,所以V 的取值范围是
0 ≤V≤210.
在数轴上表示 V 的取值范围如图所示.
在表示 0 和 210的点上画实心圆点,表示取值范围包含这两个点所对应的数.
0
210
例1 用不等式的性质解下列不等式,并在数轴上表示解集:
(1)x+5≥12; (2)-3x≤1-4x.
解:(1)根据不等式的性质 1,不等式两边减 5,不等号的方向不变,所以
x+5-5≥12-5,
x≥7.
0
7
这个不等式的解集在数轴上的表示如图所示.
例1 用不等式的性质解下列不等式,并在数轴上表示解集:
(1)x+5≥12; (2)-3x≤1-4x.
解:(2)根据不等式的性质 1,不等式两边加 4x,不等号的方向不变,所以
-3x+4x≤1-4x+4x ,
x≤1.
0
1
这个不等式的解集在数轴上的表示如图所示.
(1)在运用不等式的性质将不等式变形时,首先要注意每一步变形的依据,然后由不等式的性质判断不等号的方向是否改变.
(2)在数轴上表示不等式的解集,定边界点时,要注意是实心圆点还是空心圆圈.
总结
例2 某品牌服装 2022 年 1 月份的售价是每件 a 元,3 月份的售价上涨 10%,6 月份又比 3 月份下降 10%.
(1)用含有 a 的式子分别表示该品牌服装 3 月份和 6 月份的售价;
(2)几月份去购买该品牌服装最便宜?为什么?
解:(1)该品牌服装 3 月份的售价为每件(1+10%)a=1.1a(元),
6 月份的售价为每件(1-10%)×1.1a=0.99a(元);
(2)6 月份去购买该品牌服装最便宜.
因为 0.99<1<1.1,且 a>0,所以 0.99a<a<1.1a.
所以 6 月份去购买该品牌服装最便宜.
不等式在实际问题中的简单应用
利用不等式的性质解不等式
含“≤”“≥”的不等式
不等式的性质的应用
同课章节目录
