2025年山东省东营市中考数学真题试卷(含答案)
文档属性
| 名称 | 2025年山东省东营市中考数学真题试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 14:26:32 | ||
图片预览


文档简介
2025年山东省东营市中考数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.2025的相反数是( ).
A.2025 B.-2025 C. D.
2.下列计算正确的是( ).
A. B.
C. D.
3.下图为乒乓球男团颁奖现场,领奖台的示意图如下,则此领奖台的左视图是( ).
A. B.
C. D.
4.一次函数的函数值y随x的增大而减小,当时y的值可以是( ).
A.3 B.2 C.1 D.
5.2025年是乙巳蛇年,“巳巳如意”将蛇年与如意相结合,表达对新一年事事如意、顺遂美好的期盼.将分别印有“巳”、“巳”、“如”、“意”的四张质地均匀、大小相同的卡片放入盒中,从中随机抽取一张,则抽取到的卡片上印有汉字“巳”的概率为( ).
A. B. C. D.
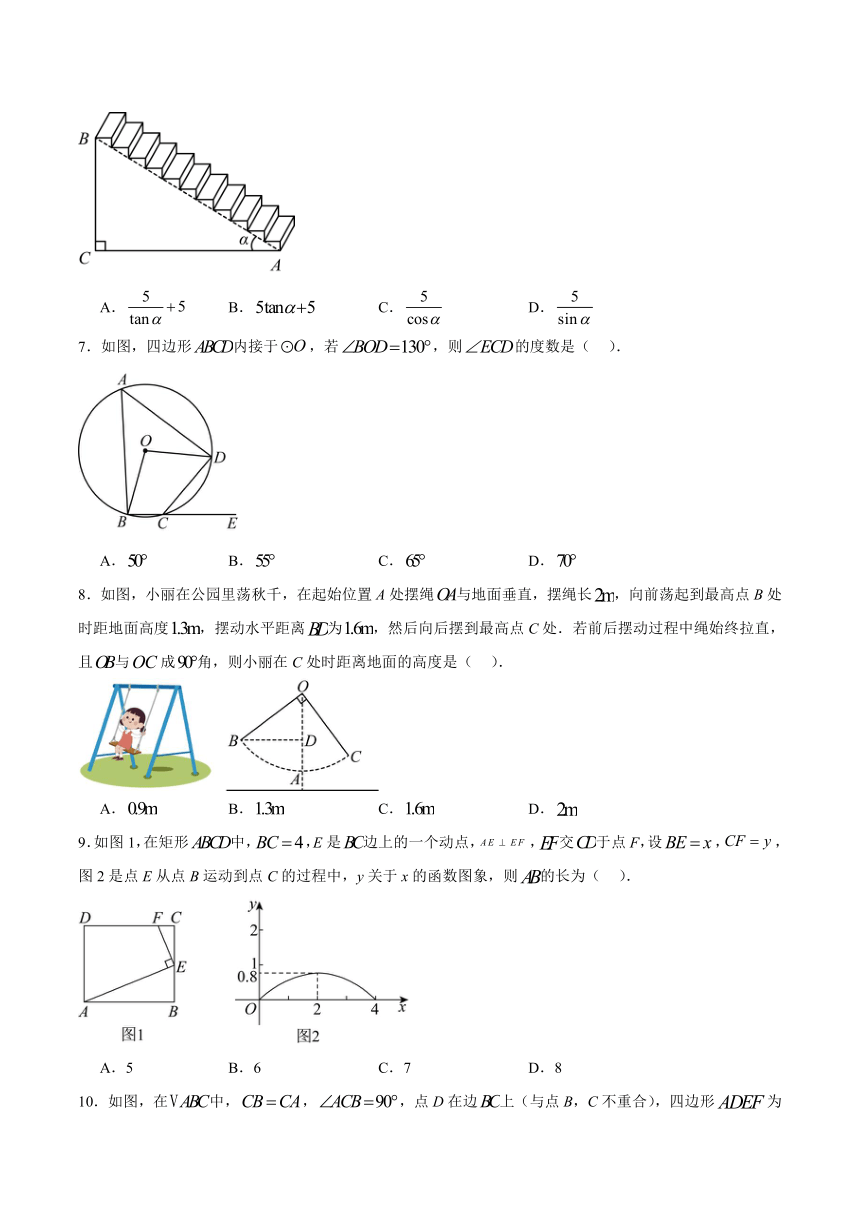
6.如图为一节楼梯的示意图,,,米.现要在楼梯上铺一块地毯,楼梯宽度为1米,则地毯的长度需要( )米.
A. B. C. D.
7.如图,四边形内接于,若,则的度数是( ).
A. B. C. D.
8.如图,小丽在公园里荡秋千,在起始位置A处摆绳与地面垂直,摆绳长,向前荡起到最高点B处时距地面高度,摆动水平距离为,然后向后摆到最高点C处.若前后摆动过程中绳始终拉直,且与成角,则小丽在C处时距离地面的高度是( ).
A. B. C. D.
9.如图1,在矩形中,,E是边上的一个动点,,交于点F,设,,图2是点E从点B运动到点C的过程中,y关于x的函数图象,则的长为( ).
A.5 B.6 C.7 D.8
10.如图,在中,,,点D在边上(与点B,C不重合),四边形为正方形,过点F作,交的延长线于点G,连接,交于点Q.下列结论:①;②;③;④.其中结论正确的序号是( ).
A.①②④ B.①②③ C.①②③④ D.②③④
二、填空题
11.2024年国家统计局发布的一份报告中宣布,中国已成为世界上第一个拥有完整高铁网络并且运行的国家,中国高铁里程达到4.6万公里,居世界首位,将4.6万用科学记数法表示为 .
12.分解因式: .
13.电影《哪吒之魔童闹海》上映七天票房破45亿元,前七日综合票房分别是:4.9 4.8 6.2 7.3 8.1 8.4 8.6(亿元),那么这组数据的中位数是 亿元.
14.若关于的方程无实根,则的取值范围是 .
15.如图,在中,,,点D为中点,点E在上,当为 时,与以点A、D、E为顶点的三角形相似.
16.《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积(弦矢+矢),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为2,则的值为 .
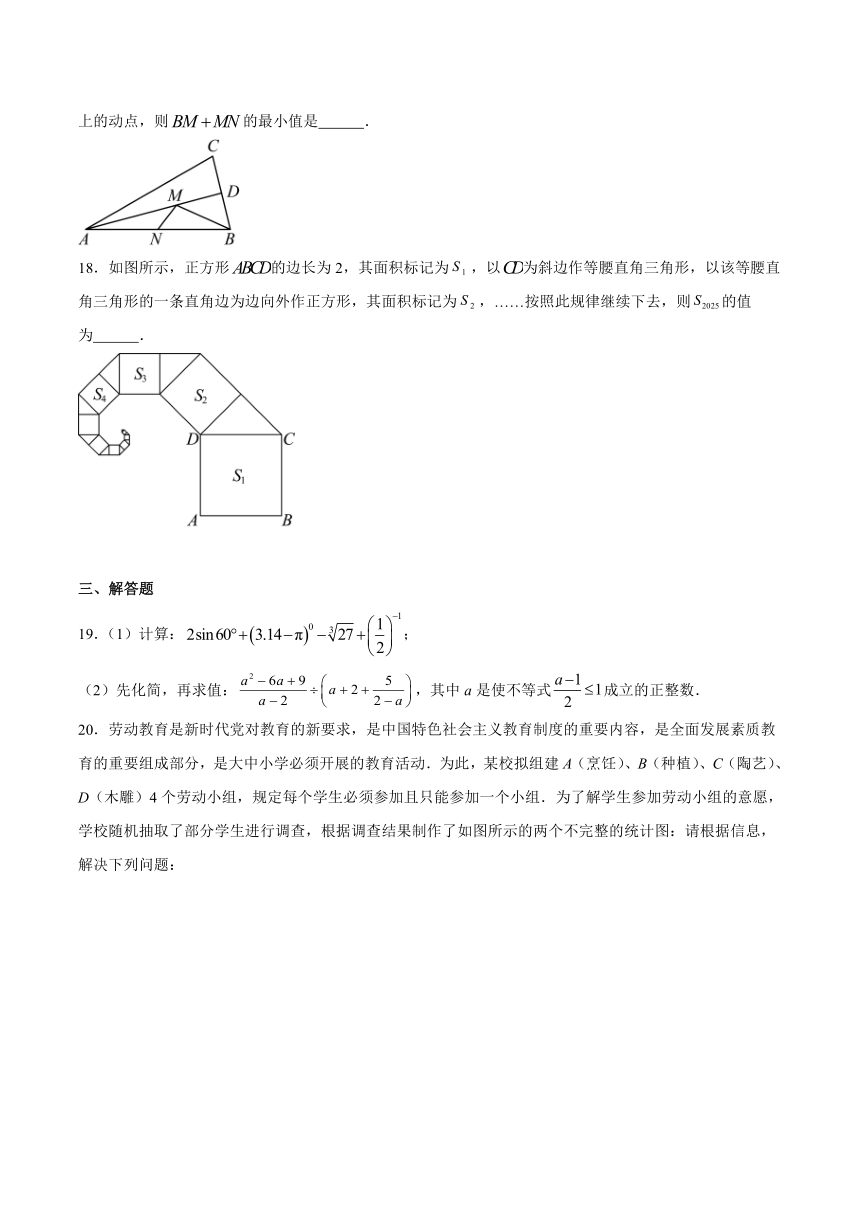
17.如图,在中,,,的平分线交于点,、分别是和上的动点,则的最小值是 .
18.如图所示,正方形的边长为2,其面积标记为,以为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为,……按照此规律继续下去,则的值为 .
三、解答题
19.(1)计算:;
(2)先化简,再求值:,其中a是使不等式成立的正整数.
20.劳动教育是新时代党对教育的新要求,是中国特色社会主义教育制度的重要内容,是全面发展素质教育的重要组成部分,是大中小学必须开展的教育活动.为此,某校拟组建A(烹饪)、B(种植)、C(陶艺)、D(木雕)4个劳动小组,规定每个学生必须参加且只能参加一个小组.为了解学生参加劳动小组的意愿,学校随机抽取了部分学生进行调查,根据调查结果制作了如图所示的两个不完整的统计图:请根据信息,解决下列问题:
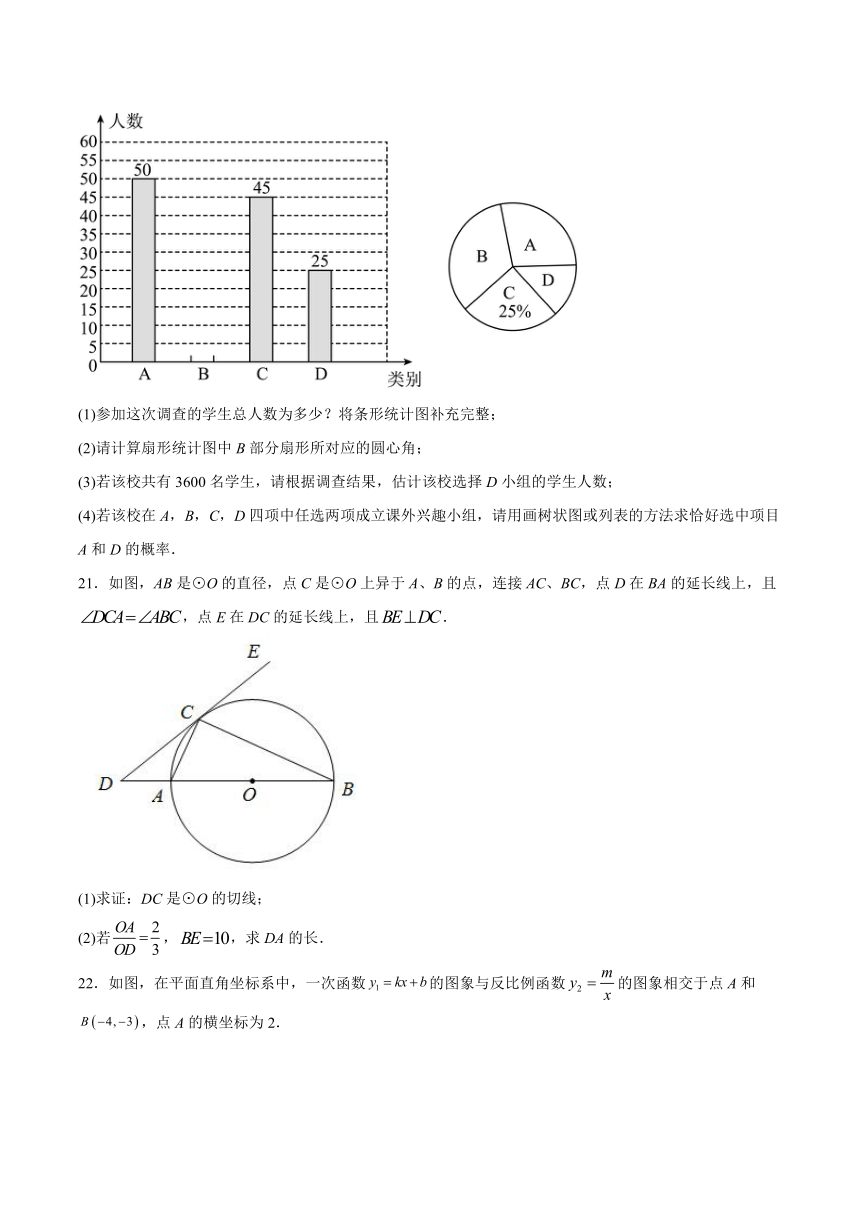
(1)参加这次调查的学生总人数为多少?将条形统计图补充完整;
(2)请计算扇形统计图中B部分扇形所对应的圆心角;
(3)若该校共有3600名学生,请根据调查结果,估计该校选择D小组的学生人数;
(4)若该校在A,B,C,D四项中任选两项成立课外兴趣小组,请用画树状图或列表的方法求恰好选中项目A和D的概率.
21.如图,AB是⊙O的直径,点C是⊙O上异于A、B的点,连接AC、BC,点D在BA的延长线上,且,点E在DC的延长线上,且.
(1)求证:DC是⊙O的切线;
(2)若,,求DA的长.
22.如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于点A和,点A的横坐标为2.
(1)求反比例函数和一次函数的解析式;
(2)观察图象,直接写出当时x的取值范围;
(3)点C为x轴上一动点,连接,若的面积为18,求点C的坐标.
23.《哪吒2魔童闹海》票房大卖,周边玩偶热销.某经销店购进A款哪吒玩偶的金额是2400元,购进B款哪吒玩偶的金额是1600元,购进A款哪吒玩偶的数量比B款哪吒玩偶少50个,A款哪吒玩偶单价是B款哪吒玩偶的2倍.
(1)A、B两款玩偶的单价分别是多少元?
(2)为满足消费者需求,在A、B两款玩偶单价不变的条件下,该超市准备再次购进A、B两款玩偶共100个,B款哪吒玩偶的数量不多于A款哪吒玩偶数量的2倍,且总金额不超过1100元,问有多少种进货方案?
24.【问题情境】在数学综合实践课上,同学们以四边形为背景,探究非动点的几何问题.若四边形是正方形,M,N分别在边上,且,我们称之为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.
(1)【初步尝试】如图1,将绕点A顺时针旋转,点D与点B重合,得到,连接.用等式写出线段的数量关系______.
(2)【类比探究】小明改变点的位置后,进一步探究:如图2,点M,N分别在正方形的边的延长线上,,连接,用等式写出线段的数量关系,并说明理由;
(3)【拓展延伸】其他小组提出新的探究方向:如图3,在四边形中,,,,点N,M分别在边上,,用等式写出线段的数量关系,并说明理由.
25.已知抛物线与x轴交于,两点,与y轴交于点.
(1)求出抛物线的解析式;
(2)如图1,点D是抛物线上位于对称轴右侧的一个动点,且点D在第一象限内,过点D作x轴的平行线交抛物线于点E,作y轴的平行线交x轴于点G,过点E作轴,垂足为点F,当四边形的周长最大时,求点D的坐标;
(3)如图2,点M是抛物线的顶点,将沿翻折得到,与y轴交于点Q,在对称轴上找一点P,使得是以为直角边的直角三角形,请直接写出点P的坐标.
《2025年山东省东营市中考数学试题》参考答案
1.B
2.D
3.C
4.A
5.D
6.B
7.C
8.A
9.A
10.C
11.
12.
13.7.3
14./
15.3或
16./
17.3
18.
19.(1)原式
;
(2)
,
是使不等式成立的正整数,
且为正整数,
,2,3,
又,,
,3,,
,
当时,原式.
20.(1)解:调查总人数为:(人);
选择B人数为:(人);
答:参加调查的总人数为180人,
补全条形图如下,
(2)解:,
答:B部分扇形所对应的圆心角为;
(3)解:(人),
答:若该校共有3600名学生估计选择D小组的学生人数为500人.
(4)由题意,列表如下:
, , ,
, , ,
, , ,
, , ,
共12种等可能的结果,其中,恰好选中项目A和D的结果有2种,
∴.
21.(1)证明:如图,连接,
,
,
是的直径,
,
,
,
,即,
,
又是的半径,
是的切线.
(2)解:∵,
设,则,
∴,,
∵,,
∴,
∴,
∴,即,
解得,
∴.
22.(1)解:一次函数的图象与反比例函数的图象相交于点A和,点A的横坐标为2
∴将代入,
则,
∴反比例函数解析式为:,
∴将代入,
则,
∴,
将,代入,
则,
解得:
∴一次函数解析式为:;
(2)解:∵,
∴观察图象,当时,的取值范围是或;
(3)解:设与轴交于点,
当时,
∴
∴,
设,
∴
∵的面积为18,
∴
∴,
∴,即
解得:或
∴点C坐标为或.
23.解:设B款玩偶的单价是元,由题意,得:
,
解得:,
经检验,是原方程的解,且符合题意;
∴;
答:A、B两款玩偶的单价分别是16元和8元;
(2)设购进款玩偶个,则购进款玩偶个,由题意,得:
,
解得:,
∵为整数,
∴,
∴,
故共有4种方案.
24.(1)解:.理由如下:
由旋转的性质,可知,,,,
∴,
∴E,B,C三线共线.
∵,
∴.
在和中, ,
∴,
∴.
∵,
∴.
(2)解:.理由如下:
如图,在上取,连接.
∵,,
∴,
∴.
∵,
∴,
∴.
在和中, ,
∴,
∴.
∵,
∴.
(3)解:.理由如下:
如图,将绕点A逆时针旋转得,
∴.
∵,
∴,
∴E,D,C三点共线.
由(1)同理可得,
∴.
25.(1)解:∵抛物线与x轴交于,两点,
设抛物线的解析式为,
把代入解析式,得,
解得:,
∴抛物线的解析式为:,即;
(2)解:∵抛物线的解析式为:,
∴抛物线图象的对称轴为:,
设,
∵轴,
∴,
∵过点D作x轴的平行线交抛物线于点E,作y轴的平行线交x轴于点G,过点E作轴,
∴四边形是矩形,
∴四边形的周长
,
∵,
∴当时,四边形的周长最大,则,
∴当四边形的周长最大时,点D的坐标为;
(3)解:过C作垂直抛物线对称轴于H,过N作轴于K,
∴,
由翻折得,
∵.
∴,
∴,
∵对称轴于H,
∴轴,
∴,
∴,
∴,即,
∴,
∴,
∵抛物线的解析式为:,
∴对称轴为,
∴,
∴,
∴,
∴,
设直线的解析式为,
∴,
解得:,
∴直线的解析式为:,
将代入,则,
∴,
设,
∴,,,
分两种情况:
①当时,,
∴,
解得:,
∴;
②当时,,
∴
解得:,
∴点的坐标为;
综上,所有符合条件的点P的坐标为或.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.2025的相反数是( ).
A.2025 B.-2025 C. D.
2.下列计算正确的是( ).
A. B.
C. D.
3.下图为乒乓球男团颁奖现场,领奖台的示意图如下,则此领奖台的左视图是( ).
A. B.
C. D.
4.一次函数的函数值y随x的增大而减小,当时y的值可以是( ).
A.3 B.2 C.1 D.
5.2025年是乙巳蛇年,“巳巳如意”将蛇年与如意相结合,表达对新一年事事如意、顺遂美好的期盼.将分别印有“巳”、“巳”、“如”、“意”的四张质地均匀、大小相同的卡片放入盒中,从中随机抽取一张,则抽取到的卡片上印有汉字“巳”的概率为( ).
A. B. C. D.
6.如图为一节楼梯的示意图,,,米.现要在楼梯上铺一块地毯,楼梯宽度为1米,则地毯的长度需要( )米.
A. B. C. D.
7.如图,四边形内接于,若,则的度数是( ).
A. B. C. D.
8.如图,小丽在公园里荡秋千,在起始位置A处摆绳与地面垂直,摆绳长,向前荡起到最高点B处时距地面高度,摆动水平距离为,然后向后摆到最高点C处.若前后摆动过程中绳始终拉直,且与成角,则小丽在C处时距离地面的高度是( ).
A. B. C. D.
9.如图1,在矩形中,,E是边上的一个动点,,交于点F,设,,图2是点E从点B运动到点C的过程中,y关于x的函数图象,则的长为( ).
A.5 B.6 C.7 D.8
10.如图,在中,,,点D在边上(与点B,C不重合),四边形为正方形,过点F作,交的延长线于点G,连接,交于点Q.下列结论:①;②;③;④.其中结论正确的序号是( ).
A.①②④ B.①②③ C.①②③④ D.②③④
二、填空题
11.2024年国家统计局发布的一份报告中宣布,中国已成为世界上第一个拥有完整高铁网络并且运行的国家,中国高铁里程达到4.6万公里,居世界首位,将4.6万用科学记数法表示为 .
12.分解因式: .
13.电影《哪吒之魔童闹海》上映七天票房破45亿元,前七日综合票房分别是:4.9 4.8 6.2 7.3 8.1 8.4 8.6(亿元),那么这组数据的中位数是 亿元.
14.若关于的方程无实根,则的取值范围是 .
15.如图,在中,,,点D为中点,点E在上,当为 时,与以点A、D、E为顶点的三角形相似.
16.《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积(弦矢+矢),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为2,则的值为 .
17.如图,在中,,,的平分线交于点,、分别是和上的动点,则的最小值是 .
18.如图所示,正方形的边长为2,其面积标记为,以为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为,……按照此规律继续下去,则的值为 .
三、解答题
19.(1)计算:;
(2)先化简,再求值:,其中a是使不等式成立的正整数.
20.劳动教育是新时代党对教育的新要求,是中国特色社会主义教育制度的重要内容,是全面发展素质教育的重要组成部分,是大中小学必须开展的教育活动.为此,某校拟组建A(烹饪)、B(种植)、C(陶艺)、D(木雕)4个劳动小组,规定每个学生必须参加且只能参加一个小组.为了解学生参加劳动小组的意愿,学校随机抽取了部分学生进行调查,根据调查结果制作了如图所示的两个不完整的统计图:请根据信息,解决下列问题:
(1)参加这次调查的学生总人数为多少?将条形统计图补充完整;
(2)请计算扇形统计图中B部分扇形所对应的圆心角;
(3)若该校共有3600名学生,请根据调查结果,估计该校选择D小组的学生人数;
(4)若该校在A,B,C,D四项中任选两项成立课外兴趣小组,请用画树状图或列表的方法求恰好选中项目A和D的概率.
21.如图,AB是⊙O的直径,点C是⊙O上异于A、B的点,连接AC、BC,点D在BA的延长线上,且,点E在DC的延长线上,且.
(1)求证:DC是⊙O的切线;
(2)若,,求DA的长.
22.如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于点A和,点A的横坐标为2.
(1)求反比例函数和一次函数的解析式;
(2)观察图象,直接写出当时x的取值范围;
(3)点C为x轴上一动点,连接,若的面积为18,求点C的坐标.
23.《哪吒2魔童闹海》票房大卖,周边玩偶热销.某经销店购进A款哪吒玩偶的金额是2400元,购进B款哪吒玩偶的金额是1600元,购进A款哪吒玩偶的数量比B款哪吒玩偶少50个,A款哪吒玩偶单价是B款哪吒玩偶的2倍.
(1)A、B两款玩偶的单价分别是多少元?
(2)为满足消费者需求,在A、B两款玩偶单价不变的条件下,该超市准备再次购进A、B两款玩偶共100个,B款哪吒玩偶的数量不多于A款哪吒玩偶数量的2倍,且总金额不超过1100元,问有多少种进货方案?
24.【问题情境】在数学综合实践课上,同学们以四边形为背景,探究非动点的几何问题.若四边形是正方形,M,N分别在边上,且,我们称之为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.
(1)【初步尝试】如图1,将绕点A顺时针旋转,点D与点B重合,得到,连接.用等式写出线段的数量关系______.
(2)【类比探究】小明改变点的位置后,进一步探究:如图2,点M,N分别在正方形的边的延长线上,,连接,用等式写出线段的数量关系,并说明理由;
(3)【拓展延伸】其他小组提出新的探究方向:如图3,在四边形中,,,,点N,M分别在边上,,用等式写出线段的数量关系,并说明理由.
25.已知抛物线与x轴交于,两点,与y轴交于点.
(1)求出抛物线的解析式;
(2)如图1,点D是抛物线上位于对称轴右侧的一个动点,且点D在第一象限内,过点D作x轴的平行线交抛物线于点E,作y轴的平行线交x轴于点G,过点E作轴,垂足为点F,当四边形的周长最大时,求点D的坐标;
(3)如图2,点M是抛物线的顶点,将沿翻折得到,与y轴交于点Q,在对称轴上找一点P,使得是以为直角边的直角三角形,请直接写出点P的坐标.
《2025年山东省东营市中考数学试题》参考答案
1.B
2.D
3.C
4.A
5.D
6.B
7.C
8.A
9.A
10.C
11.
12.
13.7.3
14./
15.3或
16./
17.3
18.
19.(1)原式
;
(2)
,
是使不等式成立的正整数,
且为正整数,
,2,3,
又,,
,3,,
,
当时,原式.
20.(1)解:调查总人数为:(人);
选择B人数为:(人);
答:参加调查的总人数为180人,
补全条形图如下,
(2)解:,
答:B部分扇形所对应的圆心角为;
(3)解:(人),
答:若该校共有3600名学生估计选择D小组的学生人数为500人.
(4)由题意,列表如下:
, , ,
, , ,
, , ,
, , ,
共12种等可能的结果,其中,恰好选中项目A和D的结果有2种,
∴.
21.(1)证明:如图,连接,
,
,
是的直径,
,
,
,
,即,
,
又是的半径,
是的切线.
(2)解:∵,
设,则,
∴,,
∵,,
∴,
∴,
∴,即,
解得,
∴.
22.(1)解:一次函数的图象与反比例函数的图象相交于点A和,点A的横坐标为2
∴将代入,
则,
∴反比例函数解析式为:,
∴将代入,
则,
∴,
将,代入,
则,
解得:
∴一次函数解析式为:;
(2)解:∵,
∴观察图象,当时,的取值范围是或;
(3)解:设与轴交于点,
当时,
∴
∴,
设,
∴
∵的面积为18,
∴
∴,
∴,即
解得:或
∴点C坐标为或.
23.解:设B款玩偶的单价是元,由题意,得:
,
解得:,
经检验,是原方程的解,且符合题意;
∴;
答:A、B两款玩偶的单价分别是16元和8元;
(2)设购进款玩偶个,则购进款玩偶个,由题意,得:
,
解得:,
∵为整数,
∴,
∴,
故共有4种方案.
24.(1)解:.理由如下:
由旋转的性质,可知,,,,
∴,
∴E,B,C三线共线.
∵,
∴.
在和中, ,
∴,
∴.
∵,
∴.
(2)解:.理由如下:
如图,在上取,连接.
∵,,
∴,
∴.
∵,
∴,
∴.
在和中, ,
∴,
∴.
∵,
∴.
(3)解:.理由如下:
如图,将绕点A逆时针旋转得,
∴.
∵,
∴,
∴E,D,C三点共线.
由(1)同理可得,
∴.
25.(1)解:∵抛物线与x轴交于,两点,
设抛物线的解析式为,
把代入解析式,得,
解得:,
∴抛物线的解析式为:,即;
(2)解:∵抛物线的解析式为:,
∴抛物线图象的对称轴为:,
设,
∵轴,
∴,
∵过点D作x轴的平行线交抛物线于点E,作y轴的平行线交x轴于点G,过点E作轴,
∴四边形是矩形,
∴四边形的周长
,
∵,
∴当时,四边形的周长最大,则,
∴当四边形的周长最大时,点D的坐标为;
(3)解:过C作垂直抛物线对称轴于H,过N作轴于K,
∴,
由翻折得,
∵.
∴,
∴,
∵对称轴于H,
∴轴,
∴,
∴,
∴,即,
∴,
∴,
∵抛物线的解析式为:,
∴对称轴为,
∴,
∴,
∴,
∴,
设直线的解析式为,
∴,
解得:,
∴直线的解析式为:,
将代入,则,
∴,
设,
∴,,,
分两种情况:
①当时,,
∴,
解得:,
∴;
②当时,,
∴
解得:,
∴点的坐标为;
综上,所有符合条件的点P的坐标为或.
同课章节目录
