11.2 一元一次不等式(第1课时)课件(共20张PPT)
文档属性
| 名称 | 11.2 一元一次不等式(第1课时)课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 13:54:17 | ||
图片预览








文档简介
(共20张PPT)
11.2一元一次不等式(第1课时)
数学人教版(2024)七年级下册
1.一元一次方程的定义是什么?它的特点是什么?
只含有一个未知数,且含有未知数的式子都是整式,未知数的次数都是 1,这样的方程叫作一元一次方程.
特点:
(1)含有未知数的式子都是整式;
(2)只含有一个未知数;
(3)未知数的次数都是 1.
2.解一元一次方程:
(1)5x+15=4x-1; (2)2(x+5)=3(x-5).
解:(1)移项,得 5x-4x=-1-15.
合并同类项,得 x=-16.
(2)去括号,得 2x+10=3x-15.
移项,得 2x-3x=-15-10.
合并同类项,得 -x=-25.
系数化为1,得 x=25.
观察下面的不等式:
x-7>26,3x<2x+1, x>50,-4x>3.
它们有哪些共同特征?
问题
(1)只含有一个未知数;(2)未知数的次数是 1;(3)含有未知数的式子都是整式.
思考:类比一元一次方程的定义,你能给出一元一次不等式的定义吗?
新知
含有一个未知数,且含有未知数的式子都是整式,未知数的次数是 1 的不等式,叫作一元一次不等式.
特点:
(1)不等号的两边都是整式;
(2)只含一个未知数;
(3)含未知数的项的次数是1.
练习
判断下列不等式是否是一元一次不等式,并说明理由.
(1)x2+1>2;(2) +2>0;(3)x>y;(4) ≤1.
解:(1)中未知数的最高次数是 2,故不是一元一次不等式;
(2)中不等号的左边不是整式,故不是一元一次不等式;
(3)中有两个未知数,故不是一元一次不等式;
(4)中不等号的两边都是整式,且只有一个未知数,未知数的次数是 1,故是一元一次不等式.
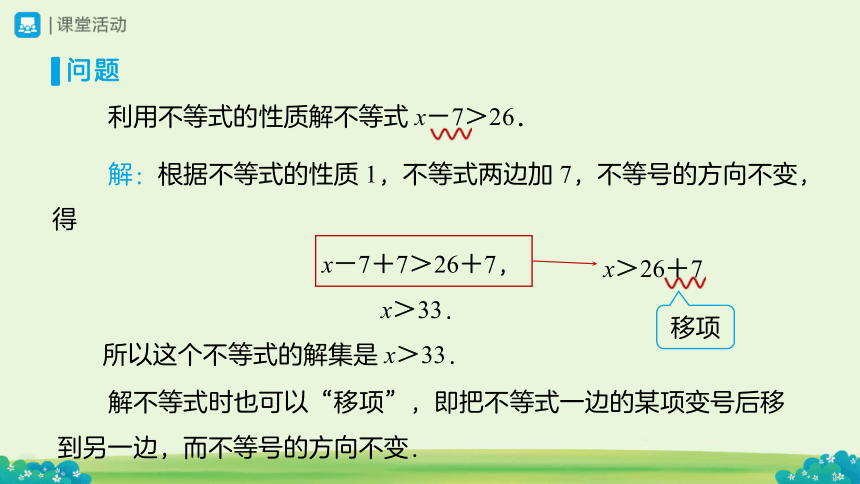
问题
利用不等式的性质解不等式 x-7>26.
解:根据不等式的性质 1,不等式两边加 7,不等号的方向不变,得
x-7+7>26+7,
x>33.
所以这个不等式的解集是 x>33.
x>26+7
移项
解不等式时也可以“移项”,即把不等式一边的某项变号后移到另一边,而不等号的方向不变.
思考
解一元一次方程的依据和一般步骤是什么?
解一元一次方程的依据是等式的性质.
解一元一次方程的一般步骤是:
去分母,去括号,移项,合并同类项,系数化为1.
一般地,利用不等式的性质,采取与解一元一次方程相类似的步骤,就可以求出一元一次不等式的解集.
解下列不等式,并在数轴上表示解集:
(1)3(x-1)<x-2; (2) +2≥ .
问题
x>m (x≥m)
或 x<m (x≤m)
依据:不等式的性质
解:(1)去括号,得 3x-3<x-2.
(1)3(x-1)<x-2;
这个不等式的解集在数轴上的表示如图所示.
0
移项,得 3x-x<-2+3.
合并同类项,得 2x<1.
系数化为 1,得 x< .
(2) +2≥ .
解:(2)去分母,得 3(x-5)+24≥2(5x+1).
这个不等式的解集在数轴上的表示如图所示.
去括号,得 3x-15+24≥10x+2.
移项,得 3x-10x≥2+15-24.
系数化为 1,得 x≤1.
合并同类项,得 -7x≥-7.
0
1
思考
对比第(1)题和第(2)题的解题过程,系数化为 1 时应注意些什么?
要看未知数系数的符号,若未知数的系数是正数,则不等号的方向不变;若未知数系数是负数,则不等号的方向要改变.
问题
解一元一次不等式的一般步骤是什么?
去分母:不等式两边乘各分母的最小公倍数;
去括号:把所有因式去括号展开;
移项:把含未知数的项移到不等号左边,常数项移到不等号右边;
合并同类项:化为 ax>b( ax≥b)或 ax<b ( ax≤b )的形式(其中 a≠0);
系数化为 1:不等式两边都除以 a,得到不等式的解集.
问题
每一步变形的依据是什么?
去分母
去括号
移项
合并同类项
系数化为 1
去括号法则
不等式的性质 1
合并同类项法则
不等式的性质 2 或 3
不等式的性质 2 或 3
思考
解一元一次不等式和解一元一次方程有哪些相同和不同之处?
相同之处:
步骤相同:去分母,去括号,移项,合并同类项,系数化为 1.
基本思想相同:都是运用化归思想,将一元一次方程或一元一
次不等式变形为最简形式.
思考
解一元一次不等式和解一元一次方程有哪些相同和不同之处?
不同之处:
解法依据不同:解一元一次不等式的主要依据是不等式的性质,解一元一次方程的主要依据是等式的性质.
最简形式不同:一元一次不等式的最简形式是 x>m (x≥m)
或 x<m (x≤m),一元一次方程的最简形式是 x=m.
例 已知 3m-2x3+2m>1 是关于 x 的一元一次不等式.
(1)求 m 的值;
(2)求出不等式的解集,并把解集表示在数轴上.
解:(1)因为 3m-2x3+2m>1 是关于 x 的一元一次不等式,
所以 3+2m=1,
解得 m=-1.
例 已知 3m-2x3+2m>1 是关于 x 的一元一次不等式.
(1)求 m 的值;
(2)求出不等式的解集,并把解集表示在数轴上.
解:(2)由(1)可知,题目中的不等式是 -3-2x>1.
移项,得 -2x>1+3.合并同类项,得 -2x>4.
系数化为 1,得 x<-2.
这个不等式的解集在数轴上的表示如图所示.
0
-2
利用一元一次不等式的概念解题时,要时刻紧扣一元一次不等式的三个特征:
(1)含有未知数的式子都是整式;
(2)只含有一个未知数;
(3)未知数的次数是 1.
一元一次不等式的解法
一元一次不等式的概念
一元一次不等式的解法
11.2一元一次不等式(第1课时)
数学人教版(2024)七年级下册
1.一元一次方程的定义是什么?它的特点是什么?
只含有一个未知数,且含有未知数的式子都是整式,未知数的次数都是 1,这样的方程叫作一元一次方程.
特点:
(1)含有未知数的式子都是整式;
(2)只含有一个未知数;
(3)未知数的次数都是 1.
2.解一元一次方程:
(1)5x+15=4x-1; (2)2(x+5)=3(x-5).
解:(1)移项,得 5x-4x=-1-15.
合并同类项,得 x=-16.
(2)去括号,得 2x+10=3x-15.
移项,得 2x-3x=-15-10.
合并同类项,得 -x=-25.
系数化为1,得 x=25.
观察下面的不等式:
x-7>26,3x<2x+1, x>50,-4x>3.
它们有哪些共同特征?
问题
(1)只含有一个未知数;(2)未知数的次数是 1;(3)含有未知数的式子都是整式.
思考:类比一元一次方程的定义,你能给出一元一次不等式的定义吗?
新知
含有一个未知数,且含有未知数的式子都是整式,未知数的次数是 1 的不等式,叫作一元一次不等式.
特点:
(1)不等号的两边都是整式;
(2)只含一个未知数;
(3)含未知数的项的次数是1.
练习
判断下列不等式是否是一元一次不等式,并说明理由.
(1)x2+1>2;(2) +2>0;(3)x>y;(4) ≤1.
解:(1)中未知数的最高次数是 2,故不是一元一次不等式;
(2)中不等号的左边不是整式,故不是一元一次不等式;
(3)中有两个未知数,故不是一元一次不等式;
(4)中不等号的两边都是整式,且只有一个未知数,未知数的次数是 1,故是一元一次不等式.
问题
利用不等式的性质解不等式 x-7>26.
解:根据不等式的性质 1,不等式两边加 7,不等号的方向不变,得
x-7+7>26+7,
x>33.
所以这个不等式的解集是 x>33.
x>26+7
移项
解不等式时也可以“移项”,即把不等式一边的某项变号后移到另一边,而不等号的方向不变.
思考
解一元一次方程的依据和一般步骤是什么?
解一元一次方程的依据是等式的性质.
解一元一次方程的一般步骤是:
去分母,去括号,移项,合并同类项,系数化为1.
一般地,利用不等式的性质,采取与解一元一次方程相类似的步骤,就可以求出一元一次不等式的解集.
解下列不等式,并在数轴上表示解集:
(1)3(x-1)<x-2; (2) +2≥ .
问题
x>m (x≥m)
或 x<m (x≤m)
依据:不等式的性质
解:(1)去括号,得 3x-3<x-2.
(1)3(x-1)<x-2;
这个不等式的解集在数轴上的表示如图所示.
0
移项,得 3x-x<-2+3.
合并同类项,得 2x<1.
系数化为 1,得 x< .
(2) +2≥ .
解:(2)去分母,得 3(x-5)+24≥2(5x+1).
这个不等式的解集在数轴上的表示如图所示.
去括号,得 3x-15+24≥10x+2.
移项,得 3x-10x≥2+15-24.
系数化为 1,得 x≤1.
合并同类项,得 -7x≥-7.
0
1
思考
对比第(1)题和第(2)题的解题过程,系数化为 1 时应注意些什么?
要看未知数系数的符号,若未知数的系数是正数,则不等号的方向不变;若未知数系数是负数,则不等号的方向要改变.
问题
解一元一次不等式的一般步骤是什么?
去分母:不等式两边乘各分母的最小公倍数;
去括号:把所有因式去括号展开;
移项:把含未知数的项移到不等号左边,常数项移到不等号右边;
合并同类项:化为 ax>b( ax≥b)或 ax<b ( ax≤b )的形式(其中 a≠0);
系数化为 1:不等式两边都除以 a,得到不等式的解集.
问题
每一步变形的依据是什么?
去分母
去括号
移项
合并同类项
系数化为 1
去括号法则
不等式的性质 1
合并同类项法则
不等式的性质 2 或 3
不等式的性质 2 或 3
思考
解一元一次不等式和解一元一次方程有哪些相同和不同之处?
相同之处:
步骤相同:去分母,去括号,移项,合并同类项,系数化为 1.
基本思想相同:都是运用化归思想,将一元一次方程或一元一
次不等式变形为最简形式.
思考
解一元一次不等式和解一元一次方程有哪些相同和不同之处?
不同之处:
解法依据不同:解一元一次不等式的主要依据是不等式的性质,解一元一次方程的主要依据是等式的性质.
最简形式不同:一元一次不等式的最简形式是 x>m (x≥m)
或 x<m (x≤m),一元一次方程的最简形式是 x=m.
例 已知 3m-2x3+2m>1 是关于 x 的一元一次不等式.
(1)求 m 的值;
(2)求出不等式的解集,并把解集表示在数轴上.
解:(1)因为 3m-2x3+2m>1 是关于 x 的一元一次不等式,
所以 3+2m=1,
解得 m=-1.
例 已知 3m-2x3+2m>1 是关于 x 的一元一次不等式.
(1)求 m 的值;
(2)求出不等式的解集,并把解集表示在数轴上.
解:(2)由(1)可知,题目中的不等式是 -3-2x>1.
移项,得 -2x>1+3.合并同类项,得 -2x>4.
系数化为 1,得 x<-2.
这个不等式的解集在数轴上的表示如图所示.
0
-2
利用一元一次不等式的概念解题时,要时刻紧扣一元一次不等式的三个特征:
(1)含有未知数的式子都是整式;
(2)只含有一个未知数;
(3)未知数的次数是 1.
一元一次不等式的解法
一元一次不等式的概念
一元一次不等式的解法
同课章节目录
