广东省湛江市岭南师院附中、东方实验学校2025届九年级下学期中考四模数学试卷(含详解)
文档属性
| 名称 | 广东省湛江市岭南师院附中、东方实验学校2025届九年级下学期中考四模数学试卷(含详解) |
|
|
| 格式 | docx | ||
| 文件大小 | 161.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 00:00:00 | ||
图片预览



文档简介
2025年广东省湛江市岭南师院附中、东方实验学校中考数学四模试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
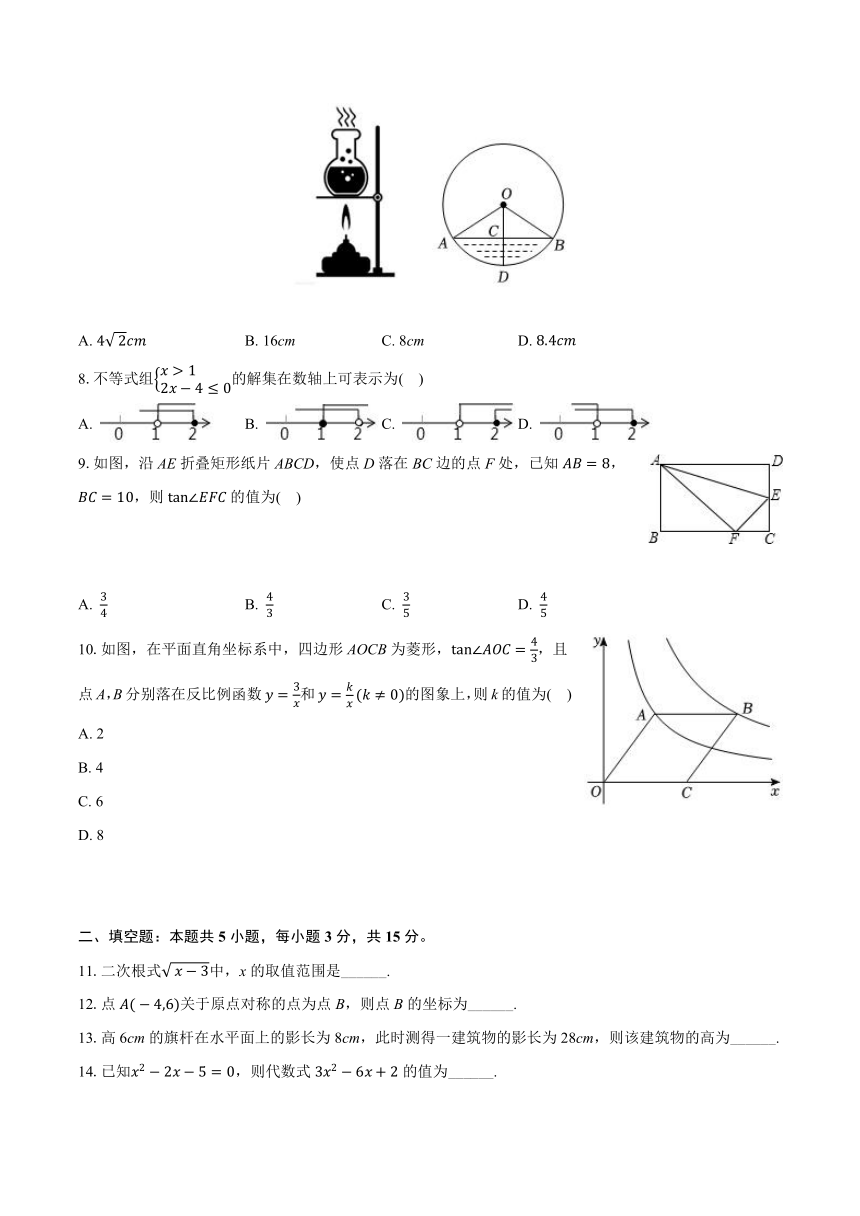
1.在,0,,3这四个数中,最小的数是( )
A. B. 2 C. D. 3
2.2025年全国高考报名人数预计约14500000人,数14500000用科学记数法表示为( )
A. B. C. D.
3.如图是一个由5个相同的正方体组成的立体图形,它的主视图是( )
A.
B.
C.
D.
4.如图,直线,的直角顶点B落在直线a上,若,则的大小为( )
A.
B.
C.
D.
5.下列各式计算正确的是( )
A. B. C. D.
6.从数据,,,125,中随机取出一个数,取出的数是负数的概率是( )
A. B. C. D.
7.如图,一个底部呈球形的烧瓶,球的半径10cm,瓶内液体的最大深度,则截面圆中弦AB的长为( )
A. B. 16cm C. 8cm D.
8.不等式组的解集在数轴上可表示为( )
A. B. C. D.
9.如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处,已知,,则的值为( )
A. B. C. D.
10.如图,在平面直角坐标系中,四边形AOCB为菱形,,且点A,B分别落在反比例函数和的图象上,则k的值为( )
A. 2
B. 4
C. 6
D. 8
二、填空题:本题共5小题,每小题3分,共15分。
11.二次根式中,x的取值范围是______.
12.点关于原点对称的点为点B,则点B的坐标为______.
13.高6cm的旗杆在水平面上的影长为8cm,此时测得一建筑物的影长为28cm,则该建筑物的高为______.
14.已知,则代数式的值为______.
15.如图,与x轴交于点,,与y轴的正半轴交于点若,则______.
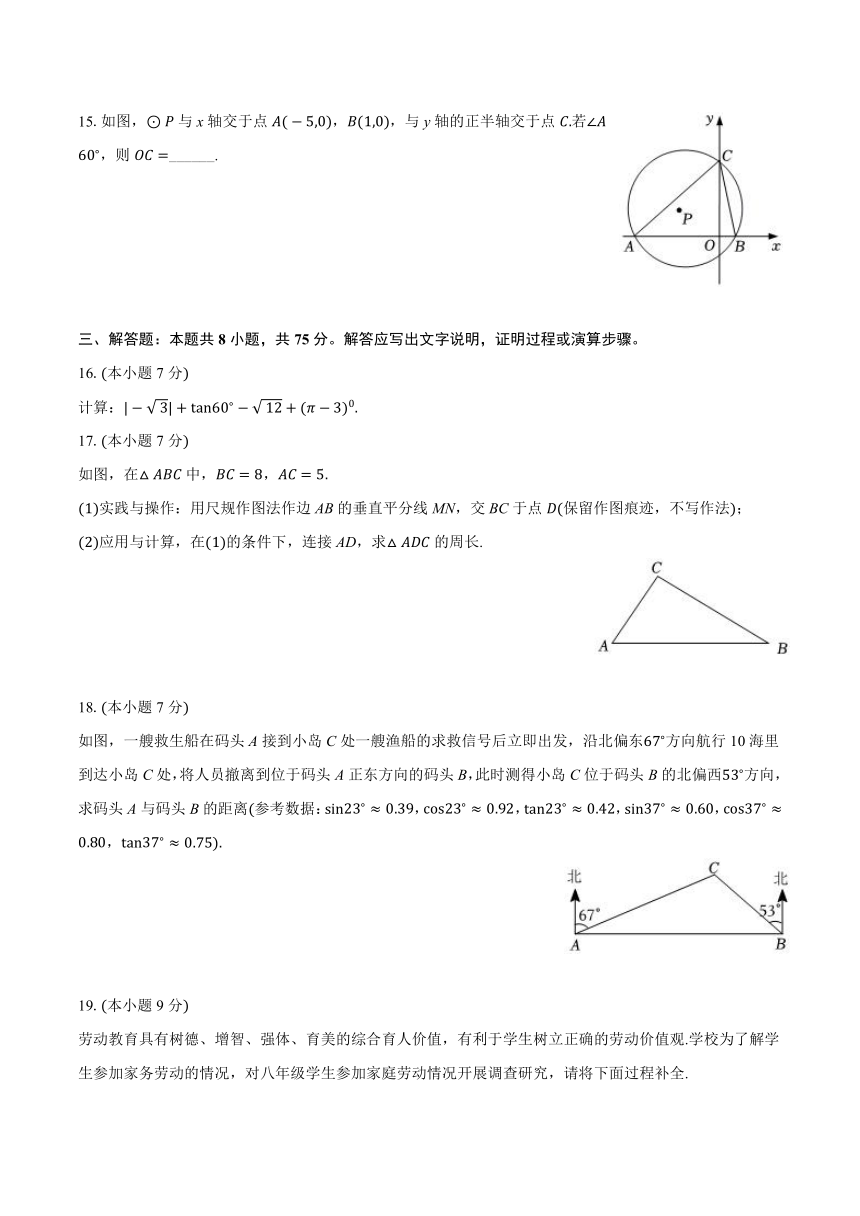
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题7分
计算:
17.本小题7分
如图,在中,,
实践与操作:用尺规作图法作边AB的垂直平分线MN,交BC于点保留作图痕迹,不写作法;
应用与计算,在的条件下,连接AD,求的周长.
18.本小题7分
如图,一艘救生船在码头A接到小岛C处一艘渔船的求救信号后立即出发,沿北偏东方向航行10海里到达小岛C处,将人员撤离到位于码头A正东方向的码头B,此时测得小岛C位于码头B的北偏西方向,求码头A与码头B的距离参考数据:,,,,,
19.本小题9分
劳动教育具有树德、增智、强体、育美的综合育人价值,有利于学生树立正确的劳动价值观.学校为了解学生参加家务劳动的情况,对八年级学生参加家庭劳动情况开展调查研究,请将下面过程补全.
收集数据,在八年级随机抽取20名学生进行问卷调查,他们一周参加家庭劳动的次数分别为:
3 1 2 2 4 3 3 2 3 4 3 4 0 5 7 2 6 4 6 6
整理数据,结果如表:
分组 频数
2
9
a
4
根据以上信息,解答下列问题:
______,补全频数分布直方图;
已知这组数据的平均数为,该校八年级现有200名学生,请估计该校八年级学生每周参加家庭劳动的次数达到平均水平及以上的学生人数;
劳动时间为的4名学生中有2名男生,2名女生,从中任意抽取2名学生参加学校开展的以“劳动美”为主题的演讲活动,用树状图或列表法求抽取的2名学生恰好是一名男生和一名女生的概率.
20.本小题9分
在运动会前夕,光明中学都会购买篮球、足球作为奖品.若购买6个篮球和8个足球共花费1700元,且购买一个篮球比购买一个足球多花50元.
求购买一个篮球,一个足球各需多少元;
今年学校计划购买这种篮球和足球共10个,恰逢商场在搞促销活动,篮球打九折,足球打八五折,若此次购买两种球的总费用不超过1150元,则最多可购买多少个篮球?
21.本小题9分
如图AB为的直径,且,点C是弧AB上的一动点不与A,B重合,过点B作的切线交AC的延长线于点D,点E是BD的中点,连接
求证:EC是的切线;
当时,求图中阴影部分面积.
22.本小题13分
综合与实践:
问题情境:数学活动课上,老师让同学们拿出大小两副三角板,按照如图1所示的方式摆放.其中,,
问题探究:将三角板DEB绕点B按顺时针方向旋转.
如图2,当点E落在边AB上时,延长DE交BC于点F,试判断BD与BF的数量关系,并说明理由;
在图2中,连接AF,请求出AF的长度;
如图3,G为DC的中点,则在旋转过程中,点G到直线AB的距离的最大值是______.
23.本小题14分
综合运用
如图,在平面直角坐标系中,矩形OABC的顶点A,C均在坐标轴上,且,,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;动点N从点C出发沿CB向终点B以同样的速度移动,当两个动点运动了x秒时,过点N作于点P,连接
直接写出点B的坐标,并求出点P的坐标用含x的式子表示;
设的面积为S,求S与x之间的函数表达式;当x为何值时,S有最大值是多少?
在两个动点运动的过程中,是否存在某一时刻,使是等腰三角形?若存在,求出M的坐标;若不存在,请说明理由.
答案和解析
1.A
解:根据有理数比较大小的方法,可得
,
在,0,,3这四个数中,最小的数是
故选:
2.B
解:
故选:
3.A
解:从正面看第一层是3个小正方形,第二层左边一个小正方形.
故选:
4.C
解:,,
,
故选:
.
5.C
解:A、,无法计算,故此选项错误;
B、,故此选项错误;
C、,正确;
D、,故此选项错误.
故选:
6.B
解:负数有,,共2个,
从数据,,,125,中随机取出一个数,取出的数是负数的概率是:
故选:
7.B
解:,,
,
,
,
故选:
8.A
解:
不等式①得:,
解不等式②得:,
不等式组的解集为,
在数轴上表示为:,
故选:
9.A
解:由折叠的性质可得≌,
,,
在中,,,
由勾股定理可得,
又,,
而故有,
故
故选
10.D
解:过点A、B作x轴的垂线,垂足分别为D、E,
,
,
设,则,
点,
由题意可得:,
负值已舍,则点,
,,
,
,,
点,
点B落在反比例函数上,
,
故选:
11.
解:根据题意得:,
解得:
故答案是:
12.
解:点关于原点对称点为点B,
点B的坐标为
故答案为:
13.21cm
解:相同时刻下物高与影长所在的三角形相似,
:建筑物高:28,
解得建筑物高为
故答案为:
14.17
解:,
,
,
故答案为:
15.
解:过P作于M,于N,连接PA,PB,PC,
,
四边形PMON是矩形,
,,
点,,
,,
,
,
,
,,
,
,
,
,
,
,
,
,,
,
,
故答案为:
16.
解:原式
17.见解析;
如图,直线MN即为所求.
直线MN为线段AB的垂直平分线,
的周长
18.码头A与码头B的距离为海里.
解:过点C作于点D,
由题意,得:,,,
在中,,
,
在中,,
则,
答:码头A与码头B的距离为海里.
19.;
如图所示;
人,
答:该校八年级学生每周参加家庭劳动的次数达到平均水平及以上的学生人数为90人.
画树状图如下:
所有等可能出现的结果总数为12个,其中抽到一男一女的情况数有8个,
恰好抽到一男一女概率为
解:由收集到的数据可知,分别有4,4,4,5,4共有5个,
,如图所示;
人,
答:该校八年级学生每周参加家庭劳动的次数达到平均水平及以上的学生人数为90人.
画树状图如下:
所有等可能出现的结果总数为12个,其中抽到一男一女的情况数有8个,
恰好抽到一男一女概率为
20.解:设购买一个篮球需x元,购买一个足球需y元,根据题意可得:
,
解得:,
答:购买一个篮球,一个足球分别需150元,100元;
设购买a个篮球,
根据题意可得:,
解得:,
答;最多可购买6个篮球.
21.见解析;
证明:如图,连接OC、BC、OE,
与相切于点B,
,
,
是的直径,
,
,
点E是BD的中点,
,
,,
≌,
,
经过的半径OC的外端,且,
是的切线;
解:,,
,
,
,
,
,
,
,
,
,
,
,
,
图中阴影部分面积
22.,
理由:,
,
将三角板DEB绕点B按顺时针方向旋转点E落在边AB上,
,
,
≌,
;
如图2,
,,,
,,
,
;
解:,
理由:,
,
将三角板DEB绕点B按顺时针方向旋转点E落在边AB上,
,
,
≌,
;
如图2,
,,,
,,
,
;
如图3,连接CD,取CD的中点G,
取BC的中点O,连接GO,则,
,
,
点G为CD的中点,点O为BC的中点,
,
点G是以点O为圆心,为半径的圆上,如图,
如图4,过点O作于K,
点O为BC的中点,,
,
,
点G到直线AB的距离的最大值是,
故答案为:
23.点P的坐标为;
,当时,S有最大值,最大值为;
M的坐标为或或
矩形OABC中,,,
点坐标为
如图,延长NP,交OA于点G,则,
,
∽,
,即,解得,
点P的坐标为;
在中,,OM边上的高为,
,
与x之间的函数表达式为
配方,得,
当时,S有最大值,最大值为;
存在某一时刻,使是等腰三角形.理由如下:
①如备用图1,若,则,
即,解得:,
所以;
②如备用图2,若,则,
即,解得:,
所以;
③如备用图3,若时,
,,
,
,
,解得:,
所以,
综上所述,M的坐标为或或
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在,0,,3这四个数中,最小的数是( )
A. B. 2 C. D. 3
2.2025年全国高考报名人数预计约14500000人,数14500000用科学记数法表示为( )
A. B. C. D.
3.如图是一个由5个相同的正方体组成的立体图形,它的主视图是( )
A.
B.
C.
D.
4.如图,直线,的直角顶点B落在直线a上,若,则的大小为( )
A.
B.
C.
D.
5.下列各式计算正确的是( )
A. B. C. D.
6.从数据,,,125,中随机取出一个数,取出的数是负数的概率是( )
A. B. C. D.
7.如图,一个底部呈球形的烧瓶,球的半径10cm,瓶内液体的最大深度,则截面圆中弦AB的长为( )
A. B. 16cm C. 8cm D.
8.不等式组的解集在数轴上可表示为( )
A. B. C. D.
9.如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处,已知,,则的值为( )
A. B. C. D.
10.如图,在平面直角坐标系中,四边形AOCB为菱形,,且点A,B分别落在反比例函数和的图象上,则k的值为( )
A. 2
B. 4
C. 6
D. 8
二、填空题:本题共5小题,每小题3分,共15分。
11.二次根式中,x的取值范围是______.
12.点关于原点对称的点为点B,则点B的坐标为______.
13.高6cm的旗杆在水平面上的影长为8cm,此时测得一建筑物的影长为28cm,则该建筑物的高为______.
14.已知,则代数式的值为______.
15.如图,与x轴交于点,,与y轴的正半轴交于点若,则______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题7分
计算:
17.本小题7分
如图,在中,,
实践与操作:用尺规作图法作边AB的垂直平分线MN,交BC于点保留作图痕迹,不写作法;
应用与计算,在的条件下,连接AD,求的周长.
18.本小题7分
如图,一艘救生船在码头A接到小岛C处一艘渔船的求救信号后立即出发,沿北偏东方向航行10海里到达小岛C处,将人员撤离到位于码头A正东方向的码头B,此时测得小岛C位于码头B的北偏西方向,求码头A与码头B的距离参考数据:,,,,,
19.本小题9分
劳动教育具有树德、增智、强体、育美的综合育人价值,有利于学生树立正确的劳动价值观.学校为了解学生参加家务劳动的情况,对八年级学生参加家庭劳动情况开展调查研究,请将下面过程补全.
收集数据,在八年级随机抽取20名学生进行问卷调查,他们一周参加家庭劳动的次数分别为:
3 1 2 2 4 3 3 2 3 4 3 4 0 5 7 2 6 4 6 6
整理数据,结果如表:
分组 频数
2
9
a
4
根据以上信息,解答下列问题:
______,补全频数分布直方图;
已知这组数据的平均数为,该校八年级现有200名学生,请估计该校八年级学生每周参加家庭劳动的次数达到平均水平及以上的学生人数;
劳动时间为的4名学生中有2名男生,2名女生,从中任意抽取2名学生参加学校开展的以“劳动美”为主题的演讲活动,用树状图或列表法求抽取的2名学生恰好是一名男生和一名女生的概率.
20.本小题9分
在运动会前夕,光明中学都会购买篮球、足球作为奖品.若购买6个篮球和8个足球共花费1700元,且购买一个篮球比购买一个足球多花50元.
求购买一个篮球,一个足球各需多少元;
今年学校计划购买这种篮球和足球共10个,恰逢商场在搞促销活动,篮球打九折,足球打八五折,若此次购买两种球的总费用不超过1150元,则最多可购买多少个篮球?
21.本小题9分
如图AB为的直径,且,点C是弧AB上的一动点不与A,B重合,过点B作的切线交AC的延长线于点D,点E是BD的中点,连接
求证:EC是的切线;
当时,求图中阴影部分面积.
22.本小题13分
综合与实践:
问题情境:数学活动课上,老师让同学们拿出大小两副三角板,按照如图1所示的方式摆放.其中,,
问题探究:将三角板DEB绕点B按顺时针方向旋转.
如图2,当点E落在边AB上时,延长DE交BC于点F,试判断BD与BF的数量关系,并说明理由;
在图2中,连接AF,请求出AF的长度;
如图3,G为DC的中点,则在旋转过程中,点G到直线AB的距离的最大值是______.
23.本小题14分
综合运用
如图,在平面直角坐标系中,矩形OABC的顶点A,C均在坐标轴上,且,,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;动点N从点C出发沿CB向终点B以同样的速度移动,当两个动点运动了x秒时,过点N作于点P,连接
直接写出点B的坐标,并求出点P的坐标用含x的式子表示;
设的面积为S,求S与x之间的函数表达式;当x为何值时,S有最大值是多少?
在两个动点运动的过程中,是否存在某一时刻,使是等腰三角形?若存在,求出M的坐标;若不存在,请说明理由.
答案和解析
1.A
解:根据有理数比较大小的方法,可得
,
在,0,,3这四个数中,最小的数是
故选:
2.B
解:
故选:
3.A
解:从正面看第一层是3个小正方形,第二层左边一个小正方形.
故选:
4.C
解:,,
,
故选:
.
5.C
解:A、,无法计算,故此选项错误;
B、,故此选项错误;
C、,正确;
D、,故此选项错误.
故选:
6.B
解:负数有,,共2个,
从数据,,,125,中随机取出一个数,取出的数是负数的概率是:
故选:
7.B
解:,,
,
,
,
故选:
8.A
解:
不等式①得:,
解不等式②得:,
不等式组的解集为,
在数轴上表示为:,
故选:
9.A
解:由折叠的性质可得≌,
,,
在中,,,
由勾股定理可得,
又,,
而故有,
故
故选
10.D
解:过点A、B作x轴的垂线,垂足分别为D、E,
,
,
设,则,
点,
由题意可得:,
负值已舍,则点,
,,
,
,,
点,
点B落在反比例函数上,
,
故选:
11.
解:根据题意得:,
解得:
故答案是:
12.
解:点关于原点对称点为点B,
点B的坐标为
故答案为:
13.21cm
解:相同时刻下物高与影长所在的三角形相似,
:建筑物高:28,
解得建筑物高为
故答案为:
14.17
解:,
,
,
故答案为:
15.
解:过P作于M,于N,连接PA,PB,PC,
,
四边形PMON是矩形,
,,
点,,
,,
,
,
,
,,
,
,
,
,
,
,
,
,,
,
,
故答案为:
16.
解:原式
17.见解析;
如图,直线MN即为所求.
直线MN为线段AB的垂直平分线,
的周长
18.码头A与码头B的距离为海里.
解:过点C作于点D,
由题意,得:,,,
在中,,
,
在中,,
则,
答:码头A与码头B的距离为海里.
19.;
如图所示;
人,
答:该校八年级学生每周参加家庭劳动的次数达到平均水平及以上的学生人数为90人.
画树状图如下:
所有等可能出现的结果总数为12个,其中抽到一男一女的情况数有8个,
恰好抽到一男一女概率为
解:由收集到的数据可知,分别有4,4,4,5,4共有5个,
,如图所示;
人,
答:该校八年级学生每周参加家庭劳动的次数达到平均水平及以上的学生人数为90人.
画树状图如下:
所有等可能出现的结果总数为12个,其中抽到一男一女的情况数有8个,
恰好抽到一男一女概率为
20.解:设购买一个篮球需x元,购买一个足球需y元,根据题意可得:
,
解得:,
答:购买一个篮球,一个足球分别需150元,100元;
设购买a个篮球,
根据题意可得:,
解得:,
答;最多可购买6个篮球.
21.见解析;
证明:如图,连接OC、BC、OE,
与相切于点B,
,
,
是的直径,
,
,
点E是BD的中点,
,
,,
≌,
,
经过的半径OC的外端,且,
是的切线;
解:,,
,
,
,
,
,
,
,
,
,
,
,
,
图中阴影部分面积
22.,
理由:,
,
将三角板DEB绕点B按顺时针方向旋转点E落在边AB上,
,
,
≌,
;
如图2,
,,,
,,
,
;
解:,
理由:,
,
将三角板DEB绕点B按顺时针方向旋转点E落在边AB上,
,
,
≌,
;
如图2,
,,,
,,
,
;
如图3,连接CD,取CD的中点G,
取BC的中点O,连接GO,则,
,
,
点G为CD的中点,点O为BC的中点,
,
点G是以点O为圆心,为半径的圆上,如图,
如图4,过点O作于K,
点O为BC的中点,,
,
,
点G到直线AB的距离的最大值是,
故答案为:
23.点P的坐标为;
,当时,S有最大值,最大值为;
M的坐标为或或
矩形OABC中,,,
点坐标为
如图,延长NP,交OA于点G,则,
,
∽,
,即,解得,
点P的坐标为;
在中,,OM边上的高为,
,
与x之间的函数表达式为
配方,得,
当时,S有最大值,最大值为;
存在某一时刻,使是等腰三角形.理由如下:
①如备用图1,若,则,
即,解得:,
所以;
②如备用图2,若,则,
即,解得:,
所以;
③如备用图3,若时,
,,
,
,
,解得:,
所以,
综上所述,M的坐标为或或
同课章节目录
