期末押题卷(含答案)-2024-2025学年数学八年级下册人教版
文档属性
| 名称 | 期末押题卷(含答案)-2024-2025学年数学八年级下册人教版 | 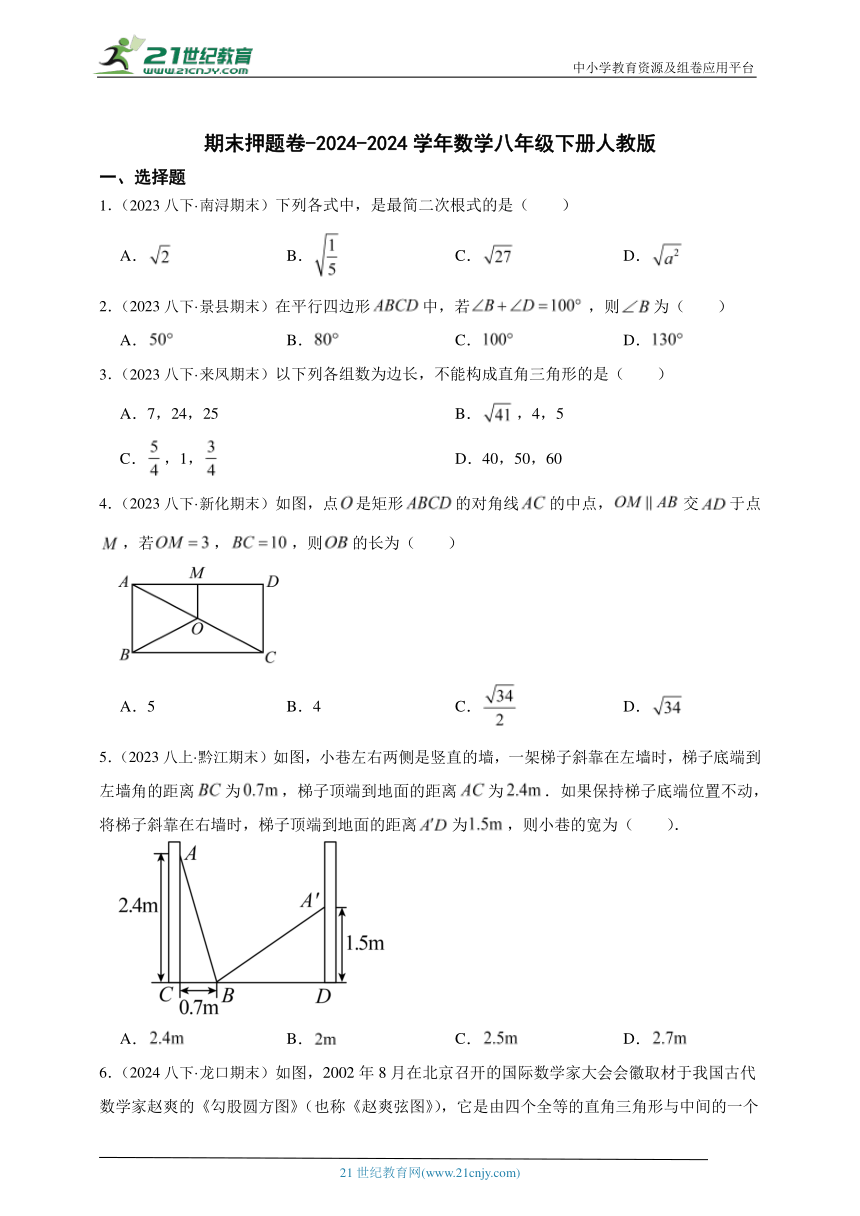 | |
| 格式 | docx | ||
| 文件大小 | 734.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 18:48:37 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末押题卷-2024-2024学年数学八年级下册人教版
一、选择题
1.(2023八下·南浔期末)下列各式中,是最简二次根式的是( )
A. B. C. D.
2.(2023八下·景县期末)在平行四边形中,若,则为( )
A. B. C. D.
3.(2023八下·来凤期末)以下列各组数为边长,不能构成直角三角形的是( )
A.7,24,25 B.,4,5
C.,1, D.40,50,60
4.(2023八下·新化期末)如图,点是矩形的对角线的中点,交于点,若,,则的长为( )
A.5 B.4 C. D.
5.(2023八上·黔江期末)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为,梯子顶端到地面的距离为.如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为,则小巷的宽为( ).
A. B. C. D.
6.(2024八下·龙口期末)如图,2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么的值为( )
A.13 B.19 C.25 D.169
7.(2023八下·郾城期末)下列计算正确的是( )
A. B.
C. D.
8.(2024八下·上海市期末)如图所示的图像中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中表示时间,表示张强离家的距离.根据图像提供的信息,以下四个说法中错误的是( )
A.体育场离张强家2.5千米
B.张强在体育场锻炼了15分钟
C.体育场离早餐店1千米
D.张强从早餐店回家的平均速度是3千米/小时
9.(2023八下·汝阳期末)小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm B.30cm C.40cm D.20cm
10.(2024八下·昆明期末)农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高(单位:cm)进行了测量.根据统计的结果,绘制出如图所示的统计图.这组数据中,众数和中位数分别是( )
A.16,15 B.16,15.5 C.16,16 D.17,16
二、填空题
11.(2024八下·莒南期末)一组数据1,6,7,4,7,5,2的中位数是 .
12.(2024八下·苍梧期末)计算: =
13.(2024九上·山亭期末)如图,一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.已知,点D为边的中点,点A、B对应的刻度为1、7,则 cm.
14.(2023八下·南安期末)如图,一次函数 与一次函数的图象交于点 ,则关于 的不等式 的解集是 .
15.(2024八下·天河期末) 已知菱形 的对角长 , 则菱形 的面积为 .
16.(2024八上·济南期末)如图,中,,,,D是线段AB上一个动点,以BD为边在外作等边.若F是DE的中点,当CF取最小值时,的周长为 .
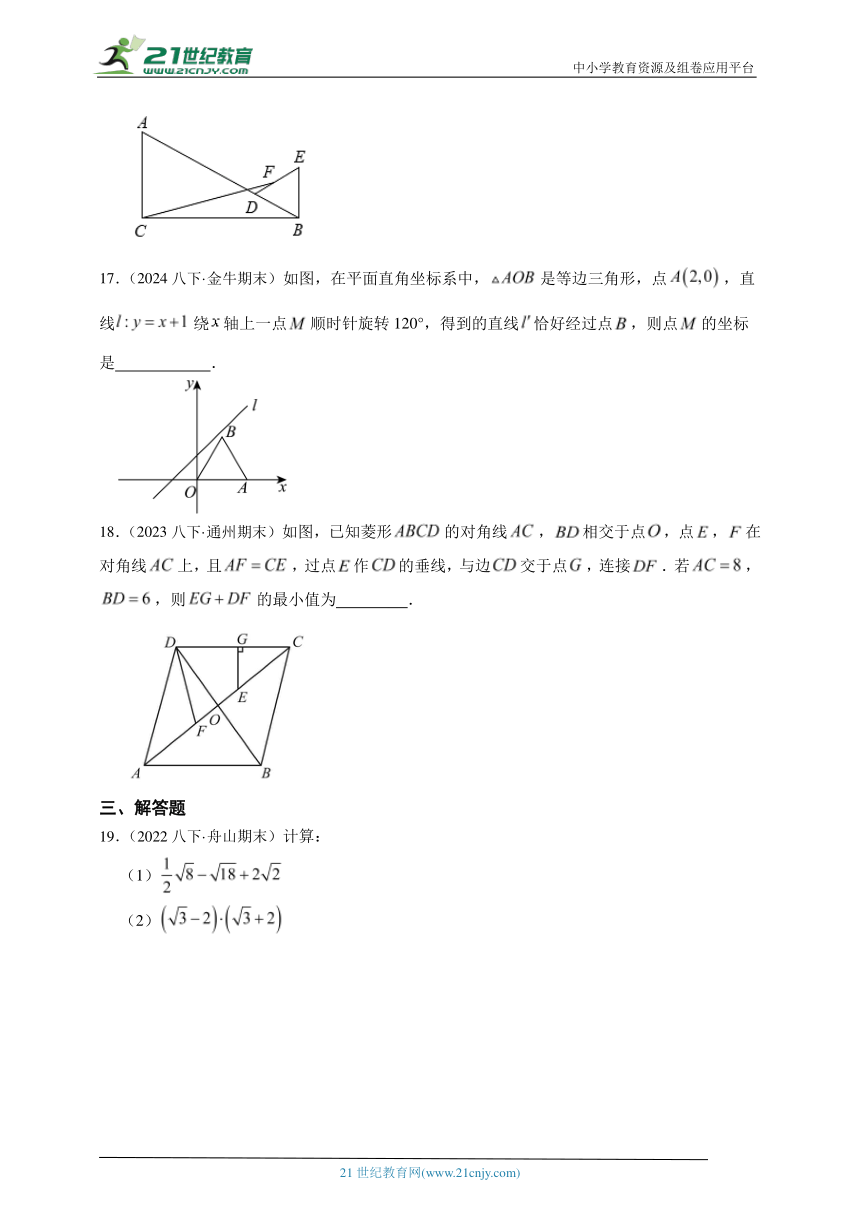
17.(2024八下·金牛期末)如图,在平面直角坐标系中,是等边三角形,点,直线绕轴上一点顺时针旋转120°,得到的直线恰好经过点,则点的坐标是 .
18.(2023八下·通州期末)如图,已知菱形的对角线,相交于点,点,在对角线上,且,过点作的垂线,与边交于点,连接.若,,则的最小值为 .
三、解答题
19.(2022八下·舟山期末)计算:
(1)
(2)
20.(2024八下·南康期末)已知,,求下列各式的值.
(1).
(2).
21.(2024八下·富顺期末)如图,在中,,平分交于点D,过点D作于点E,若,求的长.
22.(2024八上·梓潼期末)如图,矩形是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴上,点C在y轴上,.在上取一点M,使得沿翻折后,点B落在x轴上,记作点.
(1)求点的坐标;
(2)求折痕所在直线的解析式.
23.(2023八下·澄迈期末)湖的两岸有A,B两棵景观树,数学兴趣小组设计实验测量两棵景观树之间的距离,他们在与AB垂直的BC方向上取点C,测得米,米.
求:(1)两棵景观树之间的距离;
(2)点B到直线AC的距离.
24.(2024八下·汨罗期末)汉服是中国古老而美好的生活方式的一个缩影,近年来,“汉服热”席卷中国各大景区,尤其是在节假日期间,“汉服+景区”已然成为当下年轻人的创新玩法.某景区一汉服专卖店计划购进甲、乙两种汉服共120件(2种服装都要),其进价与售价如表所示:
价格类型 进价(元/件) 售价(元/件)
甲 80 100
乙 100 200
若设甲汉服的数量为件,销售完甲、乙两种汉服的利润为元.
(1)求与之间的函数关系式,写出自变量范围;
(2)若乙汉服的数量不能超过甲汉服数量的2倍,请问当甲汉服购选多少件时,该店在销售完这两种汉服后获利最多?并求出最大利润。
25.(2024八下·呼和浩特期末)如图,矩形中,点在边上,将沿折叠,点落在边上的点处,过点作交于点,连接.
(1)求证:四边形是菱形;
(2)若,求四边形的面积.
26.(2024八下·凉州期末)已知直线与直线相交于点.
(1)求m,n的值;
(2)请结合图象直接写出不等式的解集;
(3)求直线、直线与y轴围成的三角形的面积.
27.(2024八下·巴中期末)已知:如图,在四边形中,,垂足分别为E,F,延长,分别交于点H,交于点G,若,.
(1)求证:四边形为平行四边形;
(2)若,求的长.
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】D
4.【答案】D
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】D
9.【答案】D
10.【答案】C
11.【答案】5
12.【答案】1
13.【答案】3
14.【答案】
15.【答案】36
16.【答案】18
17.【答案】
18.【答案】
19.【答案】(1)解:原式=.
(2)解:原式=.
20.【答案】(1)解:∵,,
∴,
,
∴
;
(2)解:
.
21.【答案】
22.【答案】(1)点坐标为(16,0)
(2)
23.【答案】解:(1)由题意得:是直角三角形,
∴由勾股定理,得.
∵米,,
∴.
∵,
∴米.
即A,B两点间的距离是40米.
(2)过点B作于点D
因为,
所以.
所以(米),
即点B到直线AC的距离是24米.
24.【答案】(1)解:由于甲汉服的数量为件,则乙汉服的数量为(120-x)件,
由题意得:
∴y与x之间的函数关系式为:;
(2)解:由题意得:
解得:,
由(1)知,,
∵一次项系数,
∴y随x的增大而减小,
∴当时,y取最大值,y最大,
答:当甲汉服购进40件时,该店在销售完这两种汉服获利最多,最大利润为元.
25.【答案】(1)证明:∵△BCE沿BE折叠,点C落在AD边上的点F处
∴∠BEC=∠BEF,FE=CE
∵FG∥CE
∴∠FGE=∠CEB
∴∠FGE=∠FEG
∴FG=FE
∵FE=CE
∴FG=EC
∵FG∥CE
∴四边形CEFG是平行四边形
∵FE=CE
∴四边形CEFG是菱形;
(2)解:∵△BCE沿BE折叠,点C落在AD边上的点F处
∴BC=BF
∵四边形ABCD是矩形
∴AD=BC=BF=10,∠CDA=∠BAF=90°
∵AB=6
∴在Rt△ABF中,
∴DF=AB-AF=2
∴设EF=x,则CE=x,
∴DE=DC-CE=6-x
∵∠CDA=90°
∴在Rt△FDE中,
即:,
解得: ,
即,
∴平行四边形CEFG的面积是:.
26.【答案】(1)解:把代入得:
,解得:;
把,代入得:,解得
(2)解:由图象可知:不等式的解集为:
(3)结:∵,∴当时,,故,
∵,
∴当时,,解得:,则,
∴直线、直线与y轴围成的三角形的面积为:.
27.【答案】(1)证明:∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴四边形为平行四边形;
(2)解:∵四边形为平行四边形,
∴,,
∴,
∵,
∴
∴,
在中,
∵,
∴,
∴,
∴.
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末押题卷-2024-2024学年数学八年级下册人教版
一、选择题
1.(2023八下·南浔期末)下列各式中,是最简二次根式的是( )
A. B. C. D.
2.(2023八下·景县期末)在平行四边形中,若,则为( )
A. B. C. D.
3.(2023八下·来凤期末)以下列各组数为边长,不能构成直角三角形的是( )
A.7,24,25 B.,4,5
C.,1, D.40,50,60
4.(2023八下·新化期末)如图,点是矩形的对角线的中点,交于点,若,,则的长为( )
A.5 B.4 C. D.
5.(2023八上·黔江期末)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为,梯子顶端到地面的距离为.如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为,则小巷的宽为( ).
A. B. C. D.
6.(2024八下·龙口期末)如图,2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么的值为( )
A.13 B.19 C.25 D.169
7.(2023八下·郾城期末)下列计算正确的是( )
A. B.
C. D.
8.(2024八下·上海市期末)如图所示的图像中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中表示时间,表示张强离家的距离.根据图像提供的信息,以下四个说法中错误的是( )
A.体育场离张强家2.5千米
B.张强在体育场锻炼了15分钟
C.体育场离早餐店1千米
D.张强从早餐店回家的平均速度是3千米/小时
9.(2023八下·汝阳期末)小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm B.30cm C.40cm D.20cm
10.(2024八下·昆明期末)农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高(单位:cm)进行了测量.根据统计的结果,绘制出如图所示的统计图.这组数据中,众数和中位数分别是( )
A.16,15 B.16,15.5 C.16,16 D.17,16
二、填空题
11.(2024八下·莒南期末)一组数据1,6,7,4,7,5,2的中位数是 .
12.(2024八下·苍梧期末)计算: =
13.(2024九上·山亭期末)如图,一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.已知,点D为边的中点,点A、B对应的刻度为1、7,则 cm.
14.(2023八下·南安期末)如图,一次函数 与一次函数的图象交于点 ,则关于 的不等式 的解集是 .
15.(2024八下·天河期末) 已知菱形 的对角长 , 则菱形 的面积为 .
16.(2024八上·济南期末)如图,中,,,,D是线段AB上一个动点,以BD为边在外作等边.若F是DE的中点,当CF取最小值时,的周长为 .
17.(2024八下·金牛期末)如图,在平面直角坐标系中,是等边三角形,点,直线绕轴上一点顺时针旋转120°,得到的直线恰好经过点,则点的坐标是 .
18.(2023八下·通州期末)如图,已知菱形的对角线,相交于点,点,在对角线上,且,过点作的垂线,与边交于点,连接.若,,则的最小值为 .
三、解答题
19.(2022八下·舟山期末)计算:
(1)
(2)
20.(2024八下·南康期末)已知,,求下列各式的值.
(1).
(2).
21.(2024八下·富顺期末)如图,在中,,平分交于点D,过点D作于点E,若,求的长.
22.(2024八上·梓潼期末)如图,矩形是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴上,点C在y轴上,.在上取一点M,使得沿翻折后,点B落在x轴上,记作点.
(1)求点的坐标;
(2)求折痕所在直线的解析式.
23.(2023八下·澄迈期末)湖的两岸有A,B两棵景观树,数学兴趣小组设计实验测量两棵景观树之间的距离,他们在与AB垂直的BC方向上取点C,测得米,米.
求:(1)两棵景观树之间的距离;
(2)点B到直线AC的距离.
24.(2024八下·汨罗期末)汉服是中国古老而美好的生活方式的一个缩影,近年来,“汉服热”席卷中国各大景区,尤其是在节假日期间,“汉服+景区”已然成为当下年轻人的创新玩法.某景区一汉服专卖店计划购进甲、乙两种汉服共120件(2种服装都要),其进价与售价如表所示:
价格类型 进价(元/件) 售价(元/件)
甲 80 100
乙 100 200
若设甲汉服的数量为件,销售完甲、乙两种汉服的利润为元.
(1)求与之间的函数关系式,写出自变量范围;
(2)若乙汉服的数量不能超过甲汉服数量的2倍,请问当甲汉服购选多少件时,该店在销售完这两种汉服后获利最多?并求出最大利润。
25.(2024八下·呼和浩特期末)如图,矩形中,点在边上,将沿折叠,点落在边上的点处,过点作交于点,连接.
(1)求证:四边形是菱形;
(2)若,求四边形的面积.
26.(2024八下·凉州期末)已知直线与直线相交于点.
(1)求m,n的值;
(2)请结合图象直接写出不等式的解集;
(3)求直线、直线与y轴围成的三角形的面积.
27.(2024八下·巴中期末)已知:如图,在四边形中,,垂足分别为E,F,延长,分别交于点H,交于点G,若,.
(1)求证:四边形为平行四边形;
(2)若,求的长.
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】D
4.【答案】D
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】D
9.【答案】D
10.【答案】C
11.【答案】5
12.【答案】1
13.【答案】3
14.【答案】
15.【答案】36
16.【答案】18
17.【答案】
18.【答案】
19.【答案】(1)解:原式=.
(2)解:原式=.
20.【答案】(1)解:∵,,
∴,
,
∴
;
(2)解:
.
21.【答案】
22.【答案】(1)点坐标为(16,0)
(2)
23.【答案】解:(1)由题意得:是直角三角形,
∴由勾股定理,得.
∵米,,
∴.
∵,
∴米.
即A,B两点间的距离是40米.
(2)过点B作于点D
因为,
所以.
所以(米),
即点B到直线AC的距离是24米.
24.【答案】(1)解:由于甲汉服的数量为件,则乙汉服的数量为(120-x)件,
由题意得:
∴y与x之间的函数关系式为:;
(2)解:由题意得:
解得:,
由(1)知,,
∵一次项系数,
∴y随x的增大而减小,
∴当时,y取最大值,y最大,
答:当甲汉服购进40件时,该店在销售完这两种汉服获利最多,最大利润为元.
25.【答案】(1)证明:∵△BCE沿BE折叠,点C落在AD边上的点F处
∴∠BEC=∠BEF,FE=CE
∵FG∥CE
∴∠FGE=∠CEB
∴∠FGE=∠FEG
∴FG=FE
∵FE=CE
∴FG=EC
∵FG∥CE
∴四边形CEFG是平行四边形
∵FE=CE
∴四边形CEFG是菱形;
(2)解:∵△BCE沿BE折叠,点C落在AD边上的点F处
∴BC=BF
∵四边形ABCD是矩形
∴AD=BC=BF=10,∠CDA=∠BAF=90°
∵AB=6
∴在Rt△ABF中,
∴DF=AB-AF=2
∴设EF=x,则CE=x,
∴DE=DC-CE=6-x
∵∠CDA=90°
∴在Rt△FDE中,
即:,
解得: ,
即,
∴平行四边形CEFG的面积是:.
26.【答案】(1)解:把代入得:
,解得:;
把,代入得:,解得
(2)解:由图象可知:不等式的解集为:
(3)结:∵,∴当时,,故,
∵,
∴当时,,解得:,则,
∴直线、直线与y轴围成的三角形的面积为:.
27.【答案】(1)证明:∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴四边形为平行四边形;
(2)解:∵四边形为平行四边形,
∴,,
∴,
∵,
∴
∴,
在中,
∵,
∴,
∴,
∴.
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
