2025年罗湖区中考备考百师助学课程之第三讲《四边形中的十字架模型》课件
文档属性
| 名称 | 2025年罗湖区中考备考百师助学课程之第三讲《四边形中的十字架模型》课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 822.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 16:45:07 | ||
图片预览






文档简介
(共20张PPT)
四边形中的十字架模型
执教人:汤子弘
罗湖区中考备考“百师助学”课程
单位:翠园文锦中学
行业PPT模板http://www./hangye/
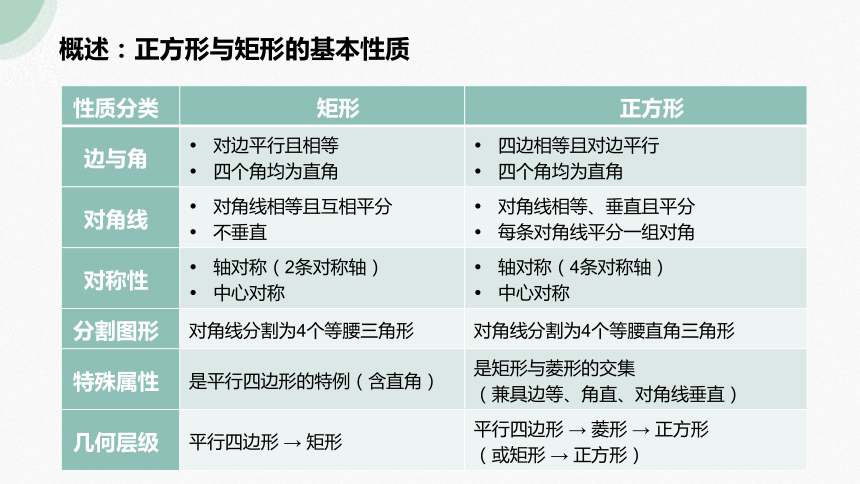
概述:正方形与矩形的基本性质
性质分类 矩形 正方形
边与角 对边平行且相等 四个角均为直角 四边相等且对边平行
四个角均为直角
对角线 对角线相等且互相平分 不垂直 对角线相等、垂直且平分
每条对角线平分一组对角
对称性 轴对称(2条对称轴) 中心对称 轴对称(4条对称轴)
中心对称
分割图形 对角线分割为4个等腰三角形 对角线分割为4个等腰直角三角形
特殊属性 是平行四边形的特例(含直角) 是矩形与菱形的交集
(兼具边等、角直、对角线垂直)
几何层级 平行四边形 → 矩形 平行四边形 → 菱形 → 正方形
(或矩形 → 正方形)
行业PPT模板http://www./hangye/
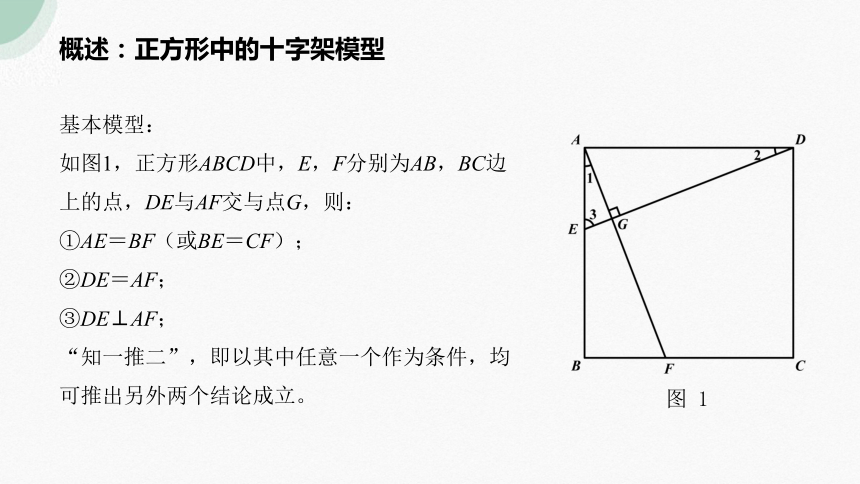
概述:正方形中的十字架模型
图 1
基本模型:
如图1,正方形ABCD中,E,F分别为AB,BC边上的点,DE与AF交与点G,则:
①AE=BF(或BE=CF);
②DE=AF;
③DE⊥AF;
“知一推二”,即以其中任意一个作为条件,均可推出另外两个结论成立。
行业PPT模板http://www./hangye/
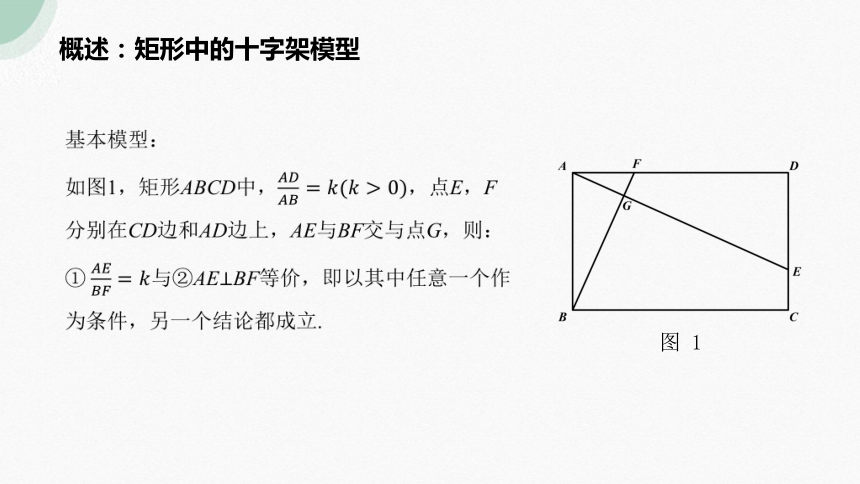
概述:矩形中的十字架模型
基本模型:
如图1,矩形ABCD中,,点E,F分别在CD边和AD边上,AE与BF交与点G,则:
① 与②AE⊥BF等价,即以其中任意一个作为条件,另一个结论都成立.
图 1
行业PPT模板http://www./hangye/
考点和题型分析
考试中常见的考察题型主要有:
(1)正方形中十字架模型的应用与变化;
(2)矩形中十字架模型的应用与变化;
(3)推理与证明在十字架模型的结合与应用。
从近几年中考真题来看,考察的核心思想是让学生以基本模型为抓手,通过自己构造创设条件,结合不同的情况综合运用图形的变化与几何证明。熟练理解和运用图形的关系包含位置关系(垂直、平行)、数量关系(全等、相似)进一步提高对几何与证明等相关知识的综合运用能力。
四边形中的十字架模型
执教人:汤子弘
罗湖区中考备考“百师助学”课程
单位:翠园文锦中学
正方形中的十字架模型
01
矩形中的十字架模型
推理与证明“+”十字架模型
目录
02
03
模块一 正方形中的十字架模型
【例题1】如图,E,G,F,H分别在正方形ABCD的各边上(不与正方形顶点重合),若EF⊥GH,求证:EF=GH.
【分析】平移思想,将EF和GH转化,转化为基本模型.
【解答】作AM//EF交BC边于点M,作DN//GH交AB边于点N
∵ 正方形ABCD
∴ AD=AB,∠DAN=∠ABM=90°
∵ AD//BC,AB//CD,
∴ 四边形AMFE和四边形DNGH均为平行四边形
∴ AM//EF,AM=EF,DN//GH,DN=GH
∵ EF⊥GH ∴ AM⊥DN,∠AND+∠DAM=90°
∵ ∠BAM+∠DAM=90°
∴ ∠AND=∠BAM
∴ △DAN≌△ABM(ASA)
∴ AM=DN,∴ EF=GH
模块一 正方形中的十字架模型
【例题2】如图,正方形ABCD中,AB=4,点P从点B出发沿着射线AB方向匀速运动,点Q从点C出发沿着射线BC方向匀速运动,P,Q两点同时出发且运动速度相等,连接DP,AQ,二者交于点E,连接CE,则CE的最小值为__________.
【分析】CE的值随E点位置的变化而变化,尝试分析E点的运动轨迹,由十字架模型得知AQ⊥DP,由“定弦定角”出隐圆可判断E点轨迹,进而确定CE的最小值。
【解答】如图,P,Q处于出发点位置时,E点为正方形的中心;
∵ 两点同时出发且运动速度相等
∴ BP=CQ,AP=BQ,则△APD≌△BQA(SAS)
∴ ∠ADP=∠BAQ
∵ ∠BAQ+∠DAQ=90°,∴ ∠ADP+∠DAQ=90°
∴ ∠AED=90°,则E点的运动轨迹为以AD中点M为圆心,以2为半径的圆弧OD;
连接MC交圆弧OD于点E,此时CE最小,此时EM=DM=2,在Rt△CDM中,CM=
则CE=CM-EM=.
模块一 正方形中的十字架模型
【例题3】如图,正方形ABCD中,AB=6,E,F分别在DC边AD边的延长线上,且CE=DF,连接AE和BF,二者交于点G,AE与BC边交于点M,BF与CD边交于点N,若阴影部分与正方形的面积之比为5:9,则△ABG的周长为__________.
【分析】由十字架模型可知,AE⊥BF,且有3组全等三角形,从而得出△ABD和四边形GMCN的面积关系,求出Rt△ABG的面积,于是得到两直角边的乘积,结合勾股定理与完全平方公式,求得其周长.
【解答】由十字架模型可知, △FAB≌△EDA,AE⊥BF, △ABM≌△BCN
∴ , ∴ , 即
∵ AB=6, ∴正方形面积为36
∵ 阴影部分与正方形的面积之比为5:9,∴ 阴影面积为20,则16
∴
设Rt△ABG的两条直角边分别为a, b,则ab=16,由勾股定理得:a +b =AB =36,
∴ a+b=,所以△ABG的周长=a+b+AB= .
四边形中的十字架模型
执教人:汤子弘
罗湖区中考备考“百师助学”课程
单位:翠园文锦中学
正方形中的十字架模型
01
矩形中的十字架模型
推理与证明“+”十字架模型
目录
02
03
模块二 矩形中的十字架模型
【例题】如图,矩形ABCD中, ,点EF分别在CD边和AD边上,AE与BF交于点G.
证明:(1)若AE⊥BF,则 ;(2)若 ,则AE⊥BF.
【分析】由AE⊥BF,根据同角的余角相等推出△ADE和△BAF的一组锐角相等,从而推出△ADE∽△BAF.
【解答】在矩形ABCD中,∠ADE=∠BAF=90°
∵ AE⊥BF,∴ ∠AGB=90°
∴ ∠ABF+∠BAG=90°且∠DAE+∠BAG=90°
∴ ∠DAE=∠ABF
∴ △ADE∽△BAF
∴
模块二 矩形中的十字架模型
【例题】如图,矩形ABCD中, ,点EF分别在CD边和AD边上,AE与BF交于点G.
证明:(1)若AE⊥BF,则 ;(2)若 ,则AE⊥BF.
【分析】证明AE⊥BF,要先证明△ADE∽△BAF,由相似三角形的判定定理得,需要证明,结合已知条件和勾股定理可推.
【解答】∵ ,∴ AD=k · AB
∵ ,∴ AE=k · BF
在Rt△ADE中,DE=;
在Rt△BAF中, AF=,∴
∴ ,又∠ADE=∠BAF=90°,∴ △ADE∽△BAF
∴ ∠DAE=∠ABF,∴ ∠DAE+∠BAG=90°,∴ ∠ABF+∠BAG=90°,即AE⊥BF
四边形中的十字架模型
执教人:汤子弘
罗湖区中考备考“百师助学”课程
单位:翠园文锦中学
正方形中的十字架模型
01
矩形中的十字架模型
推理与证明“+”十字架模型
目录
02
03
模块三 推理与证明“+”十字架模型
【探究证明】
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列题,请你给出证明:如图1,在矩形ABCD中,EF⊥GH,EF分别交AD,BC于点E,F,GH分别交AB,DC于点G,H,求证: .
【结论应用】
(2)如图2,将矩形ABCD沿EF折叠,使得点B和点D重合,若AB=2,BC=3. 求折痕EF的长;
【拓展运用】
(3)如图3,将形ABCD沿EF折叠,使得点D落在AB边上的点G处,点C落在点P处,得到四边形EFPG,若AB=2,BC=3,EF=,请求BP的长.
模块三 推理与证明“+”十字架模型
【探究证明】
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列题,请你给出证明:如图1,在矩形ABCD中,EF⊥GH,EF分别交AD,BC于点E,F,GH分别交AB,DC于点G,H,求证: .
【解答】如图,过点A作AP//EF,交BC于点P,过B作BQ//GH
∵ 四边形ABCD是矩形,∴ AB//CD,AD//BC
∴ 四边形AEFP,四边形BGHQ都是平行四边形
∴ AP=EF,GH=BQ
∵ GH⊥EF,∴ AP⊥BQ,∴ ∠BAT+∠ABT=90°
∵ 四边形ABCD是矩形,∴ ∠ABP=∠C=90°,AD=BC
∴ ∠ABT+∠CBQ=90°,∴∠BAP=∠CBQ
∴ △ABP∽△BCQ,∴ ,∴
模块三 推理与证明“+”十字架模型
【结论应用】
(2)如图2,将矩形ABCD沿EF折叠,使得点B和点D重合,若AB=2,BC=3. 求折痕EF的长;
【解答】连接BD
∵ 四边形ABCD是矩形,
∴ ∠C=90°,AB=CD=2
∴ BD=
∵ D,B关于EF对称,∴ BD⊥EF
∴ ,∴ ,∴ EF=
【分析】根据折叠的性质,连接BD,则EF⊥BD,运用相似比求解EF;
模块三 推理与证明“+”十字架模型
【拓展运用】
(3)如图3,将形ABCD沿EF折叠,使得点D落在AB边上的点G处,点C落在点P处,得到四边形EFPG,若AB=2,BC=3,EF=,请求BP的长.
【解答】∵ 四边形ABCD是矩形,∴ AB=CD=2,AD=BC=3,∠A=90°
∴ ,∴ DG=,∴ AG=
由翻折可知:PG=CD=2,ED=EG,设ED=EG=x
在Rt△AEG中,∵ EG =AE +AG ,∴ x =AG +AE ,∴ x =(3-x) +1
∴ x=,∴ DE=EG=,∴ AE=AD-DE=,在Rt△AEG中,AG=1,∴ BG=1
作PH⊥AB,交AB的延长线于H,则∠PGH+∠GPH=∠PGH+∠AGE=90°
∴ ∠GPH=∠AGE,由∵ ∠H=∠A=90°
∴ △GPH∽△EGA,∴ ,解得PH=,HG=,∴ BH=HG-BG=,在Rt△BPH中,BP=
四边形中的十字架模型
执教人:汤子弘
罗湖区中考备考“百师助学”课程
单位:翠园文锦中学
行业PPT模板http://www./hangye/
概述:正方形与矩形的基本性质
性质分类 矩形 正方形
边与角 对边平行且相等 四个角均为直角 四边相等且对边平行
四个角均为直角
对角线 对角线相等且互相平分 不垂直 对角线相等、垂直且平分
每条对角线平分一组对角
对称性 轴对称(2条对称轴) 中心对称 轴对称(4条对称轴)
中心对称
分割图形 对角线分割为4个等腰三角形 对角线分割为4个等腰直角三角形
特殊属性 是平行四边形的特例(含直角) 是矩形与菱形的交集
(兼具边等、角直、对角线垂直)
几何层级 平行四边形 → 矩形 平行四边形 → 菱形 → 正方形
(或矩形 → 正方形)
行业PPT模板http://www./hangye/
概述:正方形中的十字架模型
图 1
基本模型:
如图1,正方形ABCD中,E,F分别为AB,BC边上的点,DE与AF交与点G,则:
①AE=BF(或BE=CF);
②DE=AF;
③DE⊥AF;
“知一推二”,即以其中任意一个作为条件,均可推出另外两个结论成立。
行业PPT模板http://www./hangye/
概述:矩形中的十字架模型
基本模型:
如图1,矩形ABCD中,,点E,F分别在CD边和AD边上,AE与BF交与点G,则:
① 与②AE⊥BF等价,即以其中任意一个作为条件,另一个结论都成立.
图 1
行业PPT模板http://www./hangye/
考点和题型分析
考试中常见的考察题型主要有:
(1)正方形中十字架模型的应用与变化;
(2)矩形中十字架模型的应用与变化;
(3)推理与证明在十字架模型的结合与应用。
从近几年中考真题来看,考察的核心思想是让学生以基本模型为抓手,通过自己构造创设条件,结合不同的情况综合运用图形的变化与几何证明。熟练理解和运用图形的关系包含位置关系(垂直、平行)、数量关系(全等、相似)进一步提高对几何与证明等相关知识的综合运用能力。
四边形中的十字架模型
执教人:汤子弘
罗湖区中考备考“百师助学”课程
单位:翠园文锦中学
正方形中的十字架模型
01
矩形中的十字架模型
推理与证明“+”十字架模型
目录
02
03
模块一 正方形中的十字架模型
【例题1】如图,E,G,F,H分别在正方形ABCD的各边上(不与正方形顶点重合),若EF⊥GH,求证:EF=GH.
【分析】平移思想,将EF和GH转化,转化为基本模型.
【解答】作AM//EF交BC边于点M,作DN//GH交AB边于点N
∵ 正方形ABCD
∴ AD=AB,∠DAN=∠ABM=90°
∵ AD//BC,AB//CD,
∴ 四边形AMFE和四边形DNGH均为平行四边形
∴ AM//EF,AM=EF,DN//GH,DN=GH
∵ EF⊥GH ∴ AM⊥DN,∠AND+∠DAM=90°
∵ ∠BAM+∠DAM=90°
∴ ∠AND=∠BAM
∴ △DAN≌△ABM(ASA)
∴ AM=DN,∴ EF=GH
模块一 正方形中的十字架模型
【例题2】如图,正方形ABCD中,AB=4,点P从点B出发沿着射线AB方向匀速运动,点Q从点C出发沿着射线BC方向匀速运动,P,Q两点同时出发且运动速度相等,连接DP,AQ,二者交于点E,连接CE,则CE的最小值为__________.
【分析】CE的值随E点位置的变化而变化,尝试分析E点的运动轨迹,由十字架模型得知AQ⊥DP,由“定弦定角”出隐圆可判断E点轨迹,进而确定CE的最小值。
【解答】如图,P,Q处于出发点位置时,E点为正方形的中心;
∵ 两点同时出发且运动速度相等
∴ BP=CQ,AP=BQ,则△APD≌△BQA(SAS)
∴ ∠ADP=∠BAQ
∵ ∠BAQ+∠DAQ=90°,∴ ∠ADP+∠DAQ=90°
∴ ∠AED=90°,则E点的运动轨迹为以AD中点M为圆心,以2为半径的圆弧OD;
连接MC交圆弧OD于点E,此时CE最小,此时EM=DM=2,在Rt△CDM中,CM=
则CE=CM-EM=.
模块一 正方形中的十字架模型
【例题3】如图,正方形ABCD中,AB=6,E,F分别在DC边AD边的延长线上,且CE=DF,连接AE和BF,二者交于点G,AE与BC边交于点M,BF与CD边交于点N,若阴影部分与正方形的面积之比为5:9,则△ABG的周长为__________.
【分析】由十字架模型可知,AE⊥BF,且有3组全等三角形,从而得出△ABD和四边形GMCN的面积关系,求出Rt△ABG的面积,于是得到两直角边的乘积,结合勾股定理与完全平方公式,求得其周长.
【解答】由十字架模型可知, △FAB≌△EDA,AE⊥BF, △ABM≌△BCN
∴ , ∴ , 即
∵ AB=6, ∴正方形面积为36
∵ 阴影部分与正方形的面积之比为5:9,∴ 阴影面积为20,则16
∴
设Rt△ABG的两条直角边分别为a, b,则ab=16,由勾股定理得:a +b =AB =36,
∴ a+b=,所以△ABG的周长=a+b+AB= .
四边形中的十字架模型
执教人:汤子弘
罗湖区中考备考“百师助学”课程
单位:翠园文锦中学
正方形中的十字架模型
01
矩形中的十字架模型
推理与证明“+”十字架模型
目录
02
03
模块二 矩形中的十字架模型
【例题】如图,矩形ABCD中, ,点EF分别在CD边和AD边上,AE与BF交于点G.
证明:(1)若AE⊥BF,则 ;(2)若 ,则AE⊥BF.
【分析】由AE⊥BF,根据同角的余角相等推出△ADE和△BAF的一组锐角相等,从而推出△ADE∽△BAF.
【解答】在矩形ABCD中,∠ADE=∠BAF=90°
∵ AE⊥BF,∴ ∠AGB=90°
∴ ∠ABF+∠BAG=90°且∠DAE+∠BAG=90°
∴ ∠DAE=∠ABF
∴ △ADE∽△BAF
∴
模块二 矩形中的十字架模型
【例题】如图,矩形ABCD中, ,点EF分别在CD边和AD边上,AE与BF交于点G.
证明:(1)若AE⊥BF,则 ;(2)若 ,则AE⊥BF.
【分析】证明AE⊥BF,要先证明△ADE∽△BAF,由相似三角形的判定定理得,需要证明,结合已知条件和勾股定理可推.
【解答】∵ ,∴ AD=k · AB
∵ ,∴ AE=k · BF
在Rt△ADE中,DE=;
在Rt△BAF中, AF=,∴
∴ ,又∠ADE=∠BAF=90°,∴ △ADE∽△BAF
∴ ∠DAE=∠ABF,∴ ∠DAE+∠BAG=90°,∴ ∠ABF+∠BAG=90°,即AE⊥BF
四边形中的十字架模型
执教人:汤子弘
罗湖区中考备考“百师助学”课程
单位:翠园文锦中学
正方形中的十字架模型
01
矩形中的十字架模型
推理与证明“+”十字架模型
目录
02
03
模块三 推理与证明“+”十字架模型
【探究证明】
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列题,请你给出证明:如图1,在矩形ABCD中,EF⊥GH,EF分别交AD,BC于点E,F,GH分别交AB,DC于点G,H,求证: .
【结论应用】
(2)如图2,将矩形ABCD沿EF折叠,使得点B和点D重合,若AB=2,BC=3. 求折痕EF的长;
【拓展运用】
(3)如图3,将形ABCD沿EF折叠,使得点D落在AB边上的点G处,点C落在点P处,得到四边形EFPG,若AB=2,BC=3,EF=,请求BP的长.
模块三 推理与证明“+”十字架模型
【探究证明】
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列题,请你给出证明:如图1,在矩形ABCD中,EF⊥GH,EF分别交AD,BC于点E,F,GH分别交AB,DC于点G,H,求证: .
【解答】如图,过点A作AP//EF,交BC于点P,过B作BQ//GH
∵ 四边形ABCD是矩形,∴ AB//CD,AD//BC
∴ 四边形AEFP,四边形BGHQ都是平行四边形
∴ AP=EF,GH=BQ
∵ GH⊥EF,∴ AP⊥BQ,∴ ∠BAT+∠ABT=90°
∵ 四边形ABCD是矩形,∴ ∠ABP=∠C=90°,AD=BC
∴ ∠ABT+∠CBQ=90°,∴∠BAP=∠CBQ
∴ △ABP∽△BCQ,∴ ,∴
模块三 推理与证明“+”十字架模型
【结论应用】
(2)如图2,将矩形ABCD沿EF折叠,使得点B和点D重合,若AB=2,BC=3. 求折痕EF的长;
【解答】连接BD
∵ 四边形ABCD是矩形,
∴ ∠C=90°,AB=CD=2
∴ BD=
∵ D,B关于EF对称,∴ BD⊥EF
∴ ,∴ ,∴ EF=
【分析】根据折叠的性质,连接BD,则EF⊥BD,运用相似比求解EF;
模块三 推理与证明“+”十字架模型
【拓展运用】
(3)如图3,将形ABCD沿EF折叠,使得点D落在AB边上的点G处,点C落在点P处,得到四边形EFPG,若AB=2,BC=3,EF=,请求BP的长.
【解答】∵ 四边形ABCD是矩形,∴ AB=CD=2,AD=BC=3,∠A=90°
∴ ,∴ DG=,∴ AG=
由翻折可知:PG=CD=2,ED=EG,设ED=EG=x
在Rt△AEG中,∵ EG =AE +AG ,∴ x =AG +AE ,∴ x =(3-x) +1
∴ x=,∴ DE=EG=,∴ AE=AD-DE=,在Rt△AEG中,AG=1,∴ BG=1
作PH⊥AB,交AB的延长线于H,则∠PGH+∠GPH=∠PGH+∠AGE=90°
∴ ∠GPH=∠AGE,由∵ ∠H=∠A=90°
∴ △GPH∽△EGA,∴ ,解得PH=,HG=,∴ BH=HG-BG=,在Rt△BPH中,BP=
同课章节目录
