2024-2025学年六年级下册数学小升初重点校分班考前冲刺卷苏教版(含答案解析)
文档属性
| 名称 | 2024-2025学年六年级下册数学小升初重点校分班考前冲刺卷苏教版(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 335.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 20:13:09 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年六年级下册数学小升初重点校分班考前冲刺卷
一、填空题
1.工厂要生产240个零件,师傅单独做4小时可以完成这批零件的,徒弟6小时可以完成这批零件的,两人合作 小时可以完成。完成时,师傅做了 个零件。
2.六(1)班女生人数占全班的 , 男生人数占全班的 ,如果六 (1)班有42 人, 那么女生有 人。
3.爱心超市每月一次给社区清洁工人发放爱心小礼包,每次超市会准备72个面包、180袋小饼干,打包成若干份,要求每份里面的面包个数相同,小饼干袋数也相同。爱心超市每次最多能发放给 位社区清洁工人,每位社区清洁工人会收到 个面包、 袋小饼干。
4.下图中的两个圆大小相等,线段AB长15厘米。圆的直径是 厘米,圆的面积是 平方厘米。
5.一艘轮船从甲地到乙地每小时航行30 km,然后按原路返回,若想往返的平均速度为40km,则返回时每小时应航行 km。
6.(商品经济)某种电器上半月按定价1000元的价格出售,共销售50台,下半月降价5%,这样销售量增加了20% ,所获利润比上半月多500元。这种电器每台的成本是 元。
7.星期天妈妈要做以下家务:擦玻璃要20分钟,收拾厨房要15分钟,用全自动洗衣机洗衣服要30分钟,晾衣服要6分钟。妈妈做完这些家务至少需要 分钟。
8.小红把自己钱的 给小明以后,两人的钱数相等,则小红、小明两人原来的钱数之比是 .
9.如图,长方形长 8dm、宽 4dm,B、C 两点把长方形的一条长按1:2:1分成了三段,线段BC长 dm,三角形 ABC 的面积是长方形面积的 。
10.某工厂生产的25个零件中有一个是次品,它比正品轻一些。用天平称,至少称 次就一定能找出次品。
11.在保龄球比赛的最后一局中,小白得199分,从而把若干局的平均分由177提高到178,为了把他的平均分提高到179,下一局他必须得 分。
12.一幅地图的线段比例尺是 ,改写成数值比例尺是 。在这幅地图上量得泰兴到南京的图上距离是19.8厘米,实际距离是 千米。
13.图中,长方形的面积和圆的面积相等,已知圆的半径是3厘米,阴影部分的面积是 平方厘米.(用小数表示)
14.将一个底面周长是9.42dm的圆柱形木料,沿着底面直径垂直切一刀,切成两个半圆柱,表面积增加4.8dm2,原来这个圆柱形木料的体积是 立方分米。
15.某工厂从甲车间调出总人数的到乙车间后,甲乙两车间的人就一样多,原来甲乙两车间的人数比是 。
二、判断题
16.两个圆柱的体积相等,它们的表面积也一定相等。( )
17.甲、乙两校女生人数都占该校总人数的55%,那么甲、乙两校女生人数一定相等。( )
18.把一个长方形按5:1的比放大,就是把长方形的长和宽都放大到原来的5倍。( )
19.在比例尺是1:12500000的地图上,量得两城市问的距离是8厘米,如果画在比例尺是1:8000000的地图上,图上距离是12.5厘米。( )
20.报刊的单价一定,报刊的份数和总价成正比例。( )
21.长方体、正方体和圆柱的体积都可以用“底面积×高”计算。( )
22.甲比乙多25%,乙就比甲少20%。( )
23.正方体的表面积=棱长×棱长×6.( )
三、单选题
24.夏天多高温天气,人体会经常出汗,专家建议要适量补充含盐率为0.9%的淡盐水以防中暑。下图( )杯淡盐水的含盐率最接近0.9%。
A. B. C. D.
25.一支尖端部分是圆锥形的铅笔,圆锥部分的长度是圆柱部分的 ,则圆锥部分的体积是圆柱体积的( )。
A. B. C. D.
26.有14个同样的零件,其中有13个质量相同,另有1个质量不足,轻一些,是次品.用天平至少称( )次能保证找出这个次品。
A.2 B.3 C.4 D.5
27.下列说法中,正确的是( )。
A.降价25%就是打二五折
B.某地的麦收进度已过八成,表示已经收割的小麦面积超过了该地小麦总面积的80%
C.某超市本月的营业额是20万元,按营业额的5%缴税,本月应缴税10万元
D.一件商品先提价10%,再打九折出售,现价与原价相同
28.聪聪和明明做数学游戏,他们准备从5、7、8、9四张牌中分别抽出一张,再把两张牌上的数相乘。如果积是奇数,聪聪赢,积是偶数,明明赢。谁赢的可能性大?( )
A.聪聪赢的可能性大 B.明明赢的可能性大
C.两人赢的可能性一样大 D.无法确定
29.两根铁丝,第一根用去m,第二根用去,两根铁丝正好都剩下m,比较原来两根铁丝的长短,结果是( )。
A.第一根长 B.第二根长 C.一样 长 D.无法比较
30.210名少先队员选举大队长,有三位候选人甲、乙、丙,每人只能选他们之中的一个人,不能弃权。前190张票中,甲得75票,乙得65票,丙得50票,规定谁的票最多谁当选。若甲要当选,最少还需要( )张票.
A.6 B.7 C.8 D.10
31.一块长方形菜地,周长是120m,长和宽的比是2:1。这块长方形菜地的面积是( )m2。
A.3200 B.1600 C.800
32.下图是水滴进玻璃容器的示意图(滴水速度相同),下图表示的是容器中水的高度随滴水时间变化的情况(图中刻度、单位都相同)。下列选项中对应关系正确的是( )。
A. B. C. D.
33.一个长方体水缸,长20厘米,宽15厘米,水深6厘米,将一块石头投入水中(石头全部浸没)水面上升2厘米(水未溢出),求这块石头的体积,列式正确的是( )。
A.20×15×2 B.20×15×6
C.20×15×(6-2) D.2×2×2
四、计算题
34.直接写得数。
+ = ÷6= × = ×0÷ = 2- + =
×16= 6- = ÷ = ×3= ÷ =
35.计算下面各题,能简算的要简算。
0.25×3.2×12.5
36.解方程。
(1)0.25x+ (2) (3)0.3(6+x)=4.5
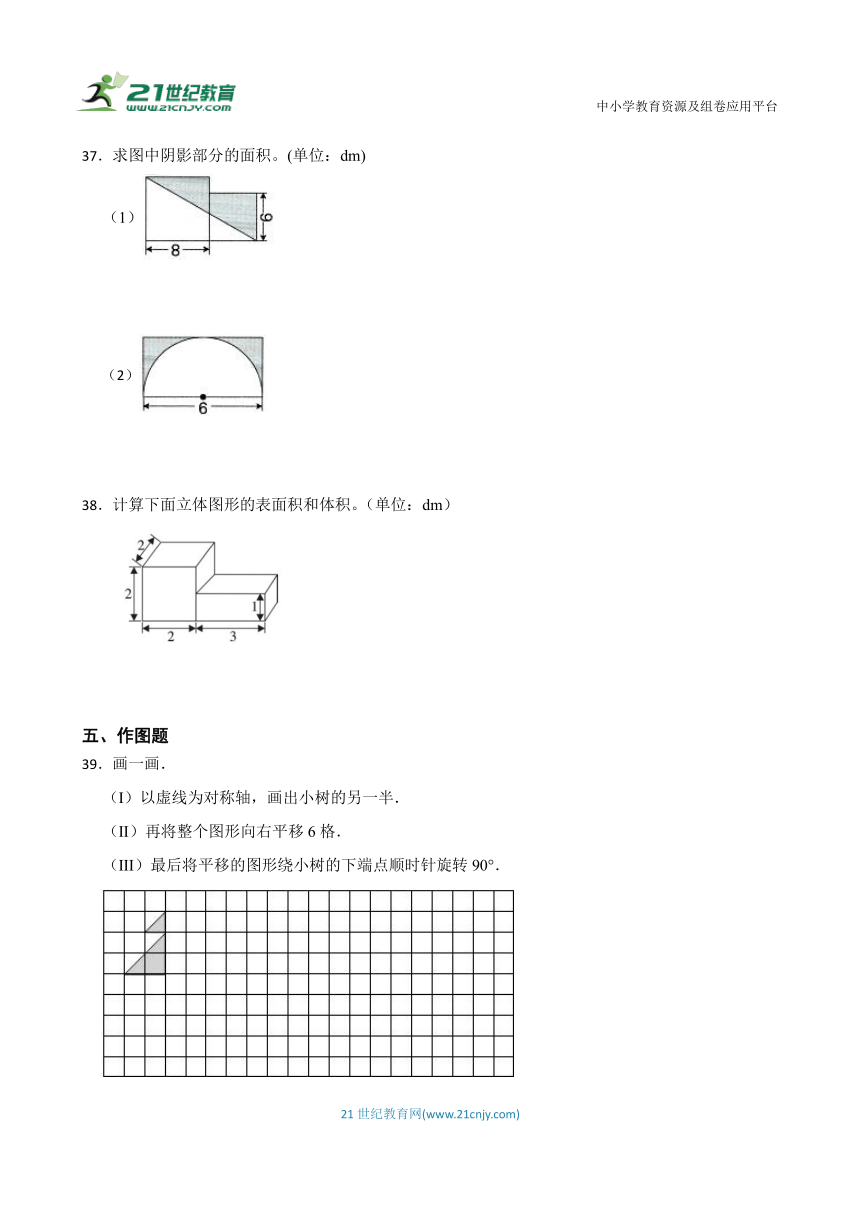
37.求图中阴影部分的面积。(单位:dm)
(1)
38.计算下面立体图形的表面积和体积。(单位:dm)
五、作图题
39.画一画.
(I)以虚线为对称轴,画出小树的另一半.
(II)再将整个图形向右平移6格.
(III)最后将平移的图形绕小树的下端点顺时针旋转90°.
六、解决问题
40. 某汽车客运站开往某市的汽车每隔15分钟开出一班。小王叔叔想搭乘6:45这班汽车到某市,但他到达车站时,已经是6:48了,他要等多少分钟下一班汽车才来?
41. 为了吸引游客,颐和园冰场正在进行抽奖活动,奖品如右图所示。如果你是冰场的运营经理,请你选择下面的一种材料设计抽奖方案,并简要说明理由。
我选择的材料: ( )。 (填序号)
我设计的方案:
42.甲、乙、丙三人同时从A城到B城。甲45分走了5千米,乙小时走了3千米,丙小时走了4千米。谁走的快些?
43. 双十一大促,某商场利用“幸运大转盘”举行抽奖活动,满99 元可以抽奖一次,指针指向哪个区域就可以获得哪种奖品,下表是转盘转动16次的结果。
奖品 纸巾 袜子 牙膏 50元代金券
次数/次 9 4 2 1
(1)下一次抽到什么奖品的可能性最大
(2)请你根据上面的结果设计出一个符合转动结果的转盘。
44.(等积变换)一个棱长60厘米的正方体容器装了一半水,把这些水的60%倒入一个底面积为48平方分米的圆柱形容器里,水的高度是多少分米?
45.石膏娃娃是雕塑和绘画融合的新艺术。妙妙用颜料给一些石膏娃娃涂色,若每个娃娃用1.8g颜料,则多出0.8g颜料,若每个娃娃用2.8g颜料,则缺3.2g颜料,有多少个石膏娃娃 多少克颜料
46. 一个圆锥形稻谷堆的底面周长是12.56m,高是1.8m。现在把这些稻谷全部装入一个底面周长是6.28m的圆柱形粮囤里,可以装多高?
47.五年级参加艺术节展演的学生有28人,六年级参加艺术节展演的学生人数比五年级多,六年级有多少人参加艺术节展演?
48.树木是氧气制造厂。1公顷阔叶林在生长季节1天大约能吸收1t二氧化碳,放出0.76t氧气。李爷爷退休后,义务维护一片长是360m,宽是250m的长方形杨树林,这片树林1天放出多少吨氧气
49.六一儿童节,305班的孩子要为福利院的小朋友们捐助爱心书包69个,大箱子每箱可装28个,每箱需快递费15元;小箱子每箱可装15个,每箱需快递费12元。如何装箱最省钱?一共需要多少元?
50.A、B相地相距1080米,甲、乙两人同时从两地相向而行, 6分钟相遇。已知甲的速度比乙的速度慢,相遇时,甲比乙少行多少米?
参考答案及试题解析
1.;144
【解析】解:÷4=
÷6=
1÷(+)
=1÷
=(小时)
×=
240×=144(个)。
故答案为:;144。
【分析】两人合作完成需要的时间=工作总量÷工作效率的和;完成时,师傅做零件的个数=师傅平均每小时完成的分率×师傅工作的时间×零件的总个数。
2.;24
【解析】解:1-=
42×=24(人)
故答案为:;24。
【分析】把 六 (1)班 的总人数看作单位“1”, 六(1)班女生人数占全班的 , 那男生人数占全班的(1-=);求女生人数,用 六 (1)班 的总人数乘 六(1)班女生人数占全班的份数,计算即可求解。
3.36;2;5
【解析】解:72 = 2×2×2×3×3,180 = 2×2×3×3×5,
因此,72和180的最大公因数是 2×2×3×3=36,
所以爱心超市每次最多能发放给36位社区清洁工人。
每位清洁工人将收到的面包和小饼干数量:
面包:72÷36 = 2(个)
小饼干:180÷36 = 5(袋)
故答案为:36;2;5。
【分析】本题要求找出爱心超市每次最多能发放给多少位社区清洁工人,同时每位清洁工人将收到多少个面包和多少袋小饼干。由题意可知,每次超市准备的面包和小饼干都需要能平均分给每位清洁工人。需要找到能同时被72(面包数量)和180(小饼干数量)整除的最大数,这个数即为最多能发放给的清洁工人数量。
4.10;78.5
【解析】解:圆的直径:15÷3×2=10(厘米),圆的面积:(平方厘米)
故答案为:10;78.5。
【分析】先算出圆的半径15除3再乘2为直径,再根据面积公式得出面积。
5.60
【解析】去时时间:
往返时间:
返回时间:
(千米/时)
故答案为60
【分析】
利用平均速度公式,设出路程和返回速度,根据已知条件列出方程,通过解方程求出返回时的速度.
6.650
【解析】解:设这种电器每台的成本是元。
1000×(1-5%)
=1000×0.95
=950(元)
50×(1+20%)
=50×1.2
=60(台)
60×(950-x)-50×(1000-x)=500
57000-60x-50000+50x=500
10x=7000-500
x=6500÷10
x=650
故答案为:650。
【分析】根据题意可得:上半月每台定价×(1-下降的百分比)=下半月每台定价,上半月销售数量×(1+增加的百分比)=下半月销售数量;
每台定价-成本=每台利润,销售数量×(每台定价-成本)=总利润,所以,下半月销售数量×(下半月每台定价-每台成本)-上半月销售数量×(上半月每台定价-每台成本)=下半月比上半月多获得的利润,据此关系式设这种电器每台的成本是元,列方程即可解答。
7.41
8.2:1
【解析】
解: 把小红原来的钱数看作"1",平均分成4份,给小明1份数后还剩下3份数,现在两人钱数相等,说明小明现在也有3份数的钱,小明现在的钱数就为3份数,原来的钱数就是2份
小红、小明原有钱数的比是:4份:2份=2:1.
故答案为:2:1.
【分析】根据题意“ 小红把自己钱的 给小明,把小红原来的钱数看作是4份,给小明1份后小红还剩下3份,再根据” 两人的钱数相等 “,可推出小明现在的钱数也是3份,原来的钱数就是2份,进而写出两人原来的钱数的比即可。
9.4;
【解析】1+2+1=4份,8÷4=2dm,BC=2×2=4dm;
长方形面积=4×8=32(dm2)
三角形面积:4×4÷2=8(dm2)
8÷32=。
故答案为:4;。
【分析】首先,根据题目描述,线段AB、BC、CD的长度比例为1:2:1可知长方形的长被平均分成了1+2+1=4份,求得每份是8÷4=2dm,而BC占2份也就是4dm;由于BC是三角形ABC的底边,且三角形ABC的高即为长方形的宽4dm,所以三角形的面积=底×高÷2=4×4÷2=8(dm2),而长方形的面积=长×宽=4×8=32(dm2),因此三角形ABC的面积是长方形面积的:8÷32=。
10.3
【解析】解:25÷3=8(个)余1(个),8+1=9(个),即三份的数量分别是8、8、9;
9÷3=3(个),即每份数量是1个;
3÷3=1(个),最后每份数量是1个;
1+1+1=3(次),所以某工厂生产的25个零件中有一个是次品,它比正品轻一些。用天平称,至少称3次就一定能找出次品。
故答案为:3。
【分析】本题可以先将25个零件分成3份,每份数量分别是8、8、9,然后进行检测。
第一次,天平检测数量相同的两组8个零件,如果重量相同,则次品在剩下的9个零件中,此时将9个零件再平均分成3份,每份3个,第二次检测其中的任意两份零件,如果重量相同,则次品就在最后的3个零件中;最后将剩下的3个零件平分成3份,每份1个零件,第三次检测任意2个零件,平衡则剩下的最后一个零件是次品。因此至少称3次就一定能找出次品。
11.201
【解析】解:设小白一共打了x局。
178x-(x-1)×177=199
178x-(177x-177)=199
178x-177x+177=199
x+177=199
x=199-177
x=22
179×23-178×22
=4117-3916
=201(分)
所以下一局他必须得201分。
故答案为:201
【分析】根据题意,先设小白一共打了x局,最后一局的199分,使平均分由177分提高到178分,列式为178x-(x-1)×177=199,解得x=22;所以下一局他必须得179×23-178×22分,据此解答。
12.1∶1000000;198
13.21.195
【解析】
3.14×32-3.14×32×
=3.14×9-3.14×9×
=28.26-7.065
=21.195(平方厘米)
答:阴影部分的面积是21.195平方厘米.
故答案为:21.195.
【分析】本题考查的主要内容是圆的面积计算问题,根据圆的面积=πr 进行分析即可.
14.5.652
【解析】解:9.42÷3.14=3(分米)
4.8÷2÷3=0.8(分米)
3.14×(3÷2)×(3÷2)×0.8
=3.14×1.5×1.5×0.8
=7.065×0.8
=5.652(立方分米)
故答案为:5.652。
【分析】表面积增加的面积是两个长方形,长方形的长就是圆柱的底面直径;
底面周长÷π=底面直径;增加的面积÷2÷底面直径=圆柱的高;
直径÷2=半径,π×底面半径的平方×高=圆柱形木料的体积。
15.5:4
【解析】解:1:(1-×2)
=1:(1-)
=1:
=5:4。
故答案为:5:4。
【分析】把原来甲车间的人数看作单位“1”,由“ 从甲车间调出总人数的到乙车间后,甲乙两车间的人就一样多 ”,说明甲车间人数比乙车间人数多甲车间人数的×2,则乙车间人数是甲车间人数的(1-×2)=,进而写出原来甲乙两车间的人数比。
16.错误
【解析】 两个圆柱的体积相等,它们的表面积可能相等,也可能不相等,原题说法错误。
故答案为:错误。
【分析】 此题主要考查了圆柱的体积、表面积的计算公式,圆柱的体积=底面积×高,圆柱的体积是由它的底面积和高两个条件决定的,而它的表面积=侧面积+底面积×2;除非它们的底面积和高分别相等,表面积才会相等,如果它们的底面积和高各不相等,表面积就不相等,据此判断 。
17.错误
【解析】因为两校的总人数不一等相等,虽然女生占的百分数相等,但女生人数不一定相等,本题错.
故答案为:错误.
【分析】女生人数=全校学生总数×女生占的百分数,据此解答.
18.正确
【解析】解:把一个长方形按5:1的比放大,就是把长方形的长和宽都放大到原来的5倍。
故答案为:正确。
【分析】把一个图形按比例放大,就是把这个图形的每条边都扩大相同的倍数。
19.正确
【解析】解:根据题意,可得
实际距离:
由于实际距离相同,所以它在比例尺是1∶8000000的地图上的图上距离为:
故答案为:正确
【分析】图上距离与实际距离的比叫作这幅图的比例尺,则图上距离=实际距离×比例尺,实际距离=图上距离÷比例尺。先根据比例尺1∶12500000和图上距离,求出实际距离,由于实际距离相同,所以再根据实际距离和比例尺1∶8000000求出图上距离。
20.正确
【解析】解:总价÷份数=单价(一定),总价和份数的商一定,二者成正比例,原题说法正确.
故答案为:正确
【分析】根据数量关系判断总价和份数的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例.
21.正确
【解析】长方体、正方体和圆柱的体积,都可以用底面积×高来计算,由此说法正确。
故答案为:正确
【分析】长方体、正方体和圆柱的体积,都可以用底面积×高来计算,由此即可判断。
22.正确
【解析】解:甲比乙多25%,乙是1,则甲就是1+25%=1.25,则乙就比甲少:(1.25-1)÷1.25=0.25÷1.25=20%。原题说法正确。
故答案为:正确。
【分析】把乙看作1,则甲就是1.25,用乙比甲少的除以甲即可求出乙比甲少百分之几。
23.正确
【解析】正方体的棱长都相等,个面的面积都相等。所以: 正方体的表面积=棱长×棱长×6.
【分析】正方体棱长,各个面的大小,形状完全相同。
24.C
25.C
【解析】解:3×3=9,
1÷9=;
故答案为:C。
【分析】根据题意,可以将圆柱看成3个与圆锥等底等高的圆柱,根据等底等高的圆柱体积是圆锥的3倍,可以得到圆柱部分体积是圆锥部分的体积的9倍,据此求解。
26.B
【解析】解:第一次把14个零件分成3份5个、5个、4个,取5个的两份分别放在天平两侧,若天平平衡,较轻的在未取的一份,若天平不平衡,取较轻的一份继续;
第二次,取含有较轻的一份(5个或4个),分成3份:2个、2个、1个,取2个的分别放在天平的两侧,若天平平衡,则未取的为较轻的次品,若天平不平衡,取较轻的继续;
第三次,把含有较轻的份(2个)分别放在天平两侧,即可找到较轻的次品。
所以至少称3次就一定能找出次品零件。
故答案为:B。
【分析】天平是用来称量物体质量的工具,此题并不是称量物体的质量,而是使用天平来比较物体质量的大小,所以在调好的天平两盘中分别放上物体,当哪边的托盘上升,则说明这边托盘中的物体质量偏小。
27.B
【解析】解:A.降价25%意味着现价为原价的75%(即100% - 25%),而打二五折对应的是原价的25%。错误。
B.“八成”表示80%,麦收进度已过八成,即收割面积超过总面积的80%。正确。
C.营业额20万元,按5%缴税,应缴税款为:20×5%=1(万元) 错误。
D.设原价为x,先提价10%后价格为1.1x,再打九折后价格为:1.1x×0.9 = 0.99x 现价为原价的99%,与原价不同,错误。
故答案为:B
【分析】本题考查百分比与折扣的对应关系,以及实际问题中的百分比应用。关键点包括:降价25%对应七五折,八成即80%,税率计算需准确,提价后折扣的复合计算。
28.C
【解析】解:积的情况有:35、40、45、56、63、72;其中,奇数有3个,偶数有3个,两人赢的可能性一样大。
故答案为:C。
【分析】从5、7、8、9四张牌中分别抽出一张,再把两张牌上的数相乘,积共有6中情况,其中,奇数有3个,偶数有3个,两人赢的可能性一样大。
29.A
【解析】解:第一根:+=(米);
第二根:÷(1-)=(米);
,所以第一根长。
故答案为:A。
【分析】把第一根用去的长度加上第一根剩下的长度求出第一根的总长度。用第二根剩下的长度除以剩下的分率求出第二根的总长度。比较后判断原来的长短即可。
30.A
【解析】解:甲得x张,乙得(210-190-x)张。
75+x=65+(210-190-x)
75+x=85-x
2x=10
x=5
5+1=6(张)
故答案为:A。
【分析】根据题意可知,还剩20张票,丙就算得了20张也比甲少,所以主要比较甲和乙,设甲得x张,乙得20-x张,根据最后两人的票数相等列方程,求出x后,令甲所得张数比x多1即可当选。
31.C
【解析】解:120÷2=60(米),60÷(2+1)×1=20(米),60-20=40(米),20×40=800(平方米),所以这块长方形菜地的面积是800m2。
故答案为:C。
【分析】菜地的长与宽的和=菜地的周长÷2,所以菜地的宽=菜地的长与宽的和÷菜地的长和宽占的份数和×菜地的宽占的份数,菜地的长=菜地的长与宽的和-菜地的宽,那么长方形菜地的面积=长×宽。
32.D
【解析】解:水面上升先快后慢,所以选择D
故答案为:D。
【分析】观察图形,玻璃容器是圆锥形,时间滴水速度一定,所以滴水时间与水的体积成正比例关系,根据圆锥的体积公式:V=Sh,底面积越来越大,所以得出水面上升是先快后慢的,据此解答即可。
33.A
【解析】解:这块石头的体积=长方体水缸的长×宽×上升水的高度,即:20×15×2。
故答案为:A。
【分析】求这块石头的体积就是求上升水的体积,石头的体积=长方体水缸的长×宽×上升水的高度。
34.+=1 ÷6= ×= ×0÷=0 2-+=
×16=6 6-= ÷= ×3= ÷=
【解析】分数乘整数,分母不变,用分子乘整数,能约分的要约分;
分数乘分数,用分子相乘的积做分子,分母相乘的积作分母,能约分的要约分;
除以一个不为0的数,等于乘这个数的倒数。
35.解:
=3÷[÷12]
=3÷
=120
=6.125+0.875-()
=7-1
=6
=1.25×5.2+1.25×3.8+1.25
=1.25×(5.2+3.8+1)
=1.25×10
=12.5
0.25×3.2×12.5
=0.25×4×(0.8×12.5)
=1×10
=10
【解析】加法交换律:两个数相加,交换加数的位置,它们的和不变,即a+b=b+a。
加法结合律:三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再和第一个数相加它们的和不变,即(a+b)+c=a+(b+c)。
乘法分配律:两个数的和与一个数相乘,可以把两个加数分别与这个数相乘再把两个积相加,即(a+b)×c=a×c+b×c。
(1)先算小括号里面的减法,再算中括号里面的除法,最后算括号外面的除法;
(2)运用加法交换律和加法结合律计算;
(3)运用乘法分配律计算;
(4)运用乘法结合律计算。
36.(1)解:0.25x+
0.25x+﹣=4﹣
0.25x=
4×0.25x=
x=11
(2)解:
0.5x=
2×0.5x= 2
x=1
(3)解:0.3(6+x)=4.5
0.3(6+x)÷0.3=4.5÷0.3
6+x=15
6+x﹣6=15﹣6
x=9
【解析】解比例时,根据比例的基本性质把比例化为方程,再根据等式性质解方程;
比例的基本性质:比例的两个外项之积等于比例的两个内项之积;
等式性质1:等式两边加上或减去同一个数,左右两边仍然相等;
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
37.(1)8×8+6×6-8×(8+6)÷2=44(dm2)
(2)
【解析】
(1) 采用 “总面积 - 空白面积 = 阴影面积” 的方法。先求出两个正方形面积之和作为总面积,再求出空白大三角形面积,最后相减得阴影面积。 三角形面积公式S= (a是底,h是高 ),正方形面积S=边长×边长。
(2) 运用 “长方形面积 - 半圆面积 = 阴影面积”。先算出长方形面积,再求出半圆面积,二者相减得阴影面积。 根据长方形面积公式S=ab(a是长,b是宽 ) , 根据圆面积公式S=πr2。
38.表面积:2×2×6+1×3×2+3×2×2
=24+6+12
=42(dm2)
体积:2×2×2+2×3×1
=8+6
=14(dm3)
答:立体图形的表面积是42平方分米,体积是14立方分米。
【解析】表面积=左边正方体的棱长×棱长×6+右边长方体的长×高×2+长×宽×2;体积=正方体的棱长×棱长×棱长+长方体的长×宽×高。
39.解:(I)根据轴对称图形的定义,画出小树的另一半,如图①.
(II)根据平移的定义将图形①向右平移6格即可得到图形②如图.
(III)利用旋转的定义将图形②绕点o顺时针旋转90°即可得到图形③.
【解析】紧扣轴对称图形的定义和图形平移和旋转的定义即可解决问题.此题考查了轴对称图形的画法以及平移和旋转的应用.
40.解:6时45分+15分=7时
7时-6时48分=12分钟
答:他要等12分钟下一班汽车才来。
【解析】用6时45分加上15分就是下班车到站的时刻,用下班车到站的时刻减去现在的时刻就是他还要等的时间。
41.解:我选择的材料:②
我设计的方案:抽到红球可以获得一等奖,抽到白球可以获得二等奖,抽到黄球可以获得三等奖。
【解析】奖品设计了三种,材料②中刚好有3种颜色的球,所以可以根据三种奖项和3种颜色的球的个数设计方案。抽到一等奖的可能性最小,二等奖次之,三等奖的可能性最大。2<6<12,抽到红球的可能性<抽到白球的可能性<抽到黄球的可能性,所以可以将抽到红球设为一等奖,抽到白球设为二等奖,抽到黄球为三等奖。
42.甲走的快些
43.(1)解:因为抽到纸巾的次数最多,所以下一次抽到纸巾的可能性最大。
(2)解:转盘区域面积由大到小依次是纸巾、袜子、牙膏、50元代金券。
【解析】(1)观察转盘中转动16次的结果,可以发现,纸巾转动的次数最多,50元代金券最少,所以,下次抽到纸巾的可能性最大
(2)根据转盘中抽到的数据显示,比较纸巾、袜子、牙膏和50元代金券的次数,即可判断
44.解:60厘米=6分米
6×6×6÷2
=36×6÷2
=216÷2
=108(立方分米)
108×60%=64.8(立方分米)
64.8÷48=1.35(分米)
答:水的高度是1.35分米。
【解析】由正方体容器装了一半水可知,水的高度是正方体容器高度的,根据正方体的体积公式:V=a3,求出水的体积。再将水的体积乘60%的积,即可求出圆柱形容器内水面的高度。
45.解:2.8-1.8=1(g),
0.8+3.2=4(g),
娃娃个数为4÷1=4(个),
颜料质量是4×1.8+0.8=8(g),
答:有4个石膏娃娃,8g颜料。
【解析】 每个娃娃所需的颜料相差:2.8 - 1.8 = 1(克),总需要的涂料是多出的0.8克加上缺少的3.2克:0.8 + 3.2 = 4(克),石膏娃娃的数量就是总需要的涂料除以每个娃娃多的1克:4 ÷ 1 = 4(个),颜料的总重量为石膏娃娃的数量乘以每个娃娃用的颜料,再加上多出的颜料:4 × 1.8 + 0.8 = 8(克)。
46.解:圆锥形稻谷堆的体积=圆柱形粮囤里谷堆的体积,
圆锥的底面半径:12.56÷3.14÷2=2(m)
圆柱的底面半径:6.28÷3.14÷2=1(m)
π×22×1.8×÷(π×12)
=2.4π÷π
=2.4(m)
答:可以装2.4m高。
【解析】底面周长÷π÷2=底面半径,π×底面半径的平方=底面积,π×圆锥的底面半径的平方×高÷3=圆锥的体积,圆锥的体积÷圆柱的底面积=可以装的高度。
47.解:28×(1+)
=28×
=40(人)
答:六年级有40人参加艺术节展演。
【解析】求比一个数多几分之几的数是多少,方法是:这个数×(1+多的几分之几)。
48.解:360×250=90000(平方米)
90000平方米=9公顷
9×0.76=6.84(吨)
答:这片树林1天放出6.84吨氧气。
【解析】这片树林1天放出氧气的质量=这片树林的面积×平均每公顷阔叶林在生长季节1天大约能放出氧气的质量,其中,这片树林的面积=长×宽,然后单位换算。
49.解:通过列表法来表示:
大箱子(个) 小箱子(个) 可装个数(个) 快递费用(元)
3 0 28×3=84 15×3=45
2 1 28×2+15=71 15×2+12=42
1 3 28+3×15=73 15+3×12=51
0 5 15×5=75 12×5=60
比较发现,使用2个小箱子,一个大箱子最省钱。
一共需要:15×2+12×1=42(元)
答:使用2个小箱子,一个大箱子最省钱。一共需要42元。
【解析】通过列表法,将所有可行方案表示出来,再进行比较,对比出最省钱方案即可。
50.解:1080÷6=180(米/分)
180×=80(米/分)
180×=100(米/分)
(100-80)×6
=20×6
=120(米)
答:相遇时,甲比乙少行120米。
【解析】甲的速度比乙的速度慢,把乙的速度看做5,甲的速度就是5-5×=4;
甲乙的速度比是4:5,甲占两人速度和的,乙占两人速度和的,
两人速度和×=甲的速度,两人速度和×=乙的速度,
甲乙两人的速度差×相遇时间=相遇时甲比乙少行的路程。
21世纪教育网(www.21cnjy.com)
2024-2025学年六年级下册数学小升初重点校分班考前冲刺卷
一、填空题
1.工厂要生产240个零件,师傅单独做4小时可以完成这批零件的,徒弟6小时可以完成这批零件的,两人合作 小时可以完成。完成时,师傅做了 个零件。
2.六(1)班女生人数占全班的 , 男生人数占全班的 ,如果六 (1)班有42 人, 那么女生有 人。
3.爱心超市每月一次给社区清洁工人发放爱心小礼包,每次超市会准备72个面包、180袋小饼干,打包成若干份,要求每份里面的面包个数相同,小饼干袋数也相同。爱心超市每次最多能发放给 位社区清洁工人,每位社区清洁工人会收到 个面包、 袋小饼干。
4.下图中的两个圆大小相等,线段AB长15厘米。圆的直径是 厘米,圆的面积是 平方厘米。
5.一艘轮船从甲地到乙地每小时航行30 km,然后按原路返回,若想往返的平均速度为40km,则返回时每小时应航行 km。
6.(商品经济)某种电器上半月按定价1000元的价格出售,共销售50台,下半月降价5%,这样销售量增加了20% ,所获利润比上半月多500元。这种电器每台的成本是 元。
7.星期天妈妈要做以下家务:擦玻璃要20分钟,收拾厨房要15分钟,用全自动洗衣机洗衣服要30分钟,晾衣服要6分钟。妈妈做完这些家务至少需要 分钟。
8.小红把自己钱的 给小明以后,两人的钱数相等,则小红、小明两人原来的钱数之比是 .
9.如图,长方形长 8dm、宽 4dm,B、C 两点把长方形的一条长按1:2:1分成了三段,线段BC长 dm,三角形 ABC 的面积是长方形面积的 。
10.某工厂生产的25个零件中有一个是次品,它比正品轻一些。用天平称,至少称 次就一定能找出次品。
11.在保龄球比赛的最后一局中,小白得199分,从而把若干局的平均分由177提高到178,为了把他的平均分提高到179,下一局他必须得 分。
12.一幅地图的线段比例尺是 ,改写成数值比例尺是 。在这幅地图上量得泰兴到南京的图上距离是19.8厘米,实际距离是 千米。
13.图中,长方形的面积和圆的面积相等,已知圆的半径是3厘米,阴影部分的面积是 平方厘米.(用小数表示)
14.将一个底面周长是9.42dm的圆柱形木料,沿着底面直径垂直切一刀,切成两个半圆柱,表面积增加4.8dm2,原来这个圆柱形木料的体积是 立方分米。
15.某工厂从甲车间调出总人数的到乙车间后,甲乙两车间的人就一样多,原来甲乙两车间的人数比是 。
二、判断题
16.两个圆柱的体积相等,它们的表面积也一定相等。( )
17.甲、乙两校女生人数都占该校总人数的55%,那么甲、乙两校女生人数一定相等。( )
18.把一个长方形按5:1的比放大,就是把长方形的长和宽都放大到原来的5倍。( )
19.在比例尺是1:12500000的地图上,量得两城市问的距离是8厘米,如果画在比例尺是1:8000000的地图上,图上距离是12.5厘米。( )
20.报刊的单价一定,报刊的份数和总价成正比例。( )
21.长方体、正方体和圆柱的体积都可以用“底面积×高”计算。( )
22.甲比乙多25%,乙就比甲少20%。( )
23.正方体的表面积=棱长×棱长×6.( )
三、单选题
24.夏天多高温天气,人体会经常出汗,专家建议要适量补充含盐率为0.9%的淡盐水以防中暑。下图( )杯淡盐水的含盐率最接近0.9%。
A. B. C. D.
25.一支尖端部分是圆锥形的铅笔,圆锥部分的长度是圆柱部分的 ,则圆锥部分的体积是圆柱体积的( )。
A. B. C. D.
26.有14个同样的零件,其中有13个质量相同,另有1个质量不足,轻一些,是次品.用天平至少称( )次能保证找出这个次品。
A.2 B.3 C.4 D.5
27.下列说法中,正确的是( )。
A.降价25%就是打二五折
B.某地的麦收进度已过八成,表示已经收割的小麦面积超过了该地小麦总面积的80%
C.某超市本月的营业额是20万元,按营业额的5%缴税,本月应缴税10万元
D.一件商品先提价10%,再打九折出售,现价与原价相同
28.聪聪和明明做数学游戏,他们准备从5、7、8、9四张牌中分别抽出一张,再把两张牌上的数相乘。如果积是奇数,聪聪赢,积是偶数,明明赢。谁赢的可能性大?( )
A.聪聪赢的可能性大 B.明明赢的可能性大
C.两人赢的可能性一样大 D.无法确定
29.两根铁丝,第一根用去m,第二根用去,两根铁丝正好都剩下m,比较原来两根铁丝的长短,结果是( )。
A.第一根长 B.第二根长 C.一样 长 D.无法比较
30.210名少先队员选举大队长,有三位候选人甲、乙、丙,每人只能选他们之中的一个人,不能弃权。前190张票中,甲得75票,乙得65票,丙得50票,规定谁的票最多谁当选。若甲要当选,最少还需要( )张票.
A.6 B.7 C.8 D.10
31.一块长方形菜地,周长是120m,长和宽的比是2:1。这块长方形菜地的面积是( )m2。
A.3200 B.1600 C.800
32.下图是水滴进玻璃容器的示意图(滴水速度相同),下图表示的是容器中水的高度随滴水时间变化的情况(图中刻度、单位都相同)。下列选项中对应关系正确的是( )。
A. B. C. D.
33.一个长方体水缸,长20厘米,宽15厘米,水深6厘米,将一块石头投入水中(石头全部浸没)水面上升2厘米(水未溢出),求这块石头的体积,列式正确的是( )。
A.20×15×2 B.20×15×6
C.20×15×(6-2) D.2×2×2
四、计算题
34.直接写得数。
+ = ÷6= × = ×0÷ = 2- + =
×16= 6- = ÷ = ×3= ÷ =
35.计算下面各题,能简算的要简算。
0.25×3.2×12.5
36.解方程。
(1)0.25x+ (2) (3)0.3(6+x)=4.5
37.求图中阴影部分的面积。(单位:dm)
(1)
38.计算下面立体图形的表面积和体积。(单位:dm)
五、作图题
39.画一画.
(I)以虚线为对称轴,画出小树的另一半.
(II)再将整个图形向右平移6格.
(III)最后将平移的图形绕小树的下端点顺时针旋转90°.
六、解决问题
40. 某汽车客运站开往某市的汽车每隔15分钟开出一班。小王叔叔想搭乘6:45这班汽车到某市,但他到达车站时,已经是6:48了,他要等多少分钟下一班汽车才来?
41. 为了吸引游客,颐和园冰场正在进行抽奖活动,奖品如右图所示。如果你是冰场的运营经理,请你选择下面的一种材料设计抽奖方案,并简要说明理由。
我选择的材料: ( )。 (填序号)
我设计的方案:
42.甲、乙、丙三人同时从A城到B城。甲45分走了5千米,乙小时走了3千米,丙小时走了4千米。谁走的快些?
43. 双十一大促,某商场利用“幸运大转盘”举行抽奖活动,满99 元可以抽奖一次,指针指向哪个区域就可以获得哪种奖品,下表是转盘转动16次的结果。
奖品 纸巾 袜子 牙膏 50元代金券
次数/次 9 4 2 1
(1)下一次抽到什么奖品的可能性最大
(2)请你根据上面的结果设计出一个符合转动结果的转盘。
44.(等积变换)一个棱长60厘米的正方体容器装了一半水,把这些水的60%倒入一个底面积为48平方分米的圆柱形容器里,水的高度是多少分米?
45.石膏娃娃是雕塑和绘画融合的新艺术。妙妙用颜料给一些石膏娃娃涂色,若每个娃娃用1.8g颜料,则多出0.8g颜料,若每个娃娃用2.8g颜料,则缺3.2g颜料,有多少个石膏娃娃 多少克颜料
46. 一个圆锥形稻谷堆的底面周长是12.56m,高是1.8m。现在把这些稻谷全部装入一个底面周长是6.28m的圆柱形粮囤里,可以装多高?
47.五年级参加艺术节展演的学生有28人,六年级参加艺术节展演的学生人数比五年级多,六年级有多少人参加艺术节展演?
48.树木是氧气制造厂。1公顷阔叶林在生长季节1天大约能吸收1t二氧化碳,放出0.76t氧气。李爷爷退休后,义务维护一片长是360m,宽是250m的长方形杨树林,这片树林1天放出多少吨氧气
49.六一儿童节,305班的孩子要为福利院的小朋友们捐助爱心书包69个,大箱子每箱可装28个,每箱需快递费15元;小箱子每箱可装15个,每箱需快递费12元。如何装箱最省钱?一共需要多少元?
50.A、B相地相距1080米,甲、乙两人同时从两地相向而行, 6分钟相遇。已知甲的速度比乙的速度慢,相遇时,甲比乙少行多少米?
参考答案及试题解析
1.;144
【解析】解:÷4=
÷6=
1÷(+)
=1÷
=(小时)
×=
240×=144(个)。
故答案为:;144。
【分析】两人合作完成需要的时间=工作总量÷工作效率的和;完成时,师傅做零件的个数=师傅平均每小时完成的分率×师傅工作的时间×零件的总个数。
2.;24
【解析】解:1-=
42×=24(人)
故答案为:;24。
【分析】把 六 (1)班 的总人数看作单位“1”, 六(1)班女生人数占全班的 , 那男生人数占全班的(1-=);求女生人数,用 六 (1)班 的总人数乘 六(1)班女生人数占全班的份数,计算即可求解。
3.36;2;5
【解析】解:72 = 2×2×2×3×3,180 = 2×2×3×3×5,
因此,72和180的最大公因数是 2×2×3×3=36,
所以爱心超市每次最多能发放给36位社区清洁工人。
每位清洁工人将收到的面包和小饼干数量:
面包:72÷36 = 2(个)
小饼干:180÷36 = 5(袋)
故答案为:36;2;5。
【分析】本题要求找出爱心超市每次最多能发放给多少位社区清洁工人,同时每位清洁工人将收到多少个面包和多少袋小饼干。由题意可知,每次超市准备的面包和小饼干都需要能平均分给每位清洁工人。需要找到能同时被72(面包数量)和180(小饼干数量)整除的最大数,这个数即为最多能发放给的清洁工人数量。
4.10;78.5
【解析】解:圆的直径:15÷3×2=10(厘米),圆的面积:(平方厘米)
故答案为:10;78.5。
【分析】先算出圆的半径15除3再乘2为直径,再根据面积公式得出面积。
5.60
【解析】去时时间:
往返时间:
返回时间:
(千米/时)
故答案为60
【分析】
利用平均速度公式,设出路程和返回速度,根据已知条件列出方程,通过解方程求出返回时的速度.
6.650
【解析】解:设这种电器每台的成本是元。
1000×(1-5%)
=1000×0.95
=950(元)
50×(1+20%)
=50×1.2
=60(台)
60×(950-x)-50×(1000-x)=500
57000-60x-50000+50x=500
10x=7000-500
x=6500÷10
x=650
故答案为:650。
【分析】根据题意可得:上半月每台定价×(1-下降的百分比)=下半月每台定价,上半月销售数量×(1+增加的百分比)=下半月销售数量;
每台定价-成本=每台利润,销售数量×(每台定价-成本)=总利润,所以,下半月销售数量×(下半月每台定价-每台成本)-上半月销售数量×(上半月每台定价-每台成本)=下半月比上半月多获得的利润,据此关系式设这种电器每台的成本是元,列方程即可解答。
7.41
8.2:1
【解析】
解: 把小红原来的钱数看作"1",平均分成4份,给小明1份数后还剩下3份数,现在两人钱数相等,说明小明现在也有3份数的钱,小明现在的钱数就为3份数,原来的钱数就是2份
小红、小明原有钱数的比是:4份:2份=2:1.
故答案为:2:1.
【分析】根据题意“ 小红把自己钱的 给小明,把小红原来的钱数看作是4份,给小明1份后小红还剩下3份,再根据” 两人的钱数相等 “,可推出小明现在的钱数也是3份,原来的钱数就是2份,进而写出两人原来的钱数的比即可。
9.4;
【解析】1+2+1=4份,8÷4=2dm,BC=2×2=4dm;
长方形面积=4×8=32(dm2)
三角形面积:4×4÷2=8(dm2)
8÷32=。
故答案为:4;。
【分析】首先,根据题目描述,线段AB、BC、CD的长度比例为1:2:1可知长方形的长被平均分成了1+2+1=4份,求得每份是8÷4=2dm,而BC占2份也就是4dm;由于BC是三角形ABC的底边,且三角形ABC的高即为长方形的宽4dm,所以三角形的面积=底×高÷2=4×4÷2=8(dm2),而长方形的面积=长×宽=4×8=32(dm2),因此三角形ABC的面积是长方形面积的:8÷32=。
10.3
【解析】解:25÷3=8(个)余1(个),8+1=9(个),即三份的数量分别是8、8、9;
9÷3=3(个),即每份数量是1个;
3÷3=1(个),最后每份数量是1个;
1+1+1=3(次),所以某工厂生产的25个零件中有一个是次品,它比正品轻一些。用天平称,至少称3次就一定能找出次品。
故答案为:3。
【分析】本题可以先将25个零件分成3份,每份数量分别是8、8、9,然后进行检测。
第一次,天平检测数量相同的两组8个零件,如果重量相同,则次品在剩下的9个零件中,此时将9个零件再平均分成3份,每份3个,第二次检测其中的任意两份零件,如果重量相同,则次品就在最后的3个零件中;最后将剩下的3个零件平分成3份,每份1个零件,第三次检测任意2个零件,平衡则剩下的最后一个零件是次品。因此至少称3次就一定能找出次品。
11.201
【解析】解:设小白一共打了x局。
178x-(x-1)×177=199
178x-(177x-177)=199
178x-177x+177=199
x+177=199
x=199-177
x=22
179×23-178×22
=4117-3916
=201(分)
所以下一局他必须得201分。
故答案为:201
【分析】根据题意,先设小白一共打了x局,最后一局的199分,使平均分由177分提高到178分,列式为178x-(x-1)×177=199,解得x=22;所以下一局他必须得179×23-178×22分,据此解答。
12.1∶1000000;198
13.21.195
【解析】
3.14×32-3.14×32×
=3.14×9-3.14×9×
=28.26-7.065
=21.195(平方厘米)
答:阴影部分的面积是21.195平方厘米.
故答案为:21.195.
【分析】本题考查的主要内容是圆的面积计算问题,根据圆的面积=πr 进行分析即可.
14.5.652
【解析】解:9.42÷3.14=3(分米)
4.8÷2÷3=0.8(分米)
3.14×(3÷2)×(3÷2)×0.8
=3.14×1.5×1.5×0.8
=7.065×0.8
=5.652(立方分米)
故答案为:5.652。
【分析】表面积增加的面积是两个长方形,长方形的长就是圆柱的底面直径;
底面周长÷π=底面直径;增加的面积÷2÷底面直径=圆柱的高;
直径÷2=半径,π×底面半径的平方×高=圆柱形木料的体积。
15.5:4
【解析】解:1:(1-×2)
=1:(1-)
=1:
=5:4。
故答案为:5:4。
【分析】把原来甲车间的人数看作单位“1”,由“ 从甲车间调出总人数的到乙车间后,甲乙两车间的人就一样多 ”,说明甲车间人数比乙车间人数多甲车间人数的×2,则乙车间人数是甲车间人数的(1-×2)=,进而写出原来甲乙两车间的人数比。
16.错误
【解析】 两个圆柱的体积相等,它们的表面积可能相等,也可能不相等,原题说法错误。
故答案为:错误。
【分析】 此题主要考查了圆柱的体积、表面积的计算公式,圆柱的体积=底面积×高,圆柱的体积是由它的底面积和高两个条件决定的,而它的表面积=侧面积+底面积×2;除非它们的底面积和高分别相等,表面积才会相等,如果它们的底面积和高各不相等,表面积就不相等,据此判断 。
17.错误
【解析】因为两校的总人数不一等相等,虽然女生占的百分数相等,但女生人数不一定相等,本题错.
故答案为:错误.
【分析】女生人数=全校学生总数×女生占的百分数,据此解答.
18.正确
【解析】解:把一个长方形按5:1的比放大,就是把长方形的长和宽都放大到原来的5倍。
故答案为:正确。
【分析】把一个图形按比例放大,就是把这个图形的每条边都扩大相同的倍数。
19.正确
【解析】解:根据题意,可得
实际距离:
由于实际距离相同,所以它在比例尺是1∶8000000的地图上的图上距离为:
故答案为:正确
【分析】图上距离与实际距离的比叫作这幅图的比例尺,则图上距离=实际距离×比例尺,实际距离=图上距离÷比例尺。先根据比例尺1∶12500000和图上距离,求出实际距离,由于实际距离相同,所以再根据实际距离和比例尺1∶8000000求出图上距离。
20.正确
【解析】解:总价÷份数=单价(一定),总价和份数的商一定,二者成正比例,原题说法正确.
故答案为:正确
【分析】根据数量关系判断总价和份数的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例.
21.正确
【解析】长方体、正方体和圆柱的体积,都可以用底面积×高来计算,由此说法正确。
故答案为:正确
【分析】长方体、正方体和圆柱的体积,都可以用底面积×高来计算,由此即可判断。
22.正确
【解析】解:甲比乙多25%,乙是1,则甲就是1+25%=1.25,则乙就比甲少:(1.25-1)÷1.25=0.25÷1.25=20%。原题说法正确。
故答案为:正确。
【分析】把乙看作1,则甲就是1.25,用乙比甲少的除以甲即可求出乙比甲少百分之几。
23.正确
【解析】正方体的棱长都相等,个面的面积都相等。所以: 正方体的表面积=棱长×棱长×6.
【分析】正方体棱长,各个面的大小,形状完全相同。
24.C
25.C
【解析】解:3×3=9,
1÷9=;
故答案为:C。
【分析】根据题意,可以将圆柱看成3个与圆锥等底等高的圆柱,根据等底等高的圆柱体积是圆锥的3倍,可以得到圆柱部分体积是圆锥部分的体积的9倍,据此求解。
26.B
【解析】解:第一次把14个零件分成3份5个、5个、4个,取5个的两份分别放在天平两侧,若天平平衡,较轻的在未取的一份,若天平不平衡,取较轻的一份继续;
第二次,取含有较轻的一份(5个或4个),分成3份:2个、2个、1个,取2个的分别放在天平的两侧,若天平平衡,则未取的为较轻的次品,若天平不平衡,取较轻的继续;
第三次,把含有较轻的份(2个)分别放在天平两侧,即可找到较轻的次品。
所以至少称3次就一定能找出次品零件。
故答案为:B。
【分析】天平是用来称量物体质量的工具,此题并不是称量物体的质量,而是使用天平来比较物体质量的大小,所以在调好的天平两盘中分别放上物体,当哪边的托盘上升,则说明这边托盘中的物体质量偏小。
27.B
【解析】解:A.降价25%意味着现价为原价的75%(即100% - 25%),而打二五折对应的是原价的25%。错误。
B.“八成”表示80%,麦收进度已过八成,即收割面积超过总面积的80%。正确。
C.营业额20万元,按5%缴税,应缴税款为:20×5%=1(万元) 错误。
D.设原价为x,先提价10%后价格为1.1x,再打九折后价格为:1.1x×0.9 = 0.99x 现价为原价的99%,与原价不同,错误。
故答案为:B
【分析】本题考查百分比与折扣的对应关系,以及实际问题中的百分比应用。关键点包括:降价25%对应七五折,八成即80%,税率计算需准确,提价后折扣的复合计算。
28.C
【解析】解:积的情况有:35、40、45、56、63、72;其中,奇数有3个,偶数有3个,两人赢的可能性一样大。
故答案为:C。
【分析】从5、7、8、9四张牌中分别抽出一张,再把两张牌上的数相乘,积共有6中情况,其中,奇数有3个,偶数有3个,两人赢的可能性一样大。
29.A
【解析】解:第一根:+=(米);
第二根:÷(1-)=(米);
,所以第一根长。
故答案为:A。
【分析】把第一根用去的长度加上第一根剩下的长度求出第一根的总长度。用第二根剩下的长度除以剩下的分率求出第二根的总长度。比较后判断原来的长短即可。
30.A
【解析】解:甲得x张,乙得(210-190-x)张。
75+x=65+(210-190-x)
75+x=85-x
2x=10
x=5
5+1=6(张)
故答案为:A。
【分析】根据题意可知,还剩20张票,丙就算得了20张也比甲少,所以主要比较甲和乙,设甲得x张,乙得20-x张,根据最后两人的票数相等列方程,求出x后,令甲所得张数比x多1即可当选。
31.C
【解析】解:120÷2=60(米),60÷(2+1)×1=20(米),60-20=40(米),20×40=800(平方米),所以这块长方形菜地的面积是800m2。
故答案为:C。
【分析】菜地的长与宽的和=菜地的周长÷2,所以菜地的宽=菜地的长与宽的和÷菜地的长和宽占的份数和×菜地的宽占的份数,菜地的长=菜地的长与宽的和-菜地的宽,那么长方形菜地的面积=长×宽。
32.D
【解析】解:水面上升先快后慢,所以选择D
故答案为:D。
【分析】观察图形,玻璃容器是圆锥形,时间滴水速度一定,所以滴水时间与水的体积成正比例关系,根据圆锥的体积公式:V=Sh,底面积越来越大,所以得出水面上升是先快后慢的,据此解答即可。
33.A
【解析】解:这块石头的体积=长方体水缸的长×宽×上升水的高度,即:20×15×2。
故答案为:A。
【分析】求这块石头的体积就是求上升水的体积,石头的体积=长方体水缸的长×宽×上升水的高度。
34.+=1 ÷6= ×= ×0÷=0 2-+=
×16=6 6-= ÷= ×3= ÷=
【解析】分数乘整数,分母不变,用分子乘整数,能约分的要约分;
分数乘分数,用分子相乘的积做分子,分母相乘的积作分母,能约分的要约分;
除以一个不为0的数,等于乘这个数的倒数。
35.解:
=3÷[÷12]
=3÷
=120
=6.125+0.875-()
=7-1
=6
=1.25×5.2+1.25×3.8+1.25
=1.25×(5.2+3.8+1)
=1.25×10
=12.5
0.25×3.2×12.5
=0.25×4×(0.8×12.5)
=1×10
=10
【解析】加法交换律:两个数相加,交换加数的位置,它们的和不变,即a+b=b+a。
加法结合律:三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再和第一个数相加它们的和不变,即(a+b)+c=a+(b+c)。
乘法分配律:两个数的和与一个数相乘,可以把两个加数分别与这个数相乘再把两个积相加,即(a+b)×c=a×c+b×c。
(1)先算小括号里面的减法,再算中括号里面的除法,最后算括号外面的除法;
(2)运用加法交换律和加法结合律计算;
(3)运用乘法分配律计算;
(4)运用乘法结合律计算。
36.(1)解:0.25x+
0.25x+﹣=4﹣
0.25x=
4×0.25x=
x=11
(2)解:
0.5x=
2×0.5x= 2
x=1
(3)解:0.3(6+x)=4.5
0.3(6+x)÷0.3=4.5÷0.3
6+x=15
6+x﹣6=15﹣6
x=9
【解析】解比例时,根据比例的基本性质把比例化为方程,再根据等式性质解方程;
比例的基本性质:比例的两个外项之积等于比例的两个内项之积;
等式性质1:等式两边加上或减去同一个数,左右两边仍然相等;
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
37.(1)8×8+6×6-8×(8+6)÷2=44(dm2)
(2)
【解析】
(1) 采用 “总面积 - 空白面积 = 阴影面积” 的方法。先求出两个正方形面积之和作为总面积,再求出空白大三角形面积,最后相减得阴影面积。 三角形面积公式S= (a是底,h是高 ),正方形面积S=边长×边长。
(2) 运用 “长方形面积 - 半圆面积 = 阴影面积”。先算出长方形面积,再求出半圆面积,二者相减得阴影面积。 根据长方形面积公式S=ab(a是长,b是宽 ) , 根据圆面积公式S=πr2。
38.表面积:2×2×6+1×3×2+3×2×2
=24+6+12
=42(dm2)
体积:2×2×2+2×3×1
=8+6
=14(dm3)
答:立体图形的表面积是42平方分米,体积是14立方分米。
【解析】表面积=左边正方体的棱长×棱长×6+右边长方体的长×高×2+长×宽×2;体积=正方体的棱长×棱长×棱长+长方体的长×宽×高。
39.解:(I)根据轴对称图形的定义,画出小树的另一半,如图①.
(II)根据平移的定义将图形①向右平移6格即可得到图形②如图.
(III)利用旋转的定义将图形②绕点o顺时针旋转90°即可得到图形③.
【解析】紧扣轴对称图形的定义和图形平移和旋转的定义即可解决问题.此题考查了轴对称图形的画法以及平移和旋转的应用.
40.解:6时45分+15分=7时
7时-6时48分=12分钟
答:他要等12分钟下一班汽车才来。
【解析】用6时45分加上15分就是下班车到站的时刻,用下班车到站的时刻减去现在的时刻就是他还要等的时间。
41.解:我选择的材料:②
我设计的方案:抽到红球可以获得一等奖,抽到白球可以获得二等奖,抽到黄球可以获得三等奖。
【解析】奖品设计了三种,材料②中刚好有3种颜色的球,所以可以根据三种奖项和3种颜色的球的个数设计方案。抽到一等奖的可能性最小,二等奖次之,三等奖的可能性最大。2<6<12,抽到红球的可能性<抽到白球的可能性<抽到黄球的可能性,所以可以将抽到红球设为一等奖,抽到白球设为二等奖,抽到黄球为三等奖。
42.甲走的快些
43.(1)解:因为抽到纸巾的次数最多,所以下一次抽到纸巾的可能性最大。
(2)解:转盘区域面积由大到小依次是纸巾、袜子、牙膏、50元代金券。
【解析】(1)观察转盘中转动16次的结果,可以发现,纸巾转动的次数最多,50元代金券最少,所以,下次抽到纸巾的可能性最大
(2)根据转盘中抽到的数据显示,比较纸巾、袜子、牙膏和50元代金券的次数,即可判断
44.解:60厘米=6分米
6×6×6÷2
=36×6÷2
=216÷2
=108(立方分米)
108×60%=64.8(立方分米)
64.8÷48=1.35(分米)
答:水的高度是1.35分米。
【解析】由正方体容器装了一半水可知,水的高度是正方体容器高度的,根据正方体的体积公式:V=a3,求出水的体积。再将水的体积乘60%的积,即可求出圆柱形容器内水面的高度。
45.解:2.8-1.8=1(g),
0.8+3.2=4(g),
娃娃个数为4÷1=4(个),
颜料质量是4×1.8+0.8=8(g),
答:有4个石膏娃娃,8g颜料。
【解析】 每个娃娃所需的颜料相差:2.8 - 1.8 = 1(克),总需要的涂料是多出的0.8克加上缺少的3.2克:0.8 + 3.2 = 4(克),石膏娃娃的数量就是总需要的涂料除以每个娃娃多的1克:4 ÷ 1 = 4(个),颜料的总重量为石膏娃娃的数量乘以每个娃娃用的颜料,再加上多出的颜料:4 × 1.8 + 0.8 = 8(克)。
46.解:圆锥形稻谷堆的体积=圆柱形粮囤里谷堆的体积,
圆锥的底面半径:12.56÷3.14÷2=2(m)
圆柱的底面半径:6.28÷3.14÷2=1(m)
π×22×1.8×÷(π×12)
=2.4π÷π
=2.4(m)
答:可以装2.4m高。
【解析】底面周长÷π÷2=底面半径,π×底面半径的平方=底面积,π×圆锥的底面半径的平方×高÷3=圆锥的体积,圆锥的体积÷圆柱的底面积=可以装的高度。
47.解:28×(1+)
=28×
=40(人)
答:六年级有40人参加艺术节展演。
【解析】求比一个数多几分之几的数是多少,方法是:这个数×(1+多的几分之几)。
48.解:360×250=90000(平方米)
90000平方米=9公顷
9×0.76=6.84(吨)
答:这片树林1天放出6.84吨氧气。
【解析】这片树林1天放出氧气的质量=这片树林的面积×平均每公顷阔叶林在生长季节1天大约能放出氧气的质量,其中,这片树林的面积=长×宽,然后单位换算。
49.解:通过列表法来表示:
大箱子(个) 小箱子(个) 可装个数(个) 快递费用(元)
3 0 28×3=84 15×3=45
2 1 28×2+15=71 15×2+12=42
1 3 28+3×15=73 15+3×12=51
0 5 15×5=75 12×5=60
比较发现,使用2个小箱子,一个大箱子最省钱。
一共需要:15×2+12×1=42(元)
答:使用2个小箱子,一个大箱子最省钱。一共需要42元。
【解析】通过列表法,将所有可行方案表示出来,再进行比较,对比出最省钱方案即可。
50.解:1080÷6=180(米/分)
180×=80(米/分)
180×=100(米/分)
(100-80)×6
=20×6
=120(米)
答:相遇时,甲比乙少行120米。
【解析】甲的速度比乙的速度慢,把乙的速度看做5,甲的速度就是5-5×=4;
甲乙的速度比是4:5,甲占两人速度和的,乙占两人速度和的,
两人速度和×=甲的速度,两人速度和×=乙的速度,
甲乙两人的速度差×相遇时间=相遇时甲比乙少行的路程。
21世纪教育网(www.21cnjy.com)
同课章节目录
