6.1几何图形暑假预习练(含解析)
图片预览
文档简介
中小学教育资源及组卷应用平台
6.1几何图形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
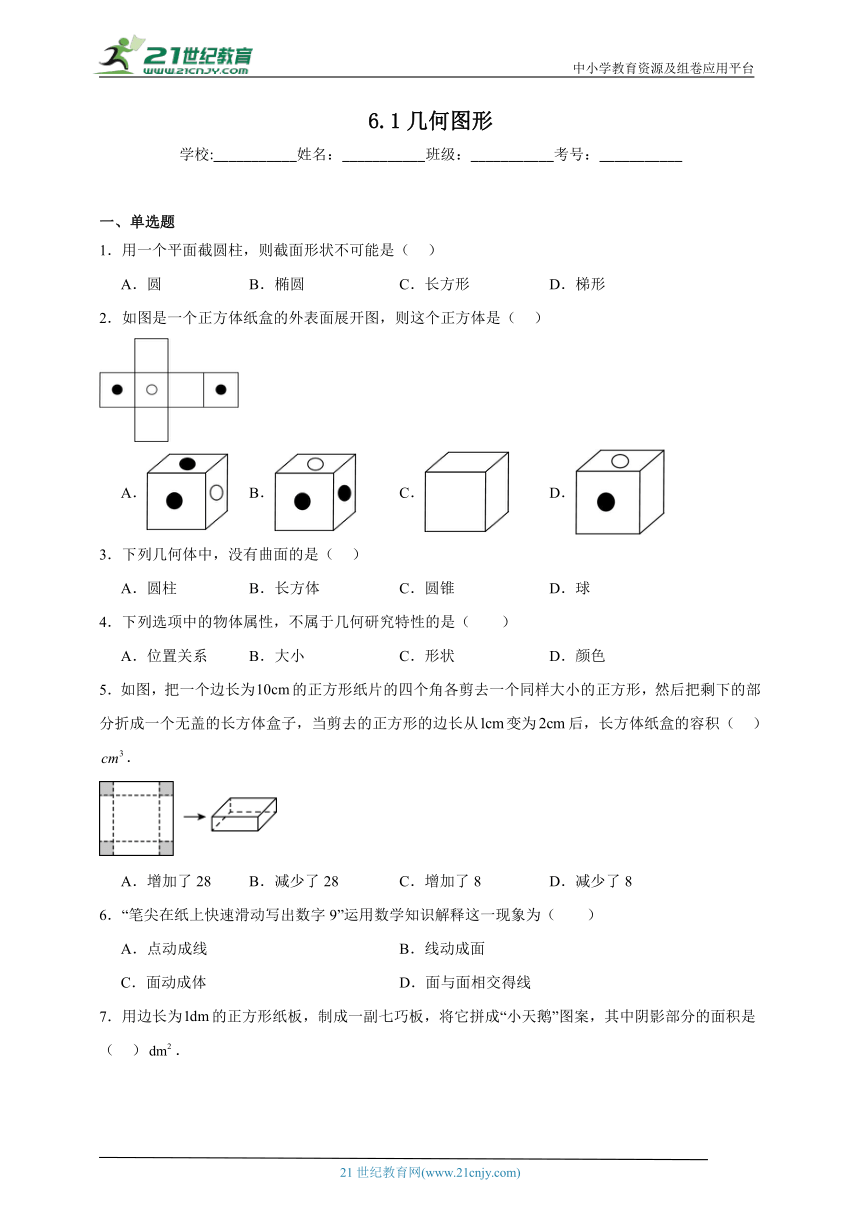
1.用一个平面截圆柱,则截面形状不可能是( )
A.圆 B.椭圆 C.长方形 D.梯形
2.如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
A. B. C. D.
3.下列几何体中,没有曲面的是( )
A.圆柱 B.长方体 C.圆锥 D.球
4.下列选项中的物体属性,不属于几何研究特性的是( )
A.位置关系 B.大小 C.形状 D.颜色
5.如图,把一个边长为的正方形纸片的四个角各剪去一个同样大小的正方形,然后把剩下的部分折成一个无盖的长方体盒子,当剪去的正方形的边长从变为后,长方体纸盒的容积( ).
A.增加了28 B.减少了28 C.增加了8 D.减少了8
6.“笔尖在纸上快速滑动写出数字9”运用数学知识解释这一现象为( )
A.点动成线 B.线动成面
C.面动成体 D.面与面相交得线
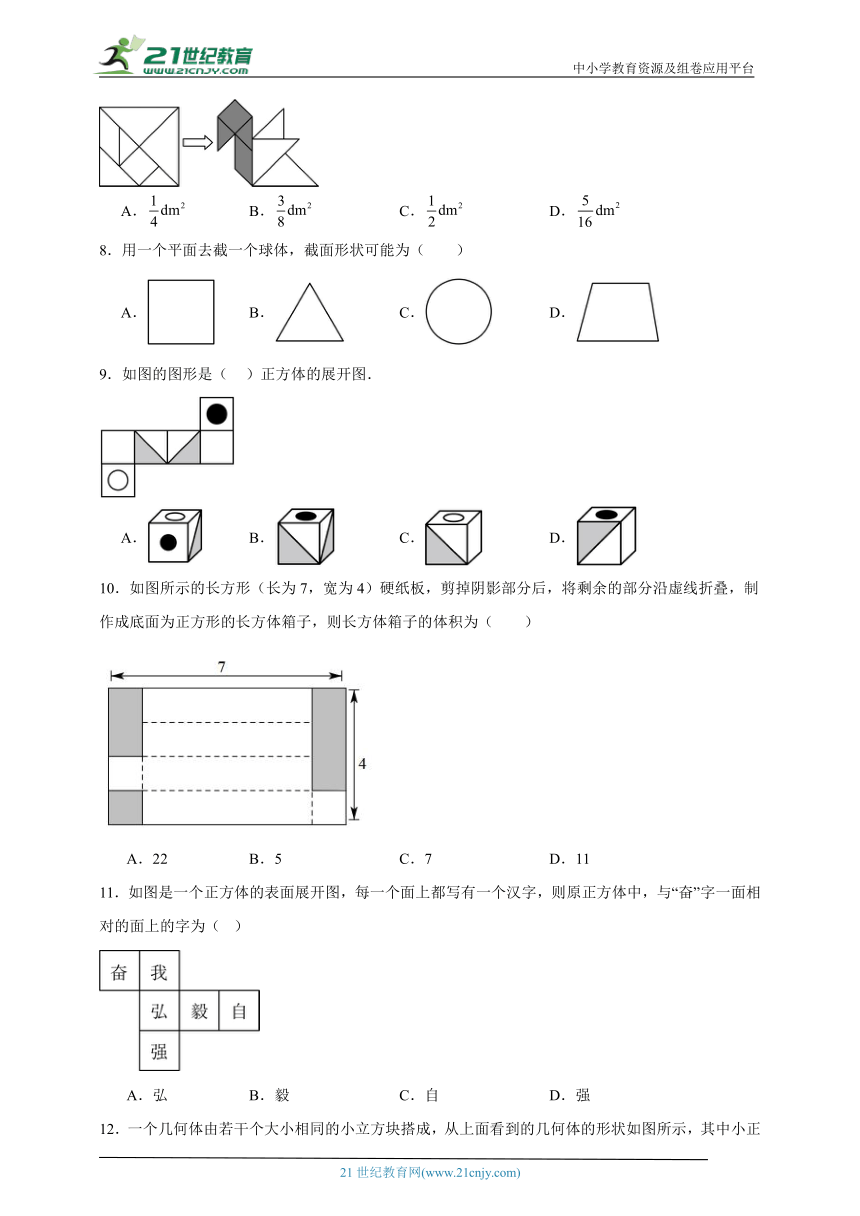
7.用边长为的正方形纸板,制成一副七巧板,将它拼成“小天鹅”图案,其中阴影部分的面积是( ).
A. B. C. D.
8.用一个平面去截一个球体,截面形状可能为( )
A. B. C. D.
9.如图的图形是( )正方体的展开图.
A. B. C. D.
10.如图所示的长方形(长为7,宽为4)硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形的长方体箱子,则长方体箱子的体积为( )
A.22 B.5 C.7 D.11
11.如图是一个正方体的表面展开图,每一个面上都写有一个汉字,则原正方体中,与“奋”字一面相对的面上的字为( )
A.弘 B.毅 C.自 D.强
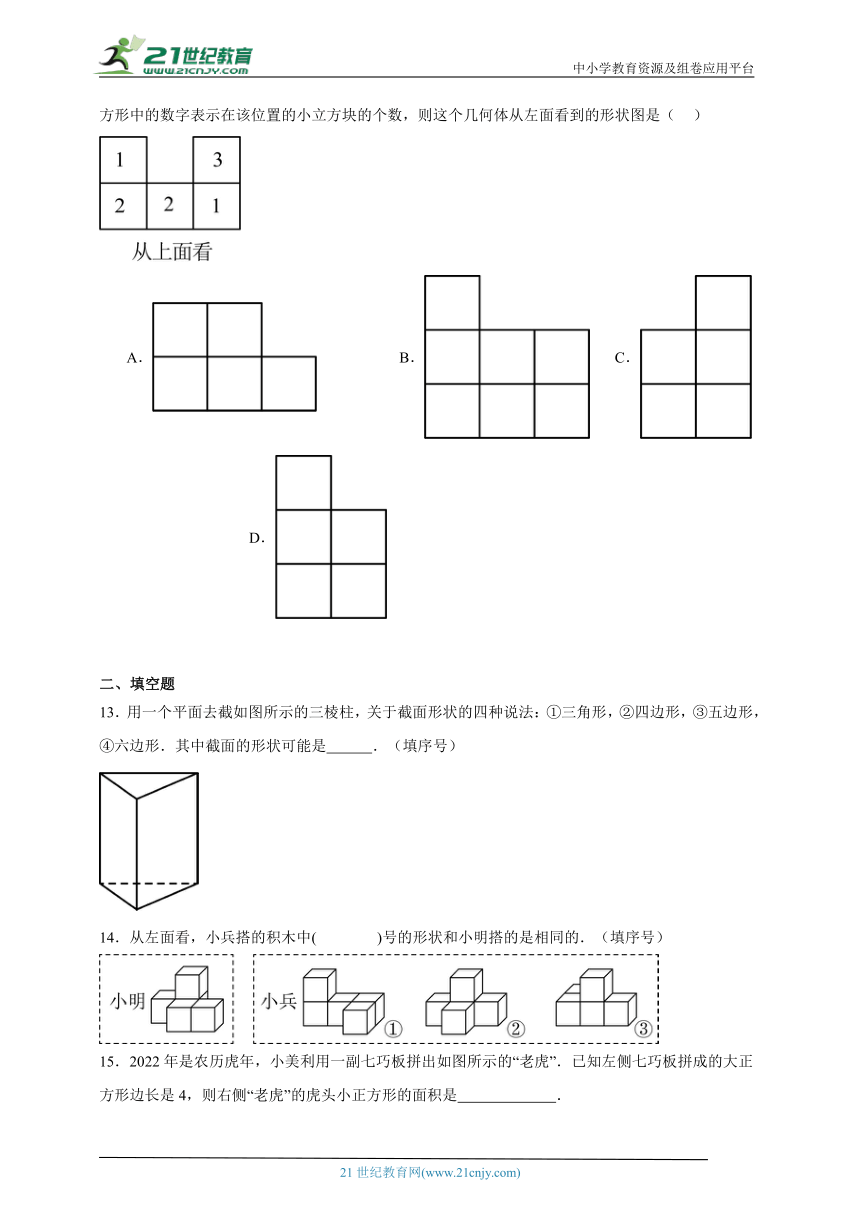
12.一个几何体由若干个大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体从左面看到的形状图是( )
A. B. C. D.
二、填空题
13.用一个平面去截如图所示的三棱柱,关于截面形状的四种说法:①三角形,②四边形,③五边形,④六边形.其中截面的形状可能是 .(填序号)
14.从左面看,小兵搭的积木中( )号的形状和小明搭的是相同的.(填序号)
15.2022年是农历虎年,小美利用一副七巧板拼出如图所示的“老虎”.已知左侧七巧板拼成的大正方形边长是4,则右侧“老虎”的虎头小正方形的面积是 .
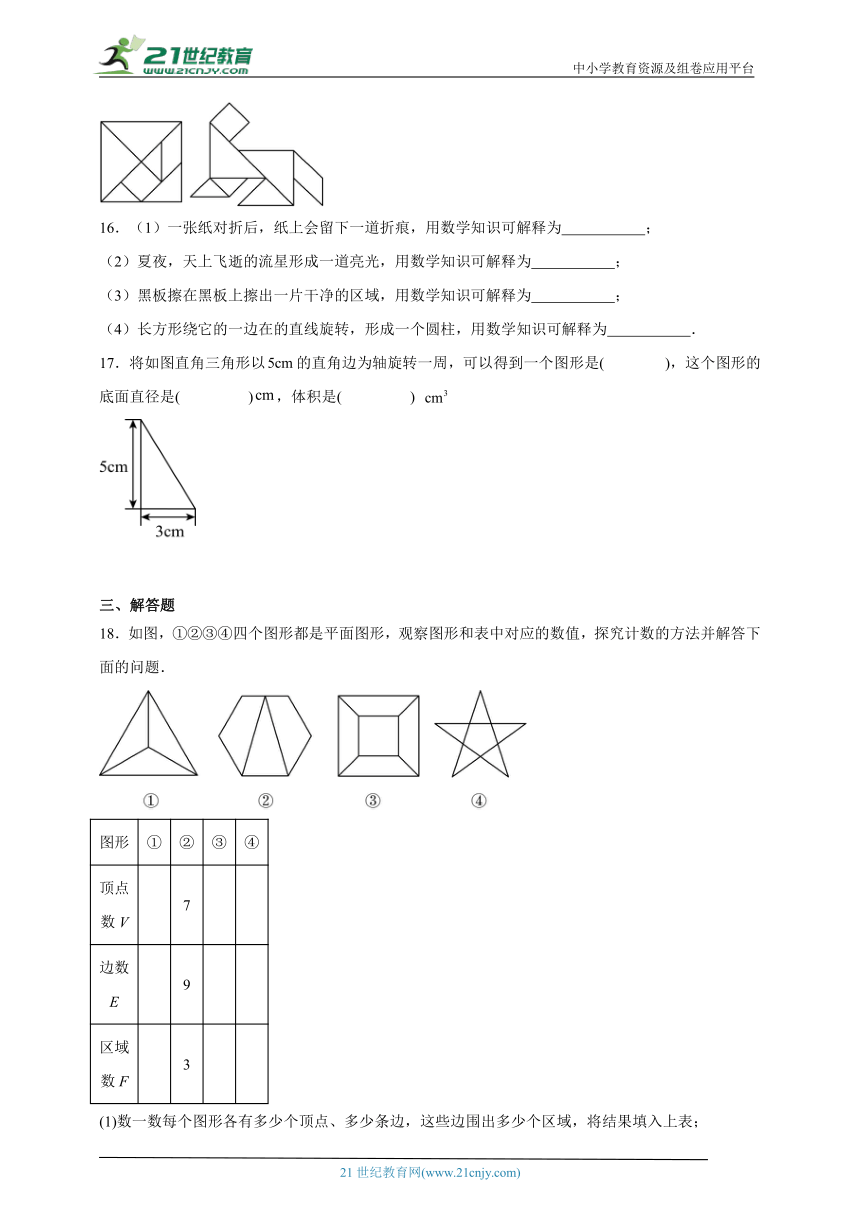
16.(1)一张纸对折后,纸上会留下一道折痕,用数学知识可解释为 ;
(2)夏夜,天上飞逝的流星形成一道亮光,用数学知识可解释为 ;
(3)黑板擦在黑板上擦出一片干净的区域,用数学知识可解释为 ;
(4)长方形绕它的一边在的直线旋转,形成一个圆柱,用数学知识可解释为 .
17.将如图直角三角形以的直角边为轴旋转一周,可以得到一个图形是( ),这个图形的底面直径是( ),体积是( )
三、解答题
18.如图,①②③④四个图形都是平面图形,观察图形和表中对应的数值,探究计数的方法并解答下面的问题.
图形 ① ② ③ ④
顶点数V 7
边数E 9
区域数F 3
(1)数一数每个图形各有多少个顶点、多少条边,这些边围出多少个区域,将结果填入上表;
(2)根据表格,猜想平面图形的顶点数、边数和区域数之间的关系;
(3)如果一个平面图形有个顶点和个区域,那么这个平面图形有几条边?
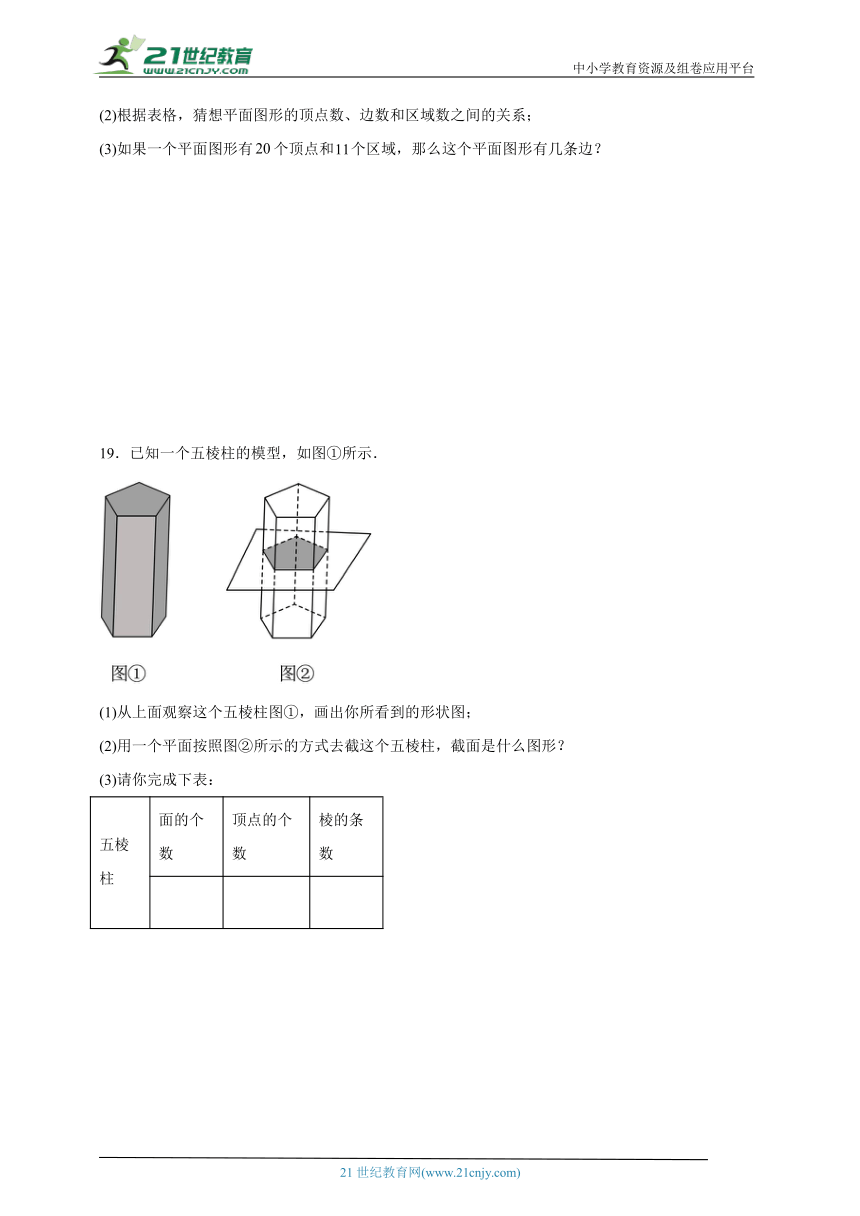
19.已知一个五棱柱的模型,如图①所示.
(1)从上面观察这个五棱柱图①,画出你所看到的形状图;
(2)用一个平面按照图②所示的方式去截这个五棱柱,截面是什么图形?
(3)请你完成下表:
五棱柱 面的个数 顶点的个数 棱的条数
20.仔细观察下面的正四面体、正六面体、正八面体,解决下列问题:
(1)填空:
①正四面体的顶点数______,面数______,棱数______;
②正六面体的顶点数______,面数______,棱数______;
③正八面体的顶点数______,面数______,棱数______;
(2)若将多面体的顶点数用v表示,面数用f表示,棱数用e表示,则v,f,e之间的数量关系可用一个公式来表示:________
21.我们所学的立体图形大致可分为柱、锥、球体,它们是否都可以展成平面图形?若不能,说明为什么;若能,说明展开图有何区别和联系.
22.七巧板起源于我国宋代,后流传于世界各国.在“综合与实践”课上,兴趣小组同学们用一张正方形纸片依据图1,制作了图2所示的七巧板.
(1)图1中与长度相等的线段是 ; (写出一条即可)
(2)从图 2所示的七巧板中任选几块拼出一个等腰梯形,画出你拼图案的形状图(在所画图中标出选取的七巧板序号).
23.如图①,②所示为用刀切去正方体一个角得到等边三角形截面的方法.请你实践并思考:将正方体用刀切去一块,它的截面可能是图③中的哪些图形?
24.如图所示:如果将图中①~④的平面图形绕虚线旋转一周,可以得到Ⅰ~Ⅴ几何体,请你把有对应关系的平面图形与几何体用线连接起来.
《6.1几何图形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B D C A B C B B
题号 11 12
答案 B D
1.D
【分析】本题考查了截一个几何体,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.对于这类题,最好是动手动脑相结合,亲自动手做一做,从中学会分析和归纳的思想方法.根据圆柱的特点,考虑截面从不同角度和方向截取的情况即可求解.
【详解】解:用一个平面截圆柱,横切就是圆,竖切就是长方形或椭圆,唯独不可能是梯形.
故选:D
2.D
【分析】根据展开图,可得空心圆与一个实心圆的面是相对的,只与一个实心圆面相邻,判断即可.
【详解】根据展开图,可得空心圆与一个实心圆的面是相对的,只与一个实心圆面相邻,
A、B、C都不符合题意,只有D符合题意,
故选D.
【点睛】本题考查了正方体的展开图,熟练掌握展开图的特点是解题的关键.
3.B
【分析】根据围成几何体的面分为多面体和曲面体,逐一进行判断即可求解.
【详解】解:A.侧面是曲面,是曲面体,故不符合题意;
B.每个面都是长方形,没有曲面,故符合题意;
C. 侧面是曲面,是曲面体,故不符合题意;
D.是曲面体,故不符合题意;
故选:B.
【点睛】本题考查了几何体的分类,理解分类的标准是解题的关键.
4.D
【分析】位置关系,大小,形状属于几何研究特性.
【详解】解:颜色不属于几何研究特性,位置关系,大小,形状属于几何研究特性.
故选D.
【点睛】本题考查认识平面图形,几何研究特性研究的是位置关系,大小,形状.
5.C
【分析】本题考查了展开图折叠成几何体,长方体的体积,熟记长方体的体积公式是解题的关键.
分别求得剪去的正方形边长从变为后,长方体的纸盒容积即可得到结论.
【详解】解:当剪去的正方形边长为时,
长方体的纸盒容积为:
当剪去的正方形边长为时,
∴当剪去的正方形的边长从变为后,长方体纸盒的容积增加了:.
即长方体纸盒的容积增加了8.
故选:C.
6.A
【分析】这一现象为:点动成线.
【详解】解:笔尖在纸上快速滑动写出数字9,用数学知识解释为点动成线.
故选A.
【点睛】本题考查点,线,面,体之间的关系.熟练掌握点动成线,线动成面,面动成体,是解题的关键.
7.B
【分析】根据图示可知,“小天鹅”图案是由边长是1分米的正方形切拼而成,所以“小天鹅”图案的面积等于这个正方形的面积.根据阴影部分的面积占整个正方形面积的分率求解即可.
【详解】解:如图:
(平方分米)
答:阴影部分的面积为.
故选:B.
【点睛】本题主要考查组合图形的面积,关键是分清阴影部分与整个图形的关系.
8.C
【分析】本题主要考查了用平面截一个几何体,熟知用平面截一个球,截面的形状只会是圆是解题的关键.
【详解】解:用平面截一个球,截面的形状只会是圆,
故选:C.
9.B
【分析】此图形为正方体展开图的“1 4 1”型,折成正方体,有空白圆与涂色圆的面相对,有两个涂色三角形的面相邻,且一个公共锐角顶点,有涂色圆的面与有两个涂色三角形的非涂色点为公共顶点,有空白圆的面与涂色三角形的两涂色点为公共顶点.据此解答即可.
【详解】解:如图:
是 的正方体展开图.
故选:B.
【点睛】解答此题的关键弄清该正方体展开图折成正方体后,各图案的位置关系.
10.B
【分析】利用图形求出长方体的宽及长即可.
【详解】解:∵长方体的底面为正方形,由图可知底面周长等于长方形纸板的宽,
∴正方形的边长为1,箱子的长为,
长方体的体积为:
故选B.
【点睛】本题主要考查长方体体积的计算方法,熟练根据图求出长宽高是解题关键.
11.B
【分析】本题主要考查正方体的展开图的性质,掌握正方体展开图的性质是解题关键;根据正方体的表面展开图,相对的面之间相隔一个正方形,根据这一特点即可求解.
【详解】解:原正方体中,与“奋”字一面相对的面上的字为“毅”,
故选:B.
12.D
【分析】此题主要考查了从不同方向看几何体.
从左面看几何体有两列,一列有3个小正方体,第二列有2个正方体,画出图形即可得出答案.
【详解】解:从左面看几何体有两列,每时一列有3个小正方体,第二列有2个正方体,即看到的形状图为:
.
故选:D.
13.①②③
【分析】本题考查了截一个几何体,熟练掌握三棱柱的截面形状是解题的关键.根据三棱柱的截面形状判断即可.
【详解】解:∵三棱柱有5个面,
∴用一个平面去截三棱柱,截面的形状可能是:三角形,四边形,五边形,不可能是六边形.
故答案为:①②③.
14.①②/②①
【分析】本题考查了从不同的角度看几何题,分别画出小明搭的从左边看到的图形和小兵搭的从左边看到的图形,即可解答.
【详解】
解:小明搭的从左面看是,
小兵搭的从左边看:
①,②,③,
∴小兵搭的积木中①②号的形状和小明搭的是相同的,
故答案为:①②.
15.2
【分析】在七巧板中小正方形的面积占整个正方形面积的,然后求出整个正方形的面积,即可求出虎头小正方形的面积.
【详解】解:大正方形的面积为4×4=16,
虎头小正方形的面积为
故答案为:2.
【点睛】本题主要考查七巧板的各图形之间的关系,大三角形占大正方形面积的,平行四边形,较小三角形和小正方形各占大正方形面积的,最小三角形占大正方形面积的.
16. 面与面相交得到线 点动成线 线动成面 面动成体
【分析】题目考查了点、线、面之间的动态关系,理解生活中的点、线、面关系是解题的关键.
【详解】(1)一张纸对折后,纸上会留下一道折痕,用数学知识可解释为面与面相交得到线;
故答案为:面与面相交得到线
(2)夏夜,天上飞逝的流星形成一道亮光,用数学知识可解释为点动成线;
故答案为:点动成线
(3)黑板擦在黑板上擦出一片干净的区域,用数学知识可解释为线动成面;
故答案为:线动成面
(4)长方形绕它的一边所在的直线旋转,形成一个圆柱,用数学知识可解释为面动成体.
故答案为:面动成体
17. 圆锥 6
【分析】本题考查了平面图形的旋转,圆锥的体积,通过空间想象确定旋转后的立体图形是解题关键.
根据面动成体的原理可知,直角三角形以直角边为轴旋转一周得到圆锥,高为轴,底面半径为另一条直角边,再根据圆锥体积公式计算,即可得到答案.
【详解】解:直角三角形以的直角边为轴旋转一周,可以得到一个图形是圆锥,这个图形的高是,底面直径是,体积是,
故答案为:①圆锥,②6,③.
18.(1)见解析
(2)
(3)条边
【分析】本题考查了平面图形,图形的规律探究.根据图形推导一般性规律是解题的关键.
(1)根据顶点,边长的定义,作答即可;
(2)推导一般性规律即可;
(3)根据,,计算求解即可.
【详解】(1)解:由题意知,填表如下;
图形 ① ② ③ ④
顶点数V 4 7 8
边数E 6 9
区域数F 3 3 5 6
(2)解:由题意知,;;;
∴可推导一般性规律为;
(3)解:由题意知,,
∴,
∴这个平面图形有条边.
19.(1)图形见解析;
(2)截面是五边形;
(3)表格见解析.
【分析】本题考查的是从不同方向看几何体,立体图形的截面的形状,五棱柱的面,顶点,棱的数量,理解基础知识是解本题的关键;
(1)画出从上面看到的平面图形即可;
(2)根据截面的位置可得答案;
(3)结合五棱柱的特点可得答案.
【详解】(1)解:如图所示:
(2)截面是五边形;
五棱柱 面的个数 顶点的个数 棱的条数
7 10 15
20.(1)①4,4,6;②8,6,12;③6,8,12
(2)
【分析】本题考查的是多面体的定义,关键点在于:多面体指四个或四个以上多边形所围成的立体图形;
(1)观察图形,结合多面体的顶点、面和棱的定义进行填空即可;
(2)根据(1)中,多面体的顶点数,面数和棱数,总结规律可得v,f,e之间的数量关系式;
【详解】(1)①正四面体的顶点数,面数,棱数;
②正六面体的顶点数,面数,棱数;
③正八面体的顶点数,面数,棱数;
故答案为:①4,4,6;②8,6,12;③6,8,12;
(2)根据(1)中数据可得:
①
②
③
故v,f,e之间的数量关系是:
21.见解析
【分析】根据柱体、锥体、球体的表面展开图解答即可.
【详解】解:柱体:圆柱展开图是两个圆和长方形,
棱柱的展开图是长方形;
锥体:圆锥的展开图一个圆加扇形,
棱锥的展开图是底面的多边形和侧面的等腰三角形;
球体不能展开,没有展开图.
【点睛】本题主要考查几何体的展开图,熟练掌握常见立体图形的展开图是解题的关键.
22.(1)(答案不唯一)
(2)见解析
【分析】本题考查七巧板,理解七巧板的分割方法以及分割的七个部分的图形性质以及相互关系是正确解答的关键.
(1)根据“七巧板”的分割方法得到第⑥部分是平行四边形,根据平行四边形的性质可得答案;
(2)取“七巧板”中的若干块,拼成等腰梯形即可.
【详解】(1)∵⑥是平行四边形,
∴,
故答案为:(答案不唯一);
(2)取③④⑤⑥按照如图所示的方式可以拼成一个等腰梯形.
23.见解析
【分析】本题主要考查了截一个几何体,关键在于弄明白平面截正方体时,穿过了几个面或与几条棱相交.若穿过了三个面或与三条棱相交,那么截面是三角形;若穿过了四个面或与四条棱相交,那么截面是四边形(正方形或长方形或梯形),依此类推,由于正方体只有六个面,所以截面最多的是六边形,而不会是七边形、八边形
【详解】解:根据题意,截面过三条棱,那么截面就是三角形,若截的三条棱长度不一,得到第一个图形,有两条相等得到第三个图形,三条都相等得到第二个图形;
沿上下底面一条对角线垂直上下底面切,得到截面是长方形第五个图形;
沿垂直上下底面或侧面的平面切,得到正方形的截面第六个图形;
不垂直上下底面,且切过上下底面各2条棱,得到梯形截面第七个图形;
切过六条棱,得到正六边形截面第八个图形.
无论怎么切,得不到截面是直角三角形,则截面不可能是第四个图形.
24.见解析
【分析】本题考查了平面图形与立体图形的联系,培养学生的观察能力和空间想象能力.根据面动成体的原理解题即可得.
【详解】解:①半圆旋转得到球体,即几何体Ⅳ;②旋转得到几何体Ⅰ;③旋转得到几何体Ⅴ;④三角形旋转得到圆锥,即几何体Ⅲ.
用线连接起来如图所示:
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.1几何图形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.用一个平面截圆柱,则截面形状不可能是( )
A.圆 B.椭圆 C.长方形 D.梯形
2.如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
A. B. C. D.
3.下列几何体中,没有曲面的是( )
A.圆柱 B.长方体 C.圆锥 D.球
4.下列选项中的物体属性,不属于几何研究特性的是( )
A.位置关系 B.大小 C.形状 D.颜色
5.如图,把一个边长为的正方形纸片的四个角各剪去一个同样大小的正方形,然后把剩下的部分折成一个无盖的长方体盒子,当剪去的正方形的边长从变为后,长方体纸盒的容积( ).
A.增加了28 B.减少了28 C.增加了8 D.减少了8
6.“笔尖在纸上快速滑动写出数字9”运用数学知识解释这一现象为( )
A.点动成线 B.线动成面
C.面动成体 D.面与面相交得线
7.用边长为的正方形纸板,制成一副七巧板,将它拼成“小天鹅”图案,其中阴影部分的面积是( ).
A. B. C. D.
8.用一个平面去截一个球体,截面形状可能为( )
A. B. C. D.
9.如图的图形是( )正方体的展开图.
A. B. C. D.
10.如图所示的长方形(长为7,宽为4)硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形的长方体箱子,则长方体箱子的体积为( )
A.22 B.5 C.7 D.11
11.如图是一个正方体的表面展开图,每一个面上都写有一个汉字,则原正方体中,与“奋”字一面相对的面上的字为( )
A.弘 B.毅 C.自 D.强
12.一个几何体由若干个大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体从左面看到的形状图是( )
A. B. C. D.
二、填空题
13.用一个平面去截如图所示的三棱柱,关于截面形状的四种说法:①三角形,②四边形,③五边形,④六边形.其中截面的形状可能是 .(填序号)
14.从左面看,小兵搭的积木中( )号的形状和小明搭的是相同的.(填序号)
15.2022年是农历虎年,小美利用一副七巧板拼出如图所示的“老虎”.已知左侧七巧板拼成的大正方形边长是4,则右侧“老虎”的虎头小正方形的面积是 .
16.(1)一张纸对折后,纸上会留下一道折痕,用数学知识可解释为 ;
(2)夏夜,天上飞逝的流星形成一道亮光,用数学知识可解释为 ;
(3)黑板擦在黑板上擦出一片干净的区域,用数学知识可解释为 ;
(4)长方形绕它的一边在的直线旋转,形成一个圆柱,用数学知识可解释为 .
17.将如图直角三角形以的直角边为轴旋转一周,可以得到一个图形是( ),这个图形的底面直径是( ),体积是( )
三、解答题
18.如图,①②③④四个图形都是平面图形,观察图形和表中对应的数值,探究计数的方法并解答下面的问题.
图形 ① ② ③ ④
顶点数V 7
边数E 9
区域数F 3
(1)数一数每个图形各有多少个顶点、多少条边,这些边围出多少个区域,将结果填入上表;
(2)根据表格,猜想平面图形的顶点数、边数和区域数之间的关系;
(3)如果一个平面图形有个顶点和个区域,那么这个平面图形有几条边?
19.已知一个五棱柱的模型,如图①所示.
(1)从上面观察这个五棱柱图①,画出你所看到的形状图;
(2)用一个平面按照图②所示的方式去截这个五棱柱,截面是什么图形?
(3)请你完成下表:
五棱柱 面的个数 顶点的个数 棱的条数
20.仔细观察下面的正四面体、正六面体、正八面体,解决下列问题:
(1)填空:
①正四面体的顶点数______,面数______,棱数______;
②正六面体的顶点数______,面数______,棱数______;
③正八面体的顶点数______,面数______,棱数______;
(2)若将多面体的顶点数用v表示,面数用f表示,棱数用e表示,则v,f,e之间的数量关系可用一个公式来表示:________
21.我们所学的立体图形大致可分为柱、锥、球体,它们是否都可以展成平面图形?若不能,说明为什么;若能,说明展开图有何区别和联系.
22.七巧板起源于我国宋代,后流传于世界各国.在“综合与实践”课上,兴趣小组同学们用一张正方形纸片依据图1,制作了图2所示的七巧板.
(1)图1中与长度相等的线段是 ; (写出一条即可)
(2)从图 2所示的七巧板中任选几块拼出一个等腰梯形,画出你拼图案的形状图(在所画图中标出选取的七巧板序号).
23.如图①,②所示为用刀切去正方体一个角得到等边三角形截面的方法.请你实践并思考:将正方体用刀切去一块,它的截面可能是图③中的哪些图形?
24.如图所示:如果将图中①~④的平面图形绕虚线旋转一周,可以得到Ⅰ~Ⅴ几何体,请你把有对应关系的平面图形与几何体用线连接起来.
《6.1几何图形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B D C A B C B B
题号 11 12
答案 B D
1.D
【分析】本题考查了截一个几何体,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.对于这类题,最好是动手动脑相结合,亲自动手做一做,从中学会分析和归纳的思想方法.根据圆柱的特点,考虑截面从不同角度和方向截取的情况即可求解.
【详解】解:用一个平面截圆柱,横切就是圆,竖切就是长方形或椭圆,唯独不可能是梯形.
故选:D
2.D
【分析】根据展开图,可得空心圆与一个实心圆的面是相对的,只与一个实心圆面相邻,判断即可.
【详解】根据展开图,可得空心圆与一个实心圆的面是相对的,只与一个实心圆面相邻,
A、B、C都不符合题意,只有D符合题意,
故选D.
【点睛】本题考查了正方体的展开图,熟练掌握展开图的特点是解题的关键.
3.B
【分析】根据围成几何体的面分为多面体和曲面体,逐一进行判断即可求解.
【详解】解:A.侧面是曲面,是曲面体,故不符合题意;
B.每个面都是长方形,没有曲面,故符合题意;
C. 侧面是曲面,是曲面体,故不符合题意;
D.是曲面体,故不符合题意;
故选:B.
【点睛】本题考查了几何体的分类,理解分类的标准是解题的关键.
4.D
【分析】位置关系,大小,形状属于几何研究特性.
【详解】解:颜色不属于几何研究特性,位置关系,大小,形状属于几何研究特性.
故选D.
【点睛】本题考查认识平面图形,几何研究特性研究的是位置关系,大小,形状.
5.C
【分析】本题考查了展开图折叠成几何体,长方体的体积,熟记长方体的体积公式是解题的关键.
分别求得剪去的正方形边长从变为后,长方体的纸盒容积即可得到结论.
【详解】解:当剪去的正方形边长为时,
长方体的纸盒容积为:
当剪去的正方形边长为时,
∴当剪去的正方形的边长从变为后,长方体纸盒的容积增加了:.
即长方体纸盒的容积增加了8.
故选:C.
6.A
【分析】这一现象为:点动成线.
【详解】解:笔尖在纸上快速滑动写出数字9,用数学知识解释为点动成线.
故选A.
【点睛】本题考查点,线,面,体之间的关系.熟练掌握点动成线,线动成面,面动成体,是解题的关键.
7.B
【分析】根据图示可知,“小天鹅”图案是由边长是1分米的正方形切拼而成,所以“小天鹅”图案的面积等于这个正方形的面积.根据阴影部分的面积占整个正方形面积的分率求解即可.
【详解】解:如图:
(平方分米)
答:阴影部分的面积为.
故选:B.
【点睛】本题主要考查组合图形的面积,关键是分清阴影部分与整个图形的关系.
8.C
【分析】本题主要考查了用平面截一个几何体,熟知用平面截一个球,截面的形状只会是圆是解题的关键.
【详解】解:用平面截一个球,截面的形状只会是圆,
故选:C.
9.B
【分析】此图形为正方体展开图的“1 4 1”型,折成正方体,有空白圆与涂色圆的面相对,有两个涂色三角形的面相邻,且一个公共锐角顶点,有涂色圆的面与有两个涂色三角形的非涂色点为公共顶点,有空白圆的面与涂色三角形的两涂色点为公共顶点.据此解答即可.
【详解】解:如图:
是 的正方体展开图.
故选:B.
【点睛】解答此题的关键弄清该正方体展开图折成正方体后,各图案的位置关系.
10.B
【分析】利用图形求出长方体的宽及长即可.
【详解】解:∵长方体的底面为正方形,由图可知底面周长等于长方形纸板的宽,
∴正方形的边长为1,箱子的长为,
长方体的体积为:
故选B.
【点睛】本题主要考查长方体体积的计算方法,熟练根据图求出长宽高是解题关键.
11.B
【分析】本题主要考查正方体的展开图的性质,掌握正方体展开图的性质是解题关键;根据正方体的表面展开图,相对的面之间相隔一个正方形,根据这一特点即可求解.
【详解】解:原正方体中,与“奋”字一面相对的面上的字为“毅”,
故选:B.
12.D
【分析】此题主要考查了从不同方向看几何体.
从左面看几何体有两列,一列有3个小正方体,第二列有2个正方体,画出图形即可得出答案.
【详解】解:从左面看几何体有两列,每时一列有3个小正方体,第二列有2个正方体,即看到的形状图为:
.
故选:D.
13.①②③
【分析】本题考查了截一个几何体,熟练掌握三棱柱的截面形状是解题的关键.根据三棱柱的截面形状判断即可.
【详解】解:∵三棱柱有5个面,
∴用一个平面去截三棱柱,截面的形状可能是:三角形,四边形,五边形,不可能是六边形.
故答案为:①②③.
14.①②/②①
【分析】本题考查了从不同的角度看几何题,分别画出小明搭的从左边看到的图形和小兵搭的从左边看到的图形,即可解答.
【详解】
解:小明搭的从左面看是,
小兵搭的从左边看:
①,②,③,
∴小兵搭的积木中①②号的形状和小明搭的是相同的,
故答案为:①②.
15.2
【分析】在七巧板中小正方形的面积占整个正方形面积的,然后求出整个正方形的面积,即可求出虎头小正方形的面积.
【详解】解:大正方形的面积为4×4=16,
虎头小正方形的面积为
故答案为:2.
【点睛】本题主要考查七巧板的各图形之间的关系,大三角形占大正方形面积的,平行四边形,较小三角形和小正方形各占大正方形面积的,最小三角形占大正方形面积的.
16. 面与面相交得到线 点动成线 线动成面 面动成体
【分析】题目考查了点、线、面之间的动态关系,理解生活中的点、线、面关系是解题的关键.
【详解】(1)一张纸对折后,纸上会留下一道折痕,用数学知识可解释为面与面相交得到线;
故答案为:面与面相交得到线
(2)夏夜,天上飞逝的流星形成一道亮光,用数学知识可解释为点动成线;
故答案为:点动成线
(3)黑板擦在黑板上擦出一片干净的区域,用数学知识可解释为线动成面;
故答案为:线动成面
(4)长方形绕它的一边所在的直线旋转,形成一个圆柱,用数学知识可解释为面动成体.
故答案为:面动成体
17. 圆锥 6
【分析】本题考查了平面图形的旋转,圆锥的体积,通过空间想象确定旋转后的立体图形是解题关键.
根据面动成体的原理可知,直角三角形以直角边为轴旋转一周得到圆锥,高为轴,底面半径为另一条直角边,再根据圆锥体积公式计算,即可得到答案.
【详解】解:直角三角形以的直角边为轴旋转一周,可以得到一个图形是圆锥,这个图形的高是,底面直径是,体积是,
故答案为:①圆锥,②6,③.
18.(1)见解析
(2)
(3)条边
【分析】本题考查了平面图形,图形的规律探究.根据图形推导一般性规律是解题的关键.
(1)根据顶点,边长的定义,作答即可;
(2)推导一般性规律即可;
(3)根据,,计算求解即可.
【详解】(1)解:由题意知,填表如下;
图形 ① ② ③ ④
顶点数V 4 7 8
边数E 6 9
区域数F 3 3 5 6
(2)解:由题意知,;;;
∴可推导一般性规律为;
(3)解:由题意知,,
∴,
∴这个平面图形有条边.
19.(1)图形见解析;
(2)截面是五边形;
(3)表格见解析.
【分析】本题考查的是从不同方向看几何体,立体图形的截面的形状,五棱柱的面,顶点,棱的数量,理解基础知识是解本题的关键;
(1)画出从上面看到的平面图形即可;
(2)根据截面的位置可得答案;
(3)结合五棱柱的特点可得答案.
【详解】(1)解:如图所示:
(2)截面是五边形;
五棱柱 面的个数 顶点的个数 棱的条数
7 10 15
20.(1)①4,4,6;②8,6,12;③6,8,12
(2)
【分析】本题考查的是多面体的定义,关键点在于:多面体指四个或四个以上多边形所围成的立体图形;
(1)观察图形,结合多面体的顶点、面和棱的定义进行填空即可;
(2)根据(1)中,多面体的顶点数,面数和棱数,总结规律可得v,f,e之间的数量关系式;
【详解】(1)①正四面体的顶点数,面数,棱数;
②正六面体的顶点数,面数,棱数;
③正八面体的顶点数,面数,棱数;
故答案为:①4,4,6;②8,6,12;③6,8,12;
(2)根据(1)中数据可得:
①
②
③
故v,f,e之间的数量关系是:
21.见解析
【分析】根据柱体、锥体、球体的表面展开图解答即可.
【详解】解:柱体:圆柱展开图是两个圆和长方形,
棱柱的展开图是长方形;
锥体:圆锥的展开图一个圆加扇形,
棱锥的展开图是底面的多边形和侧面的等腰三角形;
球体不能展开,没有展开图.
【点睛】本题主要考查几何体的展开图,熟练掌握常见立体图形的展开图是解题的关键.
22.(1)(答案不唯一)
(2)见解析
【分析】本题考查七巧板,理解七巧板的分割方法以及分割的七个部分的图形性质以及相互关系是正确解答的关键.
(1)根据“七巧板”的分割方法得到第⑥部分是平行四边形,根据平行四边形的性质可得答案;
(2)取“七巧板”中的若干块,拼成等腰梯形即可.
【详解】(1)∵⑥是平行四边形,
∴,
故答案为:(答案不唯一);
(2)取③④⑤⑥按照如图所示的方式可以拼成一个等腰梯形.
23.见解析
【分析】本题主要考查了截一个几何体,关键在于弄明白平面截正方体时,穿过了几个面或与几条棱相交.若穿过了三个面或与三条棱相交,那么截面是三角形;若穿过了四个面或与四条棱相交,那么截面是四边形(正方形或长方形或梯形),依此类推,由于正方体只有六个面,所以截面最多的是六边形,而不会是七边形、八边形
【详解】解:根据题意,截面过三条棱,那么截面就是三角形,若截的三条棱长度不一,得到第一个图形,有两条相等得到第三个图形,三条都相等得到第二个图形;
沿上下底面一条对角线垂直上下底面切,得到截面是长方形第五个图形;
沿垂直上下底面或侧面的平面切,得到正方形的截面第六个图形;
不垂直上下底面,且切过上下底面各2条棱,得到梯形截面第七个图形;
切过六条棱,得到正六边形截面第八个图形.
无论怎么切,得不到截面是直角三角形,则截面不可能是第四个图形.
24.见解析
【分析】本题考查了平面图形与立体图形的联系,培养学生的观察能力和空间想象能力.根据面动成体的原理解题即可得.
【详解】解:①半圆旋转得到球体,即几何体Ⅳ;②旋转得到几何体Ⅰ;③旋转得到几何体Ⅴ;④三角形旋转得到圆锥,即几何体Ⅲ.
用线连接起来如图所示:
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
