2025年浙江省杭州市精选期末真题重组模拟卷 含解析
文档属性
| 名称 | 2025年浙江省杭州市精选期末真题重组模拟卷 含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 304.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 18:05:13 | ||
图片预览




文档简介
/ 让教学更有效 精品试卷 | 数学学科
2025年浙江省杭州市精选期末真题重组模拟卷
满分120分 考试时间120分钟
学校:___________ 姓名:___________ 班级:___________ 考号:___________
一、选择题(共30分)
1.(24-25七年级下·浙江杭州·期末)下列方程中,是二元一次方程的是( )
A. B. C. D.
2.(23-24七年级下·浙江杭州西湖区·期末)在日本核电站排放核废水期间,我国某监测点监测到极微量的人工放射性核素碘-131,其浓度为0.0000963贝克/立方米.数据“0.0000963”用科学记数法可表示为( )
A. B. C. D.
3.(23-24七年级下·浙江杭州·期末)若分式有意义,则( )
A. B. C. D.
4.(22-23·浙江杭州·期末)下列调查中,①调查本班同学的视力;②调查一批节能灯管的使用寿命;③为保证“神舟9号”的成功发射,对其零部件进行检查;④对乘坐某班次客车的乘客进行安检.其中适合采用抽样调查的是( )
A.① B.② C.③ D.④
5.(23-24七年级下·浙江杭州·期末)下列计算中,正确的是( )
A. B.
C. D.
6.(23-24七年级下·浙江杭州·期末)若是二元一次方程的一个解,则的值是( )
A.0 B.1 C.2 D.3
7.(21-22七年级下·浙江杭州·期末)将一个直角三角板和一把直尺如图放置,如果∠α=46°,则∠β的度数是( )
A.43° B.44° C.45° D.46°
8.(21-22七年级下·浙江·期末)为了改善生态环境,防止水土流失,某村计划在荒坡上种植480棵树.由于青年志愿者的加入,每日比原计划多种,结果提前4天完成任务.设志愿者加入后每天种树x棵,则所列方程为( )
A. B. C. D.
9.(22-23·浙江杭州·期末)如图,边长为的大正方形剪去个边长为的小正方形,做成一个无盖纸盒.若无盖纸盒的底面积与表面积之比为:,则根据题意可知,满足的关系式为( )
A. B. C. D.
10.(23-24七年级下·浙江杭州·期末)设n为某一自然数,代入代数式计算其值时,四个学生算出了下列四个结果.其中正确的结果是( )
A.521 B.1413 C.3721 D.1716
二、填空题(共18分)
11.(23-24七年级下册·浙江杭州·期末真题)因式分解:= .
12.(24-25七年级下·浙江杭州·期末)运动会上将名运动员按跳远成绩分组后,组界为米的一组有人,则该组的频率是 .
13.(23-24七年级下·浙江杭州·期末)如图,将沿方向平移2个单位后得到.若,则的长是 .
14.(23-24七年级下·浙江杭州·期末)将一张长方形纸条折叠成如图形状,若,则 .
15.(22-23七年级下·浙江杭州·期末)关于的方程组,则的值等于 .
16.(22-23七年级下·浙江杭州·期末)如图,,射线,分别与,交于点M,N,若,则的度数是 .
三、解答题(共72分)
17.(8分)(23-24七年级下·浙江杭州·期末)计算
(1);
(2).
18.(8分)(23-24七年级下·浙江杭州·期末)(1)解方程组
(2)计算:.
19.(8分)(23-24七年级下·浙江杭州·期末)先化简;,再从,,,1,3中选择一个你喜欢的值代入求值.
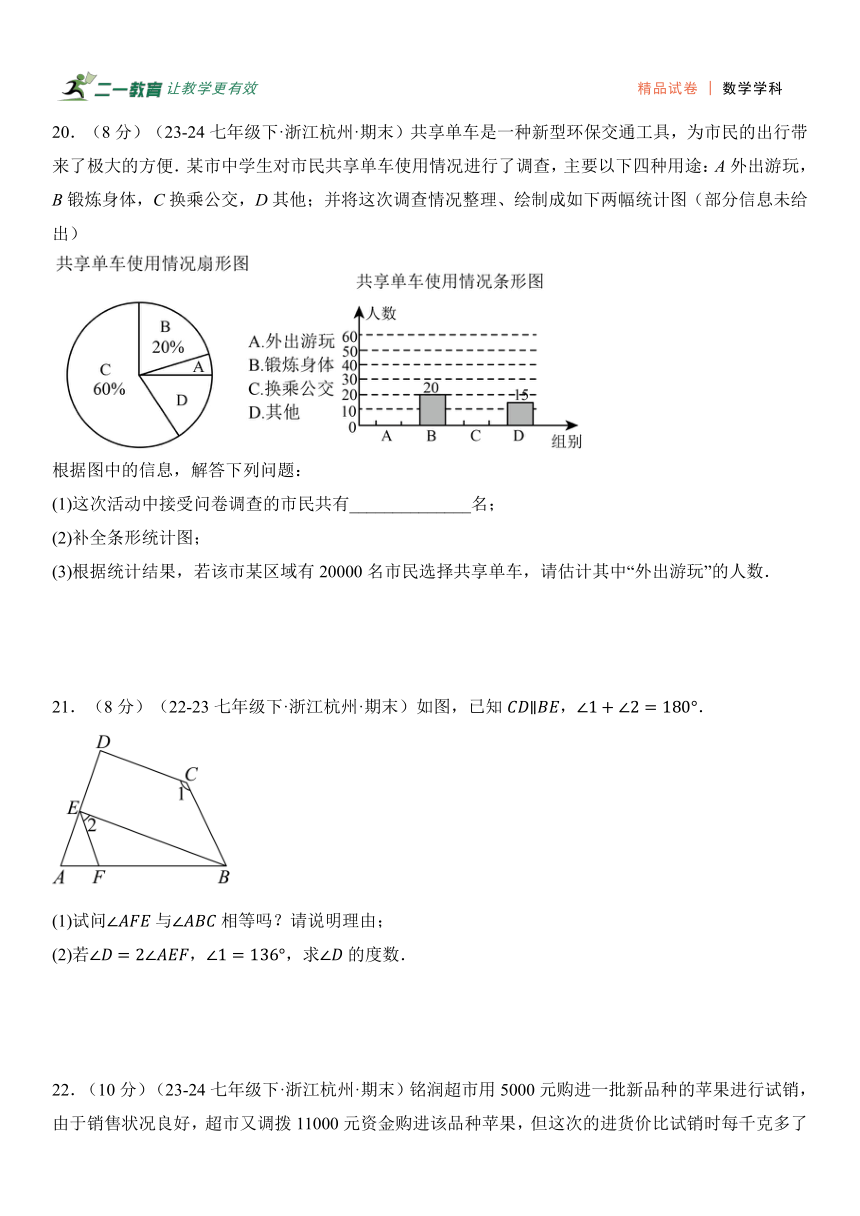
20.(8分)(23-24七年级下·浙江杭州·期末)共享单车是一种新型环保交通工具,为市民的出行带来了极大的方便.某市中学生对市民共享单车使用情况进行了调查,主要以下四种用途:A外出游玩,B锻炼身体,C换乘公交,D其他;并将这次调查情况整理、绘制成如下两幅统计图(部分信息未给出)
根据图中的信息,解答下列问题:
(1)这次活动中接受问卷调查的市民共有______________名;
(2)补全条形统计图;
(3)根据统计结果,若该市某区域有20000名市民选择共享单车,请估计其中“外出游玩”的人数.
21.(8分)(22-23七年级下·浙江杭州·期末)如图,已知,.
(1)试问与相等吗?请说明理由;
(2)若,,求的度数.
22.(10分)(23-24七年级下·浙江杭州·期末)铭润超市用5000元购进一批新品种的苹果进行试销,由于销售状况良好,超市又调拨11000元资金购进该品种苹果,但这次的进货价比试销时每千克多了元,购进苹果数量是试销时的2倍.
(1)试销时该品种苹果的进货价是每千克多少元?两次共购进多少苹果?
(2)如果超市将该品种苹果按每千克10元的定价出售,当大部分苹果售出后,余下的500千克按定价的六折售完,那么超市在这两次苹果销售中共盈利多少元?
23.(10分)(22-23七年级下·浙江杭州·期末)已知,是常数,.
(1)若,,求t;
(2)试将等式①变形成“”形式,其中A,B表示关于a,b,t的整式;
(3)若t的取值与x无关,请说明.
24.(12分)(22-23七年级下·浙江杭州·期末)在一次研究性学习中,同学们对乘法公式进行了研究.
(1)如图,大正方形的边长为,直接写出下列结果.
①中间小正方形的边长;
②用含,的等式表示:大正方形面积与小正方形面积的差等于图中一个长方形面积的倍.
(2)当,.求的值.
(3)若当,时,的值唯一确定,用含的代数式表示.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C A B C A B D A D
1.A
【分析】本题考查二元一次方程的定义,根据二元一次方程的定义:含有两个未知数,并且含有未知数的项的次数都是1,像这样的整式方程叫做二元一次方程.据此逐一判断即可得.
【详解】解:A. ,是二元一次方程,故该选项正确,符合题意;
B. ,最高次数为,不是二元一次方程,故该选项不正确,不符合题意;
C. ,不是整式方程,不是二元一次方程,故该选项不正确,不符合题意;
D. ,最高次数为,不是二元一次方程,故该选项不正确,不符合题意;
故选:A.
2.C
【分析】本题主要考查科学记数法,熟练掌握科学记数法是解题的关键;科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于或等于10时,n是正整数;当原数的绝对值小于1时,n是负整数.
【详解】解:数据“0.0000963”用科学记数法可表示为;
故选C
3.A
【分析】此题主要考查了分式有意义的条件,关键是掌握分式有意义的条件是分母不等于零.利用分式有意义的条件可得,再解不等式即可.
【详解】解:由题意得:,
解得:,
故选:A
4.B
【详解】试题分析:①适合普查,故①不适合抽样调查;
②调查具有破坏性,故适合抽样调查,故②符合题意;
③调查要求准确性,故③不适合抽样调查;
④安检适合普查,故④不适合抽样调查.
故选B.
考点:全面调查与抽样调查.
5.C
【分析】本题考查了同底数幂的乘法和除法,多项式除以单项式,以及完全平方公式,熟练掌握各知识点是解答本题的关键.根据运算法则和完全平方公式逐项分析即可.
【详解】解:A.,故原计算不正确;
B.,故原计算不正确;
C.,正确;
D.,故原计算不正确;
故选C.
6.A
【分析】本题主要考查了二元一次方程的解的定义,代数式求值,将x与y的值代入原方程,得到,再代入计算即可求出答案,熟练掌握相关知识点并灵活运用是解决此题的关键.
【详解】解:∵是二元一次方程的一个解,
∴,即,
∴,
故选:A.
7.B
【分析】过点E作EMAB,则EMCD,根据平行线的性质可得∠α+∠β=90°,再由∠α可求解.
【详解】解:如图,由题意知:ABCD,∠FEG=90°,
过点E作EMAB,则EMCD,
∴∠FEM=∠α,∠GEM=∠β,
∵∠FEM+∠GEM=∠FEG=90°,
∴∠α+∠β=90°,
∵∠α=46°,
∴∠β=90°-46°=44°.
故选:B
【点睛】本题主要考查平行线的性质,解题的关键是准确作出辅助线,掌握两直线平行,同位角相等定理的应用.
8.D
【分析】根据结果提前天完成任务,列分式方程即可.
【详解】解:根据题意,得,
故选:D.
【点睛】本题考查了分式方程的应用,理解题意并根据题意建立等量关系是解题的关键.
9.A
【分析】根据题意分别表示出底面积与表面积,根据题意列出方程即可求解.
【详解】解:依题意,底面积为,表面积为,根据题意可得.
,
即,
故选:A.
【点睛】本题考查了分式方程的应用,根据题意表示出底面积与表面积是解题的关键.
10.D
【分析】本题综合考查因式分解的应用,三个连续自然数的积为偶数等相关知识点,重点掌握因式分解的应用.代数式因式分解可得,则代数式表示三个连续正整数的积.据此分析即可.
【详解】解:由题意可知:原式,
∴为三个连续的正整数的积,
∴可写成三个连续自然数的积,其中一个因数必为偶数,
∴是一个偶数.
故选:D.
11.
【分析】本题利用平方差公式进行因式分解即可.
【详解】解:原式=(a+2b)(a-2b) .
故答案为:(a+2b)(a-2b)
12.
【分析】此题主要考查了频数与频率,正确掌握频率的求法是解题关键.频率是指每个对象出现的次数与总次数的比值(或者百分比),即频率=频数÷总数,即可得出答案.
【详解】解:∵将人的跳远成绩分组后,组界为米的一组有6人,
∴该组的频率是:.
故答案为:.
13.
【分析】本题考查的是平移的性质,根据平移的概念得到,计算即可.
【详解】解:由平移的性质可知:,
∵,
∴,
故答案为:.
14./70度
【分析】此题考查了邻补角互补,折叠的性质和平行线的性质,首先求出,然后由折叠的性质和平行线的性质求解即可.
【详解】解:如图所示,
∵
∴
由折叠可得,
由平行可得,.
故答案为:.
15.5
【分析】根据加减消元法即可求解.
【详解】解:,
得,
,
∴,
故答案为5.
【点睛】本题主要考查了加减消元法解二元一次方程组,熟练掌握加减消元法是解题的关键.
16./108度
【分析】过点F作,可得,根据平行线的性质结合已知求出,可得,即可求出的度数.
【详解】解:如图,过点F作,
∵,
∴,
∴,,
∵,
∴,
∴,
∴,
∴,
故答案为:.
【点睛】此题考查了平行线的判定与性质,熟记:①两直线平行,同位角相等;②两直线平行,内错角相等;③两直线平行,同旁内角互补是解题的关键.
17.(1)
(2)
【分析】本题考查了负整数指数幂,零指数幂,乘法公式,熟练掌握以上运算法则是解题的关键;
(1)根据有理数的乘方,负整数指数幂,零指数幂进行计算即可求解;
(2)根据完全平方公式,平方差公式进行计算即可求解.
【详解】(1)解:
;
(2)解:
.
18.(1)(2)2
【分析】本题考查解二元一次方程组,分式的加法:
(1)加减法解方程组即可;
(2)分母不变,分子相加,进行计算即可.
【详解】解:(1),
,得:,解得:,
把代入②,得:,解得:,
∴方程组的解为:;
(2)原式.
19.,4
【分析】本题考查了分式的化简求值,先通分计算括号内的运算,然后进行因式分解,计算分式乘法,得到最简分式,再结合分式有意义的条件,取合适的值代入计算,即可得到答案.
【详解】解:
,
当,1,,3时,原分式没有意义,
∴,
当时,原式.
20.(1)100
(2)见解析
(3)1000名
【分析】本题考查条形统计图和扇形统计图的关联、用样本估计总体,理解题意,能从统计图中找到有用信息是解答的关键.
(1)用“锻炼身体”的人数除以其所占的百分数即可求解;
(2)先分别求得A、C的人数,再补全条形统计图即可;
(3)用该区域总人数乘以样本中“外出游玩”的人数所占的比例求解即可.
【详解】(1)解:这次活动中接受问卷调查的市民共有(名),
故答案为:100;
(2)解:“换乘公交”的人数为(名),
“外出游玩”的人数为(名),
补全条形统计图如图:
(3)解:(名),
答:估计其中“外出游玩”的人数为1000名.
21.(1)相等,理由见解析
(2)
【分析】(1)由平行线的性质可得,结合即可得出内错角相等,进而得出;
(2)由平行线的性质可得,根据题意求出的度数即可解答.
【详解】(1)解:与相等,理由如下:
∵,
,
,
同角的补角相等,
∴(内错角相等,两直线平行,
两直线平行,同位角相等,
(2)解:∵,
,
,,
,即,
,,
,
即.
【点睛】本题考查平行线的性质和判定,熟练掌握平行线的性质和判断是解题关键.
22.(1)试销时该品种苹果的进价是每千克5元,两次共购进3000千克苹果;
(2)超市在这两次苹果销售中共盈利12000元.
【分析】(1)设试销时该品种苹果的进价是每千克x元,根据“这次的进货价比试销时每千克多了元,购进苹果数量是试销的2倍”,列出分式方程,即可求解;
(2)根据总销售额总成本销售盈利,列出算式,即可求解.
【详解】(1)解:设试销时该品种苹果的进价是每千克x元,则第二次购进该品种苹果的进价是每千克元,
根据题意得:,
解得:,
经检验,是原方程的根,且符合题意.
(千克),
答:试销时该品种苹果的进价是每千克5元,两次共购进3000千克苹果;
(2)解:(元).
答:超市在这两次苹果销售中共盈利12000元.
【点睛】本题主要考查分式方程的实际应用,找出等量关系,列出方程,是解题的关键.
23.(1)
(2),;
(3)见解析
【分析】(1)将,,代入进行计算即可;
(2)根据等式的性质,依次进行去分母、去括号、移项、合并同类项即可;
(3)由的取值与无关可得,进而得到,即,得出结论.
本题考查整式加减的无关型问题以及已知字母的值求代数式的值,正确掌握相关性质内容是解题的关键.
【详解】(1)解:∵,
∴;
(2)解:将两边都乘以得,
,
去括号得,,
移项得,,
两边都乘以得,,
即,
,;
(3)解:的取值与无关,且由(2)知
,
即,
,
即,
.
24.(1)①;②
(2)
(3)
【分析】(1)①由拼图可直接得出答案;
②用图形中面积之间的关系可得出结论;
(2)利用(1)中的结论可得,代入计算即可;
(3)用,代入即可得出结论.
【详解】(1)①由拼图可知,中间小正方形的边长为;
②大正方形的面积为,小正方形的面积为,每个小长方形的长为,宽为,因此面积为,
所以,
即大正方形面积与小正方形面积的差等于图中一个长方形面积的倍;
(2)当,时,
,
即,
;
(3)由(1)可知,,
,
即.
【点睛】本题考查完全平方公式、平方差公式,掌握完全平方公式、平方差公式的结构特征是正确解答的前提.
2025年浙江省杭州市精选期末真题重组模拟卷
满分120分 考试时间120分钟
学校:___________ 姓名:___________ 班级:___________ 考号:___________
一、选择题(共30分)
1.(24-25七年级下·浙江杭州·期末)下列方程中,是二元一次方程的是( )
A. B. C. D.
2.(23-24七年级下·浙江杭州西湖区·期末)在日本核电站排放核废水期间,我国某监测点监测到极微量的人工放射性核素碘-131,其浓度为0.0000963贝克/立方米.数据“0.0000963”用科学记数法可表示为( )
A. B. C. D.
3.(23-24七年级下·浙江杭州·期末)若分式有意义,则( )
A. B. C. D.
4.(22-23·浙江杭州·期末)下列调查中,①调查本班同学的视力;②调查一批节能灯管的使用寿命;③为保证“神舟9号”的成功发射,对其零部件进行检查;④对乘坐某班次客车的乘客进行安检.其中适合采用抽样调查的是( )
A.① B.② C.③ D.④
5.(23-24七年级下·浙江杭州·期末)下列计算中,正确的是( )
A. B.
C. D.
6.(23-24七年级下·浙江杭州·期末)若是二元一次方程的一个解,则的值是( )
A.0 B.1 C.2 D.3
7.(21-22七年级下·浙江杭州·期末)将一个直角三角板和一把直尺如图放置,如果∠α=46°,则∠β的度数是( )
A.43° B.44° C.45° D.46°
8.(21-22七年级下·浙江·期末)为了改善生态环境,防止水土流失,某村计划在荒坡上种植480棵树.由于青年志愿者的加入,每日比原计划多种,结果提前4天完成任务.设志愿者加入后每天种树x棵,则所列方程为( )
A. B. C. D.
9.(22-23·浙江杭州·期末)如图,边长为的大正方形剪去个边长为的小正方形,做成一个无盖纸盒.若无盖纸盒的底面积与表面积之比为:,则根据题意可知,满足的关系式为( )
A. B. C. D.
10.(23-24七年级下·浙江杭州·期末)设n为某一自然数,代入代数式计算其值时,四个学生算出了下列四个结果.其中正确的结果是( )
A.521 B.1413 C.3721 D.1716
二、填空题(共18分)
11.(23-24七年级下册·浙江杭州·期末真题)因式分解:= .
12.(24-25七年级下·浙江杭州·期末)运动会上将名运动员按跳远成绩分组后,组界为米的一组有人,则该组的频率是 .
13.(23-24七年级下·浙江杭州·期末)如图,将沿方向平移2个单位后得到.若,则的长是 .
14.(23-24七年级下·浙江杭州·期末)将一张长方形纸条折叠成如图形状,若,则 .
15.(22-23七年级下·浙江杭州·期末)关于的方程组,则的值等于 .
16.(22-23七年级下·浙江杭州·期末)如图,,射线,分别与,交于点M,N,若,则的度数是 .
三、解答题(共72分)
17.(8分)(23-24七年级下·浙江杭州·期末)计算
(1);
(2).
18.(8分)(23-24七年级下·浙江杭州·期末)(1)解方程组
(2)计算:.
19.(8分)(23-24七年级下·浙江杭州·期末)先化简;,再从,,,1,3中选择一个你喜欢的值代入求值.
20.(8分)(23-24七年级下·浙江杭州·期末)共享单车是一种新型环保交通工具,为市民的出行带来了极大的方便.某市中学生对市民共享单车使用情况进行了调查,主要以下四种用途:A外出游玩,B锻炼身体,C换乘公交,D其他;并将这次调查情况整理、绘制成如下两幅统计图(部分信息未给出)
根据图中的信息,解答下列问题:
(1)这次活动中接受问卷调查的市民共有______________名;
(2)补全条形统计图;
(3)根据统计结果,若该市某区域有20000名市民选择共享单车,请估计其中“外出游玩”的人数.
21.(8分)(22-23七年级下·浙江杭州·期末)如图,已知,.
(1)试问与相等吗?请说明理由;
(2)若,,求的度数.
22.(10分)(23-24七年级下·浙江杭州·期末)铭润超市用5000元购进一批新品种的苹果进行试销,由于销售状况良好,超市又调拨11000元资金购进该品种苹果,但这次的进货价比试销时每千克多了元,购进苹果数量是试销时的2倍.
(1)试销时该品种苹果的进货价是每千克多少元?两次共购进多少苹果?
(2)如果超市将该品种苹果按每千克10元的定价出售,当大部分苹果售出后,余下的500千克按定价的六折售完,那么超市在这两次苹果销售中共盈利多少元?
23.(10分)(22-23七年级下·浙江杭州·期末)已知,是常数,.
(1)若,,求t;
(2)试将等式①变形成“”形式,其中A,B表示关于a,b,t的整式;
(3)若t的取值与x无关,请说明.
24.(12分)(22-23七年级下·浙江杭州·期末)在一次研究性学习中,同学们对乘法公式进行了研究.
(1)如图,大正方形的边长为,直接写出下列结果.
①中间小正方形的边长;
②用含,的等式表示:大正方形面积与小正方形面积的差等于图中一个长方形面积的倍.
(2)当,.求的值.
(3)若当,时,的值唯一确定,用含的代数式表示.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C A B C A B D A D
1.A
【分析】本题考查二元一次方程的定义,根据二元一次方程的定义:含有两个未知数,并且含有未知数的项的次数都是1,像这样的整式方程叫做二元一次方程.据此逐一判断即可得.
【详解】解:A. ,是二元一次方程,故该选项正确,符合题意;
B. ,最高次数为,不是二元一次方程,故该选项不正确,不符合题意;
C. ,不是整式方程,不是二元一次方程,故该选项不正确,不符合题意;
D. ,最高次数为,不是二元一次方程,故该选项不正确,不符合题意;
故选:A.
2.C
【分析】本题主要考查科学记数法,熟练掌握科学记数法是解题的关键;科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于或等于10时,n是正整数;当原数的绝对值小于1时,n是负整数.
【详解】解:数据“0.0000963”用科学记数法可表示为;
故选C
3.A
【分析】此题主要考查了分式有意义的条件,关键是掌握分式有意义的条件是分母不等于零.利用分式有意义的条件可得,再解不等式即可.
【详解】解:由题意得:,
解得:,
故选:A
4.B
【详解】试题分析:①适合普查,故①不适合抽样调查;
②调查具有破坏性,故适合抽样调查,故②符合题意;
③调查要求准确性,故③不适合抽样调查;
④安检适合普查,故④不适合抽样调查.
故选B.
考点:全面调查与抽样调查.
5.C
【分析】本题考查了同底数幂的乘法和除法,多项式除以单项式,以及完全平方公式,熟练掌握各知识点是解答本题的关键.根据运算法则和完全平方公式逐项分析即可.
【详解】解:A.,故原计算不正确;
B.,故原计算不正确;
C.,正确;
D.,故原计算不正确;
故选C.
6.A
【分析】本题主要考查了二元一次方程的解的定义,代数式求值,将x与y的值代入原方程,得到,再代入计算即可求出答案,熟练掌握相关知识点并灵活运用是解决此题的关键.
【详解】解:∵是二元一次方程的一个解,
∴,即,
∴,
故选:A.
7.B
【分析】过点E作EMAB,则EMCD,根据平行线的性质可得∠α+∠β=90°,再由∠α可求解.
【详解】解:如图,由题意知:ABCD,∠FEG=90°,
过点E作EMAB,则EMCD,
∴∠FEM=∠α,∠GEM=∠β,
∵∠FEM+∠GEM=∠FEG=90°,
∴∠α+∠β=90°,
∵∠α=46°,
∴∠β=90°-46°=44°.
故选:B
【点睛】本题主要考查平行线的性质,解题的关键是准确作出辅助线,掌握两直线平行,同位角相等定理的应用.
8.D
【分析】根据结果提前天完成任务,列分式方程即可.
【详解】解:根据题意,得,
故选:D.
【点睛】本题考查了分式方程的应用,理解题意并根据题意建立等量关系是解题的关键.
9.A
【分析】根据题意分别表示出底面积与表面积,根据题意列出方程即可求解.
【详解】解:依题意,底面积为,表面积为,根据题意可得.
,
即,
故选:A.
【点睛】本题考查了分式方程的应用,根据题意表示出底面积与表面积是解题的关键.
10.D
【分析】本题综合考查因式分解的应用,三个连续自然数的积为偶数等相关知识点,重点掌握因式分解的应用.代数式因式分解可得,则代数式表示三个连续正整数的积.据此分析即可.
【详解】解:由题意可知:原式,
∴为三个连续的正整数的积,
∴可写成三个连续自然数的积,其中一个因数必为偶数,
∴是一个偶数.
故选:D.
11.
【分析】本题利用平方差公式进行因式分解即可.
【详解】解:原式=(a+2b)(a-2b) .
故答案为:(a+2b)(a-2b)
12.
【分析】此题主要考查了频数与频率,正确掌握频率的求法是解题关键.频率是指每个对象出现的次数与总次数的比值(或者百分比),即频率=频数÷总数,即可得出答案.
【详解】解:∵将人的跳远成绩分组后,组界为米的一组有6人,
∴该组的频率是:.
故答案为:.
13.
【分析】本题考查的是平移的性质,根据平移的概念得到,计算即可.
【详解】解:由平移的性质可知:,
∵,
∴,
故答案为:.
14./70度
【分析】此题考查了邻补角互补,折叠的性质和平行线的性质,首先求出,然后由折叠的性质和平行线的性质求解即可.
【详解】解:如图所示,
∵
∴
由折叠可得,
由平行可得,.
故答案为:.
15.5
【分析】根据加减消元法即可求解.
【详解】解:,
得,
,
∴,
故答案为5.
【点睛】本题主要考查了加减消元法解二元一次方程组,熟练掌握加减消元法是解题的关键.
16./108度
【分析】过点F作,可得,根据平行线的性质结合已知求出,可得,即可求出的度数.
【详解】解:如图,过点F作,
∵,
∴,
∴,,
∵,
∴,
∴,
∴,
∴,
故答案为:.
【点睛】此题考查了平行线的判定与性质,熟记:①两直线平行,同位角相等;②两直线平行,内错角相等;③两直线平行,同旁内角互补是解题的关键.
17.(1)
(2)
【分析】本题考查了负整数指数幂,零指数幂,乘法公式,熟练掌握以上运算法则是解题的关键;
(1)根据有理数的乘方,负整数指数幂,零指数幂进行计算即可求解;
(2)根据完全平方公式,平方差公式进行计算即可求解.
【详解】(1)解:
;
(2)解:
.
18.(1)(2)2
【分析】本题考查解二元一次方程组,分式的加法:
(1)加减法解方程组即可;
(2)分母不变,分子相加,进行计算即可.
【详解】解:(1),
,得:,解得:,
把代入②,得:,解得:,
∴方程组的解为:;
(2)原式.
19.,4
【分析】本题考查了分式的化简求值,先通分计算括号内的运算,然后进行因式分解,计算分式乘法,得到最简分式,再结合分式有意义的条件,取合适的值代入计算,即可得到答案.
【详解】解:
,
当,1,,3时,原分式没有意义,
∴,
当时,原式.
20.(1)100
(2)见解析
(3)1000名
【分析】本题考查条形统计图和扇形统计图的关联、用样本估计总体,理解题意,能从统计图中找到有用信息是解答的关键.
(1)用“锻炼身体”的人数除以其所占的百分数即可求解;
(2)先分别求得A、C的人数,再补全条形统计图即可;
(3)用该区域总人数乘以样本中“外出游玩”的人数所占的比例求解即可.
【详解】(1)解:这次活动中接受问卷调查的市民共有(名),
故答案为:100;
(2)解:“换乘公交”的人数为(名),
“外出游玩”的人数为(名),
补全条形统计图如图:
(3)解:(名),
答:估计其中“外出游玩”的人数为1000名.
21.(1)相等,理由见解析
(2)
【分析】(1)由平行线的性质可得,结合即可得出内错角相等,进而得出;
(2)由平行线的性质可得,根据题意求出的度数即可解答.
【详解】(1)解:与相等,理由如下:
∵,
,
,
同角的补角相等,
∴(内错角相等,两直线平行,
两直线平行,同位角相等,
(2)解:∵,
,
,,
,即,
,,
,
即.
【点睛】本题考查平行线的性质和判定,熟练掌握平行线的性质和判断是解题关键.
22.(1)试销时该品种苹果的进价是每千克5元,两次共购进3000千克苹果;
(2)超市在这两次苹果销售中共盈利12000元.
【分析】(1)设试销时该品种苹果的进价是每千克x元,根据“这次的进货价比试销时每千克多了元,购进苹果数量是试销的2倍”,列出分式方程,即可求解;
(2)根据总销售额总成本销售盈利,列出算式,即可求解.
【详解】(1)解:设试销时该品种苹果的进价是每千克x元,则第二次购进该品种苹果的进价是每千克元,
根据题意得:,
解得:,
经检验,是原方程的根,且符合题意.
(千克),
答:试销时该品种苹果的进价是每千克5元,两次共购进3000千克苹果;
(2)解:(元).
答:超市在这两次苹果销售中共盈利12000元.
【点睛】本题主要考查分式方程的实际应用,找出等量关系,列出方程,是解题的关键.
23.(1)
(2),;
(3)见解析
【分析】(1)将,,代入进行计算即可;
(2)根据等式的性质,依次进行去分母、去括号、移项、合并同类项即可;
(3)由的取值与无关可得,进而得到,即,得出结论.
本题考查整式加减的无关型问题以及已知字母的值求代数式的值,正确掌握相关性质内容是解题的关键.
【详解】(1)解:∵,
∴;
(2)解:将两边都乘以得,
,
去括号得,,
移项得,,
两边都乘以得,,
即,
,;
(3)解:的取值与无关,且由(2)知
,
即,
,
即,
.
24.(1)①;②
(2)
(3)
【分析】(1)①由拼图可直接得出答案;
②用图形中面积之间的关系可得出结论;
(2)利用(1)中的结论可得,代入计算即可;
(3)用,代入即可得出结论.
【详解】(1)①由拼图可知,中间小正方形的边长为;
②大正方形的面积为,小正方形的面积为,每个小长方形的长为,宽为,因此面积为,
所以,
即大正方形面积与小正方形面积的差等于图中一个长方形面积的倍;
(2)当,时,
,
即,
;
(3)由(1)可知,,
,
即.
【点睛】本题考查完全平方公式、平方差公式,掌握完全平方公式、平方差公式的结构特征是正确解答的前提.
同课章节目录
