4.1.1 平行线 课件(共34张PPT) 湘教版七年级数学下册
文档属性
| 名称 | 4.1.1 平行线 课件(共34张PPT) 湘教版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 36.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 20:56:20 | ||
图片预览










文档简介
(共34张PPT)
4.1.1 平行线
第4章 平面内的两条直线
【2024新教材】湘教版数学 七年级下册
授课教师:********
班 级:********
时 间:********
一)知识与技能
理解实数的概念,明确实数与数轴上的点一一对应关系。
掌握实数的分类方法,能
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情景导入
情境导入
如果两条直线只有一个公共点,那么称这两条直线相交.也称它们是相交直线.
这个公共点叫作它们的交点.
1.如果两条直线有两个公共点,那么它们一定重合.
2.今后如果没有特别说明,两条重合的直线
只当作一条.
注意:
探索新知
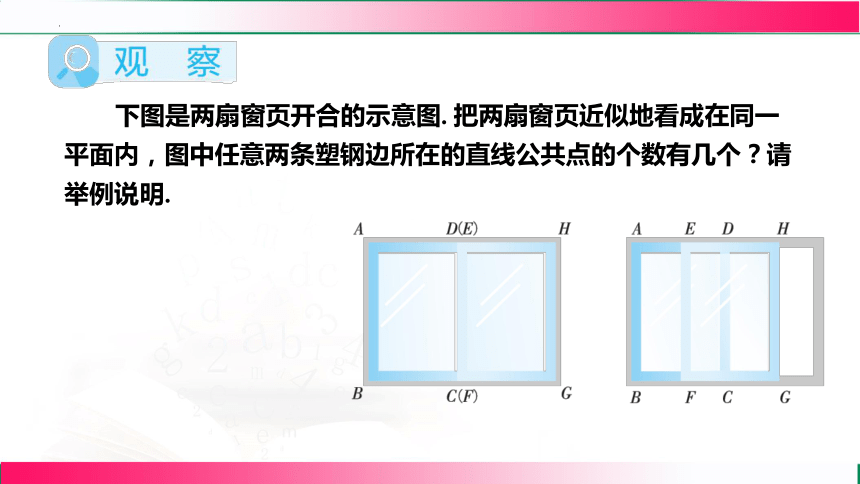
下图是两扇窗页开合的示意图. 把两扇窗页近似地看成在同一平面内,图中任意两条塑钢边所在的直线公共点的个数有几个?请举例说明.
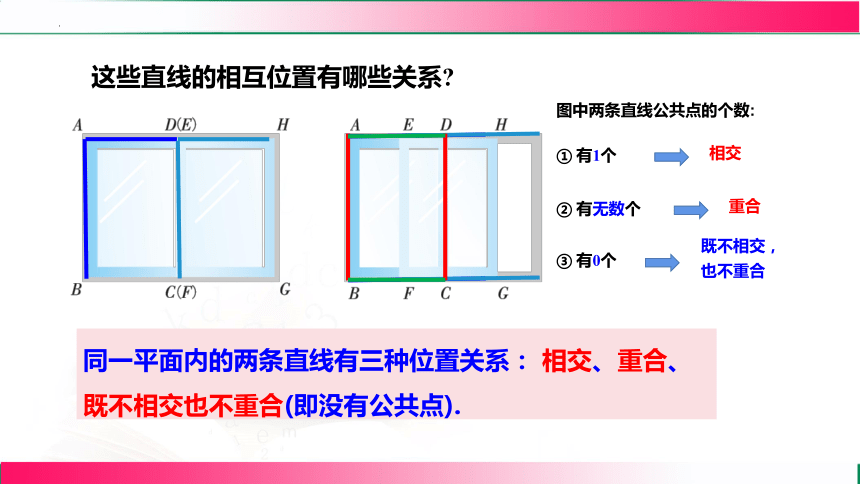
这些直线的相互位置有哪些关系
图中两条直线公共点的个数:
① 有1个
② 有无数个
③ 有0个
同一平面内的两条直线有三种位置关系: 相交、重合、既不相交也不重合(即没有公共点).
相交
重合
既不相交,
也不重合
在同一平面内,没有公共点的两条直线叫作平行线.
若直线 AB 与 CD 平行.记作“_________”,读作“_____________”.
平行线的概念
若用 a、b 表示这两条直线,那么也可以记作“ ________”,
读作“__________”.
AB∥ CD
AB 平行于 CD
a∥ b
a 平行于 b
(或“CD平行于 AB”或“AB与CD互相平行”)
(或“b平行于 a”或“a与b互相平行”)
平行符号:∥
在同一平面内,没有公共点的两条直线叫作平行线.
1.如图,直线 AB 与 CD 是平行线.记做“ ”,这里“ ”是平行符号. 读做“ ”.
平行线的概念
2.若用 a、b 表示这两条直线,那么直线 a 与直线 b 平行,记做“ ”,读做“ ”.
AB∥ CD
∥
AB 平行于 CD
a∥ b
a 平行于 b
(或“CD平行于 AB”或“AB与CD互相平行”)
(或“b平行于 a”或“a与b互相平行”)
平行符号:∥
平行线的定义包含三层意思:
① 在同一平面内
② 不相交
③ 两条直线
(前提条件)
(即两条直线没有交点)
(泛指两条直线,或两条射线、线段
或更多条直线、射线、线段)
一条线段向两端无限延伸就得到一条直线,这说明直线有两个方向,取定一个方向,就确定了另一个方向.
问题: 在每条直线上取定一个方向,两条直线平行,它们的方向有什么关系?
若两条直线平行, 则它们的方向相同或相反.
问题: 具有相同方向或相反方向的两条直线有什么位置关系?
两条直线平行
两条直线平行
两条直线的方向相同或相反
生活中平行线的实例
铁轨
电线杆
栅栏
观察教室黑板的上、下边缘所在的直线,它们可以看作平行线吗?你还能从教室里找到哪些平行线的实例?将结果与同学们交流.
墙缘所在直线、桌椅边缘所在直线、窗户边所在直线等.
任意画一条直线 a, 并在直线 a 外任取一点 P. 请用三角板和直尺画一条过点 P 且与直线 a 平行的直线.
画法:①把三角板的 BC 边靠紧直线 a,再用直尺(或另一块三角板)靠紧三角尺的另一边 AC;
②沿直尺推动三角板,使原来和直线 a重合的一边经过点 P;
③沿三角板的这条边画直线 b.
则直线 b 就是过 P 点且与直线 a 平行的直线.
B
A
C
你还可以画出其他过点P 点且与直线a 平行的直线吗?由此,你能得到什么结论?
过直线外一点有且只有一条直线与这条直线平行.
人们从长期的实践经验中抽象出如下基本事实:
如果直线 a 与 c 都和直线 b 平行,那么 a 与 c 平行吗?
若 a 与 c 不平行, 就会相交于某一点 P ,那么过点P 就有两条直线与 b 平行,
根据平行线的基本事实, 这是不可能的. 所以 a∥c.
如果直线 a 与 c 都和直线 b 平行,那么 a 与 c 平行吗?
平行公理推论:
平行于同一直线的两条直线平行.
几何语言:
如果 a∥b,c∥b,
那么 a∥c (平行于同一条直线的两条直线互相平行).
1. 请举出3个生活中的平行线实例.
大门的竖条栏栅,屹立在操场中的两根旗杆,400米跑道和单双杠等.
[选自教材P92 练习]
2. 如图,在同一平面内,若 AB∥CD,EF 与 AB 相交于点 P,EF 能与 CD 平行吗?为什么?
答:假设 EF∥CD,
则因 AB∥CD,
所以根据平行线的传递性,
便有 AB∥EF.
与 AB 和 EF 相交于 P 点矛盾,
所以 EF 与 CD 不平行.
[选自教材P92 练习]
3. 过三角形的一个顶点,画另外两个顶点所在直线的平行线。
[选自教材P92 练习]
A
B
C
(答案不唯一)
1.在同一平面内, 两条直线的位置关系有_________________.
2.在同一平面内,一条直线和两条平行线中一条直线相交 ,那么这条直线与平行线中的另一边必______ .
相交、重合、平行
相交
3.工人师傅在架设电线时,为了检验三条电线是否互相平行,只检查了其中两条是否与第三条平行,这种做法是否正确?
正确. 理由是:平行于同一条直线的两条直线互相平行 .
随堂练习
4.一个长方体如图.
(1)和 AA1平行的棱有多少条?
(2)和 AB 平行的棱有多少条?
(3)和 AD 平行的棱有多少条?请分别表示出来.
解:(1)有 3 条,分别为:BB1 , CC1 , DD1.
(2)有 3 条,分别为:A1B1 , C1D1 , CD.
(3)有 3 条,分别为:A1D1 , B1C1 , BC.
1. 在同一平面内,不重合的两条直线的位置关系是( )
C
A. 平行 B. 相交
C. 平行或相交 D. 平行或垂直
(第2题)
2. 教材P92说一说 如图, ,
过点画,则与 的位置关
系是_________,理由是______________
___________________.
平行于同一条直线的两条直线平行
3.如图,,,则点,, 在同一条直线
上,理由是__________________________________________
___.
过直线外一点有且只有一条直线与这条直线平行
(第3题)
4.分别写出下列语句表示的图形(填序号):
(1)过点的三条直线与另一条直线分别相交于,, 三点:
____.
③
(2)以直线上一点为顶点,在直线的同侧作 和
____.
②
(3)过点的一条直线和以 为端点的两条射线与另一条直
线分别相交于,, 三点:____.
①
5. 如图,在内有一点 .
(1)过点画 .
【解】如图所示.
(2)过点画 .
如图所示.
(3)用量角器量一量与的夹角与
的大小有怎样的关系?
如图,与 的夹角有两个,分别是
,, ,
所以和的夹角与 相等或互补.
与 是互补关系,容易漏掉.
6. 下列推理正确的是( )
C
A. 因为,,所以
B. 因为,,所以
C. 因为,,所以
D. 因为,,所以
7. 在同一平面内,如果直线与平行,直线与 垂直,则这
三条直线中所有交点的个数为( )
B
A. 1 B. 2 C. 3 D. 1或3
平行公理
过直线外一点有且只有一条直线与这条直线平行.
平行公理推论
平行于同一条直线的两条直线平行.
在同一平面内,没有公共点的两条直线叫作行平线.
平行线概念
课堂小结
AB∥ CD
a∥ b
平行线
谢谢观看!
4.1.1 平行线
第4章 平面内的两条直线
【2024新教材】湘教版数学 七年级下册
授课教师:********
班 级:********
时 间:********
一)知识与技能
理解实数的概念,明确实数与数轴上的点一一对应关系。
掌握实数的分类方法,能
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情景导入
情境导入
如果两条直线只有一个公共点,那么称这两条直线相交.也称它们是相交直线.
这个公共点叫作它们的交点.
1.如果两条直线有两个公共点,那么它们一定重合.
2.今后如果没有特别说明,两条重合的直线
只当作一条.
注意:
探索新知
下图是两扇窗页开合的示意图. 把两扇窗页近似地看成在同一平面内,图中任意两条塑钢边所在的直线公共点的个数有几个?请举例说明.
这些直线的相互位置有哪些关系
图中两条直线公共点的个数:
① 有1个
② 有无数个
③ 有0个
同一平面内的两条直线有三种位置关系: 相交、重合、既不相交也不重合(即没有公共点).
相交
重合
既不相交,
也不重合
在同一平面内,没有公共点的两条直线叫作平行线.
若直线 AB 与 CD 平行.记作“_________”,读作“_____________”.
平行线的概念
若用 a、b 表示这两条直线,那么也可以记作“ ________”,
读作“__________”.
AB∥ CD
AB 平行于 CD
a∥ b
a 平行于 b
(或“CD平行于 AB”或“AB与CD互相平行”)
(或“b平行于 a”或“a与b互相平行”)
平行符号:∥
在同一平面内,没有公共点的两条直线叫作平行线.
1.如图,直线 AB 与 CD 是平行线.记做“ ”,这里“ ”是平行符号. 读做“ ”.
平行线的概念
2.若用 a、b 表示这两条直线,那么直线 a 与直线 b 平行,记做“ ”,读做“ ”.
AB∥ CD
∥
AB 平行于 CD
a∥ b
a 平行于 b
(或“CD平行于 AB”或“AB与CD互相平行”)
(或“b平行于 a”或“a与b互相平行”)
平行符号:∥
平行线的定义包含三层意思:
① 在同一平面内
② 不相交
③ 两条直线
(前提条件)
(即两条直线没有交点)
(泛指两条直线,或两条射线、线段
或更多条直线、射线、线段)
一条线段向两端无限延伸就得到一条直线,这说明直线有两个方向,取定一个方向,就确定了另一个方向.
问题: 在每条直线上取定一个方向,两条直线平行,它们的方向有什么关系?
若两条直线平行, 则它们的方向相同或相反.
问题: 具有相同方向或相反方向的两条直线有什么位置关系?
两条直线平行
两条直线平行
两条直线的方向相同或相反
生活中平行线的实例
铁轨
电线杆
栅栏
观察教室黑板的上、下边缘所在的直线,它们可以看作平行线吗?你还能从教室里找到哪些平行线的实例?将结果与同学们交流.
墙缘所在直线、桌椅边缘所在直线、窗户边所在直线等.
任意画一条直线 a, 并在直线 a 外任取一点 P. 请用三角板和直尺画一条过点 P 且与直线 a 平行的直线.
画法:①把三角板的 BC 边靠紧直线 a,再用直尺(或另一块三角板)靠紧三角尺的另一边 AC;
②沿直尺推动三角板,使原来和直线 a重合的一边经过点 P;
③沿三角板的这条边画直线 b.
则直线 b 就是过 P 点且与直线 a 平行的直线.
B
A
C
你还可以画出其他过点P 点且与直线a 平行的直线吗?由此,你能得到什么结论?
过直线外一点有且只有一条直线与这条直线平行.
人们从长期的实践经验中抽象出如下基本事实:
如果直线 a 与 c 都和直线 b 平行,那么 a 与 c 平行吗?
若 a 与 c 不平行, 就会相交于某一点 P ,那么过点P 就有两条直线与 b 平行,
根据平行线的基本事实, 这是不可能的. 所以 a∥c.
如果直线 a 与 c 都和直线 b 平行,那么 a 与 c 平行吗?
平行公理推论:
平行于同一直线的两条直线平行.
几何语言:
如果 a∥b,c∥b,
那么 a∥c (平行于同一条直线的两条直线互相平行).
1. 请举出3个生活中的平行线实例.
大门的竖条栏栅,屹立在操场中的两根旗杆,400米跑道和单双杠等.
[选自教材P92 练习]
2. 如图,在同一平面内,若 AB∥CD,EF 与 AB 相交于点 P,EF 能与 CD 平行吗?为什么?
答:假设 EF∥CD,
则因 AB∥CD,
所以根据平行线的传递性,
便有 AB∥EF.
与 AB 和 EF 相交于 P 点矛盾,
所以 EF 与 CD 不平行.
[选自教材P92 练习]
3. 过三角形的一个顶点,画另外两个顶点所在直线的平行线。
[选自教材P92 练习]
A
B
C
(答案不唯一)
1.在同一平面内, 两条直线的位置关系有_________________.
2.在同一平面内,一条直线和两条平行线中一条直线相交 ,那么这条直线与平行线中的另一边必______ .
相交、重合、平行
相交
3.工人师傅在架设电线时,为了检验三条电线是否互相平行,只检查了其中两条是否与第三条平行,这种做法是否正确?
正确. 理由是:平行于同一条直线的两条直线互相平行 .
随堂练习
4.一个长方体如图.
(1)和 AA1平行的棱有多少条?
(2)和 AB 平行的棱有多少条?
(3)和 AD 平行的棱有多少条?请分别表示出来.
解:(1)有 3 条,分别为:BB1 , CC1 , DD1.
(2)有 3 条,分别为:A1B1 , C1D1 , CD.
(3)有 3 条,分别为:A1D1 , B1C1 , BC.
1. 在同一平面内,不重合的两条直线的位置关系是( )
C
A. 平行 B. 相交
C. 平行或相交 D. 平行或垂直
(第2题)
2. 教材P92说一说 如图, ,
过点画,则与 的位置关
系是_________,理由是______________
___________________.
平行于同一条直线的两条直线平行
3.如图,,,则点,, 在同一条直线
上,理由是__________________________________________
___.
过直线外一点有且只有一条直线与这条直线平行
(第3题)
4.分别写出下列语句表示的图形(填序号):
(1)过点的三条直线与另一条直线分别相交于,, 三点:
____.
③
(2)以直线上一点为顶点,在直线的同侧作 和
____.
②
(3)过点的一条直线和以 为端点的两条射线与另一条直
线分别相交于,, 三点:____.
①
5. 如图,在内有一点 .
(1)过点画 .
【解】如图所示.
(2)过点画 .
如图所示.
(3)用量角器量一量与的夹角与
的大小有怎样的关系?
如图,与 的夹角有两个,分别是
,, ,
所以和的夹角与 相等或互补.
与 是互补关系,容易漏掉.
6. 下列推理正确的是( )
C
A. 因为,,所以
B. 因为,,所以
C. 因为,,所以
D. 因为,,所以
7. 在同一平面内,如果直线与平行,直线与 垂直,则这
三条直线中所有交点的个数为( )
B
A. 1 B. 2 C. 3 D. 1或3
平行公理
过直线外一点有且只有一条直线与这条直线平行.
平行公理推论
平行于同一条直线的两条直线平行.
在同一平面内,没有公共点的两条直线叫作行平线.
平行线概念
课堂小结
AB∥ CD
a∥ b
平行线
谢谢观看!
同课章节目录
