北师版九下数学第三章圆单元测试卷(含答案)
文档属性
| 名称 | 北师版九下数学第三章圆单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 310.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 08:33:18 | ||
图片预览



文档简介
北师版九下数学-第三章 圆-单元测试卷
(时间:90分钟 满分:120分)
一、选择题(每小题4分,共40分)
1.已知☉O的直径为10 cm,圆心O到点P的距离为 6 cm,则点P与☉O的位置关系是( )
A.点在圆上 B.点在圆内 C.点在圆外 D.无法确定
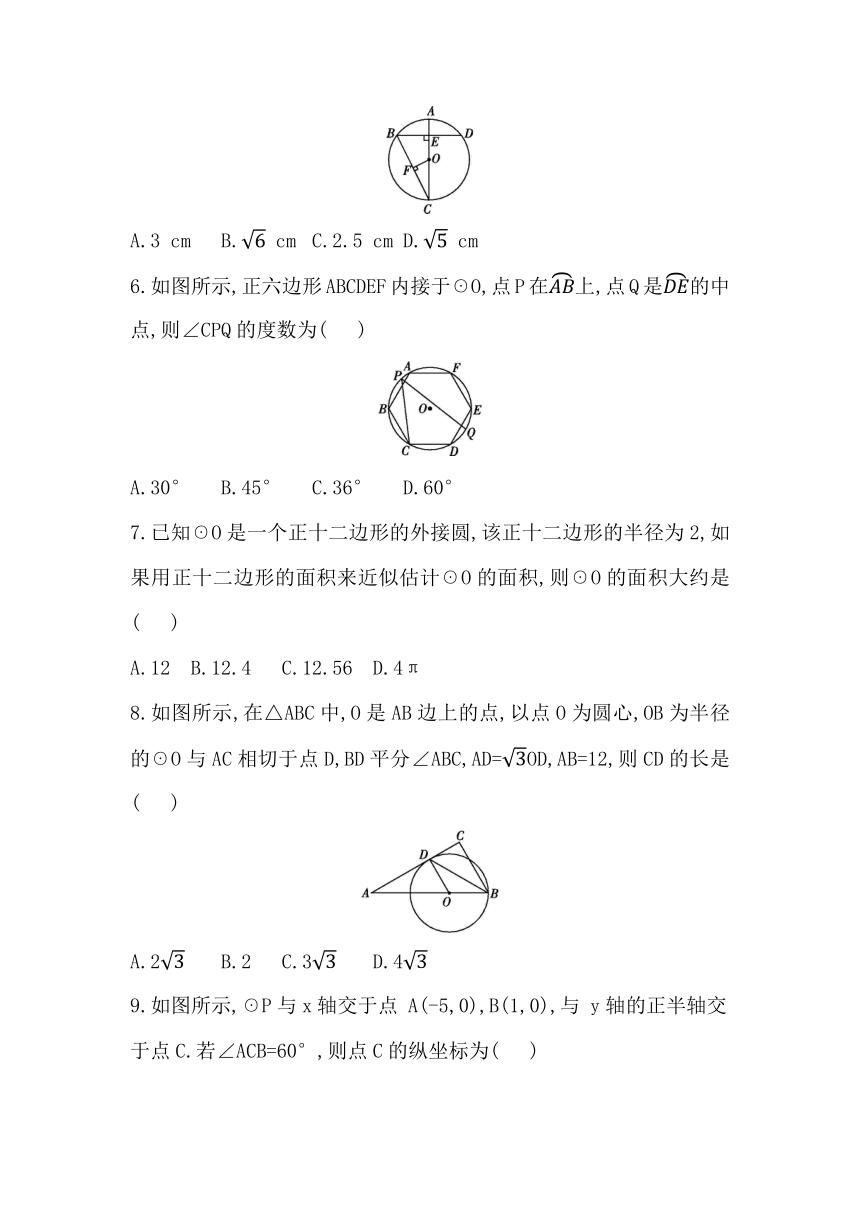
2.如图所示,☉O是△ABC的外接圆,若∠C=25°,则∠BAO等于( )
A.25° B.50° C.60° D.65°
3.一个扇形的弧长是2π,面积是4π,则该扇形的圆心角的度数是( )
A.45° B.90° C.120° D.180°
4.如图所示,AB是☉O的直径,MN是☉O的切线,切点为N,如果
∠MNB=52°,则∠NOA的度数为( )
A.76° B.56° C.54° D.52°
5.如图所示,AC是☉O的直径,弦BD⊥AO于点E,连接BC,过点O作OF⊥BC于点F,若BD=8 cm,AE=2 cm,则OF的长度是( )
A.3 cm B. cm C.2.5 cm D. cm
6.如图所示,正六边形ABCDEF内接于☉O,点P在上,点Q是的中点,则∠CPQ的度数为( )
A.30° B.45° C.36° D.60°
7.已知☉O是一个正十二边形的外接圆,该正十二边形的半径为2,如果用正十二边形的面积来近似估计☉O的面积,则☉O的面积大约是( )
A.12 B.12.4 C.12.56 D.4π
8.如图所示,在△ABC中,O是AB边上的点,以点O为圆心,OB为半径的☉O与AC相切于点D,BD平分∠ABC,AD=OD,AB=12,则CD的长是( )
A.2 B.2 C.3 D.4
9.如图所示,☉P与x轴交于点 A(-5,0),B(1,0),与 y轴的正半轴交于点C.若∠ACB=60°,则点C的纵坐标为( )
A.+ B.2+ C.4 D.2+2
10.如图所示,☉O是△ABC的外接圆,弦BD交AC于点E,AE=DE,BC=CE,过点O作OF⊥AC于点F,延长FO交BE于点G,若DE=3,EG=2,则AB的长为( )
A.4 B.7 C.8 D.4
二、填空题(每小题4分,共24分)
11.若一个正多边形的每个内角为144°,则这个正多边形的边数是 .
12.在矩形ABCD中,BC=6,CD=8,以点A为圆心画圆,且点D在☉A的内部,点B在☉A的外部,则☉A的半径r的取值范围是 .
13.如图所示,等边三角形ABC内接于☉O,BC=2,则图中阴影部分的面积是 .
14.直线y=-x-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,1个单位长度为半径作☉P,当☉P与直线AB相切时,点P的坐标是 .
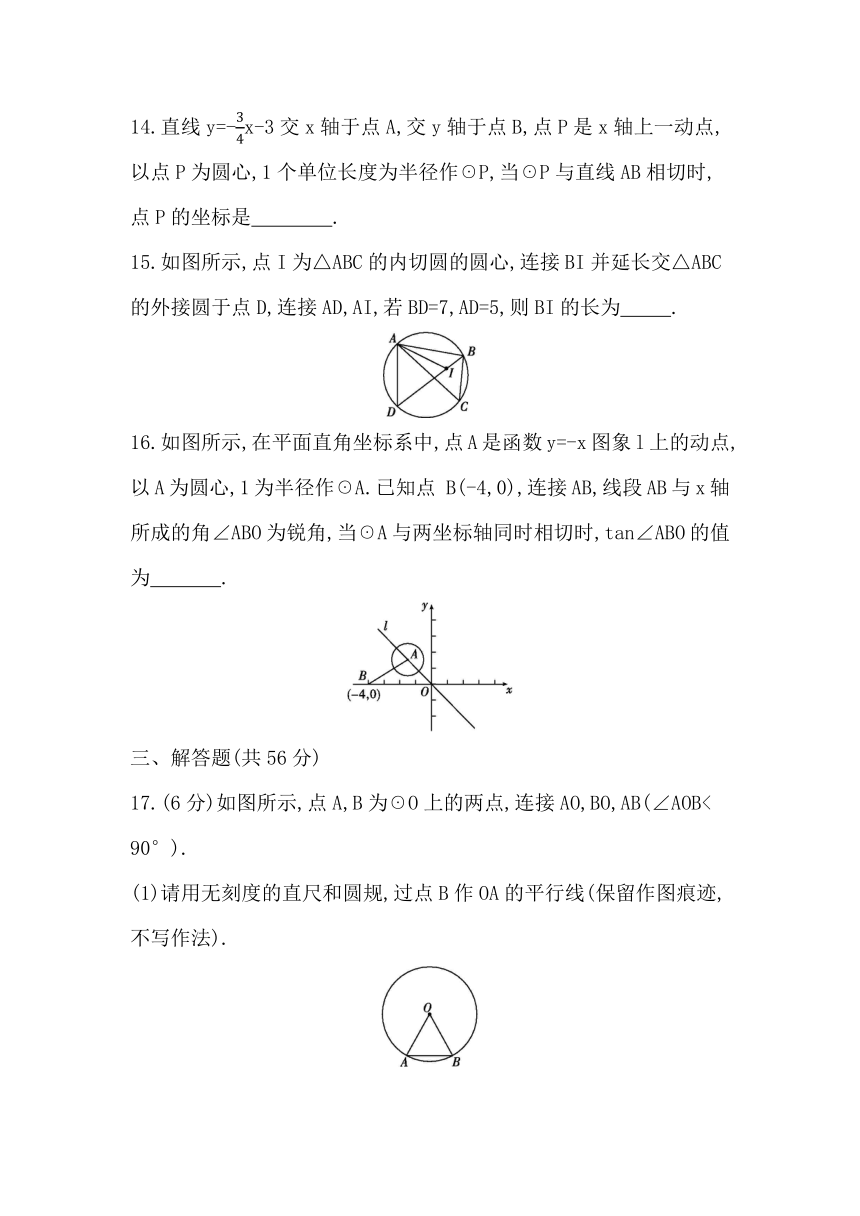
15.如图所示,点I为△ABC的内切圆的圆心,连接BI并延长交△ABC的外接圆于点D,连接AD,AI,若BD=7,AD=5,则BI的长为 .
16.如图所示,在平面直角坐标系中,点A是函数y=-x图象l上的动点,以A为圆心,1为半径作☉A.已知点 B(-4,0),连接AB,线段AB与x轴所成的角∠ABO为锐角,当☉A与两坐标轴同时相切时,tan∠ABO的值为 .
三、解答题(共56分)
17.(6分)如图所示,点A,B为☉O上的两点,连接AO,BO,AB(∠AOB<
90°).
(1)请用无刻度的直尺和圆规,过点B作OA的平行线(保留作图痕迹,不写作法).
(2)若(1)中所作的平行线与☉O交于点C,连接AC,则∠CAO与∠O有怎样的数量关系,请说明理由.
18.(8分)2023年5月30日,“神舟十六号”航天飞船成功发射.如图所示,飞船在离地球大约330 km的圆形轨道上,当运行到地球表面P点的正上方F点时,从中直接看到地球表面一个最远的点是点Q.在 Rt△OQF 中,OP=OQ≈6 400 km(参考数据:cos 16°≈0.96,cos 18°≈0.95,cos 20°≈0.94,cos 22°≈0.93,π≈3.14).
(1)求cos α的值(精确到0.01);
(2)在☉O中,求的长(结果取整数).
19.(9分)如图所示,BD为△ABC外接圆☉O的直径,且∠BAE=∠C.
(1)求证:AE是☉O的切线;
(2)若AE∥BC,BC=2,AC=2,求AD的长.
20.(10分)如图所示,AB与☉O相切于点B,AO交☉O于点C,AO的延长线交☉O于点D,E是上不与B,D重合的点,sin A=.
(1)求∠BED的大小;
(2)若☉O的半径为3,点F在AB的延长线上,且BF=3,求证:DF是☉O的切线.
21.(11分)如图所示,AB是☉O的切线,点B为切点,直线AO交☉O于C,D两点,连接BC,BD.过圆心O作BC的平行线,分别交AB的延长线、☉O及BD于点E,F,G.
(1)求证:∠D=∠E;
(2)若F是OE的中点,☉O的半径为3,求阴影部分的面积.
22.(12分)如图所示,☉O的直径AB=16,半径OC⊥AB,D为上一动点(不包括B,C两点),DE⊥OC,DF⊥AB,垂足分别为E,F.
(1)求EF的长;
(2)若点E为OC的中点,
①求的长度;
②若点P为直径AB上一动点,求出PC+PD的最小值.
参考答案
(时间:90分钟 满分:120分)
一、选择题(每小题4分,共40分)
1.(C)2.(D)3.(B)4.(A)5.(D)6.(B)7.(A)8.(A)9.(B)10.(B)
二、填空题(每小题4分,共24分)
11. 10 .12. 615. 2 . 16. 或 .
三、解答题(共56分)
17.解:(1)如图所示,直线BD即为所求.
(2)∠O=2∠CAO.理由如下:
∵BC∥OA,∴∠CAO=∠BCA.
∵∠O=2∠BCA,∴∠O=2∠CAO.
18.解:(1)由题意,知FQ是☉O的切线,
∴∠OQF=90°.
∵OP=OQ≈6 400 km,FP=330 km,
∴OF=OP+FP=6 730 km.
∴cos α==≈0.95.
(2)∵cos α≈0.95,
∴α≈18°.
∴的长为≈2 010(km).
19.(1)证明:如图所示,连接OA交BC于点F,则OA=OD,
∴∠D=∠DAO.
∵∠D=∠C,
∴∠C=∠DAO.
∵∠BAE=∠C,
∴∠BAE=∠DAO.
∵BD是☉O的直径,
∴∠DAB=90°,即∠DAO+∠OAB=90°.
∴∠BAE+∠OAB=90°,即∠OAE=90°.
∴AE⊥OA.
∵OA是☉O的半径,∴AE是☉O的切线.
(2)解:∵AE∥BC,AE⊥OA,∴OA⊥BC.
∴=,FB=BC.∴AB=AC.
∵BC=2,AC=2,∴BF=,AB=2.
在Rt△ABF中,AF==1.在Rt△OFB中,OB2=BF2+(OB-AF)2,
即OB2=()2+(OB-1)2,解得OB=4,∴BD=8.
∴在Rt△ABD中,AD====2.
20.(1)解:如图所示,连接OB,
∵AB与☉O相切于点B,
∴∠ABO=90°.
∵sin A=,∴∠A=30°.
∴∠BOD=∠ABO+∠A=120°.
∴∠BED=∠BOD=60°.
(2)证明:如图所示,连接OF,
∵AB与☉O相切于点B,∴∠OBF=90°.
∵BF=3,OB=3,∴tan∠BOF==.∴∠BOF=60°.
∵∠BOD=120°,
∴∠BOF=∠DOF=60°.
在△BOF和△DOF中,∵OB=OD,∠BOF=∠DOF,OF=OF,
∴△BOF≌△DOF(SAS).
∴∠ODF=∠OBF=90°.即OD⊥DF.
∵OD是☉O的半径,∴DF是☉O的切线.
21.(1)证明:如图所示,连接OB,
∵AB是☉O的切线,
∴∠OBE=90°.
∴∠E+∠BOE=90°.
∵CD为☉O的直径,
∴∠CBD=90°.
∴∠D+∠DCB=90°.
∵OE∥BC,∴∠BOE=∠OBC.
∵OB=OC,∴∠OBC=∠OCB.
∴∠BOE=∠OCB.
∴∠D=∠E.
(2)解:∵F是OE的中点,OB=OF,
∴OF=EF=3.∴OE=6.∴BO=OE.
∵∠OBE=90°,∴∠E=30°.
∴∠BOG=60°.
∵OE∥BC,∠DBC=90°,
∴∠OGB=90°.∴OG=,BG=.
∴S△BOG=OG·BG=××=,S扇形BOF==π.
∴S阴影部分=S扇形BOF-S△BOG=π-.
22.解:(1)如图所示,连接OD,
∵☉O的直径AB=16,
∴圆的半径为16÷2=8.
∵OC⊥AB,DE⊥OC,DF⊥AB,
∴四边形OFDE是矩形.∴EF=OD=8.
(2)①∵点E为OC的中点,
∴OE=OC=OD.
∴∠EDO=30°.
∴∠DOE=60°.
∴的长度为=.
②如图所示,延长CO交☉O于点G,连接DG交AB于点P,则PC+PD的最小值为DG.
∵∠G=∠COD=30°,EG=12,cos G=,
∴DG==8.
∴PC+PD的最小值为8.
(时间:90分钟 满分:120分)
一、选择题(每小题4分,共40分)
1.已知☉O的直径为10 cm,圆心O到点P的距离为 6 cm,则点P与☉O的位置关系是( )
A.点在圆上 B.点在圆内 C.点在圆外 D.无法确定
2.如图所示,☉O是△ABC的外接圆,若∠C=25°,则∠BAO等于( )
A.25° B.50° C.60° D.65°
3.一个扇形的弧长是2π,面积是4π,则该扇形的圆心角的度数是( )
A.45° B.90° C.120° D.180°
4.如图所示,AB是☉O的直径,MN是☉O的切线,切点为N,如果
∠MNB=52°,则∠NOA的度数为( )
A.76° B.56° C.54° D.52°
5.如图所示,AC是☉O的直径,弦BD⊥AO于点E,连接BC,过点O作OF⊥BC于点F,若BD=8 cm,AE=2 cm,则OF的长度是( )
A.3 cm B. cm C.2.5 cm D. cm
6.如图所示,正六边形ABCDEF内接于☉O,点P在上,点Q是的中点,则∠CPQ的度数为( )
A.30° B.45° C.36° D.60°
7.已知☉O是一个正十二边形的外接圆,该正十二边形的半径为2,如果用正十二边形的面积来近似估计☉O的面积,则☉O的面积大约是( )
A.12 B.12.4 C.12.56 D.4π
8.如图所示,在△ABC中,O是AB边上的点,以点O为圆心,OB为半径的☉O与AC相切于点D,BD平分∠ABC,AD=OD,AB=12,则CD的长是( )
A.2 B.2 C.3 D.4
9.如图所示,☉P与x轴交于点 A(-5,0),B(1,0),与 y轴的正半轴交于点C.若∠ACB=60°,则点C的纵坐标为( )
A.+ B.2+ C.4 D.2+2
10.如图所示,☉O是△ABC的外接圆,弦BD交AC于点E,AE=DE,BC=CE,过点O作OF⊥AC于点F,延长FO交BE于点G,若DE=3,EG=2,则AB的长为( )
A.4 B.7 C.8 D.4
二、填空题(每小题4分,共24分)
11.若一个正多边形的每个内角为144°,则这个正多边形的边数是 .
12.在矩形ABCD中,BC=6,CD=8,以点A为圆心画圆,且点D在☉A的内部,点B在☉A的外部,则☉A的半径r的取值范围是 .
13.如图所示,等边三角形ABC内接于☉O,BC=2,则图中阴影部分的面积是 .
14.直线y=-x-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,1个单位长度为半径作☉P,当☉P与直线AB相切时,点P的坐标是 .
15.如图所示,点I为△ABC的内切圆的圆心,连接BI并延长交△ABC的外接圆于点D,连接AD,AI,若BD=7,AD=5,则BI的长为 .
16.如图所示,在平面直角坐标系中,点A是函数y=-x图象l上的动点,以A为圆心,1为半径作☉A.已知点 B(-4,0),连接AB,线段AB与x轴所成的角∠ABO为锐角,当☉A与两坐标轴同时相切时,tan∠ABO的值为 .
三、解答题(共56分)
17.(6分)如图所示,点A,B为☉O上的两点,连接AO,BO,AB(∠AOB<
90°).
(1)请用无刻度的直尺和圆规,过点B作OA的平行线(保留作图痕迹,不写作法).
(2)若(1)中所作的平行线与☉O交于点C,连接AC,则∠CAO与∠O有怎样的数量关系,请说明理由.
18.(8分)2023年5月30日,“神舟十六号”航天飞船成功发射.如图所示,飞船在离地球大约330 km的圆形轨道上,当运行到地球表面P点的正上方F点时,从中直接看到地球表面一个最远的点是点Q.在 Rt△OQF 中,OP=OQ≈6 400 km(参考数据:cos 16°≈0.96,cos 18°≈0.95,cos 20°≈0.94,cos 22°≈0.93,π≈3.14).
(1)求cos α的值(精确到0.01);
(2)在☉O中,求的长(结果取整数).
19.(9分)如图所示,BD为△ABC外接圆☉O的直径,且∠BAE=∠C.
(1)求证:AE是☉O的切线;
(2)若AE∥BC,BC=2,AC=2,求AD的长.
20.(10分)如图所示,AB与☉O相切于点B,AO交☉O于点C,AO的延长线交☉O于点D,E是上不与B,D重合的点,sin A=.
(1)求∠BED的大小;
(2)若☉O的半径为3,点F在AB的延长线上,且BF=3,求证:DF是☉O的切线.
21.(11分)如图所示,AB是☉O的切线,点B为切点,直线AO交☉O于C,D两点,连接BC,BD.过圆心O作BC的平行线,分别交AB的延长线、☉O及BD于点E,F,G.
(1)求证:∠D=∠E;
(2)若F是OE的中点,☉O的半径为3,求阴影部分的面积.
22.(12分)如图所示,☉O的直径AB=16,半径OC⊥AB,D为上一动点(不包括B,C两点),DE⊥OC,DF⊥AB,垂足分别为E,F.
(1)求EF的长;
(2)若点E为OC的中点,
①求的长度;
②若点P为直径AB上一动点,求出PC+PD的最小值.
参考答案
(时间:90分钟 满分:120分)
一、选择题(每小题4分,共40分)
1.(C)2.(D)3.(B)4.(A)5.(D)6.(B)7.(A)8.(A)9.(B)10.(B)
二、填空题(每小题4分,共24分)
11. 10 .12. 6
三、解答题(共56分)
17.解:(1)如图所示,直线BD即为所求.
(2)∠O=2∠CAO.理由如下:
∵BC∥OA,∴∠CAO=∠BCA.
∵∠O=2∠BCA,∴∠O=2∠CAO.
18.解:(1)由题意,知FQ是☉O的切线,
∴∠OQF=90°.
∵OP=OQ≈6 400 km,FP=330 km,
∴OF=OP+FP=6 730 km.
∴cos α==≈0.95.
(2)∵cos α≈0.95,
∴α≈18°.
∴的长为≈2 010(km).
19.(1)证明:如图所示,连接OA交BC于点F,则OA=OD,
∴∠D=∠DAO.
∵∠D=∠C,
∴∠C=∠DAO.
∵∠BAE=∠C,
∴∠BAE=∠DAO.
∵BD是☉O的直径,
∴∠DAB=90°,即∠DAO+∠OAB=90°.
∴∠BAE+∠OAB=90°,即∠OAE=90°.
∴AE⊥OA.
∵OA是☉O的半径,∴AE是☉O的切线.
(2)解:∵AE∥BC,AE⊥OA,∴OA⊥BC.
∴=,FB=BC.∴AB=AC.
∵BC=2,AC=2,∴BF=,AB=2.
在Rt△ABF中,AF==1.在Rt△OFB中,OB2=BF2+(OB-AF)2,
即OB2=()2+(OB-1)2,解得OB=4,∴BD=8.
∴在Rt△ABD中,AD====2.
20.(1)解:如图所示,连接OB,
∵AB与☉O相切于点B,
∴∠ABO=90°.
∵sin A=,∴∠A=30°.
∴∠BOD=∠ABO+∠A=120°.
∴∠BED=∠BOD=60°.
(2)证明:如图所示,连接OF,
∵AB与☉O相切于点B,∴∠OBF=90°.
∵BF=3,OB=3,∴tan∠BOF==.∴∠BOF=60°.
∵∠BOD=120°,
∴∠BOF=∠DOF=60°.
在△BOF和△DOF中,∵OB=OD,∠BOF=∠DOF,OF=OF,
∴△BOF≌△DOF(SAS).
∴∠ODF=∠OBF=90°.即OD⊥DF.
∵OD是☉O的半径,∴DF是☉O的切线.
21.(1)证明:如图所示,连接OB,
∵AB是☉O的切线,
∴∠OBE=90°.
∴∠E+∠BOE=90°.
∵CD为☉O的直径,
∴∠CBD=90°.
∴∠D+∠DCB=90°.
∵OE∥BC,∴∠BOE=∠OBC.
∵OB=OC,∴∠OBC=∠OCB.
∴∠BOE=∠OCB.
∴∠D=∠E.
(2)解:∵F是OE的中点,OB=OF,
∴OF=EF=3.∴OE=6.∴BO=OE.
∵∠OBE=90°,∴∠E=30°.
∴∠BOG=60°.
∵OE∥BC,∠DBC=90°,
∴∠OGB=90°.∴OG=,BG=.
∴S△BOG=OG·BG=××=,S扇形BOF==π.
∴S阴影部分=S扇形BOF-S△BOG=π-.
22.解:(1)如图所示,连接OD,
∵☉O的直径AB=16,
∴圆的半径为16÷2=8.
∵OC⊥AB,DE⊥OC,DF⊥AB,
∴四边形OFDE是矩形.∴EF=OD=8.
(2)①∵点E为OC的中点,
∴OE=OC=OD.
∴∠EDO=30°.
∴∠DOE=60°.
∴的长度为=.
②如图所示,延长CO交☉O于点G,连接DG交AB于点P,则PC+PD的最小值为DG.
∵∠G=∠COD=30°,EG=12,cos G=,
∴DG==8.
∴PC+PD的最小值为8.
