【期末押题卷】期末质量检测考前冲刺预测卷(含解析)-2024-2025学年五年级下册数学人教版
文档属性
| 名称 | 【期末押题卷】期末质量检测考前冲刺预测卷(含解析)-2024-2025学年五年级下册数学人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 583.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末质量检测考前冲刺预测卷
2024-2025学年五年级下册数学人教版
一、选择题
1.气象局人员监控记录24时气温变化,用( )统计图较好。
A.条形 B.单式折线 C.复式折线
2.下图,阴影部分用分数表示,下列说法不正确的是( )。
A.一个大三角形的 B.三个大三角形的 C.三个大三角形的
3.小明看一本书,第一天看了全书的,第二天看了全书的,两天看了全书的( )。
A. B. C. D.
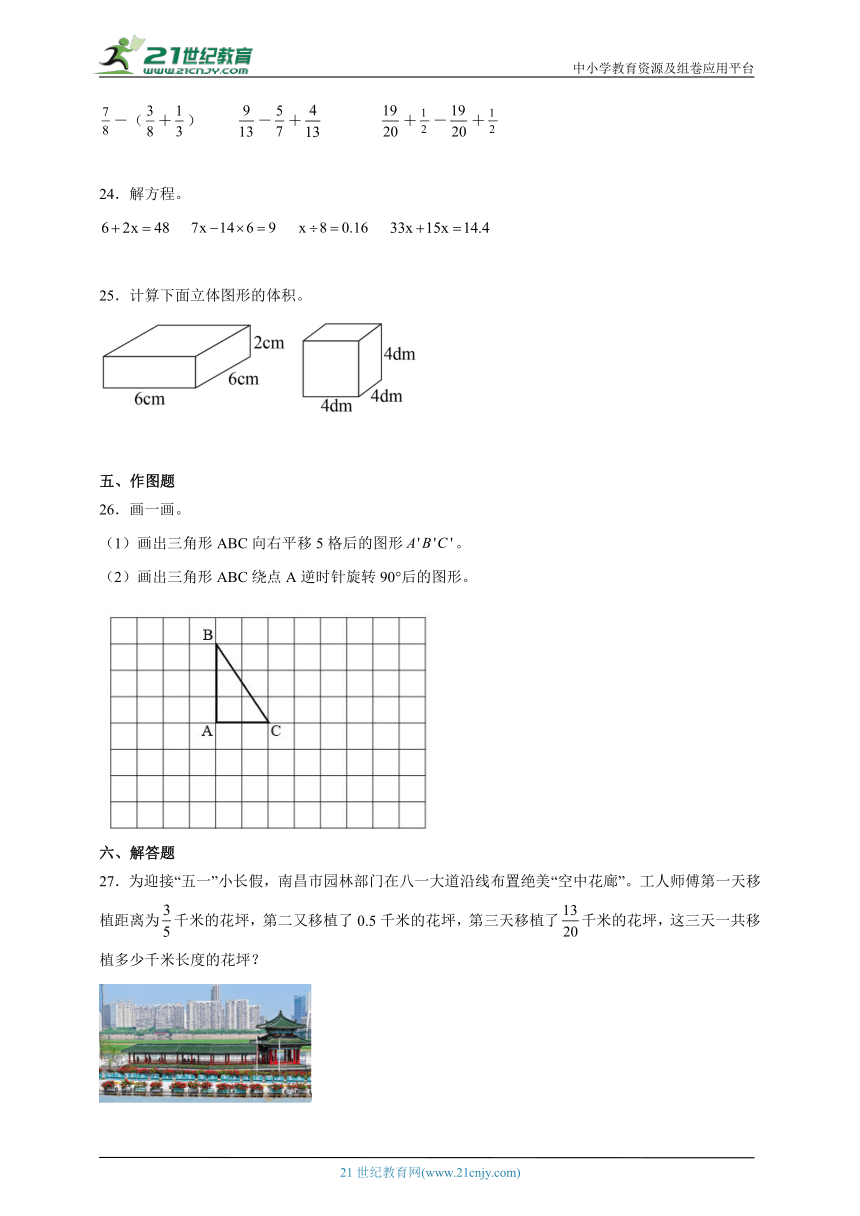
4.国美电器举行“五周年店庆”抽奖活动,王鑫分到的一张抽奖券,它的号码是一个三位数,个位上是最小的合数,十位上是最小的质数,百位上既是奇数又是合数,王鑫抽奖券的号码是( )。
A.249 B.942 C.940 D.924
5.一个正方体的表面积是24平方分米,把这个正方体的棱长增加1分米,得到的新正方体的体积比原来增加( )立方分米。
A.19 B.8 C.30
6.用8个棱长是1cm的小木块拼成一个长方体或正方体,拼成后的表面积最少是( )。
A.34cm2 B.28cm2 C.24cm2 D.20cm2
7.四个同样的礼品盒,每个长10cm,宽7cm,高2cm。下面四种不同的包装方式,( )最省包装纸。
A.B.C.D.
二、填空题
8.5个是 ,有 个,1里面有 个。
9.指针从A开始,绕点O顺时针旋转90°后到( )点;从A到C,指针绕点O按顺时针方向旋转了( )°。
10.三个质数的积是42,这三个质数是( )。
11.2500mL=( )L 小时=( )分
12.“古城一天乐”,妈妈买了4串糖葫芦,平均分给5个人,每人分得这些糖葫芦的( ),每人分得( )串。
13.在( )里填上不同的数.
(1)+ = (2)++=
三、判断题
14.一个数的倍数总比这个数的因数大。( )
15.如果a÷b=,那么a就是b的3倍。( )
16.两个数的公因数是最大公因数的因数。( )
17.一块巧克力两人分,每人分到。( )
18.在百米赛跑中,小明用了0.25分钟,小军用了分钟,小军跑得快。( )
19.的分数单位与相差。( )
20.把3kg的糖果平均分给10位同学,每人分得这些糖果的。( )
21.从正面、左面和上面看到的都是,这个几何体可以摆成。( )
四、计算题
22.直接写出得数。
23.计算下列各题,怎样算简便就怎样算。
-+ -- 4.7++5.3+
-(+) -+ +-+
24.解方程。
25.计算下面立体图形的体积。
五、作图题
26.画一画。
(1)画出三角形ABC向右平移5格后的图形。
(2)画出三角形ABC绕点A逆时针旋转90°后的图形。
六、解答题
27.为迎接“五一”小长假,南昌市园林部门在八一大道沿线布置绝美“空中花廊”。工人师傅第一天移植距离为千米的花坪,第二又移植了0.5千米的花坪,第三天移植了千米的花坪,这三天一共移植多少千米长度的花坪?
28.一筐苹果不超过50个,平均分给6个同学正好分完,平均分给8个同学也没有剩余,这筐苹果最少有多少个?最多有多少个?
29.某建筑工地运来一批水泥,砌墙用去了吨,抹地用去了吨,还剩吨,这批水泥共有多少吨?
30.花果山农场用总面积的种橙树,种杨桃树,其余的种火龙果。种火龙果的面积占总面积的几分之儿?
31.三根木条共长米,第一根和第二根共长米,第二根和第三根共长米,第二根长多少米?
32.有一个棱长为2dm的正方体玻璃容器,里面装有5L水,把一块珊瑚石完全浸没水中后,容器内水深为15cm,这块珊瑚石的体积是多少立方厘米?
33.一个长方体容器里面装有水,一块棱长24厘米的正方体铁块浸没在水中.现将铁块取出,水面下降18厘米;如果将一个长18厘米,宽16厘米,高12厘米的长方体铁块浸入水中:水面将上升多少厘米?
34.一盒饼干长30厘米,宽21厘米,高15厘米,现在要在它的四周贴上商标纸,这张商标纸的面积是多少平方厘米?
35.在南宁市“红领巾奖章”评选活动中,五(1)班获评一星章的同学占获奖人数的,获评二星章的同学占获奖人数的,剩下的同学均获评三星章,五(1)班获评三星章的同学占获奖人数的几分之几?
36.一个由小正方体搭成的物体,从上面看到的图形是,从左面看到的图形是。搭这样的物体,最少需要几个小正方体?最多可以有几个小正方体?
答案解析
1.B
【解题思路】条形统计图:用一个单位长度(如:厘米),表示一定的数量,根据数量的多少,画成长短相应成比例的直条,并按一定顺序排列起来;
折线统计图:以折线的上升或下降来表示统计数量的增减变化的统计图,分为单式统计图和复式统计图。
【精讲精析】气象局人员监控记录24时气温变化,所绘制的统计图要能够清楚地看出数量增减变化的情况,也能看出数量的多少,故选用折线统计图,由于只统计了一个项目,只用单式统计图就可以。
故答案为B。
【要点提示】学生们对于条形统计图和折线统计图特点与区别并不陌生,题目的要求也易于理解,故本题难度不大。
2.B
【解题思路】根据分数的意义,分别确定不同的单位“1”,再平均分成几份,阴影部分用分数表示出来,逐一判断各个选项的正确性。
【精讲精析】A.一个大三角形的,表示把一个大三角形看作单位“1”,平均分成3份,其中2份涂色,如图:即可表示出一个大三角形的;
B.三个大三角形的,表示把三个大三角形看作单位“1”,平均分成3份,其中2份大三角形涂色,如图:,即可表示出三个大三角形的,但与原题的图案不符;
C.三个大三角形的,表示把三个大三角形看作单位“1”,平均分成9份,其中2份涂色,如图:即可表示出三个大三角形的。
故答案为:B
【要点提示】此题的解题关键是理解掌握分数的意义,确定单位“1”,解决实际的问题。
3.B
【精讲精析】;
故答案为:B。
4.D
【解题思路】质数:一个数,除了1和它本身,不再有别的因数;合数:一个数,除了1和它本身,还有别的因数;奇数:不是2的倍数。分别根据合数、质数、奇数的概念,结合题意找到相应的数字,按照数位顺序组合起来就是答案。
【精讲精析】最小的合数是4;最小的质数是2;既是奇数又是合数的数是9;则这个数是924。
故答案为:D。
【要点提示】首先要清楚几类数的概念,能准确确定最小的合数、最小的质数及既是奇数又是合数的数,注意1既不是质数也不是合数。
5.A
【解题思路】正方体的表面积÷6,先求出一个面的面积,再确定正方体棱长,根据正方体体积=棱长×棱长×棱长,分别求出现在和原来的体积,求差即可。
【精讲精析】24÷6=4(平方分米)
4=2×2
2+1=3(分米)
3×3×3-2×2×2
=27-8
=19(立方分米)
故答案为:A
【要点提示】关键是掌握正方体表面积和体积公式,正方体表面积=棱长×棱长×6。
6.C
【解题思路】用8个棱长是1cm的小木块拼成一个长方体或正方体,拼成的这个长方体(或正方体)有3种情况:第一种是长8cm,宽1cm,高1cm;第二种是长4cm,宽2cm,高1cm;第三种是长2cm,宽2cm,高2cm;根据长方体的表面积=(长×宽+长×高+宽×高)×2;正方体的表面积=棱长×棱长×6,分别计算出这三种立体图形的表面积,再作比较,找出表面积最少的即可。
【精讲精析】第一种表面积:(8×1+8×1+1×1)×2
=(8+8+1)×2
=17×2
=34(cm2)
第二种表面积:(4×2+4×1+2×1)×2
=(8+4+2)×2
=14×2
=28(cm2)
第三种表面积:2×2×6=24(cm2)
因此拼成第三种的表面积最少,是24cm2。
故答案为:C
7.A
【解题思路】要想最省包装纸,就是求这四个长方体拼成大长方体后的表面积最小,即求出哪种包装方式下,拼成的大长方体的表面积与原来四个长方体的表面积之和相比,减少的面的面积最大,就最省包装纸。
【精讲精析】A.表面积减少了:
10×7×6
=70×6
=420(cm2)
B.表面积减少了:
10×7×4+7×2×4
=70×4+14×4
=280+56
=336(cm2)
C.表面积减少了:
10×2×4+7×2×4
=20×4+14×4
=80+56
=136(cm2)
D.表面积减少了:
10×2×6
=20×6
=120(cm2)
420>336>136>120
故答案为:A
【要点提示】掌握立体图形拼接的特点,明确要使拼成的立体图形的表面积最小,则把最大的面重合。
8. 7 6
【解题思路】分数单位是把单位“1”平均分成若干份,表示其中的一份的数;再看看分数里面有多少个这样的分数单位即可解答。
【精讲精析】5个是,有7个,1里面有6个。
9. D 180
【解题思路】在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转,据此解答。
【精讲精析】指针从A开始,绕点O顺时针旋转90°后到(D)点;从A到C,指针绕点O按顺时针方向旋转了(180)°。
【要点提示】考查了旋转,旋转要明确绕点,角度和方向。
10.2、3、7
【解题思路】从最小的质数2开始尝试,2×3=6,再乘质数7就得到42。
【精讲精析】2×3×7=42
【要点提示】此类问题可以从最容易判断的质因数开始考虑。
11. 2.5 84
【解题思路】根据进率:1L=1000mL,1时=60分;从高级单位向低级单位转换,乘进率;从低级单位向高级单位转换,除以进率;据此解答。
【精讲精析】(1)2500÷1000=2.5(L)
2500mL=2.5L
(2)×60
=×60
=84(分)
小时=84分
【要点提示】掌握各单位之间的进率以及转换方向是单位换算的关键。
12.
【解题思路】将妈妈买的糖葫芦数量看作单位“1”,求每人分得这些糖葫芦的几分之几,用1÷人数;求每人分得数量,用糖葫芦数量÷人数。
【精讲精析】1÷5=
4÷5=(串)
【要点提示】分数的分子相当于被除数,分母相当于除数。
13.(1)答案不唯一,如9 18 (2)答案不唯一,如72 24 36
【精讲精析】略
14.×
【解题思路】根据“一个数的因数最大是它本身,一个数的倍数最小是它本身”,进行分析,例如:8的最小倍数是8,最大因数是8;进而得出结论。
【精讲精析】假设这个数是8,8的最小倍数是8,最大因数是8,8=8,所以,一个数的倍数总比这个数的因数大说法错误。
故答案为:×
15.×
【解题思路】A是B的几分之几的计算方法:A÷B=,由a÷b=可知,a是b的,据此解答。
【精讲精析】假设a=1,b=3,a÷b=1÷3=,b÷a=3÷1=3,则a是b的,b是a的3倍。
故答案为:×
【要点提示】掌握一个数占另一个数几分之几的计算方法是解答题目的关键。
16.√
【解题思路】公因数是两个数公有的因数,最大公因数是公因数中最大的一个,举例进行判断即可。
【精讲精析】例如:12和20
公因数有:1、2、4,最大公因数是4,而1和2又是4的因数,所以此说法正确。
故判断为:√。
【要点提示】本题主要考查对公因数和最大公因数的理解以及求法。
17.×
【解题思路】分数的意义:把单位“1”平均分成若干份,表示其中一份或几份的数,据此解答。
【精讲精析】一块巧克力两人分,没有说平均分,所以每人不一定都分到。
故答案为:×
【要点提示】本题考查了分数的意义,注意用分数表示必须要平均分。
18.×
【解题思路】先将小军用的时间分钟转化成小数,用分子除以分母即可,再与小明用的时间作比较,路程一定时,用时越短的,跑得越快。
【精讲精析】=3÷10=0.3
0.25<0.3,小明用的时间短,所以小明跑得快。
原题说法错误。
故答案为:×
【要点提示】路程一定时,用时越少的,跑得越快。可以将两人的时间化成同分母或同分子的分数比较大小,也可化成小数比较大小。
19.√
【解题思路】把单位“1”平均分成若干份,表示其中一份的叫分数单位;算出差比较即可。
【精讲精析】-=,所以原题说法正确。
故答案为:√
【要点提示】本题考查了分数单位及分数减法,异分母分数相加减,先通分再计算。
20.×
【解题思路】把糖果看作单位“1”,平均分给10位同学,每位同学分得糖果的,据此解答即可。
【精讲精析】把3kg的糖果平均分给10位同学,每人分得这些糖果的,本题说法错误;
故答案为:×。
【要点提示】本题考查分数的意义,解答本题的关键是掌握分数的意义。
21.×
【解题思路】主视图、左视图、俯视图都是,给想象图形增加了难度,我们可以结合题意在纸上试着一步步画出立体图形,再作判断。
【精讲精析】从正面看是,说明几何体最高是2层,最低是1层;如果结合俯视图也是,基本能够确定,从正面看后排为2个小立方体,前排为1层,2列。每列各有1个小立方体;最后再结合左视图也是,可以最终确定是的形状。即。
故答案为×。
【要点提示】由三视图确定几何体,就本题来说,有一定的难度。需要我们充分发挥空间思维,在一次次试验中逐步确定几何体的形状。
22.1;2;;
8;;0;0.45
【精讲精析】略
23.;;11;
;;1
【解题思路】(1)直接找出这三个分数分母的最小公倍数作公分母进行通分,再按照同分母分数加、减法的计算方法计算。
(2)利用减法的性质进行简算。
(3)根据加法交换律、加法结合律简算。
(4)先逆用减法的性质去括号,再同分母的分数结合简算。
(5)交换第二项和第三项的位置,再同分母的分数结合简算。
(6)交换第二项和第三项的位置,再同分母的分数结合简算。
【精讲精析】-+
=
=
=
=
--
=-(+)
=
=
4.7++5.3+
=4.7+5.3+++
=(4.7+5.3)+(+)
=10+1
=11
-(+)
=--
=(-)-
=
=
=
-+
=+-
=(+)-
=1-
=
+-+
=-++
=(-)+(+)
=0+1
=1
24.;;;
【解题思路】(1)根据等式的性质1和性质2,方程左右两边先同时减去6,再同时除以2,解出方程;
(2)先计算方程左边的乘法算式,再根据等式的性质1和性质2,方程左右两边先同时加84,再同时除以7,解出方程;
(3)根据等式的性质2,方程左右两边同时乘8,解出方程;
(4)先合并方程左边含共同未知数的算式,再根据等式的性质2,方程左右两边同时除以48,解出方程。
【精讲精析】
解:
解:
解:
解:
25.72cm3;64dm3
【解题思路】根据长方体体积公式:体积=长×宽×高;正方体体积公式:体积=棱长×棱长×棱长,代入数据,分别求出长方体体积、正方体体积。
【精讲精析】6×6×2
=36×2
=72(cm3)
4×4×4
=16×4
=64(dm3)
长方体体积:72cm3;正方体体积:64dm3
26.(1)(2)见详解
【解题思路】(1)根据平移的特征,将三角形ABC的各顶点分别向右平移5格,依次连接即可得到平移后的图形。
(2)根据旋转的特征,将三角形ABC绕点A逆时针旋转90°,点A位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
【精讲精析】(1)(2)作图如下:
【要点提示】此题主要考查图形的平移和图形的旋转,掌握其作图方法是解答题目的关键。
27.千米
【解题思路】要计算三天一共移植花坪的长度,需把三天移植的长度相加+0.5+;把第二天的移植距离0.5千米化为分数,然后计算++,先通分为分母是20的分数,再计算同分母分数的加法++得出结果后约分为最简分数。
【精讲精析】+0.5+
=++
=++
=+
=
=(千米)
答:这三天一共移植千米长度的花坪。
28.24个;48个
【解题思路】这筐苹果不超过50个,平均分给6个同学正好分完,平均分给8个同学也没有剩余,这说明苹果的数量是6和8的公倍数,只需要求出50范围内6和8的公倍数的最小值和最大值就可以知道这筐苹果最少有多少个,最多有多少个。
【精讲精析】6=2×3
8=2×2×2
6和8的最小公倍数:2×2×2×3=24
50范围内6和8的公倍数有:24和48,所以这筐苹果最少有24个,最多有48个。
答:这筐苹果最少有24个,最多有48个。
【要点提示】本题考查公倍数的应用问题。
29.吨
【解题思路】将砌墙用去的吨数、抹地用去的吨数和剩下的吨数相加即可。
【精讲精析】++
=+
=(吨);
答:这批水泥共有吨。
【要点提示】熟练掌握异分母分数加法的计算方法是解答本题的关键。
30.
【解题思路】把花果山农场用总面积看作“1”,用1分别减去种橙树的面积占总面积的分率和种桃树的面积占总面积的分率,即可求出种火龙果的面积占总面积的几分之儿。
【精讲精析】1--
=-
=-
=
答:种火龙果的面积占总面积的。
【要点提示】此题的解题关键是先确定单位“1”,利用分数的加减法混合运算求出结果。
31.米
【解题思路】第三根木条的长度=三根木条的总长度-第一根和第二根木条的长度,第二根木条的长度=第二根和第三根木条的长度-第三根木条的长度,据此解答。
【精讲精析】第三根木条的长度:-=(米)
第二根木条的长度:-=(米)
答:第二根长米。
【要点提示】异分母分数相加减,先通分再按照同分母分数加减法计算。
32.1000立方厘米
【精讲精析】15cm=1.5dm
2×2×1.5-5=1(立方分米)
1立方分米=1000立方厘米
33.4.5厘米
【精讲精析】试题分析:先求出棱长为24厘米正方体铁块的体积;再根据“将铁块取出,水面下降18厘米“,进而用铁块的体积除以水面下降的厘米数,就是长方体容器的底面积;再求出长18厘米、宽16厘米、高12厘米的长方体铁块的体积,进而用长方体铁块的体积除以容器的底面积,即为水面上升的厘米数.
解:正方体铁块的体积:24×24×24=13824(立方厘米),
长方体容器的底面积:13824÷18=768(平方厘米),
长方体铁块的体积:18×16×12=3456(立方厘米),
水面上升的高度:3456÷768=4.5(厘米).
答:水面将上升4.5厘米.
点评:此题主要考查特殊物体体积的计算方法,明确将物体放入水中或从水中取出,水面上升或下降的体积就是物体的体积,从而求出容器的底面积;也考查了正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高,这两个体积公式的应用.
34.1530平方厘米
【解题思路】在它的四周贴上商标纸,即不贴上下两个面,商标纸的面积=长×高×2+宽×高×2,据此列式解答。
【精讲精析】30×15×2+21×15×2
=900+630
=1530(平方厘米)
答:这张商标纸的面积是1530平方厘米。
35.
【解题思路】把获奖人数看作单位“1”,用单位“1”减去(+)即可求出五(1)班获评三星章的同学占获奖人数的几分之几。
【精讲精析】1-(+)
=1-(+)
=1-
=
答:五(1)班获评三星章的同学占获奖人数的。
【要点提示】在计算过程中,“1”可以化成任意一个计算中需要的分子和分母相同的分数,最后结果要约成最简分数。
36.4个;6个
【解题思路】此题主要考查了观察物体的知识,从上面观察的图形可知,这个图形只有一行,一行有3个正方体;从左面看到的形状可知,这个图形有两层,最少的情况是第二层只有1个正方体,最多的情况是第二层有3个正方体,据此解答。
【精讲精析】最少需要:3+1=4(个);
最多需要:3+3=6(个)。
答:最少需要4个小正方体,最多可以有6个小正方体。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末质量检测考前冲刺预测卷
2024-2025学年五年级下册数学人教版
一、选择题
1.气象局人员监控记录24时气温变化,用( )统计图较好。
A.条形 B.单式折线 C.复式折线
2.下图,阴影部分用分数表示,下列说法不正确的是( )。
A.一个大三角形的 B.三个大三角形的 C.三个大三角形的
3.小明看一本书,第一天看了全书的,第二天看了全书的,两天看了全书的( )。
A. B. C. D.
4.国美电器举行“五周年店庆”抽奖活动,王鑫分到的一张抽奖券,它的号码是一个三位数,个位上是最小的合数,十位上是最小的质数,百位上既是奇数又是合数,王鑫抽奖券的号码是( )。
A.249 B.942 C.940 D.924
5.一个正方体的表面积是24平方分米,把这个正方体的棱长增加1分米,得到的新正方体的体积比原来增加( )立方分米。
A.19 B.8 C.30
6.用8个棱长是1cm的小木块拼成一个长方体或正方体,拼成后的表面积最少是( )。
A.34cm2 B.28cm2 C.24cm2 D.20cm2
7.四个同样的礼品盒,每个长10cm,宽7cm,高2cm。下面四种不同的包装方式,( )最省包装纸。
A.B.C.D.
二、填空题
8.5个是 ,有 个,1里面有 个。
9.指针从A开始,绕点O顺时针旋转90°后到( )点;从A到C,指针绕点O按顺时针方向旋转了( )°。
10.三个质数的积是42,这三个质数是( )。
11.2500mL=( )L 小时=( )分
12.“古城一天乐”,妈妈买了4串糖葫芦,平均分给5个人,每人分得这些糖葫芦的( ),每人分得( )串。
13.在( )里填上不同的数.
(1)+ = (2)++=
三、判断题
14.一个数的倍数总比这个数的因数大。( )
15.如果a÷b=,那么a就是b的3倍。( )
16.两个数的公因数是最大公因数的因数。( )
17.一块巧克力两人分,每人分到。( )
18.在百米赛跑中,小明用了0.25分钟,小军用了分钟,小军跑得快。( )
19.的分数单位与相差。( )
20.把3kg的糖果平均分给10位同学,每人分得这些糖果的。( )
21.从正面、左面和上面看到的都是,这个几何体可以摆成。( )
四、计算题
22.直接写出得数。
23.计算下列各题,怎样算简便就怎样算。
-+ -- 4.7++5.3+
-(+) -+ +-+
24.解方程。
25.计算下面立体图形的体积。
五、作图题
26.画一画。
(1)画出三角形ABC向右平移5格后的图形。
(2)画出三角形ABC绕点A逆时针旋转90°后的图形。
六、解答题
27.为迎接“五一”小长假,南昌市园林部门在八一大道沿线布置绝美“空中花廊”。工人师傅第一天移植距离为千米的花坪,第二又移植了0.5千米的花坪,第三天移植了千米的花坪,这三天一共移植多少千米长度的花坪?
28.一筐苹果不超过50个,平均分给6个同学正好分完,平均分给8个同学也没有剩余,这筐苹果最少有多少个?最多有多少个?
29.某建筑工地运来一批水泥,砌墙用去了吨,抹地用去了吨,还剩吨,这批水泥共有多少吨?
30.花果山农场用总面积的种橙树,种杨桃树,其余的种火龙果。种火龙果的面积占总面积的几分之儿?
31.三根木条共长米,第一根和第二根共长米,第二根和第三根共长米,第二根长多少米?
32.有一个棱长为2dm的正方体玻璃容器,里面装有5L水,把一块珊瑚石完全浸没水中后,容器内水深为15cm,这块珊瑚石的体积是多少立方厘米?
33.一个长方体容器里面装有水,一块棱长24厘米的正方体铁块浸没在水中.现将铁块取出,水面下降18厘米;如果将一个长18厘米,宽16厘米,高12厘米的长方体铁块浸入水中:水面将上升多少厘米?
34.一盒饼干长30厘米,宽21厘米,高15厘米,现在要在它的四周贴上商标纸,这张商标纸的面积是多少平方厘米?
35.在南宁市“红领巾奖章”评选活动中,五(1)班获评一星章的同学占获奖人数的,获评二星章的同学占获奖人数的,剩下的同学均获评三星章,五(1)班获评三星章的同学占获奖人数的几分之几?
36.一个由小正方体搭成的物体,从上面看到的图形是,从左面看到的图形是。搭这样的物体,最少需要几个小正方体?最多可以有几个小正方体?
答案解析
1.B
【解题思路】条形统计图:用一个单位长度(如:厘米),表示一定的数量,根据数量的多少,画成长短相应成比例的直条,并按一定顺序排列起来;
折线统计图:以折线的上升或下降来表示统计数量的增减变化的统计图,分为单式统计图和复式统计图。
【精讲精析】气象局人员监控记录24时气温变化,所绘制的统计图要能够清楚地看出数量增减变化的情况,也能看出数量的多少,故选用折线统计图,由于只统计了一个项目,只用单式统计图就可以。
故答案为B。
【要点提示】学生们对于条形统计图和折线统计图特点与区别并不陌生,题目的要求也易于理解,故本题难度不大。
2.B
【解题思路】根据分数的意义,分别确定不同的单位“1”,再平均分成几份,阴影部分用分数表示出来,逐一判断各个选项的正确性。
【精讲精析】A.一个大三角形的,表示把一个大三角形看作单位“1”,平均分成3份,其中2份涂色,如图:即可表示出一个大三角形的;
B.三个大三角形的,表示把三个大三角形看作单位“1”,平均分成3份,其中2份大三角形涂色,如图:,即可表示出三个大三角形的,但与原题的图案不符;
C.三个大三角形的,表示把三个大三角形看作单位“1”,平均分成9份,其中2份涂色,如图:即可表示出三个大三角形的。
故答案为:B
【要点提示】此题的解题关键是理解掌握分数的意义,确定单位“1”,解决实际的问题。
3.B
【精讲精析】;
故答案为:B。
4.D
【解题思路】质数:一个数,除了1和它本身,不再有别的因数;合数:一个数,除了1和它本身,还有别的因数;奇数:不是2的倍数。分别根据合数、质数、奇数的概念,结合题意找到相应的数字,按照数位顺序组合起来就是答案。
【精讲精析】最小的合数是4;最小的质数是2;既是奇数又是合数的数是9;则这个数是924。
故答案为:D。
【要点提示】首先要清楚几类数的概念,能准确确定最小的合数、最小的质数及既是奇数又是合数的数,注意1既不是质数也不是合数。
5.A
【解题思路】正方体的表面积÷6,先求出一个面的面积,再确定正方体棱长,根据正方体体积=棱长×棱长×棱长,分别求出现在和原来的体积,求差即可。
【精讲精析】24÷6=4(平方分米)
4=2×2
2+1=3(分米)
3×3×3-2×2×2
=27-8
=19(立方分米)
故答案为:A
【要点提示】关键是掌握正方体表面积和体积公式,正方体表面积=棱长×棱长×6。
6.C
【解题思路】用8个棱长是1cm的小木块拼成一个长方体或正方体,拼成的这个长方体(或正方体)有3种情况:第一种是长8cm,宽1cm,高1cm;第二种是长4cm,宽2cm,高1cm;第三种是长2cm,宽2cm,高2cm;根据长方体的表面积=(长×宽+长×高+宽×高)×2;正方体的表面积=棱长×棱长×6,分别计算出这三种立体图形的表面积,再作比较,找出表面积最少的即可。
【精讲精析】第一种表面积:(8×1+8×1+1×1)×2
=(8+8+1)×2
=17×2
=34(cm2)
第二种表面积:(4×2+4×1+2×1)×2
=(8+4+2)×2
=14×2
=28(cm2)
第三种表面积:2×2×6=24(cm2)
因此拼成第三种的表面积最少,是24cm2。
故答案为:C
7.A
【解题思路】要想最省包装纸,就是求这四个长方体拼成大长方体后的表面积最小,即求出哪种包装方式下,拼成的大长方体的表面积与原来四个长方体的表面积之和相比,减少的面的面积最大,就最省包装纸。
【精讲精析】A.表面积减少了:
10×7×6
=70×6
=420(cm2)
B.表面积减少了:
10×7×4+7×2×4
=70×4+14×4
=280+56
=336(cm2)
C.表面积减少了:
10×2×4+7×2×4
=20×4+14×4
=80+56
=136(cm2)
D.表面积减少了:
10×2×6
=20×6
=120(cm2)
420>336>136>120
故答案为:A
【要点提示】掌握立体图形拼接的特点,明确要使拼成的立体图形的表面积最小,则把最大的面重合。
8. 7 6
【解题思路】分数单位是把单位“1”平均分成若干份,表示其中的一份的数;再看看分数里面有多少个这样的分数单位即可解答。
【精讲精析】5个是,有7个,1里面有6个。
9. D 180
【解题思路】在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转,据此解答。
【精讲精析】指针从A开始,绕点O顺时针旋转90°后到(D)点;从A到C,指针绕点O按顺时针方向旋转了(180)°。
【要点提示】考查了旋转,旋转要明确绕点,角度和方向。
10.2、3、7
【解题思路】从最小的质数2开始尝试,2×3=6,再乘质数7就得到42。
【精讲精析】2×3×7=42
【要点提示】此类问题可以从最容易判断的质因数开始考虑。
11. 2.5 84
【解题思路】根据进率:1L=1000mL,1时=60分;从高级单位向低级单位转换,乘进率;从低级单位向高级单位转换,除以进率;据此解答。
【精讲精析】(1)2500÷1000=2.5(L)
2500mL=2.5L
(2)×60
=×60
=84(分)
小时=84分
【要点提示】掌握各单位之间的进率以及转换方向是单位换算的关键。
12.
【解题思路】将妈妈买的糖葫芦数量看作单位“1”,求每人分得这些糖葫芦的几分之几,用1÷人数;求每人分得数量,用糖葫芦数量÷人数。
【精讲精析】1÷5=
4÷5=(串)
【要点提示】分数的分子相当于被除数,分母相当于除数。
13.(1)答案不唯一,如9 18 (2)答案不唯一,如72 24 36
【精讲精析】略
14.×
【解题思路】根据“一个数的因数最大是它本身,一个数的倍数最小是它本身”,进行分析,例如:8的最小倍数是8,最大因数是8;进而得出结论。
【精讲精析】假设这个数是8,8的最小倍数是8,最大因数是8,8=8,所以,一个数的倍数总比这个数的因数大说法错误。
故答案为:×
15.×
【解题思路】A是B的几分之几的计算方法:A÷B=,由a÷b=可知,a是b的,据此解答。
【精讲精析】假设a=1,b=3,a÷b=1÷3=,b÷a=3÷1=3,则a是b的,b是a的3倍。
故答案为:×
【要点提示】掌握一个数占另一个数几分之几的计算方法是解答题目的关键。
16.√
【解题思路】公因数是两个数公有的因数,最大公因数是公因数中最大的一个,举例进行判断即可。
【精讲精析】例如:12和20
公因数有:1、2、4,最大公因数是4,而1和2又是4的因数,所以此说法正确。
故判断为:√。
【要点提示】本题主要考查对公因数和最大公因数的理解以及求法。
17.×
【解题思路】分数的意义:把单位“1”平均分成若干份,表示其中一份或几份的数,据此解答。
【精讲精析】一块巧克力两人分,没有说平均分,所以每人不一定都分到。
故答案为:×
【要点提示】本题考查了分数的意义,注意用分数表示必须要平均分。
18.×
【解题思路】先将小军用的时间分钟转化成小数,用分子除以分母即可,再与小明用的时间作比较,路程一定时,用时越短的,跑得越快。
【精讲精析】=3÷10=0.3
0.25<0.3,小明用的时间短,所以小明跑得快。
原题说法错误。
故答案为:×
【要点提示】路程一定时,用时越少的,跑得越快。可以将两人的时间化成同分母或同分子的分数比较大小,也可化成小数比较大小。
19.√
【解题思路】把单位“1”平均分成若干份,表示其中一份的叫分数单位;算出差比较即可。
【精讲精析】-=,所以原题说法正确。
故答案为:√
【要点提示】本题考查了分数单位及分数减法,异分母分数相加减,先通分再计算。
20.×
【解题思路】把糖果看作单位“1”,平均分给10位同学,每位同学分得糖果的,据此解答即可。
【精讲精析】把3kg的糖果平均分给10位同学,每人分得这些糖果的,本题说法错误;
故答案为:×。
【要点提示】本题考查分数的意义,解答本题的关键是掌握分数的意义。
21.×
【解题思路】主视图、左视图、俯视图都是,给想象图形增加了难度,我们可以结合题意在纸上试着一步步画出立体图形,再作判断。
【精讲精析】从正面看是,说明几何体最高是2层,最低是1层;如果结合俯视图也是,基本能够确定,从正面看后排为2个小立方体,前排为1层,2列。每列各有1个小立方体;最后再结合左视图也是,可以最终确定是的形状。即。
故答案为×。
【要点提示】由三视图确定几何体,就本题来说,有一定的难度。需要我们充分发挥空间思维,在一次次试验中逐步确定几何体的形状。
22.1;2;;
8;;0;0.45
【精讲精析】略
23.;;11;
;;1
【解题思路】(1)直接找出这三个分数分母的最小公倍数作公分母进行通分,再按照同分母分数加、减法的计算方法计算。
(2)利用减法的性质进行简算。
(3)根据加法交换律、加法结合律简算。
(4)先逆用减法的性质去括号,再同分母的分数结合简算。
(5)交换第二项和第三项的位置,再同分母的分数结合简算。
(6)交换第二项和第三项的位置,再同分母的分数结合简算。
【精讲精析】-+
=
=
=
=
--
=-(+)
=
=
4.7++5.3+
=4.7+5.3+++
=(4.7+5.3)+(+)
=10+1
=11
-(+)
=--
=(-)-
=
=
=
-+
=+-
=(+)-
=1-
=
+-+
=-++
=(-)+(+)
=0+1
=1
24.;;;
【解题思路】(1)根据等式的性质1和性质2,方程左右两边先同时减去6,再同时除以2,解出方程;
(2)先计算方程左边的乘法算式,再根据等式的性质1和性质2,方程左右两边先同时加84,再同时除以7,解出方程;
(3)根据等式的性质2,方程左右两边同时乘8,解出方程;
(4)先合并方程左边含共同未知数的算式,再根据等式的性质2,方程左右两边同时除以48,解出方程。
【精讲精析】
解:
解:
解:
解:
25.72cm3;64dm3
【解题思路】根据长方体体积公式:体积=长×宽×高;正方体体积公式:体积=棱长×棱长×棱长,代入数据,分别求出长方体体积、正方体体积。
【精讲精析】6×6×2
=36×2
=72(cm3)
4×4×4
=16×4
=64(dm3)
长方体体积:72cm3;正方体体积:64dm3
26.(1)(2)见详解
【解题思路】(1)根据平移的特征,将三角形ABC的各顶点分别向右平移5格,依次连接即可得到平移后的图形。
(2)根据旋转的特征,将三角形ABC绕点A逆时针旋转90°,点A位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
【精讲精析】(1)(2)作图如下:
【要点提示】此题主要考查图形的平移和图形的旋转,掌握其作图方法是解答题目的关键。
27.千米
【解题思路】要计算三天一共移植花坪的长度,需把三天移植的长度相加+0.5+;把第二天的移植距离0.5千米化为分数,然后计算++,先通分为分母是20的分数,再计算同分母分数的加法++得出结果后约分为最简分数。
【精讲精析】+0.5+
=++
=++
=+
=
=(千米)
答:这三天一共移植千米长度的花坪。
28.24个;48个
【解题思路】这筐苹果不超过50个,平均分给6个同学正好分完,平均分给8个同学也没有剩余,这说明苹果的数量是6和8的公倍数,只需要求出50范围内6和8的公倍数的最小值和最大值就可以知道这筐苹果最少有多少个,最多有多少个。
【精讲精析】6=2×3
8=2×2×2
6和8的最小公倍数:2×2×2×3=24
50范围内6和8的公倍数有:24和48,所以这筐苹果最少有24个,最多有48个。
答:这筐苹果最少有24个,最多有48个。
【要点提示】本题考查公倍数的应用问题。
29.吨
【解题思路】将砌墙用去的吨数、抹地用去的吨数和剩下的吨数相加即可。
【精讲精析】++
=+
=(吨);
答:这批水泥共有吨。
【要点提示】熟练掌握异分母分数加法的计算方法是解答本题的关键。
30.
【解题思路】把花果山农场用总面积看作“1”,用1分别减去种橙树的面积占总面积的分率和种桃树的面积占总面积的分率,即可求出种火龙果的面积占总面积的几分之儿。
【精讲精析】1--
=-
=-
=
答:种火龙果的面积占总面积的。
【要点提示】此题的解题关键是先确定单位“1”,利用分数的加减法混合运算求出结果。
31.米
【解题思路】第三根木条的长度=三根木条的总长度-第一根和第二根木条的长度,第二根木条的长度=第二根和第三根木条的长度-第三根木条的长度,据此解答。
【精讲精析】第三根木条的长度:-=(米)
第二根木条的长度:-=(米)
答:第二根长米。
【要点提示】异分母分数相加减,先通分再按照同分母分数加减法计算。
32.1000立方厘米
【精讲精析】15cm=1.5dm
2×2×1.5-5=1(立方分米)
1立方分米=1000立方厘米
33.4.5厘米
【精讲精析】试题分析:先求出棱长为24厘米正方体铁块的体积;再根据“将铁块取出,水面下降18厘米“,进而用铁块的体积除以水面下降的厘米数,就是长方体容器的底面积;再求出长18厘米、宽16厘米、高12厘米的长方体铁块的体积,进而用长方体铁块的体积除以容器的底面积,即为水面上升的厘米数.
解:正方体铁块的体积:24×24×24=13824(立方厘米),
长方体容器的底面积:13824÷18=768(平方厘米),
长方体铁块的体积:18×16×12=3456(立方厘米),
水面上升的高度:3456÷768=4.5(厘米).
答:水面将上升4.5厘米.
点评:此题主要考查特殊物体体积的计算方法,明确将物体放入水中或从水中取出,水面上升或下降的体积就是物体的体积,从而求出容器的底面积;也考查了正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高,这两个体积公式的应用.
34.1530平方厘米
【解题思路】在它的四周贴上商标纸,即不贴上下两个面,商标纸的面积=长×高×2+宽×高×2,据此列式解答。
【精讲精析】30×15×2+21×15×2
=900+630
=1530(平方厘米)
答:这张商标纸的面积是1530平方厘米。
35.
【解题思路】把获奖人数看作单位“1”,用单位“1”减去(+)即可求出五(1)班获评三星章的同学占获奖人数的几分之几。
【精讲精析】1-(+)
=1-(+)
=1-
=
答:五(1)班获评三星章的同学占获奖人数的。
【要点提示】在计算过程中,“1”可以化成任意一个计算中需要的分子和分母相同的分数,最后结果要约成最简分数。
36.4个;6个
【解题思路】此题主要考查了观察物体的知识,从上面观察的图形可知,这个图形只有一行,一行有3个正方体;从左面看到的形状可知,这个图形有两层,最少的情况是第二层只有1个正方体,最多的情况是第二层有3个正方体,据此解答。
【精讲精析】最少需要:3+1=4(个);
最多需要:3+3=6(个)。
答:最少需要4个小正方体,最多可以有6个小正方体。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
