5.1 认识方程 课件(共36张PPT)
文档属性
| 名称 | 5.1 认识方程 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 18:29:24 | ||
图片预览











文档简介
(共36张PPT)
5.1 认识方程
第五章 一元一次方程
北师大2024版数学七年级上册【示范课】
授课教师:********
班 级:********
时 间:********
学习目标
1. 理解方程及一元一次方程的概念,会检验一个数是不是方程的解.
2. 能根据实际问题列一元一次方程.
3. 通过列方程的过程,发展模型观念.
一元一次方程的概念
给出一元一次方程的定义:只含有一个未知数(元),未知数的次数都是 1,等号两边都是整式,这样的方程叫做一元一次方程。
举例说明:
2x 3=5
,
2
1
x+1=0
等都是一元一次方程,同时让学生判断一些式子是否为一元一次方程,如
x
2
+2x=1
(否,未知数最高次数是 2),
x
3
1=2
(否,分母含有未知数,不是整式方程)。
讲解方程的解的概念:使方程左右两边相等的未知数的值叫做方程的解。例如,
x=4
是方程
2x 3=5
的解。
等式的基本性质 步骤讲解
展示一个简单的应用题:某车间有 22 名工人,每人每天可以生产 1200 个螺钉或 2000 个螺母,1 个螺钉需要配 2 个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
讲解列方程解应用题的一般步骤:
审:认真审题,分析题目中的已知量和未知量,找出题目中的等量关系。在本题中,等量关系是生产的螺母数量是螺钉数量的 2 倍。
设:设未知数。设应安排
x
名工人生产螺钉,则
(22 x)
名工人生产螺母。
列:根据等量关系列出方程。生产螺钉的数量为
1200x
,生产螺母的数量为
2000(22 x)
,根据等量关系可列方程
2×1200x=2000(22 x)
。
解:解方程。
解:
2×1200x=2000(22 x)
去括号,得
2400x=44000 2000x
移项,得
2400x+2000x=44000
合并同类项,得
4400x=44000
系数化为 1,得
x=10
答:检验方程的解是否符合实际情况,并作答。
22 x=22 10=12
,答:应安排 10 名工人生产螺钉,12 名工人生产螺母。
练习巩固
给出一道类似的应用题:某商店以每件 60 元的价格卖出两件衣服,其中一件盈利 25%,另一件亏损 25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
让学生按照列方程解应用题的步骤进行分析和解答,教师巡视指导,最后请学生展示解答过程并进行讲解。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
探究新知
知识点 1
方程和一元一次方程的概念
1.在班级秋游活动中,全体学生和老师共购买了45张门票,学生票每张10 元,成人票每张 15元,师生总票款为475元。你知道学生和老师的人数分别是多少吗 购买学生票和成人票的票款分别是多少
(1)这个问题涉及哪些量 它们之间有怎样的等量关系
(2)如果设学生人数为x,那么师生总票款可以用含x的代数式表示为 .
(3)你能得到怎样的表示量相等的式子
10 x +15(45- x )=475.
探究新知
2.某长方形操场的面积是5850m,长比宽多 25 m。
(1)这个情境涉及哪些量 它们之间有怎样的等量关系
(2)如果设这个操场的宽为xm,那么操场的面积可以用含x的代数式表示为 .
(3)你能得到怎样的表示量相等的式子
x (x+25 )=5850
3.甲、乙两地相距 22 km,张叔叔从甲地出发到乙地,每时比原计划多行走1 km,因此提前12 min到达乙地.
(1)这个情境涉及哪些量 它们之间有怎样的等量关系
(2)如果设设张叔叔原计划每小时走xkm,那么他比原计划提前的时间可用含x的代数式表示为 .
(3)你能得到怎样的表示量相等的式子
探究新知
- = .
大家观察,这三个式子有什么特点?
- =
讨论并回答: 什么是方程?方程有什么特点?
含有未知数的表示量相等的等式称为方程.
方程的特点:
①方程中一定含有未知数;
②方程是等式.
结论
探究新知
10 x +15(45- x )=475、x (x+25 )=5850
判断下列式子是不是方程?
(1)x+2=3
(2)x+3y=6
(3)3x-6
(4)1+2=3
(5)x+3>5
(6)y-12=5
是
是
是
不是
不是
不是
变式训练
巩固练习
比较:列算式和列方程
从算式到方程是数学的进步!
列算式:列出的算式表示解题的计算过程, 只能用已知数.
对于较复杂的问题,列算式比较困难.
列方程:方程是根据题中的等量关系列出的等式. 既可用
已知数,又可用未知数,解决问题比较方便.
探究新知
一元一次方程满足的条件:
(一次)
(一元)
一元一次方程的概念
1.只含有一个未知数;
2.未知数的次数都是1;
3.等号两边都是整式.
探究新知
在一个方程中,只含有一个未知数,且方程中的代数式都是整式,未知数的次数都是 1,这样的方程叫作一元一次方程.
10 x +15(45- x )=475,2 x +3= 7 x +4都是一元一次方程.
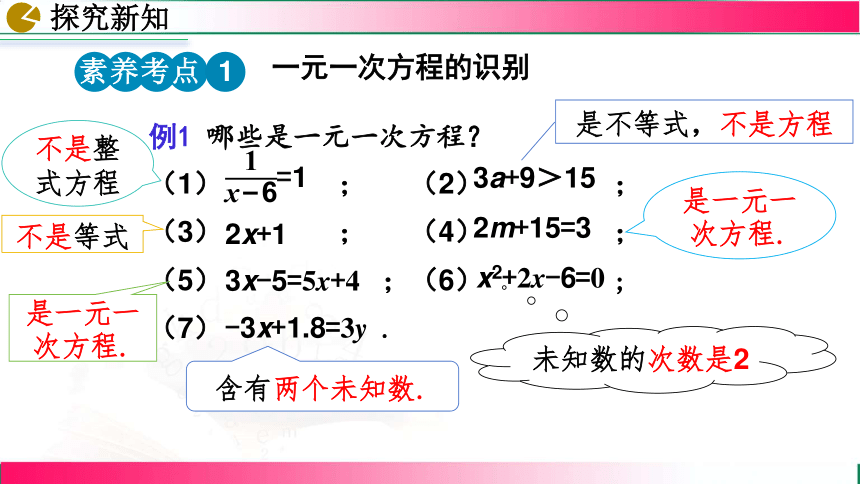
例1 哪些是一元一次方程?
(1) ; (2) ;
(3) ; (4) ;
(5) ;(6) ;
(7) .
一元一次方程的识别
不是整式方程
不是等式
素养考点 1
是不等式,不是方程
是一元一次方程.
是一元一次方程.
未知数的次数是2
含有两个未知数.
=1
3a+9>15
2x+1
2m+15=3
3x-5=5x+4
x2+2x-6=0
-3x+1.8=3y
探究新知
例2 (1)若关于x的方程2 x |n|-1 – 9 = 0是一元一次方程,则 n 的值为 .
(2)方程(m+1) x |m| + 1 = 0是关于x的一元一次方程,则m= .
2或-2
1
利用一元一次方程的定义求字母的值
素养考点 2
注:一元一次方程中求字母的值,需谨记两个条件:
①未知数的次数为1;②未知数的系数不为0.
探究新知
1.方程3x5-2k -8=0是关于x的一元一次方程,则k=_____.
2
2.方程x|m| +4=0是关于x的一元一次方程,则m=_____.
3.方程(m-1)x -2=0是关于x的一元一次方程,则m_____.
1或-1
≠1
变式训练
巩固练习
根据下列问题,设未知数并列出方程:
(1)小颖种了一株树苗,开始时树苗高为40厘米,栽种后每周树苗长高约5厘米,大约几周后树苗长高到1米?
树苗原来的高度40厘米+长的高度=1米
解:设大约x周后树苗长到1米,根据题意得:
40+5x=100.
知识点 2
根据实际问题建立方程模型
探究新知
(2)第六次全国人口普查统计数据(2010年11月1日新华社公布).
截止2010年11月1日0时,全国每10万人中具有大学文化程度的人数为8930人,比2000年7月1日0时增长了147.30%,2000年6月底每10万人中约有多少人具有大学文化程度?
解:设2000年6月底每10万人中约有x人具有大学文化程度,则:
x (1+147.30%)=8930.
2000年6月具有大学文化程度的人+增长的人数=8930
探究新知
分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法.
请同学们思考:
1. 怎样将一个实际问题转化为方程问题?
2.列方程的依据是什么?
设未知数列方程
一元一次方程
抓关键句子找等量关系
实际问题
探究新知
解:设这个学校的学生人数为x,那么女生人数为 0.52x,
男生人数为(1-0.52)x.
某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?
列方程:0.52x-(1-0.52)x=80.
等量关系:女生人数-男生人数=80,
变式训练
巩固练习
例 某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在“6·1”儿童节举行文具优惠售卖活动,铅笔按原价打8折出售,圆珠笔按原价打9折出售,结果两种笔共卖出60支,卖得金额87元.求卖出铅笔的支数.
解:设卖出铅笔x支,则卖出圆珠笔(60-x)支.
等量关系:x支铅笔的售价+(60-x)支圆珠笔的售价=87,
列方程: 1.2×0.8x+2×0.9(60-x)=87.
素养考点
根据实际问题列出方程
探究新知
方程的解
对于方程4x = 24,容易知道x = 6可以使等式成立, 对于方程 170+15x =245,你知道 x 等于什么时,等式成立吗?我们来试一试.
x 1 2 3 4 5 6 …
…
我们知道当x=5时,170+15x的值是245,所以方程170+15x = 245中的未知数的值应是5.
185
200
215
230
245
260
170+15x
思
考
知识点 3
探究新知
2x-3=5x-15
x=4是方程2x-3=5x-15的解.
左边=2×3-3 = 3,
右边=5×3-15 = 0.
x= 4, 5, 6时呢
x=3是不是方程的解呢?
把x=3代入方程,
因为左边≠右边,
所以x=3不是方程的解.
解:
探究新知
使方程左右两边的值相等的未知数的值叫方程的解.求方程解的过程叫做解方程.
x=420是 - = 1方程的解吗
方程的解
探究新知
例 x=1000和x=2000中哪一个是方程 0.52x-(1-0.52)x=80的解?
解:当x=1000时,
方程左边=0.52×1000-(1-0.52)×1000=520-480=40,右边=80,
当x=2000时,
方程左边= 0.52×2000-(1-0.52)×2000=1040-960=80,右边=80,
方程的解的识别
素养考点
左边≠右边,所以x=1000不是此方程的解.
左边=右边,所以x=2000是此方程的解.
探究新知
1. 将数值代入方程左边进行计算;
2. 将数值代入方程右边进行计算;
3. 若左边=右边,则是方程的解,反之,则不是.
判断一个数值是不是方程的解的步骤:
归纳小结
探究新知
1. [2024德州期末]在①2-5;②1+7 x =-8 y +3;③ x =
6;④3 x =2 x -9;⑤2 x >7中,方程共有( C )
A. 1个 B. 2个
C. 3个 D. 4个
2. [2024漳州期中]下列方程中,是一元一次方程的是( D )
A. -1=0 B. x2=1
C. 5 x +6 y =1 D. x +1=0
C
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
3. [2024西安交大附中期末]下列方程中,解为 x =1的是
( D )
A. x +1=0 B. 3 x =-3
C. 2( x -1)2=2 D. 2 x +2=4
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
4. [新考向·身边的数学]蛋白质和碳水化合物是我们日常饮食
中的两个重要组成部分,它们都是身体所需的营养素,能
够为我们提供能量,一瓶牛奶的营养成分中,碳水化合物
的含量是蛋白质的1.5倍,碳水化合物、蛋白质与脂肪的
含量共30 g.设蛋白质的含量为 x g,脂肪的含量为 y g,可
列出方程为 .
1.5 x + x + y =30
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
5. [2024株洲二中期中]当 a = 时,方程 a +1= x +2
a 的解是 x =3.
【点拨】
将 x =3代入 a +1= x +2 a ,得 a +1=3+2 a ,解得
a =-2.
-2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
6. [2024泉州期中]若关于 x 的方程( k -3) x| k|-2+1=0是一
元一次方程,则 k = .
【点拨】
因为( k -3) x| k|-2+1=0是关于 x 的一元一次方
程,所以| k |-2=1, k -3≠0.所以 k =-3.
-3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
7. [2024宿州期中]整式 m2 x - an 的值随 x 取值的变化而变
化,下表是当 x 取不同值时 m2 x - an 对应的值,则关于 x
的方程 m2 x - an =-4的解为 .
x … -1 0 2 3 …
m2 x - an … -6 -4 0 2 …
x =0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
8. [新考法·整体代入法·2024·深圳福田区期中]若 x =3是方程
a - bx =4的解,则-6 b +2 a +2 025值为 .
【点拨】
因为 x =3是方程 a - bx =4的解,
所以 a -3 b =4.
所以-6 b +2 a +2 025=2( a -3 b )+2 025=
2×4+2 025=2 033.
2 033
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
9. 检验下列方程后面括号内所列各数是否为相应方程的解:
(1) = x -1;
【解】把 x =- 代入方程,得
左边= =- ,
右边=- -1=- .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
因为左边≠右边,所以 x =- 不是该方程的解.
把 x =3代入方程,得左边= =2,
右边=3-1=2.
因为左边=右边,所以 x =3是该方程的解.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)2( y -2)-9(1- y )=3(4 y -1).(-10,10)
【解】把 y =-10代入方程,得
左边=2(-10-2)-9(1+10)=-123,
右边=3×[4×(-10)-1]=-123.
因为左边=右边,所以 y =-10是该方程的解.
把 y =10代入方程,得左边=2(10-2)-9(1-10)=
97,右边=3×(4×10-1)=117.
因为左边≠右边,所以 y =10不是该方程的解.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
方程
方程
建立方程模型
含有未知数的等式叫做方程
一元一次方程
在一个方程中,只含有一个未知数,且方程中的代数式都是整式,未知数的次数都是1,这样的方程叫做一元一次方程.
方程的解
使方程左右两边的值相等的未知数的值叫方程的解
实际问题
一元一次方程
设未知数
找等量关系
列方程
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
谢谢观看!
5.1 认识方程
第五章 一元一次方程
北师大2024版数学七年级上册【示范课】
授课教师:********
班 级:********
时 间:********
学习目标
1. 理解方程及一元一次方程的概念,会检验一个数是不是方程的解.
2. 能根据实际问题列一元一次方程.
3. 通过列方程的过程,发展模型观念.
一元一次方程的概念
给出一元一次方程的定义:只含有一个未知数(元),未知数的次数都是 1,等号两边都是整式,这样的方程叫做一元一次方程。
举例说明:
2x 3=5
,
2
1
x+1=0
等都是一元一次方程,同时让学生判断一些式子是否为一元一次方程,如
x
2
+2x=1
(否,未知数最高次数是 2),
x
3
1=2
(否,分母含有未知数,不是整式方程)。
讲解方程的解的概念:使方程左右两边相等的未知数的值叫做方程的解。例如,
x=4
是方程
2x 3=5
的解。
等式的基本性质 步骤讲解
展示一个简单的应用题:某车间有 22 名工人,每人每天可以生产 1200 个螺钉或 2000 个螺母,1 个螺钉需要配 2 个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
讲解列方程解应用题的一般步骤:
审:认真审题,分析题目中的已知量和未知量,找出题目中的等量关系。在本题中,等量关系是生产的螺母数量是螺钉数量的 2 倍。
设:设未知数。设应安排
x
名工人生产螺钉,则
(22 x)
名工人生产螺母。
列:根据等量关系列出方程。生产螺钉的数量为
1200x
,生产螺母的数量为
2000(22 x)
,根据等量关系可列方程
2×1200x=2000(22 x)
。
解:解方程。
解:
2×1200x=2000(22 x)
去括号,得
2400x=44000 2000x
移项,得
2400x+2000x=44000
合并同类项,得
4400x=44000
系数化为 1,得
x=10
答:检验方程的解是否符合实际情况,并作答。
22 x=22 10=12
,答:应安排 10 名工人生产螺钉,12 名工人生产螺母。
练习巩固
给出一道类似的应用题:某商店以每件 60 元的价格卖出两件衣服,其中一件盈利 25%,另一件亏损 25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
让学生按照列方程解应用题的步骤进行分析和解答,教师巡视指导,最后请学生展示解答过程并进行讲解。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
探究新知
知识点 1
方程和一元一次方程的概念
1.在班级秋游活动中,全体学生和老师共购买了45张门票,学生票每张10 元,成人票每张 15元,师生总票款为475元。你知道学生和老师的人数分别是多少吗 购买学生票和成人票的票款分别是多少
(1)这个问题涉及哪些量 它们之间有怎样的等量关系
(2)如果设学生人数为x,那么师生总票款可以用含x的代数式表示为 .
(3)你能得到怎样的表示量相等的式子
10 x +15(45- x )=475.
探究新知
2.某长方形操场的面积是5850m,长比宽多 25 m。
(1)这个情境涉及哪些量 它们之间有怎样的等量关系
(2)如果设这个操场的宽为xm,那么操场的面积可以用含x的代数式表示为 .
(3)你能得到怎样的表示量相等的式子
x (x+25 )=5850
3.甲、乙两地相距 22 km,张叔叔从甲地出发到乙地,每时比原计划多行走1 km,因此提前12 min到达乙地.
(1)这个情境涉及哪些量 它们之间有怎样的等量关系
(2)如果设设张叔叔原计划每小时走xkm,那么他比原计划提前的时间可用含x的代数式表示为 .
(3)你能得到怎样的表示量相等的式子
探究新知
- = .
大家观察,这三个式子有什么特点?
- =
讨论并回答: 什么是方程?方程有什么特点?
含有未知数的表示量相等的等式称为方程.
方程的特点:
①方程中一定含有未知数;
②方程是等式.
结论
探究新知
10 x +15(45- x )=475、x (x+25 )=5850
判断下列式子是不是方程?
(1)x+2=3
(2)x+3y=6
(3)3x-6
(4)1+2=3
(5)x+3>5
(6)y-12=5
是
是
是
不是
不是
不是
变式训练
巩固练习
比较:列算式和列方程
从算式到方程是数学的进步!
列算式:列出的算式表示解题的计算过程, 只能用已知数.
对于较复杂的问题,列算式比较困难.
列方程:方程是根据题中的等量关系列出的等式. 既可用
已知数,又可用未知数,解决问题比较方便.
探究新知
一元一次方程满足的条件:
(一次)
(一元)
一元一次方程的概念
1.只含有一个未知数;
2.未知数的次数都是1;
3.等号两边都是整式.
探究新知
在一个方程中,只含有一个未知数,且方程中的代数式都是整式,未知数的次数都是 1,这样的方程叫作一元一次方程.
10 x +15(45- x )=475,2 x +3= 7 x +4都是一元一次方程.
例1 哪些是一元一次方程?
(1) ; (2) ;
(3) ; (4) ;
(5) ;(6) ;
(7) .
一元一次方程的识别
不是整式方程
不是等式
素养考点 1
是不等式,不是方程
是一元一次方程.
是一元一次方程.
未知数的次数是2
含有两个未知数.
=1
3a+9>15
2x+1
2m+15=3
3x-5=5x+4
x2+2x-6=0
-3x+1.8=3y
探究新知
例2 (1)若关于x的方程2 x |n|-1 – 9 = 0是一元一次方程,则 n 的值为 .
(2)方程(m+1) x |m| + 1 = 0是关于x的一元一次方程,则m= .
2或-2
1
利用一元一次方程的定义求字母的值
素养考点 2
注:一元一次方程中求字母的值,需谨记两个条件:
①未知数的次数为1;②未知数的系数不为0.
探究新知
1.方程3x5-2k -8=0是关于x的一元一次方程,则k=_____.
2
2.方程x|m| +4=0是关于x的一元一次方程,则m=_____.
3.方程(m-1)x -2=0是关于x的一元一次方程,则m_____.
1或-1
≠1
变式训练
巩固练习
根据下列问题,设未知数并列出方程:
(1)小颖种了一株树苗,开始时树苗高为40厘米,栽种后每周树苗长高约5厘米,大约几周后树苗长高到1米?
树苗原来的高度40厘米+长的高度=1米
解:设大约x周后树苗长到1米,根据题意得:
40+5x=100.
知识点 2
根据实际问题建立方程模型
探究新知
(2)第六次全国人口普查统计数据(2010年11月1日新华社公布).
截止2010年11月1日0时,全国每10万人中具有大学文化程度的人数为8930人,比2000年7月1日0时增长了147.30%,2000年6月底每10万人中约有多少人具有大学文化程度?
解:设2000年6月底每10万人中约有x人具有大学文化程度,则:
x (1+147.30%)=8930.
2000年6月具有大学文化程度的人+增长的人数=8930
探究新知
分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法.
请同学们思考:
1. 怎样将一个实际问题转化为方程问题?
2.列方程的依据是什么?
设未知数列方程
一元一次方程
抓关键句子找等量关系
实际问题
探究新知
解:设这个学校的学生人数为x,那么女生人数为 0.52x,
男生人数为(1-0.52)x.
某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?
列方程:0.52x-(1-0.52)x=80.
等量关系:女生人数-男生人数=80,
变式训练
巩固练习
例 某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在“6·1”儿童节举行文具优惠售卖活动,铅笔按原价打8折出售,圆珠笔按原价打9折出售,结果两种笔共卖出60支,卖得金额87元.求卖出铅笔的支数.
解:设卖出铅笔x支,则卖出圆珠笔(60-x)支.
等量关系:x支铅笔的售价+(60-x)支圆珠笔的售价=87,
列方程: 1.2×0.8x+2×0.9(60-x)=87.
素养考点
根据实际问题列出方程
探究新知
方程的解
对于方程4x = 24,容易知道x = 6可以使等式成立, 对于方程 170+15x =245,你知道 x 等于什么时,等式成立吗?我们来试一试.
x 1 2 3 4 5 6 …
…
我们知道当x=5时,170+15x的值是245,所以方程170+15x = 245中的未知数的值应是5.
185
200
215
230
245
260
170+15x
思
考
知识点 3
探究新知
2x-3=5x-15
x=4是方程2x-3=5x-15的解.
左边=2×3-3 = 3,
右边=5×3-15 = 0.
x= 4, 5, 6时呢
x=3是不是方程的解呢?
把x=3代入方程,
因为左边≠右边,
所以x=3不是方程的解.
解:
探究新知
使方程左右两边的值相等的未知数的值叫方程的解.求方程解的过程叫做解方程.
x=420是 - = 1方程的解吗
方程的解
探究新知
例 x=1000和x=2000中哪一个是方程 0.52x-(1-0.52)x=80的解?
解:当x=1000时,
方程左边=0.52×1000-(1-0.52)×1000=520-480=40,右边=80,
当x=2000时,
方程左边= 0.52×2000-(1-0.52)×2000=1040-960=80,右边=80,
方程的解的识别
素养考点
左边≠右边,所以x=1000不是此方程的解.
左边=右边,所以x=2000是此方程的解.
探究新知
1. 将数值代入方程左边进行计算;
2. 将数值代入方程右边进行计算;
3. 若左边=右边,则是方程的解,反之,则不是.
判断一个数值是不是方程的解的步骤:
归纳小结
探究新知
1. [2024德州期末]在①2-5;②1+7 x =-8 y +3;③ x =
6;④3 x =2 x -9;⑤2 x >7中,方程共有( C )
A. 1个 B. 2个
C. 3个 D. 4个
2. [2024漳州期中]下列方程中,是一元一次方程的是( D )
A. -1=0 B. x2=1
C. 5 x +6 y =1 D. x +1=0
C
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
3. [2024西安交大附中期末]下列方程中,解为 x =1的是
( D )
A. x +1=0 B. 3 x =-3
C. 2( x -1)2=2 D. 2 x +2=4
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
4. [新考向·身边的数学]蛋白质和碳水化合物是我们日常饮食
中的两个重要组成部分,它们都是身体所需的营养素,能
够为我们提供能量,一瓶牛奶的营养成分中,碳水化合物
的含量是蛋白质的1.5倍,碳水化合物、蛋白质与脂肪的
含量共30 g.设蛋白质的含量为 x g,脂肪的含量为 y g,可
列出方程为 .
1.5 x + x + y =30
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
5. [2024株洲二中期中]当 a = 时,方程 a +1= x +2
a 的解是 x =3.
【点拨】
将 x =3代入 a +1= x +2 a ,得 a +1=3+2 a ,解得
a =-2.
-2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
6. [2024泉州期中]若关于 x 的方程( k -3) x| k|-2+1=0是一
元一次方程,则 k = .
【点拨】
因为( k -3) x| k|-2+1=0是关于 x 的一元一次方
程,所以| k |-2=1, k -3≠0.所以 k =-3.
-3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
7. [2024宿州期中]整式 m2 x - an 的值随 x 取值的变化而变
化,下表是当 x 取不同值时 m2 x - an 对应的值,则关于 x
的方程 m2 x - an =-4的解为 .
x … -1 0 2 3 …
m2 x - an … -6 -4 0 2 …
x =0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
8. [新考法·整体代入法·2024·深圳福田区期中]若 x =3是方程
a - bx =4的解,则-6 b +2 a +2 025值为 .
【点拨】
因为 x =3是方程 a - bx =4的解,
所以 a -3 b =4.
所以-6 b +2 a +2 025=2( a -3 b )+2 025=
2×4+2 025=2 033.
2 033
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
9. 检验下列方程后面括号内所列各数是否为相应方程的解:
(1) = x -1;
【解】把 x =- 代入方程,得
左边= =- ,
右边=- -1=- .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
因为左边≠右边,所以 x =- 不是该方程的解.
把 x =3代入方程,得左边= =2,
右边=3-1=2.
因为左边=右边,所以 x =3是该方程的解.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)2( y -2)-9(1- y )=3(4 y -1).(-10,10)
【解】把 y =-10代入方程,得
左边=2(-10-2)-9(1+10)=-123,
右边=3×[4×(-10)-1]=-123.
因为左边=右边,所以 y =-10是该方程的解.
把 y =10代入方程,得左边=2(10-2)-9(1-10)=
97,右边=3×(4×10-1)=117.
因为左边≠右边,所以 y =10不是该方程的解.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
方程
方程
建立方程模型
含有未知数的等式叫做方程
一元一次方程
在一个方程中,只含有一个未知数,且方程中的代数式都是整式,未知数的次数都是1,这样的方程叫做一元一次方程.
方程的解
使方程左右两边的值相等的未知数的值叫方程的解
实际问题
一元一次方程
设未知数
找等量关系
列方程
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
谢谢观看!
同课章节目录
