2024-2025学年六年级下册数学小升初重点校分班考前提升卷北师大版(含解析)
文档属性
| 名称 | 2024-2025学年六年级下册数学小升初重点校分班考前提升卷北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 696.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 08:46:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年六年级下册数学小升初重点校分班考前提升卷
一、填空题
1.一个长方体纸箱,相交于一个顶点的三条棱的长度分别是8dm、6dm、3dm,这个纸箱的体积是 。把这个纸箱放在地上,当它的占地面积最小时,纸箱的高是 dm。
2. 如图,如果把三角形ABC先向右平移3格,再向上平移4格后得到三角形A'B'C',那么点A'的位置用数对表示是( , ),点C·的位置用数对表示是( , )。
3.诗人李白写过一首诗:“危楼高百尺,手可摘星辰。不敢高声语,恐惊天上人。”若古代的一尺等于现在 am,则诗中百尺等于现在的 m;若古代的百尺约等于现在的34m,则a= m。
4.节约粮食是中华民族的传统美德,1000粒大米约重25克,1亿粒大米约重 克。
5.在括号里填上“>”“<”或“=”。
15
0.4
6.在比例25∶10=15∶6中,如果将第一个比的后项增加20,第二个比的后项应该增加 才能使该比例成立。
7.小华在30m长的跑道上走路测试了三次,第一次走了74步,第二次走了78步,第三次走了73步。照这样计算,小华沿400 m跑道走一圈大约要走 步。
8.在( )里填上最简分数。
45dm2= m2 1250dm3= m3
55秒= 分 350cm3= L
9.一个数,百万位上是7,万位上是3,百位上是5,其余各位都是0,这个数是 。
10.学校举行象棋比赛,共有10人参加,如果每两人进行1场比赛,一共要进行 场比赛。
11.七巧板中,①号和②号图形共占整个正方形的,⑦号图形共占整个正方形的,④号图形占整个正方形的。
12.一个玩具飞机292元,一个玩具火车107元,一个玩具飞机比一个玩具火车大约贵 元,买一个玩具飞机和一个玩具火车大约需要准备 元。
13.平行四边形和三角形的面积相等,底也相等,平行四边形的高是8厘米,那么三角形的高是 厘米;如果三角形的高是8厘米,那么平行四边形的高是 厘米。
14.如图所示,圆国内分别标有1,2,…,12,这 12个数字,电子跳蚤每跳一步,可以从一个圆圈逆时针跳到相邻的圆圈,若电子跳蚤所在圆圈的数字为n,则电子跳蚤连续跳(3n-2)步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳3×1-2=1步到标有数字2的圆圈内,完成一次跳跃,第二次则要连续跳 3×2-2=4步到达标有数字6的四圈,….依此规律,若电子跳蚤从①开始,那么第 2021次跳跃电子跳蚤能跳到的四圈内所标的数字为: 。
二、判断题
15.今年的钢材第一次提价15%,第二次又提价10%,现价比原价提高了25%。( )
16.16×32=512,那么(16÷4)×(32×4)=512。(
)
17.正方体的棱长扩大到原来的2倍,表面积就扩大到原来的4倍。( )
18.把20克糖溶解在100克水中。糖占糖水的20%. ( )
19.从写有1-6的6张卡片中任意抽—张,抽到2和3的可能性一样大.( )
20.两条直线相交,要么平行,要么垂直。( )
21. 一根绳子剪去,还剩下 m。 ( )
22. 一种商品价格降低了5%后又提价5%,价格和原来相比没有变化。( )
23.把一个圆柱削成一个最大的圆锥,圆锥的体积是削去的一半.( )
三、单选题
24.一本书 125 页, 看了 , 还剩 ( ) 页没看。
A. B.
C. D.
25.今年王叔叔家小表产量比去年增产三成,下面说法正确的是( )。
A.今年小麦产量是去年的130% B.今年小麦产量是去年的70%
C.去年小麦产量是今年的130% D.去年小麦产量是今年的70%
26.下面直线上的M点表示的数可能是算式( )的结果。
A.15×0.9□ B.3.□×4.□ C.15÷1.□ D.4.□×4.□
27.半导体是现代信息技术革命的关键材料。某半导体厂生产了一个底面周长为 50.24 cm,高为12 cm的圆柱体陶瓷基材,其中间位置向下挖去了一个棱长为3c m的正方体小洞,在这个小洞的下面中间位置继续向下挖去一个棱长为2cm 的正方体小洞,工厂采用真空溅射的方法对陶瓷基材剩余部分的表面镀膜,需要镀膜的面积为( )cm2。
A.401.92 B.1004.8 C.1056.8 D.1040.8
28.漳州市的方圆里国木复兴馆内陈列的《漳州战役》木雕长12.3米,最大直径是0.75米,横线部分的“3”表示( )。
A.0.3厘米 B.30分米 C.30厘米 D.0.3分米
29.如图,以点A为一个端点的线段中,最短的是( )。
A.AB B.AC C.AD D.AE
30.下面选项中与“35×79”的积相等的式子是( )。
A.35×7×9 B.35×80-1 C.35×80-35 D.79×30+5
31.某市出租车收费标准:2km以内5元;超过2km的部分,每千米1.5元(不足1km按1km计算)。王老师坐出租车去离学校12.8km远的教育局开会,应付车费( )元。
A.19.2 B.21.2 C.21.5
32.在一个三角形里,如果一个最小的角是46°,那么这个三角形一定是( )。
A.锐角三角形 B.钝角三角形 C.直角三角形
33.如下图所示,将一个正方形的变长增加1.5cm,得到一个新的正方形。用含有字母的式子表示增加的面积,其中错误的是( ) 。
A.1.5a×2+1.5 B.(a+a十1.5)×1.5 C.1.5×(a+1.5)×2 D.(a+1.5)2-a2
四、计算题
34.直接写出得数。
35.下面各题怎样简便怎样算。
①1.25×0.96×80 ②55× +3÷7
③ ×[ ÷( - )] ④ + + + (提示: - = )
解方程:
① ②
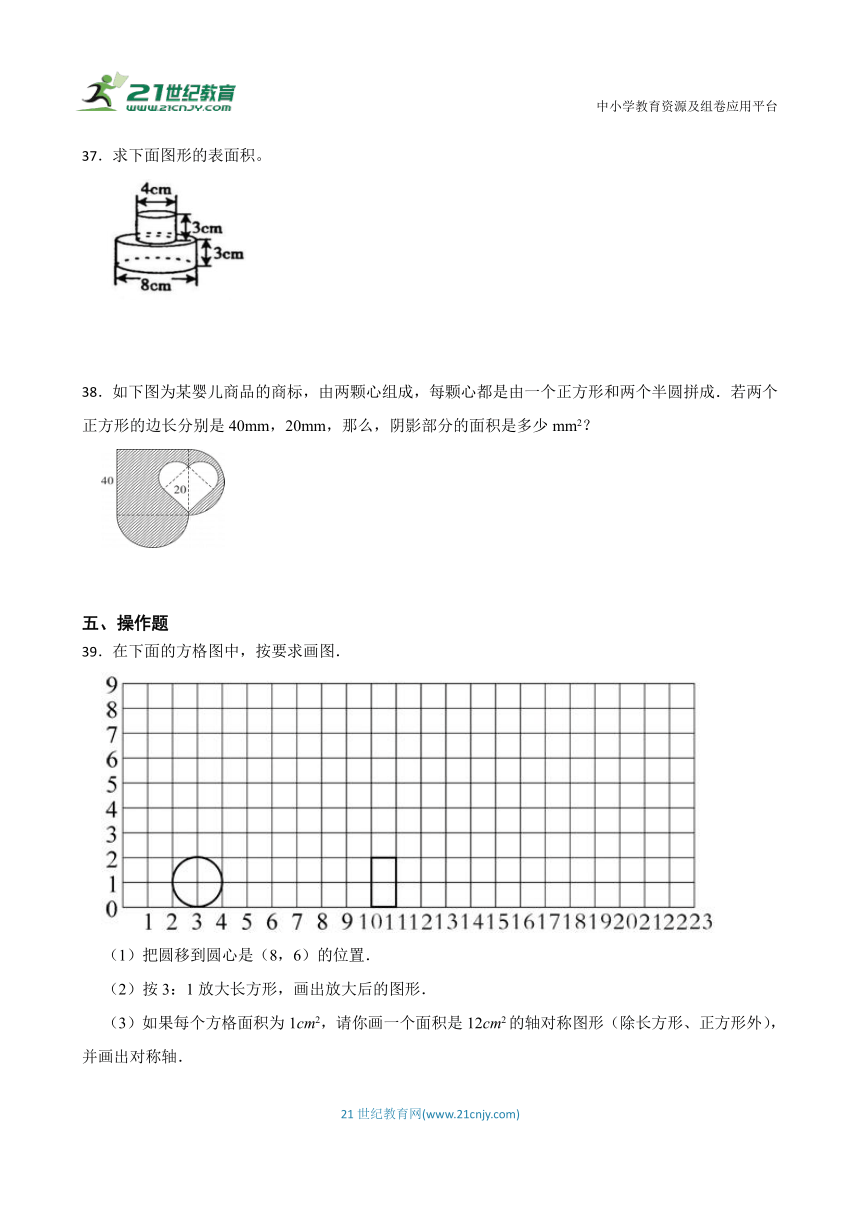
37.求下面图形的表面积。
38.如下图为某婴儿商品的商标,由两颗心组成,每颗心都是由一个正方形和两个半圆拼成.若两个正方形的边长分别是40mm,20mm,那么,阴影部分的面积是多少mm2?
五、操作题
39.在下面的方格图中,按要求画图.
(1)把圆移到圆心是(8,6)的位置.
(2)按3:1放大长方形,画出放大后的图形.
(3)如果每个方格面积为1cm2,请你画一个面积是12cm2的轴对称图形(除长方形、正方形外),并画出对称轴.
六、解决问题
40.如图1,某种油菜籽榨油机的漏斗是由圆柱和圆锥两部分组成的,它的底面半径是4分米,且这两部分的高都是6分米。已知每立方分米油菜籽重0.7千克。
(1)这个漏斗最多能装多少千克油菜籽? (结果保留1位小数)
(2)如果张师傅打算用铁皮给这个漏斗做一个圆柱形的防尘罩(如图2,没有下底面),至少需要多少平方分米铁皮?
41.旧衣服经过处理可以得到无纺布,实现资源循环利用。每吨旧衣服可以回收生产0.99吨无纺布,某公司处理了21.46吨旧衣服。
(1)相当于生产了多少吨无纺布 (得数保留两位小数)
(2)生产的这些无纺布相当于节约了17吨棉花,要节约26吨棉花需要处理多少吨无纺布
42.“垃圾分类,从我做起”。西河学校一天的可回收垃圾是52.06千克,可回收垃圾比其他垃圾多35.76千克,有害垃圾比其他垃圾少9.24千克,请问有害垃圾有多少千克?
43.李大爷擅长“变废为宝”,常常利用家里的剩余竹木做栅栏。最近,李大爷做的栅栏刚好能将一块长8米、宽4米的长方形菜地围一圈。如果用这次的栅栏围一个一面靠墙的正方形鸡舍,这个鸡舍的面积最大是多少平方米?
44.为保护树干,工作人员在树干上缠绕麻绳,工作人员裁剪了一根长12.56米的麻绳,还差1.57米才能在树干上绕满10圈,请算一算树干的直径约是多少厘米?
45.一条铁路去年的货运量比前年降低了三成,今年的货运量预计比去年增长四成,但仍比前年少80t,这条铁路前年的货运量是多少吨?(先画线段图,再解答)
46.孔明灯俗称许愿灯,是一种古老的汉族手工艺品,根据热气球原理使空气受热膨胀而升空。手工艺人张师傅将总长420cm的竹制作成一个长方体孔明灯的框架,再将它的上面和四周用安全阻燃棉纸糊成灯罩,这个孔明灯长、宽、高的比是2:2:3。这个孔明灯的体积是多少立方厘米?(接头处忽略不计)
47.《九章算术》是中国古代数学专著,它的出现标志着中国古代数学体系的形成。《九章算术》卷一中有记载如下。
(1)今有八分之五,二十五分之十六。问孰多 又有九分之八,七分之六。问孰多 意思是有两个数和,哪个数大 又有两个数和,哪个数大
(2)今有三分之一,三分之二,四分之三。问几何而平 意思是有它们的平均数是多少
48.在一个圆柱形储水桶里,把一段底面半径为3厘米的圆柱形钢材全部放入水中,这时水面上升8厘米。把这段钢材竖着拉出水面6厘米,水面下降4厘米,这段钢材的体积是多少立方厘米?
49.小明在学习了正方体的展开图后,明白了很多几何体都能展开成平面图形。于是他在家用剪刀剪开了一个长方体纸盒,如图3,可是一不小心多剪开了一条棱,把纸盒剪成了两部分,如图1、图2所示,请根据你所学的知识,回答以下问题:
(1)观察判断:
小明共剪开了 条棱。
(2)动手操作:
现在小明想将剪断的图2重新粘贴到图1上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒(如图3),请你帮助小明在图1中补全图形:
(3)解决问题:
请你设计一个长方体的包装纸箱,使每箱能装10个这种纸盒,每层放1个共放10层,要求没有空隙且要使该纸箱所用材料尽可能少(纸箱的表面积尽可能小)。请你通过计算说明最节省材料的包装纸箱的规格(单位:cm)
参考答案及试题解析
1.144;8
2.5;5;4;6
【解析】解:如图:点A'的位置用数对表示是(5,5),点C'的位置用数对表示是(4,6)。
故答案为:5;5;4;6。
【分析】数对中第一个数表示列,第二个数表示行。根据平移的方向和格数确定平移后的图形,然后确定每个点的位置。
3.100a;0.34
【解析】解:百尺=100×a=100a(m)
100a=34
a=0.34
故答案为:100a,0.34。
【分析】 古代的一尺等于现在a米,因此古代百尺等于现在100a米;古代的百尺约等于现在的34米,即100a=34,根据等式的基本性质2,将等式的两边同时除以100,得到a的值。
4.2500000
5.<;>;<;=
6.12
7.1000
【解析】解:(74+78+73)÷3
=225÷3
=75(步)
75÷30×400
=2.5×400
=1000(步)
故答案为:1000。
【分析】用三次走的步数和除以3求出平均步数,然后用平均步数除以30求出每米的步数,用每米的步数乘400即可求出400m大约要走的步数。
8.;;;
9.7030500
10.45
【解析】解:10×9÷2
=90÷2
=45(场)
故答案为:45。
【分析】如果每两个同学之间都进行一场比赛,每个同学都要和其他的9人进行一场比赛,每个同学打9场,共有10×9场比赛;由于每两个人之间重复计算了一次,再除以2即可。
11.;;
12.180;400
【解析】解:第一问:292-107≈180(元);
第二问:292+107≈400(元)。
故答案为:180;400。
【分析】从“大约”可以看出是要求估算,用减法计算一个玩具飞机比一个玩具火车大约贵的钱数;用加法估算出买一个玩具飞机和一个玩具火车大约需要准备的钱数。估算时把两个数都看作近似整百或整百整十数。
13.16;4
【解析】解:8×2=16(厘米)
8÷2=4(厘米)
故答案为:16;4。
【分析】平行四边形和三角形的面积相等,底也相等,三角形的高是平行四边形高的2倍;平行四边形的高是三角形高的一半。
14.10
【解析】仔细观察发现:
第一次跳 3x1-2=1 步到数字 2的圆圈:
第二次跳 3x2-2-4步到达标有数字6的圆圈;
第三次跳3x6-2-16步到达标有数字10的圆圈:
第四次跳3x10-2=28步到达标有数字 2的圆圈:
……
发现每三次一循环,
∵2016÷3-672
∴第 2016 次跳到的圆圈内所标的数字为10
故答案为:10.
【分析】第一次跳到数字2,第二次跳到数字6,第三次跳到数字 10,第四次跳到数字2,然后每三个一循环,用2016除以3,整除为10,余1为2,余2为6即可确定
15.错误
【解析】解:(1+10%)×(1+10%)-1
=1.1×1.1-1
=1.21-1
=21%。
故答案为:错误。
【分析】把原价看作单位“1”,第一次提价后的价格是原价的(1+10%),后来又提价10%,是在(1+10%)的基础上提价的,提价后的价格是(1+10%)的(1+10%),然后再减去1。
16.正确
【解析】解:16×32=512,那么(16÷4)×(32×4)=512,计算正确。
故答案为:正确。
【分析】积的变化规律:一个因数扩大不为0的倍数,另一个因数缩小相同的倍数,则积不变,本题据此进行判断。
17.正确
【解析】解:正方体的棱长扩大到原来的2倍,表面积就扩大到原来的4倍。原题说法正确。
故答案为:正确。
【分析】正方体表面积=棱长×棱长×6,正方体棱长扩大到原来的n(0除外)倍,那么表面积就扩大到原来的n2倍。
18.错误
【解析】解:把20克糖溶解在100克水中。糖占糖水的20÷(20+100)×100%≈16.67%。
故答案为:错误。
【分析】糖占糖水的百分之几=糖的质量÷(糖的质量+水的质量)×100%。
19.正确
【解析】解:从写有1-6的6张卡片中任意抽—张,抽到2和3的可能性一样大。
故答案为:正确。
【分析】因为卡片中2和3的张数一样多,所以抽到2和3的可能性一样大。
20.错误
【解析】解:两条直线相交,要么平行,要么相交。
故答案为:错误。
【分析】两条直线相交,要么平行,要么相交;垂直是相交的一种。
21.错误
【解析】解:一根绳子剪去,还剩下1-=。原题说法错误。
故答案为:错误。
【分析】把这根绳子看作单位“1”,用1减去剪去的分率即可求出剩下的分率。不知道绳子的长度,无法计算剩下的实际长度。
22.错误
【解析】解:1×(1-5%)×(1+5%)
=95%×105%
=99.75%
99.75%<1。
故答案为:错误。
【分析】假设这件商品的原价是1,现价=原价×(1-降价的百分率)×(1+提价的百分率),然后再比较大小。
23.正确
【解析】解:根据题干分析可得:圆柱与圆锥的体积之比是3:1,则削去部分的体积与圆锥的体积就是2:1,所以圆锥的体积是削去的一半,所以原题说法正确。
故答案为:正确。
【分析】 把一个圆柱削成一个最大的圆,圆柱的体积是圆锥体积的3倍,圆锥的体积是1份,圆柱的体积就是3份,消去的部分是2份,那么圆锥的体积是消去部分的一半。
24.C
【解析】解:看了60%,剩下这本书的1-60%,剩下的页数:。
故答案为:C。
【分析】把这本书的页数看作单位“1”,已看了60%,那么剩下(1-60%),再根据求一个数的百分之几是多少用乘法计算,据此列式。
25.A
【解析】解:1+30%=130%;
故答案为:A。
【分析】把去年小麦的产量看成单位“1”,今年的小麦产量比去年增产三成,那么今年的产量就是去年的(1+30%),由此解答即可。
26.B
27.C
【解析】解:50.243.142=8(cm)
3.14822+50.2412+334+224
=3.14128+602.88+36+16
=401.92+654.88
=1056.8(cm2)
故答案为:C。
【分析】观察图形,镀膜的面积即基材的表面积,而基材的表面积就是圆柱的表面积加上大正方体四个面的面积,再加上小正方体四个面的面积;已知圆柱的底面周长,根据圆柱的底面周长公式:C=2πr,得到半径r=50.243.142=8(cm),然后根据圆柱的表面积公式:S=2πr2+Cd,正方形四个面的面积=边长边长4,分别计算出大正方体四个面的面积和小正方体四个面的面积,相加即可得到基材的表面积,即镀膜的面积。
28.C
29.C
30.C
31.C
【解析】12.8km看做13km;
5+(13-2)×1.5=5+16.5=21.5(元)。
故答案为:C。
【分析】前2千米的车费+2千米以后的路程×单价=一共应付的车费。
32.A
【解析】解:假如另外一个角也是46°,那么最大的角是:180°-46°-46°=88°,这个三角形一定是锐角三角形。
故答案为:A。
【分析】因为46°的角是最小的角,那么另外一个角最小是46°,那么假设另外一个角也是46°,这样计算出第三个角就能确定三角形的类型。
33.C
【解析】解:A项:利用增加的面积=2×长方形面积+小正方形的面积,即增加的面积为:
1.5a×2+1.52,计算正确;
B项:( a + a +1.5)×1.5=1.5a×2+1.52,即利用增加的面积=2×长方形面积+小正方形的面积, 计算正确;
C项:1.5×( a +1.5)×2,多加了一个小正方形的面积, 计算错误;
D项:增加的面积=新的正方形的面积-原正方形的面积,即增加的面积为:
( a +1.5)2-a2, 计算正确。
故答案为: C 。
【分析】将一个正方形的边长增加1.5厘米后,增加部分的面积等于两个长等于原来正方形的边长,宽等于1.5厘米的长方形和一个边长为1.5厘米的正方形的面积;也可以用新的正方形的面积减去原正方形的面积求解即可。
34.解:
2.92 19.8
0.5
【解析】 计算小数减法时把小数点对齐再相减;计算分数加、减法时先通分,再计算;计算小数乘法时,先按照整数乘法去乘,因数中有几位小数就在积的末尾点上小数点;计算分数除法时,除以一个数等于乘这个数的倒数;计算小数除法时,先把除数和被除数同时扩大相同的倍数,然后按照除数是整数的除法去除,商的小数点和被除数的小数点对齐;分数四则混合运算的运算顺序与整数四则混合运算的运算顺序相同,都是先乘除后加减;分数除以小数,可以把分数化成小数,也可以把小数化成分数再计算。
35.解:①1.25×0.96×80
=1.25×80×0.96
=100×0.96
=96
②55× +3÷7
=55× +
= ×(55+1)
= ×56
=24
③ ×[ ÷( - )]
= ×[ ÷ ]
= ×
=1
④ + + +
= ﹣ + ﹣ + ﹣ + ﹣
= ﹣
=
【解析】①先运用乘法交换律交换后两个数的位置,再按照从左到右的顺序进行计算;
②一个相同的数分别同两个不同的数相乘,积相加,等于这个相同的数乘另外两个不同数的和,据此简算;
③运算顺序:先算乘除,再算加减,如果有括号,就先算括号里面的。如果有小括号和中括号,由内到外,先算小括号里面的,再算中括号里面的;
④分数的分子是1,分母是两个相邻自然数相乘的形式,这个分数就等于较小的自然数分之一减去较大的自然数分之一。据此先把算式写成相减的形式,再观察算式,发现中间的数相加等于0,算式就剩下两头的两个数相减,据此解答。
36.解:① ,
,
x=0.7;
② ,
,
,
x=4.5.
【解析】(1)依据等式的性质,方程两边同时除以求解,(2)依据等式的性质,方程两边同时乘,再同时除以求解.
37.解:3.14×(8÷2)2×2+3.14×8×3+3.14×4×3
=3.14×32+3.14×24+3.14×12
=3.14×68
=213.52(cm2);
答:图形的表面积是213.52cm2。
【解析】该图形的表面积就是大圆柱的表面积+小圆柱的侧面积,圆的面积=πr2,圆柱侧面积=2πrh,据此求解。
38.(402 + π ×202) - (202 +π×102)
=1600+400π-400-100π
= 1200+300π
=1200+300 × 3.14
=1200+942
=2142(平方毫米)。
答:阴影部分的面积是2142平方毫米。
【解析】如下图所示:两个大半圆可以组成一个整圆,两个小半圆也可以组成一个整圆,据此用大正方形的面积加上大圆的面积,然后减去小正方形的面积加上小圆的面积,就可以求出阴影部分的面积。
39.(1)解:
(2)解:
(3)解:
【解析】(1)用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数;
(2)放大后长方形的长、宽分别=原来长方形的长、宽分别×3,然后画出图形;
(3)等腰三角形是轴对称图形,三角形的面积=底×高÷2,据此画图。
40.(1)解:3.14×42×6+3.14×42×6×
=3.14×96+3.14×32
=3.14×128
=301.44(立方分米)
301.44×0.7=211.0(千克)
答:这个漏斗最多能装211.0千克油菜籽。
(2)解:3.14×(10÷2)2+3.14×10×2
=3.14×25+3.14×20
=78.5+62.8
=141.3(平方分米)
答:至少需要141.3平方分米铁皮。
【解析】(1)圆柱的体积=底面积×高,圆锥的体积=底面积×高×,把圆柱部分和圆锥部分的容积相加就是油菜籽的体积,然后乘每平方分米油菜籽的质量即可求出总重量;
(2)用一个底面的面积加上侧面的面积即可求出至少需要铁皮的面积。
41.(1)解:21.46×0.99≈21.25(吨),
答:相当于生产了21.25 吨无纺布。
(2)解:17÷21.25=0.8(吨),
26÷0.8=32.5(吨),
答:要节约26 吨棉花需要处理32.5 吨无纺布。
【解析】(1)根据公司处理了21.46吨旧衣服以及 每吨旧衣服可以回收生产0.99吨无纺布即可求出答案
(2)首先根据节约的棉花求出节约了一吨棉纺布相当于节约了0.8吨棉花,即可求出26吨棉花需要32.5吨棉纺布
42.7.06千克
43.64平方米
44.解:(12.56+1.57)÷10=1.413(米)=141.3(厘米),
141.3÷3.14=45(厘米);
答:树干的直径约是 45 厘米。
【解析】先求出绕满10圈所需的麻绳总长度,圆的周长公式为C=πd,据此求出直径即可。
45.解:
80÷[1-(1-30%)×(1+40%)]=4000(t)
答:这条铁路前年的货运量是4000t。
【解析】首先画出三个线段图,即可得出去年比前年降低30%,今年比去年增长40%少80吨,据此即可列式计算
46.解:长方体长宽高的和:420÷4=105(厘米)
长:105×=105×=30(厘米)
宽:105×=105×=30(厘米)
高:105×=105×=45(厘米)
体积: 30×30×45=40500(立方厘米)
答:这个孔明灯的体积是40500立方厘米。
【解析】长方体的棱长和÷4=长方体长宽高的和,长方体长宽高的和×长占长方体长宽高的和分率=长方形的长,长方体长宽高的和×宽占长方体长宽高的和分率=长方形的宽,长方体长宽高的和×高占长方体长宽高的和分率=长方形的高,长方体的长宽高的积就是长方体的体积。
47.(1)解:, 则 ;
, 则 。
(2)解:,
, 则它们的平均数为 。
【解析】(1)本题考查的是分数比较大小的问题,通过通分来将不同分母的分数转换为同分母,然后比较分子的大小来判断分数的大小。首先,需要确定两个分数的分母的最小公倍数,然后进行通分,最后通过比较分子的大小来判断原分数的大小。
(2)先对各分数进行通分,分母均为12,将三个分子相加除以3,即可得出分子的平均数。
48.解:3.14×32 ×6÷4×8
=3.14×54÷4×8
=169.56÷4×8
=339.12(立方厘米)
答:这段钢材的体积是339.12立方厘米。
【解析】用钢材的底面积乘6厘米求出拉出水面部分钢材的体积。用这部分钢材的体积除以水面下降的高度即可求出储水桶的底面积,用底面积乘原来水面上升的高度即可求出钢材的体积。
49.(1)8
(2)解:补全图形如图,一共有4种情况:
(3)解:装10件这种产品,为导致所用材料尽可能少,应尽量使得6×8的面重叠在一起,10件这种产品可以用10×6×8的包装纸箱,再考虑10×8的面积最大,所以10 x 8的面重叠在一起,纸箱所用材料就尽可能少。
所以设计的包装纸箱为10×12×8规格,该产品的侧面积分别为:
8×12 = 96(cm2)
8×10 = 80(cm2)
12×10 = 120(cm2)
纸箱的表面积:
(120+96+80)×2=592(cm2)
故答案为:规格为10×12×8。
【解析】(1)解:观察长方形纸盒的展开图,依次数出被剪开的棱的数量,数出结果为8。
故答案为:8。
【分析】(1)根据平面展开图,可以数出剪开的棱的条数。
(2)根据长方形的展开图特点,可以得出补全的四种方式,注意长度一致的边要能够重合。
(3)理解题目要求,将10件产品分层叠放时,每层只放1件,因此,纸箱的高度将等于10件产品高度的总和,而纸箱的长和宽则应等于单件产品的长和宽。在确定纸箱的长、宽、高后,计算纸箱的表面积,以找出最节省材料的设计。
21世纪教育网(www.21cnjy.com)
2024-2025学年六年级下册数学小升初重点校分班考前提升卷
一、填空题
1.一个长方体纸箱,相交于一个顶点的三条棱的长度分别是8dm、6dm、3dm,这个纸箱的体积是 。把这个纸箱放在地上,当它的占地面积最小时,纸箱的高是 dm。
2. 如图,如果把三角形ABC先向右平移3格,再向上平移4格后得到三角形A'B'C',那么点A'的位置用数对表示是( , ),点C·的位置用数对表示是( , )。
3.诗人李白写过一首诗:“危楼高百尺,手可摘星辰。不敢高声语,恐惊天上人。”若古代的一尺等于现在 am,则诗中百尺等于现在的 m;若古代的百尺约等于现在的34m,则a= m。
4.节约粮食是中华民族的传统美德,1000粒大米约重25克,1亿粒大米约重 克。
5.在括号里填上“>”“<”或“=”。
15
0.4
6.在比例25∶10=15∶6中,如果将第一个比的后项增加20,第二个比的后项应该增加 才能使该比例成立。
7.小华在30m长的跑道上走路测试了三次,第一次走了74步,第二次走了78步,第三次走了73步。照这样计算,小华沿400 m跑道走一圈大约要走 步。
8.在( )里填上最简分数。
45dm2= m2 1250dm3= m3
55秒= 分 350cm3= L
9.一个数,百万位上是7,万位上是3,百位上是5,其余各位都是0,这个数是 。
10.学校举行象棋比赛,共有10人参加,如果每两人进行1场比赛,一共要进行 场比赛。
11.七巧板中,①号和②号图形共占整个正方形的,⑦号图形共占整个正方形的,④号图形占整个正方形的。
12.一个玩具飞机292元,一个玩具火车107元,一个玩具飞机比一个玩具火车大约贵 元,买一个玩具飞机和一个玩具火车大约需要准备 元。
13.平行四边形和三角形的面积相等,底也相等,平行四边形的高是8厘米,那么三角形的高是 厘米;如果三角形的高是8厘米,那么平行四边形的高是 厘米。
14.如图所示,圆国内分别标有1,2,…,12,这 12个数字,电子跳蚤每跳一步,可以从一个圆圈逆时针跳到相邻的圆圈,若电子跳蚤所在圆圈的数字为n,则电子跳蚤连续跳(3n-2)步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳3×1-2=1步到标有数字2的圆圈内,完成一次跳跃,第二次则要连续跳 3×2-2=4步到达标有数字6的四圈,….依此规律,若电子跳蚤从①开始,那么第 2021次跳跃电子跳蚤能跳到的四圈内所标的数字为: 。
二、判断题
15.今年的钢材第一次提价15%,第二次又提价10%,现价比原价提高了25%。( )
16.16×32=512,那么(16÷4)×(32×4)=512。(
)
17.正方体的棱长扩大到原来的2倍,表面积就扩大到原来的4倍。( )
18.把20克糖溶解在100克水中。糖占糖水的20%. ( )
19.从写有1-6的6张卡片中任意抽—张,抽到2和3的可能性一样大.( )
20.两条直线相交,要么平行,要么垂直。( )
21. 一根绳子剪去,还剩下 m。 ( )
22. 一种商品价格降低了5%后又提价5%,价格和原来相比没有变化。( )
23.把一个圆柱削成一个最大的圆锥,圆锥的体积是削去的一半.( )
三、单选题
24.一本书 125 页, 看了 , 还剩 ( ) 页没看。
A. B.
C. D.
25.今年王叔叔家小表产量比去年增产三成,下面说法正确的是( )。
A.今年小麦产量是去年的130% B.今年小麦产量是去年的70%
C.去年小麦产量是今年的130% D.去年小麦产量是今年的70%
26.下面直线上的M点表示的数可能是算式( )的结果。
A.15×0.9□ B.3.□×4.□ C.15÷1.□ D.4.□×4.□
27.半导体是现代信息技术革命的关键材料。某半导体厂生产了一个底面周长为 50.24 cm,高为12 cm的圆柱体陶瓷基材,其中间位置向下挖去了一个棱长为3c m的正方体小洞,在这个小洞的下面中间位置继续向下挖去一个棱长为2cm 的正方体小洞,工厂采用真空溅射的方法对陶瓷基材剩余部分的表面镀膜,需要镀膜的面积为( )cm2。
A.401.92 B.1004.8 C.1056.8 D.1040.8
28.漳州市的方圆里国木复兴馆内陈列的《漳州战役》木雕长12.3米,最大直径是0.75米,横线部分的“3”表示( )。
A.0.3厘米 B.30分米 C.30厘米 D.0.3分米
29.如图,以点A为一个端点的线段中,最短的是( )。
A.AB B.AC C.AD D.AE
30.下面选项中与“35×79”的积相等的式子是( )。
A.35×7×9 B.35×80-1 C.35×80-35 D.79×30+5
31.某市出租车收费标准:2km以内5元;超过2km的部分,每千米1.5元(不足1km按1km计算)。王老师坐出租车去离学校12.8km远的教育局开会,应付车费( )元。
A.19.2 B.21.2 C.21.5
32.在一个三角形里,如果一个最小的角是46°,那么这个三角形一定是( )。
A.锐角三角形 B.钝角三角形 C.直角三角形
33.如下图所示,将一个正方形的变长增加1.5cm,得到一个新的正方形。用含有字母的式子表示增加的面积,其中错误的是( ) 。
A.1.5a×2+1.5 B.(a+a十1.5)×1.5 C.1.5×(a+1.5)×2 D.(a+1.5)2-a2
四、计算题
34.直接写出得数。
35.下面各题怎样简便怎样算。
①1.25×0.96×80 ②55× +3÷7
③ ×[ ÷( - )] ④ + + + (提示: - = )
解方程:
① ②
37.求下面图形的表面积。
38.如下图为某婴儿商品的商标,由两颗心组成,每颗心都是由一个正方形和两个半圆拼成.若两个正方形的边长分别是40mm,20mm,那么,阴影部分的面积是多少mm2?
五、操作题
39.在下面的方格图中,按要求画图.
(1)把圆移到圆心是(8,6)的位置.
(2)按3:1放大长方形,画出放大后的图形.
(3)如果每个方格面积为1cm2,请你画一个面积是12cm2的轴对称图形(除长方形、正方形外),并画出对称轴.
六、解决问题
40.如图1,某种油菜籽榨油机的漏斗是由圆柱和圆锥两部分组成的,它的底面半径是4分米,且这两部分的高都是6分米。已知每立方分米油菜籽重0.7千克。
(1)这个漏斗最多能装多少千克油菜籽? (结果保留1位小数)
(2)如果张师傅打算用铁皮给这个漏斗做一个圆柱形的防尘罩(如图2,没有下底面),至少需要多少平方分米铁皮?
41.旧衣服经过处理可以得到无纺布,实现资源循环利用。每吨旧衣服可以回收生产0.99吨无纺布,某公司处理了21.46吨旧衣服。
(1)相当于生产了多少吨无纺布 (得数保留两位小数)
(2)生产的这些无纺布相当于节约了17吨棉花,要节约26吨棉花需要处理多少吨无纺布
42.“垃圾分类,从我做起”。西河学校一天的可回收垃圾是52.06千克,可回收垃圾比其他垃圾多35.76千克,有害垃圾比其他垃圾少9.24千克,请问有害垃圾有多少千克?
43.李大爷擅长“变废为宝”,常常利用家里的剩余竹木做栅栏。最近,李大爷做的栅栏刚好能将一块长8米、宽4米的长方形菜地围一圈。如果用这次的栅栏围一个一面靠墙的正方形鸡舍,这个鸡舍的面积最大是多少平方米?
44.为保护树干,工作人员在树干上缠绕麻绳,工作人员裁剪了一根长12.56米的麻绳,还差1.57米才能在树干上绕满10圈,请算一算树干的直径约是多少厘米?
45.一条铁路去年的货运量比前年降低了三成,今年的货运量预计比去年增长四成,但仍比前年少80t,这条铁路前年的货运量是多少吨?(先画线段图,再解答)
46.孔明灯俗称许愿灯,是一种古老的汉族手工艺品,根据热气球原理使空气受热膨胀而升空。手工艺人张师傅将总长420cm的竹制作成一个长方体孔明灯的框架,再将它的上面和四周用安全阻燃棉纸糊成灯罩,这个孔明灯长、宽、高的比是2:2:3。这个孔明灯的体积是多少立方厘米?(接头处忽略不计)
47.《九章算术》是中国古代数学专著,它的出现标志着中国古代数学体系的形成。《九章算术》卷一中有记载如下。
(1)今有八分之五,二十五分之十六。问孰多 又有九分之八,七分之六。问孰多 意思是有两个数和,哪个数大 又有两个数和,哪个数大
(2)今有三分之一,三分之二,四分之三。问几何而平 意思是有它们的平均数是多少
48.在一个圆柱形储水桶里,把一段底面半径为3厘米的圆柱形钢材全部放入水中,这时水面上升8厘米。把这段钢材竖着拉出水面6厘米,水面下降4厘米,这段钢材的体积是多少立方厘米?
49.小明在学习了正方体的展开图后,明白了很多几何体都能展开成平面图形。于是他在家用剪刀剪开了一个长方体纸盒,如图3,可是一不小心多剪开了一条棱,把纸盒剪成了两部分,如图1、图2所示,请根据你所学的知识,回答以下问题:
(1)观察判断:
小明共剪开了 条棱。
(2)动手操作:
现在小明想将剪断的图2重新粘贴到图1上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒(如图3),请你帮助小明在图1中补全图形:
(3)解决问题:
请你设计一个长方体的包装纸箱,使每箱能装10个这种纸盒,每层放1个共放10层,要求没有空隙且要使该纸箱所用材料尽可能少(纸箱的表面积尽可能小)。请你通过计算说明最节省材料的包装纸箱的规格(单位:cm)
参考答案及试题解析
1.144;8
2.5;5;4;6
【解析】解:如图:点A'的位置用数对表示是(5,5),点C'的位置用数对表示是(4,6)。
故答案为:5;5;4;6。
【分析】数对中第一个数表示列,第二个数表示行。根据平移的方向和格数确定平移后的图形,然后确定每个点的位置。
3.100a;0.34
【解析】解:百尺=100×a=100a(m)
100a=34
a=0.34
故答案为:100a,0.34。
【分析】 古代的一尺等于现在a米,因此古代百尺等于现在100a米;古代的百尺约等于现在的34米,即100a=34,根据等式的基本性质2,将等式的两边同时除以100,得到a的值。
4.2500000
5.<;>;<;=
6.12
7.1000
【解析】解:(74+78+73)÷3
=225÷3
=75(步)
75÷30×400
=2.5×400
=1000(步)
故答案为:1000。
【分析】用三次走的步数和除以3求出平均步数,然后用平均步数除以30求出每米的步数,用每米的步数乘400即可求出400m大约要走的步数。
8.;;;
9.7030500
10.45
【解析】解:10×9÷2
=90÷2
=45(场)
故答案为:45。
【分析】如果每两个同学之间都进行一场比赛,每个同学都要和其他的9人进行一场比赛,每个同学打9场,共有10×9场比赛;由于每两个人之间重复计算了一次,再除以2即可。
11.;;
12.180;400
【解析】解:第一问:292-107≈180(元);
第二问:292+107≈400(元)。
故答案为:180;400。
【分析】从“大约”可以看出是要求估算,用减法计算一个玩具飞机比一个玩具火车大约贵的钱数;用加法估算出买一个玩具飞机和一个玩具火车大约需要准备的钱数。估算时把两个数都看作近似整百或整百整十数。
13.16;4
【解析】解:8×2=16(厘米)
8÷2=4(厘米)
故答案为:16;4。
【分析】平行四边形和三角形的面积相等,底也相等,三角形的高是平行四边形高的2倍;平行四边形的高是三角形高的一半。
14.10
【解析】仔细观察发现:
第一次跳 3x1-2=1 步到数字 2的圆圈:
第二次跳 3x2-2-4步到达标有数字6的圆圈;
第三次跳3x6-2-16步到达标有数字10的圆圈:
第四次跳3x10-2=28步到达标有数字 2的圆圈:
……
发现每三次一循环,
∵2016÷3-672
∴第 2016 次跳到的圆圈内所标的数字为10
故答案为:10.
【分析】第一次跳到数字2,第二次跳到数字6,第三次跳到数字 10,第四次跳到数字2,然后每三个一循环,用2016除以3,整除为10,余1为2,余2为6即可确定
15.错误
【解析】解:(1+10%)×(1+10%)-1
=1.1×1.1-1
=1.21-1
=21%。
故答案为:错误。
【分析】把原价看作单位“1”,第一次提价后的价格是原价的(1+10%),后来又提价10%,是在(1+10%)的基础上提价的,提价后的价格是(1+10%)的(1+10%),然后再减去1。
16.正确
【解析】解:16×32=512,那么(16÷4)×(32×4)=512,计算正确。
故答案为:正确。
【分析】积的变化规律:一个因数扩大不为0的倍数,另一个因数缩小相同的倍数,则积不变,本题据此进行判断。
17.正确
【解析】解:正方体的棱长扩大到原来的2倍,表面积就扩大到原来的4倍。原题说法正确。
故答案为:正确。
【分析】正方体表面积=棱长×棱长×6,正方体棱长扩大到原来的n(0除外)倍,那么表面积就扩大到原来的n2倍。
18.错误
【解析】解:把20克糖溶解在100克水中。糖占糖水的20÷(20+100)×100%≈16.67%。
故答案为:错误。
【分析】糖占糖水的百分之几=糖的质量÷(糖的质量+水的质量)×100%。
19.正确
【解析】解:从写有1-6的6张卡片中任意抽—张,抽到2和3的可能性一样大。
故答案为:正确。
【分析】因为卡片中2和3的张数一样多,所以抽到2和3的可能性一样大。
20.错误
【解析】解:两条直线相交,要么平行,要么相交。
故答案为:错误。
【分析】两条直线相交,要么平行,要么相交;垂直是相交的一种。
21.错误
【解析】解:一根绳子剪去,还剩下1-=。原题说法错误。
故答案为:错误。
【分析】把这根绳子看作单位“1”,用1减去剪去的分率即可求出剩下的分率。不知道绳子的长度,无法计算剩下的实际长度。
22.错误
【解析】解:1×(1-5%)×(1+5%)
=95%×105%
=99.75%
99.75%<1。
故答案为:错误。
【分析】假设这件商品的原价是1,现价=原价×(1-降价的百分率)×(1+提价的百分率),然后再比较大小。
23.正确
【解析】解:根据题干分析可得:圆柱与圆锥的体积之比是3:1,则削去部分的体积与圆锥的体积就是2:1,所以圆锥的体积是削去的一半,所以原题说法正确。
故答案为:正确。
【分析】 把一个圆柱削成一个最大的圆,圆柱的体积是圆锥体积的3倍,圆锥的体积是1份,圆柱的体积就是3份,消去的部分是2份,那么圆锥的体积是消去部分的一半。
24.C
【解析】解:看了60%,剩下这本书的1-60%,剩下的页数:。
故答案为:C。
【分析】把这本书的页数看作单位“1”,已看了60%,那么剩下(1-60%),再根据求一个数的百分之几是多少用乘法计算,据此列式。
25.A
【解析】解:1+30%=130%;
故答案为:A。
【分析】把去年小麦的产量看成单位“1”,今年的小麦产量比去年增产三成,那么今年的产量就是去年的(1+30%),由此解答即可。
26.B
27.C
【解析】解:50.243.142=8(cm)
3.14822+50.2412+334+224
=3.14128+602.88+36+16
=401.92+654.88
=1056.8(cm2)
故答案为:C。
【分析】观察图形,镀膜的面积即基材的表面积,而基材的表面积就是圆柱的表面积加上大正方体四个面的面积,再加上小正方体四个面的面积;已知圆柱的底面周长,根据圆柱的底面周长公式:C=2πr,得到半径r=50.243.142=8(cm),然后根据圆柱的表面积公式:S=2πr2+Cd,正方形四个面的面积=边长边长4,分别计算出大正方体四个面的面积和小正方体四个面的面积,相加即可得到基材的表面积,即镀膜的面积。
28.C
29.C
30.C
31.C
【解析】12.8km看做13km;
5+(13-2)×1.5=5+16.5=21.5(元)。
故答案为:C。
【分析】前2千米的车费+2千米以后的路程×单价=一共应付的车费。
32.A
【解析】解:假如另外一个角也是46°,那么最大的角是:180°-46°-46°=88°,这个三角形一定是锐角三角形。
故答案为:A。
【分析】因为46°的角是最小的角,那么另外一个角最小是46°,那么假设另外一个角也是46°,这样计算出第三个角就能确定三角形的类型。
33.C
【解析】解:A项:利用增加的面积=2×长方形面积+小正方形的面积,即增加的面积为:
1.5a×2+1.52,计算正确;
B项:( a + a +1.5)×1.5=1.5a×2+1.52,即利用增加的面积=2×长方形面积+小正方形的面积, 计算正确;
C项:1.5×( a +1.5)×2,多加了一个小正方形的面积, 计算错误;
D项:增加的面积=新的正方形的面积-原正方形的面积,即增加的面积为:
( a +1.5)2-a2, 计算正确。
故答案为: C 。
【分析】将一个正方形的边长增加1.5厘米后,增加部分的面积等于两个长等于原来正方形的边长,宽等于1.5厘米的长方形和一个边长为1.5厘米的正方形的面积;也可以用新的正方形的面积减去原正方形的面积求解即可。
34.解:
2.92 19.8
0.5
【解析】 计算小数减法时把小数点对齐再相减;计算分数加、减法时先通分,再计算;计算小数乘法时,先按照整数乘法去乘,因数中有几位小数就在积的末尾点上小数点;计算分数除法时,除以一个数等于乘这个数的倒数;计算小数除法时,先把除数和被除数同时扩大相同的倍数,然后按照除数是整数的除法去除,商的小数点和被除数的小数点对齐;分数四则混合运算的运算顺序与整数四则混合运算的运算顺序相同,都是先乘除后加减;分数除以小数,可以把分数化成小数,也可以把小数化成分数再计算。
35.解:①1.25×0.96×80
=1.25×80×0.96
=100×0.96
=96
②55× +3÷7
=55× +
= ×(55+1)
= ×56
=24
③ ×[ ÷( - )]
= ×[ ÷ ]
= ×
=1
④ + + +
= ﹣ + ﹣ + ﹣ + ﹣
= ﹣
=
【解析】①先运用乘法交换律交换后两个数的位置,再按照从左到右的顺序进行计算;
②一个相同的数分别同两个不同的数相乘,积相加,等于这个相同的数乘另外两个不同数的和,据此简算;
③运算顺序:先算乘除,再算加减,如果有括号,就先算括号里面的。如果有小括号和中括号,由内到外,先算小括号里面的,再算中括号里面的;
④分数的分子是1,分母是两个相邻自然数相乘的形式,这个分数就等于较小的自然数分之一减去较大的自然数分之一。据此先把算式写成相减的形式,再观察算式,发现中间的数相加等于0,算式就剩下两头的两个数相减,据此解答。
36.解:① ,
,
x=0.7;
② ,
,
,
x=4.5.
【解析】(1)依据等式的性质,方程两边同时除以求解,(2)依据等式的性质,方程两边同时乘,再同时除以求解.
37.解:3.14×(8÷2)2×2+3.14×8×3+3.14×4×3
=3.14×32+3.14×24+3.14×12
=3.14×68
=213.52(cm2);
答:图形的表面积是213.52cm2。
【解析】该图形的表面积就是大圆柱的表面积+小圆柱的侧面积,圆的面积=πr2,圆柱侧面积=2πrh,据此求解。
38.(402 + π ×202) - (202 +π×102)
=1600+400π-400-100π
= 1200+300π
=1200+300 × 3.14
=1200+942
=2142(平方毫米)。
答:阴影部分的面积是2142平方毫米。
【解析】如下图所示:两个大半圆可以组成一个整圆,两个小半圆也可以组成一个整圆,据此用大正方形的面积加上大圆的面积,然后减去小正方形的面积加上小圆的面积,就可以求出阴影部分的面积。
39.(1)解:
(2)解:
(3)解:
【解析】(1)用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数;
(2)放大后长方形的长、宽分别=原来长方形的长、宽分别×3,然后画出图形;
(3)等腰三角形是轴对称图形,三角形的面积=底×高÷2,据此画图。
40.(1)解:3.14×42×6+3.14×42×6×
=3.14×96+3.14×32
=3.14×128
=301.44(立方分米)
301.44×0.7=211.0(千克)
答:这个漏斗最多能装211.0千克油菜籽。
(2)解:3.14×(10÷2)2+3.14×10×2
=3.14×25+3.14×20
=78.5+62.8
=141.3(平方分米)
答:至少需要141.3平方分米铁皮。
【解析】(1)圆柱的体积=底面积×高,圆锥的体积=底面积×高×,把圆柱部分和圆锥部分的容积相加就是油菜籽的体积,然后乘每平方分米油菜籽的质量即可求出总重量;
(2)用一个底面的面积加上侧面的面积即可求出至少需要铁皮的面积。
41.(1)解:21.46×0.99≈21.25(吨),
答:相当于生产了21.25 吨无纺布。
(2)解:17÷21.25=0.8(吨),
26÷0.8=32.5(吨),
答:要节约26 吨棉花需要处理32.5 吨无纺布。
【解析】(1)根据公司处理了21.46吨旧衣服以及 每吨旧衣服可以回收生产0.99吨无纺布即可求出答案
(2)首先根据节约的棉花求出节约了一吨棉纺布相当于节约了0.8吨棉花,即可求出26吨棉花需要32.5吨棉纺布
42.7.06千克
43.64平方米
44.解:(12.56+1.57)÷10=1.413(米)=141.3(厘米),
141.3÷3.14=45(厘米);
答:树干的直径约是 45 厘米。
【解析】先求出绕满10圈所需的麻绳总长度,圆的周长公式为C=πd,据此求出直径即可。
45.解:
80÷[1-(1-30%)×(1+40%)]=4000(t)
答:这条铁路前年的货运量是4000t。
【解析】首先画出三个线段图,即可得出去年比前年降低30%,今年比去年增长40%少80吨,据此即可列式计算
46.解:长方体长宽高的和:420÷4=105(厘米)
长:105×=105×=30(厘米)
宽:105×=105×=30(厘米)
高:105×=105×=45(厘米)
体积: 30×30×45=40500(立方厘米)
答:这个孔明灯的体积是40500立方厘米。
【解析】长方体的棱长和÷4=长方体长宽高的和,长方体长宽高的和×长占长方体长宽高的和分率=长方形的长,长方体长宽高的和×宽占长方体长宽高的和分率=长方形的宽,长方体长宽高的和×高占长方体长宽高的和分率=长方形的高,长方体的长宽高的积就是长方体的体积。
47.(1)解:, 则 ;
, 则 。
(2)解:,
, 则它们的平均数为 。
【解析】(1)本题考查的是分数比较大小的问题,通过通分来将不同分母的分数转换为同分母,然后比较分子的大小来判断分数的大小。首先,需要确定两个分数的分母的最小公倍数,然后进行通分,最后通过比较分子的大小来判断原分数的大小。
(2)先对各分数进行通分,分母均为12,将三个分子相加除以3,即可得出分子的平均数。
48.解:3.14×32 ×6÷4×8
=3.14×54÷4×8
=169.56÷4×8
=339.12(立方厘米)
答:这段钢材的体积是339.12立方厘米。
【解析】用钢材的底面积乘6厘米求出拉出水面部分钢材的体积。用这部分钢材的体积除以水面下降的高度即可求出储水桶的底面积,用底面积乘原来水面上升的高度即可求出钢材的体积。
49.(1)8
(2)解:补全图形如图,一共有4种情况:
(3)解:装10件这种产品,为导致所用材料尽可能少,应尽量使得6×8的面重叠在一起,10件这种产品可以用10×6×8的包装纸箱,再考虑10×8的面积最大,所以10 x 8的面重叠在一起,纸箱所用材料就尽可能少。
所以设计的包装纸箱为10×12×8规格,该产品的侧面积分别为:
8×12 = 96(cm2)
8×10 = 80(cm2)
12×10 = 120(cm2)
纸箱的表面积:
(120+96+80)×2=592(cm2)
故答案为:规格为10×12×8。
【解析】(1)解:观察长方形纸盒的展开图,依次数出被剪开的棱的数量,数出结果为8。
故答案为:8。
【分析】(1)根据平面展开图,可以数出剪开的棱的条数。
(2)根据长方形的展开图特点,可以得出补全的四种方式,注意长度一致的边要能够重合。
(3)理解题目要求,将10件产品分层叠放时,每层只放1件,因此,纸箱的高度将等于10件产品高度的总和,而纸箱的长和宽则应等于单件产品的长和宽。在确定纸箱的长、宽、高后,计算纸箱的表面积,以找出最节省材料的设计。
21世纪教育网(www.21cnjy.com)
同课章节目录
