2024-2025学年五年级下册数学期末考前提升卷北师大版(含解析)
文档属性
| 名称 | 2024-2025学年五年级下册数学期末考前提升卷北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 438.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 08:50:21 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年五年级下学期数学期末考前提升卷(北师大版)
一、填空题
1.淘气家在学校的北偏东60°方向上700m处。则学校在淘气家 60°方向上 m处。
2.把两个棱长都是1dm的正方体拼成一个长方体,这个长方体的表面积是 。
3.一瓶水连瓶重kg,喝了一半水后连瓶重kg,瓶重 。
4.一台拖拉机 小时耕地1公顷,这台拖拉机耕地1公顷需要 小时,3小时可以耕地 平方米.
5.陈老师要用96cm长的铁丝做一个正方体教具,这个教具的棱长是 cm,在它的表面贴上彩纸,至少要 cm2的彩纸。
6.奇奇要给家里的长方体鱼缸换水。如图鱼缸长 46厘米,宽25厘米,高30厘米他打算先放掉15厘米高的水,再注入20厘米高的新水,假设放水和注水的流量均为每分钟5立方分米,则奇奇给鱼缸换水需要 分钟。(缸壁厚度和其他时间忽略不计)
7.观察线路图填空。
小东从家到公园,他先向 方向走 米到电影院,再向 方向走 米就到公园了。
8.用4个棱长是2厘米的正方体拼成长方体,所得长方体中表面积最大是 平方厘米。
9.一个长方体长8厘米,宽4.5厘米,高5厘米,(如图)把它切成两个长方体,表面积最多增加 平方厘米。
10.一个两位数,十位数字比个位数字大2,这个两位数除以十位数字与个位数字的和,商为6,余数为3,则这个两位数是 。
11.某市9月份晴天天数占本月天数的,阴天天数是晴天天数的,雨天天数比晴天天数的少2天,其余是多云天气。这个城市这个月晴天 天,阴天 天,雨天 天,多云 天。
12.如图,大正方形的边长为20厘米,小正方形的边长是大正方形边长的 。图中阴影部分的面积是 平方厘米。
13.一个长方体木块,长、宽、高分别是9dm、4dm和6dm,把它锯成若干个小正方体,再拼成一个大正方体.这个大正方体的表面积是 平方分米.
14.一根3米长的方钢,把它横截成3段时,表面积增加60平方厘米,原来方钢的体积是 立方厘米。
15.把长12厘米,宽8厘米,高5厘米的长方体木块锯成棱长2厘米的正方体木块,可锯 块。
二、判断题
16.长方体中,如果有两个相对的面是正方形,那么其余的面一定是完全一样的长方形.( ).
17.长方体中,高不变,底面积越大,体积也越大。( )
18.男生人数比女生人数多 ,女生人数就比男生人数少 。( )
19.小明沿直线向东走100米,再向西走100米,又向南走100米,这时他在出发点北100米.( ).
20.一个数的倒数小于1,这个数就大于1。( ).
21.底面积和高相等的长方体、正方体、圆柱体,它们的体积相等。( )
22.一根绳子对折一次后,量得每段长是 m,则原来的绳子长是3m。( )
23.甲数的 等于乙数的 .由于 < ,所以甲<乙.( ).
三、单选题
24.一种商品先提价,再降价,最后的价格( )。
A.原价不变 B.比原价低 C.比原价高 D.无法确定
25.用5千克棉花的 和1千克铁的 相比较,结果是( )。
A.5千克棉花的 重 B.1千克铁的 重
C.一样重 D.无法比较
26.表面积相等的长方体和正方体的体积相比( )。
A.正方体体积大 B.长方体体积大 C.相等
27.以小红家为观测点。小明家在南偏东50°方向上,则以小明家为观测点,小红家在( )方向上。
A.东偏南50° B.北偏西50° C.北偏西40° D.西偏北50”
28.如图图形是正方体平面展开图的共有( )个。
A.2 B.3 C.4
29.把一根长6分米的长方体材料平均锯成3段,表面积增加3.6平方分米,这根木料的体积是( )立方分米.
A.0.9 B.3.6 C.5.4 D.1.8
30.同学们用排水法测量土豆和红薯的体积,已知长方体容器长15cm,宽15cm,高20cm。仔细观察实验过程,比较土豆和红薯的体积,( )。
A.土豆的体积大 B.红薯的体积大
C.一样大 D.无法判断
31.把同样多的食盐溶解在下面三个长方体容器中,最咸的是( )。
A.第①杯 B.第②杯 C.第③杯 D.无法确定
32. 重点题 如下图,以数形变化的规律计算,算式 的结果是( )。
A. B.1 C. D.无法确定
33.观察下图,下列说法正确的是( )。
A.甲的表面积大于乙的表面积 B.甲的表面积等于乙的表面积
C.甲的体积小于乙的体积 D.甲的体积等于乙的体积
34.一个长方体长7cm,宽6cm,高5cm,把它的表面涂成红色。如果把这个长方体全部切割成棱长是1 cm的小正方体且没有剩余,那么切割成的小正方体中两面涂红色的有( )个。
A.8 B.210 C.94 D.48
四、极速那天
35.直接写出得数。
+ = × = 45× = 15÷ =
- = 5÷ = ÷16= ÷ =
36.用你喜欢的方法计算。
37.解方程。
(1) (2) (3)
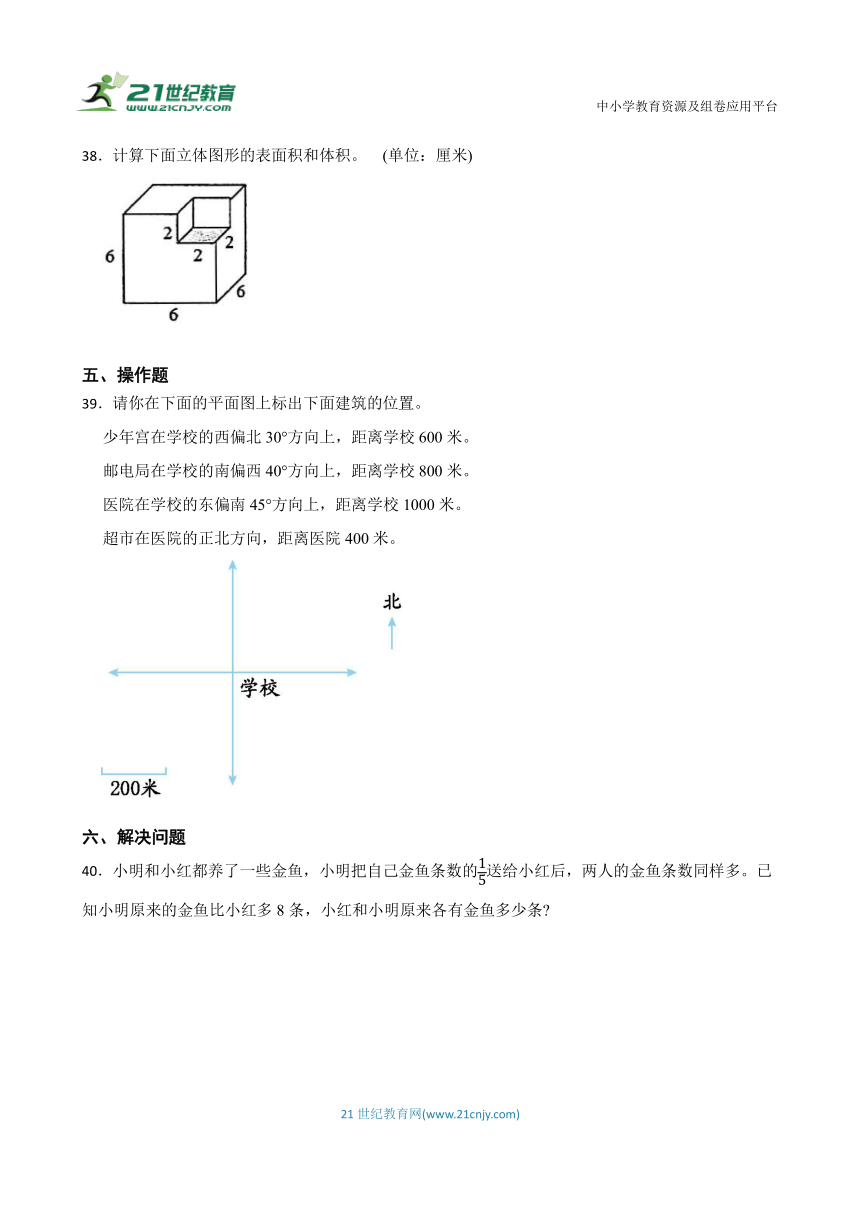
38.计算下面立体图形的表面积和体积。 (单位:厘米)
五、操作题
39.请你在下面的平面图上标出下面建筑的位置。
少年宫在学校的西偏北30°方向上,距离学校600米。
邮电局在学校的南偏西40°方向上,距离学校800米。
医院在学校的东偏南45°方向上,距离学校1000米。
超市在医院的正北方向,距离医院400米。
六、解决问题
40.小明和小红都养了一些金鱼,小明把自己金鱼条数的送给小红后,两人的金鱼条数同样多。已知小明原来的金鱼比小红多8条,小红和小明原来各有金鱼多少条
41.成都与重庆相距300千米,一辆货车从成都开往重庆,一辆轿车从重庆开往成都,货车每时行驶60千米,2时后,两车相距30千米,轿车每时行驶多少千米?
42.一个长方体简易衣柜,长0.9 m,宽0.4 m,高1.5 m,做这个简易衣柜的布罩至少需要多少平方米布?(底面不用布罩)
43.花店购进玫瑰花和百合花共200枝,占购进花的总枝数的。花店这次共购进多少枝花?
44.从一个长9厘米,宽6厘米,高6厘米的长方体中截下一个最大的正方体。剩下几何体的表面积是多少平方厘米?
45.爱动脑的小优发现,这个封闭的长方体容器平放时,水面的高度是7cm(如图①)。如果把这个容器竖起来放(如图②),水面的高度是多少厘米?(容器厚度忽略不计)
46.《资治通鉴》是司马光编撰的一部编年体通史。全书按朝代分为十六纪,其中《晋纪》有40卷,《宋纪》的卷数比《晋记》的多1卷,《齐纪》的卷数比《宋纪》少,《齐纪》有多少卷
47.五年级共有3个班,一班人数占全年级人数的,三班人数比二班人数多,如果从三班调走4人后,三班和二班的人数同样多。五年级共有多少人?
48.小红将一块棱长为4 厘米的正方体橡皮泥捏成了一个底面积是8平方厘米的长方体,这个长方体的高是多少厘米?
49.天山胜利隧道是世界在建高速公路最长的隧道。两个工程队承建了这条隧道中一段长 1500 米的隧道项目,他们分别从两端相向施工,施工完成时,甲队开凿了675米,则乙队开凿了多少米?(列方程解答)
参考答案及试题解析
1.南偏西;700
【解析】解:淘气家在学校的北偏东60°方向上700m处,
则学校在淘气家南偏西60°方向上700m处。
故答案为:南偏西;700。
【分析】甲在乙什么位置和乙在甲什么位置,他们的关系是:方向相反,角度、距离不变。
2.10平方分米
【解析】解:1×2=2(分米)
(2×1+2×1+1×1)×2
=(2+2+1)×2
=5×2
=10(平方分米)。
故答案为:10平方分米。
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,其中,长=正方体的棱长×2;宽=高=正方体的棱长。
3.kg
【解析】-=-=(kg)
-=(kg)
故答案为:kg。
【分析】根据题意可知,一瓶水连瓶的质量-喝了一半后剩下的连瓶的质量=一半的水的质量,然后用剩下的连瓶质量-一半的水的质量=瓶的质量,据此列式解答。
4.;75000
【解析】解:耕地1公顷需要:(小时);3小时可以耕地:(公顷)=75000(平方米)。
故答案为:;75000。
【分析】用耕地时间除以耕地面积即可求出耕地1公顷需要的时间;用3小时除以耕地1公顷需要的时间即可求出3小时可以耕地的面积,注意把公顷换算成平方米。
5.8;384
【解析】解:96÷12=8(cm),
8×8×6
=64×6
=384(cm2);
故答案为:8;384。
【分析】正方体共有12条棱,求出棱长,正方体表面积=棱长×棱长×6,据此求解即可。
6.8.05
【解析】解:根据题意,可得
4.6×2.5×1.5÷5+4.6×2.5×2÷5
=3.45+4.6
=8.05(分钟)
答:奇奇给鱼缸换水需要8.05分钟
故答案为:8.05
【分析】先将厘米化为分米:46厘米=4.6分米,25厘米=2.5分米,15厘米=1.5分米,20厘米=2厘米。根据长方体的体积公式:V=abh,先求出放掉15厘米高水的体积:4.6×2.5×1.5,然后除以放水的流速,求出放水的时间;再求出注水20厘米高水的体积:4.6×2.5×2,然后除以5,求出注水的时间,最后再将放水的时间加上注水的时间,即可求解
7.东偏北45°;420;东偏南30°;630
【解析】解:小东从家到公园,他先向东偏北45°方向走420米到大电影院,再向东偏南30°方向走630米就到公园了。
故答案为:东偏北45°;420;东偏南30°;630。
【分析】上北下南、左西右东,本题据此观察题中的方向以及对应的角度,再根据图上的距离即可得出答案。
8.72
【解析】解:4×2=8(厘米)
(8×2+8×2+2×2)×2
=(16+16+4)×2
=36×2
=72(平方厘米)。
故答案为:72。
【分析】所得长方体的长是8厘米、宽2厘米、高2厘米时表面积最大,表面积=(长×宽+长×高+宽×高) ×2。
9.80
【解析】 表面积最多增加 :8×5×2=80(平方厘米);
故答案为:80。
【分析】根据图示信息,长>高>宽,切成两个长方体,表面积最多增加:长×高×2,代入数值计算即可。
10.75
【解析】设这两个数为ab,则(a+b)×6+3=10a+b ,而a=b+2,
所以 (2b+2)×6+3=10(b+2)+b,
12b+15=11b+20
b=5 a=5+2=7,则原数为75,
故答案为: 75
【分析】先设数,然后根据位置原理和关系列出关系式,再结合个位与十位关系求解。
11.20;5;2;3
【解析】解:9月有30天,
30×=20(天),
20×=5(天),
20×-2
=4-2
=2(天),
30-(20+5+2)
=30-27
=3(天)
故答案为:20;5;2;3。
【分析】根据题意可知,9月有30天,9月份的天数×=晴天的天数;晴天的天数×=阴天的天数;晴天的天数×-2=雨天的天数;9月份的天数-(晴天的天数+阴天的天数+雨天的天数)=多云的天数,据此列式解答。
12.184
【解析】解:20×=8(厘米),
20×20+8×8-(20+8)×20÷2
=400+64-28×20÷2
=464-280
=184(平方厘米)
故答案为:184。
【分析】可以用两个正方形的面积之和减去左上角空白部分三角形的面积即可求出图中阴影部分的面积。
13.216
【解析】长方体木块的体积:
9×4×6
=36×6
=216(立方分米)
大正方体的体积也是216立方分米;
因为6×6×6=216(立方分米),所以大正方体的棱长是6分米;
大正方体的表面积是:
6×6×6
=36×6
=216(平方分米).
故答案为:216.
【分析】已知长方体的长、宽、高,根据公式:长方体的体积=长×宽×高,可以求出长方体体积;
因为把长方体锯成若干小正方体再拼成大正方体,体积是不变的,所以大正方体的体积就是216立方分米;
体积是216立方分米的正方体,棱长是6分米,根据正方体的表面积公式:正方体的表面积=棱长×棱长×6,据此列式解答.
14.4500
【解析】解:3米=30厘米
60÷4×300
=15×300
=4500(立方厘米)
故答案为:4500。
【分析】把它横截成3段,表面积就会增加4个横截面的面积,所以用横截面面积乘方钢的长度即可求出体积。注意统一单位。
15.48
【解析】12÷2=6,8÷2=4,5÷2=2.5, 6×4×2=48
【分析】长方体的长是12厘米,而正方体的棱长是2厘米,在成这部分,可以锯两排,宽是8厘米,可以锯两排,而高是5厘米,是正方体棱长的2.5倍,最多也只能是2排,所以总共是6×4×2=48
16.正确
【解析】解:长方体中最多会有两个相对的面是正方形,其余的四个面都是长方形且完全相同,原题说法正确.
故答案为:正确
【分析】通常长方体的六个面都是长方形,特殊的长方体有两个相对的面可以是正方形.
17.正确
【解析】解:长方体中,高不变,底面积越大,体积也越大,原题干说法正确。
故答案为:正确。
【分析】长方体的体积=底面积×高,高不变,底面积越大,体积也越大。
18.错误
【解析】÷(1+)
=÷
=
女生人数比男生人数少。
故答案为:错误
【分析】男生人数比女生人数多的几分之几÷(1+男生比女生多的几分之几)=女生人数比男生少几分之几。
19.错误
【解析】根据方向的初步认识相关知识点。【分析】据题意知,向东走100米,在向西走100米,那小明还是站在出发点,又向南走100米,这时他应该在出发点南100米的地方。
20.正确
【解析】因为一个数与它倒数乘积为1,所以这个数=1÷它的倒数,因为这数的倒数小于1,所以这个数就大于1,一个的的倒数小于1,这个数就大于1,这种说法是正确的。
【分析】1÷小于1的数>1。
21.正确
【解析】
底面积和高相等的长方体、正方体、圆柱体,它们的体积都是底面积乘以高,所以体积相等。
故答案为:正确。
【分析】长方体体积=长×宽×高=底面积×高;正方体体积=边长×边长×边长=底面积×高;圆柱体体积=底面积×高。
22.正确
【解析】解: 一根绳子对折一次后,量得每段长是m,则原来的绳子长是3m,说法正确。
故答案为:正确。
【分析】对折一次,将绳子平均分成2段,每一段绳子的长度×平均分成的段数即可得出原来绳子的总长度。
23.错误
【解析】甲数=乙数
甲数乙数=
甲数乙数=>1
甲数>乙数
故题中结论错误
【分析】先建立等量关系,然后推理得出结论,甲数>乙数
24.B
【解析】解:1×(1+)×(1-)
=×
=
<1,最后的价格比原价低。
故答案为:B。
【分析】把这件商品的原价看作单位“1”,现价=原价×(1+提价的分率)×(1-降价的分率),然后比较大小。
25.C
【解析】解:5× = (千克) 1× = (千克)
则用5千克棉花的 和1千克铁的 相比较,结果是一样重.
故答案为:C.
【分析】求一个数的几分之几是多少用乘法列式,本题中就是求5的是多少,1的是多少,分别列乘法算式,再根据分数乘整数的方法求出结果,再比较结果大小即可得出结论.
26.A
【解析】解: 可以先反过来考虑体积相等的长方体和正方体,它们的表面积哪一个大,用8个棱长1厘米正方体,可以拼成一个棱长2厘米的正方体,体积是8立方厘米,表面积是2×2×6=24(平方厘米);也可以拼成一个长8厘米,宽1厘米,高1厘米的长方体,体积同样是8立方厘米,表面积是8×1×4+1×1×2=34(平方厘米);由此可以看出体积相等,正方体的表面积小一些.所以长方体和正方体表面积相等,正方体的体积大。
故答案为:A。
【分析】(长×宽+长×高+宽×高)×2=长方体的表面积;长×宽×高=长方体的体积;
正方体的棱长×棱长×6=正方体的表面积;正方体的棱长×棱长×棱长=正方体的体积。
27.B
【解析】 以小红家为观测点。小明家在南偏东50°方向上,则以小明家为观测点,小红家在北偏西50° 方向上。
故答案为:B。
【分析】此题主要考查了方位的知识,根据方向的相对性,南和北相对,东和西相对,据此找准观测点,描述相对位置即可。
28.B
【解析】从左往右,图1、2、4是正方体的展开图。
故答案为:B。
【分析】正方体的展开图有如下类型:第一类,141型,中间四连方,两侧各一个,共六种;第二类,132型,中间三连方,两侧各有一、二个,共三种;第三类,222型,中间二连方,两侧各有二个,只有一种;第四类,33型,两排各三个,只有一种,据此判断。
29.C
【解析】解:3.6÷4×6
=0.9×6
=5.4(立方分米)
故答案为:C。
【分析】平均截成3段后表面积就会增加4各横截面面积,由此用表面积增加的部分除以4即可求出一个横截面面积,用一个横截面面积乘长即可求出这根木料的体积。
30.B
31.B
【解析】解:①号杯,12×6×3=216(cm3) ;
②号杯,14×5×3=210(cm3);
③号杯,10×7×4=280(cm3);
210<216<280,最咸的是②号杯。
故答案为:B。
【分析】此题主要考查了长方体的体积计算,加入同样多的食盐,水越少越咸,根据长方体体积=长×宽×高,分别求出三个容器中水的体积,比较即可。
32.C
【解析】解: 。
故答案为:C。
【分析】由题图可知,在图上有规律地表示出 ,,,不断累加下去,其结果越来越接近 。
33.B
【解析】解:甲比乙多了一个小正方体,多了3个小正方体面的面积,乙又多露出3个小正方体面的面积,则甲、乙的表面积相等;
甲的体积比乙的体积多了1个小正方体的体积。
故答案为:B。
【分析】甲的表面积=乙的表面积,甲的体积>乙的体积。
34.D
【解析】解:7-2=5(块)
6-2=4(块)
5-2=3(块)
5×4+4×4+3×4
=20+16+12
=36+12
=48(个)。
故答案为:D。
【分析】此题考查长方体切割后小正方体涂色情况的分析。两面涂红色的小正方体位于长方体的棱上(不包括顶点),因此需要计算每条棱上符合条件的小正方体数量,再乘以对应棱的数量。两面涂红色的小正方体位于长方体的12条棱上,但每个顶点处的小正方体会有三面涂色,因此需排除顶点处的正方体。
35.
【解析】异分母分数相加减,先通分再计算;计算分数乘法时能约分的要先约分再乘;计算分数除法时要把除法转化成乘法再计算。
36.解:
=
=
=
=
=1+1
=2
=
=
=
【解析】(1)先将分数同分,再将分子相加减;
(2)将分母相同的分数结合计算;
(3)相乘并约分即可;
(4)将除法转为乘法,再约分即可。
37.(1) x++=1
解:x+=1
x+-=1-
x=
(2) +x=
解:+x-=-
x=
(3) x-=
解:x-+=+
x=
【解析】此题应用等式的性质1:等式的两边同时加减相同的数,等式仍然成立,据此解方程。
38.解:表面积:
6×6×6
=36×6
=216(平方厘米)
体积:
6×6×6
=36×6
=216(立方厘米)
2×2×2=8(立方厘米)
216-8=208(立方厘米)
【解析】通过将凹进去的三个面分别平移到它们的对面后,发现立体图形的表面积就是外面大正方体的表面积,因此,大正方体的棱长×棱长×6=立体图形的表面积;棱长×棱长×棱长=正方体的体积,大正方体的体积-小正方体的体积=立体图形的体积。
39.解:600÷200=3(厘米)
800÷200=4(厘米)
1000÷200=5(厘米)
400÷200=2(厘米)
如下:
【解析】 由图可知,图上1厘米代表实际距离200米,找准观测点学校和医院,根据上北下南,左西右东的方向、角度,再算出距离即可解答。
40.解:原来小明有金鱼:
(8÷4)÷=20(条)
原来小红有金鱼:
20-8=12(条)
答:小明原来有20条金鱼,小红原来有 12条金鱼。
【解析】根据小明原来的金鱼比小红多8条,也就是说小明需要给小红4条,两人才会同样多,据此可知4条金鱼占小明原来金鱼总数的,据此列算式得到小明原来金鱼的数量:4÷=20(条),然后再求出小红金鱼的数量:20-8=12(条)。
41.解:设轿车每时行驶x千米。
30+60×2+2x=300
30+120+2x=300
150+2x=300
150+2x-150=300-150
2x=150
2x÷2=150÷2
x=75
答:轿车每时行驶75千米。
【解析】设轿车每时行驶x千米。依据等量关系式:两车相距的路程+货车的速度×行驶的时间+轿车的速度×行驶的时间=成都与重庆的路程,列方程,解方程。
42.解:0.9×1.5×2+0.9×0.4+0.4×1.5×2
=2.7+0.36+1.2
=4.26(m2)
答:做这个简易衣柜的布罩至少需要4.26m2布。
【解析】长×高×2+长方体的长×宽+宽×高×2=至少需要布罩的面积。
43.320枝
44.解:9-6=3(cm)
3×6×4+6×6×2
=72+72
=144(平方厘米)
答:剩下几何体的表面积是144平方厘米.
【解析】 如图:,从一个长方体中截下一个最大的正方体,则正方体的棱长是长方体中最短的棱长,因此本题中截下的正方体的棱长是6厘米。剩下部分宽和高不变还是6厘米,而长=9-6=3厘米,长方体的表面=(长×宽+长×高+宽×高)×2。
45.解:20×16×7÷(10×16)
=2240÷160
=14(厘米);
答:水面的高度是14厘米。
【解析】长方体体积=长×宽×高,据此求出水的体积,水的体积不变,高=体积÷底面积,据此求解。
46. 解:(40x+1)×(1-)=10(卷)
答:《齐纪》有10卷。
【解析】本题考验利用分数乘法解决应用问题的能力,首先分析题目找出等量关系“ 《齐纪》卷数= 《宋纪》 数目×(1-)”,“ 《宋纪》卷数= 《晋纪》×+1 ”,运用分数乘法的计算能力代入数据求得结果即可。
47.解:
(人)
答:五年级共有132人。
【解析】三班调走4人后和二班人数同样多,则原来三班比二班多4人,所以二班有人,则三班有人,又二、三班共占全体人数的,所以五年级共有人。
48.解:4×4×4÷8
=64÷8
=8(厘米)
答:这个长方体的高是8厘米。
【解析】正方体体积=棱长×棱长×棱长,长方体体积=底面积×高,用正方体橡皮泥的体积除以长方体的底面积即可求出长方体的高。
49.解:设乙队开凿了x米。
675+x=1500
675+x-675=1500-675
x=825
答:乙队开凿了825米。
【解析】设乙队开凿了x米。依据等量关系式:甲对开凿的米数+乙队开凿的米数=总米数,列方程,解方程。
21世纪教育网(www.21cnjy.com)
2024-2025学年五年级下学期数学期末考前提升卷(北师大版)
一、填空题
1.淘气家在学校的北偏东60°方向上700m处。则学校在淘气家 60°方向上 m处。
2.把两个棱长都是1dm的正方体拼成一个长方体,这个长方体的表面积是 。
3.一瓶水连瓶重kg,喝了一半水后连瓶重kg,瓶重 。
4.一台拖拉机 小时耕地1公顷,这台拖拉机耕地1公顷需要 小时,3小时可以耕地 平方米.
5.陈老师要用96cm长的铁丝做一个正方体教具,这个教具的棱长是 cm,在它的表面贴上彩纸,至少要 cm2的彩纸。
6.奇奇要给家里的长方体鱼缸换水。如图鱼缸长 46厘米,宽25厘米,高30厘米他打算先放掉15厘米高的水,再注入20厘米高的新水,假设放水和注水的流量均为每分钟5立方分米,则奇奇给鱼缸换水需要 分钟。(缸壁厚度和其他时间忽略不计)
7.观察线路图填空。
小东从家到公园,他先向 方向走 米到电影院,再向 方向走 米就到公园了。
8.用4个棱长是2厘米的正方体拼成长方体,所得长方体中表面积最大是 平方厘米。
9.一个长方体长8厘米,宽4.5厘米,高5厘米,(如图)把它切成两个长方体,表面积最多增加 平方厘米。
10.一个两位数,十位数字比个位数字大2,这个两位数除以十位数字与个位数字的和,商为6,余数为3,则这个两位数是 。
11.某市9月份晴天天数占本月天数的,阴天天数是晴天天数的,雨天天数比晴天天数的少2天,其余是多云天气。这个城市这个月晴天 天,阴天 天,雨天 天,多云 天。
12.如图,大正方形的边长为20厘米,小正方形的边长是大正方形边长的 。图中阴影部分的面积是 平方厘米。
13.一个长方体木块,长、宽、高分别是9dm、4dm和6dm,把它锯成若干个小正方体,再拼成一个大正方体.这个大正方体的表面积是 平方分米.
14.一根3米长的方钢,把它横截成3段时,表面积增加60平方厘米,原来方钢的体积是 立方厘米。
15.把长12厘米,宽8厘米,高5厘米的长方体木块锯成棱长2厘米的正方体木块,可锯 块。
二、判断题
16.长方体中,如果有两个相对的面是正方形,那么其余的面一定是完全一样的长方形.( ).
17.长方体中,高不变,底面积越大,体积也越大。( )
18.男生人数比女生人数多 ,女生人数就比男生人数少 。( )
19.小明沿直线向东走100米,再向西走100米,又向南走100米,这时他在出发点北100米.( ).
20.一个数的倒数小于1,这个数就大于1。( ).
21.底面积和高相等的长方体、正方体、圆柱体,它们的体积相等。( )
22.一根绳子对折一次后,量得每段长是 m,则原来的绳子长是3m。( )
23.甲数的 等于乙数的 .由于 < ,所以甲<乙.( ).
三、单选题
24.一种商品先提价,再降价,最后的价格( )。
A.原价不变 B.比原价低 C.比原价高 D.无法确定
25.用5千克棉花的 和1千克铁的 相比较,结果是( )。
A.5千克棉花的 重 B.1千克铁的 重
C.一样重 D.无法比较
26.表面积相等的长方体和正方体的体积相比( )。
A.正方体体积大 B.长方体体积大 C.相等
27.以小红家为观测点。小明家在南偏东50°方向上,则以小明家为观测点,小红家在( )方向上。
A.东偏南50° B.北偏西50° C.北偏西40° D.西偏北50”
28.如图图形是正方体平面展开图的共有( )个。
A.2 B.3 C.4
29.把一根长6分米的长方体材料平均锯成3段,表面积增加3.6平方分米,这根木料的体积是( )立方分米.
A.0.9 B.3.6 C.5.4 D.1.8
30.同学们用排水法测量土豆和红薯的体积,已知长方体容器长15cm,宽15cm,高20cm。仔细观察实验过程,比较土豆和红薯的体积,( )。
A.土豆的体积大 B.红薯的体积大
C.一样大 D.无法判断
31.把同样多的食盐溶解在下面三个长方体容器中,最咸的是( )。
A.第①杯 B.第②杯 C.第③杯 D.无法确定
32. 重点题 如下图,以数形变化的规律计算,算式 的结果是( )。
A. B.1 C. D.无法确定
33.观察下图,下列说法正确的是( )。
A.甲的表面积大于乙的表面积 B.甲的表面积等于乙的表面积
C.甲的体积小于乙的体积 D.甲的体积等于乙的体积
34.一个长方体长7cm,宽6cm,高5cm,把它的表面涂成红色。如果把这个长方体全部切割成棱长是1 cm的小正方体且没有剩余,那么切割成的小正方体中两面涂红色的有( )个。
A.8 B.210 C.94 D.48
四、极速那天
35.直接写出得数。
+ = × = 45× = 15÷ =
- = 5÷ = ÷16= ÷ =
36.用你喜欢的方法计算。
37.解方程。
(1) (2) (3)
38.计算下面立体图形的表面积和体积。 (单位:厘米)
五、操作题
39.请你在下面的平面图上标出下面建筑的位置。
少年宫在学校的西偏北30°方向上,距离学校600米。
邮电局在学校的南偏西40°方向上,距离学校800米。
医院在学校的东偏南45°方向上,距离学校1000米。
超市在医院的正北方向,距离医院400米。
六、解决问题
40.小明和小红都养了一些金鱼,小明把自己金鱼条数的送给小红后,两人的金鱼条数同样多。已知小明原来的金鱼比小红多8条,小红和小明原来各有金鱼多少条
41.成都与重庆相距300千米,一辆货车从成都开往重庆,一辆轿车从重庆开往成都,货车每时行驶60千米,2时后,两车相距30千米,轿车每时行驶多少千米?
42.一个长方体简易衣柜,长0.9 m,宽0.4 m,高1.5 m,做这个简易衣柜的布罩至少需要多少平方米布?(底面不用布罩)
43.花店购进玫瑰花和百合花共200枝,占购进花的总枝数的。花店这次共购进多少枝花?
44.从一个长9厘米,宽6厘米,高6厘米的长方体中截下一个最大的正方体。剩下几何体的表面积是多少平方厘米?
45.爱动脑的小优发现,这个封闭的长方体容器平放时,水面的高度是7cm(如图①)。如果把这个容器竖起来放(如图②),水面的高度是多少厘米?(容器厚度忽略不计)
46.《资治通鉴》是司马光编撰的一部编年体通史。全书按朝代分为十六纪,其中《晋纪》有40卷,《宋纪》的卷数比《晋记》的多1卷,《齐纪》的卷数比《宋纪》少,《齐纪》有多少卷
47.五年级共有3个班,一班人数占全年级人数的,三班人数比二班人数多,如果从三班调走4人后,三班和二班的人数同样多。五年级共有多少人?
48.小红将一块棱长为4 厘米的正方体橡皮泥捏成了一个底面积是8平方厘米的长方体,这个长方体的高是多少厘米?
49.天山胜利隧道是世界在建高速公路最长的隧道。两个工程队承建了这条隧道中一段长 1500 米的隧道项目,他们分别从两端相向施工,施工完成时,甲队开凿了675米,则乙队开凿了多少米?(列方程解答)
参考答案及试题解析
1.南偏西;700
【解析】解:淘气家在学校的北偏东60°方向上700m处,
则学校在淘气家南偏西60°方向上700m处。
故答案为:南偏西;700。
【分析】甲在乙什么位置和乙在甲什么位置,他们的关系是:方向相反,角度、距离不变。
2.10平方分米
【解析】解:1×2=2(分米)
(2×1+2×1+1×1)×2
=(2+2+1)×2
=5×2
=10(平方分米)。
故答案为:10平方分米。
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,其中,长=正方体的棱长×2;宽=高=正方体的棱长。
3.kg
【解析】-=-=(kg)
-=(kg)
故答案为:kg。
【分析】根据题意可知,一瓶水连瓶的质量-喝了一半后剩下的连瓶的质量=一半的水的质量,然后用剩下的连瓶质量-一半的水的质量=瓶的质量,据此列式解答。
4.;75000
【解析】解:耕地1公顷需要:(小时);3小时可以耕地:(公顷)=75000(平方米)。
故答案为:;75000。
【分析】用耕地时间除以耕地面积即可求出耕地1公顷需要的时间;用3小时除以耕地1公顷需要的时间即可求出3小时可以耕地的面积,注意把公顷换算成平方米。
5.8;384
【解析】解:96÷12=8(cm),
8×8×6
=64×6
=384(cm2);
故答案为:8;384。
【分析】正方体共有12条棱,求出棱长,正方体表面积=棱长×棱长×6,据此求解即可。
6.8.05
【解析】解:根据题意,可得
4.6×2.5×1.5÷5+4.6×2.5×2÷5
=3.45+4.6
=8.05(分钟)
答:奇奇给鱼缸换水需要8.05分钟
故答案为:8.05
【分析】先将厘米化为分米:46厘米=4.6分米,25厘米=2.5分米,15厘米=1.5分米,20厘米=2厘米。根据长方体的体积公式:V=abh,先求出放掉15厘米高水的体积:4.6×2.5×1.5,然后除以放水的流速,求出放水的时间;再求出注水20厘米高水的体积:4.6×2.5×2,然后除以5,求出注水的时间,最后再将放水的时间加上注水的时间,即可求解
7.东偏北45°;420;东偏南30°;630
【解析】解:小东从家到公园,他先向东偏北45°方向走420米到大电影院,再向东偏南30°方向走630米就到公园了。
故答案为:东偏北45°;420;东偏南30°;630。
【分析】上北下南、左西右东,本题据此观察题中的方向以及对应的角度,再根据图上的距离即可得出答案。
8.72
【解析】解:4×2=8(厘米)
(8×2+8×2+2×2)×2
=(16+16+4)×2
=36×2
=72(平方厘米)。
故答案为:72。
【分析】所得长方体的长是8厘米、宽2厘米、高2厘米时表面积最大,表面积=(长×宽+长×高+宽×高) ×2。
9.80
【解析】 表面积最多增加 :8×5×2=80(平方厘米);
故答案为:80。
【分析】根据图示信息,长>高>宽,切成两个长方体,表面积最多增加:长×高×2,代入数值计算即可。
10.75
【解析】设这两个数为ab,则(a+b)×6+3=10a+b ,而a=b+2,
所以 (2b+2)×6+3=10(b+2)+b,
12b+15=11b+20
b=5 a=5+2=7,则原数为75,
故答案为: 75
【分析】先设数,然后根据位置原理和关系列出关系式,再结合个位与十位关系求解。
11.20;5;2;3
【解析】解:9月有30天,
30×=20(天),
20×=5(天),
20×-2
=4-2
=2(天),
30-(20+5+2)
=30-27
=3(天)
故答案为:20;5;2;3。
【分析】根据题意可知,9月有30天,9月份的天数×=晴天的天数;晴天的天数×=阴天的天数;晴天的天数×-2=雨天的天数;9月份的天数-(晴天的天数+阴天的天数+雨天的天数)=多云的天数,据此列式解答。
12.184
【解析】解:20×=8(厘米),
20×20+8×8-(20+8)×20÷2
=400+64-28×20÷2
=464-280
=184(平方厘米)
故答案为:184。
【分析】可以用两个正方形的面积之和减去左上角空白部分三角形的面积即可求出图中阴影部分的面积。
13.216
【解析】长方体木块的体积:
9×4×6
=36×6
=216(立方分米)
大正方体的体积也是216立方分米;
因为6×6×6=216(立方分米),所以大正方体的棱长是6分米;
大正方体的表面积是:
6×6×6
=36×6
=216(平方分米).
故答案为:216.
【分析】已知长方体的长、宽、高,根据公式:长方体的体积=长×宽×高,可以求出长方体体积;
因为把长方体锯成若干小正方体再拼成大正方体,体积是不变的,所以大正方体的体积就是216立方分米;
体积是216立方分米的正方体,棱长是6分米,根据正方体的表面积公式:正方体的表面积=棱长×棱长×6,据此列式解答.
14.4500
【解析】解:3米=30厘米
60÷4×300
=15×300
=4500(立方厘米)
故答案为:4500。
【分析】把它横截成3段,表面积就会增加4个横截面的面积,所以用横截面面积乘方钢的长度即可求出体积。注意统一单位。
15.48
【解析】12÷2=6,8÷2=4,5÷2=2.5, 6×4×2=48
【分析】长方体的长是12厘米,而正方体的棱长是2厘米,在成这部分,可以锯两排,宽是8厘米,可以锯两排,而高是5厘米,是正方体棱长的2.5倍,最多也只能是2排,所以总共是6×4×2=48
16.正确
【解析】解:长方体中最多会有两个相对的面是正方形,其余的四个面都是长方形且完全相同,原题说法正确.
故答案为:正确
【分析】通常长方体的六个面都是长方形,特殊的长方体有两个相对的面可以是正方形.
17.正确
【解析】解:长方体中,高不变,底面积越大,体积也越大,原题干说法正确。
故答案为:正确。
【分析】长方体的体积=底面积×高,高不变,底面积越大,体积也越大。
18.错误
【解析】÷(1+)
=÷
=
女生人数比男生人数少。
故答案为:错误
【分析】男生人数比女生人数多的几分之几÷(1+男生比女生多的几分之几)=女生人数比男生少几分之几。
19.错误
【解析】根据方向的初步认识相关知识点。【分析】据题意知,向东走100米,在向西走100米,那小明还是站在出发点,又向南走100米,这时他应该在出发点南100米的地方。
20.正确
【解析】因为一个数与它倒数乘积为1,所以这个数=1÷它的倒数,因为这数的倒数小于1,所以这个数就大于1,一个的的倒数小于1,这个数就大于1,这种说法是正确的。
【分析】1÷小于1的数>1。
21.正确
【解析】
底面积和高相等的长方体、正方体、圆柱体,它们的体积都是底面积乘以高,所以体积相等。
故答案为:正确。
【分析】长方体体积=长×宽×高=底面积×高;正方体体积=边长×边长×边长=底面积×高;圆柱体体积=底面积×高。
22.正确
【解析】解: 一根绳子对折一次后,量得每段长是m,则原来的绳子长是3m,说法正确。
故答案为:正确。
【分析】对折一次,将绳子平均分成2段,每一段绳子的长度×平均分成的段数即可得出原来绳子的总长度。
23.错误
【解析】甲数=乙数
甲数乙数=
甲数乙数=>1
甲数>乙数
故题中结论错误
【分析】先建立等量关系,然后推理得出结论,甲数>乙数
24.B
【解析】解:1×(1+)×(1-)
=×
=
<1,最后的价格比原价低。
故答案为:B。
【分析】把这件商品的原价看作单位“1”,现价=原价×(1+提价的分率)×(1-降价的分率),然后比较大小。
25.C
【解析】解:5× = (千克) 1× = (千克)
则用5千克棉花的 和1千克铁的 相比较,结果是一样重.
故答案为:C.
【分析】求一个数的几分之几是多少用乘法列式,本题中就是求5的是多少,1的是多少,分别列乘法算式,再根据分数乘整数的方法求出结果,再比较结果大小即可得出结论.
26.A
【解析】解: 可以先反过来考虑体积相等的长方体和正方体,它们的表面积哪一个大,用8个棱长1厘米正方体,可以拼成一个棱长2厘米的正方体,体积是8立方厘米,表面积是2×2×6=24(平方厘米);也可以拼成一个长8厘米,宽1厘米,高1厘米的长方体,体积同样是8立方厘米,表面积是8×1×4+1×1×2=34(平方厘米);由此可以看出体积相等,正方体的表面积小一些.所以长方体和正方体表面积相等,正方体的体积大。
故答案为:A。
【分析】(长×宽+长×高+宽×高)×2=长方体的表面积;长×宽×高=长方体的体积;
正方体的棱长×棱长×6=正方体的表面积;正方体的棱长×棱长×棱长=正方体的体积。
27.B
【解析】 以小红家为观测点。小明家在南偏东50°方向上,则以小明家为观测点,小红家在北偏西50° 方向上。
故答案为:B。
【分析】此题主要考查了方位的知识,根据方向的相对性,南和北相对,东和西相对,据此找准观测点,描述相对位置即可。
28.B
【解析】从左往右,图1、2、4是正方体的展开图。
故答案为:B。
【分析】正方体的展开图有如下类型:第一类,141型,中间四连方,两侧各一个,共六种;第二类,132型,中间三连方,两侧各有一、二个,共三种;第三类,222型,中间二连方,两侧各有二个,只有一种;第四类,33型,两排各三个,只有一种,据此判断。
29.C
【解析】解:3.6÷4×6
=0.9×6
=5.4(立方分米)
故答案为:C。
【分析】平均截成3段后表面积就会增加4各横截面面积,由此用表面积增加的部分除以4即可求出一个横截面面积,用一个横截面面积乘长即可求出这根木料的体积。
30.B
31.B
【解析】解:①号杯,12×6×3=216(cm3) ;
②号杯,14×5×3=210(cm3);
③号杯,10×7×4=280(cm3);
210<216<280,最咸的是②号杯。
故答案为:B。
【分析】此题主要考查了长方体的体积计算,加入同样多的食盐,水越少越咸,根据长方体体积=长×宽×高,分别求出三个容器中水的体积,比较即可。
32.C
【解析】解: 。
故答案为:C。
【分析】由题图可知,在图上有规律地表示出 ,,,不断累加下去,其结果越来越接近 。
33.B
【解析】解:甲比乙多了一个小正方体,多了3个小正方体面的面积,乙又多露出3个小正方体面的面积,则甲、乙的表面积相等;
甲的体积比乙的体积多了1个小正方体的体积。
故答案为:B。
【分析】甲的表面积=乙的表面积,甲的体积>乙的体积。
34.D
【解析】解:7-2=5(块)
6-2=4(块)
5-2=3(块)
5×4+4×4+3×4
=20+16+12
=36+12
=48(个)。
故答案为:D。
【分析】此题考查长方体切割后小正方体涂色情况的分析。两面涂红色的小正方体位于长方体的棱上(不包括顶点),因此需要计算每条棱上符合条件的小正方体数量,再乘以对应棱的数量。两面涂红色的小正方体位于长方体的12条棱上,但每个顶点处的小正方体会有三面涂色,因此需排除顶点处的正方体。
35.
【解析】异分母分数相加减,先通分再计算;计算分数乘法时能约分的要先约分再乘;计算分数除法时要把除法转化成乘法再计算。
36.解:
=
=
=
=
=1+1
=2
=
=
=
【解析】(1)先将分数同分,再将分子相加减;
(2)将分母相同的分数结合计算;
(3)相乘并约分即可;
(4)将除法转为乘法,再约分即可。
37.(1) x++=1
解:x+=1
x+-=1-
x=
(2) +x=
解:+x-=-
x=
(3) x-=
解:x-+=+
x=
【解析】此题应用等式的性质1:等式的两边同时加减相同的数,等式仍然成立,据此解方程。
38.解:表面积:
6×6×6
=36×6
=216(平方厘米)
体积:
6×6×6
=36×6
=216(立方厘米)
2×2×2=8(立方厘米)
216-8=208(立方厘米)
【解析】通过将凹进去的三个面分别平移到它们的对面后,发现立体图形的表面积就是外面大正方体的表面积,因此,大正方体的棱长×棱长×6=立体图形的表面积;棱长×棱长×棱长=正方体的体积,大正方体的体积-小正方体的体积=立体图形的体积。
39.解:600÷200=3(厘米)
800÷200=4(厘米)
1000÷200=5(厘米)
400÷200=2(厘米)
如下:
【解析】 由图可知,图上1厘米代表实际距离200米,找准观测点学校和医院,根据上北下南,左西右东的方向、角度,再算出距离即可解答。
40.解:原来小明有金鱼:
(8÷4)÷=20(条)
原来小红有金鱼:
20-8=12(条)
答:小明原来有20条金鱼,小红原来有 12条金鱼。
【解析】根据小明原来的金鱼比小红多8条,也就是说小明需要给小红4条,两人才会同样多,据此可知4条金鱼占小明原来金鱼总数的,据此列算式得到小明原来金鱼的数量:4÷=20(条),然后再求出小红金鱼的数量:20-8=12(条)。
41.解:设轿车每时行驶x千米。
30+60×2+2x=300
30+120+2x=300
150+2x=300
150+2x-150=300-150
2x=150
2x÷2=150÷2
x=75
答:轿车每时行驶75千米。
【解析】设轿车每时行驶x千米。依据等量关系式:两车相距的路程+货车的速度×行驶的时间+轿车的速度×行驶的时间=成都与重庆的路程,列方程,解方程。
42.解:0.9×1.5×2+0.9×0.4+0.4×1.5×2
=2.7+0.36+1.2
=4.26(m2)
答:做这个简易衣柜的布罩至少需要4.26m2布。
【解析】长×高×2+长方体的长×宽+宽×高×2=至少需要布罩的面积。
43.320枝
44.解:9-6=3(cm)
3×6×4+6×6×2
=72+72
=144(平方厘米)
答:剩下几何体的表面积是144平方厘米.
【解析】 如图:,从一个长方体中截下一个最大的正方体,则正方体的棱长是长方体中最短的棱长,因此本题中截下的正方体的棱长是6厘米。剩下部分宽和高不变还是6厘米,而长=9-6=3厘米,长方体的表面=(长×宽+长×高+宽×高)×2。
45.解:20×16×7÷(10×16)
=2240÷160
=14(厘米);
答:水面的高度是14厘米。
【解析】长方体体积=长×宽×高,据此求出水的体积,水的体积不变,高=体积÷底面积,据此求解。
46. 解:(40x+1)×(1-)=10(卷)
答:《齐纪》有10卷。
【解析】本题考验利用分数乘法解决应用问题的能力,首先分析题目找出等量关系“ 《齐纪》卷数= 《宋纪》 数目×(1-)”,“ 《宋纪》卷数= 《晋纪》×+1 ”,运用分数乘法的计算能力代入数据求得结果即可。
47.解:
(人)
答:五年级共有132人。
【解析】三班调走4人后和二班人数同样多,则原来三班比二班多4人,所以二班有人,则三班有人,又二、三班共占全体人数的,所以五年级共有人。
48.解:4×4×4÷8
=64÷8
=8(厘米)
答:这个长方体的高是8厘米。
【解析】正方体体积=棱长×棱长×棱长,长方体体积=底面积×高,用正方体橡皮泥的体积除以长方体的底面积即可求出长方体的高。
49.解:设乙队开凿了x米。
675+x=1500
675+x-675=1500-675
x=825
答:乙队开凿了825米。
【解析】设乙队开凿了x米。依据等量关系式:甲对开凿的米数+乙队开凿的米数=总米数,列方程,解方程。
21世纪教育网(www.21cnjy.com)
同课章节目录
