2024-2025学年期末模拟试卷(含解析)五年级下册数学(北师大版)
文档属性
| 名称 | 2024-2025学年期末模拟试卷(含解析)五年级下册数学(北师大版) |  | |
| 格式 | docx | ||
| 文件大小 | 176.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 08:57:23 | ||
图片预览




文档简介
2024-2025学年期末模拟试卷(试题)五年级下册数学(北师大版)
一、单选题
1.一项工程,5天完成.平均每天完成这件工程的几分之几?正确的是( )
A. B. C. D.
2.下面算式中,结果最大的是( )。
A. ÷ B. × C. - D. ÷
3.一个长方体长a厘米,宽b厘米,高c厘米,如果它的长增加2厘米,那么它的表面积增加( )cm2。
A.4b+4c B.2bc C.4bc D.2b+2c
4.把化成,下面的说法中,正确的是( )。
A.分数大小不变,分数单位变小 B.分数大小不变,分数单位变大
C.分数变大,分数单位不变 D.分数变小,分数单位不变
5.甲乙两股长1米的绳子,甲剪去 米,乙剪去 ,余下的绳子( )
A.甲比乙短 B.甲乙长度相等
C.甲比乙长 D.不能确定
6.小明用一张长方形纸正好可以画上一个棱长为3厘米的无盖的正方体的表面展开图,这张长方形纸的面积最小是( )平方厘米。
A.36 B.54 C.72 D.81
7.a是大于1的自然数,下列各式中,结果最大的是( )。
A.a× B.a÷ C.a× D.a÷
8.下列图形中,能折成正方体的是( )
A. B. C.
二、判断题
9. 棱长1米的正方体可以截成100个棱长是1厘米的小正方体。 ( )
10.正方体的6个面是完全一样的正方形.( )
11.已知a和b都是自然数,且 ,则b>a。( )
12.一个正方体的棱长扩大2倍,它的体积就扩大到原来的4倍。( )
13.条形统计图能够表示一个量的增减变化情况。( )
14.一个正方体盒子容积是120立方分米,它的体积一定是120立方分米。(
)
15.用小正方体拼大正方体,所取的小正方体的个数一定是立方数。( )
16.甲数比乙数多 ,乙数就比甲数少 ( )
三、填空题
17.在横线里填入适当的运算符号,使等式成立。
= 0.6 =
=8 0.6=0.15
18.一个正方体的棱长是3分米,它的表面积是 平方分米。
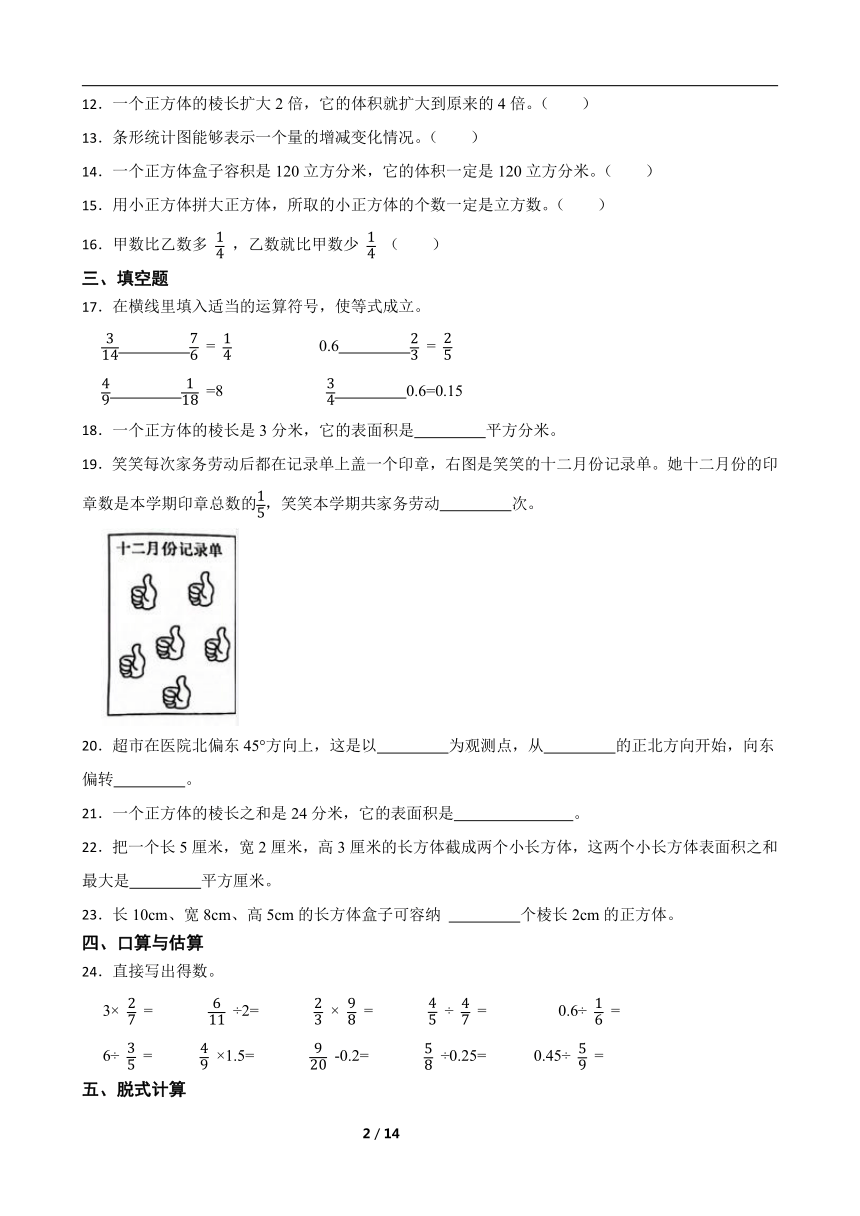
19.笑笑每次家务劳动后都在记录单上盖一个印章,右图是笑笑的十二月份记录单。她十二月份的印章数是本学期印章总数的,笑笑本学期共家务劳动 次。
20.超市在医院北偏东45°方向上,这是以 为观测点,从 的正北方向开始,向东偏转 。
21.一个正方体的棱长之和是24分米,它的表面积是 。
22.把一个长5厘米,宽2厘米,高3厘米的长方体截成两个小长方体,这两个小长方体表面积之和最大是 平方厘米。
23.长10cm、宽8cm、高5cm的长方体盒子可容纳 个棱长2cm的正方体。
四、口算与估算
24.直接写出得数。
3× = ÷2= × = ÷ = 0.6÷ =
6÷ = ×1.5= -0.2= ÷0.25= 0.45÷ =
五、脱式计算
25.脱式计算。
六、解方程
26.解方程。
(1)9-x=
(2) +x=
(3)x- =
七、操作题
27.按要求画一画。
(1)红星学校东面400米处是银行,请你用“▲”标出银行的位置。
(2)红星学校在真又美超市南面320米的位置,请你用“■”标出真又美超市的位置。
八、解决问题
28.益和药店购进一批相同数量的N95口罩和一次性普通口罩,共花了4800元。N95口罩1.5元/只,一次性普通口罩单价为0.5元。购进N95口罩多少只?(用方程解)
29.在第32届东京奥运会上,我国体育代表团共获得88枚奖牌,其中金牌占,银牌占。我国体育代表团获得金、银牌各多少枚?
30.某校五年级学生为灾区共捐款1200元,约占全校学生捐款数的 .全校学生共捐款多少元?
31.在棱长为2.5分米的正方体容器里倒入适量的水,然后放入4块大小相同的橡皮泥,橡皮泥全部浸没水中,水面上升了2厘米,算一算一块橡皮泥的体积是多少?
32.一种长方体铁皮通风管长3m,管口是边长2dm的正方形。王师傅做一节这样的通风管,至少需要多少平方米的铁皮?(接口忽略不计)
33.某学校要建一个长30米、宽20米、深1.5米的游泳池。
(1)如果游泳池的四壁和底面用瓷砖贴,贴面一共是多少平方米
(2)这个游泳池最多能装水多少立方米
34.一个自然保护区里一共有天鹅和丹顶鹤960只,天鹅的只数是丹顶鹤的2.2倍.天鹅和丹顶鹤各有多少只?(用方程解答)
35.身高是1.64 m的唐老师带领一些学生乘坐公交车去参加活动,单程全票票价为4元。根据下面的信息计算,他们来回乘车一共需要多少元?
答案解析部分
1.【答案】B
【解析】【解答】1÷5=
故答案为:B
【分析】以这项工程为单位“1”,用1除以完成的工作时间即可求出平均每天完成这件工程的几分之几.
2.【答案】A
【解析】【解答】解:,。
因为,所以A>D>B。
因为,所以;
又因为,
所以A>C。
故结果最大的是A。
故答案为:A。
【分析】除以一个数(0除外)就等于乘它的倒数;
一个因数不变,另一个因数越大,则积越大;
一个数乘另一个比1大的数,则积大于它本身。
3.【答案】A
【解析】【解答】解:原来的表面积:(ab+ac+bc)×2=2ab+2ac+2bc
现在的表面积:(a+2)×b×2+(a+2)×c×2+b×c×2
=2ab+4b+2ac+4c+2bc
=2ab+2ac+2bc+4b+4c
所以现在的表面积比原来增加了4b+4c;
故答案为:A。
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,据此求出原来的表面积和现在的表面积,再比较即可。
4.【答案】B
【解析】【解答】解:=
约分前,的分数单位是;
约分后,的分数单位是。
可以看出,约分后的分数单位变大了。
由于约分过程保持了分数值不变,所以分数的大小没有变化。
故答案为:B
【分析】本题考查对分数约分的理解,以及约分前后分数大小与分数单位变化的判断。首先,理解约分的概念,即化简分数到最简形式,同时保持其值不变。然后,对比约分前后的分数单位变化,来确定正确的选项。
5.【答案】B
【解析】【解答】解:1× = (米)
即乙剪去的和甲减去的一样多,则余下的也一样多.
故选:B.
【分析】一米的 为:1× = 米,即乙剪去的和甲减去的一样多,由于两根绳子一样长,则余下的也一样多.完成本题要注意 与 米的区别, 表示剪去的占总数的几分之几, 米表示具体的数量.
6.【答案】C
【解析】【解答】3×2×3×4=6×12=72(平方厘米)
故答案为:C
【分析】根据正方体展开图的11种形式进行解答即可。
7.【答案】B
【解析】【解答】解:A项:因为<1,所以a×<a;
B项:因为<1,所以a÷>a;
C项:因为>1,所以a×>a;
D项:因为>1,所以a÷<a;
排除A项和D项,B项:a÷=a×2;a×2>a×,结果最大的是B项。
故答案为:B。
【分析】一个非0的数除以小于1的数,所得的商大于原来的数;反之,商小于原来的数;一个非0的数乘小于1的数,所得的积小于原来的数,反之,积大于原来的数。
8.【答案】C
【解析】【解答】解:根据正方体展开图的特征,图C能折成正方体,图A和图B不能折成正方体;
故选:C.
【分析】根据正方体展开图的11种特征,图C是“1 4 1”结构,是正方体的展开图,能折成正方体;图A和图B不符全正方体展开图的11种特征,不是正方体的展开图,不能折成正方体.
9.【答案】错误
【解析】【解答】解:大正方体的体积:1×1×1=1(立方米)
小正方体的体积:1×1×1=1(立方厘米)
1立方米=1000000立方厘米
因此,棱长1米的正方体可以截成1000000个棱长是1厘米的小正方体,原题说法错误。
故答案为:错误。
【分析】根据正方体的体积=棱长×棱长×棱长,分别求出大正方体体积和小正方体体积,从而进行判断。
10.【答案】正确
【解析】【解答】 正方体的6个面是完全一样的正方形,此题说法正确.
故答案为:正确.
【分析】此题主要考查了正方体的特征,正方体的6个面是完全一样的正方形,12条棱长度相等,据此判断.
11.【答案】错误
【解析】【解答】 , 所以,所以a>b。
故答案为:错误。
【分析】如果两个乘法算式的积相等, 一个因数越大,与它相乘的另一个因数就越小。
12.【答案】错误
【解析】【解答】设原正方体的棱长为1,扩大后正方体的棱长为2。
原正方体的体积:1×1×1=1,扩大后正方体的体积:2×2×2=8,8是1的8倍。
故答案为:错误。
【分析】正方体体积=边长×边长×边长;据此解答即可。
13.【答案】错误
【解析】【解答】解:条形统计图能够清楚的看出数量的多少。
故答案为:错误。
【分析】条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
14.【答案】错误
【解析】【解答】 一个正方体盒子容积是120立方分米,它的体积≥120立方分米。
故答案为:错误
【分析】 求物体的体积是从该物体的外部来测量,而求容积却是从物体的内部来测量。一种既有体积又有容积的物体,它的体积一定大于它的容积;只有当忽略容器壁的厚度时,它的容积才等于体积。
15.【答案】正确
【解析】【解答】解:用小正方体拼大正方体,所取的小正方体的个数一定是立方数。
故答案为:正确。
【分析】大正方体需要小正方体的个数有23、33、43、……,所以用小正方体拼大正方体,所取的小正方体的个数一定是立方数。
16.【答案】错误
【解析】【解答】把乙数看作单位1,那么甲数为:1+=;
乙数比甲数少:÷=
故答案为:错误。
【分析】乙数比甲数少几分之几=乙数比甲数少的数÷甲数。
17.【答案】×;×;÷;-
【解析】【解答】解:×=
0.6×=
÷=8
-0.6=0.15
故答案为:×;×;÷;-。
【分析】一个非0的数除以一个分数,等于这个数乘它的倒数;分数和分数相乘,能约分的先约分,然后再相乘。
18.【答案】54
19.【答案】30
【解析】【解答】解:6÷=30(次)
故答案为:30。
【分析】把本学期印章总数看作单位“1”,十二月份的印章数÷十二月份印章数占本学期印章总数的分率=本学期印章总数,根据题意可知印章总数即笑笑做家务劳动次数。
20.【答案】医院;医院;45°
【解析】【解答】解:超市在医院北偏东45°方向上,这是以医院为观测点,从医院的正北方向开始,向东偏转45°。
故答案为:医院;医院;45°。
【分析】先确定观测点,然后确定从哪个方向开始,还要确定偏转的方向和偏转的度数。
21.【答案】24平方分米
【解析】【解答】解:棱长:24÷12=2(分米),
表面积:2×2×6=24(平方分米)。
故答案为:24平方分米。
【分析】正方体棱长和=棱长×12,由此用棱长和除以12求出每条棱的长度。正方体表面积=棱长×棱长×6,根据公式计算表面积即可。
22.【答案】92
【解析】【解答】解:(5×2+5×3+3×2)×2+5×3×2
=(10+15+6)×2+5×3×2
=(25+6)×2+5×3×2
=31×2+5×3×2
=62+15×2
=62+30
=92(平方厘米)
故答案为:92。
【分析】在这个长方体中,最大的面是长5厘米,高3厘米的面,那么就沿着这个面切开,这两个小长方体表面积之和最大=原来长方体的表面积+增加的2个面的面积,其中长方体的表面积=(长×宽+长×高+宽×高)×2,增加的两个面的面积=切面的面积=长×高×2,代入数值计算,据此解答即可。
23.【答案】40
【解析】【解答】解:10÷2=5(个)
8÷2=4(个)
5÷2=2(个)······2(厘米)
5×4×2
=20×2
=40(个)。
故答案为:40。
【分析】这个长方体盒子可容纳小正方体的个数=长边容纳小正方体的个数×宽边容纳小正方体的个数×高边容纳小正方体的个数。
24.【答案】3×= ÷2= ×= ÷= 0.6÷=3.6
6÷=10 ×1.5= -0.2= ÷0.25= 0.45÷=0.81
【解析】【分析】分数乘以分数计算法则:分子与分子相乘作为积的分子,分母与分母相乘作为积的分母。
分数与小数(整数)的计算方法:先将小数(整数)与分数的分母进行约分,接下来再进行相乘即可。
除以一个数等于乘以这个数的倒数。
小数与分数的混合运算,将小数化成分数,或将分数化成小数,再进行计算即可。
25.【答案】解:
=22×
=
=7×7
=49
=×1
=
=2×3
=6
=×
=
=×
=
【解析】【分析】一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
26.【答案】(1) 9-x=
解:x=9-
x=8
(2) +x=
解:+x-=-
x=-
x=
(3) x-=
解:x-+=+
x=+
x=
【解析】【分析】(1)根据减数=被减数-差即可得出x的值;
(2)两同时减去即可得出x的值;
(3)两边同时加上即可得出x的值。
27.【答案】(1)
(2)
【解析】【分析】观察此题可知,此图是按“上北下南,左西右东”来规定方向的,找准参照物,根据相对位置找出银行和真又美超市的位置。
28.【答案】解:设购进N95口罩x只。
(1.5+0.5)x=4800
2x=4800
x=4800÷2
x=2400
答:购进N95口罩2400只。
【解析】【分析】依据等量关系式:(购进N95口罩的单价+购进一次性普通口罩的单价)×购买的数量=总价,列方程,解方程。
29.【答案】解:88×=38(枚)
88×=32(枚)
答:我国体育代表团获得金、银牌分别是38枚和32枚。
【解析】【分析】我国体育代表团获得金、银牌分别的枚数=我国体育代表团共获得奖牌的枚数分别×金、银牌各占的分率。
30.【答案】解:1200÷ =3200(元)
答:全校学生共捐款3200元
【解析】【分析】把全校捐款的总钱数看成单位“1”,它的 就是五年级学生的捐款数1200元,由此用除法求出全校学生的捐款数.本题先找出单位“1”,已知一个数的几分之几是多少,求这个数用除法.
31.【答案】解:2.5分米=25厘米
25×25×2÷4
=1250÷4
=312.5(立方厘米)
答:一块橡皮泥的体积是312.5立方厘米。
【解析】【分析】正方体的棱长×棱长×水面上升的高度=4块橡皮泥的体积,4块橡皮泥的体积÷4=1块橡皮泥的体积。
32.【答案】3×2×4
=6×4
=24(平方米)
答: 至少需要24平方米的铁皮。
【解析】【分析】根据题意可知,通风管没有上、下两个底面,只有4个侧面,根据条件“ 管口是边长2dm的正方形 ”可知,这个长方体的4个侧面的面积是相等的,依据长×高×4=长方体铁皮的表面积,据此列式解答。
33.【答案】(1)解:30×20+(30×1.5+20×1.5)x 2
=600+(45+30)
=600+75×2
=600+150
=750(平方米)
答:贴面一共是750平方米。
(2)解:30×20×1.5
=600×1.5
=900(立方米)
答:这个游泳池最多能装水900立方米。
【解析】【分析】(1)长方体的表面积=(长×宽+长×高+宽×高)×2,本题中上面不贴瓷砖,所以贴瓷砖的面积=长×宽+(长×高+宽×高)×2,代入数值计算;
(2)长方体的体积=长×宽×高,能装水多少立方米即是求长方体的体积,代入数值计算即可。
34.【答案】解:设丹顶鹤有x只,那么天鹅有2.2x只。
x+2.2x=960
3.2x=960
x=300
2.2x=300×2.2=660(只)
答:丹顶鹤有300只,那么天鹅有660只。
【解析】【分析】本题可以设丹顶鹤有x只,那么天鹅有2.2x只,题中存在的等量关系是:丹顶鹤的只数+天鹅的只数=天鹅和丹顶鹤一共有的只数,据此代入数值作答即可。
35.【答案】解:4÷2=2(元)
学生免票:(1+3)×0=0(元)
半票:(14+12)×2=52(元)
全票:(1+2)×4=12(元)
教师:4元
(0+52+12+4)×2
=68×2
=136(元)
答:他们来回乘车一共需要136元。
【解析】【分析】全票4元,半票2元。免票的1+3=4人;半票的(14+12)人,全票的(1+2)人,分别计算出半票和全票的钱数,再加上老师1占全票的钱数求出去时的钱数,然后乘2求出来回一共需要的钱数。
1 / 1
一、单选题
1.一项工程,5天完成.平均每天完成这件工程的几分之几?正确的是( )
A. B. C. D.
2.下面算式中,结果最大的是( )。
A. ÷ B. × C. - D. ÷
3.一个长方体长a厘米,宽b厘米,高c厘米,如果它的长增加2厘米,那么它的表面积增加( )cm2。
A.4b+4c B.2bc C.4bc D.2b+2c
4.把化成,下面的说法中,正确的是( )。
A.分数大小不变,分数单位变小 B.分数大小不变,分数单位变大
C.分数变大,分数单位不变 D.分数变小,分数单位不变
5.甲乙两股长1米的绳子,甲剪去 米,乙剪去 ,余下的绳子( )
A.甲比乙短 B.甲乙长度相等
C.甲比乙长 D.不能确定
6.小明用一张长方形纸正好可以画上一个棱长为3厘米的无盖的正方体的表面展开图,这张长方形纸的面积最小是( )平方厘米。
A.36 B.54 C.72 D.81
7.a是大于1的自然数,下列各式中,结果最大的是( )。
A.a× B.a÷ C.a× D.a÷
8.下列图形中,能折成正方体的是( )
A. B. C.
二、判断题
9. 棱长1米的正方体可以截成100个棱长是1厘米的小正方体。 ( )
10.正方体的6个面是完全一样的正方形.( )
11.已知a和b都是自然数,且 ,则b>a。( )
12.一个正方体的棱长扩大2倍,它的体积就扩大到原来的4倍。( )
13.条形统计图能够表示一个量的增减变化情况。( )
14.一个正方体盒子容积是120立方分米,它的体积一定是120立方分米。(
)
15.用小正方体拼大正方体,所取的小正方体的个数一定是立方数。( )
16.甲数比乙数多 ,乙数就比甲数少 ( )
三、填空题
17.在横线里填入适当的运算符号,使等式成立。
= 0.6 =
=8 0.6=0.15
18.一个正方体的棱长是3分米,它的表面积是 平方分米。
19.笑笑每次家务劳动后都在记录单上盖一个印章,右图是笑笑的十二月份记录单。她十二月份的印章数是本学期印章总数的,笑笑本学期共家务劳动 次。
20.超市在医院北偏东45°方向上,这是以 为观测点,从 的正北方向开始,向东偏转 。
21.一个正方体的棱长之和是24分米,它的表面积是 。
22.把一个长5厘米,宽2厘米,高3厘米的长方体截成两个小长方体,这两个小长方体表面积之和最大是 平方厘米。
23.长10cm、宽8cm、高5cm的长方体盒子可容纳 个棱长2cm的正方体。
四、口算与估算
24.直接写出得数。
3× = ÷2= × = ÷ = 0.6÷ =
6÷ = ×1.5= -0.2= ÷0.25= 0.45÷ =
五、脱式计算
25.脱式计算。
六、解方程
26.解方程。
(1)9-x=
(2) +x=
(3)x- =
七、操作题
27.按要求画一画。
(1)红星学校东面400米处是银行,请你用“▲”标出银行的位置。
(2)红星学校在真又美超市南面320米的位置,请你用“■”标出真又美超市的位置。
八、解决问题
28.益和药店购进一批相同数量的N95口罩和一次性普通口罩,共花了4800元。N95口罩1.5元/只,一次性普通口罩单价为0.5元。购进N95口罩多少只?(用方程解)
29.在第32届东京奥运会上,我国体育代表团共获得88枚奖牌,其中金牌占,银牌占。我国体育代表团获得金、银牌各多少枚?
30.某校五年级学生为灾区共捐款1200元,约占全校学生捐款数的 .全校学生共捐款多少元?
31.在棱长为2.5分米的正方体容器里倒入适量的水,然后放入4块大小相同的橡皮泥,橡皮泥全部浸没水中,水面上升了2厘米,算一算一块橡皮泥的体积是多少?
32.一种长方体铁皮通风管长3m,管口是边长2dm的正方形。王师傅做一节这样的通风管,至少需要多少平方米的铁皮?(接口忽略不计)
33.某学校要建一个长30米、宽20米、深1.5米的游泳池。
(1)如果游泳池的四壁和底面用瓷砖贴,贴面一共是多少平方米
(2)这个游泳池最多能装水多少立方米
34.一个自然保护区里一共有天鹅和丹顶鹤960只,天鹅的只数是丹顶鹤的2.2倍.天鹅和丹顶鹤各有多少只?(用方程解答)
35.身高是1.64 m的唐老师带领一些学生乘坐公交车去参加活动,单程全票票价为4元。根据下面的信息计算,他们来回乘车一共需要多少元?
答案解析部分
1.【答案】B
【解析】【解答】1÷5=
故答案为:B
【分析】以这项工程为单位“1”,用1除以完成的工作时间即可求出平均每天完成这件工程的几分之几.
2.【答案】A
【解析】【解答】解:,。
因为,所以A>D>B。
因为,所以;
又因为,
所以A>C。
故结果最大的是A。
故答案为:A。
【分析】除以一个数(0除外)就等于乘它的倒数;
一个因数不变,另一个因数越大,则积越大;
一个数乘另一个比1大的数,则积大于它本身。
3.【答案】A
【解析】【解答】解:原来的表面积:(ab+ac+bc)×2=2ab+2ac+2bc
现在的表面积:(a+2)×b×2+(a+2)×c×2+b×c×2
=2ab+4b+2ac+4c+2bc
=2ab+2ac+2bc+4b+4c
所以现在的表面积比原来增加了4b+4c;
故答案为:A。
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,据此求出原来的表面积和现在的表面积,再比较即可。
4.【答案】B
【解析】【解答】解:=
约分前,的分数单位是;
约分后,的分数单位是。
可以看出,约分后的分数单位变大了。
由于约分过程保持了分数值不变,所以分数的大小没有变化。
故答案为:B
【分析】本题考查对分数约分的理解,以及约分前后分数大小与分数单位变化的判断。首先,理解约分的概念,即化简分数到最简形式,同时保持其值不变。然后,对比约分前后的分数单位变化,来确定正确的选项。
5.【答案】B
【解析】【解答】解:1× = (米)
即乙剪去的和甲减去的一样多,则余下的也一样多.
故选:B.
【分析】一米的 为:1× = 米,即乙剪去的和甲减去的一样多,由于两根绳子一样长,则余下的也一样多.完成本题要注意 与 米的区别, 表示剪去的占总数的几分之几, 米表示具体的数量.
6.【答案】C
【解析】【解答】3×2×3×4=6×12=72(平方厘米)
故答案为:C
【分析】根据正方体展开图的11种形式进行解答即可。
7.【答案】B
【解析】【解答】解:A项:因为<1,所以a×<a;
B项:因为<1,所以a÷>a;
C项:因为>1,所以a×>a;
D项:因为>1,所以a÷<a;
排除A项和D项,B项:a÷=a×2;a×2>a×,结果最大的是B项。
故答案为:B。
【分析】一个非0的数除以小于1的数,所得的商大于原来的数;反之,商小于原来的数;一个非0的数乘小于1的数,所得的积小于原来的数,反之,积大于原来的数。
8.【答案】C
【解析】【解答】解:根据正方体展开图的特征,图C能折成正方体,图A和图B不能折成正方体;
故选:C.
【分析】根据正方体展开图的11种特征,图C是“1 4 1”结构,是正方体的展开图,能折成正方体;图A和图B不符全正方体展开图的11种特征,不是正方体的展开图,不能折成正方体.
9.【答案】错误
【解析】【解答】解:大正方体的体积:1×1×1=1(立方米)
小正方体的体积:1×1×1=1(立方厘米)
1立方米=1000000立方厘米
因此,棱长1米的正方体可以截成1000000个棱长是1厘米的小正方体,原题说法错误。
故答案为:错误。
【分析】根据正方体的体积=棱长×棱长×棱长,分别求出大正方体体积和小正方体体积,从而进行判断。
10.【答案】正确
【解析】【解答】 正方体的6个面是完全一样的正方形,此题说法正确.
故答案为:正确.
【分析】此题主要考查了正方体的特征,正方体的6个面是完全一样的正方形,12条棱长度相等,据此判断.
11.【答案】错误
【解析】【解答】 , 所以,所以a>b。
故答案为:错误。
【分析】如果两个乘法算式的积相等, 一个因数越大,与它相乘的另一个因数就越小。
12.【答案】错误
【解析】【解答】设原正方体的棱长为1,扩大后正方体的棱长为2。
原正方体的体积:1×1×1=1,扩大后正方体的体积:2×2×2=8,8是1的8倍。
故答案为:错误。
【分析】正方体体积=边长×边长×边长;据此解答即可。
13.【答案】错误
【解析】【解答】解:条形统计图能够清楚的看出数量的多少。
故答案为:错误。
【分析】条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
14.【答案】错误
【解析】【解答】 一个正方体盒子容积是120立方分米,它的体积≥120立方分米。
故答案为:错误
【分析】 求物体的体积是从该物体的外部来测量,而求容积却是从物体的内部来测量。一种既有体积又有容积的物体,它的体积一定大于它的容积;只有当忽略容器壁的厚度时,它的容积才等于体积。
15.【答案】正确
【解析】【解答】解:用小正方体拼大正方体,所取的小正方体的个数一定是立方数。
故答案为:正确。
【分析】大正方体需要小正方体的个数有23、33、43、……,所以用小正方体拼大正方体,所取的小正方体的个数一定是立方数。
16.【答案】错误
【解析】【解答】把乙数看作单位1,那么甲数为:1+=;
乙数比甲数少:÷=
故答案为:错误。
【分析】乙数比甲数少几分之几=乙数比甲数少的数÷甲数。
17.【答案】×;×;÷;-
【解析】【解答】解:×=
0.6×=
÷=8
-0.6=0.15
故答案为:×;×;÷;-。
【分析】一个非0的数除以一个分数,等于这个数乘它的倒数;分数和分数相乘,能约分的先约分,然后再相乘。
18.【答案】54
19.【答案】30
【解析】【解答】解:6÷=30(次)
故答案为:30。
【分析】把本学期印章总数看作单位“1”,十二月份的印章数÷十二月份印章数占本学期印章总数的分率=本学期印章总数,根据题意可知印章总数即笑笑做家务劳动次数。
20.【答案】医院;医院;45°
【解析】【解答】解:超市在医院北偏东45°方向上,这是以医院为观测点,从医院的正北方向开始,向东偏转45°。
故答案为:医院;医院;45°。
【分析】先确定观测点,然后确定从哪个方向开始,还要确定偏转的方向和偏转的度数。
21.【答案】24平方分米
【解析】【解答】解:棱长:24÷12=2(分米),
表面积:2×2×6=24(平方分米)。
故答案为:24平方分米。
【分析】正方体棱长和=棱长×12,由此用棱长和除以12求出每条棱的长度。正方体表面积=棱长×棱长×6,根据公式计算表面积即可。
22.【答案】92
【解析】【解答】解:(5×2+5×3+3×2)×2+5×3×2
=(10+15+6)×2+5×3×2
=(25+6)×2+5×3×2
=31×2+5×3×2
=62+15×2
=62+30
=92(平方厘米)
故答案为:92。
【分析】在这个长方体中,最大的面是长5厘米,高3厘米的面,那么就沿着这个面切开,这两个小长方体表面积之和最大=原来长方体的表面积+增加的2个面的面积,其中长方体的表面积=(长×宽+长×高+宽×高)×2,增加的两个面的面积=切面的面积=长×高×2,代入数值计算,据此解答即可。
23.【答案】40
【解析】【解答】解:10÷2=5(个)
8÷2=4(个)
5÷2=2(个)······2(厘米)
5×4×2
=20×2
=40(个)。
故答案为:40。
【分析】这个长方体盒子可容纳小正方体的个数=长边容纳小正方体的个数×宽边容纳小正方体的个数×高边容纳小正方体的个数。
24.【答案】3×= ÷2= ×= ÷= 0.6÷=3.6
6÷=10 ×1.5= -0.2= ÷0.25= 0.45÷=0.81
【解析】【分析】分数乘以分数计算法则:分子与分子相乘作为积的分子,分母与分母相乘作为积的分母。
分数与小数(整数)的计算方法:先将小数(整数)与分数的分母进行约分,接下来再进行相乘即可。
除以一个数等于乘以这个数的倒数。
小数与分数的混合运算,将小数化成分数,或将分数化成小数,再进行计算即可。
25.【答案】解:
=22×
=
=7×7
=49
=×1
=
=2×3
=6
=×
=
=×
=
【解析】【分析】一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
26.【答案】(1) 9-x=
解:x=9-
x=8
(2) +x=
解:+x-=-
x=-
x=
(3) x-=
解:x-+=+
x=+
x=
【解析】【分析】(1)根据减数=被减数-差即可得出x的值;
(2)两同时减去即可得出x的值;
(3)两边同时加上即可得出x的值。
27.【答案】(1)
(2)
【解析】【分析】观察此题可知,此图是按“上北下南,左西右东”来规定方向的,找准参照物,根据相对位置找出银行和真又美超市的位置。
28.【答案】解:设购进N95口罩x只。
(1.5+0.5)x=4800
2x=4800
x=4800÷2
x=2400
答:购进N95口罩2400只。
【解析】【分析】依据等量关系式:(购进N95口罩的单价+购进一次性普通口罩的单价)×购买的数量=总价,列方程,解方程。
29.【答案】解:88×=38(枚)
88×=32(枚)
答:我国体育代表团获得金、银牌分别是38枚和32枚。
【解析】【分析】我国体育代表团获得金、银牌分别的枚数=我国体育代表团共获得奖牌的枚数分别×金、银牌各占的分率。
30.【答案】解:1200÷ =3200(元)
答:全校学生共捐款3200元
【解析】【分析】把全校捐款的总钱数看成单位“1”,它的 就是五年级学生的捐款数1200元,由此用除法求出全校学生的捐款数.本题先找出单位“1”,已知一个数的几分之几是多少,求这个数用除法.
31.【答案】解:2.5分米=25厘米
25×25×2÷4
=1250÷4
=312.5(立方厘米)
答:一块橡皮泥的体积是312.5立方厘米。
【解析】【分析】正方体的棱长×棱长×水面上升的高度=4块橡皮泥的体积,4块橡皮泥的体积÷4=1块橡皮泥的体积。
32.【答案】3×2×4
=6×4
=24(平方米)
答: 至少需要24平方米的铁皮。
【解析】【分析】根据题意可知,通风管没有上、下两个底面,只有4个侧面,根据条件“ 管口是边长2dm的正方形 ”可知,这个长方体的4个侧面的面积是相等的,依据长×高×4=长方体铁皮的表面积,据此列式解答。
33.【答案】(1)解:30×20+(30×1.5+20×1.5)x 2
=600+(45+30)
=600+75×2
=600+150
=750(平方米)
答:贴面一共是750平方米。
(2)解:30×20×1.5
=600×1.5
=900(立方米)
答:这个游泳池最多能装水900立方米。
【解析】【分析】(1)长方体的表面积=(长×宽+长×高+宽×高)×2,本题中上面不贴瓷砖,所以贴瓷砖的面积=长×宽+(长×高+宽×高)×2,代入数值计算;
(2)长方体的体积=长×宽×高,能装水多少立方米即是求长方体的体积,代入数值计算即可。
34.【答案】解:设丹顶鹤有x只,那么天鹅有2.2x只。
x+2.2x=960
3.2x=960
x=300
2.2x=300×2.2=660(只)
答:丹顶鹤有300只,那么天鹅有660只。
【解析】【分析】本题可以设丹顶鹤有x只,那么天鹅有2.2x只,题中存在的等量关系是:丹顶鹤的只数+天鹅的只数=天鹅和丹顶鹤一共有的只数,据此代入数值作答即可。
35.【答案】解:4÷2=2(元)
学生免票:(1+3)×0=0(元)
半票:(14+12)×2=52(元)
全票:(1+2)×4=12(元)
教师:4元
(0+52+12+4)×2
=68×2
=136(元)
答:他们来回乘车一共需要136元。
【解析】【分析】全票4元,半票2元。免票的1+3=4人;半票的(14+12)人,全票的(1+2)人,分别计算出半票和全票的钱数,再加上老师1占全票的钱数求出去时的钱数,然后乘2求出来回一共需要的钱数。
1 / 1
同课章节目录
