期末模拟测试考前预测卷(含解析)-2024-2025学年七年级下册数学人教版(2024)
文档属性
| 名称 | 期末模拟测试考前预测卷(含解析)-2024-2025学年七年级下册数学人教版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 283.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 10:18:24 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末模拟测试考前预测卷
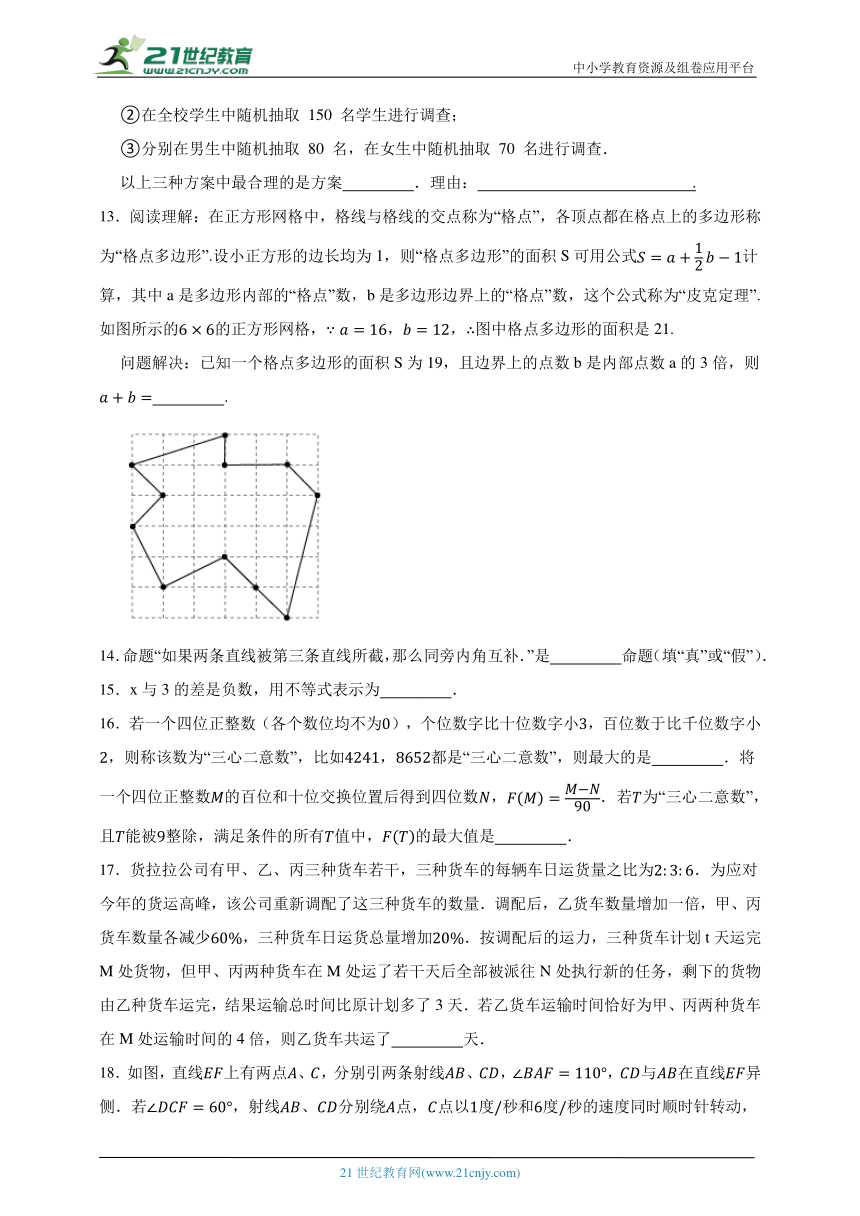
一、单选题
1.如图是红、黄两队某局比赛投壶结束后冰壶的分布图,以冰壶大本营内的中心点为原点建立平面直角坐标系,按照规则更靠近原点的壶为本局胜方,则胜方最靠近原点的壶所在位置位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.下列各方程中,是二元一次方程的是( )
A. B. C. D.
3.8的算术平方根是( )
A.4 B.2 C.±2 D.2
4.将一副三角板如图放置,则下列结论中正确的是:( )
①如果,则有;
②;
③如果,则有;
④如果,必有;
A.①②③ B.③④ C.①②④ D.①②③④
5.下列调查中,适合全面调查的是( )
A.检测载人飞船零件的质量
B.检测一批LED灯的使用寿命
C.检测杭嘉湖三地的空气质量
D.检测一批家用汽车的抗撞击能力
6.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
7.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的一组对边上,如果∠1=25°,那么∠2的度数是( )
A.30° B.25° C.20° D.15°
8.在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(3,1),则点A2017的坐标为( )
A.(0,4) B.(﹣3,1) C.(0,﹣2) D.(3,1)
9.已知方程组 ,则 的值为( )
A.14 B.2 C.-14 D.-2
10.如图,已知直线,则、、之间的关系是( )
A. B.
C. D.
二、填空题
11.若关于x,y的二元一次方程组和同解,则 .
12. 某所中学共有学生 1500 名, 其中有男生 800 名, 女生 700 名, 现对该校学生户外活动时间进行抽样调查, 如果样本容量为 150 , 小明现有三种方案:
①在七年级学生中随机抽取 150 名学生进行调查;
②在全校学生中随机抽取 150 名学生进行调查;
③分别在男生中随机抽取 80 名,在女生中随机抽取 70 名进行调查.
以上三种方案中最合理的是方案 .理由: .
13.阅读理解:在正方形网格中,格线与格线的交点称为“格点”,各顶点都在格点上的多边形称为“格点多边形”.设小正方形的边长均为1,则“格点多边形”的面积S可用公式计算,其中a是多边形内部的“格点”数,b是多边形边界上的“格点”数,这个公式称为“皮克定理”.如图所示的的正方形网格,,,图中格点多边形的面积是21.
问题解决:已知一个格点多边形的面积S为19,且边界上的点数b是内部点数a的3倍,则 .
14.命题“如果两条直线被第三条直线所截,那么同旁内角互补.”是 命题(填“真”或“假”).
15.x与3的差是负数,用不等式表示为 .
16.若一个四位正整数(各个数位均不为),个位数字比十位数字小,百位数于比千位数字小,则称该数为“三心二意数”,比如,都是“三心二意数”,则最大的是 .将一个四位正整数的百位和十位交换位置后得到四位数,.若为“三心二意数”,且能被整除,满足条件的所有值中,的最大值是 .
17.货拉拉公司有甲、乙、丙三种货车若干,三种货车的每辆车日运货量之比为.为应对今年的货运高峰,该公司重新调配了这三种货车的数量.调配后,乙货车数量增加一倍,甲、丙货车数量各减少,三种货车日运货总量增加.按调配后的运力,三种货车计划t天运完M处货物,但甲、丙两种货车在M处运了若干天后全部被派往N处执行新的任务,剩下的货物由乙种货车运完,结果运输总时间比原计划多了3天.若乙货车运输时间恰好为甲、丙两种货车在M处运输时间的4倍,则乙货车共运了 天.
18.如图,直线上有两点、,分别引两条射线、,,与在直线异侧.若,射线、分别绕点,点以度秒和度秒的速度同时顺时针转动,设时间为秒,在射线转动一周的时间内,当时间的值为时,与平行.
19.若一个四位自然数各个数位上的数字互不相同且均不为0,满足百位数字比千位数字大2,十位数字比个位数字大2,那么称这个四位数为“中二数”,一个“中二数”的千位数字为,百位数字为,十位数字为,个位数字为,记,若被9除余2,则的最大值为 ;若另一个“中二数”的千位数字为,个位数字为,且是3的倍数,则的最小值为 .
三、解答题
20.已知2a-1的平方根是±3,a+3b-1的算术平方根是4.
(1)求a,b的值;
(2)求a+b-1的立方根.
21.已知一个正数的平方根分别为和,求这个正数的值.
22.解不等式组:,并把解集在数轴上表示出来.
23.如图,已知,,,点E在线段上,,点F在直线上,.
(1)图中与相等的角有__________;
(2)若,求的度数;
(3)在(2)的条件下,点C(点C不与B,H两点重合)从点B出发,沿射线的方向运动,其他条件不变,求的度数.
24.如图,已知 , , , ,求 的度数.
25.某企业在“蜀南竹海”收购毛竹,直接销售,每吨可获利100元,进行粗加工,每天可加工8吨,每吨可获利800元;如果对毛竹进行精加工,每天可加工1吨,每吨可获利4000元.由于受条件限制,每天只能采用一种方式加工,要求将在一月内(30天)将这批毛竹93吨全部销售.为此企业厂长召集职工开会,让职工讨论如何加工销售更合算.
甲说:将毛竹全部进行粗加工后销售;
乙说:30天都进行精加工,未加工的毛竹直接销售;
丙说:30天中可用几天粗加工,再用几天精加工后销售;
请问厂长应采用哪位说的方案做,获利最大?
26.已知关于 的方程组
(1) 若用代入法求解, 可由①得, ③
把③代入(2), 解得
将其代入③, 解得
原方程组的解为
(2) 若此方程组的解 互为相反数, 求这个方程组的解及m的值
27.已知抛物线的对称轴为直线.
(1)若点在抛物线上,求t的值;
(2)若点,在抛物线上,
①当时,求a的取值范围;
②若,且,直接写出a的取值范围.
28. 如图, 直线 与 的两边交于 两点, .
(1) 过点 作 , 交射线 于点 , 依题意补全图形.
①直接写出 的度数. (用含 的式子表示)
②若点 在 的延长线上, 并且直线 , 当 平分 时,求 的度数 (用含 的式子表示). (小林在思考这道题时, 想到过点 作 交射线 于点 , 通过转化角可以求出 的度数. 你可以利用小林的思路解答此题, 也可以独立思考求出 的度数)
(2) 参考小林思考问题的方法, 解决问题: 若点 在 的延长线上, 并且直线 . 当点 在 上运动时, 直接用含 的等式表示 , 的数量关系.
29.如果一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.例如:方程的解为,不等式组的解集为,因为,所以称方程为不等式组的关联方程.
(1)在方程①;②;③中,不等式组的关联方程是___________.(填序号)
(2)若不等式组的一个关联方程的解是整数,则这个关联方程可以是___________.(写出一个即可)
(3)若方程都是关于的不等式组的关联方程,求的取值范围.
30.如图,直线,直线与直线AB、CD相交于点A、C,已知,点是射线AB上的一个动点(不包括端点).
(1) 点是直线CD上点右侧一点,且.当时,求证:.
(2)若将沿PC折叠,使顶点落在点处.
①若点刚好在直线CD上,求:的度数.
②若点落在两平行线之间,且,求:的度数.
答案解析
1.【答案】D
【知识点】点的坐标与象限的关系
2.【答案】B
【知识点】二元一次方程的概念
3.【答案】B
【知识点】求算术平方根
【解析】【解答】解:由题意得8的算术平方根是2,
故答案为:B
【分析】根据题意直接求8的算术平方根即可求解。
4.【答案】D
【知识点】角的运算;平行线的判定与性质
【解析】【解答】解:∵∠2=30°,
∴∠1=60°,
又∵∠E=60°,
∴∠1=∠E,
∴ACDE,①正确;
∵∠1+∠2=90°,∠2+∠3=90°,
即②∠BAE+∠CAD=∠1+∠2+∠2+∠3=90°+90°=180°,
故②正确;
∵BCAD,
∴∠1+∠2+∠3+∠C=180°,
又∵∠C=45°,∠1+∠2=90°,
∴∠3=45°,
∴∠2=90° 45°=45°,故③正确;
∵∠1=60°
∵∠E=60°,
∴∠1=∠E,
∴ACDE,
∴∠4=∠C,④正确.
故答案为:D.
【分析】利用平行线的判定方法,平行线的性质及角的运算和等量代换逐项分析判断即可.
5.【答案】A
【知识点】全面调查与抽样调查
【解析】【解答】解:A、检测载人飞船零件的质量很重要,必须全面调查,故选项A符合题意;
B、检测一批LED灯的使用寿命,具有破坏性,适合抽样调查,故选项B不符合题意;
C、检测杭嘉湖三地的空气质量,工作量太大,做不到全面调查,适合抽样调查,故选项C不符合题意;
D、检测一批家用汽车的抗撞击能力,具有破坏性,适合抽样调查,故选项D不符合题意;
故答案为:A
【分析】一般来说对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查;对于精确度要求高的调查,事关重大的调查往往选用普查. 根据抽样调查和全面调查的特点进行判断即可.
6.【答案】A
【知识点】解一元一次不等式组;在数轴上表示不等式的解集
7.【答案】C
【知识点】角的运算;平行线的性质
【解析】【解答】如图:
根据平行线的性质可得:∠3=∠1=25°,
∵∠ACB=45°,
∴∠2=∠ACB-∠3=45°-25°=20°,
故答案为:C.
【分析】利用平行线的性质可得∠3=∠1=25°,再利用角的运算求出∠2=∠ACB-∠3=45°-25°=20°即可。
8.【答案】D
【知识点】点的坐标
【解析】【解答】∵A1的坐标为(3,1),
∴A2(0,4),A3(﹣3,1),A4(0,﹣2),A5(3,1),
…,
依此类推,每4个点为一个循环组依次循环,
∵2017÷4=504…1,
∴点A2017的坐标与A1的坐标相同,为(3,1).
故答案为:D.
【分析】对于序号n比较大的求值题,基本方法就是循环法,通过计算几个特殊的实力观察规律,本题就是4个点为一循环,用2017除以4,余数为1,就是循环的第一个点.
9.【答案】B
【知识点】三元一次方程组解法及应用
【解析】【解答】解:在方程组 中,由①+②得 ,即 ,故B符合题意.
故答案为:B.
【分析】把①+②得 7x+7y=14 ,可得x+y的值.解答此类题目不要盲目的去解方程组,要观察方程组中各未知数的系数特点,从而找到简便方法.
10.【答案】D
【知识点】平行线的性质;平行线的判定与性质
11.【答案】0
【知识点】二元一次方程的解;加减消元法解二元一次方程组
12.【答案】③;具有代表性;结果更精确
【知识点】抽样调查的可靠性
【解析】【解答】∵学生中男生800名,女生700名,
∴男女生比为8:7,
∴设样本中男生人数:,女生人数:,
∴在男生中随机抽取80名,女生中随机抽取70名是最具有代表性,结果更精确的.
故答案为:③;具有代表性;结果更精确.
【分析】在抽样调查中,我们更习惯采用简单随机抽样,保证每个个体都有同等被抽到的机会,使抽样结果更具有代表性,结果更精确.
13.【答案】32
【知识点】二元一次方程组的应用-几何问题
【解析】【解答】解:根据题意可得,
解得,
.
故答案为:32.
【分析】将S=19代入可得a+b-1=19,根据边界上的点数b是内部点数a的3倍可得b=3a,联立求出a、b的值,进而可得a+b的值.
14.【答案】假
【知识点】真命题与假命题
15.【答案】
【知识点】列一元一次不等式
16.【答案】;
【知识点】整式的加减运算;二元一次方程的解
17.【答案】32
【知识点】三元一次方程组的应用
18.【答案】秒或秒
【知识点】平行线的判定;一元一次方程的实际应用-几何问题
19.【答案】;
【知识点】二元一次方程的解
20.【答案】(1)a=5,b=4;(2)2.
【知识点】立方根的概念与表示
21.【答案】
【知识点】平方根的概念与表示
22.【答案】解:,
解不等式得:,
解不等式得:,
,
把解集表示在数轴上:
【知识点】在数轴上表示不等式组的解集;解一元一次不等式组
【解析】【分析】分别求出两个不等式的解集,取其公共部分可得不等式组的解集,然后根据解集的表示方法表示在数轴上即可.
23.【答案】(1),,
(2)
(3)或
【知识点】余角、补角及其性质;平行线的性质
24.【答案】解:∵AD⊥BC,EF⊥BC,
∴AD∥EF,
∴∠1=∠BAD,
又∵∠1=∠2,
∴∠2=∠BAD,
∴AB∥DM,
∴∠AMD+∠BAC =180°,
∵ ,
∴∠AMD=180°-∠BAC=180°-70°=110°.
【知识点】平行线的判定与性质
【解析】【分析】 由已知条件可推出AD∥EF,得到∠1=∠BAD,结合∠1=∠2,可得∠2=∠BAD,证明AB∥DM,然后结合平行线的性质解答.
25.【答案】解:(1)若将毛竹全部进行粗加工后销售,则可以获利93×800=74 400元;(2)30天都进行精加工,可加工数量为30吨,此时获利30×4000=120 000元,
未加工的毛竹63吨直接销售可获利63×100=6300元,
因此共获利30×4000+63×100=126300元;(3)设x天粗加工,y天精加工,则
, 解之得
所以9天粗加工数量为9×8=72吨,可获利72×800=57600元,
21天精加工数量为21吨可获利21×4000=84000,因此共获利141600,
所以(3)>(2)>(1), 即第三种方案获利最大.
点睛:此题关键是把实际问题抽象到解方程组中,利用方程组来解决问题,属于基础题型.得出等量关系是解题的关键.
【知识点】二元一次方程组的其他应用
【解析】【分析】(1)、若将毛竹全部进行粗加工后销售,则获利为93×800元;(2)、30天都进行精加工,则可加工30吨,可获利30×4000,未加工的毛竹63吨直接销售可获利63×100,因此共获利30×4000+63×100;(3)、30天中可用几天粗加工,再用几天精加工后销售,则可根据“时间30天”,“共93吨”列方程组进行解答.
26.【答案】(1);;;
(2)解: 方程组的解 互为相反数, .
把 代人 , 得 ,
,
方程组的解是 .
【知识点】代入消元法解二元一次方程组;相反数的意义与性质
【解析】【解答】解:(1)由①得x=1-2y③,把③代入②,解得y=,将其代入③,解得x=.
∴原方程组的解为.
故填:;;;.
【分析】(1)运用代入消元法,由①得x=1-2y代入②,先求y,再求x;
(2)根据x,y互为相反数的条件,得出x=-y,代入①先求得y,再求x,并通过x=求出m.
27.【答案】(1)1
(2)①或;②
【知识点】解一元一次不等式组
28.【答案】(1)解:如图 1, 过点 作 , 交射线 于点 ,
① ;
②.
又 平分 .
.
(2)解:参考小林思考问题的方法: 如图 2 ,
过点 作 、交 于点 , 又 , ,
即 .
【知识点】平行线的判定与性质
【解析】【分析】(1)按要求补全图形即可。
①根据角之间的关系即可求解;
②根据平行线的性质即可求解。
(2)过点D作DH∥BC,交AM于点H,连接BD、DE,根据平行线的性质,分别讨论点D在AC(不含点A、C)上、在CF(不含点C)上、在AF的延长线上三种情况下∠BDE,∠DBC,∠BED的数量关系即可。
29.【答案】(1)①;(2);(3)
【知识点】解一元一次不等式组;解含括号的一元一次方程
30.【答案】(1)
(2)如图2,由折叠可知,
如图3,由折叠可知,
【知识点】平行线的判定与性质的应用-折叠问题
【解析】【分析】(1)根据AB∥CD,可求∠PCD的度数,根据∠AEC=∠PCD即可求解;
(2)①根据折叠可得∠FCP=∠ACP,根据平行线的性质及∠PAC=70°,可求∠ACF的度数,由此即可求解;②由折叠可知∠ACP=∠PCF,根据题意可得,根据平行线的性质可求∠DCA的度数,由此即可求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末模拟测试考前预测卷
一、单选题
1.如图是红、黄两队某局比赛投壶结束后冰壶的分布图,以冰壶大本营内的中心点为原点建立平面直角坐标系,按照规则更靠近原点的壶为本局胜方,则胜方最靠近原点的壶所在位置位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.下列各方程中,是二元一次方程的是( )
A. B. C. D.
3.8的算术平方根是( )
A.4 B.2 C.±2 D.2
4.将一副三角板如图放置,则下列结论中正确的是:( )
①如果,则有;
②;
③如果,则有;
④如果,必有;
A.①②③ B.③④ C.①②④ D.①②③④
5.下列调查中,适合全面调查的是( )
A.检测载人飞船零件的质量
B.检测一批LED灯的使用寿命
C.检测杭嘉湖三地的空气质量
D.检测一批家用汽车的抗撞击能力
6.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
7.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的一组对边上,如果∠1=25°,那么∠2的度数是( )
A.30° B.25° C.20° D.15°
8.在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(3,1),则点A2017的坐标为( )
A.(0,4) B.(﹣3,1) C.(0,﹣2) D.(3,1)
9.已知方程组 ,则 的值为( )
A.14 B.2 C.-14 D.-2
10.如图,已知直线,则、、之间的关系是( )
A. B.
C. D.
二、填空题
11.若关于x,y的二元一次方程组和同解,则 .
12. 某所中学共有学生 1500 名, 其中有男生 800 名, 女生 700 名, 现对该校学生户外活动时间进行抽样调查, 如果样本容量为 150 , 小明现有三种方案:
①在七年级学生中随机抽取 150 名学生进行调查;
②在全校学生中随机抽取 150 名学生进行调查;
③分别在男生中随机抽取 80 名,在女生中随机抽取 70 名进行调查.
以上三种方案中最合理的是方案 .理由: .
13.阅读理解:在正方形网格中,格线与格线的交点称为“格点”,各顶点都在格点上的多边形称为“格点多边形”.设小正方形的边长均为1,则“格点多边形”的面积S可用公式计算,其中a是多边形内部的“格点”数,b是多边形边界上的“格点”数,这个公式称为“皮克定理”.如图所示的的正方形网格,,,图中格点多边形的面积是21.
问题解决:已知一个格点多边形的面积S为19,且边界上的点数b是内部点数a的3倍,则 .
14.命题“如果两条直线被第三条直线所截,那么同旁内角互补.”是 命题(填“真”或“假”).
15.x与3的差是负数,用不等式表示为 .
16.若一个四位正整数(各个数位均不为),个位数字比十位数字小,百位数于比千位数字小,则称该数为“三心二意数”,比如,都是“三心二意数”,则最大的是 .将一个四位正整数的百位和十位交换位置后得到四位数,.若为“三心二意数”,且能被整除,满足条件的所有值中,的最大值是 .
17.货拉拉公司有甲、乙、丙三种货车若干,三种货车的每辆车日运货量之比为.为应对今年的货运高峰,该公司重新调配了这三种货车的数量.调配后,乙货车数量增加一倍,甲、丙货车数量各减少,三种货车日运货总量增加.按调配后的运力,三种货车计划t天运完M处货物,但甲、丙两种货车在M处运了若干天后全部被派往N处执行新的任务,剩下的货物由乙种货车运完,结果运输总时间比原计划多了3天.若乙货车运输时间恰好为甲、丙两种货车在M处运输时间的4倍,则乙货车共运了 天.
18.如图,直线上有两点、,分别引两条射线、,,与在直线异侧.若,射线、分别绕点,点以度秒和度秒的速度同时顺时针转动,设时间为秒,在射线转动一周的时间内,当时间的值为时,与平行.
19.若一个四位自然数各个数位上的数字互不相同且均不为0,满足百位数字比千位数字大2,十位数字比个位数字大2,那么称这个四位数为“中二数”,一个“中二数”的千位数字为,百位数字为,十位数字为,个位数字为,记,若被9除余2,则的最大值为 ;若另一个“中二数”的千位数字为,个位数字为,且是3的倍数,则的最小值为 .
三、解答题
20.已知2a-1的平方根是±3,a+3b-1的算术平方根是4.
(1)求a,b的值;
(2)求a+b-1的立方根.
21.已知一个正数的平方根分别为和,求这个正数的值.
22.解不等式组:,并把解集在数轴上表示出来.
23.如图,已知,,,点E在线段上,,点F在直线上,.
(1)图中与相等的角有__________;
(2)若,求的度数;
(3)在(2)的条件下,点C(点C不与B,H两点重合)从点B出发,沿射线的方向运动,其他条件不变,求的度数.
24.如图,已知 , , , ,求 的度数.
25.某企业在“蜀南竹海”收购毛竹,直接销售,每吨可获利100元,进行粗加工,每天可加工8吨,每吨可获利800元;如果对毛竹进行精加工,每天可加工1吨,每吨可获利4000元.由于受条件限制,每天只能采用一种方式加工,要求将在一月内(30天)将这批毛竹93吨全部销售.为此企业厂长召集职工开会,让职工讨论如何加工销售更合算.
甲说:将毛竹全部进行粗加工后销售;
乙说:30天都进行精加工,未加工的毛竹直接销售;
丙说:30天中可用几天粗加工,再用几天精加工后销售;
请问厂长应采用哪位说的方案做,获利最大?
26.已知关于 的方程组
(1) 若用代入法求解, 可由①得, ③
把③代入(2), 解得
将其代入③, 解得
原方程组的解为
(2) 若此方程组的解 互为相反数, 求这个方程组的解及m的值
27.已知抛物线的对称轴为直线.
(1)若点在抛物线上,求t的值;
(2)若点,在抛物线上,
①当时,求a的取值范围;
②若,且,直接写出a的取值范围.
28. 如图, 直线 与 的两边交于 两点, .
(1) 过点 作 , 交射线 于点 , 依题意补全图形.
①直接写出 的度数. (用含 的式子表示)
②若点 在 的延长线上, 并且直线 , 当 平分 时,求 的度数 (用含 的式子表示). (小林在思考这道题时, 想到过点 作 交射线 于点 , 通过转化角可以求出 的度数. 你可以利用小林的思路解答此题, 也可以独立思考求出 的度数)
(2) 参考小林思考问题的方法, 解决问题: 若点 在 的延长线上, 并且直线 . 当点 在 上运动时, 直接用含 的等式表示 , 的数量关系.
29.如果一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.例如:方程的解为,不等式组的解集为,因为,所以称方程为不等式组的关联方程.
(1)在方程①;②;③中,不等式组的关联方程是___________.(填序号)
(2)若不等式组的一个关联方程的解是整数,则这个关联方程可以是___________.(写出一个即可)
(3)若方程都是关于的不等式组的关联方程,求的取值范围.
30.如图,直线,直线与直线AB、CD相交于点A、C,已知,点是射线AB上的一个动点(不包括端点).
(1) 点是直线CD上点右侧一点,且.当时,求证:.
(2)若将沿PC折叠,使顶点落在点处.
①若点刚好在直线CD上,求:的度数.
②若点落在两平行线之间,且,求:的度数.
答案解析
1.【答案】D
【知识点】点的坐标与象限的关系
2.【答案】B
【知识点】二元一次方程的概念
3.【答案】B
【知识点】求算术平方根
【解析】【解答】解:由题意得8的算术平方根是2,
故答案为:B
【分析】根据题意直接求8的算术平方根即可求解。
4.【答案】D
【知识点】角的运算;平行线的判定与性质
【解析】【解答】解:∵∠2=30°,
∴∠1=60°,
又∵∠E=60°,
∴∠1=∠E,
∴ACDE,①正确;
∵∠1+∠2=90°,∠2+∠3=90°,
即②∠BAE+∠CAD=∠1+∠2+∠2+∠3=90°+90°=180°,
故②正确;
∵BCAD,
∴∠1+∠2+∠3+∠C=180°,
又∵∠C=45°,∠1+∠2=90°,
∴∠3=45°,
∴∠2=90° 45°=45°,故③正确;
∵∠1=60°
∵∠E=60°,
∴∠1=∠E,
∴ACDE,
∴∠4=∠C,④正确.
故答案为:D.
【分析】利用平行线的判定方法,平行线的性质及角的运算和等量代换逐项分析判断即可.
5.【答案】A
【知识点】全面调查与抽样调查
【解析】【解答】解:A、检测载人飞船零件的质量很重要,必须全面调查,故选项A符合题意;
B、检测一批LED灯的使用寿命,具有破坏性,适合抽样调查,故选项B不符合题意;
C、检测杭嘉湖三地的空气质量,工作量太大,做不到全面调查,适合抽样调查,故选项C不符合题意;
D、检测一批家用汽车的抗撞击能力,具有破坏性,适合抽样调查,故选项D不符合题意;
故答案为:A
【分析】一般来说对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查;对于精确度要求高的调查,事关重大的调查往往选用普查. 根据抽样调查和全面调查的特点进行判断即可.
6.【答案】A
【知识点】解一元一次不等式组;在数轴上表示不等式的解集
7.【答案】C
【知识点】角的运算;平行线的性质
【解析】【解答】如图:
根据平行线的性质可得:∠3=∠1=25°,
∵∠ACB=45°,
∴∠2=∠ACB-∠3=45°-25°=20°,
故答案为:C.
【分析】利用平行线的性质可得∠3=∠1=25°,再利用角的运算求出∠2=∠ACB-∠3=45°-25°=20°即可。
8.【答案】D
【知识点】点的坐标
【解析】【解答】∵A1的坐标为(3,1),
∴A2(0,4),A3(﹣3,1),A4(0,﹣2),A5(3,1),
…,
依此类推,每4个点为一个循环组依次循环,
∵2017÷4=504…1,
∴点A2017的坐标与A1的坐标相同,为(3,1).
故答案为:D.
【分析】对于序号n比较大的求值题,基本方法就是循环法,通过计算几个特殊的实力观察规律,本题就是4个点为一循环,用2017除以4,余数为1,就是循环的第一个点.
9.【答案】B
【知识点】三元一次方程组解法及应用
【解析】【解答】解:在方程组 中,由①+②得 ,即 ,故B符合题意.
故答案为:B.
【分析】把①+②得 7x+7y=14 ,可得x+y的值.解答此类题目不要盲目的去解方程组,要观察方程组中各未知数的系数特点,从而找到简便方法.
10.【答案】D
【知识点】平行线的性质;平行线的判定与性质
11.【答案】0
【知识点】二元一次方程的解;加减消元法解二元一次方程组
12.【答案】③;具有代表性;结果更精确
【知识点】抽样调查的可靠性
【解析】【解答】∵学生中男生800名,女生700名,
∴男女生比为8:7,
∴设样本中男生人数:,女生人数:,
∴在男生中随机抽取80名,女生中随机抽取70名是最具有代表性,结果更精确的.
故答案为:③;具有代表性;结果更精确.
【分析】在抽样调查中,我们更习惯采用简单随机抽样,保证每个个体都有同等被抽到的机会,使抽样结果更具有代表性,结果更精确.
13.【答案】32
【知识点】二元一次方程组的应用-几何问题
【解析】【解答】解:根据题意可得,
解得,
.
故答案为:32.
【分析】将S=19代入可得a+b-1=19,根据边界上的点数b是内部点数a的3倍可得b=3a,联立求出a、b的值,进而可得a+b的值.
14.【答案】假
【知识点】真命题与假命题
15.【答案】
【知识点】列一元一次不等式
16.【答案】;
【知识点】整式的加减运算;二元一次方程的解
17.【答案】32
【知识点】三元一次方程组的应用
18.【答案】秒或秒
【知识点】平行线的判定;一元一次方程的实际应用-几何问题
19.【答案】;
【知识点】二元一次方程的解
20.【答案】(1)a=5,b=4;(2)2.
【知识点】立方根的概念与表示
21.【答案】
【知识点】平方根的概念与表示
22.【答案】解:,
解不等式得:,
解不等式得:,
,
把解集表示在数轴上:
【知识点】在数轴上表示不等式组的解集;解一元一次不等式组
【解析】【分析】分别求出两个不等式的解集,取其公共部分可得不等式组的解集,然后根据解集的表示方法表示在数轴上即可.
23.【答案】(1),,
(2)
(3)或
【知识点】余角、补角及其性质;平行线的性质
24.【答案】解:∵AD⊥BC,EF⊥BC,
∴AD∥EF,
∴∠1=∠BAD,
又∵∠1=∠2,
∴∠2=∠BAD,
∴AB∥DM,
∴∠AMD+∠BAC =180°,
∵ ,
∴∠AMD=180°-∠BAC=180°-70°=110°.
【知识点】平行线的判定与性质
【解析】【分析】 由已知条件可推出AD∥EF,得到∠1=∠BAD,结合∠1=∠2,可得∠2=∠BAD,证明AB∥DM,然后结合平行线的性质解答.
25.【答案】解:(1)若将毛竹全部进行粗加工后销售,则可以获利93×800=74 400元;(2)30天都进行精加工,可加工数量为30吨,此时获利30×4000=120 000元,
未加工的毛竹63吨直接销售可获利63×100=6300元,
因此共获利30×4000+63×100=126300元;(3)设x天粗加工,y天精加工,则
, 解之得
所以9天粗加工数量为9×8=72吨,可获利72×800=57600元,
21天精加工数量为21吨可获利21×4000=84000,因此共获利141600,
所以(3)>(2)>(1), 即第三种方案获利最大.
点睛:此题关键是把实际问题抽象到解方程组中,利用方程组来解决问题,属于基础题型.得出等量关系是解题的关键.
【知识点】二元一次方程组的其他应用
【解析】【分析】(1)、若将毛竹全部进行粗加工后销售,则获利为93×800元;(2)、30天都进行精加工,则可加工30吨,可获利30×4000,未加工的毛竹63吨直接销售可获利63×100,因此共获利30×4000+63×100;(3)、30天中可用几天粗加工,再用几天精加工后销售,则可根据“时间30天”,“共93吨”列方程组进行解答.
26.【答案】(1);;;
(2)解: 方程组的解 互为相反数, .
把 代人 , 得 ,
,
方程组的解是 .
【知识点】代入消元法解二元一次方程组;相反数的意义与性质
【解析】【解答】解:(1)由①得x=1-2y③,把③代入②,解得y=,将其代入③,解得x=.
∴原方程组的解为.
故填:;;;.
【分析】(1)运用代入消元法,由①得x=1-2y代入②,先求y,再求x;
(2)根据x,y互为相反数的条件,得出x=-y,代入①先求得y,再求x,并通过x=求出m.
27.【答案】(1)1
(2)①或;②
【知识点】解一元一次不等式组
28.【答案】(1)解:如图 1, 过点 作 , 交射线 于点 ,
① ;
②.
又 平分 .
.
(2)解:参考小林思考问题的方法: 如图 2 ,
过点 作 、交 于点 , 又 , ,
即 .
【知识点】平行线的判定与性质
【解析】【分析】(1)按要求补全图形即可。
①根据角之间的关系即可求解;
②根据平行线的性质即可求解。
(2)过点D作DH∥BC,交AM于点H,连接BD、DE,根据平行线的性质,分别讨论点D在AC(不含点A、C)上、在CF(不含点C)上、在AF的延长线上三种情况下∠BDE,∠DBC,∠BED的数量关系即可。
29.【答案】(1)①;(2);(3)
【知识点】解一元一次不等式组;解含括号的一元一次方程
30.【答案】(1)
(2)如图2,由折叠可知,
如图3,由折叠可知,
【知识点】平行线的判定与性质的应用-折叠问题
【解析】【分析】(1)根据AB∥CD,可求∠PCD的度数,根据∠AEC=∠PCD即可求解;
(2)①根据折叠可得∠FCP=∠ACP,根据平行线的性质及∠PAC=70°,可求∠ACF的度数,由此即可求解;②由折叠可知∠ACP=∠PCF,根据题意可得,根据平行线的性质可求∠DCA的度数,由此即可求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
