期末模拟测试考前冲刺卷(含解析)-2024-2025学年七年级下册数学人教版(2024)
文档属性
| 名称 | 期末模拟测试考前冲刺卷(含解析)-2024-2025学年七年级下册数学人教版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 325.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 11:32:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末模拟测试考前冲刺卷
一、单选题
1.已知,下列各式正确的是( )
A. B. C. D.
2.二元一次方程组的解是( )
A. B. C. D.
3.下列各数中,属于无理数的是( )
A. B. C. D.3.14
4.实数,(相邻的两个3之间依次多一个0),, ,,中,无理数的个数有( )
A.2个 B.3个 C.4个 D.5个
5.把一副三角板摆放成如图所示的形状,使两个直角顶点重合,已知,,,若,则的度数是( )
A. B. C. D.
6.把方程改写成用含的式子表示,下列正确的为( )
A. B. C. D.
7.在平面直角坐标系中,,,以点为圆心,长为半径画弧交轴负半轴于点,则点的坐标为( )
A. B. C. D.
8.不等式组的解集在数轴上表示正确的为( )
A. B.
C. D.
9.如图,已知于点E,,,则的度数是( )
A. B. C. D.
10.已知 , , 表示取三个数中最小的那个数﹒例如:当 , , , = , , =3﹒当 , , = 时,则 的值为( )
A. B. C. D.
11.如图,已知,,点是射线上一动点(与点不重合),、分别平分和,分别交射线于点、,下列结论:①;②;③当时,;④当点运动时,的数量关系不变.其中正确结论有( )个.
A.1 B.2 C.3 D.4
12.已知、、满足,,且、、都为正数.设,则的取值范围为( )
A. B. C. D.
二、填空题
13.如图,直线a,b相交于点O,∠1=130°,则∠2的度数是 .
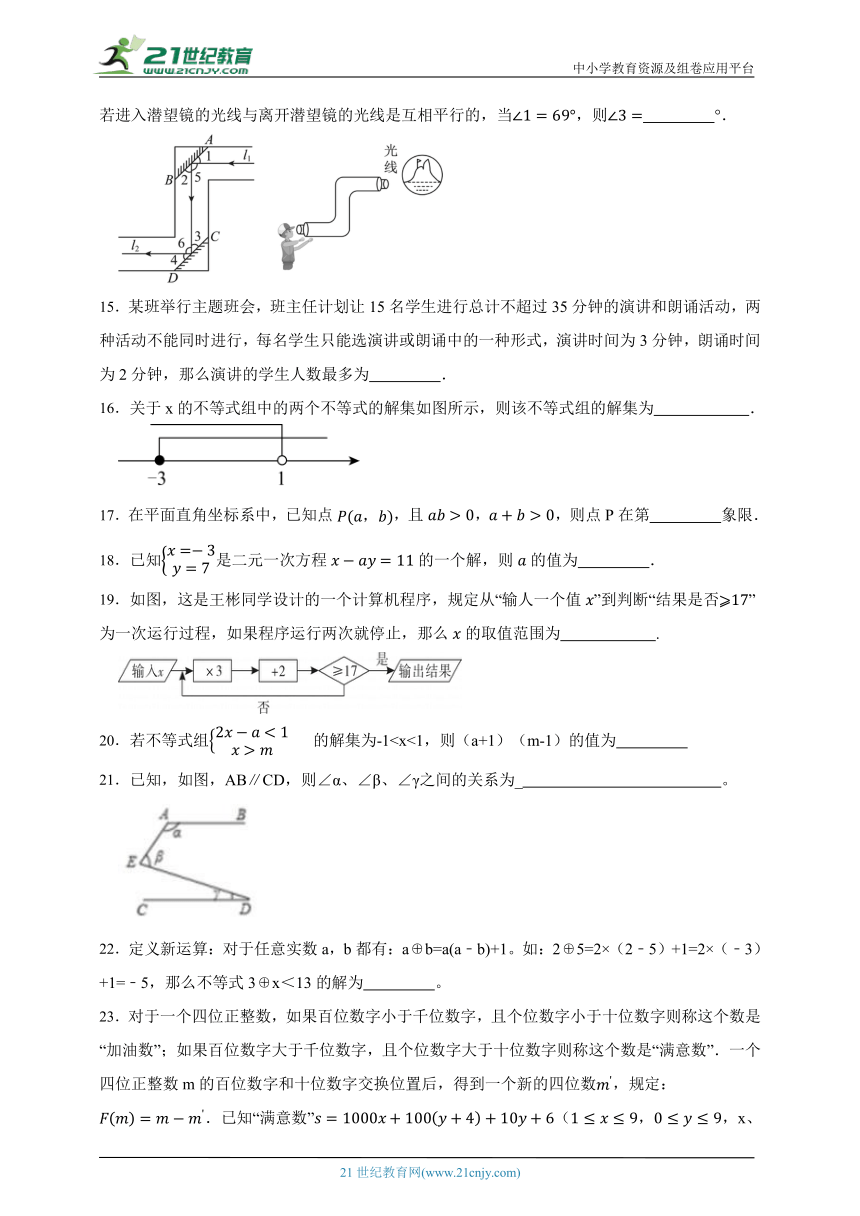
14.如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,,,若进入潜望镜的光线与离开潜望镜的光线是互相平行的,当,则 °.
15.某班举行主题班会,班主任计划让15名学生进行总计不超过35分钟的演讲和朗诵活动,两种活动不能同时进行,每名学生只能选演讲或朗诵中的一种形式,演讲时间为3分钟,朗诵时间为2分钟,那么演讲的学生人数最多为 .
16.关于x的不等式组中的两个不等式的解集如图所示,则该不等式组的解集为 .
17.在平面直角坐标系中,已知点,且,,则点P在第 象限.
18.已知是二元一次方程的一个解,则的值为 .
19.如图,这是王彬同学设计的一个计算机程序,规定从“输人一个值”到判断“结果是否”为一次运行过程,如果程序运行两次就停止,那么的取值范围为 .
20.若不等式组 的解集为-121.已知,如图,AB∥CD,则∠α、∠β、∠γ之间的关系为_ 。
22.定义新运算:对于任意实数a,b都有:a b=a(a﹣b)+1。如:2 5=2×(2﹣5)+1=2×(﹣3)+1=﹣5,那么不等式3 x<13的解为 。
23.对于一个四位正整数,如果百位数字小于千位数字,且个位数字小于十位数字则称这个数是“加油数”;如果百位数字大于千位数字,且个位数字大于十位数字则称这个数是“满意数”.一个四位正整数m的百位数字和十位数字交换位置后,得到一个新的四位数,规定:.已知“满意数”(,,x、y是整数),“加油数”(,,a、b是整数),且t的各个数位上的数字之和能被12整除.现规定,当k取最大值时, .
三、解答题
24.长沙交警正在全市范围内开展“一盔一带”安全守护行动,旨在提升摩托车、电动自行车骑乘人员和机动车驾乘人员的交通安全防护水平.某超市计划购进一批头盔用于销售.已知购进4个型头盔和3个型头盔需要315元,购进3个型头盔和4个型头盔需要350元.
(1)求,两种型号的头盔单价分别为多少元;
(2)若该商场准备购进100个这两种型号的头盔,总费用不超过4400元,则最多可购进型头盔多少个?
25.(1)解方程组
(2)解不等式组,并把它的解集在数轴上表示出来.
26.某班为了丰富学生的课外活动和体育健身,计划购买10个足球和20根跳绳,共花费980元,其中足球的价格是跳绳价格的3倍多8元.
(1)求跳绳和足球的单价;
(2)在实际课外活动中,发现如果全班同学根据自身的爱好总有部分学生无法玩足球或跳绳,若使用剩余班费233元,并要求至少购买一个足球,那么最多可购买多少根跳绳?
27. 若是的算术平方根,为的立方根,试求的平方根
28.小明的妈妈在菜市场买回1千克萝卜和0.5千克排骨,准备做萝卜排骨汤,妈妈说,今天买的这两样共花了23.6元,上个星期同等质量的这两样只要17元.爸爸说今天电视新闻上说萝卜每千克上涨了,排骨每千克上涨了.求今天萝卜和排骨的价格?
29.北京丰台站是亚洲最大铁路枢纽客站.北京丰台站交通枢纽是北京丰台站的重要配套工程,设计施工中采用了绿色建筑设计及建造技术,通过设置空气源热泵、节能灯具、高性能建材等,节约能源及建筑材料.北京丰台站交通枢纽将在2023年年内实现主体结构封顶.施工单位租用两种车型为交通枢纽运送高性能建材,若用2辆A型车和1辆B型车载满高性能建材,一次可运送10吨:用1辆A型车和2辆B型车载满高性能建材,一次可运送11吨.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满高性能建材,一次分别可运送多少吨?
(2)现有高性能建材31吨,计划同时租用A型车a辆,B型车b辆,一次运完且恰好每辆车都载满高性能建材.
①请你帮施工单位列出所有可能的租车方案:
②若1辆A型车需租金300元/次,1辆B型车需租金320元/次,则最少的租车费是元
30.若一个三位正整数(各个数位上的数字均不为0)满足,则称这个三位正整数为“长久数”.对于一个“长久数”m,将它的百位数字和个位数字交换以后得到新数n,记.如:满足,则216为“长久数”,那么,所以.
(1)求、的值;
(2)对于任意一个“长久数”m,若能被5整除,求所有满足条件的“长久数”.
31.甲乙两人以不变的速度在环形路上跑步,相向而行每隔两分钟相遇一次;同向而行,每隔6分相遇一次,已知甲比乙跑的快,求甲、乙两人每分钟各跑多少圈?
32.平面直角坐标系中,若点的坐标满足,则称点是原点的阶外围点.
(1)已知点,是否存在,使得是原点的3阶外围点;
(2)点在第二象限,且是原点的3阶外围点,将向右平移2个单位,再向下平移1个单位得到点,若点也是原点的3阶外围点,求的坐标;
(3)平面直角坐标系中,平移后得到,点的对应点为,点的对应点为,点的对应点为.若的横坐标为,在轴上,,的面积为4.是否存在,使得点,均是原点的阶外围点.若存在,求的值,若不存在,请说明理由.
33.如图,在以点为原点的平面直角坐标系中点,的坐标分别为,,点在轴上,且轴,,满足点从原点出发,以每秒个单位长度的速度沿着的路线运动回到为止.
(1)直接写出点,,的坐标;
(2)当点运动秒时,连接,,求出点的坐标,并直接写出,,之间满足的数量关系;
(3)点运动秒后,是否存在点到轴的距离为个单位长度的情况.若存在,求出点的坐标;若不存在,请说明理由.
答案解析
1.【答案】D
【知识点】不等式的性质
2.【答案】D
【知识点】加减消元法解二元一次方程组
3.【答案】B
【知识点】无理数的概念;求算术平方根
4.【答案】B
【知识点】无理数的概念;求算术平方根
5.【答案】C
【知识点】两直线平行,内错角相等
【解析】【解答】解:∵,,
∴,
∵,,,
∴
∴
故答案为:C
【分析】由平行线的性质求出,由三角形内角和定理求出∠BCE的度数,利用三角形的内角和定理可求出∠ACB,∠DCE的度数,根据周角的定义即可求出的度数.
6.【答案】D
【知识点】解二元一次方程
【解析】【解答】解:∵,
∴5y=2x-3,
∴,
故答案为:D.
【分析】将x当作常数,再利用一元一次方程的计算方法求解即可.
7.【答案】B
【知识点】坐标与图形性质
【解析】【解答】解:如图,
∵点A(,0),
∴OA=,
∵AC=AB=,
∴OC=AC-OA=,
∵点C在x轴的负半轴上,
∴点C(,0).
故答案为:B.
【分析】画出示意图,由点A的坐标可得OA的长,进而根据同圆半径相等可得AC的长,根据CO=AC-OA求出OC的长,最后根据点C在x轴的负半轴上可写出其坐标.
8.【答案】B
【知识点】在数轴上表示不等式组的解集;解一元一次不等式组
【解析】【解答】解:
解①得:x≤3,
解②得:x>2,
∴不等式组的解集为2<x≤3,
在数轴上表示为:
【分析】先分别解出两个不等式的解集,然后根据“同大取大,同小取小,大小小大中间找,大大小小无处找”的规律找出不等式组的解集,再利用数轴画出解集即可.
9.【答案】C
【知识点】平行线的判定与性质的应用-求角度;平行公理的推论
【解析】【解答】解:如图,过点H作HM∥AB,过点F作FN∥AB,
∵AB∥HM,∠AEH=20°,
∴∠EHM=∠AEH=20°,
∵∠EHG=50°,
∴∠MHG=∠EHG-∠EHM=30°,
∵AB∥CD,HM∥AB,
∴HM∥CD,
∴∠MHG=∠HGC=30°,
∴∠CGF=∠CGH+∠HGF=30°+20°=50°,
∵EF⊥AB,
∴∠BEF=90°,
∵AB∥FN,
∴∠EFN=180°-∠BEF=90°,
∵AB∥CD,FN∥AB,
∴FN∥CD,
∴∠NFG=∠CGF=50°,
∴∠EFG=∠EFN+∠NFG=90°+50°=140°.
故答案为:C.
【分析】过点H作HM∥AB,过点F作FN∥AB,由二直线平行,内错角相等得∠EHM=∠AEH=20°,由角的构成得∠MHG=∠EHG-∠EHM=30°,由平行于同一直线的两条直线互相平行得HM∥CD,由二直线平行内错角相等得∠MHG=∠HGC=30°,由角的构成得∠CGF=∠CGH+∠HGF=30°+20°=50°;由垂直的定义得∠BEF=90°,由二直线平行,同旁内角互补,得∠EFN=180°-∠BEF=90°,由平行于同一直线的两条直线互相平行得FN∥CD,由二直线平行内错角相等得∠NFG=∠CGF=50°,最后根据角的构成,由∠EFG=∠EFN+∠NFG代值计算即可.
10.【答案】C
【知识点】平方根;无理数的大小比较
【解析】【解答】解:
当01时, ,
∴ , , ,则x=.
故答案为:C
【分析】当底数大于零而小于1时,指数越大值反而越小,当底数大于1时,指数越大,值越大。据此原理,先找出最小值是x2, 再列方程解出x即可。
11.【答案】D
【知识点】角的运算;平行线的判定与性质
【解析】【解答】解:∵,
∴,
故①符合题意;
∵,,
∴,
∵、分别平分和,
∴,,
∴,
故②符合题意;
∵,
∴,
又,
∴,
∴,
又,,
∴,
故③符合题意;
∵,
∴,,
又,
∴,
∴,
故④符合题意.
故答案为:D.
【分析】利用平行线的判定方法、平行线的性质及角的运算逐项判断即可。
12.【答案】A
【知识点】解一元一次不等式组;加减消元法解二元一次方程组
13.【答案】130°
【知识点】对顶角及其性质
14.【答案】69
【知识点】平行线的性质
【解析】【解答】解:∵潜望镜中的两面镜子是互相平行放置的,即,
∴,
∵,,
∴,
∴.
故答案为:69.
【分析】先利用平行线的性质可得,再根据,,利用等量代换可得.
15.【答案】5
【知识点】一元一次不等式的应用
16.【答案】
【知识点】在数轴上表示不等式组的解集
【解析】【解答】解:由题意得该不等式组的解集为,
故答案为:
【分析】根据数轴结合题意即可求解。
17.【答案】一
【知识点】点的坐标与象限的关系;不等式的性质
【解析】【解答】解:∵ab>0,∴a、b同号,即两者要么都是正数,要么都是负数,
若a、b都是负数,则a+b也是负数,与题意a+b>0矛盾,
∴a、b都是正数,那么点P在第一象限.
故答案为:一.
【分析】考虑不等式 再结合 可知a、b都是正数;根据各个象限中点的坐标特点即可判断出点P在第一象限.
18.【答案】
【知识点】已知二元一次方程的解求参数
【解析】【解答】解:∵是二元一次方程的一个解,
∴,
解得:,
故答案为:.
【分析】把解代入方程,转化为待求字母的方程求解.
19.【答案】1≤x<5
【知识点】一元一次不等式组的应用
【解析】【解答】解:根据题意得,
解得.
故答案为:.
【分析】根据程序运行两次就停止,即可得出关于x的一元一次不等式组,解之即可得出x的取值范围.
20.【答案】-4.
【知识点】解一元一次不等式组
21.【答案】∠α+∠β-∠γ=180°
【知识点】平行线的判定与性质
【解析】【解答】解:过点E作EF∥AB
∴∠α+∠AEF=180° (两直线平行,同旁内角互补)
∵AB∥CD(已知)
∴EF∥CD
∴∠FED=∠EDC(两直线平行,内错角相等)
∵∠β=∠AEP+∠FED
又∵∠γ=∠EDC(已知)
∴∠α+∠β-∠γ=180°
【分析】过E作EF∥AB∥CD由平行线的质可得∠α+∠AEF=180°,∠FED=∠γ,由∠β=∠AEP=∠FED,可得∠α、∠β、∠γ之间的关系。
22.【答案】x>—1
【知识点】解一元一次不等式
【解析】【解答】解:由a b=a(a﹣b)+1
得3 x=3(3-x)+1
∴3(3-x)+1﹤13
解得x>—1
故答案为x>—1
【分析】定义新运算关键要看清对应数字和字母的位置,可得结果。
23.【答案】
【知识点】整式的加减运算;二元一次方程的解
24.【答案】(1)解:设购进1个型头盔需要元,购进1个型头盔需要元.
根据题意,得,
解得,;
答:购进1个型头盔需要30元,购进1个型头盔需要65元;
(2)解:设购进型头盔个,则购进型头盔个,根据题意,得:,
解得:,
∴的最大值为40,
答:最多可购进B型头盔40个.
【知识点】一元一次不等式的应用;二元一次方程组的实际应用-销售问题
【解析】【分析】本题主要对二元一次方程组和一元一次不等式的应用进行考查.
(1)设A型x元,B型y元,根据题意列出方程组,解得;
(2)设B型头盔个,则购进A型个,根据题意列出不等式,解得,所以最多可购进B型头盔40个.
(1)解:设购进1个型头盔需要元,购进1个型头盔需要元.
根据题意,得,
解得,;
答:购进1个型头盔需要30元,购进1个型头盔需要65元;
(2)解:设购进型头盔个,则购进型头盔个,
根据题意,得:,
解得:,
∴的最大值为40,
答:最多可购进B型头盔40个.
25.【答案】(1);(2)
【知识点】解一元一次不等式组;在数轴上表示不等式的解集;加减消元法解二元一次方程组
26.【答案】(1)解:设跳绳的价格为元,则足球的价格为元,
由题意得:,
解得:,
(元),
跳绳的价格为元,则足球的价格为元;
(2)解:设最多可购买根跳绳,
由题意得:,
解得:,
为正整数,
最大为,
最多可购买根跳绳.
【知识点】一元一次不等式的应用;一元一次方程的实际应用-销售问题
【解析】【分析】(1)基本关系:总花费=10个足球的花费+20根跳绳的花费,根据“计划购买10个足球和20根跳绳,共花费980元”,列出一元一次方程,解方程即可得出答案;
(2)设购买m根跳绳,根据“使用剩余班费233元,并要求至少购买一个足球”,列出一元一次不等式,解不等式即可.
27.【答案】解:由题意得:
,,
的平方根是。
【知识点】开平方(求平方根);算术平方根的概念与表示;立方根的概念与表示
【解析】【分析】先根据算术平方根和立方根的定义列出方程组,解出、,再代入、求出结果,进而得到的平方根.
28.【答案】萝卜元千克,排骨元千克
【知识点】二元一次方程组的其他应用
29.【答案】(1)解:设1辆A型车一次可运送x吨,1辆B型车一次可运送y吨.根据题意,得:
,
解得,
答:1辆A型车一次可运送3吨,1辆B型车一次可运送4吨.
(2)解:①根据题意,得
∵x、y均为非负整数∴或或
∴有三种租车方案:
方案一:租用9辆A型车,1辆B型车;
方案二:租用5辆A型车,4辆B型车;
方案三:租用1辆A型车,7辆B型车.
②2540.
【知识点】二元一次方程的应用;二元一次方程组的应用-和差倍分问题
【解析】【解答】解:(2)② 方案一费用:9×300+320=3020元,
方案二费用:5×300+320×4=2780元,
方案三费用:300+320×7=2540元,
∴方案三租车费用最少,最少费用为2540元.
【分析】(1)设1辆A型车一次可运送x吨,1辆B型车一次可运送y吨,根据“ 用2辆A型车和1辆B型车载满高性能建材,一次可运送10吨:用1辆A型车和2辆B型车载满高性能建材,一次可运送11吨”列出方程组并解之即可;
(2)①由题意得,求出方程的非负整数解即得租车方案;
②分别求出每种方案的费用,再比较即可.
30.【答案】(1),
(2)144或243或342或441
【知识点】有理数的加减乘除混合运算的法则;整式的加减运算;二元一次方程组的应用-数字问题
31.【答案】解:设甲每分跑x圈,乙每分跑y圈,
根据题意得: ,
解得: .
则甲、乙二人每分各跑 圈与 圈.
【知识点】二元一次方程组的实际应用-行程问题
【解析】【分析】由题意可知,题中关键的已知条件为:相向而行每隔两分钟相遇一次;同向而行,每隔6分相遇一次,隐含了两个等量关系,然后设未知数,列方程组,然后求出方程组的解。
32.【答案】(1)不存在,使得是原点的3阶外围点;
(2)
(3)存在,
【知识点】坐标与图形性质;坐标与图形变化﹣平移;二元一次方程组的应用-几何问题
33.【答案】(1)
,,;
(2)解:如图,当运动秒时,点运动了个单位长度,
,
点运动秒时,点在线段上,且,
点的坐标是;
如图,作.
,,
,
,,
;
(3)解:存在.
,
点可能运动到或或上.
当点运动到上时,,
,,
,解得:,
,
点的坐标为;
当点运动到上时,,即,
点到轴的距离为,
,解得,
,
此种情况不符合题意;
当点运动到上时,,即,
,
,解得:,
,
点的坐标为
综上所述,点运动秒后,存在点到轴的距离为个单位长度的情况,点的坐标为:或
【知识点】解一元一次方程;点的坐标;点到直线的距离;算术平方根的性质(双重非负性);绝对值的非负性
【解析】【解答】解:(1)且,,
,,
,,
,,;
【分析】 (1)利用非负数的性质列出方程求解,再写出A、B、C三点坐标;
(2)作PE∥AO.利用平行线的性质证明;
(3)根据P点运动的位置分三种情况讨论:当点运动到上时 ; 当点运动到上时 ; 当点运动到上时 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末模拟测试考前冲刺卷
一、单选题
1.已知,下列各式正确的是( )
A. B. C. D.
2.二元一次方程组的解是( )
A. B. C. D.
3.下列各数中,属于无理数的是( )
A. B. C. D.3.14
4.实数,(相邻的两个3之间依次多一个0),, ,,中,无理数的个数有( )
A.2个 B.3个 C.4个 D.5个
5.把一副三角板摆放成如图所示的形状,使两个直角顶点重合,已知,,,若,则的度数是( )
A. B. C. D.
6.把方程改写成用含的式子表示,下列正确的为( )
A. B. C. D.
7.在平面直角坐标系中,,,以点为圆心,长为半径画弧交轴负半轴于点,则点的坐标为( )
A. B. C. D.
8.不等式组的解集在数轴上表示正确的为( )
A. B.
C. D.
9.如图,已知于点E,,,则的度数是( )
A. B. C. D.
10.已知 , , 表示取三个数中最小的那个数﹒例如:当 , , , = , , =3﹒当 , , = 时,则 的值为( )
A. B. C. D.
11.如图,已知,,点是射线上一动点(与点不重合),、分别平分和,分别交射线于点、,下列结论:①;②;③当时,;④当点运动时,的数量关系不变.其中正确结论有( )个.
A.1 B.2 C.3 D.4
12.已知、、满足,,且、、都为正数.设,则的取值范围为( )
A. B. C. D.
二、填空题
13.如图,直线a,b相交于点O,∠1=130°,则∠2的度数是 .
14.如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,,,若进入潜望镜的光线与离开潜望镜的光线是互相平行的,当,则 °.
15.某班举行主题班会,班主任计划让15名学生进行总计不超过35分钟的演讲和朗诵活动,两种活动不能同时进行,每名学生只能选演讲或朗诵中的一种形式,演讲时间为3分钟,朗诵时间为2分钟,那么演讲的学生人数最多为 .
16.关于x的不等式组中的两个不等式的解集如图所示,则该不等式组的解集为 .
17.在平面直角坐标系中,已知点,且,,则点P在第 象限.
18.已知是二元一次方程的一个解,则的值为 .
19.如图,这是王彬同学设计的一个计算机程序,规定从“输人一个值”到判断“结果是否”为一次运行过程,如果程序运行两次就停止,那么的取值范围为 .
20.若不等式组 的解集为-1
22.定义新运算:对于任意实数a,b都有:a b=a(a﹣b)+1。如:2 5=2×(2﹣5)+1=2×(﹣3)+1=﹣5,那么不等式3 x<13的解为 。
23.对于一个四位正整数,如果百位数字小于千位数字,且个位数字小于十位数字则称这个数是“加油数”;如果百位数字大于千位数字,且个位数字大于十位数字则称这个数是“满意数”.一个四位正整数m的百位数字和十位数字交换位置后,得到一个新的四位数,规定:.已知“满意数”(,,x、y是整数),“加油数”(,,a、b是整数),且t的各个数位上的数字之和能被12整除.现规定,当k取最大值时, .
三、解答题
24.长沙交警正在全市范围内开展“一盔一带”安全守护行动,旨在提升摩托车、电动自行车骑乘人员和机动车驾乘人员的交通安全防护水平.某超市计划购进一批头盔用于销售.已知购进4个型头盔和3个型头盔需要315元,购进3个型头盔和4个型头盔需要350元.
(1)求,两种型号的头盔单价分别为多少元;
(2)若该商场准备购进100个这两种型号的头盔,总费用不超过4400元,则最多可购进型头盔多少个?
25.(1)解方程组
(2)解不等式组,并把它的解集在数轴上表示出来.
26.某班为了丰富学生的课外活动和体育健身,计划购买10个足球和20根跳绳,共花费980元,其中足球的价格是跳绳价格的3倍多8元.
(1)求跳绳和足球的单价;
(2)在实际课外活动中,发现如果全班同学根据自身的爱好总有部分学生无法玩足球或跳绳,若使用剩余班费233元,并要求至少购买一个足球,那么最多可购买多少根跳绳?
27. 若是的算术平方根,为的立方根,试求的平方根
28.小明的妈妈在菜市场买回1千克萝卜和0.5千克排骨,准备做萝卜排骨汤,妈妈说,今天买的这两样共花了23.6元,上个星期同等质量的这两样只要17元.爸爸说今天电视新闻上说萝卜每千克上涨了,排骨每千克上涨了.求今天萝卜和排骨的价格?
29.北京丰台站是亚洲最大铁路枢纽客站.北京丰台站交通枢纽是北京丰台站的重要配套工程,设计施工中采用了绿色建筑设计及建造技术,通过设置空气源热泵、节能灯具、高性能建材等,节约能源及建筑材料.北京丰台站交通枢纽将在2023年年内实现主体结构封顶.施工单位租用两种车型为交通枢纽运送高性能建材,若用2辆A型车和1辆B型车载满高性能建材,一次可运送10吨:用1辆A型车和2辆B型车载满高性能建材,一次可运送11吨.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满高性能建材,一次分别可运送多少吨?
(2)现有高性能建材31吨,计划同时租用A型车a辆,B型车b辆,一次运完且恰好每辆车都载满高性能建材.
①请你帮施工单位列出所有可能的租车方案:
②若1辆A型车需租金300元/次,1辆B型车需租金320元/次,则最少的租车费是元
30.若一个三位正整数(各个数位上的数字均不为0)满足,则称这个三位正整数为“长久数”.对于一个“长久数”m,将它的百位数字和个位数字交换以后得到新数n,记.如:满足,则216为“长久数”,那么,所以.
(1)求、的值;
(2)对于任意一个“长久数”m,若能被5整除,求所有满足条件的“长久数”.
31.甲乙两人以不变的速度在环形路上跑步,相向而行每隔两分钟相遇一次;同向而行,每隔6分相遇一次,已知甲比乙跑的快,求甲、乙两人每分钟各跑多少圈?
32.平面直角坐标系中,若点的坐标满足,则称点是原点的阶外围点.
(1)已知点,是否存在,使得是原点的3阶外围点;
(2)点在第二象限,且是原点的3阶外围点,将向右平移2个单位,再向下平移1个单位得到点,若点也是原点的3阶外围点,求的坐标;
(3)平面直角坐标系中,平移后得到,点的对应点为,点的对应点为,点的对应点为.若的横坐标为,在轴上,,的面积为4.是否存在,使得点,均是原点的阶外围点.若存在,求的值,若不存在,请说明理由.
33.如图,在以点为原点的平面直角坐标系中点,的坐标分别为,,点在轴上,且轴,,满足点从原点出发,以每秒个单位长度的速度沿着的路线运动回到为止.
(1)直接写出点,,的坐标;
(2)当点运动秒时,连接,,求出点的坐标,并直接写出,,之间满足的数量关系;
(3)点运动秒后,是否存在点到轴的距离为个单位长度的情况.若存在,求出点的坐标;若不存在,请说明理由.
答案解析
1.【答案】D
【知识点】不等式的性质
2.【答案】D
【知识点】加减消元法解二元一次方程组
3.【答案】B
【知识点】无理数的概念;求算术平方根
4.【答案】B
【知识点】无理数的概念;求算术平方根
5.【答案】C
【知识点】两直线平行,内错角相等
【解析】【解答】解:∵,,
∴,
∵,,,
∴
∴
故答案为:C
【分析】由平行线的性质求出,由三角形内角和定理求出∠BCE的度数,利用三角形的内角和定理可求出∠ACB,∠DCE的度数,根据周角的定义即可求出的度数.
6.【答案】D
【知识点】解二元一次方程
【解析】【解答】解:∵,
∴5y=2x-3,
∴,
故答案为:D.
【分析】将x当作常数,再利用一元一次方程的计算方法求解即可.
7.【答案】B
【知识点】坐标与图形性质
【解析】【解答】解:如图,
∵点A(,0),
∴OA=,
∵AC=AB=,
∴OC=AC-OA=,
∵点C在x轴的负半轴上,
∴点C(,0).
故答案为:B.
【分析】画出示意图,由点A的坐标可得OA的长,进而根据同圆半径相等可得AC的长,根据CO=AC-OA求出OC的长,最后根据点C在x轴的负半轴上可写出其坐标.
8.【答案】B
【知识点】在数轴上表示不等式组的解集;解一元一次不等式组
【解析】【解答】解:
解①得:x≤3,
解②得:x>2,
∴不等式组的解集为2<x≤3,
在数轴上表示为:
【分析】先分别解出两个不等式的解集,然后根据“同大取大,同小取小,大小小大中间找,大大小小无处找”的规律找出不等式组的解集,再利用数轴画出解集即可.
9.【答案】C
【知识点】平行线的判定与性质的应用-求角度;平行公理的推论
【解析】【解答】解:如图,过点H作HM∥AB,过点F作FN∥AB,
∵AB∥HM,∠AEH=20°,
∴∠EHM=∠AEH=20°,
∵∠EHG=50°,
∴∠MHG=∠EHG-∠EHM=30°,
∵AB∥CD,HM∥AB,
∴HM∥CD,
∴∠MHG=∠HGC=30°,
∴∠CGF=∠CGH+∠HGF=30°+20°=50°,
∵EF⊥AB,
∴∠BEF=90°,
∵AB∥FN,
∴∠EFN=180°-∠BEF=90°,
∵AB∥CD,FN∥AB,
∴FN∥CD,
∴∠NFG=∠CGF=50°,
∴∠EFG=∠EFN+∠NFG=90°+50°=140°.
故答案为:C.
【分析】过点H作HM∥AB,过点F作FN∥AB,由二直线平行,内错角相等得∠EHM=∠AEH=20°,由角的构成得∠MHG=∠EHG-∠EHM=30°,由平行于同一直线的两条直线互相平行得HM∥CD,由二直线平行内错角相等得∠MHG=∠HGC=30°,由角的构成得∠CGF=∠CGH+∠HGF=30°+20°=50°;由垂直的定义得∠BEF=90°,由二直线平行,同旁内角互补,得∠EFN=180°-∠BEF=90°,由平行于同一直线的两条直线互相平行得FN∥CD,由二直线平行内错角相等得∠NFG=∠CGF=50°,最后根据角的构成,由∠EFG=∠EFN+∠NFG代值计算即可.
10.【答案】C
【知识点】平方根;无理数的大小比较
【解析】【解答】解:
当0
∴ , , ,则x=.
故答案为:C
【分析】当底数大于零而小于1时,指数越大值反而越小,当底数大于1时,指数越大,值越大。据此原理,先找出最小值是x2, 再列方程解出x即可。
11.【答案】D
【知识点】角的运算;平行线的判定与性质
【解析】【解答】解:∵,
∴,
故①符合题意;
∵,,
∴,
∵、分别平分和,
∴,,
∴,
故②符合题意;
∵,
∴,
又,
∴,
∴,
又,,
∴,
故③符合题意;
∵,
∴,,
又,
∴,
∴,
故④符合题意.
故答案为:D.
【分析】利用平行线的判定方法、平行线的性质及角的运算逐项判断即可。
12.【答案】A
【知识点】解一元一次不等式组;加减消元法解二元一次方程组
13.【答案】130°
【知识点】对顶角及其性质
14.【答案】69
【知识点】平行线的性质
【解析】【解答】解:∵潜望镜中的两面镜子是互相平行放置的,即,
∴,
∵,,
∴,
∴.
故答案为:69.
【分析】先利用平行线的性质可得,再根据,,利用等量代换可得.
15.【答案】5
【知识点】一元一次不等式的应用
16.【答案】
【知识点】在数轴上表示不等式组的解集
【解析】【解答】解:由题意得该不等式组的解集为,
故答案为:
【分析】根据数轴结合题意即可求解。
17.【答案】一
【知识点】点的坐标与象限的关系;不等式的性质
【解析】【解答】解:∵ab>0,∴a、b同号,即两者要么都是正数,要么都是负数,
若a、b都是负数,则a+b也是负数,与题意a+b>0矛盾,
∴a、b都是正数,那么点P在第一象限.
故答案为:一.
【分析】考虑不等式 再结合 可知a、b都是正数;根据各个象限中点的坐标特点即可判断出点P在第一象限.
18.【答案】
【知识点】已知二元一次方程的解求参数
【解析】【解答】解:∵是二元一次方程的一个解,
∴,
解得:,
故答案为:.
【分析】把解代入方程,转化为待求字母的方程求解.
19.【答案】1≤x<5
【知识点】一元一次不等式组的应用
【解析】【解答】解:根据题意得,
解得.
故答案为:.
【分析】根据程序运行两次就停止,即可得出关于x的一元一次不等式组,解之即可得出x的取值范围.
20.【答案】-4.
【知识点】解一元一次不等式组
21.【答案】∠α+∠β-∠γ=180°
【知识点】平行线的判定与性质
【解析】【解答】解:过点E作EF∥AB
∴∠α+∠AEF=180° (两直线平行,同旁内角互补)
∵AB∥CD(已知)
∴EF∥CD
∴∠FED=∠EDC(两直线平行,内错角相等)
∵∠β=∠AEP+∠FED
又∵∠γ=∠EDC(已知)
∴∠α+∠β-∠γ=180°
【分析】过E作EF∥AB∥CD由平行线的质可得∠α+∠AEF=180°,∠FED=∠γ,由∠β=∠AEP=∠FED,可得∠α、∠β、∠γ之间的关系。
22.【答案】x>—1
【知识点】解一元一次不等式
【解析】【解答】解:由a b=a(a﹣b)+1
得3 x=3(3-x)+1
∴3(3-x)+1﹤13
解得x>—1
故答案为x>—1
【分析】定义新运算关键要看清对应数字和字母的位置,可得结果。
23.【答案】
【知识点】整式的加减运算;二元一次方程的解
24.【答案】(1)解:设购进1个型头盔需要元,购进1个型头盔需要元.
根据题意,得,
解得,;
答:购进1个型头盔需要30元,购进1个型头盔需要65元;
(2)解:设购进型头盔个,则购进型头盔个,根据题意,得:,
解得:,
∴的最大值为40,
答:最多可购进B型头盔40个.
【知识点】一元一次不等式的应用;二元一次方程组的实际应用-销售问题
【解析】【分析】本题主要对二元一次方程组和一元一次不等式的应用进行考查.
(1)设A型x元,B型y元,根据题意列出方程组,解得;
(2)设B型头盔个,则购进A型个,根据题意列出不等式,解得,所以最多可购进B型头盔40个.
(1)解:设购进1个型头盔需要元,购进1个型头盔需要元.
根据题意,得,
解得,;
答:购进1个型头盔需要30元,购进1个型头盔需要65元;
(2)解:设购进型头盔个,则购进型头盔个,
根据题意,得:,
解得:,
∴的最大值为40,
答:最多可购进B型头盔40个.
25.【答案】(1);(2)
【知识点】解一元一次不等式组;在数轴上表示不等式的解集;加减消元法解二元一次方程组
26.【答案】(1)解:设跳绳的价格为元,则足球的价格为元,
由题意得:,
解得:,
(元),
跳绳的价格为元,则足球的价格为元;
(2)解:设最多可购买根跳绳,
由题意得:,
解得:,
为正整数,
最大为,
最多可购买根跳绳.
【知识点】一元一次不等式的应用;一元一次方程的实际应用-销售问题
【解析】【分析】(1)基本关系:总花费=10个足球的花费+20根跳绳的花费,根据“计划购买10个足球和20根跳绳,共花费980元”,列出一元一次方程,解方程即可得出答案;
(2)设购买m根跳绳,根据“使用剩余班费233元,并要求至少购买一个足球”,列出一元一次不等式,解不等式即可.
27.【答案】解:由题意得:
,,
的平方根是。
【知识点】开平方(求平方根);算术平方根的概念与表示;立方根的概念与表示
【解析】【分析】先根据算术平方根和立方根的定义列出方程组,解出、,再代入、求出结果,进而得到的平方根.
28.【答案】萝卜元千克,排骨元千克
【知识点】二元一次方程组的其他应用
29.【答案】(1)解:设1辆A型车一次可运送x吨,1辆B型车一次可运送y吨.根据题意,得:
,
解得,
答:1辆A型车一次可运送3吨,1辆B型车一次可运送4吨.
(2)解:①根据题意,得
∵x、y均为非负整数∴或或
∴有三种租车方案:
方案一:租用9辆A型车,1辆B型车;
方案二:租用5辆A型车,4辆B型车;
方案三:租用1辆A型车,7辆B型车.
②2540.
【知识点】二元一次方程的应用;二元一次方程组的应用-和差倍分问题
【解析】【解答】解:(2)② 方案一费用:9×300+320=3020元,
方案二费用:5×300+320×4=2780元,
方案三费用:300+320×7=2540元,
∴方案三租车费用最少,最少费用为2540元.
【分析】(1)设1辆A型车一次可运送x吨,1辆B型车一次可运送y吨,根据“ 用2辆A型车和1辆B型车载满高性能建材,一次可运送10吨:用1辆A型车和2辆B型车载满高性能建材,一次可运送11吨”列出方程组并解之即可;
(2)①由题意得,求出方程的非负整数解即得租车方案;
②分别求出每种方案的费用,再比较即可.
30.【答案】(1),
(2)144或243或342或441
【知识点】有理数的加减乘除混合运算的法则;整式的加减运算;二元一次方程组的应用-数字问题
31.【答案】解:设甲每分跑x圈,乙每分跑y圈,
根据题意得: ,
解得: .
则甲、乙二人每分各跑 圈与 圈.
【知识点】二元一次方程组的实际应用-行程问题
【解析】【分析】由题意可知,题中关键的已知条件为:相向而行每隔两分钟相遇一次;同向而行,每隔6分相遇一次,隐含了两个等量关系,然后设未知数,列方程组,然后求出方程组的解。
32.【答案】(1)不存在,使得是原点的3阶外围点;
(2)
(3)存在,
【知识点】坐标与图形性质;坐标与图形变化﹣平移;二元一次方程组的应用-几何问题
33.【答案】(1)
,,;
(2)解:如图,当运动秒时,点运动了个单位长度,
,
点运动秒时,点在线段上,且,
点的坐标是;
如图,作.
,,
,
,,
;
(3)解:存在.
,
点可能运动到或或上.
当点运动到上时,,
,,
,解得:,
,
点的坐标为;
当点运动到上时,,即,
点到轴的距离为,
,解得,
,
此种情况不符合题意;
当点运动到上时,,即,
,
,解得:,
,
点的坐标为
综上所述,点运动秒后,存在点到轴的距离为个单位长度的情况,点的坐标为:或
【知识点】解一元一次方程;点的坐标;点到直线的距离;算术平方根的性质(双重非负性);绝对值的非负性
【解析】【解答】解:(1)且,,
,,
,,
,,;
【分析】 (1)利用非负数的性质列出方程求解,再写出A、B、C三点坐标;
(2)作PE∥AO.利用平行线的性质证明;
(3)根据P点运动的位置分三种情况讨论:当点运动到上时 ; 当点运动到上时 ; 当点运动到上时 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
