初中数学北师大版八年级下册 第一章 三角形的证明---三角形全等之三垂直模型(无答案)
文档属性
| 名称 | 初中数学北师大版八年级下册 第一章 三角形的证明---三角形全等之三垂直模型(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 131.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 14:05:50 | ||
图片预览



文档简介
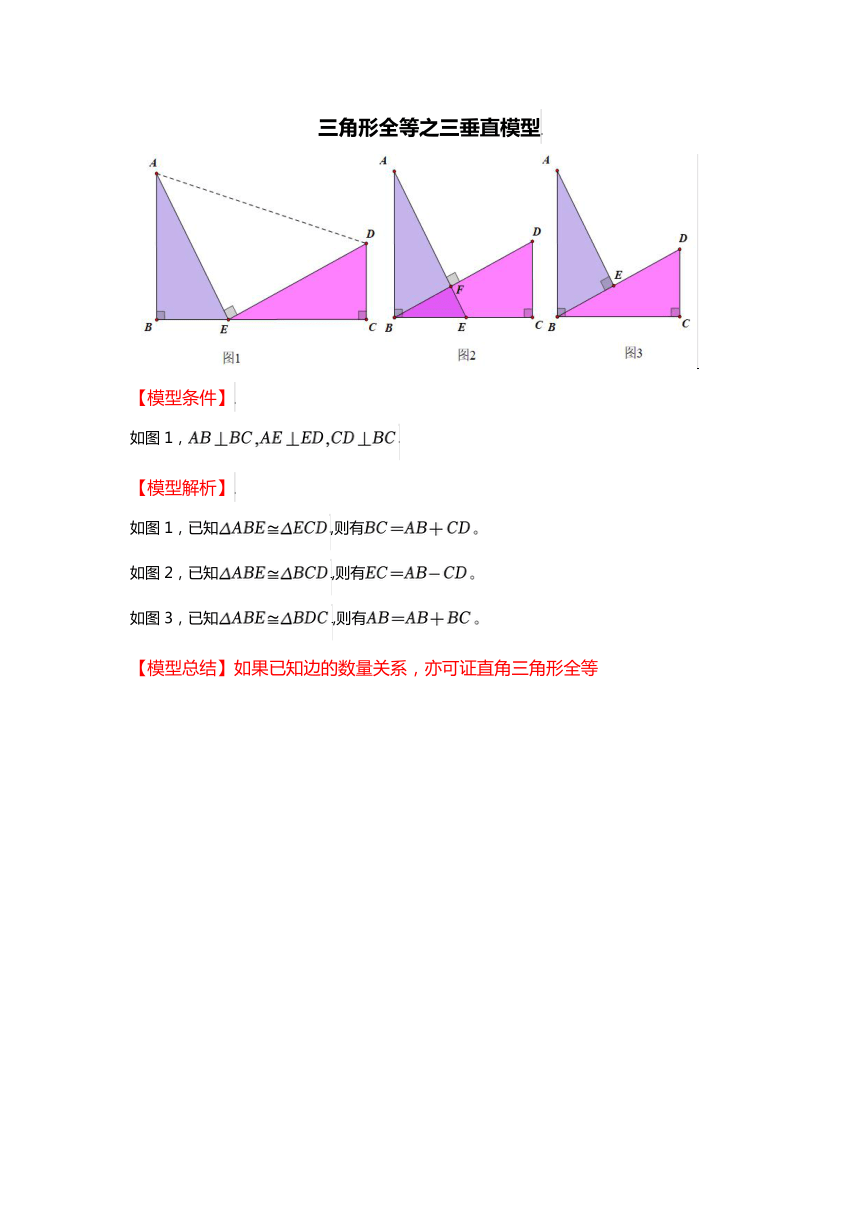
三角形全等之三垂直模型
【模型条件】
如图1,
【模型解析】
如图1,已知,则有
如图2,已知,则有
如图3,已知,则有
【模型总结】如果已知边的数量关系,亦可证直角三角形全等
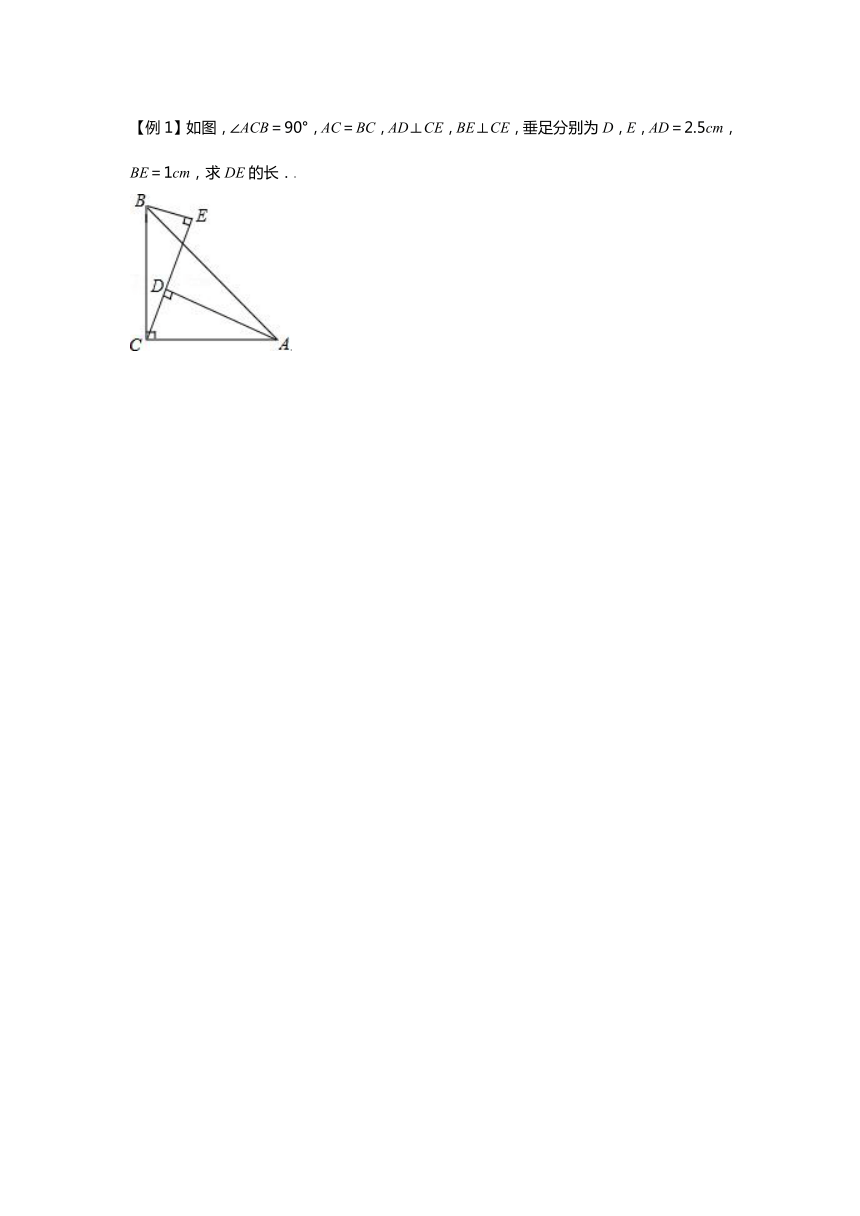
【例1】如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,BE=1cm,求DE的长.
【例2】如图,在Rt△ABC中,∠ACB=90°,CA=CB,M是AB的中点,点D在BM上,AE⊥CD,BF⊥CD,垂足分别为E,F,连接EM.
(1)求证:CE=BF;
(2)求证:∠AEM=∠DEM.
【例3】如图所示,直线MN一侧有一个等腰Rt△ABC,其中∠ACB=90°,CA=CB.直线MN过顶点C,分别过点A,B作AE⊥MN,BF⊥MN,垂足分别为点E,F,∠CAB的角平分线AG交BC于点O,交MN于点G,连接BG,恰好满足AG⊥BG.延长AC,BG交于点D.
(1)求证:CE=BF;
(2)求证:AC+CO=AB.
【例4】问题1:如图①,在四边形ABCD中,∠B=∠C=90°,P是BC上一点,PA=PD,∠APD=90°.求证:AB+CD=BC.
问题2:如图②,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,PA=PD,∠APD=90°.求的值.
【例5】在△ABC中,∠ACB=90°,BC=AC.
(1)如图①,DE是过点C的一条直线,且A,B在DE的同侧,AD⊥DE于D,BE⊥DE于E.写出AD,BE,ED间的数量关系,并写明理由;
(2)如图②,DE是过点C的一条直线,且A,B在DE的两侧,AD⊥DE于D,BE⊥DE于E.写出AD,BE,ED间的数量关系,并写明理由.
【例6】已知,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)如图1,求证:DE=AD+BE;
(2)如图2,点O为AB的中点,连接OD,OE.请判断△ODE的形状?并说明理由.
【例7】如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC,(1)求C点的坐标;
(2)如图2,P为y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OP﹣DE的值;
(3)如图3,已知点F坐标为(﹣2,﹣2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90°,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,以下两个结论:①m﹣n为定值;②m+n为定值,其中只有一个结论是正确的,请找出正确的结论,并求出其值.
【模型条件】
如图1,
【模型解析】
如图1,已知,则有
如图2,已知,则有
如图3,已知,则有
【模型总结】如果已知边的数量关系,亦可证直角三角形全等
【例1】如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,BE=1cm,求DE的长.
【例2】如图,在Rt△ABC中,∠ACB=90°,CA=CB,M是AB的中点,点D在BM上,AE⊥CD,BF⊥CD,垂足分别为E,F,连接EM.
(1)求证:CE=BF;
(2)求证:∠AEM=∠DEM.
【例3】如图所示,直线MN一侧有一个等腰Rt△ABC,其中∠ACB=90°,CA=CB.直线MN过顶点C,分别过点A,B作AE⊥MN,BF⊥MN,垂足分别为点E,F,∠CAB的角平分线AG交BC于点O,交MN于点G,连接BG,恰好满足AG⊥BG.延长AC,BG交于点D.
(1)求证:CE=BF;
(2)求证:AC+CO=AB.
【例4】问题1:如图①,在四边形ABCD中,∠B=∠C=90°,P是BC上一点,PA=PD,∠APD=90°.求证:AB+CD=BC.
问题2:如图②,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,PA=PD,∠APD=90°.求的值.
【例5】在△ABC中,∠ACB=90°,BC=AC.
(1)如图①,DE是过点C的一条直线,且A,B在DE的同侧,AD⊥DE于D,BE⊥DE于E.写出AD,BE,ED间的数量关系,并写明理由;
(2)如图②,DE是过点C的一条直线,且A,B在DE的两侧,AD⊥DE于D,BE⊥DE于E.写出AD,BE,ED间的数量关系,并写明理由.
【例6】已知,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)如图1,求证:DE=AD+BE;
(2)如图2,点O为AB的中点,连接OD,OE.请判断△ODE的形状?并说明理由.
【例7】如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC,(1)求C点的坐标;
(2)如图2,P为y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OP﹣DE的值;
(3)如图3,已知点F坐标为(﹣2,﹣2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90°,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,以下两个结论:①m﹣n为定值;②m+n为定值,其中只有一个结论是正确的,请找出正确的结论,并求出其值.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
