第1章 三角函数 2.1 角的概念推广 2.2 象限角及其表示--北师大版高中数学必修第二册课件(共38页PPT)
文档属性
| 名称 | 第1章 三角函数 2.1 角的概念推广 2.2 象限角及其表示--北师大版高中数学必修第二册课件(共38页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 17:59:44 | ||
图片预览










文档简介
(共38张PPT)
第一章
2.1 角的概念推广 2.2 象限角及其表示
基础落实·必备知识一遍过
重难探究·能力素养速提升
目录索引
学以致用·随堂检测促达标
课程标准 1.理解正角、负角和零角的概念.
2.掌握象限角的特征及其表示方法.
3.理解终边相同的角的概念,会表示终边相同的角的集合.
基础落实·必备知识一遍过
知识点一 角的概念推广
1.角的概念
平面内一条射线OA绕着它的端点O按箭头所示方向旋转到终止位置OB,形成角α.其中点O是角α的顶点,射线OA是角α的始边,射线OB是角α的终边.
2.角的分类
按旋转方向可将角分为如下三类:
类型 定义 图示
正角 一条射线按 形成的角
负角 一条射线按 形成的角
零角 一条射线没有作任何旋转形成的角
不能理解为始边和终边重合
逆时针方向旋转
顺时针方向旋转
名师点睛
1.在不引起混淆的前提下,“角α”或“∠α”可以简记成“α”.
2.角的范围由0°~360°推广到任意角后,角的加减运算就类似于实数的加减运算.
思考辨析
角的概念推广后角的范围有怎样的变化
提示 角的概念推广后,角度的范围不限于0°~360°,而是任意的角,包括正角、负角与零角.
自主诊断
1.判断正误.(正确的画“√”,错误的画“×”)
(1)经过1 h,时针转过30°.( )
(2)把30°的角终边按顺时针旋转10°后终边所对应的角为30°-10°
=20°.( )
(3)如果两个角的旋转量相等,那么这两个角是相等角.( )
(4)任意角α按逆时针旋转越旋转越大.( )
×
×
×
√
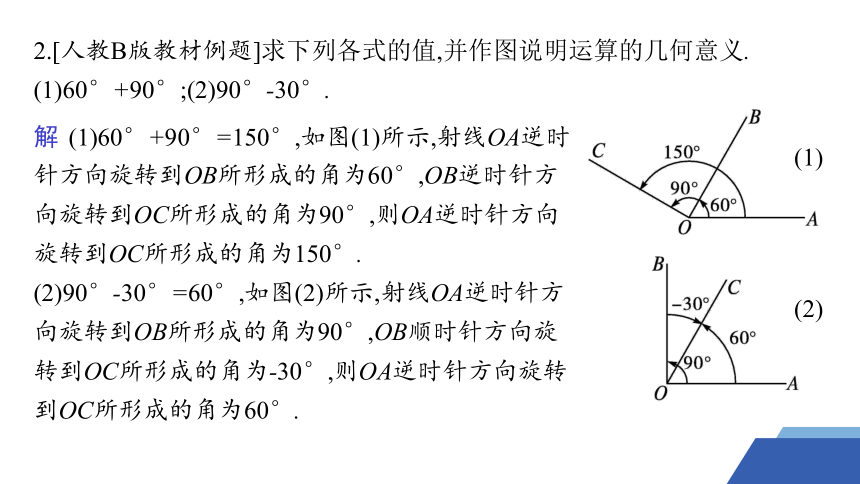
2.[人教B版教材例题]求下列各式的值,并作图说明运算的几何意义.
(1)60°+90°;(2)90°-30°.
解 (1)60°+90°=150°,如图(1)所示,射线OA逆时针方向旋转到OB所形成的角为60°,OB逆时针方向旋转到OC所形成的角为90°,则OA逆时针方向旋转到OC所形成的角为150°.
(2)90°-30°=60°,如图(2)所示,射线OA逆时针方向旋转到OB所形成的角为90°,OB顺时针方向旋转到OC所形成的角为-30°,则OA逆时针方向旋转到OC所形成的角为60°.
(1)
(2)
知识点二 象限角
在平面直角坐标系中研究角时,角的顶点在坐标 ,始边在x轴的 .以角的终边(除端点外)在平面直角坐标系的位置对角分类:角的终边在第几象限,就说这个角是第几象限角.
名师点睛
1.在角的顶点与坐标原点重合,角的始边与x轴的非负半轴重合的前提下,才能对象限角进行定义,否则不能判断角的终边在哪一个象限,也就不能称作象限角.
2.若角的终边落在坐标轴上,则这个角不属于任何象限.
原点
非负半轴
思考辨析
锐角是第几象限角 第一象限角一定是锐角吗
提示 锐角是第一象限角,第一象限角不一定是锐角.
自主诊断
判断正误.(正确的画“√”,错误的画“×”)
(1)象限角的终边不能落在坐标轴上.( )
(2)小于90°的角是锐角.( )
(3)钝角是第二象限角.( )
√
×
√
知识点三 终边相同的角
一般地,给定一个角α,所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β= ,k∈Z},即任何一个与角α终边相同的角,都可以表示成角α与 的和.
名师点睛
理解集合S={β|β=α+k·360°,k∈Z}要注意以下几点:
(1)集合中角α为任意角;
(2)k∈Z这一条件必不可少;
(3)k·360°与α之间是“+”,如k·360°-30°应看成k·360°+(-30°),即与-30°角终边相同;
(4)当α与β的终边相同时,α-β=k·360°,k∈Z,反之亦然.
α+k·360°
周角的整数倍
自主诊断
1.判断正误.(正确的画“√”,错误的画“×”)
(1)一个角的始边和终边重合,则这个角是零角.( )
(2)始边和终边重合的角相差k·360°(k∈Z).( )
(3)-936°化为α+k·360°(0°≤α<360°,k∈Z)的形式为
-216°+(-2)×360°.( )
×
√
×
2.[人教A版教材例题]写出终边在y轴上的角的集合.
解 在0°~360°范围内,终边在y轴上的角有两个,即90°,270°角.因此,所有与90°角终边相同的角构成集合S1={β|β=90°+k·360°,k∈Z},
而所有与270°角终边相同的角构成集合
S2={β|β=270°+k·360°,k∈Z},
于是,终边在y轴上的角的集合
S=S1∪S2
={β|β=90°+2k·180°,k∈Z}∪{β|β=90°+180°+2k·180°,k∈Z}
={β|β=90°+2k·180°,k∈Z}∪{β|β=90°+(2k+1)180°,k∈Z}
={β|β=90°+n·180°,n∈Z}.
重难探究·能力素养速提升
探究点一 角的概念推广
【例1】 下列说法正确的是( )
A.终边与始边重合的角是零角
B.终边和始边都相同的两个角一定相等
C.象限角为钝角的终边在第二象限
D.小于90°的角是锐角
C
解析 终边与始边重合的角还可能是360°,720°,故A错误;终边和始边都相同的两个角可能相差360°的整数倍,如30°与-330°,故B错误;钝角的范围是(90°,180°),钝角的终边在第二象限,故C正确;小于90°的角还可以是零角或负角,故D错误.故选C.
规律方法 概念辨析问题的求解方略
对于概念辨析题,一是利用反例排除错误答案,二是利用定义直接判断.本题需要准确理解象限角、锐角、钝角、终边相同的角等基本概念才能作出正确的判断.
变式训练1一个角为30°,其终边按逆时针方向旋转三周后的角度是多少 按顺时针方向旋转三周后又是多少
解 终边按逆时针方向旋转三周,转过的角度为360°×3=1 080°,所以按逆时针旋转后的角度数是1 110°.同理按顺时针方向旋转三周后的角度是-3×360°+30°=-1 050°.
探究点二 终边相同的角
【例2】 写出与75°角终边相同的角的集合S,并把S中适合
360°≤β<1 080°的元素β写出来.
解 与75°角终边相同的角的集合为
S={β|β=75°+k·360°,k∈Z}.
当360°≤β<1 080°时,
即360°≤75°+k·360°<1 080°,
又因为k∈Z,
所以k=1,或k=2.
当k=1时,β=435°;当k=2时,β=795°.
规律方法 终边相同的角的求解方法
求与已知角α终边相同的角时,要先将这样的角表示成k·360°+α,k∈Z的形式,然后采用赋值法求解或解不等式,确定整数k的值,求出满足条件的角.
变式训练2与-2 024°角终边相同的最小正角是 .
136°
解析 因为-2 024°=136°-6×360°,
所以与-2 024°角终边相同的最小正角是136°.
探究点三 象限角
【例3】 (1)分别判断角α=-130°和角β=-940°是第几象限角.
解 由于α=-130°=-360°+230°,即α角与230°角终边相同,而230°角是第三象限角,故α是第三象限角.
由于β=-940°=-3×360°+140°,即β角与140°角终边相同,而140°角是第二象限角,故β是第二象限角.
(2)若角α是第二象限角,试判断180°-α及2α是第几象限角.
解 由α是第二象限角可得,90°+k·360°<α<180°+k·360°,k∈Z,所以180°-(180°+k·360°)<180°-α<180°-(90°+k·360°),k∈Z,即
-k·360°<180°-α<90°-k·360°,k∈Z.所以180°-α为第一象限角.
同理,180°+2k·360°<2α<360°+2k·360°,k∈Z,
所以角2α可能是第三、第四象限角或者终边落在y轴的非正半轴上.
规律方法 象限角的判定
(1)已知一个角的大小判断其所在象限时,可先根据终边相同的角的表示方法,找到在[0°,360°)内与之终边相同的角,再确定其象限.
(2)已知角的终边所在的象限,求待求角的终边所在的位置时,通常首先根据所给已知角的范围,得到待求角的范围,然后判断待求角终边所在的位置.
变式训练3(1)已知角α=2 024°.把α改写成k·360°+β(k∈Z,0°≤β<360°)的形式,并指出它是第几象限角.
解 把α写成k·360°+β的形式为α=5×360°+224°.
又224°是第三象限角,
∴α为第三象限角.
(2)若α是第二象限角,试分别确定2α, 的终边所在位置.
解 ∵α是第二象限角,∴90°+k·360°<α<180°+k·360°(k∈Z).
∵180°+2k·360°<2α<360°+2k·360°(k∈Z),∴2α的终边位于第三象限或第四象限,或在y轴的非正半轴上.
(方法二)将坐标系的每个象限二等分,得到8个区域.自x轴正向按逆时针方向把每个区域依次标上Ⅰ,Ⅱ,Ⅲ,Ⅳ,如图所示:
将坐标系的每个象限三等分,得到12个区域.自x轴正向按逆时针方向把每个区域依次标上Ⅰ,Ⅱ,Ⅲ,Ⅳ,如图所示:
本节要点归纳
1.知识清单:
(1)任意角的概念;
(2)终边相同的角;
(3)象限角、区域角的表示.
2.方法归纳:数形结合、分类讨论.
3.常见误区:锐角与小于90°角的区别,终边相同角的表示中漏掉k∈Z.
学以致用·随堂检测促达标
1
2
3
4
1.660°是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
C
解析 因为660°=300°+360°,所以在0°~360°范围内,与660°角终边相同的角是300°角,它是第四象限角.
1
2
3
4
2.集合M={α|α=k·90°,k∈Z}中各角的终边都在( )
A.x轴非负半轴上
B.y轴非负半轴上
C.x轴或y轴上
D.x轴非负半轴或y轴非负半轴上
C
解析 当k=4n,n∈Z时,α=n·360°;当k=4n+1,n∈Z时,α=90°+n·360°;当k=4n+2,n∈Z时,α=180°+n·360°;当k=4n+3,n∈Z时,α=270°+n·360°.因此,集合M中各角的终边都在x轴或y轴上.
1
2
3
4
3.在0°~360°范围内,与角-60°的终边在同一条直线上的角为 .
120°,300°
解析 与角-60°的终边在同一条直线上的角可表示为
β=-60°+k·180°,k∈Z.
∵所求角在0°~360°范围内,∴0°≤-60°+k·180°≤360°,解得 ,k∈Z,∴k=1或2,
当k=1时,β=120°,当k=2时,β=300°.
1
2
3
4
4.已知角α的终边落在图中阴影部分表示的范围内(不包括边界),则角α的集合是 .
{α|45°+k·360°<α<150°+k·360°,k∈Z}
解析 在0°~360°范围内,阴影部分的边界射线所表示的角分别是45°和150°,因此,所求α的范围是45°+k·360°<α<150°+k·360°,k∈Z.
1
2
3
4
5.若β是第二象限角,则270°+β是第 象限角;-β是第
象限角.
一
三
解析 因为β是第二象限角,所以k·360°+90°<β所以(k+1)·360°<270°+β<(k+1)·360°+90°,-180°-k·360°<-β<-90°-k·360°,所以270°+β是第一象限角,-β是第三象限角.
本 课 结 束
第一章
2.1 角的概念推广 2.2 象限角及其表示
基础落实·必备知识一遍过
重难探究·能力素养速提升
目录索引
学以致用·随堂检测促达标
课程标准 1.理解正角、负角和零角的概念.
2.掌握象限角的特征及其表示方法.
3.理解终边相同的角的概念,会表示终边相同的角的集合.
基础落实·必备知识一遍过
知识点一 角的概念推广
1.角的概念
平面内一条射线OA绕着它的端点O按箭头所示方向旋转到终止位置OB,形成角α.其中点O是角α的顶点,射线OA是角α的始边,射线OB是角α的终边.
2.角的分类
按旋转方向可将角分为如下三类:
类型 定义 图示
正角 一条射线按 形成的角
负角 一条射线按 形成的角
零角 一条射线没有作任何旋转形成的角
不能理解为始边和终边重合
逆时针方向旋转
顺时针方向旋转
名师点睛
1.在不引起混淆的前提下,“角α”或“∠α”可以简记成“α”.
2.角的范围由0°~360°推广到任意角后,角的加减运算就类似于实数的加减运算.
思考辨析
角的概念推广后角的范围有怎样的变化
提示 角的概念推广后,角度的范围不限于0°~360°,而是任意的角,包括正角、负角与零角.
自主诊断
1.判断正误.(正确的画“√”,错误的画“×”)
(1)经过1 h,时针转过30°.( )
(2)把30°的角终边按顺时针旋转10°后终边所对应的角为30°-10°
=20°.( )
(3)如果两个角的旋转量相等,那么这两个角是相等角.( )
(4)任意角α按逆时针旋转越旋转越大.( )
×
×
×
√
2.[人教B版教材例题]求下列各式的值,并作图说明运算的几何意义.
(1)60°+90°;(2)90°-30°.
解 (1)60°+90°=150°,如图(1)所示,射线OA逆时针方向旋转到OB所形成的角为60°,OB逆时针方向旋转到OC所形成的角为90°,则OA逆时针方向旋转到OC所形成的角为150°.
(2)90°-30°=60°,如图(2)所示,射线OA逆时针方向旋转到OB所形成的角为90°,OB顺时针方向旋转到OC所形成的角为-30°,则OA逆时针方向旋转到OC所形成的角为60°.
(1)
(2)
知识点二 象限角
在平面直角坐标系中研究角时,角的顶点在坐标 ,始边在x轴的 .以角的终边(除端点外)在平面直角坐标系的位置对角分类:角的终边在第几象限,就说这个角是第几象限角.
名师点睛
1.在角的顶点与坐标原点重合,角的始边与x轴的非负半轴重合的前提下,才能对象限角进行定义,否则不能判断角的终边在哪一个象限,也就不能称作象限角.
2.若角的终边落在坐标轴上,则这个角不属于任何象限.
原点
非负半轴
思考辨析
锐角是第几象限角 第一象限角一定是锐角吗
提示 锐角是第一象限角,第一象限角不一定是锐角.
自主诊断
判断正误.(正确的画“√”,错误的画“×”)
(1)象限角的终边不能落在坐标轴上.( )
(2)小于90°的角是锐角.( )
(3)钝角是第二象限角.( )
√
×
√
知识点三 终边相同的角
一般地,给定一个角α,所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β= ,k∈Z},即任何一个与角α终边相同的角,都可以表示成角α与 的和.
名师点睛
理解集合S={β|β=α+k·360°,k∈Z}要注意以下几点:
(1)集合中角α为任意角;
(2)k∈Z这一条件必不可少;
(3)k·360°与α之间是“+”,如k·360°-30°应看成k·360°+(-30°),即与-30°角终边相同;
(4)当α与β的终边相同时,α-β=k·360°,k∈Z,反之亦然.
α+k·360°
周角的整数倍
自主诊断
1.判断正误.(正确的画“√”,错误的画“×”)
(1)一个角的始边和终边重合,则这个角是零角.( )
(2)始边和终边重合的角相差k·360°(k∈Z).( )
(3)-936°化为α+k·360°(0°≤α<360°,k∈Z)的形式为
-216°+(-2)×360°.( )
×
√
×
2.[人教A版教材例题]写出终边在y轴上的角的集合.
解 在0°~360°范围内,终边在y轴上的角有两个,即90°,270°角.因此,所有与90°角终边相同的角构成集合S1={β|β=90°+k·360°,k∈Z},
而所有与270°角终边相同的角构成集合
S2={β|β=270°+k·360°,k∈Z},
于是,终边在y轴上的角的集合
S=S1∪S2
={β|β=90°+2k·180°,k∈Z}∪{β|β=90°+180°+2k·180°,k∈Z}
={β|β=90°+2k·180°,k∈Z}∪{β|β=90°+(2k+1)180°,k∈Z}
={β|β=90°+n·180°,n∈Z}.
重难探究·能力素养速提升
探究点一 角的概念推广
【例1】 下列说法正确的是( )
A.终边与始边重合的角是零角
B.终边和始边都相同的两个角一定相等
C.象限角为钝角的终边在第二象限
D.小于90°的角是锐角
C
解析 终边与始边重合的角还可能是360°,720°,故A错误;终边和始边都相同的两个角可能相差360°的整数倍,如30°与-330°,故B错误;钝角的范围是(90°,180°),钝角的终边在第二象限,故C正确;小于90°的角还可以是零角或负角,故D错误.故选C.
规律方法 概念辨析问题的求解方略
对于概念辨析题,一是利用反例排除错误答案,二是利用定义直接判断.本题需要准确理解象限角、锐角、钝角、终边相同的角等基本概念才能作出正确的判断.
变式训练1一个角为30°,其终边按逆时针方向旋转三周后的角度是多少 按顺时针方向旋转三周后又是多少
解 终边按逆时针方向旋转三周,转过的角度为360°×3=1 080°,所以按逆时针旋转后的角度数是1 110°.同理按顺时针方向旋转三周后的角度是-3×360°+30°=-1 050°.
探究点二 终边相同的角
【例2】 写出与75°角终边相同的角的集合S,并把S中适合
360°≤β<1 080°的元素β写出来.
解 与75°角终边相同的角的集合为
S={β|β=75°+k·360°,k∈Z}.
当360°≤β<1 080°时,
即360°≤75°+k·360°<1 080°,
又因为k∈Z,
所以k=1,或k=2.
当k=1时,β=435°;当k=2时,β=795°.
规律方法 终边相同的角的求解方法
求与已知角α终边相同的角时,要先将这样的角表示成k·360°+α,k∈Z的形式,然后采用赋值法求解或解不等式,确定整数k的值,求出满足条件的角.
变式训练2与-2 024°角终边相同的最小正角是 .
136°
解析 因为-2 024°=136°-6×360°,
所以与-2 024°角终边相同的最小正角是136°.
探究点三 象限角
【例3】 (1)分别判断角α=-130°和角β=-940°是第几象限角.
解 由于α=-130°=-360°+230°,即α角与230°角终边相同,而230°角是第三象限角,故α是第三象限角.
由于β=-940°=-3×360°+140°,即β角与140°角终边相同,而140°角是第二象限角,故β是第二象限角.
(2)若角α是第二象限角,试判断180°-α及2α是第几象限角.
解 由α是第二象限角可得,90°+k·360°<α<180°+k·360°,k∈Z,所以180°-(180°+k·360°)<180°-α<180°-(90°+k·360°),k∈Z,即
-k·360°<180°-α<90°-k·360°,k∈Z.所以180°-α为第一象限角.
同理,180°+2k·360°<2α<360°+2k·360°,k∈Z,
所以角2α可能是第三、第四象限角或者终边落在y轴的非正半轴上.
规律方法 象限角的判定
(1)已知一个角的大小判断其所在象限时,可先根据终边相同的角的表示方法,找到在[0°,360°)内与之终边相同的角,再确定其象限.
(2)已知角的终边所在的象限,求待求角的终边所在的位置时,通常首先根据所给已知角的范围,得到待求角的范围,然后判断待求角终边所在的位置.
变式训练3(1)已知角α=2 024°.把α改写成k·360°+β(k∈Z,0°≤β<360°)的形式,并指出它是第几象限角.
解 把α写成k·360°+β的形式为α=5×360°+224°.
又224°是第三象限角,
∴α为第三象限角.
(2)若α是第二象限角,试分别确定2α, 的终边所在位置.
解 ∵α是第二象限角,∴90°+k·360°<α<180°+k·360°(k∈Z).
∵180°+2k·360°<2α<360°+2k·360°(k∈Z),∴2α的终边位于第三象限或第四象限,或在y轴的非正半轴上.
(方法二)将坐标系的每个象限二等分,得到8个区域.自x轴正向按逆时针方向把每个区域依次标上Ⅰ,Ⅱ,Ⅲ,Ⅳ,如图所示:
将坐标系的每个象限三等分,得到12个区域.自x轴正向按逆时针方向把每个区域依次标上Ⅰ,Ⅱ,Ⅲ,Ⅳ,如图所示:
本节要点归纳
1.知识清单:
(1)任意角的概念;
(2)终边相同的角;
(3)象限角、区域角的表示.
2.方法归纳:数形结合、分类讨论.
3.常见误区:锐角与小于90°角的区别,终边相同角的表示中漏掉k∈Z.
学以致用·随堂检测促达标
1
2
3
4
1.660°是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
C
解析 因为660°=300°+360°,所以在0°~360°范围内,与660°角终边相同的角是300°角,它是第四象限角.
1
2
3
4
2.集合M={α|α=k·90°,k∈Z}中各角的终边都在( )
A.x轴非负半轴上
B.y轴非负半轴上
C.x轴或y轴上
D.x轴非负半轴或y轴非负半轴上
C
解析 当k=4n,n∈Z时,α=n·360°;当k=4n+1,n∈Z时,α=90°+n·360°;当k=4n+2,n∈Z时,α=180°+n·360°;当k=4n+3,n∈Z时,α=270°+n·360°.因此,集合M中各角的终边都在x轴或y轴上.
1
2
3
4
3.在0°~360°范围内,与角-60°的终边在同一条直线上的角为 .
120°,300°
解析 与角-60°的终边在同一条直线上的角可表示为
β=-60°+k·180°,k∈Z.
∵所求角在0°~360°范围内,∴0°≤-60°+k·180°≤360°,解得 ,k∈Z,∴k=1或2,
当k=1时,β=120°,当k=2时,β=300°.
1
2
3
4
4.已知角α的终边落在图中阴影部分表示的范围内(不包括边界),则角α的集合是 .
{α|45°+k·360°<α<150°+k·360°,k∈Z}
解析 在0°~360°范围内,阴影部分的边界射线所表示的角分别是45°和150°,因此,所求α的范围是45°+k·360°<α<150°+k·360°,k∈Z.
1
2
3
4
5.若β是第二象限角,则270°+β是第 象限角;-β是第
象限角.
一
三
解析 因为β是第二象限角,所以k·360°+90°<β
本 课 结 束
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
