第1章 三角函数 总结提升--北师大版高中数学必修第二册课件(共44页PPT)
文档属性
| 名称 | 第1章 三角函数 总结提升--北师大版高中数学必修第二册课件(共44页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 20:10:35 | ||
图片预览







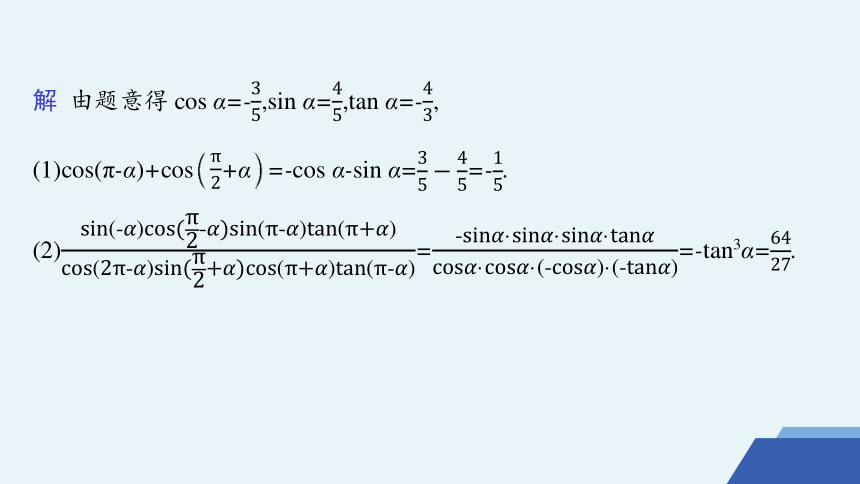



文档简介
(共44张PPT)
第一章
本章总结提升
知识网络·整合构建
专题突破·素养提升
目录索引
易错易混·衔接高考
知识网络·整合构建
三角函数
三角函数
专题突破·素养提升
专题一 三角函数的化简与求值
1.三角函数的化简与求值主要用到任意角三角函数的定义,三角函数的诱导公式等知识,其中熟练掌握诱导公式是关键.
2.通过三角函数的化简与求值,能提升逻辑推理和数学运算能力.
【例1】 已知角α的顶点在原点,始边与x轴的非负半轴重合,终边经过点P(-3,4).
规律方法 解决三角函数的化简与求值问题一般先化简再求值,充分利用诱导公式.
专题二 三角函数的图象及变换
1.用“五点法”作y=Asin(ωx+φ)的图象,确定五个关键点的方法是分别令
2.对于y=Asin(ωx+φ)+h,应明确A,ω决定“形变”,φ,h决定“位变”,A影响值域,ω影响周期,A,ω,φ影响单调性.
3.通过三角函数的图象及变换的应用,能提升直观想象和逻辑推理能力.
【例2】 将函数y=f(x)的图象向左平移1个单位长度,然后将图象上各点的纵坐标不变,横坐标伸长到原来的 倍,然后将图象向上平移1个单位长度,得到函数y= sin x的图象.
(1)求f(x)的最小正周期和单调递增区间;
(2)若函数y=g(x)与y=f(x)的图象关于直线x=2对称,求当x∈[0,1]时,函数y=g(x)的最小值和最大值.
(2)∵函数y=g(x)与y=f(x)的图象关于直线x=2对称,
∴当x∈[0,1]时,y=g(x)的最值即为x∈[3,4]时,y=f(x)的最值.
(1)求f(x)的解析式;
(2)把f(x)的图象向左至少平移多少个单位长度,才能使得到的图象对应的函数为偶函数
规律方法 关于平移变换要注意是在x的基础上加或减的变换,还要注意先“平移”后“伸缩”与先“伸缩”后“平移”的区别.
专题三 三角函数的图象与性质
1.整体代换思想、数形结合思想是研究三角函数的图象与性质的主要思想方法.
2.通过研究三角函数的图象与性质,能提升直观想象和数学运算的能力.
规律方法 研究y=Asin(ωx+φ)的单调性、最值问题时,把ωx+φ看作一个整体来解决.
专题四 数形结合思想在三角函数中的应用
1.在三角函数学习和解题过程中,要善于运用数形结合的方法寻找解题的突破口,解题先想图,以图促解题,养成数形结合的习惯,用好数形结合的思想方法,能起到事半功倍的效果.
2.通过数形结合思想方法的应用,能促进直观想象素养的提升.
【例4】 如果关于x的方程sin2x-(2+a)sin x+2a=0在x∈ 上有两个实数根,求实数a的取值范围.
解 sin2x-(2+a)sin x+2a=0,
即(sin x-2)(sin x-a)=0.
∵sin x-2≠0,∴sin x=a,
规律方法 数形结合思想贯穿了三角函数的始终,对于与方程解有关的问题以及在研究y=Asin(ωx+φ)(A>0,ω>0)的性质和由性质研究图象时,常利用数形结合思想.
变式训练4方程lg|x|=sin(x+ )的实数根的个数为( )
A.4 B.5 C.6 D.7
C
两图象共有6个公共点,从而方程有6个实数根,故选C.
易错易混·衔接高考
1
2
3
4
1.[2024北京,6]已知f(x)=sin ωx(ω>0),f(x1)=-1,f(x2)=1,|x1-x2|min= ,则ω=( )
A.1 B.2 C.3 D.4
B
1
2
3
4
2.(多选)[2024新高考Ⅱ,9]对于函数f(x)=sin 2x和 ,下列正确的有( )
A.f(x)与g(x)有相同的零点
B.f(x)与g(x)有相同的最大值
C.f(x)与g(x)有相同的最小正周期
D.f(x)与g(x)的图象有相同的对称轴
BC
1
2
3
4
1
2
3
4
A
1
2
3
4
1
2
3
4
4.[2024新高考Ⅰ,7]当x∈[0,2π]时,曲线y=sin x与y=2sin(3x- )的交点个数为( )
A.3 B.4 C.6 D.8
C
1
2
3
4
本 课 结 束
第一章
本章总结提升
知识网络·整合构建
专题突破·素养提升
目录索引
易错易混·衔接高考
知识网络·整合构建
三角函数
三角函数
专题突破·素养提升
专题一 三角函数的化简与求值
1.三角函数的化简与求值主要用到任意角三角函数的定义,三角函数的诱导公式等知识,其中熟练掌握诱导公式是关键.
2.通过三角函数的化简与求值,能提升逻辑推理和数学运算能力.
【例1】 已知角α的顶点在原点,始边与x轴的非负半轴重合,终边经过点P(-3,4).
规律方法 解决三角函数的化简与求值问题一般先化简再求值,充分利用诱导公式.
专题二 三角函数的图象及变换
1.用“五点法”作y=Asin(ωx+φ)的图象,确定五个关键点的方法是分别令
2.对于y=Asin(ωx+φ)+h,应明确A,ω决定“形变”,φ,h决定“位变”,A影响值域,ω影响周期,A,ω,φ影响单调性.
3.通过三角函数的图象及变换的应用,能提升直观想象和逻辑推理能力.
【例2】 将函数y=f(x)的图象向左平移1个单位长度,然后将图象上各点的纵坐标不变,横坐标伸长到原来的 倍,然后将图象向上平移1个单位长度,得到函数y= sin x的图象.
(1)求f(x)的最小正周期和单调递增区间;
(2)若函数y=g(x)与y=f(x)的图象关于直线x=2对称,求当x∈[0,1]时,函数y=g(x)的最小值和最大值.
(2)∵函数y=g(x)与y=f(x)的图象关于直线x=2对称,
∴当x∈[0,1]时,y=g(x)的最值即为x∈[3,4]时,y=f(x)的最值.
(1)求f(x)的解析式;
(2)把f(x)的图象向左至少平移多少个单位长度,才能使得到的图象对应的函数为偶函数
规律方法 关于平移变换要注意是在x的基础上加或减的变换,还要注意先“平移”后“伸缩”与先“伸缩”后“平移”的区别.
专题三 三角函数的图象与性质
1.整体代换思想、数形结合思想是研究三角函数的图象与性质的主要思想方法.
2.通过研究三角函数的图象与性质,能提升直观想象和数学运算的能力.
规律方法 研究y=Asin(ωx+φ)的单调性、最值问题时,把ωx+φ看作一个整体来解决.
专题四 数形结合思想在三角函数中的应用
1.在三角函数学习和解题过程中,要善于运用数形结合的方法寻找解题的突破口,解题先想图,以图促解题,养成数形结合的习惯,用好数形结合的思想方法,能起到事半功倍的效果.
2.通过数形结合思想方法的应用,能促进直观想象素养的提升.
【例4】 如果关于x的方程sin2x-(2+a)sin x+2a=0在x∈ 上有两个实数根,求实数a的取值范围.
解 sin2x-(2+a)sin x+2a=0,
即(sin x-2)(sin x-a)=0.
∵sin x-2≠0,∴sin x=a,
规律方法 数形结合思想贯穿了三角函数的始终,对于与方程解有关的问题以及在研究y=Asin(ωx+φ)(A>0,ω>0)的性质和由性质研究图象时,常利用数形结合思想.
变式训练4方程lg|x|=sin(x+ )的实数根的个数为( )
A.4 B.5 C.6 D.7
C
两图象共有6个公共点,从而方程有6个实数根,故选C.
易错易混·衔接高考
1
2
3
4
1.[2024北京,6]已知f(x)=sin ωx(ω>0),f(x1)=-1,f(x2)=1,|x1-x2|min= ,则ω=( )
A.1 B.2 C.3 D.4
B
1
2
3
4
2.(多选)[2024新高考Ⅱ,9]对于函数f(x)=sin 2x和 ,下列正确的有( )
A.f(x)与g(x)有相同的零点
B.f(x)与g(x)有相同的最大值
C.f(x)与g(x)有相同的最小正周期
D.f(x)与g(x)的图象有相同的对称轴
BC
1
2
3
4
1
2
3
4
A
1
2
3
4
1
2
3
4
4.[2024新高考Ⅰ,7]当x∈[0,2π]时,曲线y=sin x与y=2sin(3x- )的交点个数为( )
A.3 B.4 C.6 D.8
C
1
2
3
4
本 课 结 束
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
