高中数学人教A版必修2期末限时训练6(含解析)
文档属性
| 名称 | 高中数学人教A版必修2期末限时训练6(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 917.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 20:21:21 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
限时训练6
一、单选题
1.已知向量,若,则( )
A.10 B. C. D.
2.下列说法正确的是( )
A.有两个平面平行,其余各面都是四边形的几何体是棱柱 B.底面是正六边形的棱锥是正六棱锥
C.棱台的所有侧棱的延长线交于同一个点 D.绕直角梯形的一条边所在直线旋转一周得到的几何体是圆台
3.已知,是两条不同的直线,,是两个不同的平面,则下列结论一定正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
4.小明在手工课上用硬纸板做了一个圆锥形容器,若该圆锥形容器的轴截面是边长为分米的等边三角形,忽略硬纸板的厚度,则该圆锥形容器的容积是( )
A.立方分米 B.立方分米 C.立方分米 D.立方分米
5.正五角星是一个非常优美的几何图形,且与黄金分割有着密切的联系.在如图所示的正五角星中,,是该正五角星的中心,则( )
A. B. C.12 D.18
二、多选题
6.在中,角,,的对边分别是,,,若,,,则的值可以是( )
A. B. C. D.
7.已知三棱锥的底面是直角三角形,平面,,则( )
A.三棱锥外接球的表面积为 B.三棱锥外接球的表面积为
C.三棱锥内切球的半径为 D.三棱锥内切球的半径为
三、填空题
8.如图所示,一个水平放置的四边形的斜二测画法的直观图是边长为2的正方形,则原四边形的面积是 .
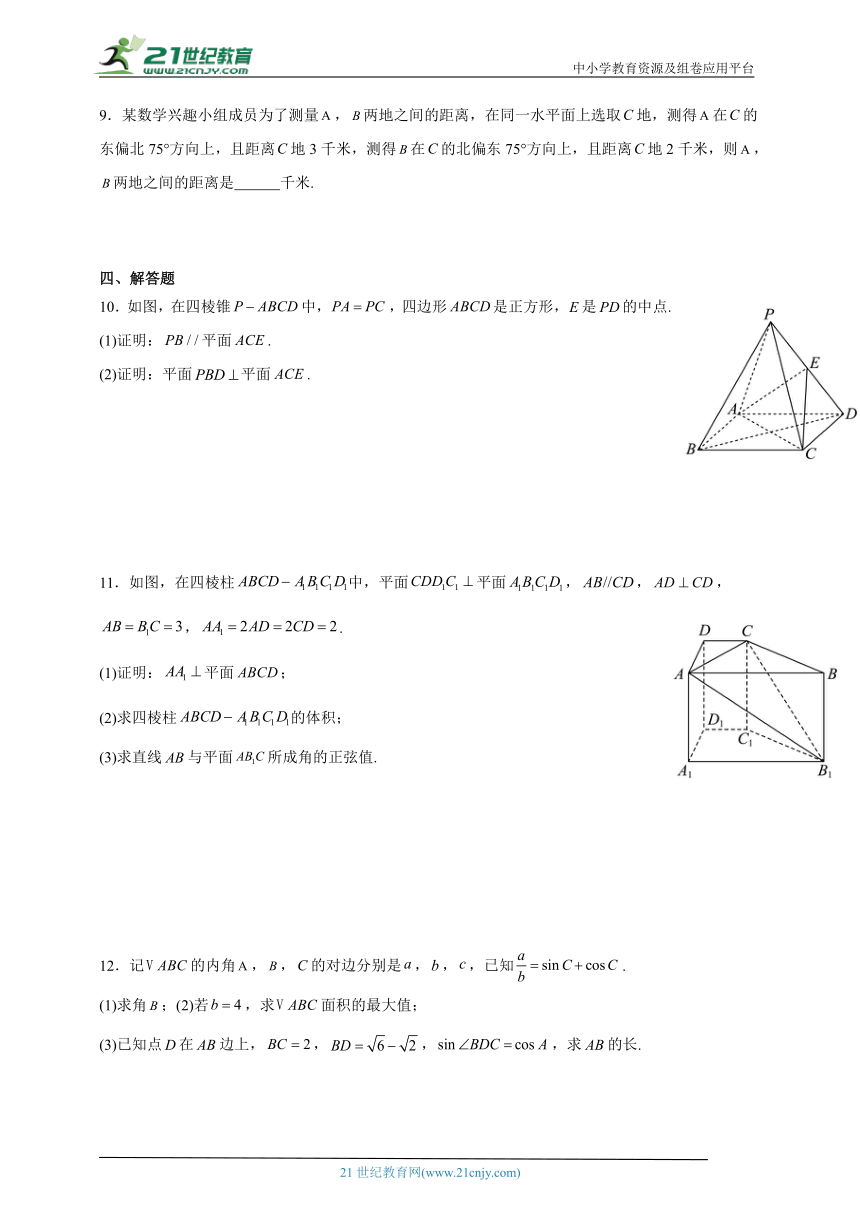
9.某数学兴趣小组成员为了测量,两地之间的距离,在同一水平面上选取地,测得在的东偏北75°方向上,且距离地3千米,测得在的北偏东75°方向上,且距离地2千米,则,两地之间的距离是 千米.
四、解答题
10.如图,在四棱锥中,,四边形是正方形,是的中点.
(1)证明:平面.
(2)证明:平面平面.
11.如图,在四棱柱中,平面平面,,,,.
(1)证明:平面;
(2)求四棱柱的体积;
(3)求直线与平面所成角的正弦值.
12.记的内角,,的对边分别是,,,已知.
(1)求角;(2)若,求面积的最大值;
(3)已知点在边上,,,,求的长.
《限时训练6》参考答案
题号 1 2 3 4 5 6 7
答案 A C D A D AD AC
1.由题意可得,解得.故选:A
2.棱台有两个平面平行,其余各面都是梯形,则A错误;底面是正六边形,且所有侧棱相等的棱锥是正六棱锥,则B错误;由棱台的定义可知棱台的所有侧棱的延长线交于同一个点,则C正确;绕直角梯形的直角腰所在直线旋转一周得到的几何体是圆台,则D错误.故选:C
3.若,,则或,故A错误.若,,则或,相交,故B错误.
若,,则或或,故C错误.若,,则,故D正确.故选:D.
4.设该圆锥形的容器的底面圆的半径为,高为,则分米,分米,
则小明制作的圆锥形的容器的容积是立方分米.故选:.
5.作,垂足为,如下图所示:
则为的中点,故.
故选:D
6.因为,且,所以.由正弦定理可得,则,又,有,故或.故选:AD
7.由题意可知,,两两垂直,则三棱锥外接球的半径满足,
从而三棱锥外接球的表面积为,故A正确,B错误.
由题意可得三棱锥的体积,三棱锥的表面积.设三棱锥内切球的半径为,
因为,所以,则C正确,D错误.故选:AC
8.在正方形中可得,由斜二测画法可知,
且,所以四边形为平行四边形,所以原四边形的面积是,故答案为:.
9.由题意可得,,在的东偏北75°方向,在的北偏东75°方向可得.
在中,由余弦定理可得,则千米.
故答案为:.
10.(1)记,连接.因为四边形是正方形,所以是的中点.因为是的中点,所以.因为平面,平面,所以平面.
(2)连接.因为四边形是正方形,所以是的中点.
因为,所以.因为四边形是正方形,所以.
因为平面,且,所以平面.因为平面,所以平面平面.
11.(1)在上取点,使得,连接,因为,,所以,,又,即,所以四边形是正方形.因为,,所以.
因为,,所以,所以,因为平面平面,且平面平面,,平面,所以平面.因为平面,所以.因为,平面,且与相交,所以平面.因为平面平面,,所以平面.
(2)由题意可得梯形的面积,则四棱柱的体积.
(3)作平面,垂足为,连接,
则是直线与平面所成的角,由题意可得的面积,由(1)可知平面,
所以三棱锥的体积,因为,且,所以.由(1)可知平面,平面,所以.又,,所以.在中由余弦定理可知,则,所以,则的面积,故三棱锥的体积.因为,所以,解得,则,即直线与平面所成角的正弦值为.
12.(1)由正弦定理得,,所以,所以,又因为,
所以,所以,所以,所以,因为,
所以,即,因为,所以.
(2)由余弦定理得,即.因为,当且仅当时,等号成立,
所以,所以,即,则的面积,
即面积的最大值为.
(3)在中,由余弦定理得,,
所以.所以,所以,
又因为,所以,
所以,即,又因为所以,即,
因为,所以
所以,即,在中,由锐角三角函数得,,所以,故.
【点睛】关键点点睛:本题主要考查了正弦定理,两角和的正弦函数公式,余弦定理,三角形面积公式在解三角形中的综合应用,解题的关键是合理利用正弦定理的边角互化,以及余弦定理列出方程求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
限时训练6
一、单选题
1.已知向量,若,则( )
A.10 B. C. D.
2.下列说法正确的是( )
A.有两个平面平行,其余各面都是四边形的几何体是棱柱 B.底面是正六边形的棱锥是正六棱锥
C.棱台的所有侧棱的延长线交于同一个点 D.绕直角梯形的一条边所在直线旋转一周得到的几何体是圆台
3.已知,是两条不同的直线,,是两个不同的平面,则下列结论一定正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
4.小明在手工课上用硬纸板做了一个圆锥形容器,若该圆锥形容器的轴截面是边长为分米的等边三角形,忽略硬纸板的厚度,则该圆锥形容器的容积是( )
A.立方分米 B.立方分米 C.立方分米 D.立方分米
5.正五角星是一个非常优美的几何图形,且与黄金分割有着密切的联系.在如图所示的正五角星中,,是该正五角星的中心,则( )
A. B. C.12 D.18
二、多选题
6.在中,角,,的对边分别是,,,若,,,则的值可以是( )
A. B. C. D.
7.已知三棱锥的底面是直角三角形,平面,,则( )
A.三棱锥外接球的表面积为 B.三棱锥外接球的表面积为
C.三棱锥内切球的半径为 D.三棱锥内切球的半径为
三、填空题
8.如图所示,一个水平放置的四边形的斜二测画法的直观图是边长为2的正方形,则原四边形的面积是 .
9.某数学兴趣小组成员为了测量,两地之间的距离,在同一水平面上选取地,测得在的东偏北75°方向上,且距离地3千米,测得在的北偏东75°方向上,且距离地2千米,则,两地之间的距离是 千米.
四、解答题
10.如图,在四棱锥中,,四边形是正方形,是的中点.
(1)证明:平面.
(2)证明:平面平面.
11.如图,在四棱柱中,平面平面,,,,.
(1)证明:平面;
(2)求四棱柱的体积;
(3)求直线与平面所成角的正弦值.
12.记的内角,,的对边分别是,,,已知.
(1)求角;(2)若,求面积的最大值;
(3)已知点在边上,,,,求的长.
《限时训练6》参考答案
题号 1 2 3 4 5 6 7
答案 A C D A D AD AC
1.由题意可得,解得.故选:A
2.棱台有两个平面平行,其余各面都是梯形,则A错误;底面是正六边形,且所有侧棱相等的棱锥是正六棱锥,则B错误;由棱台的定义可知棱台的所有侧棱的延长线交于同一个点,则C正确;绕直角梯形的直角腰所在直线旋转一周得到的几何体是圆台,则D错误.故选:C
3.若,,则或,故A错误.若,,则或,相交,故B错误.
若,,则或或,故C错误.若,,则,故D正确.故选:D.
4.设该圆锥形的容器的底面圆的半径为,高为,则分米,分米,
则小明制作的圆锥形的容器的容积是立方分米.故选:.
5.作,垂足为,如下图所示:
则为的中点,故.
故选:D
6.因为,且,所以.由正弦定理可得,则,又,有,故或.故选:AD
7.由题意可知,,两两垂直,则三棱锥外接球的半径满足,
从而三棱锥外接球的表面积为,故A正确,B错误.
由题意可得三棱锥的体积,三棱锥的表面积.设三棱锥内切球的半径为,
因为,所以,则C正确,D错误.故选:AC
8.在正方形中可得,由斜二测画法可知,
且,所以四边形为平行四边形,所以原四边形的面积是,故答案为:.
9.由题意可得,,在的东偏北75°方向,在的北偏东75°方向可得.
在中,由余弦定理可得,则千米.
故答案为:.
10.(1)记,连接.因为四边形是正方形,所以是的中点.因为是的中点,所以.因为平面,平面,所以平面.
(2)连接.因为四边形是正方形,所以是的中点.
因为,所以.因为四边形是正方形,所以.
因为平面,且,所以平面.因为平面,所以平面平面.
11.(1)在上取点,使得,连接,因为,,所以,,又,即,所以四边形是正方形.因为,,所以.
因为,,所以,所以,因为平面平面,且平面平面,,平面,所以平面.因为平面,所以.因为,平面,且与相交,所以平面.因为平面平面,,所以平面.
(2)由题意可得梯形的面积,则四棱柱的体积.
(3)作平面,垂足为,连接,
则是直线与平面所成的角,由题意可得的面积,由(1)可知平面,
所以三棱锥的体积,因为,且,所以.由(1)可知平面,平面,所以.又,,所以.在中由余弦定理可知,则,所以,则的面积,故三棱锥的体积.因为,所以,解得,则,即直线与平面所成角的正弦值为.
12.(1)由正弦定理得,,所以,所以,又因为,
所以,所以,所以,所以,因为,
所以,即,因为,所以.
(2)由余弦定理得,即.因为,当且仅当时,等号成立,
所以,所以,即,则的面积,
即面积的最大值为.
(3)在中,由余弦定理得,,
所以.所以,所以,
又因为,所以,
所以,即,又因为所以,即,
因为,所以
所以,即,在中,由锐角三角函数得,,所以,故.
【点睛】关键点点睛:本题主要考查了正弦定理,两角和的正弦函数公式,余弦定理,三角形面积公式在解三角形中的综合应用,解题的关键是合理利用正弦定理的边角互化,以及余弦定理列出方程求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
