第6章 立体几何初步 总结提升--北师大版高中数学必修第二册课件(共47页PPT)
文档属性
| 名称 | 第6章 立体几何初步 总结提升--北师大版高中数学必修第二册课件(共47页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-26 17:21:08 | ||
图片预览








文档简介
(共47张PPT)
第六章
本章总结提升
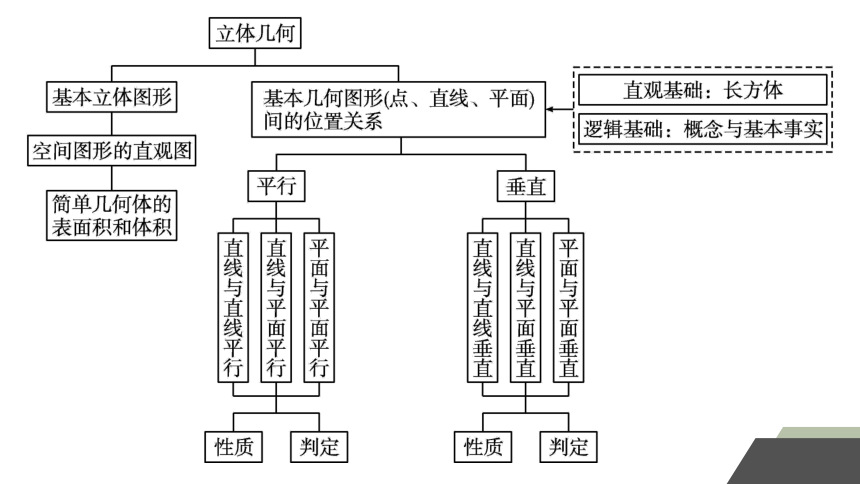
知识网络·整合构建
专题突破·素养提升
目录索引
易错易混·衔接高考
知识网络·整合构建
专题突破·素养提升
专题一 几何体的表面积与体积
1.主要考查多面体、旋转体的表面积,旋转体的侧面展开图,柱体、锥体、台体的体积,球的表面积和体积,不规则几何体常用等体积法、分割法、补形法等进行求解.
2.利用公式求解表面积、体积,提高数学运算素养.
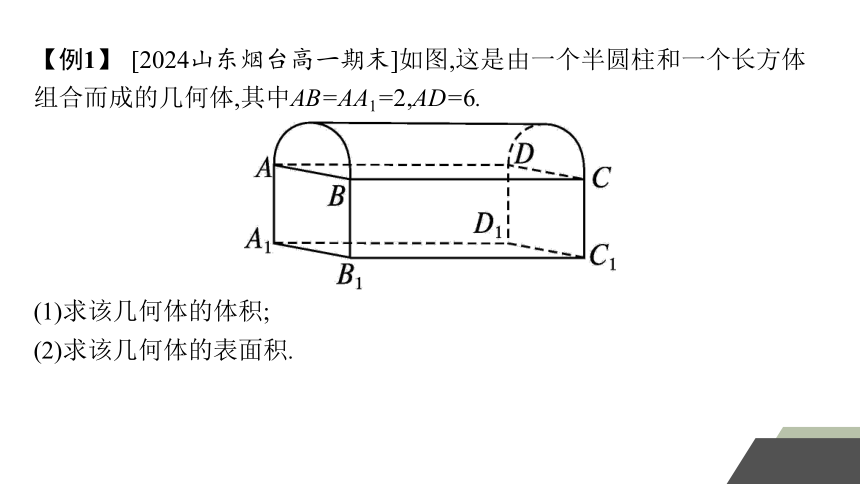
【例1】 [2024山东烟台高一期末]如图,这是由一个半圆柱和一个长方体组合而成的几何体,其中AB=AA1=2,AD=6.
(1)求该几何体的体积;
(2)求该几何体的表面积.
解 (1)由题得,长方体的体积为2×2×6=24,
故该几何体的体积为24+3π.
(2)长方体去掉上底面后的表面积为2×6+2×2×2+2×6×2=44.
规律方法 1.空间几何体表面积的求法
(1)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.
(2)旋转体的表面积问题注意其侧面展开图的应用.
2.空间几何体体积问题的常见类型及解题策略
(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解.
(2)若所给定的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等方法进行求解.特别地,求三棱锥体积时经常要转换顶点和底面,从而达到方便求高的目的.
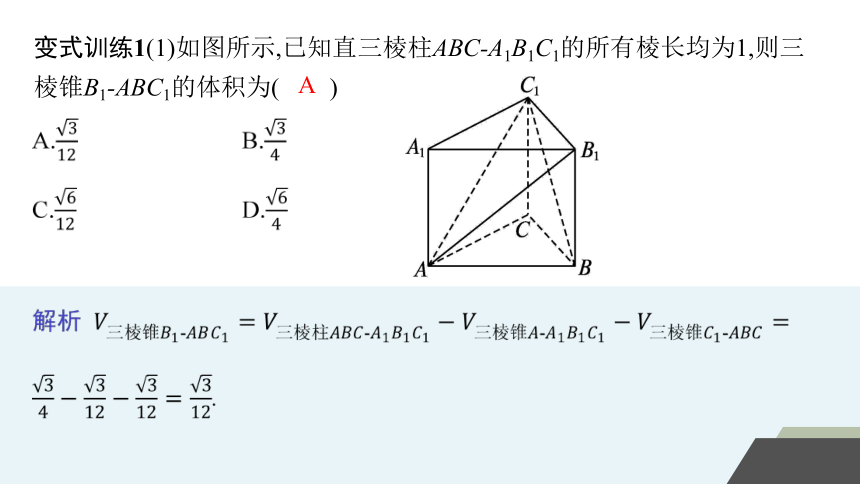
变式训练1(1)如图所示,已知直三棱柱ABC-A1B1C1的所有棱长均为1,则三棱锥B1-ABC1的体积为( )
A
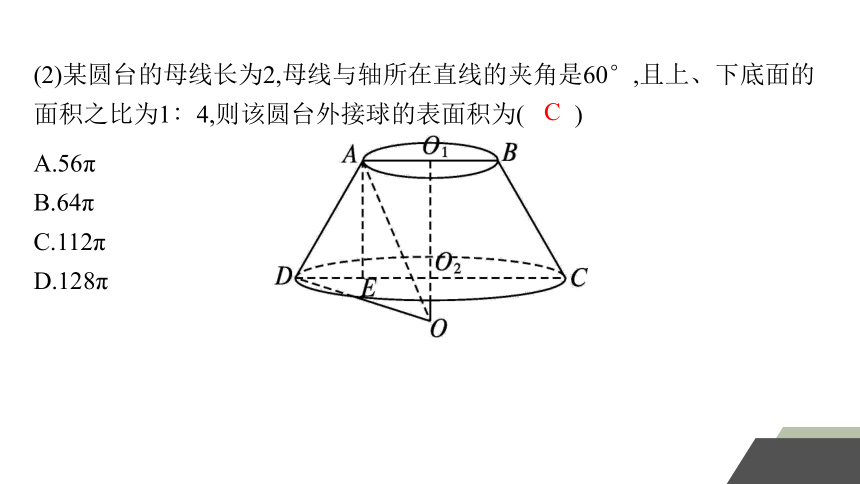
(2)某圆台的母线长为2,母线与轴所在直线的夹角是60°,且上、下底面的面积之比为1∶4,则该圆台外接球的表面积为( )
A.56π
B.64π
C.112π
D.128π
C
专题二 空间中的平行关系
1.空间中的平行主要有线线平行、线面平行、面面平行,主要考查在空间几何体中证明线面平行、面面平行以及线线平行.
2.通过线线平行、线面平行、面面平行之间的相互转化,提升逻辑推理和直观想象素养.
【例2】 已知M,N分别是底面为平行四边形的四棱锥P-ABCD的棱AB,PC的中点,平面CMN与平面PAD交于PE.求证:
(1)MN∥平面PAD;
(2)MN∥PE.
证明 (1)如图,取DC的中点Q,连接MQ,NQ.
∵NQ是△PDC的中位线,∴NQ∥PD.∵NQ 平面PAD,
PD 平面PAD,
∴NQ∥平面PAD.
∵M是AB的中点,四边形ABCD是平行四边形,
∴MQ∥AD.∵MQ 平面PAD,AD 平面PAD,
∴MQ∥平面PAD.∵MQ∩NQ=Q,MQ 平面MNQ,NQ 平面MNQ,
∴平面MNQ∥平面PAD.
∵MN 平面MNQ,∴MN∥平面PAD.
(2)∵平面MNQ∥平面PAD,平面PEC∩平面MNQ=MN,平面PEC∩平面PAD=PE,∴MN∥PE.
规律方法 线线平行、线面平行、面面平行相互间的转化
变式训练2如图,正方体ABCD-A1B1C1D1的棱长为2,E,F分别为DD1,BB1的
中点.
(1)求证:CF∥平面A1EC1;
(2)过点D作正方体截面使其与平面A1EC1平行,请给以证明并求出该截面图形的面积.
(1)证明 取CC1中点M,连接ME,B1M.
由MC∥FB1且MC=FB1,可得四边形MCFB1为平行四边形,则FC∥MB1.
由ME∥A1B1且ME=A1B1,可得四边形MEA1B1为平行四边形,则A1E∥MB1,
则A1E∥FC.又A1E 平面A1EC1,CF 平面A1EC1,
则CF∥平面A1EC1.
(2)解取AA1,CC1中点G,H,连接DG,GB1,B1H,HD.
易知四边形DGB1H为平行四边形,且DH∥C1E,DG∥A1E.
又因为DH,DG 平面DGB1H,DH∩DG=D,A1E,C1E 平面A1EC1,A1E∩C1E=E,所以平面DGB1H∥平面A1EC1,
平面DGB1H即为所求截面.
专题三 空间中的垂直关系
1.主要考查空间中线面垂直、面面垂直的判定定理与性质定理,以及线线垂直、线面垂直、面面垂直三者之间的联系与转化.
2.通过线线垂直、线面垂直、面面垂直三者之间的转化,提升直观想象和逻辑推理素养.
【例3】 如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.求证:
(1)平面ADE⊥平面BCC1B1;
(2)直线A1F∥平面ADE.
(1)证明 因为三棱柱ABC-A1B1C1是直三棱柱,
所以CC1⊥平面ABC.又AD 平面ABC,所以CC1⊥AD.
又因为AD⊥DE,CC1,DE 平面BCC1B1,CC1∩DE=E,
所以AD⊥平面BCC1B1.
又AD 平面ADE,所以平面ADE⊥平面BCC1B1.
(2)证明 因为A1B1=A1C1,F为B1C1的中点,所以A1F⊥B1C1.因为CC1⊥平面A1B1C1,且A1F 平面A1B1C1,所以CC1⊥A1F.又因为CC1,B1C1 平面BCC1B1,CC1∩B1C1=C1,所以A1F⊥平面BCC1B1.由(1)知AD⊥平面BCC1B1,所以A1F∥AD.又AD 平面ADE,A1F 平面ADE,所以A1F∥平面ADE.
规律方法 线线垂直、线面垂直、面面垂直相互间的转化
变式训练3在四棱锥P-ABCD中,已知AB∥CD,平面PAB与平面PCD的交线为l.
(1)求证:AB∥l;
(2)若PA⊥平面ABCD,且BC=2AB,∠ABC=60°,求证:AB⊥PC.
证明 (1)因为AB∥CD,AB 平面PCD,CD 平面PCD,所以AB∥平面PCD,AB 平面PAB,平面PCD∩平面PAB=l,所以AB∥l.
(2)因为四边形ABCD中,BC=2AB,∠ABC=60°,
所以在△ABC中,AB⊥AC.
又因为PA⊥平面ABCD,AB 平面ABCD,
所以PA⊥AB,PA∩AC=A,所以AB⊥平面PAC.
因为PC 平面PAC,所以AB⊥PC.
专题四 空间角的求法
1.空间角包括异面直线所成的角、线面角及二面角,主要考查空间角的定义及求法,求角时要先找角,再证角,最后在三角形中求角.
2.通过找角、证角、求角,提升逻辑推理与数学运算素养.
【例4】 如图,正方体的棱长为1,B'C∩BC'=O,求:
(1)AO与A'C'所成的角的大小;
(2)AO与平面ABCD所成的角的正切值;
(3)二面角B-AO-C的大小.
解 (1)∵A'C'∥AC,
∴AO与A'C'所成的角就是∠OAC.
∵AB⊥平面BCC'B',OC 平面BCC'B',∴OC⊥AB.
又OC⊥BO,AB∩BO=B,AB,BO 平面ABO,
∴OC⊥平面ABO.又OA 平面ABO,∴OC⊥OA.
(2)如图,作OE⊥BC于E,连接AE.
∵平面BCC'B'⊥平面ABCD,平面BCC'B'∩平面ABCD=BC,OE 平面BCC'B',∴OE⊥平面ABCD,
∴∠OAE为OA与平面ABCD所成的角.在Rt△OAE
(3)由(1)可知OC⊥平面AOB.
∵OC 平面AOC,∴平面AOB⊥平面AOC,即二面角B-AO-C的大小为90°.
规律方法 1.求异面直线所成的角常用平移转化法(转化为相交直线的夹角).
2.求直线与平面所成的角常用射影转化法(即作垂线、找射影).
3.二面角的平面角的作法常有三种:(1)定义法;(2)三垂线法;(3)垂面法.
变式训练4(1)在直三棱柱ABC-A1B1C1中,CA=CB=4,AB=2 ,CC1=2 ,E,F分别为AC,CC1的中点,则直线EF与平面AA1B1B所成的角是( )
A.30° B.45° C.60° D.90°
A
解析 如图,连接AC1,取A1B1的中点记为O,连接C1O,AO.
∵C1A1=C1B1,O为A1B1的中点,
∴C1O⊥A1B1.
又AA1⊥平面A1B1C1,∴AA1⊥C1O.
又AA1∩A1B1=A1,AA1 平面AA1B1B,A1B1 平面AA1B1B,
∴C1O⊥平面AA1B1B.又EF∥AC1,
∴EF与平面AA1B1B所成的角即为∠C1AO.
在Rt△C1AO中,∠C1OA=90°,
(2)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD为直角梯形, AB∥CD,AB⊥AD.若AB=AD,直线PB与CD所成的角为45°,求二面角
P-CD-B的大小.
解∵AB⊥AD,CD∥AB,∴CD⊥AD.
又PA⊥底面ABCD,CD 平面ABCD,∴PA⊥CD.
又PA∩AD=A,PA,AD 平面PAD,
∴CD⊥平面PAD.又PD 平面PAD,∴CD⊥PD,
∴∠PDA是二面角P-CD-B的平面角.
又直线PB与CD所成的角为45°,
∴∠PBA=45°,PA=AB,∴在Rt△PAD中,PA=AD,
∴∠PDA=45°,即二面角P-CD-B的大小为45°.
易错易混·衔接高考
1
2
3
4
5
1.[2024天津,6]若m,n为两条不同的直线,α为一个平面,则下列结论中正确的是( )
A.若m∥α,n α,则m∥n
B.若m∥α,n∥α,则m∥n
C.若m∥α,n⊥α,则m⊥n
D.若m∥α,n⊥α,则m与n相交
C
1
2
3
4
5
解析 对于A,若m∥α,n α,则m与n平行或异面,A错误;对于B,若m∥α,n∥α,则m与n平行或异面或相交,B错误;对于C,已知m∥α,n⊥α,如图,过直线m作平面β,使得α∩β=s.∵m β,∴m∥s,又s α,∴n⊥s,∴m⊥n,C正确;对于D,若m∥α,n⊥α,则m与n相交或异面,D错误.故选C.
1
2
3
4
5
2.[2024北京,8]已知以边长为4的正方形为底面的四棱锥,四条侧棱分别为4,4,2 ,2 ,则该四棱锥的高为( )
D
解析 如图所示,底面ABCD是边长为4的正方形,设SA=SD=4,SB=SC=2 .分别取AD,BC的中点E,F,则SE⊥AD,EF⊥AD.∴AD⊥平面SEF.作SO⊥EF,
O为垂足,则AD⊥SO.∴SO⊥平面ABCD,∴SO是四棱锥S-ABCD的高.
∵SE=2 ,EF=4,SF=2,∴EF2=SE2+SF2,∴∠ESF=90°.在Rt△ESF中,
1
2
3
4
5
1
2
3
4
5
3.[2024新高考Ⅰ,5]已知圆柱和圆锥的底面半径相等,侧面积相等,且它们的高均为 ,则圆锥的体积为( )
B
1
2
3
4
5
4.[2024新高考Ⅱ,7]已知正三棱台ABC-A1B1C1的体积为 ,AB=6,A1B1=2,则A1A与平面ABC所成角的正切值为( )
A. B.1 C.2 D.3
B
1
2
3
4
5
解析 (方法一)设棱台的高为h,三条侧棱延长后相交于一点S.正三角形ABC与正三角形A1B1C1的中心分别是点O,O1.连接AO,SO,易知点O1在SO上.
1
2
3
4
5
(方法二)设棱台的高为h,正三角形ABC与正三角形A1B1C1的中心分别是点O,O1,连接OO1,A1O1,AO,作A1H⊥AO,H为垂足.
1
2
3
4
5
5.[2024全国甲,文19]如图,在以A,B,C,D,E,F为顶点的五面体中,四边形ABCD与四边形ADEF均为等腰梯形,EF∥AD,BC∥AD,AD=4, AB=BC=EF=2,ED= ,FB=2,M为AD的中点.
(1)证明:BM∥平面CDE;
(2)求M到平面FAB的距离.
1
2
3
4
5
(1)证明由题意知MD=2,BC=2,MD∥BC,
所以四边形BCDM为平行四边形,
故BM∥CD,
又因为BM 平面CDE,
所以BM∥平面CDE.
1
2
3
4
5
(2)解 取AM的中点为G,连接FG,BG,FM,
因为BM=CD=AB,所以BG⊥AM,同理FG⊥AM.
本 课 结 束
第六章
本章总结提升
知识网络·整合构建
专题突破·素养提升
目录索引
易错易混·衔接高考
知识网络·整合构建
专题突破·素养提升
专题一 几何体的表面积与体积
1.主要考查多面体、旋转体的表面积,旋转体的侧面展开图,柱体、锥体、台体的体积,球的表面积和体积,不规则几何体常用等体积法、分割法、补形法等进行求解.
2.利用公式求解表面积、体积,提高数学运算素养.
【例1】 [2024山东烟台高一期末]如图,这是由一个半圆柱和一个长方体组合而成的几何体,其中AB=AA1=2,AD=6.
(1)求该几何体的体积;
(2)求该几何体的表面积.
解 (1)由题得,长方体的体积为2×2×6=24,
故该几何体的体积为24+3π.
(2)长方体去掉上底面后的表面积为2×6+2×2×2+2×6×2=44.
规律方法 1.空间几何体表面积的求法
(1)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.
(2)旋转体的表面积问题注意其侧面展开图的应用.
2.空间几何体体积问题的常见类型及解题策略
(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解.
(2)若所给定的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等方法进行求解.特别地,求三棱锥体积时经常要转换顶点和底面,从而达到方便求高的目的.
变式训练1(1)如图所示,已知直三棱柱ABC-A1B1C1的所有棱长均为1,则三棱锥B1-ABC1的体积为( )
A
(2)某圆台的母线长为2,母线与轴所在直线的夹角是60°,且上、下底面的面积之比为1∶4,则该圆台外接球的表面积为( )
A.56π
B.64π
C.112π
D.128π
C
专题二 空间中的平行关系
1.空间中的平行主要有线线平行、线面平行、面面平行,主要考查在空间几何体中证明线面平行、面面平行以及线线平行.
2.通过线线平行、线面平行、面面平行之间的相互转化,提升逻辑推理和直观想象素养.
【例2】 已知M,N分别是底面为平行四边形的四棱锥P-ABCD的棱AB,PC的中点,平面CMN与平面PAD交于PE.求证:
(1)MN∥平面PAD;
(2)MN∥PE.
证明 (1)如图,取DC的中点Q,连接MQ,NQ.
∵NQ是△PDC的中位线,∴NQ∥PD.∵NQ 平面PAD,
PD 平面PAD,
∴NQ∥平面PAD.
∵M是AB的中点,四边形ABCD是平行四边形,
∴MQ∥AD.∵MQ 平面PAD,AD 平面PAD,
∴MQ∥平面PAD.∵MQ∩NQ=Q,MQ 平面MNQ,NQ 平面MNQ,
∴平面MNQ∥平面PAD.
∵MN 平面MNQ,∴MN∥平面PAD.
(2)∵平面MNQ∥平面PAD,平面PEC∩平面MNQ=MN,平面PEC∩平面PAD=PE,∴MN∥PE.
规律方法 线线平行、线面平行、面面平行相互间的转化
变式训练2如图,正方体ABCD-A1B1C1D1的棱长为2,E,F分别为DD1,BB1的
中点.
(1)求证:CF∥平面A1EC1;
(2)过点D作正方体截面使其与平面A1EC1平行,请给以证明并求出该截面图形的面积.
(1)证明 取CC1中点M,连接ME,B1M.
由MC∥FB1且MC=FB1,可得四边形MCFB1为平行四边形,则FC∥MB1.
由ME∥A1B1且ME=A1B1,可得四边形MEA1B1为平行四边形,则A1E∥MB1,
则A1E∥FC.又A1E 平面A1EC1,CF 平面A1EC1,
则CF∥平面A1EC1.
(2)解取AA1,CC1中点G,H,连接DG,GB1,B1H,HD.
易知四边形DGB1H为平行四边形,且DH∥C1E,DG∥A1E.
又因为DH,DG 平面DGB1H,DH∩DG=D,A1E,C1E 平面A1EC1,A1E∩C1E=E,所以平面DGB1H∥平面A1EC1,
平面DGB1H即为所求截面.
专题三 空间中的垂直关系
1.主要考查空间中线面垂直、面面垂直的判定定理与性质定理,以及线线垂直、线面垂直、面面垂直三者之间的联系与转化.
2.通过线线垂直、线面垂直、面面垂直三者之间的转化,提升直观想象和逻辑推理素养.
【例3】 如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.求证:
(1)平面ADE⊥平面BCC1B1;
(2)直线A1F∥平面ADE.
(1)证明 因为三棱柱ABC-A1B1C1是直三棱柱,
所以CC1⊥平面ABC.又AD 平面ABC,所以CC1⊥AD.
又因为AD⊥DE,CC1,DE 平面BCC1B1,CC1∩DE=E,
所以AD⊥平面BCC1B1.
又AD 平面ADE,所以平面ADE⊥平面BCC1B1.
(2)证明 因为A1B1=A1C1,F为B1C1的中点,所以A1F⊥B1C1.因为CC1⊥平面A1B1C1,且A1F 平面A1B1C1,所以CC1⊥A1F.又因为CC1,B1C1 平面BCC1B1,CC1∩B1C1=C1,所以A1F⊥平面BCC1B1.由(1)知AD⊥平面BCC1B1,所以A1F∥AD.又AD 平面ADE,A1F 平面ADE,所以A1F∥平面ADE.
规律方法 线线垂直、线面垂直、面面垂直相互间的转化
变式训练3在四棱锥P-ABCD中,已知AB∥CD,平面PAB与平面PCD的交线为l.
(1)求证:AB∥l;
(2)若PA⊥平面ABCD,且BC=2AB,∠ABC=60°,求证:AB⊥PC.
证明 (1)因为AB∥CD,AB 平面PCD,CD 平面PCD,所以AB∥平面PCD,AB 平面PAB,平面PCD∩平面PAB=l,所以AB∥l.
(2)因为四边形ABCD中,BC=2AB,∠ABC=60°,
所以在△ABC中,AB⊥AC.
又因为PA⊥平面ABCD,AB 平面ABCD,
所以PA⊥AB,PA∩AC=A,所以AB⊥平面PAC.
因为PC 平面PAC,所以AB⊥PC.
专题四 空间角的求法
1.空间角包括异面直线所成的角、线面角及二面角,主要考查空间角的定义及求法,求角时要先找角,再证角,最后在三角形中求角.
2.通过找角、证角、求角,提升逻辑推理与数学运算素养.
【例4】 如图,正方体的棱长为1,B'C∩BC'=O,求:
(1)AO与A'C'所成的角的大小;
(2)AO与平面ABCD所成的角的正切值;
(3)二面角B-AO-C的大小.
解 (1)∵A'C'∥AC,
∴AO与A'C'所成的角就是∠OAC.
∵AB⊥平面BCC'B',OC 平面BCC'B',∴OC⊥AB.
又OC⊥BO,AB∩BO=B,AB,BO 平面ABO,
∴OC⊥平面ABO.又OA 平面ABO,∴OC⊥OA.
(2)如图,作OE⊥BC于E,连接AE.
∵平面BCC'B'⊥平面ABCD,平面BCC'B'∩平面ABCD=BC,OE 平面BCC'B',∴OE⊥平面ABCD,
∴∠OAE为OA与平面ABCD所成的角.在Rt△OAE
(3)由(1)可知OC⊥平面AOB.
∵OC 平面AOC,∴平面AOB⊥平面AOC,即二面角B-AO-C的大小为90°.
规律方法 1.求异面直线所成的角常用平移转化法(转化为相交直线的夹角).
2.求直线与平面所成的角常用射影转化法(即作垂线、找射影).
3.二面角的平面角的作法常有三种:(1)定义法;(2)三垂线法;(3)垂面法.
变式训练4(1)在直三棱柱ABC-A1B1C1中,CA=CB=4,AB=2 ,CC1=2 ,E,F分别为AC,CC1的中点,则直线EF与平面AA1B1B所成的角是( )
A.30° B.45° C.60° D.90°
A
解析 如图,连接AC1,取A1B1的中点记为O,连接C1O,AO.
∵C1A1=C1B1,O为A1B1的中点,
∴C1O⊥A1B1.
又AA1⊥平面A1B1C1,∴AA1⊥C1O.
又AA1∩A1B1=A1,AA1 平面AA1B1B,A1B1 平面AA1B1B,
∴C1O⊥平面AA1B1B.又EF∥AC1,
∴EF与平面AA1B1B所成的角即为∠C1AO.
在Rt△C1AO中,∠C1OA=90°,
(2)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD为直角梯形, AB∥CD,AB⊥AD.若AB=AD,直线PB与CD所成的角为45°,求二面角
P-CD-B的大小.
解∵AB⊥AD,CD∥AB,∴CD⊥AD.
又PA⊥底面ABCD,CD 平面ABCD,∴PA⊥CD.
又PA∩AD=A,PA,AD 平面PAD,
∴CD⊥平面PAD.又PD 平面PAD,∴CD⊥PD,
∴∠PDA是二面角P-CD-B的平面角.
又直线PB与CD所成的角为45°,
∴∠PBA=45°,PA=AB,∴在Rt△PAD中,PA=AD,
∴∠PDA=45°,即二面角P-CD-B的大小为45°.
易错易混·衔接高考
1
2
3
4
5
1.[2024天津,6]若m,n为两条不同的直线,α为一个平面,则下列结论中正确的是( )
A.若m∥α,n α,则m∥n
B.若m∥α,n∥α,则m∥n
C.若m∥α,n⊥α,则m⊥n
D.若m∥α,n⊥α,则m与n相交
C
1
2
3
4
5
解析 对于A,若m∥α,n α,则m与n平行或异面,A错误;对于B,若m∥α,n∥α,则m与n平行或异面或相交,B错误;对于C,已知m∥α,n⊥α,如图,过直线m作平面β,使得α∩β=s.∵m β,∴m∥s,又s α,∴n⊥s,∴m⊥n,C正确;对于D,若m∥α,n⊥α,则m与n相交或异面,D错误.故选C.
1
2
3
4
5
2.[2024北京,8]已知以边长为4的正方形为底面的四棱锥,四条侧棱分别为4,4,2 ,2 ,则该四棱锥的高为( )
D
解析 如图所示,底面ABCD是边长为4的正方形,设SA=SD=4,SB=SC=2 .分别取AD,BC的中点E,F,则SE⊥AD,EF⊥AD.∴AD⊥平面SEF.作SO⊥EF,
O为垂足,则AD⊥SO.∴SO⊥平面ABCD,∴SO是四棱锥S-ABCD的高.
∵SE=2 ,EF=4,SF=2,∴EF2=SE2+SF2,∴∠ESF=90°.在Rt△ESF中,
1
2
3
4
5
1
2
3
4
5
3.[2024新高考Ⅰ,5]已知圆柱和圆锥的底面半径相等,侧面积相等,且它们的高均为 ,则圆锥的体积为( )
B
1
2
3
4
5
4.[2024新高考Ⅱ,7]已知正三棱台ABC-A1B1C1的体积为 ,AB=6,A1B1=2,则A1A与平面ABC所成角的正切值为( )
A. B.1 C.2 D.3
B
1
2
3
4
5
解析 (方法一)设棱台的高为h,三条侧棱延长后相交于一点S.正三角形ABC与正三角形A1B1C1的中心分别是点O,O1.连接AO,SO,易知点O1在SO上.
1
2
3
4
5
(方法二)设棱台的高为h,正三角形ABC与正三角形A1B1C1的中心分别是点O,O1,连接OO1,A1O1,AO,作A1H⊥AO,H为垂足.
1
2
3
4
5
5.[2024全国甲,文19]如图,在以A,B,C,D,E,F为顶点的五面体中,四边形ABCD与四边形ADEF均为等腰梯形,EF∥AD,BC∥AD,AD=4, AB=BC=EF=2,ED= ,FB=2,M为AD的中点.
(1)证明:BM∥平面CDE;
(2)求M到平面FAB的距离.
1
2
3
4
5
(1)证明由题意知MD=2,BC=2,MD∥BC,
所以四边形BCDM为平行四边形,
故BM∥CD,
又因为BM 平面CDE,
所以BM∥平面CDE.
1
2
3
4
5
(2)解 取AM的中点为G,连接FG,BG,FM,
因为BM=CD=AB,所以BG⊥AM,同理FG⊥AM.
本 课 结 束
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
