2024-2025学年苏州市吴中、吴江、相城七年级下册数学期末试卷(PDF版,无答案)
文档属性
| 名称 | 2024-2025学年苏州市吴中、吴江、相城七年级下册数学期末试卷(PDF版,无答案) |

|
|
| 格式 | |||
| 文件大小 | 180.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 00:00:00 | ||
图片预览


文档简介
2024- 2025学年苏州市吴中、吴江、相城初一年级数学期末试卷
2025.6
一、选择题 (本大题共 8小题,每小题 3分,共 24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,
请将答案填涂在答题卡相应位置上)
1.剪纸是我国最具代表性的民间艺术之一,下列剪纸作品中,是中心对称图形的为 ( )
A. B. C. D.
2.下列各数中属于无理数的是 ( )
A. 3 B. 227 C. 5 D. 0.3
3.下列计算正确的是 ( )
A. a2·a3= a5 B. a5- a3= a2 C. a4÷ a4= a D. (a3)4= a7
4.已知 a> b,则下列不等式成立的是 ( )
A. 2a< 2b B. a+ 1< b+ 1 C. a- 1< b- 1 D. - 2a<-2b
5.已知一个多边形的内角和为 540°,则这个多边形是 ( )
A. 四边形 B. 五边形 C. 六边形 D. 七边形
6.有一首古算诗:“林下牧童闹如簇,不知人数不知竹,每人六竿多十四,每人八竿恰齐足.”大意:牧童们在树下拿
着竹竿玩耍,不知有多少人和竹竿.每人 6竿,多 14竿;每人 8竿,恰好用完,牧童有多少人,竹竿有多少根?请
你解决这个问题.设牧童 x人,竹竿 y根,则可列出方程组为 ( )
6x+14=yA. B.
6x-14=7 6(x+14)=y 6(x-14)=y
8x=y 8x= C.y D.8x=y 8x=y
7.如图,把一块含 30°角的三角板OAB沿一条直角边OB翻折到△OCB的位置,然后沿斜边OC翻折到△OCD
的位置,下列说法正确的是 ( )
A. 将△OAB绕着点O顺时针旋转 60°得到△OCD
B. 将△OAB绕着点O逆时针旋转 60°得到△OCD
C. 将△OAB绕着点O顺时针旋转 90°得到△OCD
D. 将△OAB绕着点O逆时针旋转 90°得到△OCD
8.如图,在△ABC中,∠C= 90°,点C,D关于AB对称,过点C作EF∥AB,若EF= 3AB,△ABC的面积等于 2,
则△DEF的面积为 ( )
D A
D
A. 4 B. 6
C. 12 D. 24 C E
C B
O B
A
(第7题图) (第8题图) F
初一期末 第1页 共6页
二、填空题 (本大题共 8小题,每小题 3分,共 24分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)
9.某人红细胞的截面半径约为 0.0000037m,数据 0.0000037用科学记数法表示为 .
10.已知 x3- 2= 25,则 x= .
11.命题“对顶角相等”的逆命题是 .
12.比较大小: 66 8.(在横线上填“>”,“=”或“<”)
3x-ay=16 x=713.已知关于 x,y的方程组 2x+ = 的解是 = ,则 ab= .by 15 y 1
14.如图,AB∥CD,已知∠B= 66°,∠D= 21°,则∠E= °.
A
A B
D
E
C D
E B C
(第14题图) (第15题图)
15.如图,在△ABC中,∠B=∠C,∠A= 50°,点D,E分别是边AB,AC上的点,连接DE.将△ADE绕点A顺时
针旋转一定角度,当AD∥BC时,∠BAE的度数为 °.
16.定义:关于 x,y的二元一次方程 cx- ay= b(其中 a,b,c是常数)叫做方程 ax+ by= c的“移变方程“.例如:
3x+ 5y= 7的”移变方程“为 7x- 3y= 5.已知常数m,n,k满足条件 3m< k< n,并且 3x+ (m- n+ 3)y=
2n + 6k + 3是关于 x,y的二元一次方程 (7m - k)x + (3m + 2n)y= 3的“移变方程”,则 k的取值范围为
.
三、解答题 (本大题共 11小题,共 82分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步
骤)
17. (本题满分 8分,每小题 4分)计算:
(1)| -4| - (π- 5 )0+ (- 1 )-12 ;(2) 9 +
3 -8- 3 (-1)3 .
18. (本题满分 8分,每小题 4分)计算:
(1) (a3)2+ (a2)3- a·a5;(2)2(x+ 3) (x- 3) - (2x- 1) (x- 2).
19. (本题满分 5分)
先化简再求值:(2a+ b)2+ 5a(a- b) - (3a- b)2 2 3,其中 a= 5 ,b= 4 .
初一期末 第2页 共6页
20. (本题满分 8分,每小题 4分)
x+2y=0
x-2(x-1)≤1
(1)解方程组 + = (2)解不等式组 3x 4y 6 1+x3 >x-1
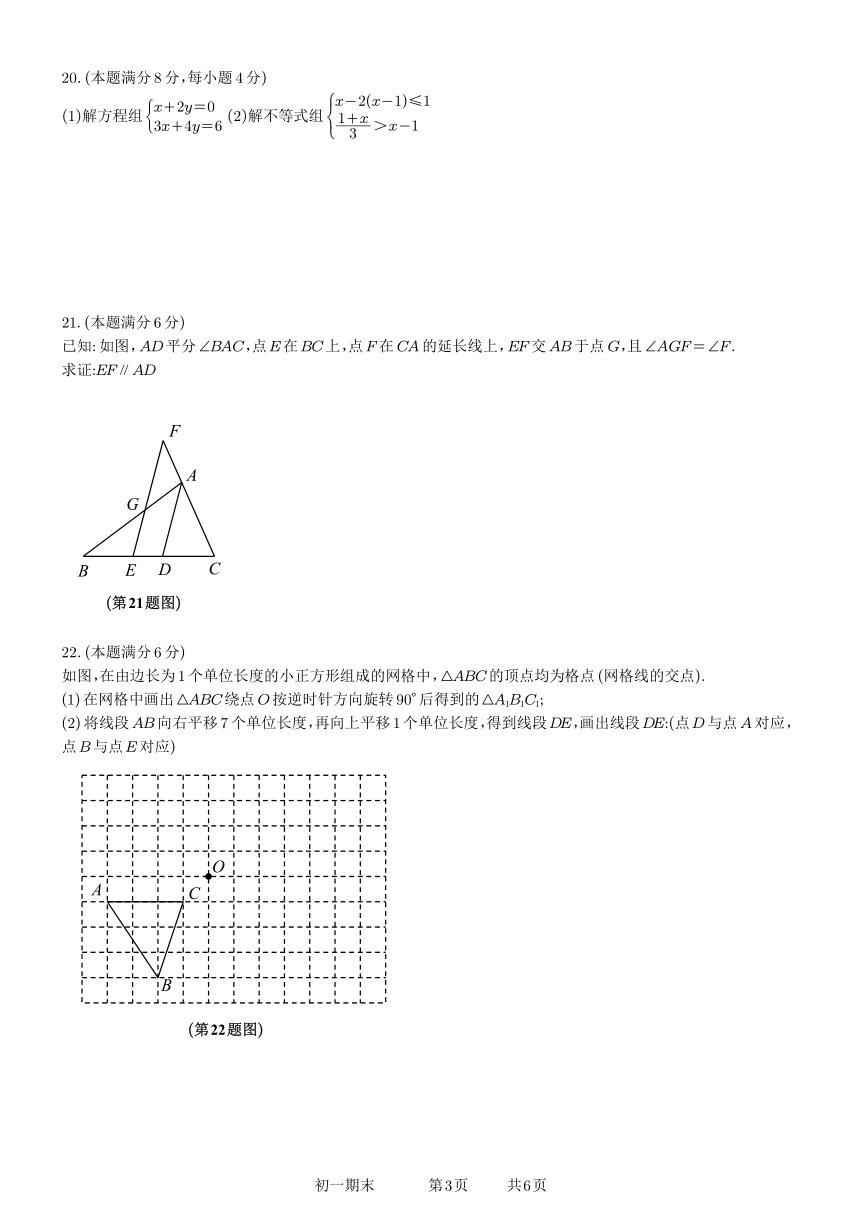
21. (本题满分 6分)
已知:如图,AD平分∠BAC,点E在BC上,点F在CA的延长线上,EF交AB于点G,且∠AGF=∠F.
求证:EF∥AD
F
A
G
B E D C
(第21题图)
22. (本题满分 6分)
如图,在由边长为 1个单位长度的小正方形组成的网格中,△ABC的顶点均为格点 (网格线的交点).
(1)在网格中画出△ABC绕点O按逆时针方向旋转 90°后得到的△A1B1C1;
(2)将线段AB向右平移 7个单位长度,再向上平移 1个单位长度,得到线段DE,画出线段DE:(点D与点A对应,
点B与点E对应)
O
A C
B
(第22题图)
初一期末 第3页 共6页
23. (本题满分 6分)
已知 am= 8,an= 32(m,n是整数).
(1)求 am+n的值;
(2)求 am-2n的值.
24. (本题满分 7分)
观察下列等式,探究其中的规律并解答问题:
2× 4+ 1= 9,①
4× 6+ 1= 25,②
6× 8+ 1= 49,③
(1)根据上述规律,试写出第 4个等式: ;
(2)①根据上述规律,试写出第n个等式: ;
②证明①中的等式成立.
25. (本题满分 8分)
我们已经学移,知道了平移的性质,请探索完成下列问题.
A D H
A
M
B C
E G F K
B C
图① 图②
【知识激活】
(1)如图①,沿AA 的方向平移△ABC,使点A移动到点A′的位置,得到△A′B′C′,分别连接AA ,BB′.则AA 与
BB 的关系为 ;
【知识应用】
(2)如图②,将△DEF沿EF方向向右平移得到△HGK,已知∠E= 90°,若FK= 6cm,MG= 3cm,MH= 4cm,求
四边形MHKF的面积;
初一期末 第4页 共6页
【知识拓展】
(3)为切实保障居民用气安全,某地开展天然气设施改造工程.如图③所示,某小区 (点A)和天然气站 (点B),分别
位于公路两侧,若公路的宽度是一定的 (公路的两边 a∥ b),现要在地下通一条天然气管道接通A,B两地,管道通
过马路时,为了尽量少破坏马路,管道通过马路的部分与马路的一边 a互相垂直,求作管道的位置,使得从点A到
点B的管道长度最短.(要求:用无刻度的直尺和圆规作图,保留作图痕迹,如有必要可写出文字说明,不写说明不
扣分)
A
a
b
图③ B
26. (本题满分 10分)
综合与实践:七年级某学习小组围绕“学校膳食结构”开展主题学习活动.他们发现学校为学生提供的每份早餐包
含一份 150g的蔬菜,一份牛肉和一份牛奶.(食物的营养成分见表一)学校每天为学生提供的午餐有A,B两种套
餐 (见表二),为了平衡膳食,该小组建议学生控制主食和肉类的摄入量,每周每位学生午餐主食的摄入量不超过
870g,午餐肉类摄入量不超过 390g.(一周按五天计算)
(1)若一份早餐包含一份 150g的蔬菜,一份 100g的牛肉和一份 200g的牛奶,则该份早餐中蛋白质总含量为
g;
(2)学校为学生提供的每份早餐的总质量为 500g,每份早餐的蛋白质总含量占早餐总质量的 5.78%,则每份早餐中
牛肉和牛奶食品各多少克;
(3)为平衡膳食,每个学生每周午餐可以选择A,B套餐各几天?
表二:学校每天提供的A,B两种套餐
表一:食物的营养成分表 表二:学校提供的A,B两种套餐
食物 蛋白质 碳水化合物 脂肪 套餐 主食 肉类 其他
A 160 g 80g 260g
100g蔬菜 1.0g 4.0g 0.4g
B 180g 65g 255g
100g牛肉 19.9g 2.0g 4.2g
100g牛奶 3.0g 4.5g 3.6g
初一期末 第5页 共6页
27. (本题满分 10分)
阅读下列材料并解答问题:
已知 a2+ b2= 13,(a+ b)2= 25,求 ab的值,可直接代入 (a+ b)2= a2+ b2+ 2ab得:ab= 6;
若 (12- c)2+ (c- 4)2= 6,求 (12- c) (c- 4)的值.如何解答?可令 12- c= a,c- 4= b,
则 a+ b= 8,a2+ b2= 6,代入 (a+ b)2= a2+ b2+ 2ab得:ab= 29.像这样把某个式子看成一个整体,用一个字母去
代替它,从而使问题得到简化的方法叫做换元法.
(1)已知 (m-n)2= 7,令 a= (n-m)2,则 a的值为 ;
(2)若 c满足 (c- 2026)2+ (c- 2025)2= 2024,求 (2026- c) (c- 2025)的值:
(3)如图,在长方形ABCD中,AB= 15,AD= 10,点E,K分别是BC,CD上的点,且BE=DK,分别以EC,CK
为边在长方形ABCD外侧作正方形EFGC和正方形CMNK,连接EK.若△CEK的面积为 50,设正方形EFGC
的面积为S1,正方形CMNK的面积为S2,求S1+S2的值.
N M
D K C G
E F
A B
(第27题图)
初一期末 第6页 共6页
2025.6
一、选择题 (本大题共 8小题,每小题 3分,共 24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,
请将答案填涂在答题卡相应位置上)
1.剪纸是我国最具代表性的民间艺术之一,下列剪纸作品中,是中心对称图形的为 ( )
A. B. C. D.
2.下列各数中属于无理数的是 ( )
A. 3 B. 227 C. 5 D. 0.3
3.下列计算正确的是 ( )
A. a2·a3= a5 B. a5- a3= a2 C. a4÷ a4= a D. (a3)4= a7
4.已知 a> b,则下列不等式成立的是 ( )
A. 2a< 2b B. a+ 1< b+ 1 C. a- 1< b- 1 D. - 2a<-2b
5.已知一个多边形的内角和为 540°,则这个多边形是 ( )
A. 四边形 B. 五边形 C. 六边形 D. 七边形
6.有一首古算诗:“林下牧童闹如簇,不知人数不知竹,每人六竿多十四,每人八竿恰齐足.”大意:牧童们在树下拿
着竹竿玩耍,不知有多少人和竹竿.每人 6竿,多 14竿;每人 8竿,恰好用完,牧童有多少人,竹竿有多少根?请
你解决这个问题.设牧童 x人,竹竿 y根,则可列出方程组为 ( )
6x+14=yA. B.
6x-14=7 6(x+14)=y 6(x-14)=y
8x=y 8x= C.y D.8x=y 8x=y
7.如图,把一块含 30°角的三角板OAB沿一条直角边OB翻折到△OCB的位置,然后沿斜边OC翻折到△OCD
的位置,下列说法正确的是 ( )
A. 将△OAB绕着点O顺时针旋转 60°得到△OCD
B. 将△OAB绕着点O逆时针旋转 60°得到△OCD
C. 将△OAB绕着点O顺时针旋转 90°得到△OCD
D. 将△OAB绕着点O逆时针旋转 90°得到△OCD
8.如图,在△ABC中,∠C= 90°,点C,D关于AB对称,过点C作EF∥AB,若EF= 3AB,△ABC的面积等于 2,
则△DEF的面积为 ( )
D A
D
A. 4 B. 6
C. 12 D. 24 C E
C B
O B
A
(第7题图) (第8题图) F
初一期末 第1页 共6页
二、填空题 (本大题共 8小题,每小题 3分,共 24分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)
9.某人红细胞的截面半径约为 0.0000037m,数据 0.0000037用科学记数法表示为 .
10.已知 x3- 2= 25,则 x= .
11.命题“对顶角相等”的逆命题是 .
12.比较大小: 66 8.(在横线上填“>”,“=”或“<”)
3x-ay=16 x=713.已知关于 x,y的方程组 2x+ = 的解是 = ,则 ab= .by 15 y 1
14.如图,AB∥CD,已知∠B= 66°,∠D= 21°,则∠E= °.
A
A B
D
E
C D
E B C
(第14题图) (第15题图)
15.如图,在△ABC中,∠B=∠C,∠A= 50°,点D,E分别是边AB,AC上的点,连接DE.将△ADE绕点A顺时
针旋转一定角度,当AD∥BC时,∠BAE的度数为 °.
16.定义:关于 x,y的二元一次方程 cx- ay= b(其中 a,b,c是常数)叫做方程 ax+ by= c的“移变方程“.例如:
3x+ 5y= 7的”移变方程“为 7x- 3y= 5.已知常数m,n,k满足条件 3m< k< n,并且 3x+ (m- n+ 3)y=
2n + 6k + 3是关于 x,y的二元一次方程 (7m - k)x + (3m + 2n)y= 3的“移变方程”,则 k的取值范围为
.
三、解答题 (本大题共 11小题,共 82分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步
骤)
17. (本题满分 8分,每小题 4分)计算:
(1)| -4| - (π- 5 )0+ (- 1 )-12 ;(2) 9 +
3 -8- 3 (-1)3 .
18. (本题满分 8分,每小题 4分)计算:
(1) (a3)2+ (a2)3- a·a5;(2)2(x+ 3) (x- 3) - (2x- 1) (x- 2).
19. (本题满分 5分)
先化简再求值:(2a+ b)2+ 5a(a- b) - (3a- b)2 2 3,其中 a= 5 ,b= 4 .
初一期末 第2页 共6页
20. (本题满分 8分,每小题 4分)
x+2y=0
x-2(x-1)≤1
(1)解方程组 + = (2)解不等式组 3x 4y 6 1+x3 >x-1
21. (本题满分 6分)
已知:如图,AD平分∠BAC,点E在BC上,点F在CA的延长线上,EF交AB于点G,且∠AGF=∠F.
求证:EF∥AD
F
A
G
B E D C
(第21题图)
22. (本题满分 6分)
如图,在由边长为 1个单位长度的小正方形组成的网格中,△ABC的顶点均为格点 (网格线的交点).
(1)在网格中画出△ABC绕点O按逆时针方向旋转 90°后得到的△A1B1C1;
(2)将线段AB向右平移 7个单位长度,再向上平移 1个单位长度,得到线段DE,画出线段DE:(点D与点A对应,
点B与点E对应)
O
A C
B
(第22题图)
初一期末 第3页 共6页
23. (本题满分 6分)
已知 am= 8,an= 32(m,n是整数).
(1)求 am+n的值;
(2)求 am-2n的值.
24. (本题满分 7分)
观察下列等式,探究其中的规律并解答问题:
2× 4+ 1= 9,①
4× 6+ 1= 25,②
6× 8+ 1= 49,③
(1)根据上述规律,试写出第 4个等式: ;
(2)①根据上述规律,试写出第n个等式: ;
②证明①中的等式成立.
25. (本题满分 8分)
我们已经学移,知道了平移的性质,请探索完成下列问题.
A D H
A
M
B C
E G F K
B C
图① 图②
【知识激活】
(1)如图①,沿AA 的方向平移△ABC,使点A移动到点A′的位置,得到△A′B′C′,分别连接AA ,BB′.则AA 与
BB 的关系为 ;
【知识应用】
(2)如图②,将△DEF沿EF方向向右平移得到△HGK,已知∠E= 90°,若FK= 6cm,MG= 3cm,MH= 4cm,求
四边形MHKF的面积;
初一期末 第4页 共6页
【知识拓展】
(3)为切实保障居民用气安全,某地开展天然气设施改造工程.如图③所示,某小区 (点A)和天然气站 (点B),分别
位于公路两侧,若公路的宽度是一定的 (公路的两边 a∥ b),现要在地下通一条天然气管道接通A,B两地,管道通
过马路时,为了尽量少破坏马路,管道通过马路的部分与马路的一边 a互相垂直,求作管道的位置,使得从点A到
点B的管道长度最短.(要求:用无刻度的直尺和圆规作图,保留作图痕迹,如有必要可写出文字说明,不写说明不
扣分)
A
a
b
图③ B
26. (本题满分 10分)
综合与实践:七年级某学习小组围绕“学校膳食结构”开展主题学习活动.他们发现学校为学生提供的每份早餐包
含一份 150g的蔬菜,一份牛肉和一份牛奶.(食物的营养成分见表一)学校每天为学生提供的午餐有A,B两种套
餐 (见表二),为了平衡膳食,该小组建议学生控制主食和肉类的摄入量,每周每位学生午餐主食的摄入量不超过
870g,午餐肉类摄入量不超过 390g.(一周按五天计算)
(1)若一份早餐包含一份 150g的蔬菜,一份 100g的牛肉和一份 200g的牛奶,则该份早餐中蛋白质总含量为
g;
(2)学校为学生提供的每份早餐的总质量为 500g,每份早餐的蛋白质总含量占早餐总质量的 5.78%,则每份早餐中
牛肉和牛奶食品各多少克;
(3)为平衡膳食,每个学生每周午餐可以选择A,B套餐各几天?
表二:学校每天提供的A,B两种套餐
表一:食物的营养成分表 表二:学校提供的A,B两种套餐
食物 蛋白质 碳水化合物 脂肪 套餐 主食 肉类 其他
A 160 g 80g 260g
100g蔬菜 1.0g 4.0g 0.4g
B 180g 65g 255g
100g牛肉 19.9g 2.0g 4.2g
100g牛奶 3.0g 4.5g 3.6g
初一期末 第5页 共6页
27. (本题满分 10分)
阅读下列材料并解答问题:
已知 a2+ b2= 13,(a+ b)2= 25,求 ab的值,可直接代入 (a+ b)2= a2+ b2+ 2ab得:ab= 6;
若 (12- c)2+ (c- 4)2= 6,求 (12- c) (c- 4)的值.如何解答?可令 12- c= a,c- 4= b,
则 a+ b= 8,a2+ b2= 6,代入 (a+ b)2= a2+ b2+ 2ab得:ab= 29.像这样把某个式子看成一个整体,用一个字母去
代替它,从而使问题得到简化的方法叫做换元法.
(1)已知 (m-n)2= 7,令 a= (n-m)2,则 a的值为 ;
(2)若 c满足 (c- 2026)2+ (c- 2025)2= 2024,求 (2026- c) (c- 2025)的值:
(3)如图,在长方形ABCD中,AB= 15,AD= 10,点E,K分别是BC,CD上的点,且BE=DK,分别以EC,CK
为边在长方形ABCD外侧作正方形EFGC和正方形CMNK,连接EK.若△CEK的面积为 50,设正方形EFGC
的面积为S1,正方形CMNK的面积为S2,求S1+S2的值.
N M
D K C G
E F
A B
(第27题图)
初一期末 第6页 共6页
同课章节目录
