初中数学北师大版九年级上册 第四章 三角形相似复习(无答案)
文档属性
| 名称 | 初中数学北师大版九年级上册 第四章 三角形相似复习(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 165.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 00:00:00 | ||
图片预览




文档简介
相似模型
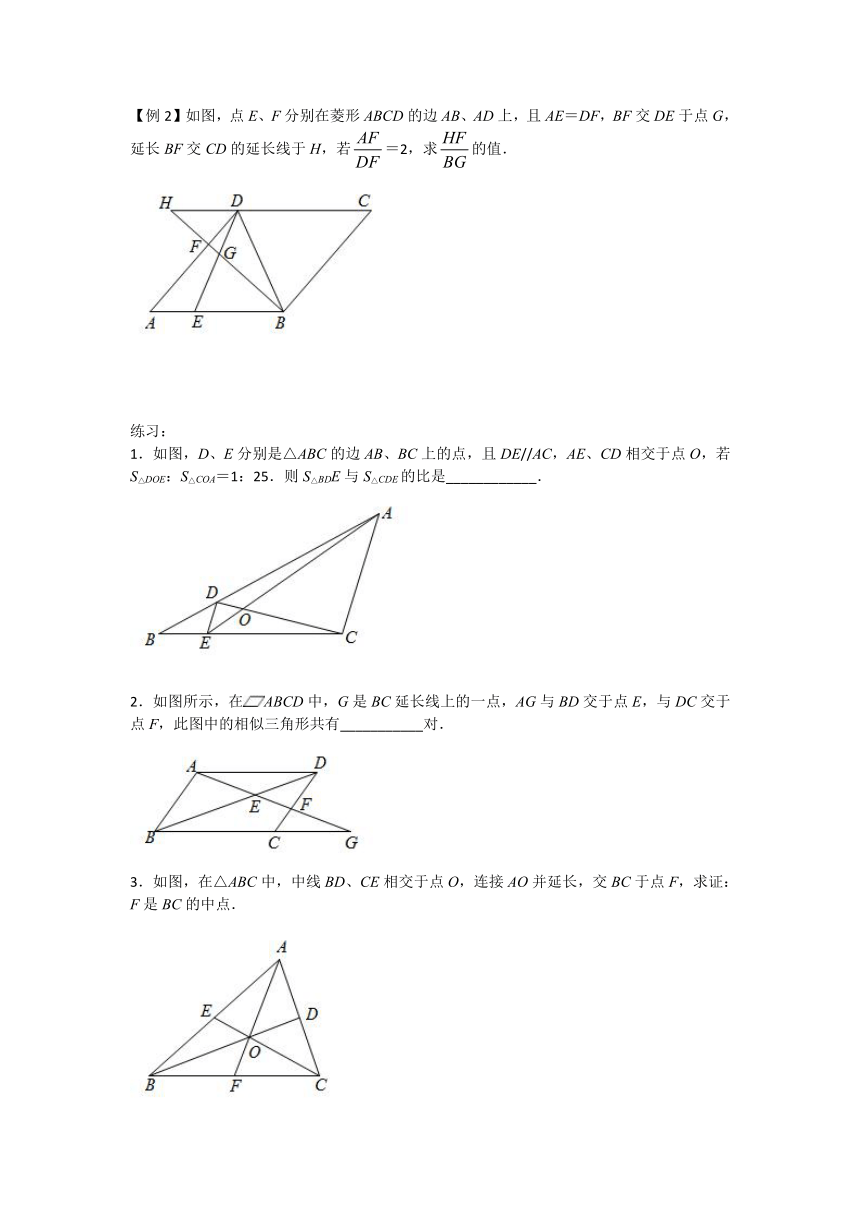
模型1:A型、8型
已知∠1=∠2
结论:△ADE∽△ABC
模型浅析
如图,在相似三角形的判定中,我们通过做平行线,从而得出A型或8型相似.
模型题源
【例1】如图,在ABC中,中线AF、BD、CE相交于点O,求证:.
【例2】如图,点E、F分别在菱形ABCD的边AB、AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若=2,求的值.
练习:
1.如图,D、E分别是△ABC的边AB、BC上的点,且DE//AC,AE、CD相交于点O,若S△DOE:S△COA=1:25.则S△BDE与S△CDE的比是____________.
2.如图所示,在ABCD中,G是BC延长线上的一点,AG与BD交于点E,与DC交于点F,此图中的相似三角形共有___________对.
3.如图,在△ABC中,中线BD、CE相交于点O,连接AO并延长,交BC于点F,求证:F是BC的中点.
4.在△ABC中,AD是角平分线,求证:.
5.如图,△ABC为等腰直角三角形,D是直角边BC的中点,E在AB上,且AE:EB=2:1,求证:CE⊥AD.
模型2 子母型
已知: ∠1=∠2 结论:△ACD ∽△ABC
模型浅析
上图中,不仅要熟悉模型,还要熟记模型的结论,有时候题目中会给出三角形边的乘积关系或者比例关系,我们要能快速判断题中的相似三角形,模型中由△ACD ∽△ABC进而可以得到:AC2=
模型题源
【例1】如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B,如果△ABD的面积为15.那么△ACD的面积为 .
【例2】如图,在Rt△ABC中,∠BAC=90o,AD⊥BC于D.
(1)图中有多少对相似三角形?
(2)求证:AB2=,AC2=,AD2=
(3)求证:=
练习:
1.如图所示,能判定△ABC∽△DAC的有 .
①∠B=∠DAC
②∠BAC=∠ADC
③AC2=
④AD2=
2.已知△AMN是等边三角形,∠BAC=120o.求证:
(1)AB2==;
(2)AC2=;
(3)MN2= .
3.如图,AB是半圆O的直径,C是半圆上一点,过C作CD⊥AB于D,AC=,AD:DB=4:1.求CD的长.
4.如图①,Rt△ABC中,∠ACB=90o,CD⊥AB,我们可以利用△ABC∽△ACD证明AC2=,这个结论我们称之为射影定理,结论运用:如图②,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF.
(1)试利用射影定理证明△BOF∽△BED;
(2)若DE=2CE,求OF的长.
模型3 一线三等角型
已知,如图①②③中:∠B=∠ACE=∠D
结论:△ABC∽△CDE
模型浅析
如图①,∵∠ACE+∠DCE=∠B+∠A,又∵∠B=∠ACE,∴∠DCE=∠A.
∴△ABC∽△CDE.图②③同理可证△ABC∽△CDE.
在一线三等角的模型中,难点在于当已知三个相等的角的时候,容易忽略隐含的其他相等的角,此模型中三垂直相似应用较多,当看见该模型的时候,应立刻能看出相应的相似三角形.
模型题源
【例1】如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60o,BP=1,CD=.则△ABC的边长为 .
【例2】如图,∠A=∠B=90o,AB=7,AD=2,BC=3,在边AB上取一点P,使得△PAD与△PBC相似,则这样的P点共有 个.
练习:
1.如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上一动点(不与B、C点重合),∠ADE=45°.
(1)求证:△ABD∽△DCE;
(2)设,,求关于的函数关系式;
(3)当△ADE是等腰三角形时,求AE的长.
2.如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=a,DE交AC于点E,且.下列结论:
①△ADE∽△ACD;
②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD等于8或;
④
其中正确的结论是 .
3.如图,已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折叠与边BC交于O,连接AP、OP、OA.
(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1∶4,求边AB的长.
模型4 倒数型
条件:AF∥DE∥BC
结论:
仔细观察,会发现模型中含有两个A型相似模型,它的结论是由两个A型相似的结论相加而得到的,该模型的练习有助于提高综合能力水平.
模型题源
如图,AF∥BC,AC、BF相交于E,过E作ED∥AF交AB于D.
求证:.
练习
如图,在△ABC中,CD⊥AB于点D,正方形EFGH的四个顶点都在△ABC的边上.
求证:
2.正方形ABCD中,以AB为边作等边三角形ABE,连接DE交AC于F,交AB于G,连接BF.求证:
(1) AF+BF=EF;
(2)
模型5 相似和旋转
如图①,已知DE∥BC,将△ADE绕点A旋转一定的角度,连接BD、CE,得到如图②.
结论:△ABD∽△ACE.
该模型难度较大,常出现在压轴题中,以直角三角形为背景出题,对学生的综合能力要求较高,考察知识点有相似、旋转、勾股定理、三角函数等,是优等生必须掌握的—种题型.
模型题源
如图,在Rt△ABC中,∠BAC=60°,点P在△ABC内,且,PB=5,PC=2.
求.
练习
1.如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CA E+∠ CBE=90°,连接BF.
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
2.已知,在△ABC中,∠BAC=60°.
(1)如图①.若AB=AC,点P在△ABC内,且∠APC=150°,PA=3,PC=4,把△APC绕着点A顺时针旋转,使点C旋转到点B处,得到△ADB,连接DP.①依题意补全图1; ②直接写出PB的长;
(2)如图②,若AB=AC,点P在△ABC外,且PA=3,PB=5,PC=4,求∠APC的度数;
(3)如图③,若AB=2AC,点P在△ABC内,且PA=,PB=5,∠APC=120°,请直接写出PC的长.
模型1:A型、8型
已知∠1=∠2
结论:△ADE∽△ABC
模型浅析
如图,在相似三角形的判定中,我们通过做平行线,从而得出A型或8型相似.
模型题源
【例1】如图,在ABC中,中线AF、BD、CE相交于点O,求证:.
【例2】如图,点E、F分别在菱形ABCD的边AB、AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若=2,求的值.
练习:
1.如图,D、E分别是△ABC的边AB、BC上的点,且DE//AC,AE、CD相交于点O,若S△DOE:S△COA=1:25.则S△BDE与S△CDE的比是____________.
2.如图所示,在ABCD中,G是BC延长线上的一点,AG与BD交于点E,与DC交于点F,此图中的相似三角形共有___________对.
3.如图,在△ABC中,中线BD、CE相交于点O,连接AO并延长,交BC于点F,求证:F是BC的中点.
4.在△ABC中,AD是角平分线,求证:.
5.如图,△ABC为等腰直角三角形,D是直角边BC的中点,E在AB上,且AE:EB=2:1,求证:CE⊥AD.
模型2 子母型
已知: ∠1=∠2 结论:△ACD ∽△ABC
模型浅析
上图中,不仅要熟悉模型,还要熟记模型的结论,有时候题目中会给出三角形边的乘积关系或者比例关系,我们要能快速判断题中的相似三角形,模型中由△ACD ∽△ABC进而可以得到:AC2=
模型题源
【例1】如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B,如果△ABD的面积为15.那么△ACD的面积为 .
【例2】如图,在Rt△ABC中,∠BAC=90o,AD⊥BC于D.
(1)图中有多少对相似三角形?
(2)求证:AB2=,AC2=,AD2=
(3)求证:=
练习:
1.如图所示,能判定△ABC∽△DAC的有 .
①∠B=∠DAC
②∠BAC=∠ADC
③AC2=
④AD2=
2.已知△AMN是等边三角形,∠BAC=120o.求证:
(1)AB2==;
(2)AC2=;
(3)MN2= .
3.如图,AB是半圆O的直径,C是半圆上一点,过C作CD⊥AB于D,AC=,AD:DB=4:1.求CD的长.
4.如图①,Rt△ABC中,∠ACB=90o,CD⊥AB,我们可以利用△ABC∽△ACD证明AC2=,这个结论我们称之为射影定理,结论运用:如图②,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF.
(1)试利用射影定理证明△BOF∽△BED;
(2)若DE=2CE,求OF的长.
模型3 一线三等角型
已知,如图①②③中:∠B=∠ACE=∠D
结论:△ABC∽△CDE
模型浅析
如图①,∵∠ACE+∠DCE=∠B+∠A,又∵∠B=∠ACE,∴∠DCE=∠A.
∴△ABC∽△CDE.图②③同理可证△ABC∽△CDE.
在一线三等角的模型中,难点在于当已知三个相等的角的时候,容易忽略隐含的其他相等的角,此模型中三垂直相似应用较多,当看见该模型的时候,应立刻能看出相应的相似三角形.
模型题源
【例1】如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60o,BP=1,CD=.则△ABC的边长为 .
【例2】如图,∠A=∠B=90o,AB=7,AD=2,BC=3,在边AB上取一点P,使得△PAD与△PBC相似,则这样的P点共有 个.
练习:
1.如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上一动点(不与B、C点重合),∠ADE=45°.
(1)求证:△ABD∽△DCE;
(2)设,,求关于的函数关系式;
(3)当△ADE是等腰三角形时,求AE的长.
2.如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=a,DE交AC于点E,且.下列结论:
①△ADE∽△ACD;
②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD等于8或;
④
其中正确的结论是 .
3.如图,已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折叠与边BC交于O,连接AP、OP、OA.
(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1∶4,求边AB的长.
模型4 倒数型
条件:AF∥DE∥BC
结论:
仔细观察,会发现模型中含有两个A型相似模型,它的结论是由两个A型相似的结论相加而得到的,该模型的练习有助于提高综合能力水平.
模型题源
如图,AF∥BC,AC、BF相交于E,过E作ED∥AF交AB于D.
求证:.
练习
如图,在△ABC中,CD⊥AB于点D,正方形EFGH的四个顶点都在△ABC的边上.
求证:
2.正方形ABCD中,以AB为边作等边三角形ABE,连接DE交AC于F,交AB于G,连接BF.求证:
(1) AF+BF=EF;
(2)
模型5 相似和旋转
如图①,已知DE∥BC,将△ADE绕点A旋转一定的角度,连接BD、CE,得到如图②.
结论:△ABD∽△ACE.
该模型难度较大,常出现在压轴题中,以直角三角形为背景出题,对学生的综合能力要求较高,考察知识点有相似、旋转、勾股定理、三角函数等,是优等生必须掌握的—种题型.
模型题源
如图,在Rt△ABC中,∠BAC=60°,点P在△ABC内,且,PB=5,PC=2.
求.
练习
1.如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CA E+∠ CBE=90°,连接BF.
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
2.已知,在△ABC中,∠BAC=60°.
(1)如图①.若AB=AC,点P在△ABC内,且∠APC=150°,PA=3,PC=4,把△APC绕着点A顺时针旋转,使点C旋转到点B处,得到△ADB,连接DP.①依题意补全图1; ②直接写出PB的长;
(2)如图②,若AB=AC,点P在△ABC外,且PA=3,PB=5,PC=4,求∠APC的度数;
(3)如图③,若AB=2AC,点P在△ABC内,且PA=,PB=5,∠APC=120°,请直接写出PC的长.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
