期末模拟测试考前押题卷(含解析)-2024-2025学年八年级下册数学人教版
文档属性
| 名称 | 期末模拟测试考前押题卷(含解析)-2024-2025学年八年级下册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 504.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 21:27:04 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末模拟测试考前押题卷
一、单选题
1.下列条件中,能判断四边形是平行四边形的是( )
A., B.,
C., D.,
2.对于函数,下列结论正确的是( )
A.它的图象必经过点
B.它的图象经过第一、三、四象限
C.当时,
D.y的值随x值的增大而减小
3.已知一次函数的图像如图所示,则,的取值范围是( )
A., B., C., D.,
4.如图,下列条件中,不能判定四边形是平行四边形的是( )
A., B.,
C., D.,
5.甲、乙两人以各自的交通工具、相同路线,前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②乙走了8km后遇到甲;③乙出发6分钟后追上甲;④甲走了28分钟时,甲乙相距3km.其中正确的是( )
A.只有① B.①③ C.②③④ D.①③④
6.图1所示的教具是用钉子将四根木条钉成的平行四边形框架,在与,与两点之间分别用一根橡皮筋拉直固定.老师推动框架至如图2所示,下列判断一定正确的是( )
A.在图2中, B.在图2中,
C.四边形的周长变大 D.四边形的面积不变
7.关于函数,给出下列说法正确的是:( )
①当时,该函数是一次函数;
②若点在该函数图象上,且,则;
③若该函数不经过第四象限,则;
④该函数恒过定点.
A.①②④ B.①③④ C.②③④ D.①②③
8.如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=2,BC=4,一动点P从点B出发,沿着B﹣A﹣D﹣C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )
A.点C B.点O C.点E D.点F
9.如图,在中,于点,交于点,,四边形和都是正方形(正方形的四边相等,四个内角都是直角),下列四个说法:
(1);
(2)若连接,则且;
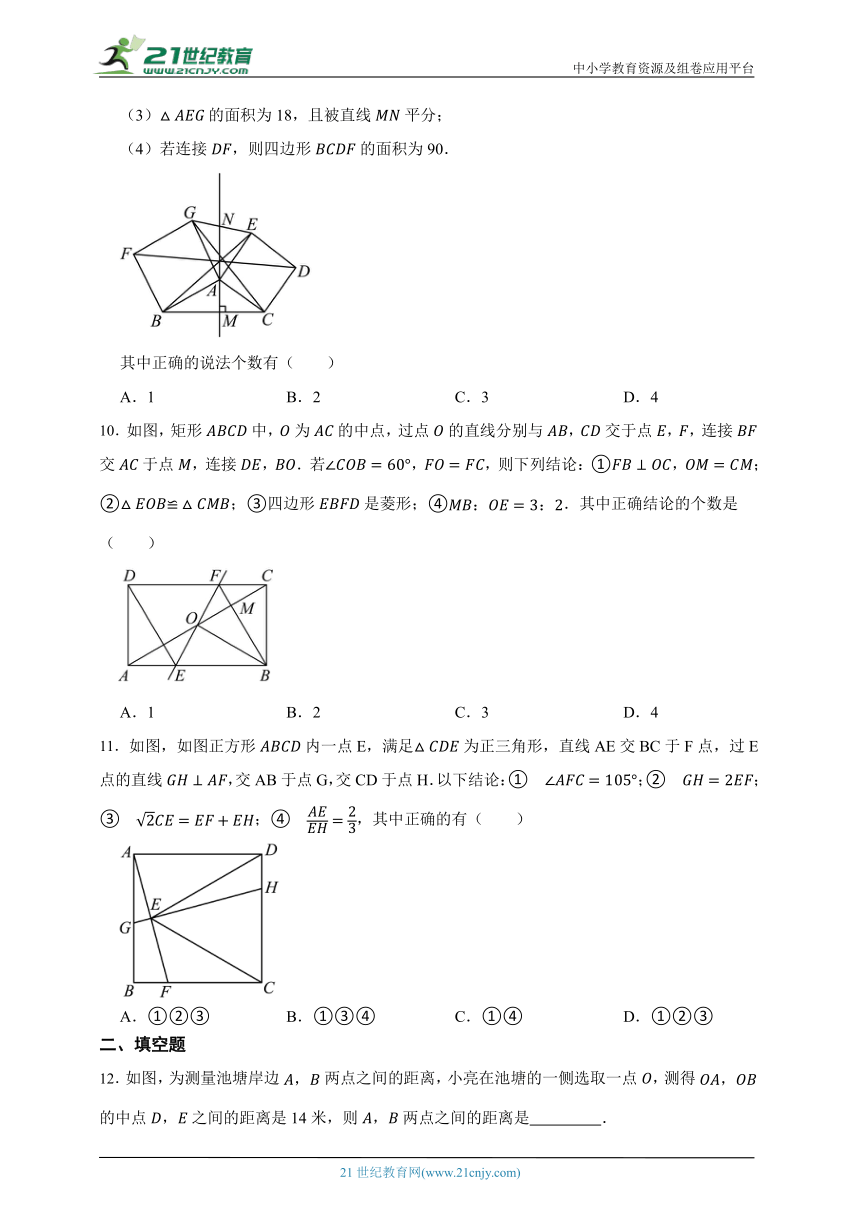
(3)的面积为18,且被直线平分;
(4)若连接,则四边形的面积为90.
其中正确的说法个数有( )
A.1 B.2 C.3 D.4
10.如图,矩形中,为的中点,过点的直线分别与,交于点,,连接交于点,连接,.若,,则下列结论:①,;②;③四边形是菱形;④.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
11.如图,如图正方形内一点E,满足为正三角形,直线AE交BC于F点,过E点的直线,交AB于点G,交CD于点H.以下结论:① ;② ;③ ;④ ,其中正确的有( )
A.①②③ B.①③④ C.①④ D.①②③
二、填空题
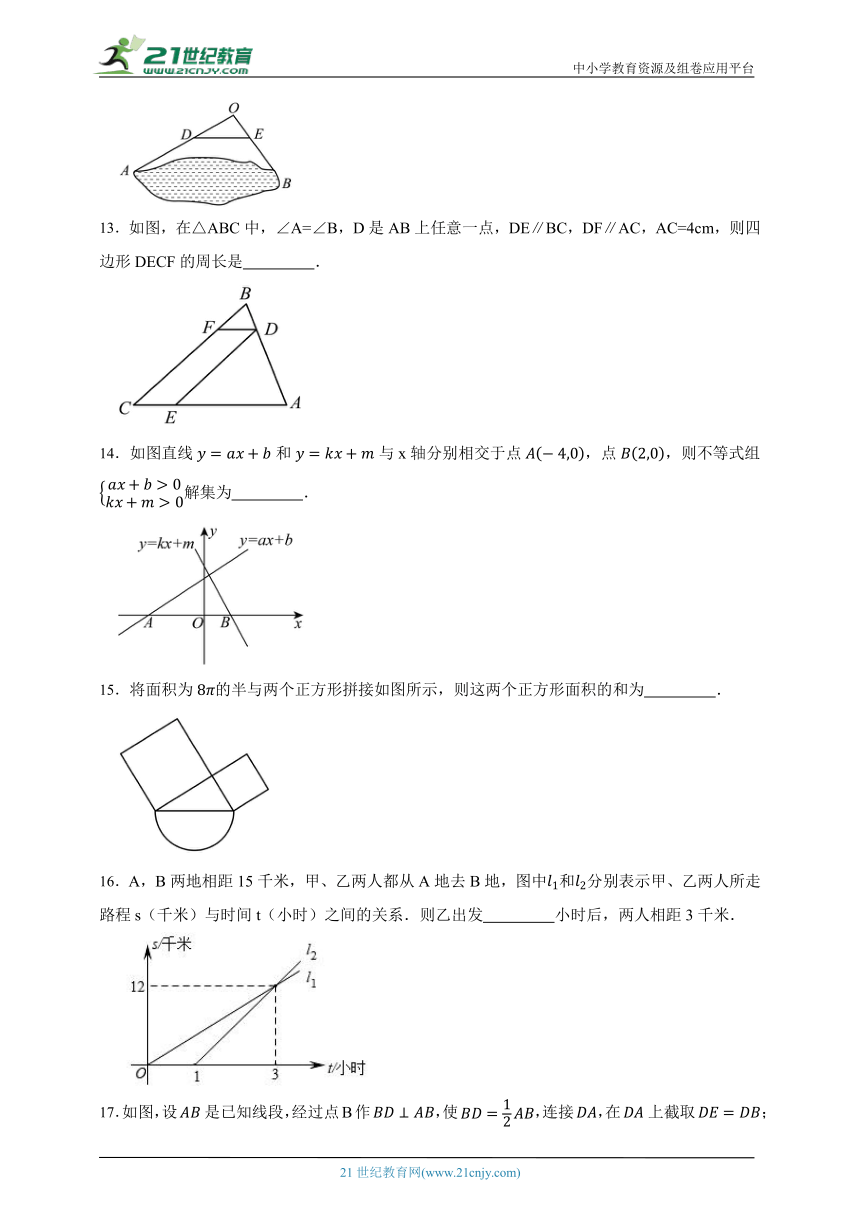
12.如图,为测量池塘岸边两点之间的距离,小亮在池塘的一侧选取一点,测得的中点,之间的距离是14米,则,两点之间的距离是 .
13.如图,在△ABC中,∠A=∠B,D是AB上任意一点,DE∥BC,DF∥AC,AC=4cm,则四边形DECF的周长是 .
14.如图直线和与x轴分别相交于点,点,则不等式组解集为 .
15.将面积为的半与两个正方形拼接如图所示,则这两个正方形面积的和为 .
16.A,B两地相距15千米,甲、乙两人都从A地去B地,图中和分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系.则乙出发 小时后,两人相距3千米.
17.如图,设是已知线段,经过点B作,使,连接,在上截取;在上截取.已知线段的长为2,则线段的长为 .
18.如图,的顶点在等边的边上,点在的延长线上,为的中点,连接.若,,则的长为 .
19.如图,矩形中,对角线,相交于点,,,是的平分线,于点,点是直线上的一个动点,则的最小值是 .
20.如图,在中,于点,为上一点,且,,连接,若为的中点,则 .
21.如图,长方形中,,,点为射线上的一个动点,若与关于直线对称,若为直角三角形,则的长为 .
三、解答题
22.在平面直角坐标系中有两点,.
(1)如图1,点是轴上的点,当最小时,点坐标为________;(直接写出答案)
(2)如图2,点,在轴上,且,当最小时,点的坐标________(直接写出答案,请用含的式子表示).
(3)如图3,在平面直角坐标系中,点的坐标为,点是直线上的一个动点,以为边,在的右侧作等腰直角,使得,点落在第一象限,连接,当的最小值时,求点的坐标.
23.已知关于的函数.
(1)若该函数是正比例函数,求的值;
(2)若点在函数图象上,求的值.
24.为推进中原经济区建设,促进中部地区崛起,我省汽车领头企业郑州日产实行技术革新,在保证原有生产线的同时,引进新的生产线,今年某月公司接到装配汽车2400辆的订单,定价为每辆6万元,若只采用新的生产线生产,则与原生产线相比可以提前8天完成订单任务,已知新的生产线使汽车装配效率比以前提高了.
(1)求原生产线每天可以装配多少辆汽车?
(2)已知原生产线装配一辆汽车需要成本5万元,新生产线比原生产线每辆节省1万元,于是公司决定两条生产线同时生产,且新生产线装配的数量最多是原生产线装配数量的2倍,问:如何分配两条生产线才能使获得的利润最大,最大利润为多少万元?
25.已知与成正比例,当时,.
(1)求y与x的函数表达式;
(2)若点关于y轴的对称点恰好落在该函数的图象上,求m的值.
26.A,B两地分别有垃圾20吨,30吨,现要把这些垃圾全部运到C,D两个垃圾处理厂,其中24吨运到C厂.运费标准(单位:元/吨)如下表:
目的地 始发地 C厂 D厂
A地 26 25
B地 15 20
当从A地运送多少吨垃圾到C厂时,从A,B两地运到C厂的总运费大于运到D厂的总运费?
(1)建立函数模型:设从A地运到C厂x吨垃圾.从A,B两地运到C厂的总运费为元,运到D厂的总运费为元.分别求出关于x的函数关系式;
(2)根据函数的图象与性质,解决问题:当时,求x的取值范围.
27.如图,已知正比例函数经过点A,点A在第四象限,过点A作轴,垂足为点H,点A的横坐标为3,且的面积为3.
(1)求正比例函数的解析式;
(2)点P在x轴上,使的面积为5,求点P的坐标.
28.劳动教育是新时代教育体系中的重要组成部分.如图,三角形ABC区域是云岩区某学校为劳动课开辟的劳动场地,小路AD将场地分为“水果培育”和“蔬菜种植”两个部分,现用皮尺测量得到.
(1)请判断小路AD是否与BC垂直,并说明理由;
(2)求劳动场地三角形ABC的面积.
29.冬奥会期间,冰墩墩玩偶非常畅销.小冬在某网店选中A,B两款冰墩墩玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:
A款玩偶 B款玩偶
进货价(元/个) 20 15
销售价(元/个) 28 20
(1)第一次小冬550元购进了A,B两款玩偶共30个,求两款玩偶各购进多少个.
(2)第二次小冬进货时,网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半.小冬计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?
30.已知点,且.
(1)求直线的函数表达式;
(2)如图,已知直线与直线相交于点C,点P为直线上一动点,若有,请求出点P的坐标;
(3)点T为平面内一动点,连接,将线段绕点T旋转得到线段.若点Q恰好落在直线上,且当取到最小值时,请求出点T的坐标.
31.如图①,小明家、食堂、图书倌在同一条直线上. 小明从食堂吃完早餐, 摘着骑自行车去图书馆读书, 然后以相同的速度原路返回家. 如图 ②, 反映了小明离家的距离 与他所用时间 之间的函数关系.
(1) 小明家与图书馆的距离为 ,小明骑自行车速度为 ;
(2)求小明从图书馆返回家的过程中, 与 的函数解析式;
(3)当小明离家的距离为 时,求 的值.
32.如图,在平面直角坐标系中,点A,B均在x轴上,点C在第一象限,直线AC与y轴交于点D,且直线AC上所有点的坐标都是二元一次方程的解,直线BC上所有点的坐标都是二元一次方程的解.
(1)求点C的坐标时,小聪是这样想的:先设点C的坐标为,因为点C在直线AC上,所以是方程的解;又因为点C在直线BC上,所以是方程的解,从而m,n满足据此可求出点C的坐标为______,再求出点A的坐标为______,点B的坐标为 ;
(2)求四边形BODC的面积;
(3)点是线段BC上一点,若点E的纵坐标,则点E的横坐标x的取值范围是 ;
(4)在y轴上是否存在点P,使三角形ACP的面积等于三角形ABC面积的倍?若存在,请求出点P的坐标;若不存在,请说明理由.
33.一次函数 =ax-a+1(a为常数,且a≠0).
(1)若点(-1,3)在一次函数=ax-a+1的图象上,求a的值;
(2)当-1≤x≤2时,函数有最大值5,求出此时一次函数的表达式;
(3)对于一次函数=kx+2k-4(k≠0),若对任意实数x,> 都成立,求k的取值范围.
答案解析
1.【答案】D
【知识点】平行四边形的判定
【解析】【解答】解:A、不能判断四边形是平行四边形,本选项不符合题意;
B、不能判断四边形是平行四边形,本选项不符合题意;
C、不能判断四边形是平行四边形,本选项不符合题意;
D、由对边平行且相等,能判断四边形是平行四边形,本选项符合题意;
故答案为:D
【分析】根据平行四边形判定定理逐项进行判断即可求出答案.
2.【答案】D
【知识点】一次函数的概念
3.【答案】B
【知识点】一次函数图象、性质与系数的关系
4.【答案】D
【知识点】平行四边形的判定
5.【答案】B
【知识点】线段垂直平分线的性质;等边三角形的判定与性质;菱形的性质
6.【答案】B
【知识点】平行四边形的性质;矩形的判定与性质
7.【答案】A
【知识点】一次函数的概念;一次函数图象、性质与系数的关系
【解析】【解答】解:当时,该函数是一次函数,正确,故①符合题意;
若点在该函数图象上,且,
,
y随x的增大而增大,则正确,故②符合题意;
若该函数不经过第四象限,则,
原说法错误,故③不符合题意;
令,则该函数恒过定点,正确,故④符合题意;
故符合题意的有①②④,
故答案为:A.
【分析】 根据一次函数的定义判断①、利用一次函数的增减性判断②、根据一次函数的图象经过的象限判断③,根据一次函数图象上点的坐标特征判断④即可.
8.【答案】B
【知识点】函数的图象;矩形的性质
【解析】【解答】解:∵AB=2,BC=4,四边形ABCD是矩形,
∴当x=6时,点P到达D点,此时△BPM的面积为0,说明点M一定在BD上,
∴从选项中可得只有O点符合,所以点M的位置可能是图1中的点O.
故答案为:B.
【分析】根据矩形的性质,得到当x=6时,点P到达D点,此时△BPM的面积为0,说明点M一定在BD上,从选项中可得只有O点符合,所以点M的位置可能是图1中的点O.
9.【答案】D
【知识点】三角形的角平分线、中线和高;三角形全等及其性质;正方形的性质
10.【答案】C
【知识点】三角形全等及其性质;等边三角形的判定与性质;菱形的判定与性质;矩形的性质;线段垂直平分线的判定
【解析】【解答】解:∵四边形ABCD是矩形
∴OB=OC,
∵∠COB=60°,
∴是等边三角形,∠FCO=∠FOC
∴∠COB=∠OCB=∠CBO=60°
∴∠FCO=∠FOC=30°
∴EF⊥OB
∴OM=CM,FB⊥OC,所以①正确;
由①可知,FB平分∠OBC,∠BOE=∠BCD=90°
∴∠CBO=∠MBC=30°
又∵是等边三角形
∴OB=BC
∴,所以②错误;
∵FO=FC=OE,∠FOC=∠EOA
∴
∴AE=CF
∴DF=BE
又∵DC//BE
∴四边形是平行四边形
∵
∴BE=BF
∴四边形是菱形 ,所以③正确;
设OE=x,则在含30°角的中,可得BE=2x
∴BO==
又在含30°角的中,可得OM=BO=
∴MB==
∴MB:OE=:x=3∶2,所以④正确.
所以正确答案为:①③④.
故答案为:C.
【分析】根据矩形的性质,得出OB=OC,∠BCD=90°;
根据线段的垂直平分线的性质,可得OM=CM,FBOC;
根据等边三角形的判定和性质,得出;
根据一组对边平行且相等的四边形是平行四边形,得出四边形是平行四边形;
根据一组邻边相等的平行四边形是菱形,得出四边形是菱形;
根据含30°角的直角三角形的性质,30°角的直角三角形斜边是30°角的对角的2倍,以及勾股定理可以得出MB和OE的值,最后算出MB:OE的值即可.
11.【答案】A
【知识点】勾股定理;平行四边形的判定与性质;正方形的性质
12.【答案】米
【知识点】三角形的中位线定理
13.【答案】8cm
【知识点】等腰三角形的判定与性质;平行四边形的判定与性质
14.【答案】
【知识点】解一元一次不等式组;一次函数与不等式(组)的关系
15.【答案】64
【知识点】勾股定理
16.【答案】0.5
【知识点】一次函数的实际应用-行程问题
17.【答案】
【知识点】勾股定理;线段的和、差、倍、分的简单计算
【解析】【解答】解:线段的长为2,
,
又,
,
由勾股定理得:,
,
,
故答案为:.
【分析】本题考查了勾股定理,以及线段的和差,由线段的长为2,且,利用构成定理,求得,得到,结合,列式计算,即可得到答案.
18.【答案】
【知识点】平行线的性质;三角形全等及其性质;三角形全等的判定;等边三角形的判定与性质;平行四边形的性质
【解析】【解答】解:∵四边形是平行四边形,,,
∴,,,
∴,
如图所示,延长交于点H,
∵,
∴,
在和中,
,
∴,
∴,,
∴,
∵,,
∴是等边三角形,
∴,
∴,
故答案为:.
【分析】根据平行四边形的性质得,,,即可得,延长交于点H,根据直线平行性质可得,再根据全等三角形判定定理可得,则,,即可得,再根据等边三角形判定定理可得是等边三角形,则,即可得,即可求出答案.
19.【答案】
【知识点】等腰三角形的判定与性质;勾股定理;矩形的性质;轴对称的性质
20.【答案】
【知识点】二次根式的混合运算;直角三角形全等的判定-HL;等腰三角形的判定与性质;勾股定理
21.【答案】2或18
【知识点】勾股定理;轴对称的性质
22.【答案】(1)
(2)
(3)
【知识点】坐标与图形性质;待定系数法求一次函数解析式;一次函数的实际应用-几何问题
23.【答案】(1)
(2)
【知识点】列一次函数关系式;正比例函数的概念
24.【答案】(1)原生产线每天可以装配120辆汽车(2)当原生产线生产800辆汽车,新生产线生产1600辆汽车时,利润最大,最大利润为4000万元
【知识点】分式方程的实际应用;一次函数的实际应用-销售问题
25.【答案】(1)
(2)
【知识点】一次函数的概念;待定系数法求一次函数解析式;坐标与图形变化﹣对称
26.【答案】(1),
(2)
【知识点】一元一次不等式的应用;函数自变量的取值范围;用关系式表示变量间的关系
27.【答案】(1)解:由题意,因为点的横坐标为3,且的面积为3,
所以点的纵坐标为,点的坐标为,
又因为正比例函数经过点,所以,解得,
所以正比例函数的解析式是.
(2)解:由 的面积为5,且点的坐标为,
因为点P在x轴上,可得,解得,
所以点的坐标为或.
【知识点】待定系数法求一次函数解析式;一次函数的实际应用-几何问题
【解析】【分析】(1)根据题意,求得点的坐标,然后利用待定系数法求得正比例函数的解析式;
(2)根据题意,利用三角形的面积公式,列出方程,求得,结合点P在x轴上,即可求得点的坐标,得到答案.
(1)点的横坐标为3,且的面积为3
点的纵坐标为,点的坐标为,
正比例函数经过点,
解得,
正比例函数的解析式是;
(2)的面积为5,点的坐标为,
∴
,
点的坐标为或.
28.【答案】(1)解:AD与BC垂直,理由:
为直角三角形且.
∴AD与BC垂直;
(2)解:
【知识点】三角形的面积;勾股定理;勾股定理的逆定理
【解析】【分析】(1)由可推导出为直角三角形且从而推导出 为直角三角形,于是得到结论
(2)利用勾股定理计算得CD,从而完成求解.
29.【答案】(1)A款玩偶购进20个,B款玩偶购进10个
(2)按照A款玩偶购进10个、B款玩偶购进20个的方案进货才能获得最大利润,最大利润是180元
【知识点】一元一次方程的其他应用;一元一次不等式的应用;一次函数的实际应用-销售问题
30.【答案】(1)
(2)P的坐标为或
(3)或
【知识点】二次根式的混合运算;等腰三角形的判定与性质;勾股定理;一次函数的实际应用-几何问题
31.【答案】(1)2000;200
(2)解:∵小明的速度为200m/min,
∴小明回家所用时间为:2000÷200=10min,
∴小明最终到家用时总时长为:36+10=46min,
∴小明从图书馆回家的直线经过(36,2000),(46,0),
设小明从图书馆回家的直线的解析式为y=kx+b,将(36,2000),(46,0)代入得,
,解得,
∴ 小明从图书馆返回家的过程中, 与 的函数解析式为.
(3)解:当小明离家的距离为 时,
情况一:当小明从食堂去图书馆离家的距离为1000米时,此时他距离食堂2000 - 1000 = 1000米,速度是200米/分钟,根据时间等于路程除以速度,所用的时间x=1000÷200=5分钟,因为是从食堂出发,所以从开始计时是1分钟;
情况二:当小明从图书馆返回家的过程中,当y = 1000时,将y = 1000代入y=-200x + 9200,解得x = 41。
故 的值为 41 或 1.
【知识点】一次函数的实际应用;一次函数的实际应用-行程问题
【解析】【解答】解:(1)由图像可知,小明家与图书馆的距离为2000m,
由图可知食堂与图书馆的距离为2000-800=1200m,小明从食堂去图书馆所用时间为6min,则小明的速度为:1200÷6=200m/min;
故答案为:2000;200.
【分析】(1)由图像可以知道小明家与图书馆得距离,在结合图像,利用速度=路程÷时间求出 小明骑自行车速度 ;
(2)首先根据小明骑车的速度求出小明回家的时间,再根据待定系数法求出解析式;
(3)分两种情况讨论,一是从食堂去图书馆时离家距离为1000米的情况,二是从图书馆返回家时离家距离为1000米的情况,分别计算出对应的时间.
32.【答案】(1)点,,
(2)
(3)
(4)或
【知识点】坐标与图形性质;一次函数与二元一次方程(组)的关系;加减消元法解二元一次方程组
33.【答案】(1)a= -1;(2)y=4x-3或y= -2x+3;(3)k<0或0<k<.
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系;一次函数的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末模拟测试考前押题卷
一、单选题
1.下列条件中,能判断四边形是平行四边形的是( )
A., B.,
C., D.,
2.对于函数,下列结论正确的是( )
A.它的图象必经过点
B.它的图象经过第一、三、四象限
C.当时,
D.y的值随x值的增大而减小
3.已知一次函数的图像如图所示,则,的取值范围是( )
A., B., C., D.,
4.如图,下列条件中,不能判定四边形是平行四边形的是( )
A., B.,
C., D.,
5.甲、乙两人以各自的交通工具、相同路线,前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②乙走了8km后遇到甲;③乙出发6分钟后追上甲;④甲走了28分钟时,甲乙相距3km.其中正确的是( )
A.只有① B.①③ C.②③④ D.①③④
6.图1所示的教具是用钉子将四根木条钉成的平行四边形框架,在与,与两点之间分别用一根橡皮筋拉直固定.老师推动框架至如图2所示,下列判断一定正确的是( )
A.在图2中, B.在图2中,
C.四边形的周长变大 D.四边形的面积不变
7.关于函数,给出下列说法正确的是:( )
①当时,该函数是一次函数;
②若点在该函数图象上,且,则;
③若该函数不经过第四象限,则;
④该函数恒过定点.
A.①②④ B.①③④ C.②③④ D.①②③
8.如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=2,BC=4,一动点P从点B出发,沿着B﹣A﹣D﹣C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )
A.点C B.点O C.点E D.点F
9.如图,在中,于点,交于点,,四边形和都是正方形(正方形的四边相等,四个内角都是直角),下列四个说法:
(1);
(2)若连接,则且;
(3)的面积为18,且被直线平分;
(4)若连接,则四边形的面积为90.
其中正确的说法个数有( )
A.1 B.2 C.3 D.4
10.如图,矩形中,为的中点,过点的直线分别与,交于点,,连接交于点,连接,.若,,则下列结论:①,;②;③四边形是菱形;④.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
11.如图,如图正方形内一点E,满足为正三角形,直线AE交BC于F点,过E点的直线,交AB于点G,交CD于点H.以下结论:① ;② ;③ ;④ ,其中正确的有( )
A.①②③ B.①③④ C.①④ D.①②③
二、填空题
12.如图,为测量池塘岸边两点之间的距离,小亮在池塘的一侧选取一点,测得的中点,之间的距离是14米,则,两点之间的距离是 .
13.如图,在△ABC中,∠A=∠B,D是AB上任意一点,DE∥BC,DF∥AC,AC=4cm,则四边形DECF的周长是 .
14.如图直线和与x轴分别相交于点,点,则不等式组解集为 .
15.将面积为的半与两个正方形拼接如图所示,则这两个正方形面积的和为 .
16.A,B两地相距15千米,甲、乙两人都从A地去B地,图中和分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系.则乙出发 小时后,两人相距3千米.
17.如图,设是已知线段,经过点B作,使,连接,在上截取;在上截取.已知线段的长为2,则线段的长为 .
18.如图,的顶点在等边的边上,点在的延长线上,为的中点,连接.若,,则的长为 .
19.如图,矩形中,对角线,相交于点,,,是的平分线,于点,点是直线上的一个动点,则的最小值是 .
20.如图,在中,于点,为上一点,且,,连接,若为的中点,则 .
21.如图,长方形中,,,点为射线上的一个动点,若与关于直线对称,若为直角三角形,则的长为 .
三、解答题
22.在平面直角坐标系中有两点,.
(1)如图1,点是轴上的点,当最小时,点坐标为________;(直接写出答案)
(2)如图2,点,在轴上,且,当最小时,点的坐标________(直接写出答案,请用含的式子表示).
(3)如图3,在平面直角坐标系中,点的坐标为,点是直线上的一个动点,以为边,在的右侧作等腰直角,使得,点落在第一象限,连接,当的最小值时,求点的坐标.
23.已知关于的函数.
(1)若该函数是正比例函数,求的值;
(2)若点在函数图象上,求的值.
24.为推进中原经济区建设,促进中部地区崛起,我省汽车领头企业郑州日产实行技术革新,在保证原有生产线的同时,引进新的生产线,今年某月公司接到装配汽车2400辆的订单,定价为每辆6万元,若只采用新的生产线生产,则与原生产线相比可以提前8天完成订单任务,已知新的生产线使汽车装配效率比以前提高了.
(1)求原生产线每天可以装配多少辆汽车?
(2)已知原生产线装配一辆汽车需要成本5万元,新生产线比原生产线每辆节省1万元,于是公司决定两条生产线同时生产,且新生产线装配的数量最多是原生产线装配数量的2倍,问:如何分配两条生产线才能使获得的利润最大,最大利润为多少万元?
25.已知与成正比例,当时,.
(1)求y与x的函数表达式;
(2)若点关于y轴的对称点恰好落在该函数的图象上,求m的值.
26.A,B两地分别有垃圾20吨,30吨,现要把这些垃圾全部运到C,D两个垃圾处理厂,其中24吨运到C厂.运费标准(单位:元/吨)如下表:
目的地 始发地 C厂 D厂
A地 26 25
B地 15 20
当从A地运送多少吨垃圾到C厂时,从A,B两地运到C厂的总运费大于运到D厂的总运费?
(1)建立函数模型:设从A地运到C厂x吨垃圾.从A,B两地运到C厂的总运费为元,运到D厂的总运费为元.分别求出关于x的函数关系式;
(2)根据函数的图象与性质,解决问题:当时,求x的取值范围.
27.如图,已知正比例函数经过点A,点A在第四象限,过点A作轴,垂足为点H,点A的横坐标为3,且的面积为3.
(1)求正比例函数的解析式;
(2)点P在x轴上,使的面积为5,求点P的坐标.
28.劳动教育是新时代教育体系中的重要组成部分.如图,三角形ABC区域是云岩区某学校为劳动课开辟的劳动场地,小路AD将场地分为“水果培育”和“蔬菜种植”两个部分,现用皮尺测量得到.
(1)请判断小路AD是否与BC垂直,并说明理由;
(2)求劳动场地三角形ABC的面积.
29.冬奥会期间,冰墩墩玩偶非常畅销.小冬在某网店选中A,B两款冰墩墩玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:
A款玩偶 B款玩偶
进货价(元/个) 20 15
销售价(元/个) 28 20
(1)第一次小冬550元购进了A,B两款玩偶共30个,求两款玩偶各购进多少个.
(2)第二次小冬进货时,网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半.小冬计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?
30.已知点,且.
(1)求直线的函数表达式;
(2)如图,已知直线与直线相交于点C,点P为直线上一动点,若有,请求出点P的坐标;
(3)点T为平面内一动点,连接,将线段绕点T旋转得到线段.若点Q恰好落在直线上,且当取到最小值时,请求出点T的坐标.
31.如图①,小明家、食堂、图书倌在同一条直线上. 小明从食堂吃完早餐, 摘着骑自行车去图书馆读书, 然后以相同的速度原路返回家. 如图 ②, 反映了小明离家的距离 与他所用时间 之间的函数关系.
(1) 小明家与图书馆的距离为 ,小明骑自行车速度为 ;
(2)求小明从图书馆返回家的过程中, 与 的函数解析式;
(3)当小明离家的距离为 时,求 的值.
32.如图,在平面直角坐标系中,点A,B均在x轴上,点C在第一象限,直线AC与y轴交于点D,且直线AC上所有点的坐标都是二元一次方程的解,直线BC上所有点的坐标都是二元一次方程的解.
(1)求点C的坐标时,小聪是这样想的:先设点C的坐标为,因为点C在直线AC上,所以是方程的解;又因为点C在直线BC上,所以是方程的解,从而m,n满足据此可求出点C的坐标为______,再求出点A的坐标为______,点B的坐标为 ;
(2)求四边形BODC的面积;
(3)点是线段BC上一点,若点E的纵坐标,则点E的横坐标x的取值范围是 ;
(4)在y轴上是否存在点P,使三角形ACP的面积等于三角形ABC面积的倍?若存在,请求出点P的坐标;若不存在,请说明理由.
33.一次函数 =ax-a+1(a为常数,且a≠0).
(1)若点(-1,3)在一次函数=ax-a+1的图象上,求a的值;
(2)当-1≤x≤2时,函数有最大值5,求出此时一次函数的表达式;
(3)对于一次函数=kx+2k-4(k≠0),若对任意实数x,> 都成立,求k的取值范围.
答案解析
1.【答案】D
【知识点】平行四边形的判定
【解析】【解答】解:A、不能判断四边形是平行四边形,本选项不符合题意;
B、不能判断四边形是平行四边形,本选项不符合题意;
C、不能判断四边形是平行四边形,本选项不符合题意;
D、由对边平行且相等,能判断四边形是平行四边形,本选项符合题意;
故答案为:D
【分析】根据平行四边形判定定理逐项进行判断即可求出答案.
2.【答案】D
【知识点】一次函数的概念
3.【答案】B
【知识点】一次函数图象、性质与系数的关系
4.【答案】D
【知识点】平行四边形的判定
5.【答案】B
【知识点】线段垂直平分线的性质;等边三角形的判定与性质;菱形的性质
6.【答案】B
【知识点】平行四边形的性质;矩形的判定与性质
7.【答案】A
【知识点】一次函数的概念;一次函数图象、性质与系数的关系
【解析】【解答】解:当时,该函数是一次函数,正确,故①符合题意;
若点在该函数图象上,且,
,
y随x的增大而增大,则正确,故②符合题意;
若该函数不经过第四象限,则,
原说法错误,故③不符合题意;
令,则该函数恒过定点,正确,故④符合题意;
故符合题意的有①②④,
故答案为:A.
【分析】 根据一次函数的定义判断①、利用一次函数的增减性判断②、根据一次函数的图象经过的象限判断③,根据一次函数图象上点的坐标特征判断④即可.
8.【答案】B
【知识点】函数的图象;矩形的性质
【解析】【解答】解:∵AB=2,BC=4,四边形ABCD是矩形,
∴当x=6时,点P到达D点,此时△BPM的面积为0,说明点M一定在BD上,
∴从选项中可得只有O点符合,所以点M的位置可能是图1中的点O.
故答案为:B.
【分析】根据矩形的性质,得到当x=6时,点P到达D点,此时△BPM的面积为0,说明点M一定在BD上,从选项中可得只有O点符合,所以点M的位置可能是图1中的点O.
9.【答案】D
【知识点】三角形的角平分线、中线和高;三角形全等及其性质;正方形的性质
10.【答案】C
【知识点】三角形全等及其性质;等边三角形的判定与性质;菱形的判定与性质;矩形的性质;线段垂直平分线的判定
【解析】【解答】解:∵四边形ABCD是矩形
∴OB=OC,
∵∠COB=60°,
∴是等边三角形,∠FCO=∠FOC
∴∠COB=∠OCB=∠CBO=60°
∴∠FCO=∠FOC=30°
∴EF⊥OB
∴OM=CM,FB⊥OC,所以①正确;
由①可知,FB平分∠OBC,∠BOE=∠BCD=90°
∴∠CBO=∠MBC=30°
又∵是等边三角形
∴OB=BC
∴,所以②错误;
∵FO=FC=OE,∠FOC=∠EOA
∴
∴AE=CF
∴DF=BE
又∵DC//BE
∴四边形是平行四边形
∵
∴BE=BF
∴四边形是菱形 ,所以③正确;
设OE=x,则在含30°角的中,可得BE=2x
∴BO==
又在含30°角的中,可得OM=BO=
∴MB==
∴MB:OE=:x=3∶2,所以④正确.
所以正确答案为:①③④.
故答案为:C.
【分析】根据矩形的性质,得出OB=OC,∠BCD=90°;
根据线段的垂直平分线的性质,可得OM=CM,FBOC;
根据等边三角形的判定和性质,得出;
根据一组对边平行且相等的四边形是平行四边形,得出四边形是平行四边形;
根据一组邻边相等的平行四边形是菱形,得出四边形是菱形;
根据含30°角的直角三角形的性质,30°角的直角三角形斜边是30°角的对角的2倍,以及勾股定理可以得出MB和OE的值,最后算出MB:OE的值即可.
11.【答案】A
【知识点】勾股定理;平行四边形的判定与性质;正方形的性质
12.【答案】米
【知识点】三角形的中位线定理
13.【答案】8cm
【知识点】等腰三角形的判定与性质;平行四边形的判定与性质
14.【答案】
【知识点】解一元一次不等式组;一次函数与不等式(组)的关系
15.【答案】64
【知识点】勾股定理
16.【答案】0.5
【知识点】一次函数的实际应用-行程问题
17.【答案】
【知识点】勾股定理;线段的和、差、倍、分的简单计算
【解析】【解答】解:线段的长为2,
,
又,
,
由勾股定理得:,
,
,
故答案为:.
【分析】本题考查了勾股定理,以及线段的和差,由线段的长为2,且,利用构成定理,求得,得到,结合,列式计算,即可得到答案.
18.【答案】
【知识点】平行线的性质;三角形全等及其性质;三角形全等的判定;等边三角形的判定与性质;平行四边形的性质
【解析】【解答】解:∵四边形是平行四边形,,,
∴,,,
∴,
如图所示,延长交于点H,
∵,
∴,
在和中,
,
∴,
∴,,
∴,
∵,,
∴是等边三角形,
∴,
∴,
故答案为:.
【分析】根据平行四边形的性质得,,,即可得,延长交于点H,根据直线平行性质可得,再根据全等三角形判定定理可得,则,,即可得,再根据等边三角形判定定理可得是等边三角形,则,即可得,即可求出答案.
19.【答案】
【知识点】等腰三角形的判定与性质;勾股定理;矩形的性质;轴对称的性质
20.【答案】
【知识点】二次根式的混合运算;直角三角形全等的判定-HL;等腰三角形的判定与性质;勾股定理
21.【答案】2或18
【知识点】勾股定理;轴对称的性质
22.【答案】(1)
(2)
(3)
【知识点】坐标与图形性质;待定系数法求一次函数解析式;一次函数的实际应用-几何问题
23.【答案】(1)
(2)
【知识点】列一次函数关系式;正比例函数的概念
24.【答案】(1)原生产线每天可以装配120辆汽车(2)当原生产线生产800辆汽车,新生产线生产1600辆汽车时,利润最大,最大利润为4000万元
【知识点】分式方程的实际应用;一次函数的实际应用-销售问题
25.【答案】(1)
(2)
【知识点】一次函数的概念;待定系数法求一次函数解析式;坐标与图形变化﹣对称
26.【答案】(1),
(2)
【知识点】一元一次不等式的应用;函数自变量的取值范围;用关系式表示变量间的关系
27.【答案】(1)解:由题意,因为点的横坐标为3,且的面积为3,
所以点的纵坐标为,点的坐标为,
又因为正比例函数经过点,所以,解得,
所以正比例函数的解析式是.
(2)解:由 的面积为5,且点的坐标为,
因为点P在x轴上,可得,解得,
所以点的坐标为或.
【知识点】待定系数法求一次函数解析式;一次函数的实际应用-几何问题
【解析】【分析】(1)根据题意,求得点的坐标,然后利用待定系数法求得正比例函数的解析式;
(2)根据题意,利用三角形的面积公式,列出方程,求得,结合点P在x轴上,即可求得点的坐标,得到答案.
(1)点的横坐标为3,且的面积为3
点的纵坐标为,点的坐标为,
正比例函数经过点,
解得,
正比例函数的解析式是;
(2)的面积为5,点的坐标为,
∴
,
点的坐标为或.
28.【答案】(1)解:AD与BC垂直,理由:
为直角三角形且.
∴AD与BC垂直;
(2)解:
【知识点】三角形的面积;勾股定理;勾股定理的逆定理
【解析】【分析】(1)由可推导出为直角三角形且从而推导出 为直角三角形,于是得到结论
(2)利用勾股定理计算得CD,从而完成求解.
29.【答案】(1)A款玩偶购进20个,B款玩偶购进10个
(2)按照A款玩偶购进10个、B款玩偶购进20个的方案进货才能获得最大利润,最大利润是180元
【知识点】一元一次方程的其他应用;一元一次不等式的应用;一次函数的实际应用-销售问题
30.【答案】(1)
(2)P的坐标为或
(3)或
【知识点】二次根式的混合运算;等腰三角形的判定与性质;勾股定理;一次函数的实际应用-几何问题
31.【答案】(1)2000;200
(2)解:∵小明的速度为200m/min,
∴小明回家所用时间为:2000÷200=10min,
∴小明最终到家用时总时长为:36+10=46min,
∴小明从图书馆回家的直线经过(36,2000),(46,0),
设小明从图书馆回家的直线的解析式为y=kx+b,将(36,2000),(46,0)代入得,
,解得,
∴ 小明从图书馆返回家的过程中, 与 的函数解析式为.
(3)解:当小明离家的距离为 时,
情况一:当小明从食堂去图书馆离家的距离为1000米时,此时他距离食堂2000 - 1000 = 1000米,速度是200米/分钟,根据时间等于路程除以速度,所用的时间x=1000÷200=5分钟,因为是从食堂出发,所以从开始计时是1分钟;
情况二:当小明从图书馆返回家的过程中,当y = 1000时,将y = 1000代入y=-200x + 9200,解得x = 41。
故 的值为 41 或 1.
【知识点】一次函数的实际应用;一次函数的实际应用-行程问题
【解析】【解答】解:(1)由图像可知,小明家与图书馆的距离为2000m,
由图可知食堂与图书馆的距离为2000-800=1200m,小明从食堂去图书馆所用时间为6min,则小明的速度为:1200÷6=200m/min;
故答案为:2000;200.
【分析】(1)由图像可以知道小明家与图书馆得距离,在结合图像,利用速度=路程÷时间求出 小明骑自行车速度 ;
(2)首先根据小明骑车的速度求出小明回家的时间,再根据待定系数法求出解析式;
(3)分两种情况讨论,一是从食堂去图书馆时离家距离为1000米的情况,二是从图书馆返回家时离家距离为1000米的情况,分别计算出对应的时间.
32.【答案】(1)点,,
(2)
(3)
(4)或
【知识点】坐标与图形性质;一次函数与二元一次方程(组)的关系;加减消元法解二元一次方程组
33.【答案】(1)a= -1;(2)y=4x-3或y= -2x+3;(3)k<0或0<k<.
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系;一次函数的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
