期末模拟测试考前预测卷(含解析)-2024-2025学年八年级下册数学人教版
文档属性
| 名称 | 期末模拟测试考前预测卷(含解析)-2024-2025学年八年级下册数学人教版 | 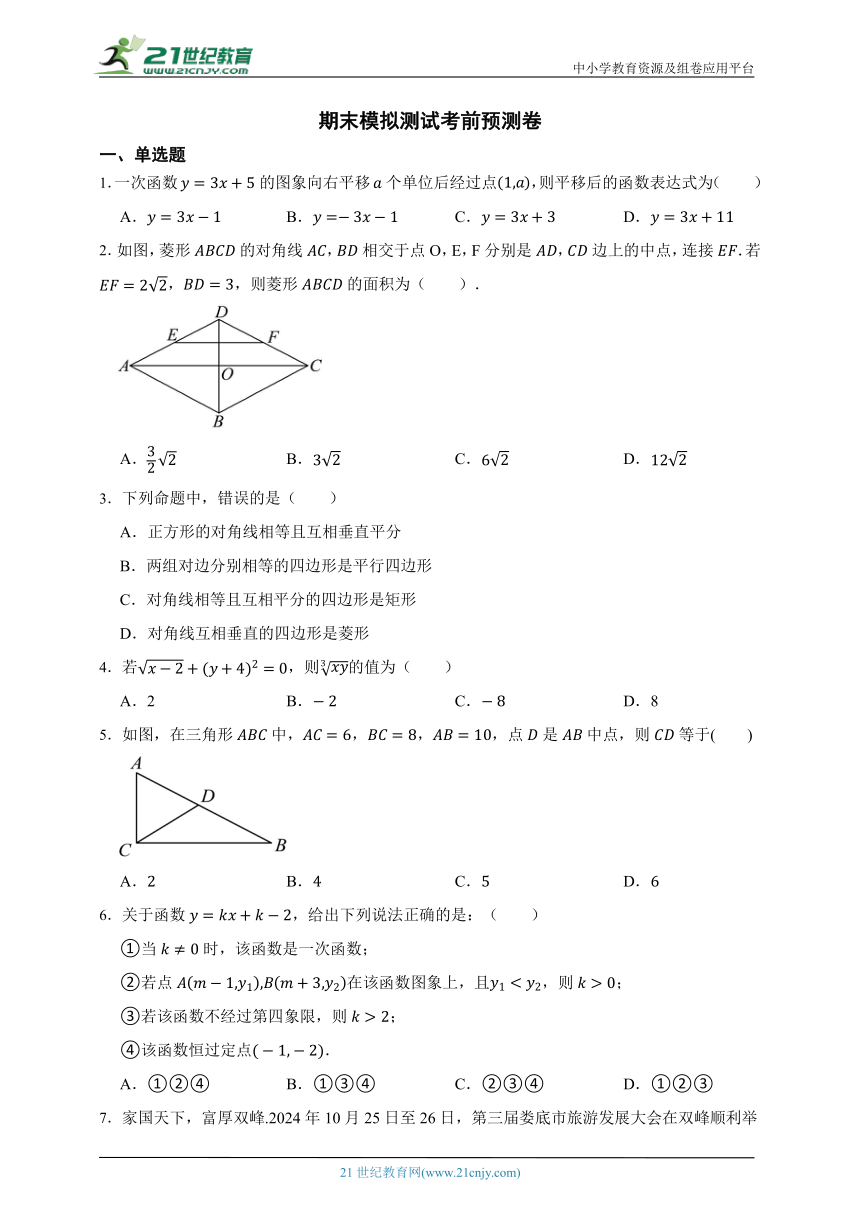 | |
| 格式 | docx | ||
| 文件大小 | 528.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 21:28:02 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末模拟测试考前预测卷
一、单选题
1.一次函数的图象向右平移个单位后经过点,则平移后的函数表达式为( )
A. B. C. D.
2.如图,菱形的对角线,相交于点O,E,F分别是,边上的中点,连接.若,,则菱形的面积为( ).
A. B. C. D.
3.下列命题中,错误的是( )
A.正方形的对角线相等且互相垂直平分
B.两组对边分别相等的四边形是平行四边形
C.对角线相等且互相平分的四边形是矩形
D.对角线互相垂直的四边形是菱形
4.若,则的值为( )
A.2 B. C. D.8
5.如图,在三角形中,,,,点是中点,则等于( )
A. B. C. D.
6.关于函数,给出下列说法正确的是:( )
①当时,该函数是一次函数;
②若点在该函数图象上,且,则;
③若该函数不经过第四象限,则;
④该函数恒过定点.
A.①②④ B.①③④ C.②③④ D.①②③
7.家国天下,富厚双峰.2024年10月25日至26日,第三届娄底市旅游发展大会在双峰顺利举办,多个场所举办趣味活动吸引游客参与.在某游乐场,甲、乙两人进行射击测试,每人10次射击成绩平均数均是9环,两人射击成绩的折线统计图如图所示,方差分别为,则下列判断正确的是( )
A. B. C. D.
8.如图,正方形和等边三角形夹在两条平行线之间,顶点,分别在两条平行线上.若,,在一条直线上,则与的数量关系是( )
A. B.
C. D.
9.如图,直线和相交于点,则关于的不等式的解集为( )
A. B. C. D.
10.如图,在中,,的平分线与边相交于点,,垂足为,若的周长为6,则的面积为( ).
A.36 B.18 C.12 D.9
11.如图,正方形的边长为2,点从点出发沿着线段向点运动(不与点、重合),点从点出发沿着线段向点运动(不与点、重合),点与点的运动速度相同.与相交于点,为中点.
①是定值;
②平分;
③当运动到中点时,;
④当时,四边形的面积是.
其中正确的是( )
A.①③ B.①②③ C.①③④ D.①④
12.如图,正方形ABCD中,点E在BC上,且CE= BC,点F是CD的中点,延长AF与BC的延长线交于点M.以下论:①AB=CM;②AE=AB+CE;③S△AEF= S四边形ABCF;④∠AFE=90°.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
13.如图,在△ABC中,∠A=∠B,D是AB上任意一点,DE∥BC,DF∥AC,AC=4cm,则四边形DECF的周长是 .
14.菱形的对角线长分别为,,则该菱形的面积为 .
15.正方形的对角线长为8,O是的中点,点E、F分别在、边上,且,那么四边形的面积为 .
16.已知是y关于x的一次函数,则 .
17.如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=24 cm,BC=26 cm.点P从A出发,以1 cm/s的速度向点D运动,点Q从点C同时出发,以3 cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使PQ=CD需要 秒
18.如图,菱形的对角线相交于点,过点作于点,连接,若菱形的面积为,则的长为 .
19.如图,在中,,E为中点,若,则四边形的周长是 .
20.如图所示,在Rt△ABC中,∠C=90°,∠A=30°,AB边中点D到BC边距离为3 cm,现在AC边找点E,使BE+ED值最小,则BE+ED的最小值是 cm.
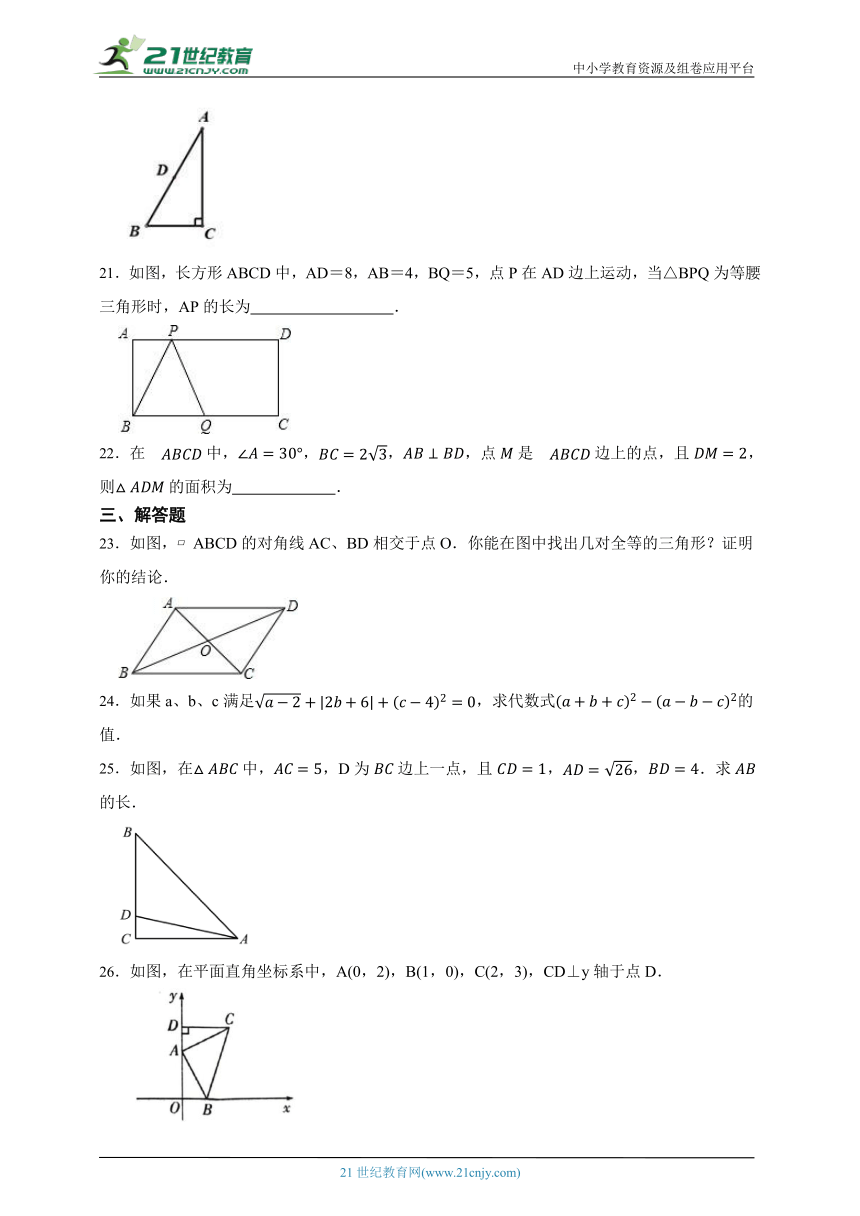
21.如图,长方形ABCD中,AD=8,AB=4,BQ=5,点P在AD边上运动,当△BPQ为等腰三角形时,AP的长为 .
22.在中,,,,点是边上的点,且,则的面积为 .
三、解答题
23.如图, ABCD的对角线AC、BD相交于点O.你能在图中找出几对全等的三角形?证明你的结论.
24.如果a、b、c满足,求代数式的值.
25.如图,在中,,D为边上一点,且,,.求的长.
26.如图,在平面直角坐标系中,A(0,2),B(1,0),C(2,3),CD⊥y轴于点D.
(1)求证:△AOB≌△CDA;
(2)连接BC,判断AB与CA的长度及位置的关系,并说明理由.
27. “和谐号”火车从车站出发,在行驶过程中速度y(单位:)与时间x(单位:s)的关系如图所示,其中线段轴.
请根据图象提供的信息解答下列问题:
(1)当,求y关于x的函数关系式;
(2)求C点的坐标.
28. 如图,
在等腰三角形ABC中,点B在坐标原点,∠BAC= 120°,AB=AC=2,求点A的坐标.
29.在平面直角坐标系中,点为坐标原点,直线交轴的正半轴于点,交轴的正半轴于点.
(1)求的长;
(2)如图1,点在轴的负半轴上,点在上,连接交轴于点,点为的中点,设点的横坐标为的面积为,求与的函数解析式;
(3)如图2,在(2)的条件下,将射线绕点顺时针旋转,交轴的负半轴于点,连接,若,求S的值.
30.如图,在平面直角坐标系中,点为坐标原点,的直角顶点在轴的正半轴上,A点坐标为,点在射线上,点以每秒个单位长度的速度从点出发向终点运动,同时动点以每秒个单位长度的速度从点出发向终点运动,点,同时到达终点,点为的中点,连接,,以,为边构造 设点的运动时间为秒.
(1) ______ ,点的坐标是______ (用含的代数式表示);
(2)在点,运动过程中,是否存在直线将 的面积分成:的两部分?若存在,则求出此时的值;若不存在,请说明理由.
(3)若,交于点,作点关于直线的对称点为点,连接,,当是以为腰的等腰三角形时,的值是______ (直接写出答案).
31.如图,在长方形中,,点分别是线段上的点,其中,连线,动点从点出发,以的速度沿着路径匀速运动,运动到点即停止运动,连接,设点运动的时间为.
(1)如图1,线段 ;当时,线段 ;
(2)如图1,点在线段上运动的过程中,连接,当是以为直角边的直角三角形时,请求出对应的时间的值;
(3)如图2,连接,点在整个运动过程中,的面积总是随着时间的变化而变化,请直接写出面积与运动时间的关系式.
32.菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为菱形或矩形的“接近度”.
(1)如图1,已知菱形ABCD的边长为2,设菱形ABCD的对角线AC,BD的长分别为m,n.若我们将菱形的“接近度”定义为(即“接近度”=),于是越小,菱形就越接近正方形.
①若菱形的“接近度”=_____________,菱形就是正方形;
②若菱形的一个内角为60°,则“接近度”=________________.
(2)如图2,已知矩形ABCD的对角线AC,BD相交于点O,设AB,BC的长分别为m,n,我们将矩形的“接近度”定义为(即“接近度”=).
①若矩形的“接近度”=______________,矩形就是正方形;
②若∠AOD=45°,求矩形的“接近度”.
33.在平面直角坐标系中,已知点,,两点坐标中,、的值使式子 成立.
(1)求,两点的坐标.
(2)如图1,若为轴负半轴上的一个动点,当时,与的平分线交于点,求的度数;
(3)如图2,连接交轴于点,若为轴负半轴上的一个动点,连接交轴于点.问是否存在点,使得?若存在,请求出点的纵坐标的取值范围;若不存在,请说明理由.
答案解析
1.【答案】A
【知识点】待定系数法求一次函数解析式;一次函数图象的平移变换
2.【答案】C
【知识点】菱形的性质;三角形的中位线定理
3.【答案】D
【知识点】平行四边形的判定;菱形的判定;矩形的判定;正方形的性质
4.【答案】B
【知识点】算术平方根的性质(双重非负性);开立方(求立方根)
5.【答案】C
【知识点】勾股定理的逆定理;直角三角形斜边上的中线
6.【答案】A
【知识点】一次函数的概念;一次函数图象、性质与系数的关系
【解析】【解答】解:当时,该函数是一次函数,正确,故①符合题意;
若点在该函数图象上,且,
,
y随x的增大而增大,则正确,故②符合题意;
若该函数不经过第四象限,则,
原说法错误,故③不符合题意;
令,则该函数恒过定点,正确,故④符合题意;
故符合题意的有①②④,
故答案为:A.
【分析】 根据一次函数的定义判断①、利用一次函数的增减性判断②、根据一次函数的图象经过的象限判断③,根据一次函数图象上点的坐标特征判断④即可.
7.【答案】B
【知识点】折线统计图;方差
【解析】【解答】解:由折线统计图可知,乙射击成绩比甲射击成绩更为分散、稳定性更差,
则由方差的意义得:,
故答案为:B.
【分析】利用据甲、乙两人射击成绩的波动大小、方差的意义解题即可.
8.【答案】A
【知识点】平行线的性质;等边三角形的性质;正方形的性质
9.【答案】B
【知识点】一次函数与不等式(组)的关系
10.【答案】D
【知识点】角平分线的性质;勾股定理
11.【答案】C
【知识点】勾股定理;正方形的性质;三角形全等的判定-SAS;直角三角形斜边上的中线
12.【答案】C
【知识点】三角形的面积;全等三角形的判定与性质;等腰三角形的性质;正方形的性质
【解析】【解答】由题意知,∵点F是CD的中点,∴DF=CF,
又∵∠D=∠FCM,∠DFA=∠CFM,
∴△ADF≌△MCF,
∴CM=AD=AB,
①正确;
设正方形ABCD边长为4,
∵CE= BC=1,
∴BE=3,
∴AE=5,
∴AE=AB+CE,
②正确;
EM=CM+CE=5=AE,
又∵F为AM的中点,
∴EF⊥AM,
④正确,
由CF=2,CE=1得EF= ,
由DF=2,AD=4得AF= ,
∴S△AEF=5,
又S△ADF=4,
∴S四边形ABCF=S□ABCD S△ADF=12,
③不正确,
故正确的有3个,选C.
【分析】根据正方形的性质和已知,根据ASA可以得到△ADF≌△MCF,得到对应边CM=AD=AB;由已知得到AE=AB+CE;由F为AM的中点,根据三线合一得到EF⊥AM;由四边形和三角形的面积进行比较得到③不正确.
13.【答案】8cm
【知识点】等腰三角形的判定与性质;平行四边形的判定与性质
14.【答案】24
【知识点】菱形的性质
15.【答案】8
【知识点】正方形的性质;三角形全等的判定-SAS
16.【答案】
【知识点】一次函数的概念
17.【答案】6或7
【知识点】平行四边形的判定与性质;一元一次方程的实际应用-几何问题
18.【答案】4
【知识点】勾股定理;菱形的性质;直角三角形斜边上的中线
19.【答案】24
【知识点】菱形的判定与性质;三角形的中位线定理
【解析】【解答】解:∵四边形ABCD为平行四边形,,
∴四边形ABCD为菱形,O为AC的中点,
∴AB=BC=CD=AD,
∵E为中点,,
∴BC=6,
∴四边形ABCD的周长为4BC=24,
故答案为:24
【分析】先根据菱形的判定与性质得到四边形ABCD为菱形,O为AC的中点,AB=BC=CD=AD,进而根据三角形中位线定理得到CB,从而即可求解。
20.【答案】6
【知识点】勾股定理;菱形的性质;轴对称的应用-最短距离问题
【解析】【解答】解:作D关于AC的对称点F,连接BF交AC于点E,连接DE,BE
这时BC+CF>BE+EF,
即当B、E、F三点共线时,BE+ED=BF最短,
过D作DH⊥BC,
∵D为AB的中点,DH=3,
∴AC=2DH=6,
∵DF∥BC,DF=BC,
∴四边形BCFD为平行四边形,
∵∠A=30°,
∴AB=2BC,
∵D为AB的中点,
∴BC=BD,
∴四边形BCFD为菱形,
∴BF=2BO,BF⊥CD,
∵BC2+AC2=AB2,
BC2+62=4BC2,
解得BC=2,
则BO=3,
∴BF=2BO=6,即BE+ED=6.
故答案为:6.
【分析】作D关于AC的对称点F,连接BF交AC于点E,连接DE,BE,根据对称图形的特点,结合三角形两边之和大于第三边,得出当B、E、F三点共线时,BE+EF最短. 由三角形中位线定理,结合对称的性质求得四边形BCFD为平行四边形,再由30°所对的直角边等于斜边的一半和D为AB的中点,得出BC=BD,
从而推出四边形BCFD为菱形,再由勾股求出BC的长,于是根据菱形的性质,BO的长度可求,则BF的长度可知.
21.【答案】3或2或或8
【知识点】等腰三角形的性质;勾股定理;矩形的判定与性质
【解析】【解答】解:∵矩形ABCD,
∴∠A=∠ABC=90°,
∵△BPQ为等腰三角形,
∴当BP=BQ=5时,
;
当QP=QB=5时,过点Q作QE⊥AD于点E,
∴∠A=∠AEQ=∠ABQ=90°,
∴四边形AEQB是矩形,
∴AE=BQ=5,AB=EQ=4;
∴,
∴AP=AE-PE=5-3=2;
当PB=PQ时,过点P作PM⊥BC于点M,
∴四边形APMB是矩形,
∴AP=BM=BQ=;
当点P与点D重合时,AP=8
∴AP的长为3或2或或8.
故答案为:3或2或或8.
【分析】利用矩形的性质可知∠A=∠ABC=90°,利用等腰三角形的定义分情况讨论:当BP=BQ=5时,利用勾股定理求出AP的长;当QP=QB=5时,过点Q作QE⊥AD于点E,易证四边形AEQB是矩形,利用矩形的性质可知AE=BQ=5,AB=EQ=4;再利用勾股定理求出PE的长,根据AP=AE-PE,可求出AP的长;当PB=PQ时,过点P作PM⊥BC于点M,易证四边形APMB是矩形,利用矩形的性质及等腰三角形的性质可求出AP的长.
22.【答案】或
【知识点】三角形的面积;含30°角的直角三角形;勾股定理;平行四边形的性质
【解析】【解答】解:∵四边形ABCD是平行四边形,BC=,
∴AD=BC=,BC∥AD,AB∥CD,
∵,,,
∴BD=AD=,AB=3,
图1 图2 图3
当M在CD边上时,如图1,过点M作ME⊥AD交延长线于点E,
∵AB∥CD,DM=2
∴∠MED=∠A=30°,
∴ME=DM=1,
∴的面积为 AD·ME=××1=;
当M在AB边上时,如图2,在Rt△MBD中,MD=2,DB=,
由勾股定理得MB=1,
∴AM=AB-MB=3-1=2,
∴的面积为 AM·DB=×2×=;
当M在BC 边上时,如图3,过点B作BE⊥AD,
∵AB=3,∠A=30°,
∴BE=AB=,
∴的面积为 AD·BE=××=;
当M在AD 边上时,不能构成三角形,不符合题意;
综上所述:的面积为 或 ;
故答案为: 或 .
【分析】利用平行四边形的性质及直角三角形的性质,先求出BD=AD=,AB=3,分四种情况:当M在CD边上时,当M在AB边上时,当M在BC 边上时和当M在AD 边上时,据此分别画出图形,分别求解即可.
23.【答案】解:图中的全等三角形:△AOB≌△COD,△AOD≌△COB,△ABD≌△CDB,△ABC≌△CDA,
∵四边形ABCD是平行四边形,
∴AB=CD,
在△AOB与△COD中,
∴△AOB≌△COD(SSS).
∵四边形ABCD是平行四边形,
∴AD=BC,
在△AOD与△BOC中,
∴△AOD≌△COB(SSS).
∵四边形ABCD是平行四边形,
∴AB=CD ,AD=BC,
在△ABD与△CDB中,
∴△ABD≌△CDB(SSS).
∵四边形ABCD是平行四边形,
∴AB=CD ,AD=BC,
在△ABC与ADC中,
∴△ABC≌△CDA(SSS).
【知识点】全等三角形的判定与性质;平行四边形的判定与性质
【解析】【分析】根据平行四边形性质可得,平行四边形对边相等,对角线互相平分,利用全等三角形判定定理(SSS)即可判定△AOB≌△COD,△AOD≌△COB,△ABD≌△CDB,△ABC≌△CDA.
24.【答案】的值为8
【知识点】算术平方根的性质(双重非负性);绝对值的非负性;求代数式的值-整体代入求值
25.【答案】
【知识点】勾股定理;勾股定理的逆定理
26.【答案】(1)证明:∵C(2,3),CD⊥y轴于点D,
∴D(0,3).
∴OD=3,CD=2
∵A(0,2),B(1,0),
∴OA=2,OB=1.
∴DA=1.
∴OB= DA.
在△AOB和△CDA中,
∴△AOB≌△CDA(SAS).
(2)解:AB=CA且AB⊥CA,理由如下:
由(1)知△AOB≌△CDA,
∴∠ABO=∠CAD,AB=CA.
∵∠ABO+∠BAO= 90°,
∴∠CAD+∠BAO=90°.
∴∠BAC= 90°.
∴AB⊥CA.
∴AB=CA且AB⊥CA.
【知识点】坐标与图形性质;三角形全等的判定;勾股定理
【解析】【分析】(1)根据点在直角坐标系中的位置,可以得出相应线段的长度,即OA=2,OB=1,DA=1;根据全等三角形的判定(SAS),可以得出△AOB≌△CDA;
(2)根据全等三角形的性质,可得∠ABO=∠CAD,AB=CA;根据等量代换原则,可以判定∠CAD+∠BAO=90°;根据平角是,已知其中一角,可以得出AB⊥CA.
27.【答案】(1)解:当时,设y关于x的函数关系式为,
将代入得,
,得,
即当时,y关于x的函数关系式为.
(2)解:当时,设y关于x的函数关系式为,
将,代入得
,解得,
即当时,y关于x的函数关系式为,
当时,,所以.
因为线段轴,所以点C的坐标为.
【知识点】待定系数法求一次函数解析式;一次函数图象上点的坐标特征
【解析】【分析】(1)根据待定系数法求一次函数,即可求得;
(2)根据待定系数法求直线AB的函数解析式,求出B点纵坐标,也是C点的纵坐标,即为所求.
28.【答案】解:过点作于点,
,
∴∠ABC=∠ACB=30°,∠ADB=90°.
在Rt中,∠ABC=30°,∠ADB=90°,
.
由勾股定理,得,
点的坐标为.
【知识点】坐标与图形性质;等腰三角形的性质;含30°角的直角三角形;勾股定理
【解析】【分析】过点A作AD⊥BC于点D,由等腰三角形的性质得∠ABC=∠ACB=30°,∠ADB=90°,由含30°角直角三角形的性质得AD=1,进而根据勾股定理算出BD的长,从而即可得出点A的坐标.
29.【答案】(1)
(2)
(3)
【知识点】三角形全等及其性质;勾股定理;一次函数的实际应用-几何问题
30.【答案】(1)
(2)存在,的值为或
(3)或
【知识点】坐标与图形性质;等腰三角形的判定与性质;平行四边形的性质;一次函数的实际应用-几何问题
31.【答案】(1)13;9
(2)或
(3)①当时:;②当时:;③当时:
【知识点】勾股定理;一元一次方程的实际应用-几何问题;一次函数的实际应用-几何问题
32.【答案】(1)①0;②
(2)①1;②
【知识点】勾股定理;菱形的性质;正方形的判定与性质
33.【答案】(1)、
(2)
(3)存在,的纵坐标的取值范围是
【知识点】坐标与图形性质;平行线的判定与性质;算术平方根的性质(双重非负性)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末模拟测试考前预测卷
一、单选题
1.一次函数的图象向右平移个单位后经过点,则平移后的函数表达式为( )
A. B. C. D.
2.如图,菱形的对角线,相交于点O,E,F分别是,边上的中点,连接.若,,则菱形的面积为( ).
A. B. C. D.
3.下列命题中,错误的是( )
A.正方形的对角线相等且互相垂直平分
B.两组对边分别相等的四边形是平行四边形
C.对角线相等且互相平分的四边形是矩形
D.对角线互相垂直的四边形是菱形
4.若,则的值为( )
A.2 B. C. D.8
5.如图,在三角形中,,,,点是中点,则等于( )
A. B. C. D.
6.关于函数,给出下列说法正确的是:( )
①当时,该函数是一次函数;
②若点在该函数图象上,且,则;
③若该函数不经过第四象限,则;
④该函数恒过定点.
A.①②④ B.①③④ C.②③④ D.①②③
7.家国天下,富厚双峰.2024年10月25日至26日,第三届娄底市旅游发展大会在双峰顺利举办,多个场所举办趣味活动吸引游客参与.在某游乐场,甲、乙两人进行射击测试,每人10次射击成绩平均数均是9环,两人射击成绩的折线统计图如图所示,方差分别为,则下列判断正确的是( )
A. B. C. D.
8.如图,正方形和等边三角形夹在两条平行线之间,顶点,分别在两条平行线上.若,,在一条直线上,则与的数量关系是( )
A. B.
C. D.
9.如图,直线和相交于点,则关于的不等式的解集为( )
A. B. C. D.
10.如图,在中,,的平分线与边相交于点,,垂足为,若的周长为6,则的面积为( ).
A.36 B.18 C.12 D.9
11.如图,正方形的边长为2,点从点出发沿着线段向点运动(不与点、重合),点从点出发沿着线段向点运动(不与点、重合),点与点的运动速度相同.与相交于点,为中点.
①是定值;
②平分;
③当运动到中点时,;
④当时,四边形的面积是.
其中正确的是( )
A.①③ B.①②③ C.①③④ D.①④
12.如图,正方形ABCD中,点E在BC上,且CE= BC,点F是CD的中点,延长AF与BC的延长线交于点M.以下论:①AB=CM;②AE=AB+CE;③S△AEF= S四边形ABCF;④∠AFE=90°.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
13.如图,在△ABC中,∠A=∠B,D是AB上任意一点,DE∥BC,DF∥AC,AC=4cm,则四边形DECF的周长是 .
14.菱形的对角线长分别为,,则该菱形的面积为 .
15.正方形的对角线长为8,O是的中点,点E、F分别在、边上,且,那么四边形的面积为 .
16.已知是y关于x的一次函数,则 .
17.如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=24 cm,BC=26 cm.点P从A出发,以1 cm/s的速度向点D运动,点Q从点C同时出发,以3 cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使PQ=CD需要 秒
18.如图,菱形的对角线相交于点,过点作于点,连接,若菱形的面积为,则的长为 .
19.如图,在中,,E为中点,若,则四边形的周长是 .
20.如图所示,在Rt△ABC中,∠C=90°,∠A=30°,AB边中点D到BC边距离为3 cm,现在AC边找点E,使BE+ED值最小,则BE+ED的最小值是 cm.
21.如图,长方形ABCD中,AD=8,AB=4,BQ=5,点P在AD边上运动,当△BPQ为等腰三角形时,AP的长为 .
22.在中,,,,点是边上的点,且,则的面积为 .
三、解答题
23.如图, ABCD的对角线AC、BD相交于点O.你能在图中找出几对全等的三角形?证明你的结论.
24.如果a、b、c满足,求代数式的值.
25.如图,在中,,D为边上一点,且,,.求的长.
26.如图,在平面直角坐标系中,A(0,2),B(1,0),C(2,3),CD⊥y轴于点D.
(1)求证:△AOB≌△CDA;
(2)连接BC,判断AB与CA的长度及位置的关系,并说明理由.
27. “和谐号”火车从车站出发,在行驶过程中速度y(单位:)与时间x(单位:s)的关系如图所示,其中线段轴.
请根据图象提供的信息解答下列问题:
(1)当,求y关于x的函数关系式;
(2)求C点的坐标.
28. 如图,
在等腰三角形ABC中,点B在坐标原点,∠BAC= 120°,AB=AC=2,求点A的坐标.
29.在平面直角坐标系中,点为坐标原点,直线交轴的正半轴于点,交轴的正半轴于点.
(1)求的长;
(2)如图1,点在轴的负半轴上,点在上,连接交轴于点,点为的中点,设点的横坐标为的面积为,求与的函数解析式;
(3)如图2,在(2)的条件下,将射线绕点顺时针旋转,交轴的负半轴于点,连接,若,求S的值.
30.如图,在平面直角坐标系中,点为坐标原点,的直角顶点在轴的正半轴上,A点坐标为,点在射线上,点以每秒个单位长度的速度从点出发向终点运动,同时动点以每秒个单位长度的速度从点出发向终点运动,点,同时到达终点,点为的中点,连接,,以,为边构造 设点的运动时间为秒.
(1) ______ ,点的坐标是______ (用含的代数式表示);
(2)在点,运动过程中,是否存在直线将 的面积分成:的两部分?若存在,则求出此时的值;若不存在,请说明理由.
(3)若,交于点,作点关于直线的对称点为点,连接,,当是以为腰的等腰三角形时,的值是______ (直接写出答案).
31.如图,在长方形中,,点分别是线段上的点,其中,连线,动点从点出发,以的速度沿着路径匀速运动,运动到点即停止运动,连接,设点运动的时间为.
(1)如图1,线段 ;当时,线段 ;
(2)如图1,点在线段上运动的过程中,连接,当是以为直角边的直角三角形时,请求出对应的时间的值;
(3)如图2,连接,点在整个运动过程中,的面积总是随着时间的变化而变化,请直接写出面积与运动时间的关系式.
32.菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为菱形或矩形的“接近度”.
(1)如图1,已知菱形ABCD的边长为2,设菱形ABCD的对角线AC,BD的长分别为m,n.若我们将菱形的“接近度”定义为(即“接近度”=),于是越小,菱形就越接近正方形.
①若菱形的“接近度”=_____________,菱形就是正方形;
②若菱形的一个内角为60°,则“接近度”=________________.
(2)如图2,已知矩形ABCD的对角线AC,BD相交于点O,设AB,BC的长分别为m,n,我们将矩形的“接近度”定义为(即“接近度”=).
①若矩形的“接近度”=______________,矩形就是正方形;
②若∠AOD=45°,求矩形的“接近度”.
33.在平面直角坐标系中,已知点,,两点坐标中,、的值使式子 成立.
(1)求,两点的坐标.
(2)如图1,若为轴负半轴上的一个动点,当时,与的平分线交于点,求的度数;
(3)如图2,连接交轴于点,若为轴负半轴上的一个动点,连接交轴于点.问是否存在点,使得?若存在,请求出点的纵坐标的取值范围;若不存在,请说明理由.
答案解析
1.【答案】A
【知识点】待定系数法求一次函数解析式;一次函数图象的平移变换
2.【答案】C
【知识点】菱形的性质;三角形的中位线定理
3.【答案】D
【知识点】平行四边形的判定;菱形的判定;矩形的判定;正方形的性质
4.【答案】B
【知识点】算术平方根的性质(双重非负性);开立方(求立方根)
5.【答案】C
【知识点】勾股定理的逆定理;直角三角形斜边上的中线
6.【答案】A
【知识点】一次函数的概念;一次函数图象、性质与系数的关系
【解析】【解答】解:当时,该函数是一次函数,正确,故①符合题意;
若点在该函数图象上,且,
,
y随x的增大而增大,则正确,故②符合题意;
若该函数不经过第四象限,则,
原说法错误,故③不符合题意;
令,则该函数恒过定点,正确,故④符合题意;
故符合题意的有①②④,
故答案为:A.
【分析】 根据一次函数的定义判断①、利用一次函数的增减性判断②、根据一次函数的图象经过的象限判断③,根据一次函数图象上点的坐标特征判断④即可.
7.【答案】B
【知识点】折线统计图;方差
【解析】【解答】解:由折线统计图可知,乙射击成绩比甲射击成绩更为分散、稳定性更差,
则由方差的意义得:,
故答案为:B.
【分析】利用据甲、乙两人射击成绩的波动大小、方差的意义解题即可.
8.【答案】A
【知识点】平行线的性质;等边三角形的性质;正方形的性质
9.【答案】B
【知识点】一次函数与不等式(组)的关系
10.【答案】D
【知识点】角平分线的性质;勾股定理
11.【答案】C
【知识点】勾股定理;正方形的性质;三角形全等的判定-SAS;直角三角形斜边上的中线
12.【答案】C
【知识点】三角形的面积;全等三角形的判定与性质;等腰三角形的性质;正方形的性质
【解析】【解答】由题意知,∵点F是CD的中点,∴DF=CF,
又∵∠D=∠FCM,∠DFA=∠CFM,
∴△ADF≌△MCF,
∴CM=AD=AB,
①正确;
设正方形ABCD边长为4,
∵CE= BC=1,
∴BE=3,
∴AE=5,
∴AE=AB+CE,
②正确;
EM=CM+CE=5=AE,
又∵F为AM的中点,
∴EF⊥AM,
④正确,
由CF=2,CE=1得EF= ,
由DF=2,AD=4得AF= ,
∴S△AEF=5,
又S△ADF=4,
∴S四边形ABCF=S□ABCD S△ADF=12,
③不正确,
故正确的有3个,选C.
【分析】根据正方形的性质和已知,根据ASA可以得到△ADF≌△MCF,得到对应边CM=AD=AB;由已知得到AE=AB+CE;由F为AM的中点,根据三线合一得到EF⊥AM;由四边形和三角形的面积进行比较得到③不正确.
13.【答案】8cm
【知识点】等腰三角形的判定与性质;平行四边形的判定与性质
14.【答案】24
【知识点】菱形的性质
15.【答案】8
【知识点】正方形的性质;三角形全等的判定-SAS
16.【答案】
【知识点】一次函数的概念
17.【答案】6或7
【知识点】平行四边形的判定与性质;一元一次方程的实际应用-几何问题
18.【答案】4
【知识点】勾股定理;菱形的性质;直角三角形斜边上的中线
19.【答案】24
【知识点】菱形的判定与性质;三角形的中位线定理
【解析】【解答】解:∵四边形ABCD为平行四边形,,
∴四边形ABCD为菱形,O为AC的中点,
∴AB=BC=CD=AD,
∵E为中点,,
∴BC=6,
∴四边形ABCD的周长为4BC=24,
故答案为:24
【分析】先根据菱形的判定与性质得到四边形ABCD为菱形,O为AC的中点,AB=BC=CD=AD,进而根据三角形中位线定理得到CB,从而即可求解。
20.【答案】6
【知识点】勾股定理;菱形的性质;轴对称的应用-最短距离问题
【解析】【解答】解:作D关于AC的对称点F,连接BF交AC于点E,连接DE,BE
这时BC+CF>BE+EF,
即当B、E、F三点共线时,BE+ED=BF最短,
过D作DH⊥BC,
∵D为AB的中点,DH=3,
∴AC=2DH=6,
∵DF∥BC,DF=BC,
∴四边形BCFD为平行四边形,
∵∠A=30°,
∴AB=2BC,
∵D为AB的中点,
∴BC=BD,
∴四边形BCFD为菱形,
∴BF=2BO,BF⊥CD,
∵BC2+AC2=AB2,
BC2+62=4BC2,
解得BC=2,
则BO=3,
∴BF=2BO=6,即BE+ED=6.
故答案为:6.
【分析】作D关于AC的对称点F,连接BF交AC于点E,连接DE,BE,根据对称图形的特点,结合三角形两边之和大于第三边,得出当B、E、F三点共线时,BE+EF最短. 由三角形中位线定理,结合对称的性质求得四边形BCFD为平行四边形,再由30°所对的直角边等于斜边的一半和D为AB的中点,得出BC=BD,
从而推出四边形BCFD为菱形,再由勾股求出BC的长,于是根据菱形的性质,BO的长度可求,则BF的长度可知.
21.【答案】3或2或或8
【知识点】等腰三角形的性质;勾股定理;矩形的判定与性质
【解析】【解答】解:∵矩形ABCD,
∴∠A=∠ABC=90°,
∵△BPQ为等腰三角形,
∴当BP=BQ=5时,
;
当QP=QB=5时,过点Q作QE⊥AD于点E,
∴∠A=∠AEQ=∠ABQ=90°,
∴四边形AEQB是矩形,
∴AE=BQ=5,AB=EQ=4;
∴,
∴AP=AE-PE=5-3=2;
当PB=PQ时,过点P作PM⊥BC于点M,
∴四边形APMB是矩形,
∴AP=BM=BQ=;
当点P与点D重合时,AP=8
∴AP的长为3或2或或8.
故答案为:3或2或或8.
【分析】利用矩形的性质可知∠A=∠ABC=90°,利用等腰三角形的定义分情况讨论:当BP=BQ=5时,利用勾股定理求出AP的长;当QP=QB=5时,过点Q作QE⊥AD于点E,易证四边形AEQB是矩形,利用矩形的性质可知AE=BQ=5,AB=EQ=4;再利用勾股定理求出PE的长,根据AP=AE-PE,可求出AP的长;当PB=PQ时,过点P作PM⊥BC于点M,易证四边形APMB是矩形,利用矩形的性质及等腰三角形的性质可求出AP的长.
22.【答案】或
【知识点】三角形的面积;含30°角的直角三角形;勾股定理;平行四边形的性质
【解析】【解答】解:∵四边形ABCD是平行四边形,BC=,
∴AD=BC=,BC∥AD,AB∥CD,
∵,,,
∴BD=AD=,AB=3,
图1 图2 图3
当M在CD边上时,如图1,过点M作ME⊥AD交延长线于点E,
∵AB∥CD,DM=2
∴∠MED=∠A=30°,
∴ME=DM=1,
∴的面积为 AD·ME=××1=;
当M在AB边上时,如图2,在Rt△MBD中,MD=2,DB=,
由勾股定理得MB=1,
∴AM=AB-MB=3-1=2,
∴的面积为 AM·DB=×2×=;
当M在BC 边上时,如图3,过点B作BE⊥AD,
∵AB=3,∠A=30°,
∴BE=AB=,
∴的面积为 AD·BE=××=;
当M在AD 边上时,不能构成三角形,不符合题意;
综上所述:的面积为 或 ;
故答案为: 或 .
【分析】利用平行四边形的性质及直角三角形的性质,先求出BD=AD=,AB=3,分四种情况:当M在CD边上时,当M在AB边上时,当M在BC 边上时和当M在AD 边上时,据此分别画出图形,分别求解即可.
23.【答案】解:图中的全等三角形:△AOB≌△COD,△AOD≌△COB,△ABD≌△CDB,△ABC≌△CDA,
∵四边形ABCD是平行四边形,
∴AB=CD,
在△AOB与△COD中,
∴△AOB≌△COD(SSS).
∵四边形ABCD是平行四边形,
∴AD=BC,
在△AOD与△BOC中,
∴△AOD≌△COB(SSS).
∵四边形ABCD是平行四边形,
∴AB=CD ,AD=BC,
在△ABD与△CDB中,
∴△ABD≌△CDB(SSS).
∵四边形ABCD是平行四边形,
∴AB=CD ,AD=BC,
在△ABC与ADC中,
∴△ABC≌△CDA(SSS).
【知识点】全等三角形的判定与性质;平行四边形的判定与性质
【解析】【分析】根据平行四边形性质可得,平行四边形对边相等,对角线互相平分,利用全等三角形判定定理(SSS)即可判定△AOB≌△COD,△AOD≌△COB,△ABD≌△CDB,△ABC≌△CDA.
24.【答案】的值为8
【知识点】算术平方根的性质(双重非负性);绝对值的非负性;求代数式的值-整体代入求值
25.【答案】
【知识点】勾股定理;勾股定理的逆定理
26.【答案】(1)证明:∵C(2,3),CD⊥y轴于点D,
∴D(0,3).
∴OD=3,CD=2
∵A(0,2),B(1,0),
∴OA=2,OB=1.
∴DA=1.
∴OB= DA.
在△AOB和△CDA中,
∴△AOB≌△CDA(SAS).
(2)解:AB=CA且AB⊥CA,理由如下:
由(1)知△AOB≌△CDA,
∴∠ABO=∠CAD,AB=CA.
∵∠ABO+∠BAO= 90°,
∴∠CAD+∠BAO=90°.
∴∠BAC= 90°.
∴AB⊥CA.
∴AB=CA且AB⊥CA.
【知识点】坐标与图形性质;三角形全等的判定;勾股定理
【解析】【分析】(1)根据点在直角坐标系中的位置,可以得出相应线段的长度,即OA=2,OB=1,DA=1;根据全等三角形的判定(SAS),可以得出△AOB≌△CDA;
(2)根据全等三角形的性质,可得∠ABO=∠CAD,AB=CA;根据等量代换原则,可以判定∠CAD+∠BAO=90°;根据平角是,已知其中一角,可以得出AB⊥CA.
27.【答案】(1)解:当时,设y关于x的函数关系式为,
将代入得,
,得,
即当时,y关于x的函数关系式为.
(2)解:当时,设y关于x的函数关系式为,
将,代入得
,解得,
即当时,y关于x的函数关系式为,
当时,,所以.
因为线段轴,所以点C的坐标为.
【知识点】待定系数法求一次函数解析式;一次函数图象上点的坐标特征
【解析】【分析】(1)根据待定系数法求一次函数,即可求得;
(2)根据待定系数法求直线AB的函数解析式,求出B点纵坐标,也是C点的纵坐标,即为所求.
28.【答案】解:过点作于点,
,
∴∠ABC=∠ACB=30°,∠ADB=90°.
在Rt中,∠ABC=30°,∠ADB=90°,
.
由勾股定理,得,
点的坐标为.
【知识点】坐标与图形性质;等腰三角形的性质;含30°角的直角三角形;勾股定理
【解析】【分析】过点A作AD⊥BC于点D,由等腰三角形的性质得∠ABC=∠ACB=30°,∠ADB=90°,由含30°角直角三角形的性质得AD=1,进而根据勾股定理算出BD的长,从而即可得出点A的坐标.
29.【答案】(1)
(2)
(3)
【知识点】三角形全等及其性质;勾股定理;一次函数的实际应用-几何问题
30.【答案】(1)
(2)存在,的值为或
(3)或
【知识点】坐标与图形性质;等腰三角形的判定与性质;平行四边形的性质;一次函数的实际应用-几何问题
31.【答案】(1)13;9
(2)或
(3)①当时:;②当时:;③当时:
【知识点】勾股定理;一元一次方程的实际应用-几何问题;一次函数的实际应用-几何问题
32.【答案】(1)①0;②
(2)①1;②
【知识点】勾股定理;菱形的性质;正方形的判定与性质
33.【答案】(1)、
(2)
(3)存在,的纵坐标的取值范围是
【知识点】坐标与图形性质;平行线的判定与性质;算术平方根的性质(双重非负性)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
