人教版九年级数学下册期末考试卷(无答案)
文档属性
| 名称 | 人教版九年级数学下册期末考试卷(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 655.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 14:53:43 | ||
图片预览

文档简介
人教版九年级数学下册期末考试卷
班级 姓名 成绩班级
(考试时间:120分钟 )
一、选择题(下列各题的四个选项中,只有一项符合题意)
1.下列说法中正确的是( ) 来源:www./tiku/
A.“打开电视,正在播放《新闻联播》”是必然事件;
B.某次抽奖活动中奖的概率为,说明每买100张奖券,一定有一次中奖;
C.数据1,1,2,2,3的众数是3;
D.想了解台州市城镇居民人均年收入水平,宜采用抽样调查.
2.一个袋子里装有8个球,其中6个红球2个绿球,这些球除颜色外,形状、大小、质地等完全 相同.搅匀后,在看不到球的条件下,随机从这个袋子中摸出一个红球的概率是( ).
(A) (B) (C) (D)
3.在抛物线y=x2-4上的一个点是( ).
(A)(4,4) (B)(1,一4) (C)(2,0) (D)(0,4)
4.如图,两条抛物线、与分别经过点,且平行于轴的两条平行线围成的阴影部分的面积为
A.8 B.6 C.10 D.4
5.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
6.如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
A. 2 cm2 B. 4 cm2 C. 8 cm2 D. 16 cm2
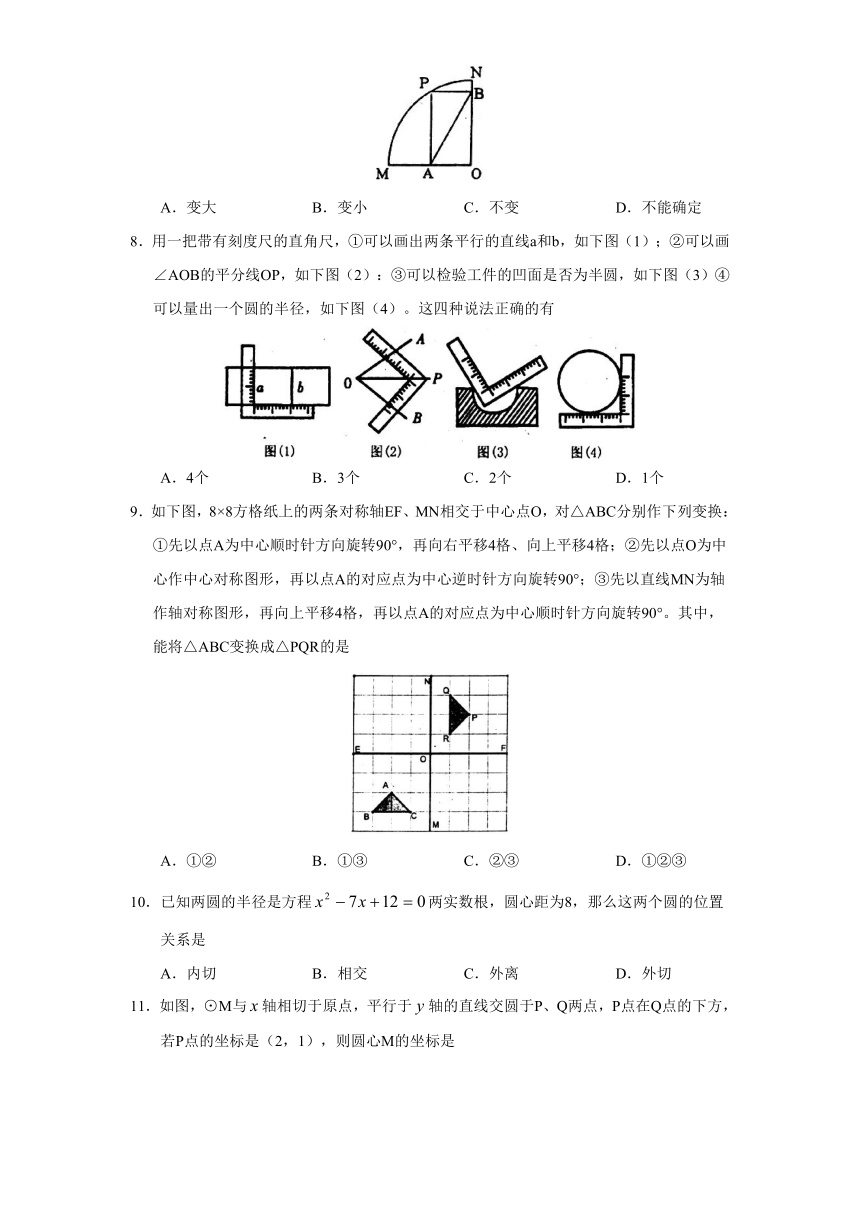
7.如下图,四边形PAOB是扇形OMN的内接矩形,顶点P在MN上,且不与M、N重合,当P 点在MN上移动时,矩形PAOB的形状、大小随之变化,则AB的长度
A.变大 B.变小 C.不变 D.不能确定
8.用一把带有刻度尺的直角尺,①可以画出两条平行的直线a和b,如下图(1);②可以画∠AOB的平分线OP,如下图(2):③可以检验工件的凹面是否为半圆,如下图(3)④可以量出一个圆的半径,如下图(4)。这四种说法正确的有
A.4个 B.3个 C.2个 D.1个
9.如下图,8×8方格纸上的两条对称轴EF、MN相交于中心点O,对△ABC分别作下列变换:①先以点A为中心顺时针方向旋转90°,再向右平移4格、向上平移4格;②先以点O为中心作中心对称图形,再以点A的对应点为中心逆时针方向旋转90°;③先以直线MN为轴作轴对称图形,再向上平移4格,再以点A的对应点为中心顺时针方向旋转90°。其中,能将△ABC变换成△PQR的是
A.①② B.①③ C.②③ D.①②③
10.已知两圆的半径是方程两实数根,圆心距为8,那么这两个圆的位置关系是
A.内切 B.相交 C.外离 D.外切
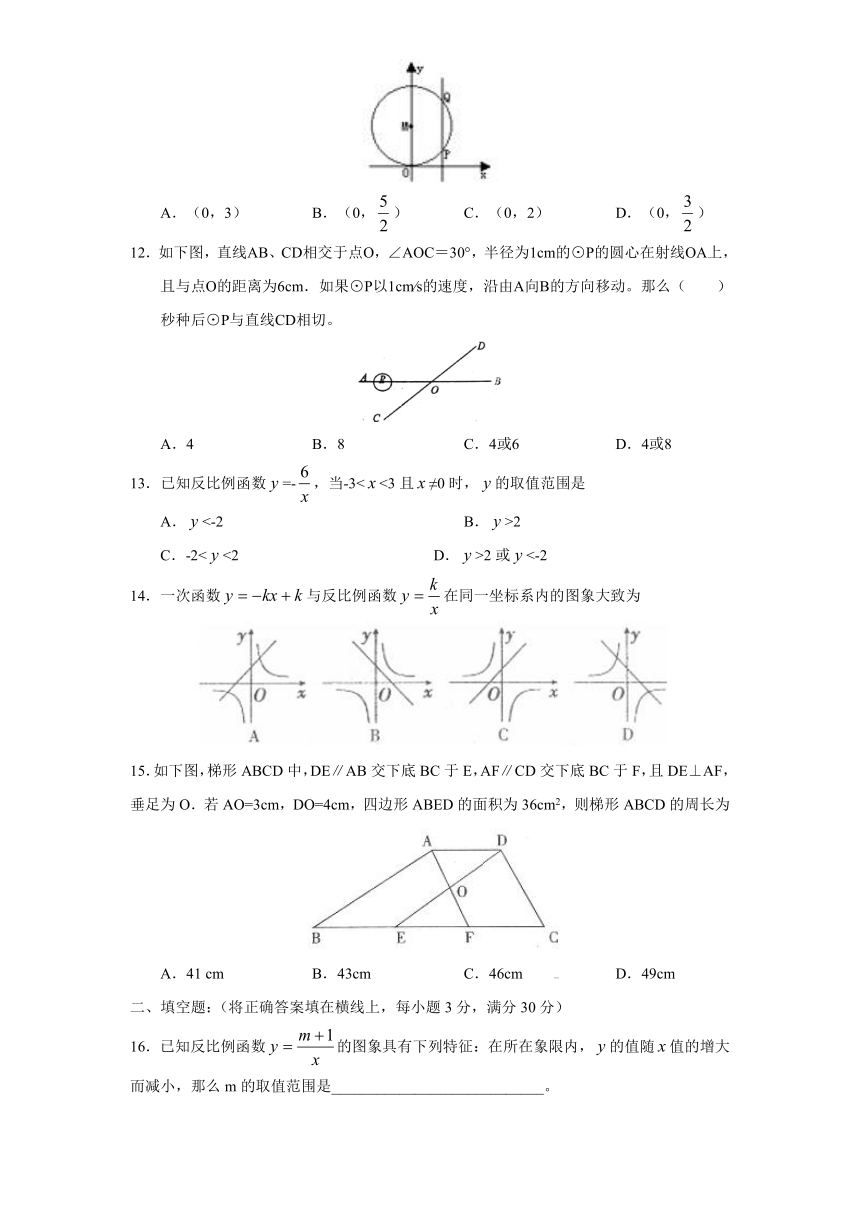
11.如图,⊙M与轴相切于原点,平行于轴的直线交圆于P、Q两点,P点在Q点的下方,若P点的坐标是(2,1),则圆心M的坐标是
A.(0,3) B.(0,) C.(0,2) D.(0,)
12.如下图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm.如果⊙P以1cm∕s的速度,沿由A向B的方向移动。那么( )秒种后⊙P与直线CD相切。
A.4 B.8 C.4或6 D.4或8
13.已知反比例函数=-,当-3<<3且≠0时,的取值范围是
A.<-2 B.>2
C.-2<<2 D.>2或<-2
14.一次函数与反比例函数在同一坐标系内的图象大致为
15.如下图,梯形ABCD中,DE∥AB交下底BC于E,AF∥CD交下底BC于F,且DE⊥AF,垂足为O.若AO=3cm,DO=4cm,四边形ABED的面积为36cm2,则梯形ABCD的周长为
A.41 cm B.43cm C.46cm D.49cm
二、填空题:(将正确答案填在横线上,每小题3分,满分30分)
16.已知反比例函数的图象具有下列特征:在所在象限内,的值随值的增大而减小,那么m的取值范围是____________________________。
17.元旦晚会上,有一个闯关活动:将20个大小、质量完全相同的乒乓球放入一个箱子里,其中8个黄色的,5个白色的,5个黑色的,2个红色的.若从箱子里任意摸出一个乒乓球是红色,就可以过关,那么一次过关的概率为_________________________。
18.如下图,ABC中,AB=AC,D为BC中点,∠BAD=30°,E为AC上一点,且AE=AD,则∠EDC的度数为____________________。
19.已知=1是一元二次方程2++=0的一个根,则()2011的值____________。
20.如下图,菱形ABCD的边长为,∠B=60°,点E,F分别是边BC,CD的中点,则△AEF的周长是_________________。
21.四条线段的长分别是2,4,6,8,从中任意取出三条线段能围成三角形的概率是_______。
22.如下图,点A在反比例函数(≠0)的图象上,AM⊥轴于点M,若AOM的面积为3,则的值是________________。
23.如下图,将矩形纸片ABCD的两个直角折叠,使点B,D都落在AC的中点O处,若AB=3,则BC的长为_______________________。
24.若是方程2-3-5=0的两根,则代数式9-32-+5的值是__________。
25.如下图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把ABC沿着AD方向平移,得到△A′B′C′.若两个三角形重叠部分的面积是1cm2,则移动的距离AA′等于___cm。
三、解答题(共54分,解答应写出文字说明、证明过程或推演步骤)
19.计算:(耐心做一做,试试我能行!每小题4分,共8分)
(1) (2)
20.(9分)如图,已知二次函数y=— x2+bx+c的图象经过A(2,0)、B(0,—6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数图象的对称轴与x轴交于点C,连结BA、BC,求△ABC的面积.
来源:www./tiku/
21、(9分)如图,在方格纸中
(1)请在方格纸上建立平面直角坐标系,使,并求出点坐标;
(2)以原点为位似中心,相似比为2,在第一象限内将放大,画出放大后的图形;
(3)计算的面积.
22.(10分)为迎接第四届世界太阳城大会,德州市把主要路段路灯更换为太阳能路灯.已知太阳能路灯售价为5000元/个,目前两个商家有此产品.甲商家用如下方法促销:若购买路灯不超过100个,按原价付款;若一次购买100个以上,且购买的个数每增加一个,其价格减少10元,但太阳能路灯的售价不得低于3500元/个.乙店一律按原价的80℅销售.现购买太阳能路灯x个,如果全部在甲商家购买,则所需金额为y1元;如果全部在乙商家购买,则所需金额为y2元.
(1)分别求出y1、y2与x之间的函数关系式;
(2)若市政府投资140万元,最多能购买多少个太阳能路灯?
23.(12分)如图,已知抛物线与交于A(-1,0)、E(3,0)两点,与轴交于点B(0,3)。
求抛物线的解析式;
设抛物线顶点为D,求四边形AEDB的面积;
△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由。
24.(本题满分8分)某村计划建造如下图所示的矩形蔬菜温室,要求长与宽的比为2︰1。在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道。当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288m2?
25.(本题满分8分)如下图,在直角坐标系中,M为轴上一点,⊙M交轴于A、B两点,交轴于C、D两点,P为BC上的一个动点,CQ平分∠PCD,A(-1,0),如(1,0)。
(1)求C点的坐标;
(2)当P点运动时,线段AQ的长度是否改变?若不变,请求其值;若改变请说明理由。
(4题图)
O
第20题
y
A
x
C
B
A
B
C
(第21题)
班级 姓名 成绩班级
(考试时间:120分钟 )
一、选择题(下列各题的四个选项中,只有一项符合题意)
1.下列说法中正确的是( ) 来源:www./tiku/
A.“打开电视,正在播放《新闻联播》”是必然事件;
B.某次抽奖活动中奖的概率为,说明每买100张奖券,一定有一次中奖;
C.数据1,1,2,2,3的众数是3;
D.想了解台州市城镇居民人均年收入水平,宜采用抽样调查.
2.一个袋子里装有8个球,其中6个红球2个绿球,这些球除颜色外,形状、大小、质地等完全 相同.搅匀后,在看不到球的条件下,随机从这个袋子中摸出一个红球的概率是( ).
(A) (B) (C) (D)
3.在抛物线y=x2-4上的一个点是( ).
(A)(4,4) (B)(1,一4) (C)(2,0) (D)(0,4)
4.如图,两条抛物线、与分别经过点,且平行于轴的两条平行线围成的阴影部分的面积为
A.8 B.6 C.10 D.4
5.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
6.如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
A. 2 cm2 B. 4 cm2 C. 8 cm2 D. 16 cm2
7.如下图,四边形PAOB是扇形OMN的内接矩形,顶点P在MN上,且不与M、N重合,当P 点在MN上移动时,矩形PAOB的形状、大小随之变化,则AB的长度
A.变大 B.变小 C.不变 D.不能确定
8.用一把带有刻度尺的直角尺,①可以画出两条平行的直线a和b,如下图(1);②可以画∠AOB的平分线OP,如下图(2):③可以检验工件的凹面是否为半圆,如下图(3)④可以量出一个圆的半径,如下图(4)。这四种说法正确的有
A.4个 B.3个 C.2个 D.1个
9.如下图,8×8方格纸上的两条对称轴EF、MN相交于中心点O,对△ABC分别作下列变换:①先以点A为中心顺时针方向旋转90°,再向右平移4格、向上平移4格;②先以点O为中心作中心对称图形,再以点A的对应点为中心逆时针方向旋转90°;③先以直线MN为轴作轴对称图形,再向上平移4格,再以点A的对应点为中心顺时针方向旋转90°。其中,能将△ABC变换成△PQR的是
A.①② B.①③ C.②③ D.①②③
10.已知两圆的半径是方程两实数根,圆心距为8,那么这两个圆的位置关系是
A.内切 B.相交 C.外离 D.外切
11.如图,⊙M与轴相切于原点,平行于轴的直线交圆于P、Q两点,P点在Q点的下方,若P点的坐标是(2,1),则圆心M的坐标是
A.(0,3) B.(0,) C.(0,2) D.(0,)
12.如下图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm.如果⊙P以1cm∕s的速度,沿由A向B的方向移动。那么( )秒种后⊙P与直线CD相切。
A.4 B.8 C.4或6 D.4或8
13.已知反比例函数=-,当-3<<3且≠0时,的取值范围是
A.<-2 B.>2
C.-2<<2 D.>2或<-2
14.一次函数与反比例函数在同一坐标系内的图象大致为
15.如下图,梯形ABCD中,DE∥AB交下底BC于E,AF∥CD交下底BC于F,且DE⊥AF,垂足为O.若AO=3cm,DO=4cm,四边形ABED的面积为36cm2,则梯形ABCD的周长为
A.41 cm B.43cm C.46cm D.49cm
二、填空题:(将正确答案填在横线上,每小题3分,满分30分)
16.已知反比例函数的图象具有下列特征:在所在象限内,的值随值的增大而减小,那么m的取值范围是____________________________。
17.元旦晚会上,有一个闯关活动:将20个大小、质量完全相同的乒乓球放入一个箱子里,其中8个黄色的,5个白色的,5个黑色的,2个红色的.若从箱子里任意摸出一个乒乓球是红色,就可以过关,那么一次过关的概率为_________________________。
18.如下图,ABC中,AB=AC,D为BC中点,∠BAD=30°,E为AC上一点,且AE=AD,则∠EDC的度数为____________________。
19.已知=1是一元二次方程2++=0的一个根,则()2011的值____________。
20.如下图,菱形ABCD的边长为,∠B=60°,点E,F分别是边BC,CD的中点,则△AEF的周长是_________________。
21.四条线段的长分别是2,4,6,8,从中任意取出三条线段能围成三角形的概率是_______。
22.如下图,点A在反比例函数(≠0)的图象上,AM⊥轴于点M,若AOM的面积为3,则的值是________________。
23.如下图,将矩形纸片ABCD的两个直角折叠,使点B,D都落在AC的中点O处,若AB=3,则BC的长为_______________________。
24.若是方程2-3-5=0的两根,则代数式9-32-+5的值是__________。
25.如下图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把ABC沿着AD方向平移,得到△A′B′C′.若两个三角形重叠部分的面积是1cm2,则移动的距离AA′等于___cm。
三、解答题(共54分,解答应写出文字说明、证明过程或推演步骤)
19.计算:(耐心做一做,试试我能行!每小题4分,共8分)
(1) (2)
20.(9分)如图,已知二次函数y=— x2+bx+c的图象经过A(2,0)、B(0,—6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数图象的对称轴与x轴交于点C,连结BA、BC,求△ABC的面积.
来源:www./tiku/
21、(9分)如图,在方格纸中
(1)请在方格纸上建立平面直角坐标系,使,并求出点坐标;
(2)以原点为位似中心,相似比为2,在第一象限内将放大,画出放大后的图形;
(3)计算的面积.
22.(10分)为迎接第四届世界太阳城大会,德州市把主要路段路灯更换为太阳能路灯.已知太阳能路灯售价为5000元/个,目前两个商家有此产品.甲商家用如下方法促销:若购买路灯不超过100个,按原价付款;若一次购买100个以上,且购买的个数每增加一个,其价格减少10元,但太阳能路灯的售价不得低于3500元/个.乙店一律按原价的80℅销售.现购买太阳能路灯x个,如果全部在甲商家购买,则所需金额为y1元;如果全部在乙商家购买,则所需金额为y2元.
(1)分别求出y1、y2与x之间的函数关系式;
(2)若市政府投资140万元,最多能购买多少个太阳能路灯?
23.(12分)如图,已知抛物线与交于A(-1,0)、E(3,0)两点,与轴交于点B(0,3)。
求抛物线的解析式;
设抛物线顶点为D,求四边形AEDB的面积;
△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由。
24.(本题满分8分)某村计划建造如下图所示的矩形蔬菜温室,要求长与宽的比为2︰1。在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道。当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288m2?
25.(本题满分8分)如下图,在直角坐标系中,M为轴上一点,⊙M交轴于A、B两点,交轴于C、D两点,P为BC上的一个动点,CQ平分∠PCD,A(-1,0),如(1,0)。
(1)求C点的坐标;
(2)当P点运动时,线段AQ的长度是否改变?若不变,请求其值;若改变请说明理由。
(4题图)
O
第20题
y
A
x
C
B
A
B
C
(第21题)
同课章节目录
