9.1.1 平面直角坐标系的概念 课件(共25张PPT) 初中数学人教版(2024)七年级下册
文档属性
| 名称 | 9.1.1 平面直角坐标系的概念 课件(共25张PPT) 初中数学人教版(2024)七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 585.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 15:36:40 | ||
图片预览






文档简介
(共25张PPT)
9.1.1平面直角坐标系的概念
学习目标
1.理解平面直角坐标系的相关概念.
2.掌握平面直角坐标系内点与坐标是一一对应的.
3.理解在平面直角坐标系中四个象限的点对应坐标的符号特征.
4.能运用点的坐标的符号特征解决问题,进一步体会数形结合思想的作用.
-4
-3
-2
2
3
4
0
-1
1
5
-5
什么是数轴?请画出一条数轴.
数轴是一条规定了原点、正方向和单位长度的直线.
-4
-3
-2
2
3
4
0
-1
1
5
-5
如图,A,B 两点所表示的数分别是什么?
A
B
在数轴上描出“5”
表示的点.
C
数轴上每个点都对应一个实数,这个实数叫做这个点在数轴上的坐标.
点 A 的坐标为-4,点 B 的坐标为 2,点 C 的坐标为 5.
数轴上的点
坐标
-4
-3
-2
2
3
4
0
-1
1
5
-5
A
B
C
在数轴上已知点能说出它的坐标,由坐标能在数轴上找到对应点的位置.那么数轴上的点与坐标有怎样的关系?
一一对应
我们知道,平面上点的位置可以用一对有序数对来表示(如用水平和竖直方向上的两个距离表示)。水平方向的数轴可以表示水平方向上的点的距离,竖直方向上的数轴可以表示竖直方向上点的距离,两条数轴结合起来表示平面上点的位置。
平面直角坐标系
新知讲解
平面直角坐标系的概念
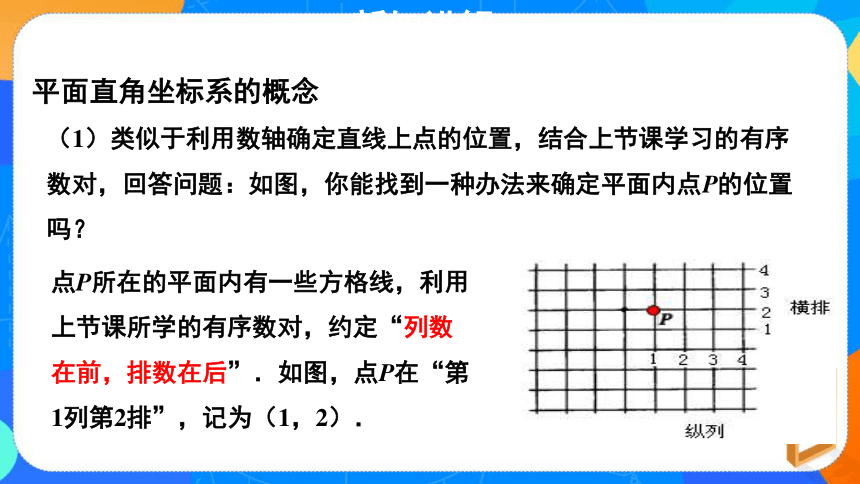
(1)类似于利用数轴确定直线上点的位置,结合上节课学习的有序数对,回答问题:如图,你能找到一种办法来确定平面内点P的位置吗?
点P所在的平面内有一些方格线,利用上节课所学的有序数对,约定“列数在前,排数在后”.如图,点P在“第1列第2排”,记为(1,2).
3
1
4
2
5
-2
-4
-1
-3
O
y
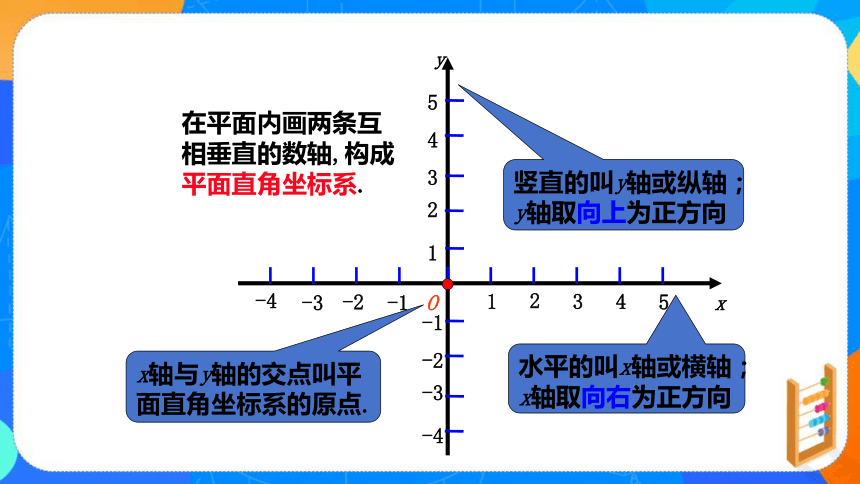
在平面内画两条互相垂直的数轴,构成平面直角坐标系.
1
2
3
4
5
-4
-3
-2
-1
x
竖直的叫y轴或纵轴;
y轴取向上为正方向
水平的叫x轴或横轴;
x轴取向右为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
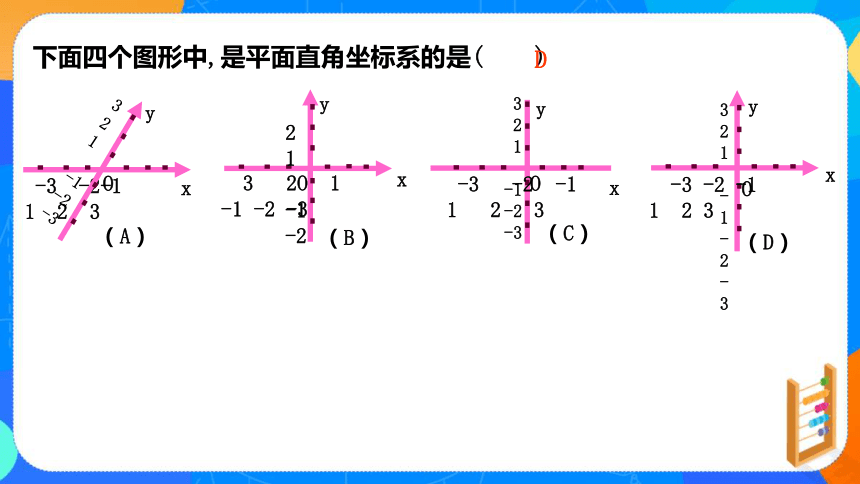
下面四个图形中,是平面直角坐标系的是( )
-3 -2-1 1 2 3
3
2
1
-1
-2
-3
y
x
O
(A)
3 2 1 -1 -2 -3
x
y
(B)
2
1
-1
-2
O
x
y
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
(C)
O
x
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
(D)
O
D
这样P点的横坐标是-2,纵坐标是3,规定把横坐标写在前,纵坐标在后,记作:P(-2,3)
P(-2,3)就叫做点P在平面直角坐标系中的坐标,简称点P的坐标.
-4 -3 -2 -1 0 1 2 3
1
2
3
4
-1
-2
-3
-4
x
y
【思考】如图点P如何表示呢?
后由P点向y轴画垂线,垂足N在y轴上的坐标是3.称为P点的纵坐标.
先由P点向x轴画垂线,垂足M在x轴上的坐标是-2;称为P点的横坐标.
P
N
M
例 下列选项中,平面直角坐标系的画法正确的是 ( )
B
x
y
x
y
x
y
归纳
辨识平面直角坐标系的“三要素”:
(1) 两条数轴;
(2) 有公共原点;
(3) 互相垂直.
注意:一般取向上、向右为正方向.
早在 1637 年以前,法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上可以看成是平面内互相垂直的两条直线,所以笛卡尔的方法就是在平面内画两条原点重合,互相垂直且具有相同单位长度的数轴建立直角坐标系,从而解决了用一对实数表示平面内点的位置的问题.
扩展
几个象限内点的特点
第一象限:(+,+)
第二象限:(-,+)
第三象限:(-,-)
第四象限:(+,-)
考考你:1、请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
A(-5、2) B(3、-2) C(0、4), D(-6、0) E(1、8) F(0、0), G(5、0),H(-6、-4)K(0、-3)
解:A在第二象限,
B在第四象限,
C在Y的正半轴,
E在第一象限,
D在X轴的负半轴,
F在原点,
G在X轴的正半轴,
H在第三象限,
K在Y轴的负半轴。
A
B
C
D
E
F
写出图中多边形ABCDEF各个顶点的坐标。
(-2,0)
(0,-3)
(3,-3)
(4,0)
(3,3)
(0,3)
点B与点C的纵坐标有什么特点,线段BC的位置 有什么特点?
线段CE的位置 有什么特点?
坐标轴上点的坐标有什么特点?
点 M(a,b) 为平面直角坐标系中的点.
(1) 当 a>0,b<0 时,点 M 位于第几象限?
(2) 当 ab>0 时,点M 位于第几象限?
(3) 当 a 为任意实数,且 b<0 时,点 M 位于第几象限?
解析:在平面直角坐标系内,点的坐标特点为:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
原点的坐标是(0,0) ;
x轴上的点:纵坐标都是 0;
y轴上的点:横坐标都是 0;
坐标轴上的点不属于任何象限.
点 M(a,b) 为平面直角坐标系中的点.
(1) 当 a>0,b<0 时,点 M 位于第几象限?
第四象限
解析:在平面直角坐标系内,点的坐标特点为:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
原点的坐标是(0,0) ;
x轴上的点:纵坐标都是 0;
y轴上的点:横坐标都是 0;
坐标轴上的点不属于任何象限.
a>0,b>0 时,点M在第一象限;
点 M(a,b) 为平面直角坐标系中的点.
(2) 当 ab>0 时,点M 位于第几象限?
a<0,b<0 时,点M在第三象限.
解析:在平面直角坐标系内,点的坐标特点为:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
原点的坐标是(0,0) ;
x轴上的点:纵坐标都是 0;
y轴上的点:横坐标都是 0;
坐标轴上的点不属于任何象限.
a<0,b<0 时,点 M 在第三象限;
a>0,b<0 时,点 M 在第四象限;
点 M(a,b) 为平面直角坐标系中的点.
(3) 当 a 为任意实数,且 b<0 时,点 M 位于第几象限?
a=0,b<0 时,点 M 在 y 轴的负半轴.
解析:在平面直角坐标系内,点的坐标特点为:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
原点的坐标是(0,0) ;
x轴上的点:纵坐标都是 0;
y轴上的点:横坐标都是 0;
坐标轴上的点不属于任何象限.
平面直角坐标系及点的坐标
各象限内的点的坐标的特征
坐标轴及平行于坐标轴的直线上的点的坐标的特征
课堂总结
1.在平面直角坐标系中,点A(2,-3)位( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
课堂练习
B
B
2.如果点P(m+3,2m+4)在y轴上,那么点P的坐标是( )
A.(-2,0) B.(0,-2)
C.(1,1) D.(0,2)
3.在平面直角坐标系中,点(-4,m2+1)一定在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.右图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(-2,-1),求黑棋 、白棋③的坐标.
解:由已知白棋①的坐标是(-2,-1)构建平面直角坐标系,如图:
y
x
y轴应在从左往右数的第四条格线上,且向上为正方向,
x轴在从上往下数第二条格线上,且向右为正方向,
这两条直线的交点为坐标原点,
由此可得黑棋 (1,-2)、
白棋③(-1,-3)
o
五、课堂总结
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.
(一)平面直角坐标系的概念
如图所示,有序数对(a,b)叫做点P的坐标.
1
a
3
1
b
3
O
x
y
P(a,b)
(二)坐标特点及象限划分
原点O的坐标为(0,0);
x轴上的点的纵坐标为0;
y轴上的点的横坐标为0;
第二象限
第一象限
第三象限
第四象限
1
2
3
-1
-2
-3
-1
-2
-3
1
2
3
x
y
9.1.1平面直角坐标系的概念
学习目标
1.理解平面直角坐标系的相关概念.
2.掌握平面直角坐标系内点与坐标是一一对应的.
3.理解在平面直角坐标系中四个象限的点对应坐标的符号特征.
4.能运用点的坐标的符号特征解决问题,进一步体会数形结合思想的作用.
-4
-3
-2
2
3
4
0
-1
1
5
-5
什么是数轴?请画出一条数轴.
数轴是一条规定了原点、正方向和单位长度的直线.
-4
-3
-2
2
3
4
0
-1
1
5
-5
如图,A,B 两点所表示的数分别是什么?
A
B
在数轴上描出“5”
表示的点.
C
数轴上每个点都对应一个实数,这个实数叫做这个点在数轴上的坐标.
点 A 的坐标为-4,点 B 的坐标为 2,点 C 的坐标为 5.
数轴上的点
坐标
-4
-3
-2
2
3
4
0
-1
1
5
-5
A
B
C
在数轴上已知点能说出它的坐标,由坐标能在数轴上找到对应点的位置.那么数轴上的点与坐标有怎样的关系?
一一对应
我们知道,平面上点的位置可以用一对有序数对来表示(如用水平和竖直方向上的两个距离表示)。水平方向的数轴可以表示水平方向上的点的距离,竖直方向上的数轴可以表示竖直方向上点的距离,两条数轴结合起来表示平面上点的位置。
平面直角坐标系
新知讲解
平面直角坐标系的概念
(1)类似于利用数轴确定直线上点的位置,结合上节课学习的有序数对,回答问题:如图,你能找到一种办法来确定平面内点P的位置吗?
点P所在的平面内有一些方格线,利用上节课所学的有序数对,约定“列数在前,排数在后”.如图,点P在“第1列第2排”,记为(1,2).
3
1
4
2
5
-2
-4
-1
-3
O
y
在平面内画两条互相垂直的数轴,构成平面直角坐标系.
1
2
3
4
5
-4
-3
-2
-1
x
竖直的叫y轴或纵轴;
y轴取向上为正方向
水平的叫x轴或横轴;
x轴取向右为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
下面四个图形中,是平面直角坐标系的是( )
-3 -2-1 1 2 3
3
2
1
-1
-2
-3
y
x
O
(A)
3 2 1 -1 -2 -3
x
y
(B)
2
1
-1
-2
O
x
y
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
(C)
O
x
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
(D)
O
D
这样P点的横坐标是-2,纵坐标是3,规定把横坐标写在前,纵坐标在后,记作:P(-2,3)
P(-2,3)就叫做点P在平面直角坐标系中的坐标,简称点P的坐标.
-4 -3 -2 -1 0 1 2 3
1
2
3
4
-1
-2
-3
-4
x
y
【思考】如图点P如何表示呢?
后由P点向y轴画垂线,垂足N在y轴上的坐标是3.称为P点的纵坐标.
先由P点向x轴画垂线,垂足M在x轴上的坐标是-2;称为P点的横坐标.
P
N
M
例 下列选项中,平面直角坐标系的画法正确的是 ( )
B
x
y
x
y
x
y
归纳
辨识平面直角坐标系的“三要素”:
(1) 两条数轴;
(2) 有公共原点;
(3) 互相垂直.
注意:一般取向上、向右为正方向.
早在 1637 年以前,法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上可以看成是平面内互相垂直的两条直线,所以笛卡尔的方法就是在平面内画两条原点重合,互相垂直且具有相同单位长度的数轴建立直角坐标系,从而解决了用一对实数表示平面内点的位置的问题.
扩展
几个象限内点的特点
第一象限:(+,+)
第二象限:(-,+)
第三象限:(-,-)
第四象限:(+,-)
考考你:1、请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
A(-5、2) B(3、-2) C(0、4), D(-6、0) E(1、8) F(0、0), G(5、0),H(-6、-4)K(0、-3)
解:A在第二象限,
B在第四象限,
C在Y的正半轴,
E在第一象限,
D在X轴的负半轴,
F在原点,
G在X轴的正半轴,
H在第三象限,
K在Y轴的负半轴。
A
B
C
D
E
F
写出图中多边形ABCDEF各个顶点的坐标。
(-2,0)
(0,-3)
(3,-3)
(4,0)
(3,3)
(0,3)
点B与点C的纵坐标有什么特点,线段BC的位置 有什么特点?
线段CE的位置 有什么特点?
坐标轴上点的坐标有什么特点?
点 M(a,b) 为平面直角坐标系中的点.
(1) 当 a>0,b<0 时,点 M 位于第几象限?
(2) 当 ab>0 时,点M 位于第几象限?
(3) 当 a 为任意实数,且 b<0 时,点 M 位于第几象限?
解析:在平面直角坐标系内,点的坐标特点为:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
原点的坐标是(0,0) ;
x轴上的点:纵坐标都是 0;
y轴上的点:横坐标都是 0;
坐标轴上的点不属于任何象限.
点 M(a,b) 为平面直角坐标系中的点.
(1) 当 a>0,b<0 时,点 M 位于第几象限?
第四象限
解析:在平面直角坐标系内,点的坐标特点为:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
原点的坐标是(0,0) ;
x轴上的点:纵坐标都是 0;
y轴上的点:横坐标都是 0;
坐标轴上的点不属于任何象限.
a>0,b>0 时,点M在第一象限;
点 M(a,b) 为平面直角坐标系中的点.
(2) 当 ab>0 时,点M 位于第几象限?
a<0,b<0 时,点M在第三象限.
解析:在平面直角坐标系内,点的坐标特点为:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
原点的坐标是(0,0) ;
x轴上的点:纵坐标都是 0;
y轴上的点:横坐标都是 0;
坐标轴上的点不属于任何象限.
a<0,b<0 时,点 M 在第三象限;
a>0,b<0 时,点 M 在第四象限;
点 M(a,b) 为平面直角坐标系中的点.
(3) 当 a 为任意实数,且 b<0 时,点 M 位于第几象限?
a=0,b<0 时,点 M 在 y 轴的负半轴.
解析:在平面直角坐标系内,点的坐标特点为:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
原点的坐标是(0,0) ;
x轴上的点:纵坐标都是 0;
y轴上的点:横坐标都是 0;
坐标轴上的点不属于任何象限.
平面直角坐标系及点的坐标
各象限内的点的坐标的特征
坐标轴及平行于坐标轴的直线上的点的坐标的特征
课堂总结
1.在平面直角坐标系中,点A(2,-3)位( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
课堂练习
B
B
2.如果点P(m+3,2m+4)在y轴上,那么点P的坐标是( )
A.(-2,0) B.(0,-2)
C.(1,1) D.(0,2)
3.在平面直角坐标系中,点(-4,m2+1)一定在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.右图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(-2,-1),求黑棋 、白棋③的坐标.
解:由已知白棋①的坐标是(-2,-1)构建平面直角坐标系,如图:
y
x
y轴应在从左往右数的第四条格线上,且向上为正方向,
x轴在从上往下数第二条格线上,且向右为正方向,
这两条直线的交点为坐标原点,
由此可得黑棋 (1,-2)、
白棋③(-1,-3)
o
五、课堂总结
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.
(一)平面直角坐标系的概念
如图所示,有序数对(a,b)叫做点P的坐标.
1
a
3
1
b
3
O
x
y
P(a,b)
(二)坐标特点及象限划分
原点O的坐标为(0,0);
x轴上的点的纵坐标为0;
y轴上的点的横坐标为0;
第二象限
第一象限
第三象限
第四象限
1
2
3
-1
-2
-3
-1
-2
-3
1
2
3
x
y
同课章节目录
