2025年山东省东营市中考数学模拟试卷(含答案)
文档属性
| 名称 | 2025年山东省东营市中考数学模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 126.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 19:00:18 | ||
图片预览



文档简介
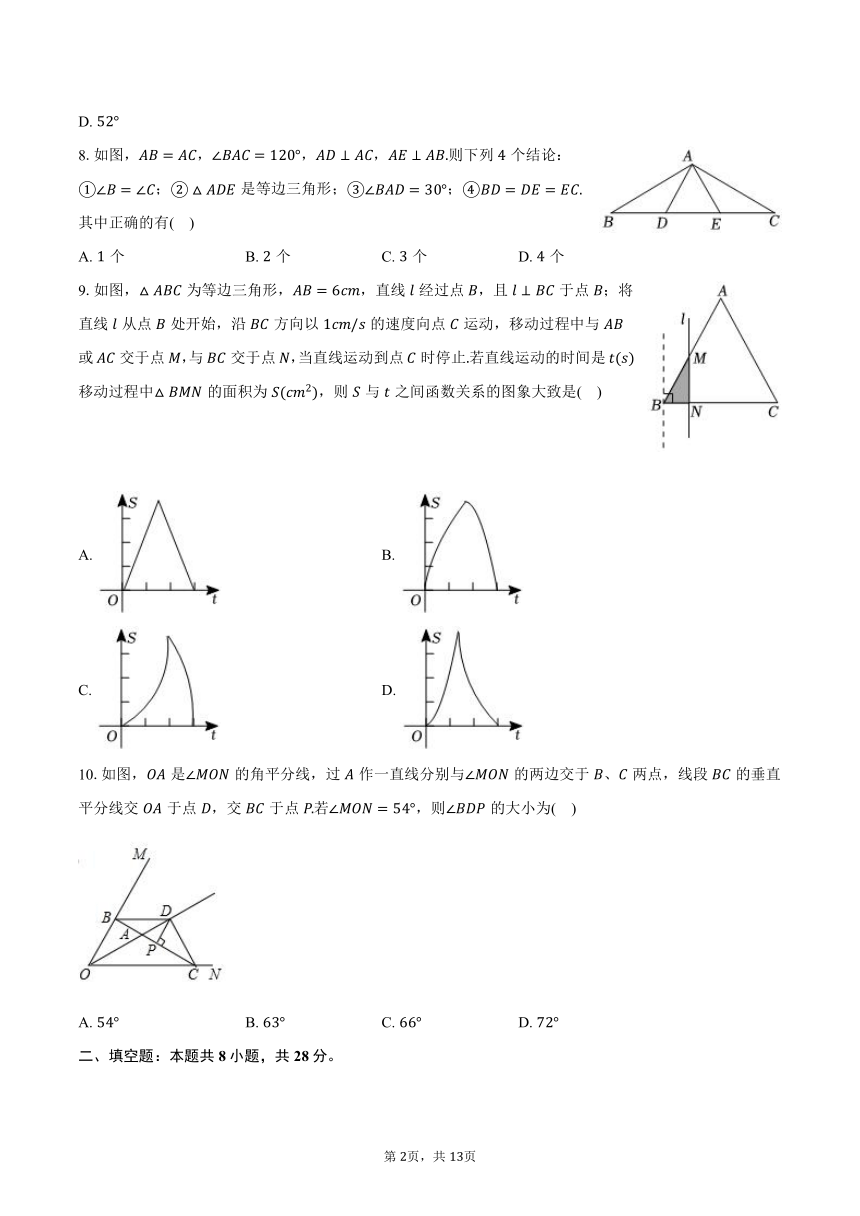
2025年山东省东营市中考数学模拟试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的相反数是( )
A. B. C. D.
2.下列运算正确的是( )
A. B. C. D.
3.将五个相同的小正方体堆成如图所示的物体,它的左视图是( )
A. B.
C. D.
4.在平面直角坐标系中,点在正比例函数的图象上,且随的增大而减小,则在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5.抛一枚硬币,正面朝上的概率为;掷一枚普通的正方体骰子,掷得的点数小于的概率为;口袋中有红、黄、白球各一个,从中一次摸出两个红球的概率为则、、的大小关系是( )
A. B. C. D.
6.如图,先锋村准备在坡角为的山坡上栽树,要求相邻两树之间的水平距离为米,那么这两树在坡面上的距离为( )
A.
B.
C.
D.
7.如图,点,,在上,,,则的度数为( )
A.
B.
C.
D.
8.如图,,,,则下列个结论:;是等边三角形;;其中正确的有( )
A. 个 B. 个 C. 个 D. 个
9.如图,为等边三角形,,直线经过点,且于点;将直线从点处开始,沿方向以的速度向点运动,移动过程中与或交于点,与交于点,当直线运动到点时停止若直线运动的时间是,移动过程中的面积为,则与之间函数关系的图象大致是( )
A. B.
C. D.
10.如图,是的角平分线,过作一直线分别与的两边交于、两点,线段的垂直平分线交于点,交于点若,则的大小为( )
A. B. C. D.
二、填空题:本题共8小题,共28分。
11.中国首次火星探测任务天问一号探测器实施近火捕获制动,环绕器轨控发动机点火工作约分钟,探测器顺利进人近火点高度约米,将用科学记数法表示为______.
12.因式分解: .
13.学校举办跳绳比赛,九年班参加比赛的名同学每分钟跳绳次数分别是,,,,,这个数据的中位数是______.
14.关于的一元二次方程没有实数根,则的取值范围是______.
15.如图,已知等腰三角形中,,,点从点出发沿以的速度向点运动;同时点从点出发沿以的速度向点运动,在运动过程中,当与相似时, ______.
16.如图,,,点是直线上的一个动点,连结,作与的角平分线与,两角平分线所在的直线交于点,求点在运动过程中线段的最小值为______.
17.若一个直角三角形的两条边分别为和,则此直角三角形的外接圆半径为______.
18.如图,在正六边形中,,将一个含的直角三角板的直角放入正六边形内,保证点,同时在三角板的边,上,转动三角板连接,则线段的最小值为______.
三、解答题:本题共7小题,共62分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
先化简,再求值:,其中.
20.本小题分
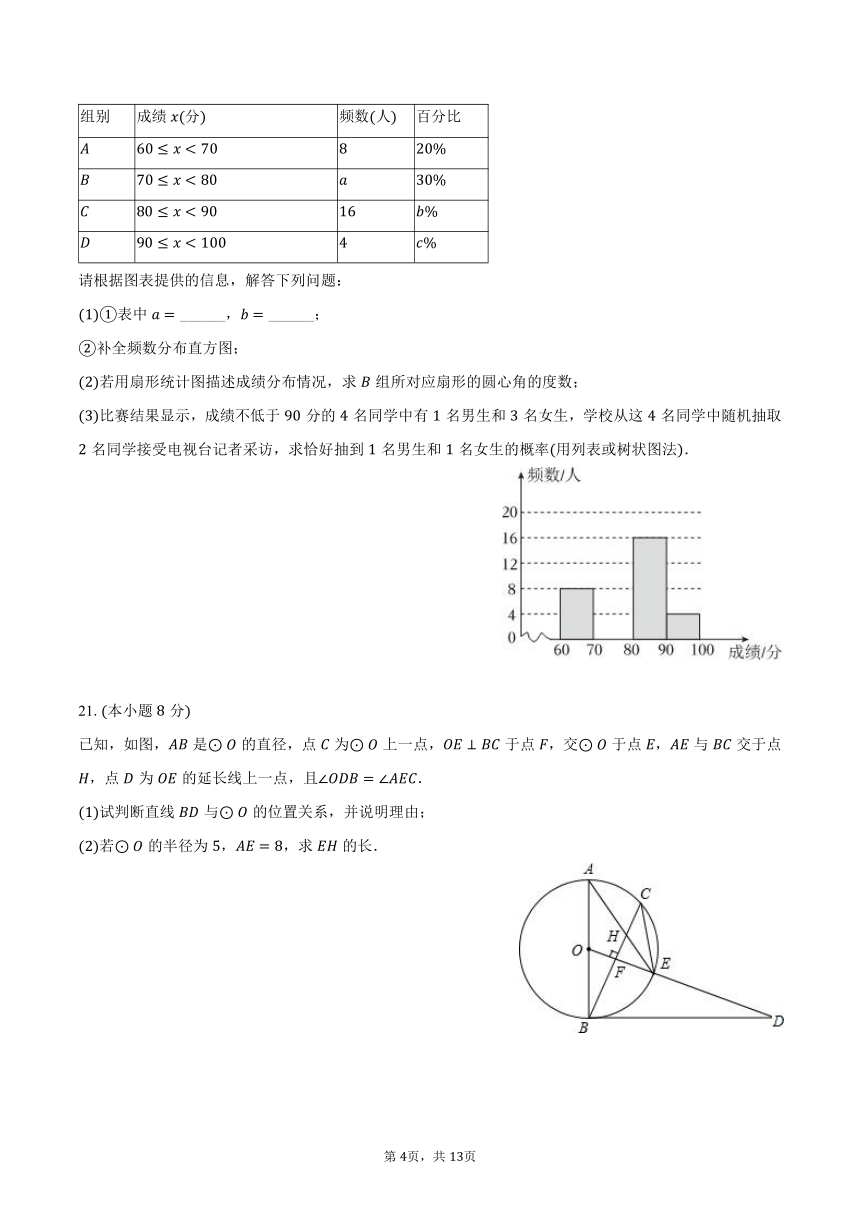
某学校举行了以“美丽鼓楼”为主题的演讲比赛赛后组委会整理参赛同学成绩,将成绩按分数段分为,,,四组,并制作了如下不完整的频数分布表和频数分布直方图.
组别 成绩分 频数人 百分比
请根据图表提供的信息,解答下列问题:
表中 ______, ______;
补全频数分布直方图;
若用扇形统计图描述成绩分布情况,求组所对应扇形的圆心角的度数;
比赛结果显示,成绩不低于分的名同学中有名男生和名女生,学校从这名同学中随机抽取名同学接受电视台记者采访,求恰好抽到名男生和名女生的概率用列表或树状图法.
21.本小题分
已知,如图,是的直径,点为上一点,于点,交于点,与交于点,点为的延长线上一点,且.
试判断直线与的位置关系,并说明理由;
若的半径为,,求的长.
22.本小题分
如图,平面直角坐标系中,正方形的顶点,在轴上,反比例函数的图象经过点,交于点.
求该反比例函数的解析式;
求的面积.
23.本小题分
某市市政府提出年将申报国家级卫生城市,全市各小区积极响应,红星小区决定在小区内安装垃圾分类的型固定垃圾箱和型移动垃圾箱,已知购买个型固定垃圾箱和个型移动垃圾箱共需元,且型固定垃圾箱的单价是型移动垃圾箱单价的倍.
求型固定垃圾箱和型移动垃圾箱的单价各是多少元;
如果需要购买型固定垃圾箱和型移动垃圾箱共个,且费用不超过元,问:那么该小区最多可以购买型固定垃圾箱多少个?
24.本小题分
如图,在中,,,,另有一直角梯形的底边落在上,腰落在上,且,,::.
延长交于,求的面积.
操作:固定,将直角梯形以每秒个单位的速度沿方向向右移动,直到点与点重合时停止,设运动的时间为秒,运动后的直角梯形为如图.
探究:在运动中,四边形能否为正方形?若能,请求出此时的值;若不能,请说明理由.
探究:在运动过程中,延长交于,三角形能否为等腰三角形?若能,求出此时的值;若不能,请说明理由.
25.本小题分
如图,抛物线经过,两点,作轴于点点是抛物线上一点.
求该抛物线的解析式;
连接,交直线于点,作轴,若,求点的坐标;
若点为抛物线上一点,且在第四象限内,已知直线,与轴分别交于、两点,当点运动时,是否为定值?若是,请求出该定值;若不是,请说明理由.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】或
16.【答案】
17.【答案】或.
18.【答案】
19.【答案】解:原式
,
当时,原式.
20.【解析】由题意得,参赛人数为人,
,,
.
故答案为:;.
补全频数分布直方图如图所示.
组所对应扇形的圆心角的度数为.
列表如下:
男 女 女 女
男 男,女 男,女 男,女
女 女,男 女,女 女,女
女 女,男 女,女 女,女
女 女,男 女,女 女,女
共有种等可能的结果,其中恰好抽到名男生和名女生的结果有种,
恰好抽到名男生和名女生的概率为.
21.【答案】证明:,,
,
,
,
,
,
即,
,
是的切线;
解:连接,如图所示:
是的直径,
,
,,
,
,
,
,
,
,
∽,
,
;
,
.
22.【答案】解:反比例函数的图象经过点,
,
该反比例函数的解析式为;
四边形是正方形,,
,,
,
把代入得,,
,
.
23.【答案】解:设型固定垃圾箱的单价是元,型移动垃圾箱的单价是元,根据题意可得:
,
解得:,
答:型固定垃圾箱的单价是元,型移动垃圾箱的单价是元;
设购买型固定垃圾箱个,则购买型移动垃圾箱个,根据题意可得:
,
解得:,
的最大值为,
答:该小区最多可以购买型固定垃圾箱个.
24.【答案】解:::,
又,
,
∽
,
即,
,
.
能为正方形
,,
四边形为平行四边形,
又,
四边形为矩形,
又
当时,四边形为正方形
此时可得秒时,四边形为正方形.
Ⅰ,
当秒时,直角梯形的腰与重合.
当时,重叠部分的面积为直角梯形的面积.
过作于,
,
,
,
直角梯形的面积为,
.
Ⅱ当时,重叠部分的面积为四边形的面积一矩形的面积.
而,
,
.
Ⅲ当时,如图,设交于,
,
又,
,
重叠部分的面积,
.
重叠部分面积与的函数关系式:
.
25.【解析】解:抛物线经过,两点,
,
解得:,
该抛物线的解析式为:;
,
设直线的解析式为,
,
解得:,
直线的解析式为,
设,
,
,
解得:或舍去,
;
是定值,该定值为,理由如下.
令,
解得,,即抛物线与轴的交点是:和,
设点的坐标是,则,
设直线的解析式是:,
将点、代入得:,
解得:,
直线的解析式是:,
令,
解得:,即,
,
设直线的解析式是:,
将点、代入得:,
解得:,
直线的解析式是:,
令,
解得:,即,
,,
.
是定值,该定值为.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的相反数是( )
A. B. C. D.
2.下列运算正确的是( )
A. B. C. D.
3.将五个相同的小正方体堆成如图所示的物体,它的左视图是( )
A. B.
C. D.
4.在平面直角坐标系中,点在正比例函数的图象上,且随的增大而减小,则在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5.抛一枚硬币,正面朝上的概率为;掷一枚普通的正方体骰子,掷得的点数小于的概率为;口袋中有红、黄、白球各一个,从中一次摸出两个红球的概率为则、、的大小关系是( )
A. B. C. D.
6.如图,先锋村准备在坡角为的山坡上栽树,要求相邻两树之间的水平距离为米,那么这两树在坡面上的距离为( )
A.
B.
C.
D.
7.如图,点,,在上,,,则的度数为( )
A.
B.
C.
D.
8.如图,,,,则下列个结论:;是等边三角形;;其中正确的有( )
A. 个 B. 个 C. 个 D. 个
9.如图,为等边三角形,,直线经过点,且于点;将直线从点处开始,沿方向以的速度向点运动,移动过程中与或交于点,与交于点,当直线运动到点时停止若直线运动的时间是,移动过程中的面积为,则与之间函数关系的图象大致是( )
A. B.
C. D.
10.如图,是的角平分线,过作一直线分别与的两边交于、两点,线段的垂直平分线交于点,交于点若,则的大小为( )
A. B. C. D.
二、填空题:本题共8小题,共28分。
11.中国首次火星探测任务天问一号探测器实施近火捕获制动,环绕器轨控发动机点火工作约分钟,探测器顺利进人近火点高度约米,将用科学记数法表示为______.
12.因式分解: .
13.学校举办跳绳比赛,九年班参加比赛的名同学每分钟跳绳次数分别是,,,,,这个数据的中位数是______.
14.关于的一元二次方程没有实数根,则的取值范围是______.
15.如图,已知等腰三角形中,,,点从点出发沿以的速度向点运动;同时点从点出发沿以的速度向点运动,在运动过程中,当与相似时, ______.
16.如图,,,点是直线上的一个动点,连结,作与的角平分线与,两角平分线所在的直线交于点,求点在运动过程中线段的最小值为______.
17.若一个直角三角形的两条边分别为和,则此直角三角形的外接圆半径为______.
18.如图,在正六边形中,,将一个含的直角三角板的直角放入正六边形内,保证点,同时在三角板的边,上,转动三角板连接,则线段的最小值为______.
三、解答题:本题共7小题,共62分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
先化简,再求值:,其中.
20.本小题分
某学校举行了以“美丽鼓楼”为主题的演讲比赛赛后组委会整理参赛同学成绩,将成绩按分数段分为,,,四组,并制作了如下不完整的频数分布表和频数分布直方图.
组别 成绩分 频数人 百分比
请根据图表提供的信息,解答下列问题:
表中 ______, ______;
补全频数分布直方图;
若用扇形统计图描述成绩分布情况,求组所对应扇形的圆心角的度数;
比赛结果显示,成绩不低于分的名同学中有名男生和名女生,学校从这名同学中随机抽取名同学接受电视台记者采访,求恰好抽到名男生和名女生的概率用列表或树状图法.
21.本小题分
已知,如图,是的直径,点为上一点,于点,交于点,与交于点,点为的延长线上一点,且.
试判断直线与的位置关系,并说明理由;
若的半径为,,求的长.
22.本小题分
如图,平面直角坐标系中,正方形的顶点,在轴上,反比例函数的图象经过点,交于点.
求该反比例函数的解析式;
求的面积.
23.本小题分
某市市政府提出年将申报国家级卫生城市,全市各小区积极响应,红星小区决定在小区内安装垃圾分类的型固定垃圾箱和型移动垃圾箱,已知购买个型固定垃圾箱和个型移动垃圾箱共需元,且型固定垃圾箱的单价是型移动垃圾箱单价的倍.
求型固定垃圾箱和型移动垃圾箱的单价各是多少元;
如果需要购买型固定垃圾箱和型移动垃圾箱共个,且费用不超过元,问:那么该小区最多可以购买型固定垃圾箱多少个?
24.本小题分
如图,在中,,,,另有一直角梯形的底边落在上,腰落在上,且,,::.
延长交于,求的面积.
操作:固定,将直角梯形以每秒个单位的速度沿方向向右移动,直到点与点重合时停止,设运动的时间为秒,运动后的直角梯形为如图.
探究:在运动中,四边形能否为正方形?若能,请求出此时的值;若不能,请说明理由.
探究:在运动过程中,延长交于,三角形能否为等腰三角形?若能,求出此时的值;若不能,请说明理由.
25.本小题分
如图,抛物线经过,两点,作轴于点点是抛物线上一点.
求该抛物线的解析式;
连接,交直线于点,作轴,若,求点的坐标;
若点为抛物线上一点,且在第四象限内,已知直线,与轴分别交于、两点,当点运动时,是否为定值?若是,请求出该定值;若不是,请说明理由.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】或
16.【答案】
17.【答案】或.
18.【答案】
19.【答案】解:原式
,
当时,原式.
20.【解析】由题意得,参赛人数为人,
,,
.
故答案为:;.
补全频数分布直方图如图所示.
组所对应扇形的圆心角的度数为.
列表如下:
男 女 女 女
男 男,女 男,女 男,女
女 女,男 女,女 女,女
女 女,男 女,女 女,女
女 女,男 女,女 女,女
共有种等可能的结果,其中恰好抽到名男生和名女生的结果有种,
恰好抽到名男生和名女生的概率为.
21.【答案】证明:,,
,
,
,
,
,
即,
,
是的切线;
解:连接,如图所示:
是的直径,
,
,,
,
,
,
,
,
,
∽,
,
;
,
.
22.【答案】解:反比例函数的图象经过点,
,
该反比例函数的解析式为;
四边形是正方形,,
,,
,
把代入得,,
,
.
23.【答案】解:设型固定垃圾箱的单价是元,型移动垃圾箱的单价是元,根据题意可得:
,
解得:,
答:型固定垃圾箱的单价是元,型移动垃圾箱的单价是元;
设购买型固定垃圾箱个,则购买型移动垃圾箱个,根据题意可得:
,
解得:,
的最大值为,
答:该小区最多可以购买型固定垃圾箱个.
24.【答案】解:::,
又,
,
∽
,
即,
,
.
能为正方形
,,
四边形为平行四边形,
又,
四边形为矩形,
又
当时,四边形为正方形
此时可得秒时,四边形为正方形.
Ⅰ,
当秒时,直角梯形的腰与重合.
当时,重叠部分的面积为直角梯形的面积.
过作于,
,
,
,
直角梯形的面积为,
.
Ⅱ当时,重叠部分的面积为四边形的面积一矩形的面积.
而,
,
.
Ⅲ当时,如图,设交于,
,
又,
,
重叠部分的面积,
.
重叠部分面积与的函数关系式:
.
25.【解析】解:抛物线经过,两点,
,
解得:,
该抛物线的解析式为:;
,
设直线的解析式为,
,
解得:,
直线的解析式为,
设,
,
,
解得:或舍去,
;
是定值,该定值为,理由如下.
令,
解得,,即抛物线与轴的交点是:和,
设点的坐标是,则,
设直线的解析式是:,
将点、代入得:,
解得:,
直线的解析式是:,
令,
解得:,即,
,
设直线的解析式是:,
将点、代入得:,
解得:,
直线的解析式是:,
令,
解得:,即,
,,
.
是定值,该定值为.
第1页,共1页
同课章节目录
