2025年四川省宜宾市中考数学模拟试卷(含答案)
文档属性
| 名称 | 2025年四川省宜宾市中考数学模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 170.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 16:02:18 | ||
图片预览



文档简介
2025年四川省宜宾市中考数学模拟试卷
一、选择题:本题共12小题,每小题4分,共48分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列四个数:,,,其中负数的个数是( )
A. 个 B. 个 C. 个 D. 个
2.下图几何体中是三棱锥是( )
A. B. C. D.
3.某校举办“青春励志”主题演讲比赛,规定每位选手演讲时长不超过分钟初赛结束后,随机抽取名选手,编号为,统计这名选手的实际演讲时长单位:分钟如图所示为了更全面评估选手水平,组委会决定再抽取名选手的成绩纳入统计若名选手演讲时长的中位数与原来名选手演讲时长的中位数保持一致,则新增的名选手演讲时长可能是( )
A. 分钟,分钟 B. 分钟,分钟
C. 分钟,分钟 D. 分钟,分钟
4.若方程组的解,满足,则的取值范围是( )
A. B. C. D.
5.下列计算中,正确的是( )
A. B. C. D.
6.某厂商为中小学智慧课堂提供学生平板,成本为元,标价为元,如果厂商要以利润不低于的售价打折出售,最低可打几折( )
A. 折 B. 折 C. 折 D. 折
7.如图,正六边形内接于,,则的周长为( )
A.
B.
C.
D.
8.九章算术是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十枚,称之重适等,交易其一,金轻十三两,问金、银一枚各重几何?”意思是:甲袋中装有黄金枚每枚黄金重量相同,乙袋中装有白银枚每枚白银重量相同,称重两袋相等,两袋互相交换枚后,甲袋比乙袋轻了两袋子重量忽略不计,问黄金、白银每枚各重多少两?设每枚黄金重两,每枚白银重两,根据题意可列方程组为( )
A. B.
C. D.
9.如图,直线与轴交于点,与双曲线交于点,过点作轴于点,且,则的值为( )
A.
B.
C.
D.
10.如图,在中,,,分别以点,为圆心,以大于的长为半径作弧,两弧相交于,两点,作直线分别交,于点,,连接,以下结论不正确的是( )
A. B. C. D.
11.如图,内接于圆,,则圆的半径为( )
A.
B.
C.
D.
12.如图,在平行四边形中,,,,是的中点,连接,平分,且,则的长为( )
A.
B.
C.
D.
二、填空题:本题共6小题,每小题4分,共24分。
13.分解因式;______.
14.若关于的分式方程,有负数解,则实数的取值范围是______.
15.如图,是的直径,是延长线上一点,点在上,且,的延长线交于点若,则的度数为______.
16.如图,在矩形中,,,垂足为,,点、分别在,上,则的最小值为______.
17.如图,、、、为直线上的个动点,其中,在直线上,线段以每秒个单位的速度向左运动,同时线段以每秒个单位的速度向右运动,则运动______秒时,点到点的距离与点到点的距离相等.
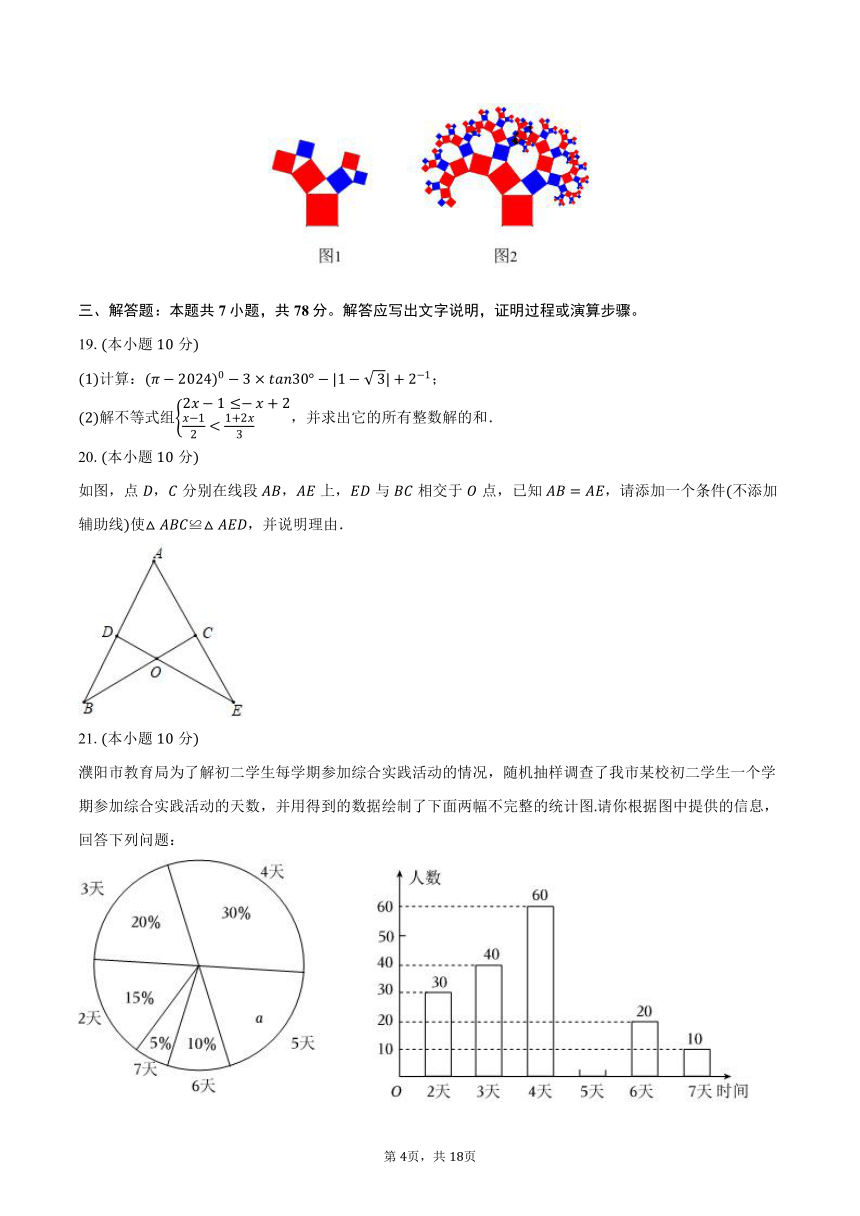
18.如图,有一个边长为的大正方形,经过次“生长”后,在它的左右屑上生出两个小正方形,其中三个正方形围成的三角形是直角三角形,再经过次生长”后,形成的图形如图所示如果继续“生长”下去,它将变得“枝繁叶茂”,若“生长”了次后形成的图形如图所示,则图中所有的正方形的面积和是______.
三、解答题:本题共7小题,共78分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
计算:;
解不等式组,并求出它的所有整数解的和.
20.本小题分
如图,点,分别在线段,上,与相交于点,已知,请添加一个条件不添加辅助线使≌,并说明理由.
21.本小题分
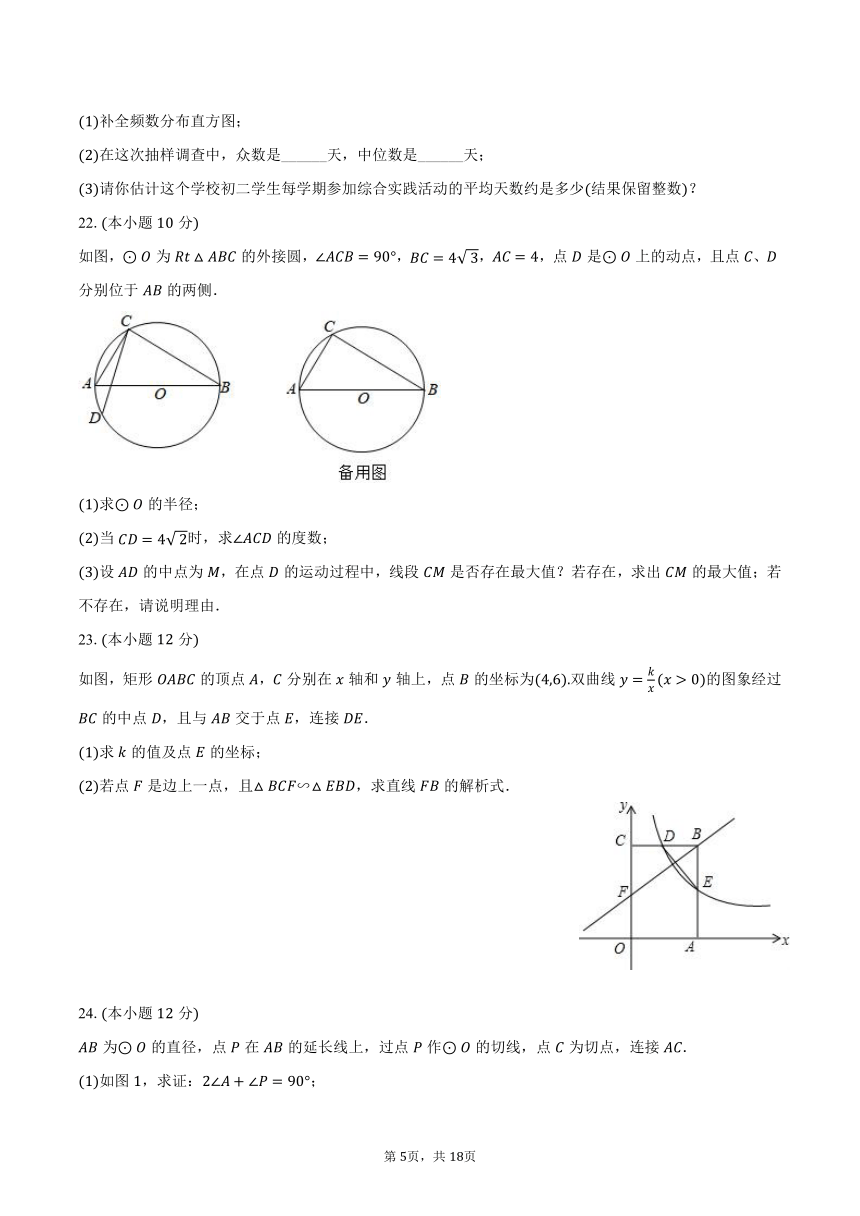
濮阳市教育局为了解初二学生每学期参加综合实践活动的情况,随机抽样调查了我市某校初二学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图请你根据图中提供的信息,回答下列问题:
补全频数分布直方图;
在这次抽样调查中,众数是______天,中位数是______天;
请你估计这个学校初二学生每学期参加综合实践活动的平均天数约是多少结果保留整数?
22.本小题分
如图,为的外接圆,,,,点是上的动点,且点、分别位于的两侧.
求的半径;
当时,求的度数;
设的中点为,在点的运动过程中,线段是否存在最大值?若存在,求出的最大值;若不存在,请说明理由.
23.本小题分
如图,矩形的顶点,分别在轴和轴上,点的坐标为双曲线的图象经过的中点,且与交于点,连接.
求的值及点的坐标;
若点是边上一点,且∽,求直线的解析式.
24.本小题分
为的直径,点在的延长线上,过点作的切线,点为切点,连接.
如图,求证:;
如图,过点作的垂线,点为垂足,点在上,,连接,求证:;
如图,在的条件下,点为的中点,点在上,连接,若,,,求的长.
25.本小题分
如图,在平面直角坐标系中,抛物线与轴交于点,,交轴于点,且.
求该抛物线的函数表达式;
如图,点为直线上方抛物线上的一动点,过点作交于点,,为轴上的动点,在的下方,满足,连接,,当取得最大值时,求点的坐标及的最小值;
将抛物线沿着射线方向平移个单位长度得到新抛物线,在当取得最大值的条件下,点为新抛物线上一点,连接,,当时,请直接写出点的横坐标.
答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.且
15.
16.
17.或
18.
19.【解析】
;
,
解得,
解得,
则不等式组的解集为:,
所有整数解的和为.
20.解:条件
在和中,
≌.
21.解:一个学期参加综合实践活动的天数为天的人数占总人数的百分比为:
,
本次调查的总人数为:人,
一个学期参加综合实践活动的天数为天的人数为:
人,
补全频数分布直方图,如图所示:
众数是天,中位数为天.
故答案为:,.
天,
答:估计该市初二学生每学期参加综合实践活动的平均天数约为天.
22.解:为的外接圆,,
是直径,
在中,,,
,
的半径为.
如图中,连接,.
,,
,,
,
,
,
,
是等边三角形,
,
.
存在;
如图中,连接,.
是的中点,
,
,
点的运动轨迹以为直径的,
.
连接,,则,
是等边三角形,,
,
,
,
的最大值为.
23.解:在矩形中,
,
边中点的坐标为,
又曲线的图象经过点,
,
点在上,
点的横坐标为,
经过点,
点纵坐标为,
点坐标为;
由得,,,,
∽,
,即,
,
,即点的坐标为,
设直线的解析式为,而直线经过,,
,解得,
直线的解析式为.
24.证明:连接,如图,
为的切线,
,
,
,
,
;
证明:连接,如图,
为的切线,
,
,
,
.
,
,
.
在和中,
,
≌,
;
解:连接,,,,交于点,如图,
点为的中点,为的直径,
,
,
,
.
,
,
,
,
.
,
,
为的切线,
,
,
,
,
设圆的半径为,则,
,,
为的切线,
,
,
或不合题意,舍去,
,,
由知:≌,
,
,
,
,
∽,
,
设,则,
,.
为的直径,
,
,
∽,
,
,
解得:或不合题意,舍去,
,
由知:.
25..解:点,
,
,
,,
把,代入,
得:,
解得:,
抛物线的解析式为:;
过点作,交于点,过点作,交于点,如图所示:
设直线的解析式为,把,代入得:,
解得:,
直线的解析式为:,
同理可得:直线的解析式为:,
,
直线的解析式为:,
联立,
解得:,
点,
,
,,
,
,
,
,
,
,
∽,
,
即,
,
设,则,
,
,
,
当时,有最大值,
,
此时点的坐标为;
作轴,在点下方取,连接,取点关于轴的对称点,连接,如图所示:
则,,
,,
四边形为平行四边形,
,
根据轴对称可知:,
,
两点之间线段最短,
当、、三点在同一直线上时,最小,即最小,
为定值,
此时最小,且最小值为:;
,
抛物线的顶点坐标为,
将抛物线沿着射线方向平移个单位长度得到新抛物线,
,,
将抛物线向右平移个单位,向上平移个单位,正好得出新抛物线,
新抛物线的顶点坐标为,
新抛物线的解析式为:,
根据解析可知:当取得最大值时,,
,
轴,
,
,,
,,
,
作,点在轴正半轴上,过点作于点,如图所示:
则,
设,则,
为等腰直角三角形,
,
,
,
,
,,
,
,
∽,
,即,
解得:,
,
,,,
≌,
,
,
设直线的解析式为:,把代入得:,
解得:,
直线的解析式为:,
令,
解得:舍去;
当与轴的交点正好为关于轴的对称点时,,此时点符合题意,
设直线的解析式为:,
把代入得:,
解得:,
直线的解析式为:,
令,
解得:舍去;
综上分析可知:点的横坐标为或.
第8页,共18页
一、选择题:本题共12小题,每小题4分,共48分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列四个数:,,,其中负数的个数是( )
A. 个 B. 个 C. 个 D. 个
2.下图几何体中是三棱锥是( )
A. B. C. D.
3.某校举办“青春励志”主题演讲比赛,规定每位选手演讲时长不超过分钟初赛结束后,随机抽取名选手,编号为,统计这名选手的实际演讲时长单位:分钟如图所示为了更全面评估选手水平,组委会决定再抽取名选手的成绩纳入统计若名选手演讲时长的中位数与原来名选手演讲时长的中位数保持一致,则新增的名选手演讲时长可能是( )
A. 分钟,分钟 B. 分钟,分钟
C. 分钟,分钟 D. 分钟,分钟
4.若方程组的解,满足,则的取值范围是( )
A. B. C. D.
5.下列计算中,正确的是( )
A. B. C. D.
6.某厂商为中小学智慧课堂提供学生平板,成本为元,标价为元,如果厂商要以利润不低于的售价打折出售,最低可打几折( )
A. 折 B. 折 C. 折 D. 折
7.如图,正六边形内接于,,则的周长为( )
A.
B.
C.
D.
8.九章算术是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十枚,称之重适等,交易其一,金轻十三两,问金、银一枚各重几何?”意思是:甲袋中装有黄金枚每枚黄金重量相同,乙袋中装有白银枚每枚白银重量相同,称重两袋相等,两袋互相交换枚后,甲袋比乙袋轻了两袋子重量忽略不计,问黄金、白银每枚各重多少两?设每枚黄金重两,每枚白银重两,根据题意可列方程组为( )
A. B.
C. D.
9.如图,直线与轴交于点,与双曲线交于点,过点作轴于点,且,则的值为( )
A.
B.
C.
D.
10.如图,在中,,,分别以点,为圆心,以大于的长为半径作弧,两弧相交于,两点,作直线分别交,于点,,连接,以下结论不正确的是( )
A. B. C. D.
11.如图,内接于圆,,则圆的半径为( )
A.
B.
C.
D.
12.如图,在平行四边形中,,,,是的中点,连接,平分,且,则的长为( )
A.
B.
C.
D.
二、填空题:本题共6小题,每小题4分,共24分。
13.分解因式;______.
14.若关于的分式方程,有负数解,则实数的取值范围是______.
15.如图,是的直径,是延长线上一点,点在上,且,的延长线交于点若,则的度数为______.
16.如图,在矩形中,,,垂足为,,点、分别在,上,则的最小值为______.
17.如图,、、、为直线上的个动点,其中,在直线上,线段以每秒个单位的速度向左运动,同时线段以每秒个单位的速度向右运动,则运动______秒时,点到点的距离与点到点的距离相等.
18.如图,有一个边长为的大正方形,经过次“生长”后,在它的左右屑上生出两个小正方形,其中三个正方形围成的三角形是直角三角形,再经过次生长”后,形成的图形如图所示如果继续“生长”下去,它将变得“枝繁叶茂”,若“生长”了次后形成的图形如图所示,则图中所有的正方形的面积和是______.
三、解答题:本题共7小题,共78分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
计算:;
解不等式组,并求出它的所有整数解的和.
20.本小题分
如图,点,分别在线段,上,与相交于点,已知,请添加一个条件不添加辅助线使≌,并说明理由.
21.本小题分
濮阳市教育局为了解初二学生每学期参加综合实践活动的情况,随机抽样调查了我市某校初二学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图请你根据图中提供的信息,回答下列问题:
补全频数分布直方图;
在这次抽样调查中,众数是______天,中位数是______天;
请你估计这个学校初二学生每学期参加综合实践活动的平均天数约是多少结果保留整数?
22.本小题分
如图,为的外接圆,,,,点是上的动点,且点、分别位于的两侧.
求的半径;
当时,求的度数;
设的中点为,在点的运动过程中,线段是否存在最大值?若存在,求出的最大值;若不存在,请说明理由.
23.本小题分
如图,矩形的顶点,分别在轴和轴上,点的坐标为双曲线的图象经过的中点,且与交于点,连接.
求的值及点的坐标;
若点是边上一点,且∽,求直线的解析式.
24.本小题分
为的直径,点在的延长线上,过点作的切线,点为切点,连接.
如图,求证:;
如图,过点作的垂线,点为垂足,点在上,,连接,求证:;
如图,在的条件下,点为的中点,点在上,连接,若,,,求的长.
25.本小题分
如图,在平面直角坐标系中,抛物线与轴交于点,,交轴于点,且.
求该抛物线的函数表达式;
如图,点为直线上方抛物线上的一动点,过点作交于点,,为轴上的动点,在的下方,满足,连接,,当取得最大值时,求点的坐标及的最小值;
将抛物线沿着射线方向平移个单位长度得到新抛物线,在当取得最大值的条件下,点为新抛物线上一点,连接,,当时,请直接写出点的横坐标.
答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.且
15.
16.
17.或
18.
19.【解析】
;
,
解得,
解得,
则不等式组的解集为:,
所有整数解的和为.
20.解:条件
在和中,
≌.
21.解:一个学期参加综合实践活动的天数为天的人数占总人数的百分比为:
,
本次调查的总人数为:人,
一个学期参加综合实践活动的天数为天的人数为:
人,
补全频数分布直方图,如图所示:
众数是天,中位数为天.
故答案为:,.
天,
答:估计该市初二学生每学期参加综合实践活动的平均天数约为天.
22.解:为的外接圆,,
是直径,
在中,,,
,
的半径为.
如图中,连接,.
,,
,,
,
,
,
,
是等边三角形,
,
.
存在;
如图中,连接,.
是的中点,
,
,
点的运动轨迹以为直径的,
.
连接,,则,
是等边三角形,,
,
,
,
的最大值为.
23.解:在矩形中,
,
边中点的坐标为,
又曲线的图象经过点,
,
点在上,
点的横坐标为,
经过点,
点纵坐标为,
点坐标为;
由得,,,,
∽,
,即,
,
,即点的坐标为,
设直线的解析式为,而直线经过,,
,解得,
直线的解析式为.
24.证明:连接,如图,
为的切线,
,
,
,
,
;
证明:连接,如图,
为的切线,
,
,
,
.
,
,
.
在和中,
,
≌,
;
解:连接,,,,交于点,如图,
点为的中点,为的直径,
,
,
,
.
,
,
,
,
.
,
,
为的切线,
,
,
,
,
设圆的半径为,则,
,,
为的切线,
,
,
或不合题意,舍去,
,,
由知:≌,
,
,
,
,
∽,
,
设,则,
,.
为的直径,
,
,
∽,
,
,
解得:或不合题意,舍去,
,
由知:.
25..解:点,
,
,
,,
把,代入,
得:,
解得:,
抛物线的解析式为:;
过点作,交于点,过点作,交于点,如图所示:
设直线的解析式为,把,代入得:,
解得:,
直线的解析式为:,
同理可得:直线的解析式为:,
,
直线的解析式为:,
联立,
解得:,
点,
,
,,
,
,
,
,
,
,
∽,
,
即,
,
设,则,
,
,
,
当时,有最大值,
,
此时点的坐标为;
作轴,在点下方取,连接,取点关于轴的对称点,连接,如图所示:
则,,
,,
四边形为平行四边形,
,
根据轴对称可知:,
,
两点之间线段最短,
当、、三点在同一直线上时,最小,即最小,
为定值,
此时最小,且最小值为:;
,
抛物线的顶点坐标为,
将抛物线沿着射线方向平移个单位长度得到新抛物线,
,,
将抛物线向右平移个单位,向上平移个单位,正好得出新抛物线,
新抛物线的顶点坐标为,
新抛物线的解析式为:,
根据解析可知:当取得最大值时,,
,
轴,
,
,,
,,
,
作,点在轴正半轴上,过点作于点,如图所示:
则,
设,则,
为等腰直角三角形,
,
,
,
,
,,
,
,
∽,
,即,
解得:,
,
,,,
≌,
,
,
设直线的解析式为:,把代入得:,
解得:,
直线的解析式为:,
令,
解得:舍去;
当与轴的交点正好为关于轴的对称点时,,此时点符合题意,
设直线的解析式为:,
把代入得:,
解得:,
直线的解析式为:,
令,
解得:舍去;
综上分析可知:点的横坐标为或.
第8页,共18页
同课章节目录
