2025年江苏省小升初数学备考真题分类汇编专题六《概率与统计》(含解析)
文档属性
| 名称 | 2025年江苏省小升初数学备考真题分类汇编专题六《概率与统计》(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 18:38:18 | ||
图片预览



文档简介
2025学年小升初总复习真题分类汇编·江苏地区专版
专题六《概率与统计》
选择题 典例+压轴20题
填空题 典例+压轴10题
解答题 典例+压轴20题
一、选择题。
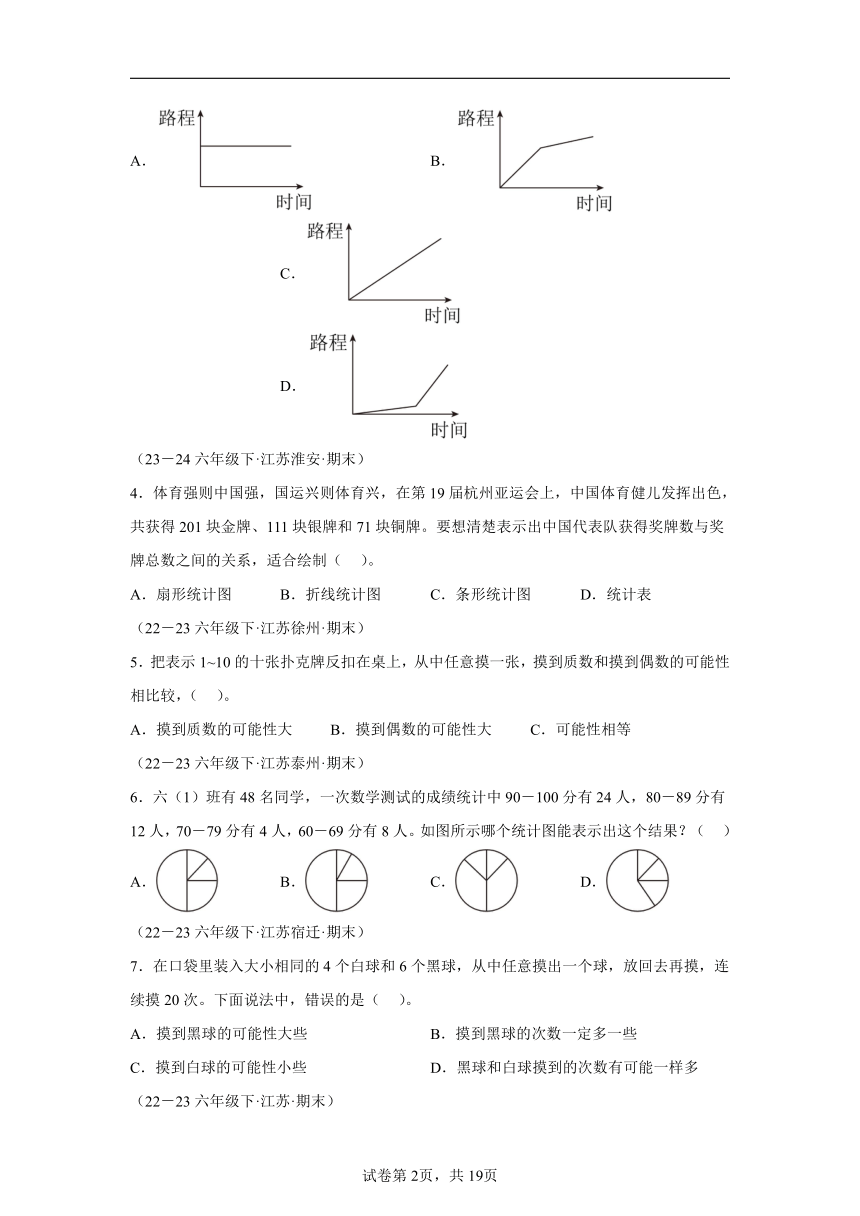
(23-24六年级下·江苏淮安·期末)
1.一个正方体,有1个面上写“1”,2个面上写“2”,3个面上写“3”,任意抛起这个正方体,落下后数字( )朝上的可能性最大。
A.1 B.2 C.3 D.无法确定
(22-23六年级下·江苏·期末)
2.有一幅家庭支出扇形统计图,表示伙食费支出的扇形圆心角是45°,那么伙食费支出占家庭总支出的( )。
A.45% B.25% C.12.5% D.50%
(22-23六年级下·江苏南京·期末)
3.小力觉得上学要迟到了,就跑步上学,跑累了,便走着到学校。下列( )幅图描述了他的行为。
A. B. C. D.
(23-24六年级下·江苏淮安·期末)
4.体育强则中国强,国运兴则体育兴,在第19届杭州亚运会上,中国体育健儿发挥出色,共获得201块金牌、111块银牌和71块铜牌。要想清楚表示出中国代表队获得奖牌数与奖牌总数之间的关系,适合绘制( )。
A.扇形统计图 B.折线统计图 C.条形统计图 D.统计表
(22-23六年级下·江苏徐州·期末)
5.把表示1~10的十张扑克牌反扣在桌上,从中任意摸一张,摸到质数和摸到偶数的可能性相比较,( )。
A.摸到质数的可能性大 B.摸到偶数的可能性大 C.可能性相等
(22-23六年级下·江苏泰州·期末)
6.六(1)班有48名同学,一次数学测试的成绩统计中90-100分有24人,80-89分有12人,70-79分有4人,60-69分有8人。如图所示哪个统计图能表示出这个结果?( )
A. B. C. D.
(22-23六年级下·江苏宿迁·期末)
7.在口袋里装入大小相同的4个白球和6个黑球,从中任意摸出一个球,放回去再摸,连续摸20次。下面说法中,错误的是( )。
A.摸到黑球的可能性大些 B.摸到黑球的次数一定多一些
C.摸到白球的可能性小些 D.黑球和白球摸到的次数有可能一样多
(22-23六年级下·江苏·期末)
8.钱老师在3月15日想要了解某商品的状况,他想要拨打服务热线,但是忘了一个数字,只记得是1231●,他任意拨打最后一个数字,正好打通电话的可能性是( )。
A.20% B.11.1% C.10% D.15%
(22-23六年级下·江苏·期末)
9.某校学生当天参与课后服务类型情况如图:校内作业400人,校内兴趣1000人,校外兴趣400人,校内托管200人,如将该校当天学生参与课后服务类型制成如图的扇形统计图,那么B表示( )。
A.校内兴趣 B.校外兴趣 C.校内托管 D.校内作业
(22-23六年级下·江苏南通·期末)
10.连续六个自然数,前三个数的和是90,那么后三个数的和是( )。
A.93 B.96 C.99 D.90
(22-23六年级下·江苏淮安·期末)
11.将分别标有数字2、3、4、5、6、7的六个同样小球放在一个不透明的袋子里,从袋子里任意摸出一个球,摸到标有( )的球可能性最小。
A.奇数 B.偶数 C.质数 D.合数
(22-23六年级下·江苏无锡·期末)
12.小华向花瓶中匀速注水,描述水面高度随注水时间变化而变化的情况如图,则这个花瓶是( )。
A. B. C. D.
(23-24六年级下·江苏苏州·期末)
13.一个正方体的六个面,有3个面上写“1”,2个面上写“2”,1个面上写“3”,抛起这个正方体,落下后数字“1”朝上的可能性( )。
A.最大 B.与数学“2”朝上的可能性相等
C.最小 D.与数学“3”朝上的可能性相等
(23-24六年级下·江苏苏州·期末)
14.4月23日是“世界读书日”,刘校长想了解全校学生去年阅读量的整体情况。以下信息中( )对他最有帮助。
A.去年全校人均阅读书籍16.4本。 B.三(2)班李浩平时不喜欢看书。
C.阅读之星王斌一年阅读书籍47本。 D.六年级借阅图书数量最多的是六(6)班。
(23-24六年级下·江苏苏州·期末)
15.如表,六年级四个班学生近视情况统计表,要对比四个班的近视人数,绘制( )统计图最合适。
班级 一班 二班 三班 四班
近视人数 20人 22人 34人 24人
A.条形 B.折线 C.扇形 D.无法确定
(23-24六年级下·江苏连云港·期末)
16.萍萍想通过一个调查来了解哪一种口味的冰淇淋在她的学校中最流行。如果她在学校中任意抽样,方法( )是最好的。
A.从每个班中抽10名学生 B.从女子垒球队中选一些成员
C.从男子篮球队中选一些成员 D.选一些有自己喜欢的冰淇淋口味的学生
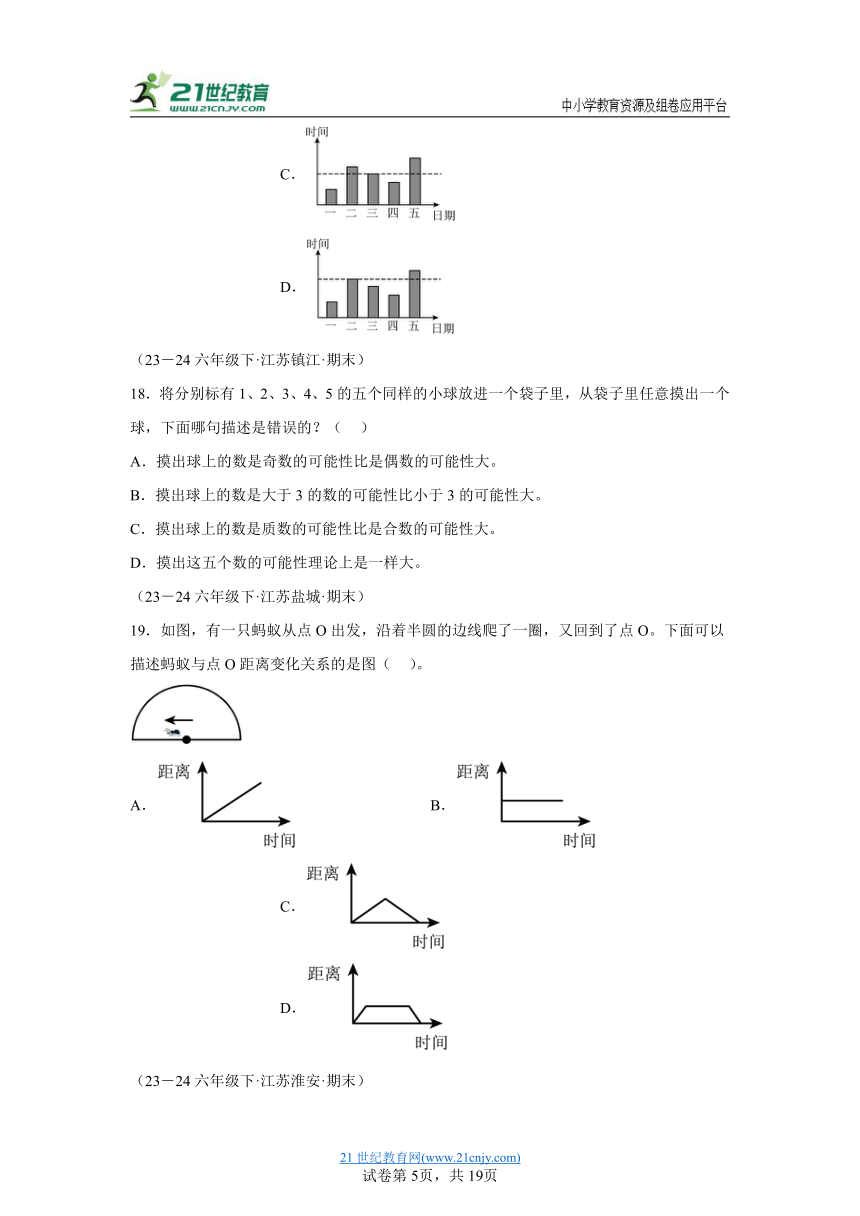
(23-24六年级下·江苏连云港·期末)
17.下面是小军周一到周五每天的运动时间统计图,图( )中的虚线表示小军这5天运动的平均时间。
A. B. C. D.
(23-24六年级下·江苏镇江·期末)
18.将分别标有1、2、3、4、5的五个同样的小球放进一个袋子里,从袋子里任意摸出一个球,下面哪句描述是错误的?( )
A.摸出球上的数是奇数的可能性比是偶数的可能性大。
B.摸出球上的数是大于3的数的可能性比小于3的可能性大。
C.摸出球上的数是质数的可能性比是合数的可能性大。
D.摸出这五个数的可能性理论上是一样大。
(23-24六年级下·江苏盐城·期末)
19.如图,有一只蚂蚁从点O出发,沿着半圆的边线爬了一圈,又回到了点O。下面可以描述蚂蚁与点O距离变化关系的是图( )。
A. B. C. D.
(23-24六年级下·江苏淮安·期末)
20.科学实验课上,同学们往一个玻璃容器中滴水(滴水速度相同,如图),四位同学将滴水时间和容器中水面高度变化情况绘制成示意图,其中正确的是( )。
A. B. C. D.
二、填空题。
(22-23六年级下·江苏·课前预习)
21.要清楚地描述数据的多少,选用( )统计图;要清楚地反映事物的增减变化情况,选用( )统计图;要清楚地表示出各部分数量占总数量的百分比,选用( )统计图。
(22-23六年级下·江苏无锡·期末)
22.小华在30米长的跑道上走路测试了三次,第一次走了74步,第二次走了78步,第三次走了73步。照这样算,小华沿400米跑道走一圈大约要走( )步。
(22-23六年级下·江苏扬州·期末)
23.如图是某校六年级学生上学出行方式情况统计图。已知由家长接送的有75人,步行的有 人,乘公交车和骑车的共有 人,家长接送的人数比乘公交车的少 %。
(22-23六年级下·江苏连云港·期末)
24.在一次科学课实验中,小菲同学记录一壶水加热过程中水温变化情况,并把它制作成了下面的统计图。
(1)加热前,水的温度是( )℃。
(2)水温从50℃上升到100℃用了( )分钟。
(3)烧开这壶水(达到100℃)一共用了( )分钟。
(4)如果继续加热到第10分钟,水温是( )℃。
(21-22六年级下·江苏苏州·期末)
25.下图是小明和弟弟两人进行100米赛跑的情况。
(1)从图上看,小明跑的路程和时间成( )比例。
(2)弟弟每秒跑( )米。
(23-24六年级下·江苏徐州·期末)
26.下图是学校红领巾广播站每星期播出各类节目的时间统计图。若《书香校园》每星期播出38分钟,则红领巾广播站一星期共播出( )分钟,《儿童大合唱》每星期播出的时间比《古诗欣赏》少( )分钟。
(23-24六年级下·江苏苏州·期末)
27.如图是一件毛线衣中各种材质占总质量的统计图,根据如图回答问题。
(1)棉的含量占这件衣服的( )%。
(2)( )的含量最多,( )的含量最少。
(3)这件毛线衣重200克,羊毛有( )克。
(4)如果羊毛含量120克,那么棉含量是( )克。
(23-24六年级下·福建福州·期末)
28.王阿姨从单位下班先到菜场买菜再回家。如图①和图②记录了她的行程。
(1)王阿姨从单位下班,先买菜再回家,一共用了( )分钟。
(2)王阿姨买菜后步行回家时,平均每分钟走( )米。
(22-23六年级下·江苏南京·期末)
29.图为林老师的移动硬盘目前的储存状态。
(1)林老师的移动硬盘中储存的( )最多,储存的( )和( )一样多。
(2)如果移动硬盘中可用空间是,那么总储存量大约是( )G。
(23-24六年级下·江苏南京·期末)
30.如图是某种食物中所含各种成分的统计图。如果食物有100克,那么其中含有脂肪 克,蛋白质 克。如果食物中含有200克碳水化合物,那么这份食物约有 克。(保留一位小数)
三、解答题。
(23-24六年级下·江苏·期末)
31.下边的图像表示甲、乙两辆汽车行驶的路程和时间的关系。
(1)甲汽车的速度是( )千米/分。
(2)行驶12千米路程,甲汽车比乙汽车少用( )分钟。
(3)两车同时出发,8分钟后甲汽车比乙汽车多行( )千米。
(22-23六年级下·江苏·期末)
32.六(1)班同学2023年上半年阅读课外书情况如下:共阅读360本,科普书占40%,小说占25%,漫画与童话各占10%,其他占15%。
(1)在图中表示出六(1)班同学阅读课外书情况。
(2)科普书比小说多阅读了多少本?
(23-24六年级下·江苏·期末)
33.六(1)班书橱里有320本书,分类情况如图。科普书和文艺书一共有多少本?学习指导书比科普书多多少本?
(22-23六年级下·江苏连云港·期末)
34.某市科学学科测试结果以等级形式呈现,分A、B、C、D四个等级。某校六年级进行了一次模拟测试,随机抽取部分学生的科学成绩进行调查统计,绘制成如图所示两幅不完整的统计图。
(1)这次模拟测试共抽取了( )名学生的科学成绩。
(2)将上面的条形统计图补充完整。
(3)如果该学校六年级共有800名学生,估计一下这次模拟测试有( )名同学的科学成绩等级为A。
(22-23六年级下·江苏宿迁·期末)
35.今年的“世界环境日”,某校环保兴趣小组对全校部分师生进行调查后,制成了下面两个还不完整的统计图。其中:
A:能将垃圾放到规定的地方,而且还考虑垃圾的分类;
B:能将垃圾放到规定的地方,但不考虑垃圾的分类;
C:偶尔会将垃圾放到规定的地方;
D:随手乱扔垃圾。
(1)该校课外活动小组共调查了多少人?在调查的人中,偶尔会将垃圾放到规定地方的有多少人?
(2)照这样计算,如果该校共有师生2600人,那么随手乱扔垃圾的约有多少人?
(22-23六年级下·江苏宿迁·期末)
36.如图是学校图书馆的故事书、科技书和连环画三类图书的统计图,已知这三类图书共有2000本。看图回答下面问题:
(1)故事书占总数的百分之几?
(2)学校图书馆哪类书最少,是多少本?
(3)故事书比连环画多百分之几?
(22-23六年级下·江苏无锡·期末)
37.某学校为组建校内课后服务小组,随机抽取了部分同学进行兴趣爱好的调查。将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)学校这次调查共抽取了( )名学生;
(2)在条形统计图中,把喜欢书法的人数用直条表示出来;
(3)喜欢“音乐”的人数在扇形统计图中所占圆心角度数为( );
(4)若该校共有学生1200名,请你估计该校约有名学生喜欢足球?
(22-23六年级下·江苏淮安·期末)
38.今年6月22日是端午节,某小学在节前就学生对端午节文化习俗了解情况进行了随机调查,了解程度分为:A很了解、B比较了解、C了解较少、D不了解;并将调查结果绘制成下图所示不完整的统计图。
(1)在实际调查收集数据的过程中,下面方法中( )是最好的。
A.以一个年级的学生为调查对象 B.从每个班中随机抽10名学生调查
C.以学校合唱队成员为调查对象 D.选一些对端午节文化习俗有了解的学生
(2)本次共调查了( )人,对端午节文化习俗“不了解”的占总人数的( )%。
(3)本次调查的学生中对端午节文化习俗“了解较少”的有( )人。请根据数据用直条(直条内画上斜线)将条形统计图补充完整。
(4)如果这所小学共有学生2000人,你估计全校学生对端午节文化习俗“比较了解”的大约有( )人。
(22-23六年级下·江苏南通·期末)
39.王阿姨从单位下班先到菜场买菜,再回家。下面图①和图②记录了她的行程。
(1)王阿姨从单位下班,先买菜再回家,一共用了多少分钟?
(2)王阿姨买菜后步行回家时,平均每分钟走多少米?
(22-23六年级下·江苏盐城·期末)
40.新明小学于5月份隆重举行了第四届数学文化节。文化节期间,学校为同学们安排了丰富多彩的数学活动,每人只参与其中一项。志愿者小明统计了部分同学参与活动的情况,并绘制了如图所示统计图,其中条形统计图不完整。请根据图中的信息,回答下列问题。
(1)小明共统计了( )人。
(2)在被统计的同学中,参与“趣味运动会”的有( )人。
(3)若该校共有1170名学生,请根据以上数据推算出该校约有多少人参加“真人五子棋”。(通过计算说明)
(23-24六年级下·江苏无锡·期末)
41.某小学六年级学生参加社团活动,人数分布情况如图所示(每人都参加且只参加了一个社团活动)。已知美术社团有160人,六年级一共有多少人?
(23-24六年级下·江苏泰州·期末)
42.研学结束后,48名队员都提交了研学报告。老师根据队员的研学报告作出评价,并绘制了以下两个不完整的统计图。
六(1)中队研学报告评价等级条形统计图
六(1)中队研学报告评价等级扇形统计图
请根据以上提供的信息解答下列问题。(两幅不完整的统计图仅供数据分析,不需补充完整。)
(1)获A等级的人数占总人数的( )%(百分号前保留一位小数),获B等级的有( )人。
(2)如果获C等级的人数比获D等级的多,获D等级有多少人?
(23-24六年级下·江苏徐州·期末)
43.李明家5月份水电费、燃气费、电话费和收视费文出情况如下图。
(1)李明家四项支出一共多少元?
(2)收视费比水电费少支出百分之几?
(3)把条形图补充完整。
(23-24六年级下·江苏苏州·期末)
44.下图是昆山某商场2023年冰箱销售情况,相关信息如下:
(1)2023年一共卖出( )台冰箱;第一季度卖出的冰箱是全年的( )%,第二季度占全年的( )%。
(2)根据上面图中信息,将上面条形统计图填写完整。
(3)算一算,这个商场第一季度比第三季度少销售冰箱少百分之几?(百分号前保留一位小数)
(23-24六年级下·江苏徐州·期末)
45.科技小组的甲、乙两队进行无人机穿越障碍比赛,每人穿越15个障碍。下面的统计图表示他们越过障碍的个数。
(1)甲、乙两队谁的比赛成绩好?请说明理由。
(2)如果乙队想超过甲队,那么新加入的⑥号队员至少要穿过多少个障碍?
(23-24六年级下·江苏连云港·期末)
46.小强记录了一杯水加热过程中水温变化情况,数据如下表:
实验记录单2024年6月
时间/分 0 1 2 3 4 5 6 7 8 9 10 …
温度/℃ 16 25 37 54 69 84 90 94 97 98 100 …
水加热温度变化情况统计图
(1)根据实验数据完成上面的折线统计图。
(2)加热前,水的温度是( )。
(3)通过折线统计图可以看出,在加热过程中,水温上升的趋势是( )。(填“先慢后快”或“先快后慢”)
(4)预测一下,如果加热到第11分钟,水温大约是( )。
(23-24六年级下·江苏宿迁·期末)
47.端午节期间,阳光小学就学生对端午节习俗的了解情况进行了随机调查(了解程度:A很了解;B比较了解;C了解较少;D不了解),并将调查结果绘制成如下统计图。
阳光小学学生对端午节文化习俗了解情况扇形统计图 阳光小学学生对端午节文化习俗了解情况条形统计图
(1)调查时,如果在学校中任意抽样,那么方法( )是最好的。
A. 从每个班随机抽10名学生 B. 从女子舞蹈队中选一些队员
C. 从男子排球队中选一些队员 D. 选一些对端午节文化习俗有了解的学生
(2)本次调查共调查了( )人,调查的学生中对端午节文化习俗“很了解”的人数占总人数的( )%。
(3)本次调查的学生中对端午节文化习俗“了解较少”的有( )人。请将条形统计图补充完整。
(4)若阳光小学共有学生2400人,估计全校所有学生对端午节文化习俗“比较了解”的有( )人。
(23-24六年级下·江苏盐城·期末)
48.学校为做好校内课后服务工作,针对学生兴趣爱好情况作了调查。被调查的学生按A(球类)、B(乐器类)、C(书法绘画类)、D(舞蹈类)四个类型进行统计,每个学生只选其中一类,然后绘制了如下两幅统计图:图1和图2。
(1)经检查图1是正确的,图2中A、B、C、D四类中有一类出现错误,有错误的是( )类,喜欢该类的学生应该有( )人。
(2)喜欢舞蹈类的人数在扇形统计图中所占圆心角度数为( )。
(3)喜欢B类的学生比喜欢D类的学生少( )%。
(4)如果从被调查的学生中随意抽取1名学生,那么这名学生喜欢( )类的可能性最大。
(23-24六年级下·江苏南京·期末)
49.李叔叔每个月的工资收入是元,如图是他五月份工资的安排情况统计图。
(1)购书费占工资的_________。
(2)李叔叔四、五月份的生活费之比为,四月份他的生活费是多少钱?(用比例解答)
(3)李叔叔将五月份的储蓄金存入银行,存期为两年定期,年利率为,到期支取时,他可以得到多少利息?
(22-23六年级下·江苏盐城·期末)
50.某城市的育才路(南北方向)和向阳路(东西方向)相交形成一个十字路口,下面是该十字路口日常情况下某一天部分时段的车流量统计表。阅读下表,回答后面的问题。
时段路名(方向) 7:00~8:00 10:00~11:00 13:00~14:00 16:00~17:00 19:00~20:00
育才路(南北方向) 356 257 174 388 90
向阳路(东西方向) 231 169 114 258 59
(1)根据上表,如果要统计该十字路口不同时段车流量的增减变化情况,应该绘制成________统计图;如果要统计某一时段车流量占全天车流量的百分比,应绘制成________统计图。
(2)19:00~20:00时段,向阳路(东西方向)的车流量大约是育才路(南北方向)车流量的百分之几?(百分号前保留一位小数)
(3)交通管理部门要根据车流量设定不同方向的红绿灯时长,根据统计的数据制定了以下四个方案,你认为最合理的方案是________。
A.南北方向、东西方向绿灯时长相等,都是60秒。
B.南北方向绿灯时长为60秒,东西方向绿灯时长为40秒。
C.南北方向绿灯时长为60秒,东西方向绿灯时长为20秒。
D.南北方向绿灯时长为20秒,东西方向绿灯时长为40秒。
(4)请写出你选择该方案的理由。
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
试卷第1页,共3页
《2024-2025学年江苏省苏教版六年级下册小升初备考真题分类汇编专题六《概率与统计》数学试卷》参考答案:
1.C
【分析】可能性的大小与数量的多少有关,数量越多,出现的可能性越大,据此解答。
【详解】3>2>1
即任意抛起这个正方体,落下后数字3朝上的可能性最大。
故答案为:C
2.C
【分析】伙食费支出所占圆心角大小占总圆心角(360°)的百分比即为伙食费支出在扇形统计图所占百分比,即用45°÷360°×100%解答。
【详解】45°÷360°×100%
=0.125×100%
=12.5%
有一幅家庭支出扇形统计图,表示伙食费支出的扇形圆心角是45°,那么伙食费支出占家庭总支出的12.5%。
故答案为:C
【点睛】此题主要考查扇形统计图中的百分数问题,熟练掌握求一个数是另一个数的百分之几的计算方法是解答本题的关键。
3.B
【分析】小力先跑步走,也就是先快,后慢,反映到统计图上是先陡后相对平缓,据此逐项分析解答。
【详解】
A.,观察图意可知,静止状态,不符合题意;
B.,先陡后相对平缓,即先快后慢,描述了小力的行为,符合题意;
C.,观察图意可知,速度保持不变,不符合题意;
D.,先平缓后陡,即先慢后快,不符合题意。
小力觉得上学要迟到了,就跑步上学,跑累了,便走着到学校。描述了他的行为。
故答案为:B
4.A
【分析】统计表以表格呈现数据,条形统计图以直条呈现数据,都能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;据此解答。
【详解】通过分析可得:要想清楚表示出中国代表队获得奖牌数与奖牌总数之间的关系,适合绘制扇形统计图。
故答案为:A
5.B
【分析】找出1~10中质数、偶数的个数,若个数相同,则可能性相等,若个数不同,则个数多的可能性大;据此解答。
【详解】1~10中质数有2、3、5、7共4个;偶数有2、4、6、8、10共5个。
4<5,所以摸到偶数的可能性大。
故答案为:B
【点睛】本题主要考查可能性的大小,找出质数、偶数的个数是解题的关键。
6.B
【分析】用“部分量÷总数量”算出各分数段人数占总人数的百分比,再根据部分占整体的百分比的大小选择即可。
【详解】90-100分所占的百分数:
24÷48×100%
=0.5×100%
=50%
80-89分所占的百分数:
12÷48×100%
=0.25×100%
=25%
70-79分所占的百分数:
4÷48×100%
≈0.08×100%
=8%
60-69分所占的百分数:
8÷48×100%
≈0.17×100%
=17%
90-100分所占的百分数为50%,因为50%是和1的一半,所以有一个扇形的面积是圆面积的一半,所以排除C和D,又因为70-79分所占的百分数为8%,60-69分所占的百分数为17%,8%近似17%的一半,所以有一个小扇形的面积近似另一个小扇形面积的一半,所以排除A。
故答案为:B
【点睛】本题考查扇形统计图的应用,注意:扇形统计图的特征是可以清楚的看出部分与整体的关系。
7.B
【分析】因为从中任意摸出一个球,放回去再摸,所以里面始终都是4个白球和6个黑球,因为黑球比白球多,那么摸到黑球的可能性大些,摸到白球的可能性小些,因为只摸了20次,次数较少,所以摸到黑球的次数可能多一些,黑球和白球摸到的次数也有可能一样多;据此解答。
【详解】由分析可知:
A.因为摸到黑球的可能性大些,所以此说法正确;
B.因为摸到黑球的次数可能多一些,所以此说法错误;
C.因为摸到白球的可能性小些,所以此说法正确;
D.因为黑球和白球摸到的次数有可能一样多,所以此说法正确。
故答案为:B
【点睛】本题考查可能性,摸球游戏中,条件相同情况下,哪种颜色的球较多,摸到哪种颜色球的可能性就越大。
8.C
【分析】最后一个数字可能是0,1,2,3、4,5,6,7,8,9这10个数字中的一个数字,他任意拨打一个数字,正好打通的可能性,即求1为10的百分之几,即1÷10×100%,据此解答。
【详解】1÷10×100%
=0.1×100%
=10%
钱老师在3月15日想要了解某商品的状况,他想要拨打服务热线,但是忘了一个数字,只记得是1231●,他任意拨打最后一个数字,正好打通电话的可能性是10%。
故答案为:C
【点睛】熟练掌握求一个数是另一个数的百分之几的计算方法是解答本题的关键。
9.A
【分析】根据求一个数是另一个数的百分之几的计算方法,用一个数÷另一个数×100%,分别求出校内作业人数、校内兴趣人数、校外兴趣人数、校内托管人数占总人数的百分比,再结合扇形统计图特征,即可得B表示的内容。
【详解】总人数:400+1000+400+200=2000(人)
校外兴趣小组:400÷2000×100%
=0.2×100%
=20%
校内兴趣小组:1000÷2000×100%
=0.5×100%
=50%
校内作业:400÷2000×100%
=0.2×100%
=20%
校内托管:200÷2000×100%
=0.1×100%
=10%
50%>20%=20%>10%,由于B占了总人数的一半,B表示校内兴趣。
故答案为:A
10.C
【分析】前三个数的和是90,根据“三个数的和数的个数=平均数”求出前三个数中间的数,为,进而得出前三个数和后三个数,然后求出和即可选择。
【详解】前三个数中间的数为:,所以前三个数为29,30,31
后三个数应为32,33,34
后三个数的和为:
故答案为:C
【点睛】根据总数、个数和平均数三者之间的关系求出前三个数中间的数,是解答此题的关键所在。
11.D
【分析】在自然数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数;一个数只有1和它本身两个因数,这个数叫做质数;一个数除了1和它本身两个因数,还有其他的因数,这个数叫做合数。不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。所以合数最少,摸到标有合数的球可能性最小。
【详解】奇数有3、5、7,共3个;偶数有2、4、6,共3个;质数有2、3、5、7,共4个;合数有4、6,共2个。
2<3<4
合数最少,摸到标有合数的球可能性最小。
故答案为:D
【点睛】本题主要考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
12.A
【分析】由图像可知,向容器中匀速注水时,随时间的增加,水面高度也增加,先是缓慢上升,然后很快上升,最后处趋于平缓。据此解答。
【详解】
A.,该容器水面上升缓慢,较快,趋于平稳,与图形相符,符合题意;
B.该容器水面上升较快,较慢,趋于平稳,与图形不符,不符合题意;
C.,该容器水面上升较快,趋于平稳,与图形不符,不符合题意;
D.,该容器水面上升较慢,较快,与图形不符,不符合题意。
小华向花瓶中匀速注水,描述水面高度随注水时间变化而变化的情况如图,则这个花瓶。
故答案为:A
【点睛】简单折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
13.A
【分析】要比较可能性的大小,可以直接比较写有三个数字的面数,因为有3个面上写“1”,2个面上写“2”,1个面上写“3”,3>2>1,所以抛起这个正方体,落下后数字“1”朝上的可能性最大,据此解答。
【详解】根据分析可知,3>2>1
所以落下后数字“1”朝上的可能性最大。
故答案为:A
14.A
【分析】根据题意,要了解全校学生年阅读量情况,注意关键词“全校”“年阅读量”,据此逐项分析。
【详解】A.去年全校人均阅读书籍16.4本;可以用16.4乘全校人数,即可知道全校学生年阅读量情况,符合题意;
B.三(2)班李浩平时不喜欢看书;只说明一个同学不喜欢看书,不代表其他同学不喜欢阅读,不符合题意;
C.阅读之星王斌一年阅读书籍47本;只说明王斌一个同学一年读书的本数,不代表全校学生读书的本数,不符合题意;
D.六年级借阅图书数量最多的是六(6)班,只是说明六(6)班借阅图书数量最多,不能说明其他年级借阅图书的数量,不符合题意。
4月23日是“世界读书日”,刘校长想了解全校学生去年阅读量的整体情况。以下信息中去年全校人均阅读书籍16.4本对他最有帮助。
故答案为:A
15.A
【分析】条形统计图可以反映数量的多少,条形高度越高,表示的数量越多。折线统计图可以反映数据的变化情况,扇形统计图可以反映部分和总体之间的百分比情况。
【详解】要对比四个班的近视人数,绘制条形统计图最合适。这样可以清晰看出哪个班近视的人数最多,哪个班近视的人数最少。
故答案为:A
16.A
【分析】抽样调查的定义:被调查的样本中的每个个体都有相等的被抽到的机会;据此逐项分析,进行解答。
【详解】A.从每个班中抽10名学生,有普遍性,符合题意;
B.从女子垒球队中选一些成员,没有普遍性,不符合题意;
C.从男子篮球队中选一些成员,没有普遍性,不符合题意;
D.选一些有自己喜欢的冰淇淋口味的学生,不符合任意抽样的方法,不符合题意。
萍萍想通过一个调查来了解哪一种口味的冰淇淋在她的学校中最流行。如果她在学校中任意抽样,方法从每个班中抽10名学生是最好的。
故答案为:A
17.C
【分析】根据平均数的意义,一组数据的平均数一定大于这组数据中的最小数,一定小于这组数据中的最大数,据此解答即可。
【详解】A.虚线表示的是最小的数,不能作为平均数;
B.图中的虚线表示的是第二小的数,其它三个数据都比平均数高挺多,所以不能作为平均数;
C.虚线表示的是第三小的数,能够作为平均数;
D.虚线表示的是第二大的数,最大的数比平均数多一点,不能够弥补其它比平均数少的部分,所以不能作为平均数。
故答案为:C
18.B
【分析】在1、2、3、4、5这五个数中,合数只有一个4,质数有三个2、3、5,1既不是质数也不是合数。奇数有三个1、3、5,偶数有两个2和4。在摸球活动中,哪种球的数量多,被摸出的可能性就大,据此逐项分析。
【详解】A.奇数有三个1、3、5,偶数有两个2和4。3>2,所以,摸出球上的数是奇数的可能性比是偶数的可能性大,原题说法正确。
B.大于3的数有两个4和5,小于3的数有两个1和2,2=2,所以,摸出球上的数是大于3的数的可能性等于小于3的可能性,原题说法错误。
C.合数只有一个4,质数有三个2、3、5,1<3,所以,摸出球上的数是质数的可能性比是合数的可能性大,原题说法正确。
D.标有1、2、3、4、5的球各一个,所以,摸出这五个数的可能性理论上是一样大,原题说法正确。
故答案为:B
19.D
【分析】蚂蚁从点O出发,沿着半径往左爬行时,蚂蚁与点O的距离越来越远,折线往上;当蚂蚁到达圆上,沿着圆爬行时,因为同一个圆的半径都相等,蚂蚁与点O的距离不变,折线平缓无变化;当蚂蚁沿着半径返回时,蚂蚁与点0的距离越来越近,折线往下,直至距离为0,据此分析。
【详解】
A.,没有反映出沿着圆爬行时,蚂蚁与点O的距离不变,和当蚂蚁沿着半径返回时,蚂蚁与点0的距离越来越近,排除;
B.,没有反映出沿着半径往左爬行时,蚂蚁与点O的距离越来越远,和当蚂蚁沿着半径返回时,蚂蚁与点0的距离越来越近,排除;
C.,没有反映出沿着圆爬行时,蚂蚁与点O的距离不变,排除
D. 可以描述蚂蚁与点O距离变化关系。
故答案为:D
20.D
【分析】容器的形状下宽上窄,水上升的高度会先慢后快,图像表现为先缓后陡;一段时间后,因为容器最上面一段宽度不变,则水上升的高度很明显,图像表现为很陡。据此分析解答。
【详解】
A.,由于容器的形状是下宽上窄,所以水的深度上升是先慢后快;表现出的图形为先缓,后陡,本图表现出的图形为先陡,后缓,不符合题意;
B.,由于容器的形状是下宽上窄,所以水的深度上升是先慢后快;表现出的图形为先缓,后陡,本图表现的图形为一直缓,不符合题意;
C.,由于容器的形状是下宽上窄,所以水的深度上升是先慢后快,本图表现的图形为一直陡,不符合题意;
D.,容器的形状下宽上窄,水上升的高度会先慢后快,图像表现为先缓,后陡,符合题意。
科学实验课上,同学们往一个玻璃容器中滴水(滴水速度相同,如图),四位同学将滴水时间和容器中水面高度变化情况绘制成示意图,其中正确的是。
故答案为:D
21. 条形 折线 扇形
【分析】根据各个统计图的特点,结合统计需求,直接填空即可。
【详解】要清楚地描述数据的多少,选用条形统计图;要清楚地反映事物的增减变化情况,选用折线统计图;要清楚地表示出各部分数量占总数量的百分比,选用扇形统计图。
【点睛】本题考查了统计图的选择,掌握常见统计图的特点是解题的关键。
22.1000
【分析】先求出3次的平均数,然后再求出沿400米跑道走一圈大约要走多少步即可。
【详解】(74+78+73)÷3÷30×400
=225÷3÷30×400
=2.5×400
=1000(步)
小华沿400米跑道走一圈大约要走1000步。
【点睛】熟练掌握平均数的含义和求法,是解答此题的关键。
23. 200 225 40
【分析】扇形统计图是把某校六年级学生的总人数看作单位“1”,用360°表示,其中乘公交车的人数用90°表示,根据求一个数是另一个数的百分之几,用除法计算,用90°÷360°=25%,可知乘公交车的人数是总人数的25%,观察可知,家长接送的人数是总人数的,根据已知一个数的百分之几是多少,求这个数用除法计算,用家长接送的人数除以其对应的百分率可得总人数,再根据求一个数的百分之几是多少,用乘法计算,用总人数分别乘步行人数对应的百分率可分别得步行人数,再用总人数减步行人数再减家长接送人数得乘公交车和骑车的人数,再用总人数乘25%得乘公交车人数,最后根据求一个数比另一个数少百分之几,用少的数量除以另一个数即可得解。
【详解】1-20%-40%-25%=15%
75÷15%=500(人)
步行人数:500×40%=200(人)
乘公交车和骑车的人数:500-200-75=225(人)
500×25%=125(人)
(125-75)÷125
=50÷125
=40%
如图是某校六年级学生上学出行方式情况统计图。已知由家长接送的有75人,步行的有200人,乘公交车和骑车的共有225人,家长接送的人数比乘公交车的少40%。
24.(1)10
(2)3
(3)9
(4)100
【分析】(1)观察此统计图,横轴表示的是加热的时间,纵轴表示的是温度,在时间为0时对应的温度是10℃,由此得出未加热时水温是10℃;
(2)50℃对应的时间是6分,100℃对应的时间是9分,9-6=3(分);
(3)结合水烧开表示水温为100℃,找出水温是100℃对应的时间,即可解答题目。
(4)水沸点是100℃,如果继续加热到第10分钟,水温仍是100℃。
【详解】(1)加热前,水的温度是10℃。
(2)水温从50℃上升到100℃用了3分钟。
(3)烧开这壶水(达到100℃)一共用了9分钟。
(4)如果继续加热到第10分钟,水温是100℃。
【点睛】此题考查的目的是理解在折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
25.(1)正
(2)3
【分析】(1)根据正比例的意义,两种相关联的量,一种量变化另一种量也随着变化,两种量中相对应的两个数的比值一定,这两种量成正比例关系;从图上看,小明跑的路程和时间比是20∶5=40∶10=60∶15=4(一定),所以小明跑的路程和时间成正比例;
(2)根据“速度=路程÷时间”求出弟弟每秒跑的路程,据此解答。
【详解】(1)
如图所示,(一定),所以小明跑的路程和时间成正比例。
(2)60÷20=3(米)
所以,弟弟每秒跑3米。
【点睛】掌握正比例的意义并且能够根据折线统计图提供的信息解决有关的实际问题是解答题目的关键。
26. 100 5
【分析】将播出总时间看作单位“1”,《书香校园》播出时间÷对应百分率=播出总时间;播出总时间×《儿童大合唱》和《古诗欣赏》对应百分率的差=《儿童大合唱》比《古诗欣赏》少播出的时间。
【详解】38÷38%=38÷0.38=100(分钟)
100×(21%-16%)
=100×0.05
=5(分钟)
红领巾广播站一星期共播出100分钟,《儿童大合唱》每星期播出的时间比《古诗欣赏》少5分钟。
27.(1)7
(2) 羊毛 棉
(3)120
(4)14
【分析】(1)把这件衣服总质量看作单位“1”,用1减去羊毛占总质量的百分比,减去兔毛占总质量的百分比,减去涤纶占总质量的百分比,即可求出棉占这件衣服总质量的百分比;
(2)比较羊毛、兔毛、棉、涤纶占总重量的百分比,即可解答;
(3)用这件毛衣的总重量×羊毛占这件衣服的总重量的百分比,即可求出羊毛的重量;
(4)把这件衣服的总重量看作单位“1”,羊毛占总重量的60%,对应的是120克,求单位“1”,用120÷60%,求出这件衣服的总重量。再用衣服的总质量×棉占衣服总质量的百分比,即可解答。
【详解】(1)1-60%-8%-25%
=40%-8%-25%
=32%-25%
=7%
棉的含量占这件衣服的7%。
(2)60%>25%>8%>7%,即羊毛含量>涤纶含量>兔毛含量>棉含量;
羊毛的含量最多,棉的含量最少。
(3)200×60%=120(克)
这件毛线衣重200克,羊毛有120克。
(4)120÷60%×7%
=200×7%
=14(克)
如果羊毛含量120克,那么棉含量是14克。
28.(1)60
(2)80
【分析】(1)根据扇形统计图可知,将全程用时看作单位“1”,因步行回家的扇形的圆心角是,即占全程用时的,那么坐公交到菜场和买菜的用时是全程的(1-)。根据折线统计图可知,坐公交到菜场和买菜一共用时45分钟。单位“1”未知,将45分钟除以对应的分率,即可求出全程用时;
(2)将全程用时减去坐公交和买菜一共的用时,求出步行回家用的时间。根据折线统计图,步行回家的路程是1.2千米,1千米=1000米,把单位千米转换为米,再根据“路程÷时间=速度”求出平均每分钟走多少米。
【详解】(1)45÷(1-)
=45÷
=60(分钟)
一共用了60分钟。
(2)60×=15(分钟)
1.2千米=1200米
1200÷15=80(米)
平均每分钟走80米。
29.(1) 照片 音乐 视频
(2)500
【分析】(1)比价数据,找出移动硬盘中储存最多的,储存一样多的;
(2)把总储存量看作单位“1”,可以空间占总储存量的20%,对应的是100G,求单位“1”,用100÷20%解答。
【详解】(1)50%>20%>15%=15%
林老师的移动硬盘中储存的照片最多,储存的音乐和视频一样多。
(2)100÷20%=500(G)
如果移动硬盘中可用空间是,那么总储存量大约是500G。
30. 16 8.3 266.7
【分析】(1)根据扇形图所示,脂肪含量占了16%,已知食物有100克,用食物总量乘脂肪含量百分比即可。
(2)根据扇形图所示,蛋白质含量8.3%,已知食物有100克,用食物总量乘蛋白质含量百分比即可。
(3)先求出碳水化合物的占比,1-(16%+8.3%+0.7%)即可,根据已知一个数的百分之几是多少,求这个数用除法,用200除得出的结果即可得到含有200克碳水化合物食物的总重量。
【详解】(1)100×16%=100×0.16=16(克)
其中含有脂肪16克;
(2)100×8.3%=100×0.083=8.3(克)
蛋白质8.3克。
(3)1-(16%+8.3%+0.7%)
=100%-25%
=75%
200÷75%=200÷0.75≈266.7(克)
那么这份食物约有266.7克。
31.(1)2
(2)6
(3)8
【分析】(1)根据“速度=路程÷时间”,由图可知,甲汽车8分钟行驶了16千米,所以,用16÷8即可求出甲汽车的速度;
(2)由图可知,甲车行驶12千米所用时间为6分,乙车行驶12千米所用时间为12分,两者所用时间作差即可求得甲汽车比乙汽车少用多少分钟;
(3)由图可知,8分钟后甲汽车行驶了16千米,乙汽车行驶了8千米,两者所行驶路程作差即可求得8分钟后甲汽车比乙汽车多行多少千米。
【详解】(1)16÷8=2(千米/分)
所以,甲汽车的速度是2千米/分。
(2)12-6=6(分钟)
所以,甲汽车比乙汽车少用6分钟。
(3)16-8=8(千米)
所以,两车同时出发,8分钟后甲汽车比乙汽车多行8千米。
32.(1)见详解
(2)54本
【分析】(1)根据题中提供的数据,绘制完整的扇形统计图;
(2)用阅读的总本数×科普书占的百分比,求出阅读科普书多少本,再用阅读总本数×小说占的百分比,求出小说阅读多少本,再用阅读科普书的本数-阅读小说的本数,即可解答。
【详解】
(1)
(2)360×40%-360×25%
=144-90
=54(本)
答:科普书比小说阅读多了54本。
【点睛】本题考查扇形统计图的应用,并且考查根据扇形统计图提供的信息解答问题的能力。
33.144本;64本
【分析】将书的总本数看作单位“1”,总本数×科普书和文艺书对应百分率的和=科普书和文艺书的本数;总本数×学习指导书和科普书对应百分率的差=学习指导书比科普书多的本数,据此列式解答。
【详解】320×(25%+20%)
=320×0.45
=144(本)
320×(45%-25%)
=320×0.2
=64(本)
答:科普书和文艺书一共有144本,学习指导书比科普书多64本。
34.(1)50;
(2)见详解;
(3)240
【分析】(1)把调测的总人数看作单位“1”,D等级的5人,占10%,根据已知一个数的百分之几是多少,求这个数,用除法解答。
(2)用总人数减去B、C、D各个等级的人数之和,进而求出A等级的人数,完成统计图。
(3)根据求一个数是另一个数的百分之几,先用除法求出等级A占总人数的百分之几,再依据求一个数的百分之几是多少,用乘法解答。
【详解】(1)因为:5÷10%=5÷0.1=50(名)
所以:这次模拟测试共抽取了50名学生的科学成绩。
(2)50-(22+8+5)
=50-35
=15(名)
统计图如下:
(3)15÷30=0.3=30%
800×30%=800×0.3=240(人)
所以:如果该学校六年级共有800名学生,估计一下这次模拟测试有240名同学的科学成绩等级为A。
【点睛】此题主要考查学生对扇形统计图、条形统计图特点及作用的掌握,关键是能够根据统计图提供的信息,解决有关的实际问题。
35.(1)300人;90人
(2)780人
【分析】(1)根据扇形统计图和条形统计图可知,把调查总人数看作单位“1”,其中A:能将垃圾放到规定的地方,而且还考虑垃圾的分类占总调查人数的50%,对应的是150人,求单位“1”,用150÷50%解答;再用总人数-能将垃圾放到规定的地方,而且还考虑垃圾的分类的人数- 能将垃圾放到规定的地方,但不考虑垃圾的分类的人数- 随手乱扔垃圾的人数,即可求出偶尔会将垃圾放到规定地方的人数。
(2)用调查随手乱扔垃圾的人数÷总调查的人数×100%,求出随手乱扔垃圾人数占总调查人数的百分比,再用2600×随手乱扔垃圾的人数占总人数的百分比,即可解答。
【详解】(1)150÷50%=300(人)
300-150-30-30
=150-30-30
=120-30
=90(人)
答:该校课外活动小组共调查了300人,在调查的人中,偶尔会将垃圾放到规定地方的有90人。
(2)90÷300×100%
=0.3×100%
=30%
2600×30%=780(人)
答:随手乱扔垃圾的约有780人。
【点睛】本题考查扇形统计图和条形统计图的应用,并且考查根据扇形统计图和条形统计图提供的信息解答问题的能力。
36.(1)30%;(2)连环画;500本;(3)20%
【分析】(1)把总数看作单位“1”,根据减法的意义,用1-45%-25%即可求出故事书占总数的百分之几;
(2)比较三种图书占的百分比,可知连环画的数量最少,根据百分数乘法的意义,用2000×25%即可求出连环画的本数;
(3)根据百分数乘法的意义,用2000×30%即可求出故事书的本数,根据求一个数比另一个数多百分之几,用相差数除以另一个数再乘100%,则用故事书的本数减去连环画的本数的差,除以连环画的本数再乘100%,即可求出故事书比连环画多百分之几。
【详解】(1)1-45%-25%=30%
答:故事书占总数的30%。
(2)25%<30%<45%
连环画最少;
2000×25%=500(本)
答:学校图书馆连环画的本数最少,是500本。
(3)2000×30%=600(本)
(600-500)÷500×100%
=100÷500×100%
=20%
答:故事书比连环画多20%。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
37.(1)100;
(2)见详解;
(3)72°;
(4)360名;
【分析】(1)用喜欢舞蹈的人数除以喜欢舞蹈的人数占总人数的百分数,就是学校这次调查共抽取的学生数。
(2)先求喜欢书法的人数所占的百分数,用1减去参加舞蹈、音乐、围棋和足球所占的总人数的百分数;再用总人数乘喜欢书法人数所占的百分数,就是喜欢书法的人数。
(3)圆心角的度数是360°,用喜欢音乐的人数所占的百分数乘360°,就是喜欢“音乐”的人数在扇形统计图中所占圆心角度数。
(4)用总人数乘喜欢足球人数所占的百分数,就是喜欢足球的人数。
【详解】(1)25÷25%
=25÷0.25
=100(人)
(2)1-25%-20%-10%-30%
=1-(25%+20%+10%+30%)
=1-85%
=15%
100×15%
=100×0.15
=15(人)
(3)360°×20%
=360°×0.2
=72°
喜欢“音乐”的人数在扇形统计图中所占圆心角度数为72°。
(4)1200×30%
=120×0.3
=360(人)
该校约有360名学生喜欢足球。
【点睛】此题主要考查的是如何观察扇形统计图和条形统计图并且从统计图中获取信息,然后再进行计算、解答即可。
38.(1)B;(2)400;5;(3)80;(4)800
【分析】(1)根据题意可知,从每个班中随机抽10名学生调查最合适;
(2)把调查总人数看作单位“1”,根据百分数除法的意义,用比较了解的人数除以比较了解的人数的百分比,即可求出调查总人数;再根据求一个数占另一个数的几分之几,用一个数除以另一个数再乘100%,则用不了解的人数除以总人数再乘100%就是不了解的占总人数的百分比;
(3)根据减法的意义,用总人数减A很了解、比较了解、不了解的人数就是了解较少的人数;
(4)把2000人看作单位“1”,根据百分数乘法的意义,用2000×40%即可求出全校学生对端午节文化习俗“比较了解”的大约人数。
【详解】(1)在实际调查收集数据的过程中,从每个班中随机抽10名学生调查是最好的。
(2)160÷40%=400(人)
20÷400×100%=5%
本次共调查了400人,对端午节文化习俗“不了解”的占总人数的5%。
(3)400-140-160-20=80(人)
本次调查的学生中对端午节文化习俗“了解较少”的有80人。
如图:
(4)2000×40%=800(人)
全校学生对端午节文化习俗“比较了解”的大约有800人。
【点睛】此题主要考查的是如何观察扇形统计图和条形统计图并且从统计图中获取信息,然后再进行计算、解答和画图。
39.(1)60分钟
(2)80米
【分析】(1)通过观察统计图可知,步行回家用的时间占总时间的,坐公交车到菜场和买菜用的时间占总时间的,坐公交车到菜场和买菜共用45分钟,根据已知一个数的百分之几是多少,求这个数,用除法求出总时间。
(2)首先根据求一个数的百分之几是多少用乘法求出步行回家用的时间,然后根据速度=路程时间,列式解答即可。
【详解】(1)
分钟)
答:一共用了60分钟。
(2)分钟)
千米米
米)
答:平均每分钟走80米。
【点睛】此题考查的目的是理解掌握扇形统计图、折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
40.(1)72
(2)16
(3)260人
【分析】(1)由扇形统计图可知,参加魔方超人赛的人数占参与统计总人数的,结合条形统计图可知,参加魔方超人赛的人数是12,根据已知一个数的几分之几是多少,求这个数,用除法解答;
(2)用参与活动的总人数减去参与真人五子棋、魔方超人赛、数学游园会、小论文答辩的人数和就是参与“趣味运动会”的人数;
(3)先用参加“真人五子棋”的人数除以小明统计的总人数,求出参加“真人五子棋”的人数占统计人数的几分之几,根据求一个数的几分之几是多少,用乘法解答;用该校的学生人数乘参加“真人五子棋”的人数占参加活动的人数的分率即可解答。
【详解】(1)12÷
=12×6
=72(人)
所以小明共统计了72人。
(2)72-(16+12+20+8)
=72-(28+28)
=72-56
=16(人)
所以参与“趣味运动会”的有16人。
(3)16÷72=
(人)
答:该校约有260人参加“真人五子棋”。
41.400人
【分析】把六年级学生人数看作单位“1”,用1减去合唱社团占六年级学生人数的百分比,减去足球社团占六年级人数的百分比,求出美术社团占六年级学生人数的百分比,对应的是美术社团人数160人,求出单位“1”,用160÷美术社团占六年级人数的百分比,即可解答。
【详解】160÷(1-34%-26%)
=160÷(66%-26%)
=160÷40%
=400(人)
答:六年级一共有400人。
42.(1)45.8;12
(2)6人
【分析】(1)将总人数看作单位“1”,获A等级的人数÷总人数=获A等级的人数占总人数的百分之几;观察扇形统计图,获B等级的占总人数的,总人数×获B等级的对应分率=获B等级的人数。
(2)总人数-获A等级的人数-获B等级的人数=获C等级和获D等级的总人数,将获D等级的人数看作单位“1”,获C等级的人数是获D等级的(1+),获C等级和获D等级的总人数是获D等级的人数的(1++1),获C等级和获D等级的总人数÷对应分率=获D等级的人数。
【详解】(1)22÷48≈0.458=45.8%
48×=12(人)
获A等级的人数占总人数的45.8%,获B等级的有12人。
(2)48-22-12=14(人)
14÷(1++1)
=14÷
=14×
=6(人)
答:获D等级有6人。
43.(1)600元;
(2)75%;
(3)见详解
【分析】(1)我们观察统计图可知,收视费占总支出的10%,对应的具体金额是60元,根据“总支出=部分量÷该部分量所占百分比”,求出总支出是多少钱;
(2)用水电费减去收视费求出差,再除以水电费即可解答;
(3)用总支出乘电话费占总支出的分率即可求出电话费支出的钱数,用总支出减去电话费、收视费、水电费的支出即可求出燃气费的支出,再补充统计图即可。
【详解】(1)60÷10%=600(元)
答:李明家四项支出一共600元。
(2)(240-60)÷240×100%
=180÷240×100%
=0.75×100%
=75%
答:收视费比水电费少支出75%。
(3)电话费:600×30%=180(元)
燃气费:600-180-240-60=120(元)
44.(1)800;22.5%;12.5%
(2)图见详解
(3)35.7%
【分析】(1)把全年一共卖出冰箱的台数看作单位“1”,第三季度占卖出冰箱的35%,对应的是280台,求单位“1”,用280÷35%解答;用第一季度卖出冰箱的台数÷全年一共卖出冰箱的台数×100%,求出第一季度卖出的冰箱占全年的百分比;用全年一共卖出冰箱的台数×第四季度占卖出冰箱的百分比,求出第四季度卖出冰箱的台数,再用全年一共卖出冰箱的台数-第一季度卖出冰箱的台数-第三季度卖出冰箱的台数-第四季度卖出冰箱的台数,求出第二季度卖出冰箱的台数,再除以全年卖出冰箱的台数,再乘100%,即可求出第二季度买出的冰箱占全年的百分比;
(2)用全年卖出冰箱的台数×第四季度卖出冰箱占全年的百分比,求出第四季度卖出冰箱的台数;用全年卖出冰箱的台数-第一季度卖出冰箱的台数-第三季度卖出冰箱的台数-第四季度卖出冰箱的台数,求出第二季度卖出冰箱的台数;补充完整的条形统计图;
(3)用第一季度卖出冰箱的台数与第三季度卖出冰箱的台数差,除以第三季度卖出冰箱的台数,再乘100%,即可求出第一季度比第三季度少销售冰箱少百分之几,据此解答。
【详解】(1)280÷35%=800(台)
180÷800×100%
=0.225×100%
=22.5%
800×30%=240(台)
(800-180-280-240)÷800×100%
=(620-280-240)÷800×100%
=(340-240)÷800×100%
=100÷800×100%
=0.125×100%
=12.5%
2023年一共卖出800台冰箱;第一季度卖出的冰箱是全年的22.5%%,第二季度占全年的12.5%。
(2)800×30%=240(台)
800-180-280-240
=620-280-240
=340-240
=100(台)
如图:
(3)(280-180)÷280×100%
=100÷280×100%
≈0.357×100%
=35.7%
答:这个商场第一季度比第三季度少销售冰箱少35.7%。
45.(1)甲队;理由见详解
(2)13个
【分析】(1)用甲队6名队员穿越障碍的总个数除以6,计算出甲队的平均成绩;用乙队5名队员穿越障碍的总个数除以5,计算出乙队的平均成绩;通过比较甲、乙两队的平均成绩来判断两队成绩的好坏;
(2)分别计算甲、乙两队的总成绩,乙队要想超过甲队,用(甲队的总成绩+1)减去乙队的总成绩,所得差即为⑥号队员至少要穿过障碍的个数。
【详解】(1)甲队的平均成绩:
(7+6+8+9+4+8)÷6
=42÷6
=7(个)
乙队的平均成绩:
(9+5+7+3+6)÷5
=30÷5
=6(个)
因为7>6,所以甲队的平均成绩大于乙队的平均成绩,因此甲队的比赛成绩好些。
答:甲队。理由是:甲队的平均成绩比乙队的平均成绩高。
(2)(7+6+8+9+4+8+1)-(9+5+7+3+6)
=43-30
=13(个)
答:新加入的⑥号队员至少要穿过13个障碍。
46.(1)见详解
(2)16
(3)先快后慢
(4)100
【分析】(1)根据绘制折线统计图的方法,先描点,在统计图上找到对应的数据,再连线即可;
(2)加热前,是指没有加热的时候,即时间是0分的时候,对应的水温是16℃。
(3)根据折线统计图可知,刚开始的水温上涨的非常快,到最后上涨的速度比较平缓;由此即可填空;
(4)由于在第10分钟的时候水温是100℃,水的沸点在100℃,所以第11分钟的时候,水温不会有变化,即还是100℃,据此即可填空。
【详解】(1)如下图所示:
(2)加热前,水的温度是16℃;
(3)通过折线统计图可以看出,在加热过程中,水温上升的趋势是先快后慢。
(4)预测一下,如果加热到第11分钟,水温大约是100。
47.(1)A
(2)400;35
(3)80;图见详解
(4)960
【分析】(1)抽样调查的定义:被调查的样本中的每个个体都有相等的被抽到的机会;据此逐项分析;
(2)用B比较了解的人数除以B比较了解的人数的百分比,就是调查的总人数;用“很了解”的人数除以总人数就是“很了解”的占总人数的百分比;
(3)用总人数减去A很了解、B比较了解、D不了解的人数就是“了解较少”的人数,即可求出本次调查中对端午节文化习俗“了解较少”的学生有多少人,然后再在条形统计图中画出直方图即可。
(4)用学校的总人数乘B比较了解的人数的百分比,即可求出全校所有学生对端午节文化习俗“比较了解”的有多少人。
【详解】(1)A.从每个班中抽10名学生,有普遍性,符合题意;
B.从女子舞蹈队中选一些队员,没有普遍性,不符合题意;
C.从男子排球队中选一些队员,没有普遍性,不符合题意;
D.选一些对端午节文化习俗有了解的学生,不符合任意抽样的方法,不符合题意。
故答案为:A
(2)160÷40%=400(人)
140÷400×100%
=0.35×100%
=35%
本次调查共调查了400人,被调查的学生中对端午节文化习俗“很了解”的占总人数的35%。
(3)400-140-160-20
=260-160-20
=100-20
=80(人)
所以本次调查中对端午节文化习俗“了解较少的学生有80人。
作图如下:
(4)2400×40%=960(人)
若阳光小学共有学生2400人,估计全校所有学生对端午节文化习俗“比较了解”的有960人。
48.(1)C;60
(2)90°
(3)40
(4)A
【分析】(1)由图1可知,C类比D类少,比B类多。而图2中,C类比B类和D类都多,则C类是错误的。由图1可知,A类有120人,占被调查的学生人数的40%,根据已知一个数的百分之几,求这个数,用120÷40%求出被调查的学生人数,再根据求一个数的百分之几,用乘法分别求出B、C、D的人数,再与图2中的人数进行比较,即可验证结论;
(2)圆心角的度数是360度,由图1可知,喜欢舞蹈类的人数占总人数的25%,把360度看作单位“1”,根据求一个数的百分之几是多少,用乘法解答;
(3)求喜欢B类的学生比喜欢D类的学生少百分之几,用两个百分率的差除以D类的百分率;列式:(25%-15%)÷25%计算即可。
(4)扇形统计图中哪种兴趣爱好所占的百分比最大,那么这名学生喜欢哪类的可能性最大;据此进行比较即可解答。
【详解】(1)120÷40%=300(人)
300×15%=45(人)
300×20%=60(人)
300×25%=75(人)
所以有错误的类是C类,喜欢该类的学生应该有60人。
(2)360×25%=90°
所以喜欢舞蹈类的人数在扇形统计图中所占圆心角度数为90°。
(3)(25%-15%)÷25%
=10%÷25%
=0.1÷0.25
=40%
所以喜欢B类的学生比喜欢D类的学生少40%。
(4)15%<20%<25%<40%
喜欢A类的学生占的百分率最大,所以这名学生喜欢A类的可能性最大。
49.(1)(2)元(3)元
【分析】(1)将五月份的工资看作单位“”,再用“”减去生活费、储蓄、其他、水电费房租费解答即可;
(2)根据五月份的工资为元,生活费所占百分数为可知五月份的生活费,再根据四月份与五月份的生活费之比为即可解答;
(3)根据五月份的工资为元,储存所占百分数为可知五月份储存的金额为,再根据利息本金年利率存期解答即可。
【详解】(1)
答:购书费占工资的;
(2)设四月份李叔叔的生活费为元,
答:四月份李叔叔的生活费为元;
(3)
(元)
答:他可以得到元利息。
【点睛】本题考查了扇形统计图,比例方程与实际问题,利息本金年利率存期,审清题意找准数量关系是解题的关键。
50.(1)折线;扇形
(2)65.6%
(3)B
(4)见详解
【分析】(1)条形统计图能清楚地表示出数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;扇形统计图表示部分与整体之间的关系;
(2)用向阳路(东西方向)的车流量÷育才路(南北方向)车流量的×100%,代入数据;
(3)(4)356÷231≈1.5,257÷169≈1.5,174÷114≈1.5,388÷258≈1.5,90÷59≈1.5,育才路(南北方向)车流量大约是向阳路(东西方向)的车流量的1.5倍,所以最合理的方案是南北方向绿灯时长是东西方向绿灯时长的1.5倍,据此解答即可。
【详解】(1)根据上表,如果要统计该十字路口不同时段车流量的增减变化情况,应该绘制成折线统计图;如果要统计某一时段车流量占全天车流量的百分比,应绘制成扇形统计图。
(2)59÷90×100%
≈0.656×100%
=65.6%
答:19:00~20:00时段,向阳路(东西方向)的车流量大约是育才路(南北方向)车流量的65.6%。
(3)60÷40=1.5
我认为最合理的方案是南北方向绿灯时长为60秒,东西方向绿灯时长为40秒。
故答案为:B
(4)我选择的方案的理由是:红绿灯的设置时长主要取决于路口的具体位置,交通流量,车道使用比例以及路面的行车条件等因素,育才路(南北方向)车流量大约是向阳路(东西方向)的车流量的1.5倍,所以选择南北方向绿灯时长大约是东西方向绿灯时长的1.5倍。
答案第1页,共2页
21世纪教育网(www.21cnjy.com)
答案第1页,共2页
专题六《概率与统计》
选择题 典例+压轴20题
填空题 典例+压轴10题
解答题 典例+压轴20题
一、选择题。
(23-24六年级下·江苏淮安·期末)
1.一个正方体,有1个面上写“1”,2个面上写“2”,3个面上写“3”,任意抛起这个正方体,落下后数字( )朝上的可能性最大。
A.1 B.2 C.3 D.无法确定
(22-23六年级下·江苏·期末)
2.有一幅家庭支出扇形统计图,表示伙食费支出的扇形圆心角是45°,那么伙食费支出占家庭总支出的( )。
A.45% B.25% C.12.5% D.50%
(22-23六年级下·江苏南京·期末)
3.小力觉得上学要迟到了,就跑步上学,跑累了,便走着到学校。下列( )幅图描述了他的行为。
A. B. C. D.
(23-24六年级下·江苏淮安·期末)
4.体育强则中国强,国运兴则体育兴,在第19届杭州亚运会上,中国体育健儿发挥出色,共获得201块金牌、111块银牌和71块铜牌。要想清楚表示出中国代表队获得奖牌数与奖牌总数之间的关系,适合绘制( )。
A.扇形统计图 B.折线统计图 C.条形统计图 D.统计表
(22-23六年级下·江苏徐州·期末)
5.把表示1~10的十张扑克牌反扣在桌上,从中任意摸一张,摸到质数和摸到偶数的可能性相比较,( )。
A.摸到质数的可能性大 B.摸到偶数的可能性大 C.可能性相等
(22-23六年级下·江苏泰州·期末)
6.六(1)班有48名同学,一次数学测试的成绩统计中90-100分有24人,80-89分有12人,70-79分有4人,60-69分有8人。如图所示哪个统计图能表示出这个结果?( )
A. B. C. D.
(22-23六年级下·江苏宿迁·期末)
7.在口袋里装入大小相同的4个白球和6个黑球,从中任意摸出一个球,放回去再摸,连续摸20次。下面说法中,错误的是( )。
A.摸到黑球的可能性大些 B.摸到黑球的次数一定多一些
C.摸到白球的可能性小些 D.黑球和白球摸到的次数有可能一样多
(22-23六年级下·江苏·期末)
8.钱老师在3月15日想要了解某商品的状况,他想要拨打服务热线,但是忘了一个数字,只记得是1231●,他任意拨打最后一个数字,正好打通电话的可能性是( )。
A.20% B.11.1% C.10% D.15%
(22-23六年级下·江苏·期末)
9.某校学生当天参与课后服务类型情况如图:校内作业400人,校内兴趣1000人,校外兴趣400人,校内托管200人,如将该校当天学生参与课后服务类型制成如图的扇形统计图,那么B表示( )。
A.校内兴趣 B.校外兴趣 C.校内托管 D.校内作业
(22-23六年级下·江苏南通·期末)
10.连续六个自然数,前三个数的和是90,那么后三个数的和是( )。
A.93 B.96 C.99 D.90
(22-23六年级下·江苏淮安·期末)
11.将分别标有数字2、3、4、5、6、7的六个同样小球放在一个不透明的袋子里,从袋子里任意摸出一个球,摸到标有( )的球可能性最小。
A.奇数 B.偶数 C.质数 D.合数
(22-23六年级下·江苏无锡·期末)
12.小华向花瓶中匀速注水,描述水面高度随注水时间变化而变化的情况如图,则这个花瓶是( )。
A. B. C. D.
(23-24六年级下·江苏苏州·期末)
13.一个正方体的六个面,有3个面上写“1”,2个面上写“2”,1个面上写“3”,抛起这个正方体,落下后数字“1”朝上的可能性( )。
A.最大 B.与数学“2”朝上的可能性相等
C.最小 D.与数学“3”朝上的可能性相等
(23-24六年级下·江苏苏州·期末)
14.4月23日是“世界读书日”,刘校长想了解全校学生去年阅读量的整体情况。以下信息中( )对他最有帮助。
A.去年全校人均阅读书籍16.4本。 B.三(2)班李浩平时不喜欢看书。
C.阅读之星王斌一年阅读书籍47本。 D.六年级借阅图书数量最多的是六(6)班。
(23-24六年级下·江苏苏州·期末)
15.如表,六年级四个班学生近视情况统计表,要对比四个班的近视人数,绘制( )统计图最合适。
班级 一班 二班 三班 四班
近视人数 20人 22人 34人 24人
A.条形 B.折线 C.扇形 D.无法确定
(23-24六年级下·江苏连云港·期末)
16.萍萍想通过一个调查来了解哪一种口味的冰淇淋在她的学校中最流行。如果她在学校中任意抽样,方法( )是最好的。
A.从每个班中抽10名学生 B.从女子垒球队中选一些成员
C.从男子篮球队中选一些成员 D.选一些有自己喜欢的冰淇淋口味的学生
(23-24六年级下·江苏连云港·期末)
17.下面是小军周一到周五每天的运动时间统计图,图( )中的虚线表示小军这5天运动的平均时间。
A. B. C. D.
(23-24六年级下·江苏镇江·期末)
18.将分别标有1、2、3、4、5的五个同样的小球放进一个袋子里,从袋子里任意摸出一个球,下面哪句描述是错误的?( )
A.摸出球上的数是奇数的可能性比是偶数的可能性大。
B.摸出球上的数是大于3的数的可能性比小于3的可能性大。
C.摸出球上的数是质数的可能性比是合数的可能性大。
D.摸出这五个数的可能性理论上是一样大。
(23-24六年级下·江苏盐城·期末)
19.如图,有一只蚂蚁从点O出发,沿着半圆的边线爬了一圈,又回到了点O。下面可以描述蚂蚁与点O距离变化关系的是图( )。
A. B. C. D.
(23-24六年级下·江苏淮安·期末)
20.科学实验课上,同学们往一个玻璃容器中滴水(滴水速度相同,如图),四位同学将滴水时间和容器中水面高度变化情况绘制成示意图,其中正确的是( )。
A. B. C. D.
二、填空题。
(22-23六年级下·江苏·课前预习)
21.要清楚地描述数据的多少,选用( )统计图;要清楚地反映事物的增减变化情况,选用( )统计图;要清楚地表示出各部分数量占总数量的百分比,选用( )统计图。
(22-23六年级下·江苏无锡·期末)
22.小华在30米长的跑道上走路测试了三次,第一次走了74步,第二次走了78步,第三次走了73步。照这样算,小华沿400米跑道走一圈大约要走( )步。
(22-23六年级下·江苏扬州·期末)
23.如图是某校六年级学生上学出行方式情况统计图。已知由家长接送的有75人,步行的有 人,乘公交车和骑车的共有 人,家长接送的人数比乘公交车的少 %。
(22-23六年级下·江苏连云港·期末)
24.在一次科学课实验中,小菲同学记录一壶水加热过程中水温变化情况,并把它制作成了下面的统计图。
(1)加热前,水的温度是( )℃。
(2)水温从50℃上升到100℃用了( )分钟。
(3)烧开这壶水(达到100℃)一共用了( )分钟。
(4)如果继续加热到第10分钟,水温是( )℃。
(21-22六年级下·江苏苏州·期末)
25.下图是小明和弟弟两人进行100米赛跑的情况。
(1)从图上看,小明跑的路程和时间成( )比例。
(2)弟弟每秒跑( )米。
(23-24六年级下·江苏徐州·期末)
26.下图是学校红领巾广播站每星期播出各类节目的时间统计图。若《书香校园》每星期播出38分钟,则红领巾广播站一星期共播出( )分钟,《儿童大合唱》每星期播出的时间比《古诗欣赏》少( )分钟。
(23-24六年级下·江苏苏州·期末)
27.如图是一件毛线衣中各种材质占总质量的统计图,根据如图回答问题。
(1)棉的含量占这件衣服的( )%。
(2)( )的含量最多,( )的含量最少。
(3)这件毛线衣重200克,羊毛有( )克。
(4)如果羊毛含量120克,那么棉含量是( )克。
(23-24六年级下·福建福州·期末)
28.王阿姨从单位下班先到菜场买菜再回家。如图①和图②记录了她的行程。
(1)王阿姨从单位下班,先买菜再回家,一共用了( )分钟。
(2)王阿姨买菜后步行回家时,平均每分钟走( )米。
(22-23六年级下·江苏南京·期末)
29.图为林老师的移动硬盘目前的储存状态。
(1)林老师的移动硬盘中储存的( )最多,储存的( )和( )一样多。
(2)如果移动硬盘中可用空间是,那么总储存量大约是( )G。
(23-24六年级下·江苏南京·期末)
30.如图是某种食物中所含各种成分的统计图。如果食物有100克,那么其中含有脂肪 克,蛋白质 克。如果食物中含有200克碳水化合物,那么这份食物约有 克。(保留一位小数)
三、解答题。
(23-24六年级下·江苏·期末)
31.下边的图像表示甲、乙两辆汽车行驶的路程和时间的关系。
(1)甲汽车的速度是( )千米/分。
(2)行驶12千米路程,甲汽车比乙汽车少用( )分钟。
(3)两车同时出发,8分钟后甲汽车比乙汽车多行( )千米。
(22-23六年级下·江苏·期末)
32.六(1)班同学2023年上半年阅读课外书情况如下:共阅读360本,科普书占40%,小说占25%,漫画与童话各占10%,其他占15%。
(1)在图中表示出六(1)班同学阅读课外书情况。
(2)科普书比小说多阅读了多少本?
(23-24六年级下·江苏·期末)
33.六(1)班书橱里有320本书,分类情况如图。科普书和文艺书一共有多少本?学习指导书比科普书多多少本?
(22-23六年级下·江苏连云港·期末)
34.某市科学学科测试结果以等级形式呈现,分A、B、C、D四个等级。某校六年级进行了一次模拟测试,随机抽取部分学生的科学成绩进行调查统计,绘制成如图所示两幅不完整的统计图。
(1)这次模拟测试共抽取了( )名学生的科学成绩。
(2)将上面的条形统计图补充完整。
(3)如果该学校六年级共有800名学生,估计一下这次模拟测试有( )名同学的科学成绩等级为A。
(22-23六年级下·江苏宿迁·期末)
35.今年的“世界环境日”,某校环保兴趣小组对全校部分师生进行调查后,制成了下面两个还不完整的统计图。其中:
A:能将垃圾放到规定的地方,而且还考虑垃圾的分类;
B:能将垃圾放到规定的地方,但不考虑垃圾的分类;
C:偶尔会将垃圾放到规定的地方;
D:随手乱扔垃圾。
(1)该校课外活动小组共调查了多少人?在调查的人中,偶尔会将垃圾放到规定地方的有多少人?
(2)照这样计算,如果该校共有师生2600人,那么随手乱扔垃圾的约有多少人?
(22-23六年级下·江苏宿迁·期末)
36.如图是学校图书馆的故事书、科技书和连环画三类图书的统计图,已知这三类图书共有2000本。看图回答下面问题:
(1)故事书占总数的百分之几?
(2)学校图书馆哪类书最少,是多少本?
(3)故事书比连环画多百分之几?
(22-23六年级下·江苏无锡·期末)
37.某学校为组建校内课后服务小组,随机抽取了部分同学进行兴趣爱好的调查。将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)学校这次调查共抽取了( )名学生;
(2)在条形统计图中,把喜欢书法的人数用直条表示出来;
(3)喜欢“音乐”的人数在扇形统计图中所占圆心角度数为( );
(4)若该校共有学生1200名,请你估计该校约有名学生喜欢足球?
(22-23六年级下·江苏淮安·期末)
38.今年6月22日是端午节,某小学在节前就学生对端午节文化习俗了解情况进行了随机调查,了解程度分为:A很了解、B比较了解、C了解较少、D不了解;并将调查结果绘制成下图所示不完整的统计图。
(1)在实际调查收集数据的过程中,下面方法中( )是最好的。
A.以一个年级的学生为调查对象 B.从每个班中随机抽10名学生调查
C.以学校合唱队成员为调查对象 D.选一些对端午节文化习俗有了解的学生
(2)本次共调查了( )人,对端午节文化习俗“不了解”的占总人数的( )%。
(3)本次调查的学生中对端午节文化习俗“了解较少”的有( )人。请根据数据用直条(直条内画上斜线)将条形统计图补充完整。
(4)如果这所小学共有学生2000人,你估计全校学生对端午节文化习俗“比较了解”的大约有( )人。
(22-23六年级下·江苏南通·期末)
39.王阿姨从单位下班先到菜场买菜,再回家。下面图①和图②记录了她的行程。
(1)王阿姨从单位下班,先买菜再回家,一共用了多少分钟?
(2)王阿姨买菜后步行回家时,平均每分钟走多少米?
(22-23六年级下·江苏盐城·期末)
40.新明小学于5月份隆重举行了第四届数学文化节。文化节期间,学校为同学们安排了丰富多彩的数学活动,每人只参与其中一项。志愿者小明统计了部分同学参与活动的情况,并绘制了如图所示统计图,其中条形统计图不完整。请根据图中的信息,回答下列问题。
(1)小明共统计了( )人。
(2)在被统计的同学中,参与“趣味运动会”的有( )人。
(3)若该校共有1170名学生,请根据以上数据推算出该校约有多少人参加“真人五子棋”。(通过计算说明)
(23-24六年级下·江苏无锡·期末)
41.某小学六年级学生参加社团活动,人数分布情况如图所示(每人都参加且只参加了一个社团活动)。已知美术社团有160人,六年级一共有多少人?
(23-24六年级下·江苏泰州·期末)
42.研学结束后,48名队员都提交了研学报告。老师根据队员的研学报告作出评价,并绘制了以下两个不完整的统计图。
六(1)中队研学报告评价等级条形统计图
六(1)中队研学报告评价等级扇形统计图
请根据以上提供的信息解答下列问题。(两幅不完整的统计图仅供数据分析,不需补充完整。)
(1)获A等级的人数占总人数的( )%(百分号前保留一位小数),获B等级的有( )人。
(2)如果获C等级的人数比获D等级的多,获D等级有多少人?
(23-24六年级下·江苏徐州·期末)
43.李明家5月份水电费、燃气费、电话费和收视费文出情况如下图。
(1)李明家四项支出一共多少元?
(2)收视费比水电费少支出百分之几?
(3)把条形图补充完整。
(23-24六年级下·江苏苏州·期末)
44.下图是昆山某商场2023年冰箱销售情况,相关信息如下:
(1)2023年一共卖出( )台冰箱;第一季度卖出的冰箱是全年的( )%,第二季度占全年的( )%。
(2)根据上面图中信息,将上面条形统计图填写完整。
(3)算一算,这个商场第一季度比第三季度少销售冰箱少百分之几?(百分号前保留一位小数)
(23-24六年级下·江苏徐州·期末)
45.科技小组的甲、乙两队进行无人机穿越障碍比赛,每人穿越15个障碍。下面的统计图表示他们越过障碍的个数。
(1)甲、乙两队谁的比赛成绩好?请说明理由。
(2)如果乙队想超过甲队,那么新加入的⑥号队员至少要穿过多少个障碍?
(23-24六年级下·江苏连云港·期末)
46.小强记录了一杯水加热过程中水温变化情况,数据如下表:
实验记录单2024年6月
时间/分 0 1 2 3 4 5 6 7 8 9 10 …
温度/℃ 16 25 37 54 69 84 90 94 97 98 100 …
水加热温度变化情况统计图
(1)根据实验数据完成上面的折线统计图。
(2)加热前,水的温度是( )。
(3)通过折线统计图可以看出,在加热过程中,水温上升的趋势是( )。(填“先慢后快”或“先快后慢”)
(4)预测一下,如果加热到第11分钟,水温大约是( )。
(23-24六年级下·江苏宿迁·期末)
47.端午节期间,阳光小学就学生对端午节习俗的了解情况进行了随机调查(了解程度:A很了解;B比较了解;C了解较少;D不了解),并将调查结果绘制成如下统计图。
阳光小学学生对端午节文化习俗了解情况扇形统计图 阳光小学学生对端午节文化习俗了解情况条形统计图
(1)调查时,如果在学校中任意抽样,那么方法( )是最好的。
A. 从每个班随机抽10名学生 B. 从女子舞蹈队中选一些队员
C. 从男子排球队中选一些队员 D. 选一些对端午节文化习俗有了解的学生
(2)本次调查共调查了( )人,调查的学生中对端午节文化习俗“很了解”的人数占总人数的( )%。
(3)本次调查的学生中对端午节文化习俗“了解较少”的有( )人。请将条形统计图补充完整。
(4)若阳光小学共有学生2400人,估计全校所有学生对端午节文化习俗“比较了解”的有( )人。
(23-24六年级下·江苏盐城·期末)
48.学校为做好校内课后服务工作,针对学生兴趣爱好情况作了调查。被调查的学生按A(球类)、B(乐器类)、C(书法绘画类)、D(舞蹈类)四个类型进行统计,每个学生只选其中一类,然后绘制了如下两幅统计图:图1和图2。
(1)经检查图1是正确的,图2中A、B、C、D四类中有一类出现错误,有错误的是( )类,喜欢该类的学生应该有( )人。
(2)喜欢舞蹈类的人数在扇形统计图中所占圆心角度数为( )。
(3)喜欢B类的学生比喜欢D类的学生少( )%。
(4)如果从被调查的学生中随意抽取1名学生,那么这名学生喜欢( )类的可能性最大。
(23-24六年级下·江苏南京·期末)
49.李叔叔每个月的工资收入是元,如图是他五月份工资的安排情况统计图。
(1)购书费占工资的_________。
(2)李叔叔四、五月份的生活费之比为,四月份他的生活费是多少钱?(用比例解答)
(3)李叔叔将五月份的储蓄金存入银行,存期为两年定期,年利率为,到期支取时,他可以得到多少利息?
(22-23六年级下·江苏盐城·期末)
50.某城市的育才路(南北方向)和向阳路(东西方向)相交形成一个十字路口,下面是该十字路口日常情况下某一天部分时段的车流量统计表。阅读下表,回答后面的问题。
时段路名(方向) 7:00~8:00 10:00~11:00 13:00~14:00 16:00~17:00 19:00~20:00
育才路(南北方向) 356 257 174 388 90
向阳路(东西方向) 231 169 114 258 59
(1)根据上表,如果要统计该十字路口不同时段车流量的增减变化情况,应该绘制成________统计图;如果要统计某一时段车流量占全天车流量的百分比,应绘制成________统计图。
(2)19:00~20:00时段,向阳路(东西方向)的车流量大约是育才路(南北方向)车流量的百分之几?(百分号前保留一位小数)
(3)交通管理部门要根据车流量设定不同方向的红绿灯时长,根据统计的数据制定了以下四个方案,你认为最合理的方案是________。
A.南北方向、东西方向绿灯时长相等,都是60秒。
B.南北方向绿灯时长为60秒,东西方向绿灯时长为40秒。
C.南北方向绿灯时长为60秒,东西方向绿灯时长为20秒。
D.南北方向绿灯时长为20秒,东西方向绿灯时长为40秒。
(4)请写出你选择该方案的理由。
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
试卷第1页,共3页
《2024-2025学年江苏省苏教版六年级下册小升初备考真题分类汇编专题六《概率与统计》数学试卷》参考答案:
1.C
【分析】可能性的大小与数量的多少有关,数量越多,出现的可能性越大,据此解答。
【详解】3>2>1
即任意抛起这个正方体,落下后数字3朝上的可能性最大。
故答案为:C
2.C
【分析】伙食费支出所占圆心角大小占总圆心角(360°)的百分比即为伙食费支出在扇形统计图所占百分比,即用45°÷360°×100%解答。
【详解】45°÷360°×100%
=0.125×100%
=12.5%
有一幅家庭支出扇形统计图,表示伙食费支出的扇形圆心角是45°,那么伙食费支出占家庭总支出的12.5%。
故答案为:C
【点睛】此题主要考查扇形统计图中的百分数问题,熟练掌握求一个数是另一个数的百分之几的计算方法是解答本题的关键。
3.B
【分析】小力先跑步走,也就是先快,后慢,反映到统计图上是先陡后相对平缓,据此逐项分析解答。
【详解】
A.,观察图意可知,静止状态,不符合题意;
B.,先陡后相对平缓,即先快后慢,描述了小力的行为,符合题意;
C.,观察图意可知,速度保持不变,不符合题意;
D.,先平缓后陡,即先慢后快,不符合题意。
小力觉得上学要迟到了,就跑步上学,跑累了,便走着到学校。描述了他的行为。
故答案为:B
4.A
【分析】统计表以表格呈现数据,条形统计图以直条呈现数据,都能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;据此解答。
【详解】通过分析可得:要想清楚表示出中国代表队获得奖牌数与奖牌总数之间的关系,适合绘制扇形统计图。
故答案为:A
5.B
【分析】找出1~10中质数、偶数的个数,若个数相同,则可能性相等,若个数不同,则个数多的可能性大;据此解答。
【详解】1~10中质数有2、3、5、7共4个;偶数有2、4、6、8、10共5个。
4<5,所以摸到偶数的可能性大。
故答案为:B
【点睛】本题主要考查可能性的大小,找出质数、偶数的个数是解题的关键。
6.B
【分析】用“部分量÷总数量”算出各分数段人数占总人数的百分比,再根据部分占整体的百分比的大小选择即可。
【详解】90-100分所占的百分数:
24÷48×100%
=0.5×100%
=50%
80-89分所占的百分数:
12÷48×100%
=0.25×100%
=25%
70-79分所占的百分数:
4÷48×100%
≈0.08×100%
=8%
60-69分所占的百分数:
8÷48×100%
≈0.17×100%
=17%
90-100分所占的百分数为50%,因为50%是和1的一半,所以有一个扇形的面积是圆面积的一半,所以排除C和D,又因为70-79分所占的百分数为8%,60-69分所占的百分数为17%,8%近似17%的一半,所以有一个小扇形的面积近似另一个小扇形面积的一半,所以排除A。
故答案为:B
【点睛】本题考查扇形统计图的应用,注意:扇形统计图的特征是可以清楚的看出部分与整体的关系。
7.B
【分析】因为从中任意摸出一个球,放回去再摸,所以里面始终都是4个白球和6个黑球,因为黑球比白球多,那么摸到黑球的可能性大些,摸到白球的可能性小些,因为只摸了20次,次数较少,所以摸到黑球的次数可能多一些,黑球和白球摸到的次数也有可能一样多;据此解答。
【详解】由分析可知:
A.因为摸到黑球的可能性大些,所以此说法正确;
B.因为摸到黑球的次数可能多一些,所以此说法错误;
C.因为摸到白球的可能性小些,所以此说法正确;
D.因为黑球和白球摸到的次数有可能一样多,所以此说法正确。
故答案为:B
【点睛】本题考查可能性,摸球游戏中,条件相同情况下,哪种颜色的球较多,摸到哪种颜色球的可能性就越大。
8.C
【分析】最后一个数字可能是0,1,2,3、4,5,6,7,8,9这10个数字中的一个数字,他任意拨打一个数字,正好打通的可能性,即求1为10的百分之几,即1÷10×100%,据此解答。
【详解】1÷10×100%
=0.1×100%
=10%
钱老师在3月15日想要了解某商品的状况,他想要拨打服务热线,但是忘了一个数字,只记得是1231●,他任意拨打最后一个数字,正好打通电话的可能性是10%。
故答案为:C
【点睛】熟练掌握求一个数是另一个数的百分之几的计算方法是解答本题的关键。
9.A
【分析】根据求一个数是另一个数的百分之几的计算方法,用一个数÷另一个数×100%,分别求出校内作业人数、校内兴趣人数、校外兴趣人数、校内托管人数占总人数的百分比,再结合扇形统计图特征,即可得B表示的内容。
【详解】总人数:400+1000+400+200=2000(人)
校外兴趣小组:400÷2000×100%
=0.2×100%
=20%
校内兴趣小组:1000÷2000×100%
=0.5×100%
=50%
校内作业:400÷2000×100%
=0.2×100%
=20%
校内托管:200÷2000×100%
=0.1×100%
=10%
50%>20%=20%>10%,由于B占了总人数的一半,B表示校内兴趣。
故答案为:A
10.C
【分析】前三个数的和是90,根据“三个数的和数的个数=平均数”求出前三个数中间的数,为,进而得出前三个数和后三个数,然后求出和即可选择。
【详解】前三个数中间的数为:,所以前三个数为29,30,31
后三个数应为32,33,34
后三个数的和为:
故答案为:C
【点睛】根据总数、个数和平均数三者之间的关系求出前三个数中间的数,是解答此题的关键所在。
11.D
【分析】在自然数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数;一个数只有1和它本身两个因数,这个数叫做质数;一个数除了1和它本身两个因数,还有其他的因数,这个数叫做合数。不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。所以合数最少,摸到标有合数的球可能性最小。
【详解】奇数有3、5、7,共3个;偶数有2、4、6,共3个;质数有2、3、5、7,共4个;合数有4、6,共2个。
2<3<4
合数最少,摸到标有合数的球可能性最小。
故答案为:D
【点睛】本题主要考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
12.A
【分析】由图像可知,向容器中匀速注水时,随时间的增加,水面高度也增加,先是缓慢上升,然后很快上升,最后处趋于平缓。据此解答。
【详解】
A.,该容器水面上升缓慢,较快,趋于平稳,与图形相符,符合题意;
B.该容器水面上升较快,较慢,趋于平稳,与图形不符,不符合题意;
C.,该容器水面上升较快,趋于平稳,与图形不符,不符合题意;
D.,该容器水面上升较慢,较快,与图形不符,不符合题意。
小华向花瓶中匀速注水,描述水面高度随注水时间变化而变化的情况如图,则这个花瓶。
故答案为:A
【点睛】简单折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
13.A
【分析】要比较可能性的大小,可以直接比较写有三个数字的面数,因为有3个面上写“1”,2个面上写“2”,1个面上写“3”,3>2>1,所以抛起这个正方体,落下后数字“1”朝上的可能性最大,据此解答。
【详解】根据分析可知,3>2>1
所以落下后数字“1”朝上的可能性最大。
故答案为:A
14.A
【分析】根据题意,要了解全校学生年阅读量情况,注意关键词“全校”“年阅读量”,据此逐项分析。
【详解】A.去年全校人均阅读书籍16.4本;可以用16.4乘全校人数,即可知道全校学生年阅读量情况,符合题意;
B.三(2)班李浩平时不喜欢看书;只说明一个同学不喜欢看书,不代表其他同学不喜欢阅读,不符合题意;
C.阅读之星王斌一年阅读书籍47本;只说明王斌一个同学一年读书的本数,不代表全校学生读书的本数,不符合题意;
D.六年级借阅图书数量最多的是六(6)班,只是说明六(6)班借阅图书数量最多,不能说明其他年级借阅图书的数量,不符合题意。
4月23日是“世界读书日”,刘校长想了解全校学生去年阅读量的整体情况。以下信息中去年全校人均阅读书籍16.4本对他最有帮助。
故答案为:A
15.A
【分析】条形统计图可以反映数量的多少,条形高度越高,表示的数量越多。折线统计图可以反映数据的变化情况,扇形统计图可以反映部分和总体之间的百分比情况。
【详解】要对比四个班的近视人数,绘制条形统计图最合适。这样可以清晰看出哪个班近视的人数最多,哪个班近视的人数最少。
故答案为:A
16.A
【分析】抽样调查的定义:被调查的样本中的每个个体都有相等的被抽到的机会;据此逐项分析,进行解答。
【详解】A.从每个班中抽10名学生,有普遍性,符合题意;
B.从女子垒球队中选一些成员,没有普遍性,不符合题意;
C.从男子篮球队中选一些成员,没有普遍性,不符合题意;
D.选一些有自己喜欢的冰淇淋口味的学生,不符合任意抽样的方法,不符合题意。
萍萍想通过一个调查来了解哪一种口味的冰淇淋在她的学校中最流行。如果她在学校中任意抽样,方法从每个班中抽10名学生是最好的。
故答案为:A
17.C
【分析】根据平均数的意义,一组数据的平均数一定大于这组数据中的最小数,一定小于这组数据中的最大数,据此解答即可。
【详解】A.虚线表示的是最小的数,不能作为平均数;
B.图中的虚线表示的是第二小的数,其它三个数据都比平均数高挺多,所以不能作为平均数;
C.虚线表示的是第三小的数,能够作为平均数;
D.虚线表示的是第二大的数,最大的数比平均数多一点,不能够弥补其它比平均数少的部分,所以不能作为平均数。
故答案为:C
18.B
【分析】在1、2、3、4、5这五个数中,合数只有一个4,质数有三个2、3、5,1既不是质数也不是合数。奇数有三个1、3、5,偶数有两个2和4。在摸球活动中,哪种球的数量多,被摸出的可能性就大,据此逐项分析。
【详解】A.奇数有三个1、3、5,偶数有两个2和4。3>2,所以,摸出球上的数是奇数的可能性比是偶数的可能性大,原题说法正确。
B.大于3的数有两个4和5,小于3的数有两个1和2,2=2,所以,摸出球上的数是大于3的数的可能性等于小于3的可能性,原题说法错误。
C.合数只有一个4,质数有三个2、3、5,1<3,所以,摸出球上的数是质数的可能性比是合数的可能性大,原题说法正确。
D.标有1、2、3、4、5的球各一个,所以,摸出这五个数的可能性理论上是一样大,原题说法正确。
故答案为:B
19.D
【分析】蚂蚁从点O出发,沿着半径往左爬行时,蚂蚁与点O的距离越来越远,折线往上;当蚂蚁到达圆上,沿着圆爬行时,因为同一个圆的半径都相等,蚂蚁与点O的距离不变,折线平缓无变化;当蚂蚁沿着半径返回时,蚂蚁与点0的距离越来越近,折线往下,直至距离为0,据此分析。
【详解】
A.,没有反映出沿着圆爬行时,蚂蚁与点O的距离不变,和当蚂蚁沿着半径返回时,蚂蚁与点0的距离越来越近,排除;
B.,没有反映出沿着半径往左爬行时,蚂蚁与点O的距离越来越远,和当蚂蚁沿着半径返回时,蚂蚁与点0的距离越来越近,排除;
C.,没有反映出沿着圆爬行时,蚂蚁与点O的距离不变,排除
D. 可以描述蚂蚁与点O距离变化关系。
故答案为:D
20.D
【分析】容器的形状下宽上窄,水上升的高度会先慢后快,图像表现为先缓后陡;一段时间后,因为容器最上面一段宽度不变,则水上升的高度很明显,图像表现为很陡。据此分析解答。
【详解】
A.,由于容器的形状是下宽上窄,所以水的深度上升是先慢后快;表现出的图形为先缓,后陡,本图表现出的图形为先陡,后缓,不符合题意;
B.,由于容器的形状是下宽上窄,所以水的深度上升是先慢后快;表现出的图形为先缓,后陡,本图表现的图形为一直缓,不符合题意;
C.,由于容器的形状是下宽上窄,所以水的深度上升是先慢后快,本图表现的图形为一直陡,不符合题意;
D.,容器的形状下宽上窄,水上升的高度会先慢后快,图像表现为先缓,后陡,符合题意。
科学实验课上,同学们往一个玻璃容器中滴水(滴水速度相同,如图),四位同学将滴水时间和容器中水面高度变化情况绘制成示意图,其中正确的是。
故答案为:D
21. 条形 折线 扇形
【分析】根据各个统计图的特点,结合统计需求,直接填空即可。
【详解】要清楚地描述数据的多少,选用条形统计图;要清楚地反映事物的增减变化情况,选用折线统计图;要清楚地表示出各部分数量占总数量的百分比,选用扇形统计图。
【点睛】本题考查了统计图的选择,掌握常见统计图的特点是解题的关键。
22.1000
【分析】先求出3次的平均数,然后再求出沿400米跑道走一圈大约要走多少步即可。
【详解】(74+78+73)÷3÷30×400
=225÷3÷30×400
=2.5×400
=1000(步)
小华沿400米跑道走一圈大约要走1000步。
【点睛】熟练掌握平均数的含义和求法,是解答此题的关键。
23. 200 225 40
【分析】扇形统计图是把某校六年级学生的总人数看作单位“1”,用360°表示,其中乘公交车的人数用90°表示,根据求一个数是另一个数的百分之几,用除法计算,用90°÷360°=25%,可知乘公交车的人数是总人数的25%,观察可知,家长接送的人数是总人数的,根据已知一个数的百分之几是多少,求这个数用除法计算,用家长接送的人数除以其对应的百分率可得总人数,再根据求一个数的百分之几是多少,用乘法计算,用总人数分别乘步行人数对应的百分率可分别得步行人数,再用总人数减步行人数再减家长接送人数得乘公交车和骑车的人数,再用总人数乘25%得乘公交车人数,最后根据求一个数比另一个数少百分之几,用少的数量除以另一个数即可得解。
【详解】1-20%-40%-25%=15%
75÷15%=500(人)
步行人数:500×40%=200(人)
乘公交车和骑车的人数:500-200-75=225(人)
500×25%=125(人)
(125-75)÷125
=50÷125
=40%
如图是某校六年级学生上学出行方式情况统计图。已知由家长接送的有75人,步行的有200人,乘公交车和骑车的共有225人,家长接送的人数比乘公交车的少40%。
24.(1)10
(2)3
(3)9
(4)100
【分析】(1)观察此统计图,横轴表示的是加热的时间,纵轴表示的是温度,在时间为0时对应的温度是10℃,由此得出未加热时水温是10℃;
(2)50℃对应的时间是6分,100℃对应的时间是9分,9-6=3(分);
(3)结合水烧开表示水温为100℃,找出水温是100℃对应的时间,即可解答题目。
(4)水沸点是100℃,如果继续加热到第10分钟,水温仍是100℃。
【详解】(1)加热前,水的温度是10℃。
(2)水温从50℃上升到100℃用了3分钟。
(3)烧开这壶水(达到100℃)一共用了9分钟。
(4)如果继续加热到第10分钟,水温是100℃。
【点睛】此题考查的目的是理解在折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
25.(1)正
(2)3
【分析】(1)根据正比例的意义,两种相关联的量,一种量变化另一种量也随着变化,两种量中相对应的两个数的比值一定,这两种量成正比例关系;从图上看,小明跑的路程和时间比是20∶5=40∶10=60∶15=4(一定),所以小明跑的路程和时间成正比例;
(2)根据“速度=路程÷时间”求出弟弟每秒跑的路程,据此解答。
【详解】(1)
如图所示,(一定),所以小明跑的路程和时间成正比例。
(2)60÷20=3(米)
所以,弟弟每秒跑3米。
【点睛】掌握正比例的意义并且能够根据折线统计图提供的信息解决有关的实际问题是解答题目的关键。
26. 100 5
【分析】将播出总时间看作单位“1”,《书香校园》播出时间÷对应百分率=播出总时间;播出总时间×《儿童大合唱》和《古诗欣赏》对应百分率的差=《儿童大合唱》比《古诗欣赏》少播出的时间。
【详解】38÷38%=38÷0.38=100(分钟)
100×(21%-16%)
=100×0.05
=5(分钟)
红领巾广播站一星期共播出100分钟,《儿童大合唱》每星期播出的时间比《古诗欣赏》少5分钟。
27.(1)7
(2) 羊毛 棉
(3)120
(4)14
【分析】(1)把这件衣服总质量看作单位“1”,用1减去羊毛占总质量的百分比,减去兔毛占总质量的百分比,减去涤纶占总质量的百分比,即可求出棉占这件衣服总质量的百分比;
(2)比较羊毛、兔毛、棉、涤纶占总重量的百分比,即可解答;
(3)用这件毛衣的总重量×羊毛占这件衣服的总重量的百分比,即可求出羊毛的重量;
(4)把这件衣服的总重量看作单位“1”,羊毛占总重量的60%,对应的是120克,求单位“1”,用120÷60%,求出这件衣服的总重量。再用衣服的总质量×棉占衣服总质量的百分比,即可解答。
【详解】(1)1-60%-8%-25%
=40%-8%-25%
=32%-25%
=7%
棉的含量占这件衣服的7%。
(2)60%>25%>8%>7%,即羊毛含量>涤纶含量>兔毛含量>棉含量;
羊毛的含量最多,棉的含量最少。
(3)200×60%=120(克)
这件毛线衣重200克,羊毛有120克。
(4)120÷60%×7%
=200×7%
=14(克)
如果羊毛含量120克,那么棉含量是14克。
28.(1)60
(2)80
【分析】(1)根据扇形统计图可知,将全程用时看作单位“1”,因步行回家的扇形的圆心角是,即占全程用时的,那么坐公交到菜场和买菜的用时是全程的(1-)。根据折线统计图可知,坐公交到菜场和买菜一共用时45分钟。单位“1”未知,将45分钟除以对应的分率,即可求出全程用时;
(2)将全程用时减去坐公交和买菜一共的用时,求出步行回家用的时间。根据折线统计图,步行回家的路程是1.2千米,1千米=1000米,把单位千米转换为米,再根据“路程÷时间=速度”求出平均每分钟走多少米。
【详解】(1)45÷(1-)
=45÷
=60(分钟)
一共用了60分钟。
(2)60×=15(分钟)
1.2千米=1200米
1200÷15=80(米)
平均每分钟走80米。
29.(1) 照片 音乐 视频
(2)500
【分析】(1)比价数据,找出移动硬盘中储存最多的,储存一样多的;
(2)把总储存量看作单位“1”,可以空间占总储存量的20%,对应的是100G,求单位“1”,用100÷20%解答。
【详解】(1)50%>20%>15%=15%
林老师的移动硬盘中储存的照片最多,储存的音乐和视频一样多。
(2)100÷20%=500(G)
如果移动硬盘中可用空间是,那么总储存量大约是500G。
30. 16 8.3 266.7
【分析】(1)根据扇形图所示,脂肪含量占了16%,已知食物有100克,用食物总量乘脂肪含量百分比即可。
(2)根据扇形图所示,蛋白质含量8.3%,已知食物有100克,用食物总量乘蛋白质含量百分比即可。
(3)先求出碳水化合物的占比,1-(16%+8.3%+0.7%)即可,根据已知一个数的百分之几是多少,求这个数用除法,用200除得出的结果即可得到含有200克碳水化合物食物的总重量。
【详解】(1)100×16%=100×0.16=16(克)
其中含有脂肪16克;
(2)100×8.3%=100×0.083=8.3(克)
蛋白质8.3克。
(3)1-(16%+8.3%+0.7%)
=100%-25%
=75%
200÷75%=200÷0.75≈266.7(克)
那么这份食物约有266.7克。
31.(1)2
(2)6
(3)8
【分析】(1)根据“速度=路程÷时间”,由图可知,甲汽车8分钟行驶了16千米,所以,用16÷8即可求出甲汽车的速度;
(2)由图可知,甲车行驶12千米所用时间为6分,乙车行驶12千米所用时间为12分,两者所用时间作差即可求得甲汽车比乙汽车少用多少分钟;
(3)由图可知,8分钟后甲汽车行驶了16千米,乙汽车行驶了8千米,两者所行驶路程作差即可求得8分钟后甲汽车比乙汽车多行多少千米。
【详解】(1)16÷8=2(千米/分)
所以,甲汽车的速度是2千米/分。
(2)12-6=6(分钟)
所以,甲汽车比乙汽车少用6分钟。
(3)16-8=8(千米)
所以,两车同时出发,8分钟后甲汽车比乙汽车多行8千米。
32.(1)见详解
(2)54本
【分析】(1)根据题中提供的数据,绘制完整的扇形统计图;
(2)用阅读的总本数×科普书占的百分比,求出阅读科普书多少本,再用阅读总本数×小说占的百分比,求出小说阅读多少本,再用阅读科普书的本数-阅读小说的本数,即可解答。
【详解】
(1)
(2)360×40%-360×25%
=144-90
=54(本)
答:科普书比小说阅读多了54本。
【点睛】本题考查扇形统计图的应用,并且考查根据扇形统计图提供的信息解答问题的能力。
33.144本;64本
【分析】将书的总本数看作单位“1”,总本数×科普书和文艺书对应百分率的和=科普书和文艺书的本数;总本数×学习指导书和科普书对应百分率的差=学习指导书比科普书多的本数,据此列式解答。
【详解】320×(25%+20%)
=320×0.45
=144(本)
320×(45%-25%)
=320×0.2
=64(本)
答:科普书和文艺书一共有144本,学习指导书比科普书多64本。
34.(1)50;
(2)见详解;
(3)240
【分析】(1)把调测的总人数看作单位“1”,D等级的5人,占10%,根据已知一个数的百分之几是多少,求这个数,用除法解答。
(2)用总人数减去B、C、D各个等级的人数之和,进而求出A等级的人数,完成统计图。
(3)根据求一个数是另一个数的百分之几,先用除法求出等级A占总人数的百分之几,再依据求一个数的百分之几是多少,用乘法解答。
【详解】(1)因为:5÷10%=5÷0.1=50(名)
所以:这次模拟测试共抽取了50名学生的科学成绩。
(2)50-(22+8+5)
=50-35
=15(名)
统计图如下:
(3)15÷30=0.3=30%
800×30%=800×0.3=240(人)
所以:如果该学校六年级共有800名学生,估计一下这次模拟测试有240名同学的科学成绩等级为A。
【点睛】此题主要考查学生对扇形统计图、条形统计图特点及作用的掌握,关键是能够根据统计图提供的信息,解决有关的实际问题。
35.(1)300人;90人
(2)780人
【分析】(1)根据扇形统计图和条形统计图可知,把调查总人数看作单位“1”,其中A:能将垃圾放到规定的地方,而且还考虑垃圾的分类占总调查人数的50%,对应的是150人,求单位“1”,用150÷50%解答;再用总人数-能将垃圾放到规定的地方,而且还考虑垃圾的分类的人数- 能将垃圾放到规定的地方,但不考虑垃圾的分类的人数- 随手乱扔垃圾的人数,即可求出偶尔会将垃圾放到规定地方的人数。
(2)用调查随手乱扔垃圾的人数÷总调查的人数×100%,求出随手乱扔垃圾人数占总调查人数的百分比,再用2600×随手乱扔垃圾的人数占总人数的百分比,即可解答。
【详解】(1)150÷50%=300(人)
300-150-30-30
=150-30-30
=120-30
=90(人)
答:该校课外活动小组共调查了300人,在调查的人中,偶尔会将垃圾放到规定地方的有90人。
(2)90÷300×100%
=0.3×100%
=30%
2600×30%=780(人)
答:随手乱扔垃圾的约有780人。
【点睛】本题考查扇形统计图和条形统计图的应用,并且考查根据扇形统计图和条形统计图提供的信息解答问题的能力。
36.(1)30%;(2)连环画;500本;(3)20%
【分析】(1)把总数看作单位“1”,根据减法的意义,用1-45%-25%即可求出故事书占总数的百分之几;
(2)比较三种图书占的百分比,可知连环画的数量最少,根据百分数乘法的意义,用2000×25%即可求出连环画的本数;
(3)根据百分数乘法的意义,用2000×30%即可求出故事书的本数,根据求一个数比另一个数多百分之几,用相差数除以另一个数再乘100%,则用故事书的本数减去连环画的本数的差,除以连环画的本数再乘100%,即可求出故事书比连环画多百分之几。
【详解】(1)1-45%-25%=30%
答:故事书占总数的30%。
(2)25%<30%<45%
连环画最少;
2000×25%=500(本)
答:学校图书馆连环画的本数最少,是500本。
(3)2000×30%=600(本)
(600-500)÷500×100%
=100÷500×100%
=20%
答:故事书比连环画多20%。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
37.(1)100;
(2)见详解;
(3)72°;
(4)360名;
【分析】(1)用喜欢舞蹈的人数除以喜欢舞蹈的人数占总人数的百分数,就是学校这次调查共抽取的学生数。
(2)先求喜欢书法的人数所占的百分数,用1减去参加舞蹈、音乐、围棋和足球所占的总人数的百分数;再用总人数乘喜欢书法人数所占的百分数,就是喜欢书法的人数。
(3)圆心角的度数是360°,用喜欢音乐的人数所占的百分数乘360°,就是喜欢“音乐”的人数在扇形统计图中所占圆心角度数。
(4)用总人数乘喜欢足球人数所占的百分数,就是喜欢足球的人数。
【详解】(1)25÷25%
=25÷0.25
=100(人)
(2)1-25%-20%-10%-30%
=1-(25%+20%+10%+30%)
=1-85%
=15%
100×15%
=100×0.15
=15(人)
(3)360°×20%
=360°×0.2
=72°
喜欢“音乐”的人数在扇形统计图中所占圆心角度数为72°。
(4)1200×30%
=120×0.3
=360(人)
该校约有360名学生喜欢足球。
【点睛】此题主要考查的是如何观察扇形统计图和条形统计图并且从统计图中获取信息,然后再进行计算、解答即可。
38.(1)B;(2)400;5;(3)80;(4)800
【分析】(1)根据题意可知,从每个班中随机抽10名学生调查最合适;
(2)把调查总人数看作单位“1”,根据百分数除法的意义,用比较了解的人数除以比较了解的人数的百分比,即可求出调查总人数;再根据求一个数占另一个数的几分之几,用一个数除以另一个数再乘100%,则用不了解的人数除以总人数再乘100%就是不了解的占总人数的百分比;
(3)根据减法的意义,用总人数减A很了解、比较了解、不了解的人数就是了解较少的人数;
(4)把2000人看作单位“1”,根据百分数乘法的意义,用2000×40%即可求出全校学生对端午节文化习俗“比较了解”的大约人数。
【详解】(1)在实际调查收集数据的过程中,从每个班中随机抽10名学生调查是最好的。
(2)160÷40%=400(人)
20÷400×100%=5%
本次共调查了400人,对端午节文化习俗“不了解”的占总人数的5%。
(3)400-140-160-20=80(人)
本次调查的学生中对端午节文化习俗“了解较少”的有80人。
如图:
(4)2000×40%=800(人)
全校学生对端午节文化习俗“比较了解”的大约有800人。
【点睛】此题主要考查的是如何观察扇形统计图和条形统计图并且从统计图中获取信息,然后再进行计算、解答和画图。
39.(1)60分钟
(2)80米
【分析】(1)通过观察统计图可知,步行回家用的时间占总时间的,坐公交车到菜场和买菜用的时间占总时间的,坐公交车到菜场和买菜共用45分钟,根据已知一个数的百分之几是多少,求这个数,用除法求出总时间。
(2)首先根据求一个数的百分之几是多少用乘法求出步行回家用的时间,然后根据速度=路程时间,列式解答即可。
【详解】(1)
分钟)
答:一共用了60分钟。
(2)分钟)
千米米
米)
答:平均每分钟走80米。
【点睛】此题考查的目的是理解掌握扇形统计图、折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
40.(1)72
(2)16
(3)260人
【分析】(1)由扇形统计图可知,参加魔方超人赛的人数占参与统计总人数的,结合条形统计图可知,参加魔方超人赛的人数是12,根据已知一个数的几分之几是多少,求这个数,用除法解答;
(2)用参与活动的总人数减去参与真人五子棋、魔方超人赛、数学游园会、小论文答辩的人数和就是参与“趣味运动会”的人数;
(3)先用参加“真人五子棋”的人数除以小明统计的总人数,求出参加“真人五子棋”的人数占统计人数的几分之几,根据求一个数的几分之几是多少,用乘法解答;用该校的学生人数乘参加“真人五子棋”的人数占参加活动的人数的分率即可解答。
【详解】(1)12÷
=12×6
=72(人)
所以小明共统计了72人。
(2)72-(16+12+20+8)
=72-(28+28)
=72-56
=16(人)
所以参与“趣味运动会”的有16人。
(3)16÷72=
(人)
答:该校约有260人参加“真人五子棋”。
41.400人
【分析】把六年级学生人数看作单位“1”,用1减去合唱社团占六年级学生人数的百分比,减去足球社团占六年级人数的百分比,求出美术社团占六年级学生人数的百分比,对应的是美术社团人数160人,求出单位“1”,用160÷美术社团占六年级人数的百分比,即可解答。
【详解】160÷(1-34%-26%)
=160÷(66%-26%)
=160÷40%
=400(人)
答:六年级一共有400人。
42.(1)45.8;12
(2)6人
【分析】(1)将总人数看作单位“1”,获A等级的人数÷总人数=获A等级的人数占总人数的百分之几;观察扇形统计图,获B等级的占总人数的,总人数×获B等级的对应分率=获B等级的人数。
(2)总人数-获A等级的人数-获B等级的人数=获C等级和获D等级的总人数,将获D等级的人数看作单位“1”,获C等级的人数是获D等级的(1+),获C等级和获D等级的总人数是获D等级的人数的(1++1),获C等级和获D等级的总人数÷对应分率=获D等级的人数。
【详解】(1)22÷48≈0.458=45.8%
48×=12(人)
获A等级的人数占总人数的45.8%,获B等级的有12人。
(2)48-22-12=14(人)
14÷(1++1)
=14÷
=14×
=6(人)
答:获D等级有6人。
43.(1)600元;
(2)75%;
(3)见详解
【分析】(1)我们观察统计图可知,收视费占总支出的10%,对应的具体金额是60元,根据“总支出=部分量÷该部分量所占百分比”,求出总支出是多少钱;
(2)用水电费减去收视费求出差,再除以水电费即可解答;
(3)用总支出乘电话费占总支出的分率即可求出电话费支出的钱数,用总支出减去电话费、收视费、水电费的支出即可求出燃气费的支出,再补充统计图即可。
【详解】(1)60÷10%=600(元)
答:李明家四项支出一共600元。
(2)(240-60)÷240×100%
=180÷240×100%
=0.75×100%
=75%
答:收视费比水电费少支出75%。
(3)电话费:600×30%=180(元)
燃气费:600-180-240-60=120(元)
44.(1)800;22.5%;12.5%
(2)图见详解
(3)35.7%
【分析】(1)把全年一共卖出冰箱的台数看作单位“1”,第三季度占卖出冰箱的35%,对应的是280台,求单位“1”,用280÷35%解答;用第一季度卖出冰箱的台数÷全年一共卖出冰箱的台数×100%,求出第一季度卖出的冰箱占全年的百分比;用全年一共卖出冰箱的台数×第四季度占卖出冰箱的百分比,求出第四季度卖出冰箱的台数,再用全年一共卖出冰箱的台数-第一季度卖出冰箱的台数-第三季度卖出冰箱的台数-第四季度卖出冰箱的台数,求出第二季度卖出冰箱的台数,再除以全年卖出冰箱的台数,再乘100%,即可求出第二季度买出的冰箱占全年的百分比;
(2)用全年卖出冰箱的台数×第四季度卖出冰箱占全年的百分比,求出第四季度卖出冰箱的台数;用全年卖出冰箱的台数-第一季度卖出冰箱的台数-第三季度卖出冰箱的台数-第四季度卖出冰箱的台数,求出第二季度卖出冰箱的台数;补充完整的条形统计图;
(3)用第一季度卖出冰箱的台数与第三季度卖出冰箱的台数差,除以第三季度卖出冰箱的台数,再乘100%,即可求出第一季度比第三季度少销售冰箱少百分之几,据此解答。
【详解】(1)280÷35%=800(台)
180÷800×100%
=0.225×100%
=22.5%
800×30%=240(台)
(800-180-280-240)÷800×100%
=(620-280-240)÷800×100%
=(340-240)÷800×100%
=100÷800×100%
=0.125×100%
=12.5%
2023年一共卖出800台冰箱;第一季度卖出的冰箱是全年的22.5%%,第二季度占全年的12.5%。
(2)800×30%=240(台)
800-180-280-240
=620-280-240
=340-240
=100(台)
如图:
(3)(280-180)÷280×100%
=100÷280×100%
≈0.357×100%
=35.7%
答:这个商场第一季度比第三季度少销售冰箱少35.7%。
45.(1)甲队;理由见详解
(2)13个
【分析】(1)用甲队6名队员穿越障碍的总个数除以6,计算出甲队的平均成绩;用乙队5名队员穿越障碍的总个数除以5,计算出乙队的平均成绩;通过比较甲、乙两队的平均成绩来判断两队成绩的好坏;
(2)分别计算甲、乙两队的总成绩,乙队要想超过甲队,用(甲队的总成绩+1)减去乙队的总成绩,所得差即为⑥号队员至少要穿过障碍的个数。
【详解】(1)甲队的平均成绩:
(7+6+8+9+4+8)÷6
=42÷6
=7(个)
乙队的平均成绩:
(9+5+7+3+6)÷5
=30÷5
=6(个)
因为7>6,所以甲队的平均成绩大于乙队的平均成绩,因此甲队的比赛成绩好些。
答:甲队。理由是:甲队的平均成绩比乙队的平均成绩高。
(2)(7+6+8+9+4+8+1)-(9+5+7+3+6)
=43-30
=13(个)
答:新加入的⑥号队员至少要穿过13个障碍。
46.(1)见详解
(2)16
(3)先快后慢
(4)100
【分析】(1)根据绘制折线统计图的方法,先描点,在统计图上找到对应的数据,再连线即可;
(2)加热前,是指没有加热的时候,即时间是0分的时候,对应的水温是16℃。
(3)根据折线统计图可知,刚开始的水温上涨的非常快,到最后上涨的速度比较平缓;由此即可填空;
(4)由于在第10分钟的时候水温是100℃,水的沸点在100℃,所以第11分钟的时候,水温不会有变化,即还是100℃,据此即可填空。
【详解】(1)如下图所示:
(2)加热前,水的温度是16℃;
(3)通过折线统计图可以看出,在加热过程中,水温上升的趋势是先快后慢。
(4)预测一下,如果加热到第11分钟,水温大约是100。
47.(1)A
(2)400;35
(3)80;图见详解
(4)960
【分析】(1)抽样调查的定义:被调查的样本中的每个个体都有相等的被抽到的机会;据此逐项分析;
(2)用B比较了解的人数除以B比较了解的人数的百分比,就是调查的总人数;用“很了解”的人数除以总人数就是“很了解”的占总人数的百分比;
(3)用总人数减去A很了解、B比较了解、D不了解的人数就是“了解较少”的人数,即可求出本次调查中对端午节文化习俗“了解较少”的学生有多少人,然后再在条形统计图中画出直方图即可。
(4)用学校的总人数乘B比较了解的人数的百分比,即可求出全校所有学生对端午节文化习俗“比较了解”的有多少人。
【详解】(1)A.从每个班中抽10名学生,有普遍性,符合题意;
B.从女子舞蹈队中选一些队员,没有普遍性,不符合题意;
C.从男子排球队中选一些队员,没有普遍性,不符合题意;
D.选一些对端午节文化习俗有了解的学生,不符合任意抽样的方法,不符合题意。
故答案为:A
(2)160÷40%=400(人)
140÷400×100%
=0.35×100%
=35%
本次调查共调查了400人,被调查的学生中对端午节文化习俗“很了解”的占总人数的35%。
(3)400-140-160-20
=260-160-20
=100-20
=80(人)
所以本次调查中对端午节文化习俗“了解较少的学生有80人。
作图如下:
(4)2400×40%=960(人)
若阳光小学共有学生2400人,估计全校所有学生对端午节文化习俗“比较了解”的有960人。
48.(1)C;60
(2)90°
(3)40
(4)A
【分析】(1)由图1可知,C类比D类少,比B类多。而图2中,C类比B类和D类都多,则C类是错误的。由图1可知,A类有120人,占被调查的学生人数的40%,根据已知一个数的百分之几,求这个数,用120÷40%求出被调查的学生人数,再根据求一个数的百分之几,用乘法分别求出B、C、D的人数,再与图2中的人数进行比较,即可验证结论;
(2)圆心角的度数是360度,由图1可知,喜欢舞蹈类的人数占总人数的25%,把360度看作单位“1”,根据求一个数的百分之几是多少,用乘法解答;
(3)求喜欢B类的学生比喜欢D类的学生少百分之几,用两个百分率的差除以D类的百分率;列式:(25%-15%)÷25%计算即可。
(4)扇形统计图中哪种兴趣爱好所占的百分比最大,那么这名学生喜欢哪类的可能性最大;据此进行比较即可解答。
【详解】(1)120÷40%=300(人)
300×15%=45(人)
300×20%=60(人)
300×25%=75(人)
所以有错误的类是C类,喜欢该类的学生应该有60人。
(2)360×25%=90°
所以喜欢舞蹈类的人数在扇形统计图中所占圆心角度数为90°。
(3)(25%-15%)÷25%
=10%÷25%
=0.1÷0.25
=40%
所以喜欢B类的学生比喜欢D类的学生少40%。
(4)15%<20%<25%<40%
喜欢A类的学生占的百分率最大,所以这名学生喜欢A类的可能性最大。
49.(1)(2)元(3)元
【分析】(1)将五月份的工资看作单位“”,再用“”减去生活费、储蓄、其他、水电费房租费解答即可;
(2)根据五月份的工资为元,生活费所占百分数为可知五月份的生活费,再根据四月份与五月份的生活费之比为即可解答;
(3)根据五月份的工资为元,储存所占百分数为可知五月份储存的金额为,再根据利息本金年利率存期解答即可。
【详解】(1)
答:购书费占工资的;
(2)设四月份李叔叔的生活费为元,
答:四月份李叔叔的生活费为元;
(3)
(元)
答:他可以得到元利息。
【点睛】本题考查了扇形统计图,比例方程与实际问题,利息本金年利率存期,审清题意找准数量关系是解题的关键。
50.(1)折线;扇形
(2)65.6%
(3)B
(4)见详解
【分析】(1)条形统计图能清楚地表示出数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;扇形统计图表示部分与整体之间的关系;
(2)用向阳路(东西方向)的车流量÷育才路(南北方向)车流量的×100%,代入数据;
(3)(4)356÷231≈1.5,257÷169≈1.5,174÷114≈1.5,388÷258≈1.5,90÷59≈1.5,育才路(南北方向)车流量大约是向阳路(东西方向)的车流量的1.5倍,所以最合理的方案是南北方向绿灯时长是东西方向绿灯时长的1.5倍,据此解答即可。
【详解】(1)根据上表,如果要统计该十字路口不同时段车流量的增减变化情况,应该绘制成折线统计图;如果要统计某一时段车流量占全天车流量的百分比,应绘制成扇形统计图。
(2)59÷90×100%
≈0.656×100%
=65.6%
答:19:00~20:00时段,向阳路(东西方向)的车流量大约是育才路(南北方向)车流量的65.6%。
(3)60÷40=1.5
我认为最合理的方案是南北方向绿灯时长为60秒,东西方向绿灯时长为40秒。
故答案为:B
(4)我选择的方案的理由是:红绿灯的设置时长主要取决于路口的具体位置,交通流量,车道使用比例以及路面的行车条件等因素,育才路(南北方向)车流量大约是向阳路(东西方向)的车流量的1.5倍,所以选择南北方向绿灯时长大约是东西方向绿灯时长的1.5倍。
答案第1页,共2页
21世纪教育网(www.21cnjy.com)
答案第1页,共2页
同课章节目录
