2025年6月甘肃省中考数学模拟试卷(含答案)
文档属性
| 名称 | 2025年6月甘肃省中考数学模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 248.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 10:24:10 | ||
图片预览



文档简介
2025年甘肃省中考数学模拟试卷(6月份)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.杰伦最近几次英语测验的成绩如下:第一次考了分,第二次比第一次高分,第三次比第二次高分,那么杰伦第三次英语成绩是( )
A. 分 B. 分 C. 分 D. 分
2.二十大报告中,一组组亮眼的数字,吸引无数目光,折射出新时代十年的非凡成就.其中,国内生产总值从万亿元增长到万亿元.请你把万亿元用科学记数法表示为( )
A. 元 B. 元 C. 元 D. 元
3.下列运算中,正确的是( )
A. B.
C. D.
4.如图,在中,,将绕点逆时针旋转到的位置,使得,则的度数是( )
A.
B.
C.
D.
5.若关于的一元二次方程有两个不相等的实数根,则的值可以是( )
A. B. C. D.
6.石墨烯在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景它的分子结构如图所示,所有多边形都是正六边形一个正六边形的内角和为( )
A.
B.
C.
D.
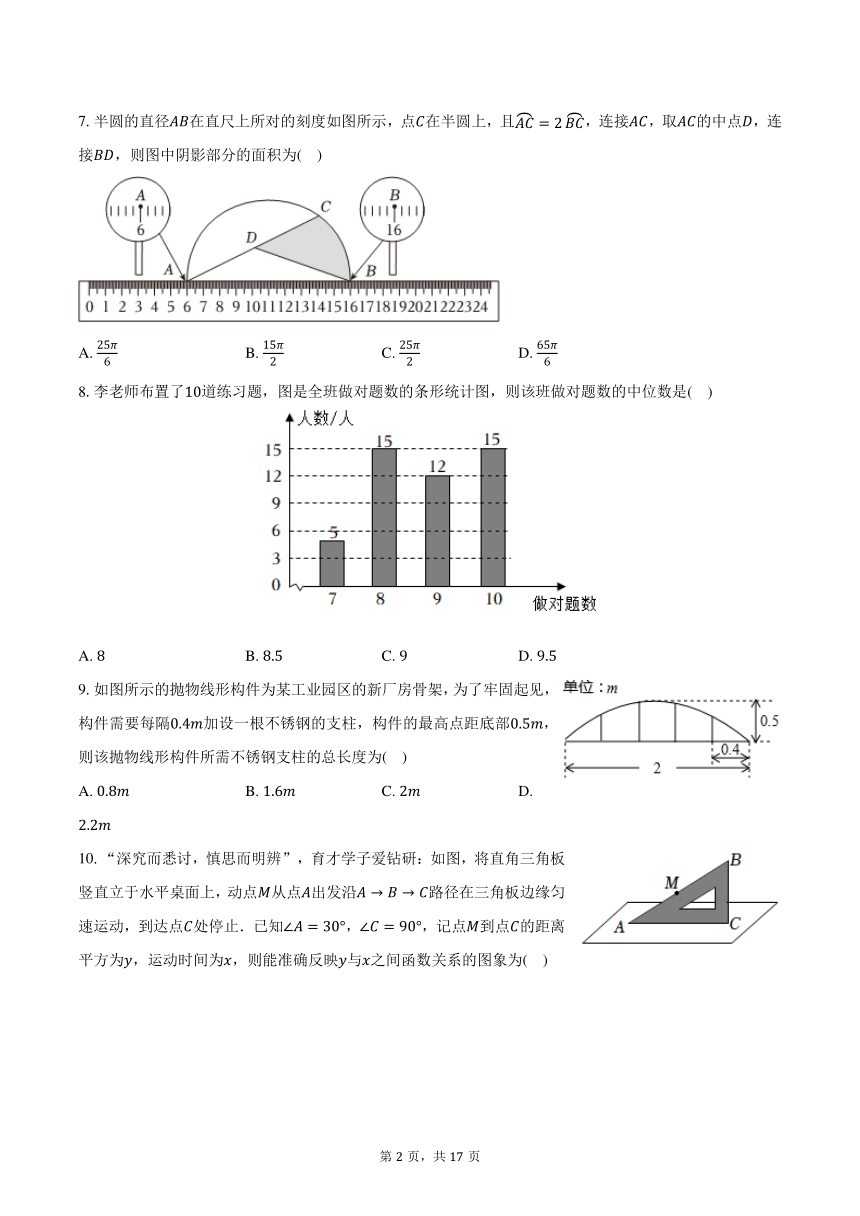
7.半圆的直径在直尺上所对的刻度如图所示,点在半圆上,且,连接,取的中点,连接,则图中阴影部分的面积为( )
A. B. C. D.
8.李老师布置了道练习题,图是全班做对题数的条形统计图,则该班做对题数的中位数是( )
A. B. C. D.
9.如图所示的抛物线形构件为某工业园区的新厂房骨架,为了牢固起见,构件需要每隔加设一根不锈钢的支柱,构件的最高点距底部,则该抛物线形构件所需不锈钢支柱的总长度为( )
A. B. C. D.
10.“深究而悉讨,慎思而明辨”,育才学子爱钻研:如图,将直角三角板竖直立于水平桌面上,动点从点出发沿路径在三角板边缘匀速运动,到达点处停止.已知,,记点到点的距离平方为,运动时间为,则能准确反映与之间函数关系的图象为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.分解因式: .
12.当 ______时,关于的方程的解是.
13.若反比例函数的图象上有两点,,若,则,的大小关系是______.
14.矩形纸片,,,在矩形边上有一点,且将矩形纸片折叠,使点与点重合,折痕所在直线交矩形两边于点,,则______.
15.我们假设把两边平方和等于第三边平方的两倍的三角形叫做奇异三角形.如果是奇异三角形,在中,,,,,且,其中,,那么 .
16.如图,在正六边形中,,将一个含的直角三角板的直角放入正六边形内,保证点,同时在三角板的边,上,转动三角板连接,则线段的最小值为______.
三、解答题:本题共11小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:;
化简:
18.本小题分
解不式组.
19.本小题分
小芳解答问题“已知,求的值”的过程如下:
,
,即,
.
.
请你根据小芳的解答过程,解决下列问题:
,求的值;
化简.
20.本小题分
如图,在中,是一条不过圆心的弦,,是的三等分点,直径交于点,连接交于点,连接,过点的切线交的延长线于点.
求证:;
若,求的值;
连接交于点,连接,若的半径为,,求与的周长比.
21.本小题分
学校为了践行“立德树人,实践育人”的目标,开展劳动课程,组织学生走进农业基地,欣赏田园风光,体验劳作的艰辛和乐趣,该劳动课程有以下小组:搭豇豆架、斩草除根趣挖番薯、开垦播种,学校要求每人只能参加一个小组,甲和乙准备随机报名一个小组.
甲选择“趣挖番薯”小组的概率是______;
请利用列表或画树状图的方法,求甲、乙两人选择同一个小组的概率.
22.本小题分
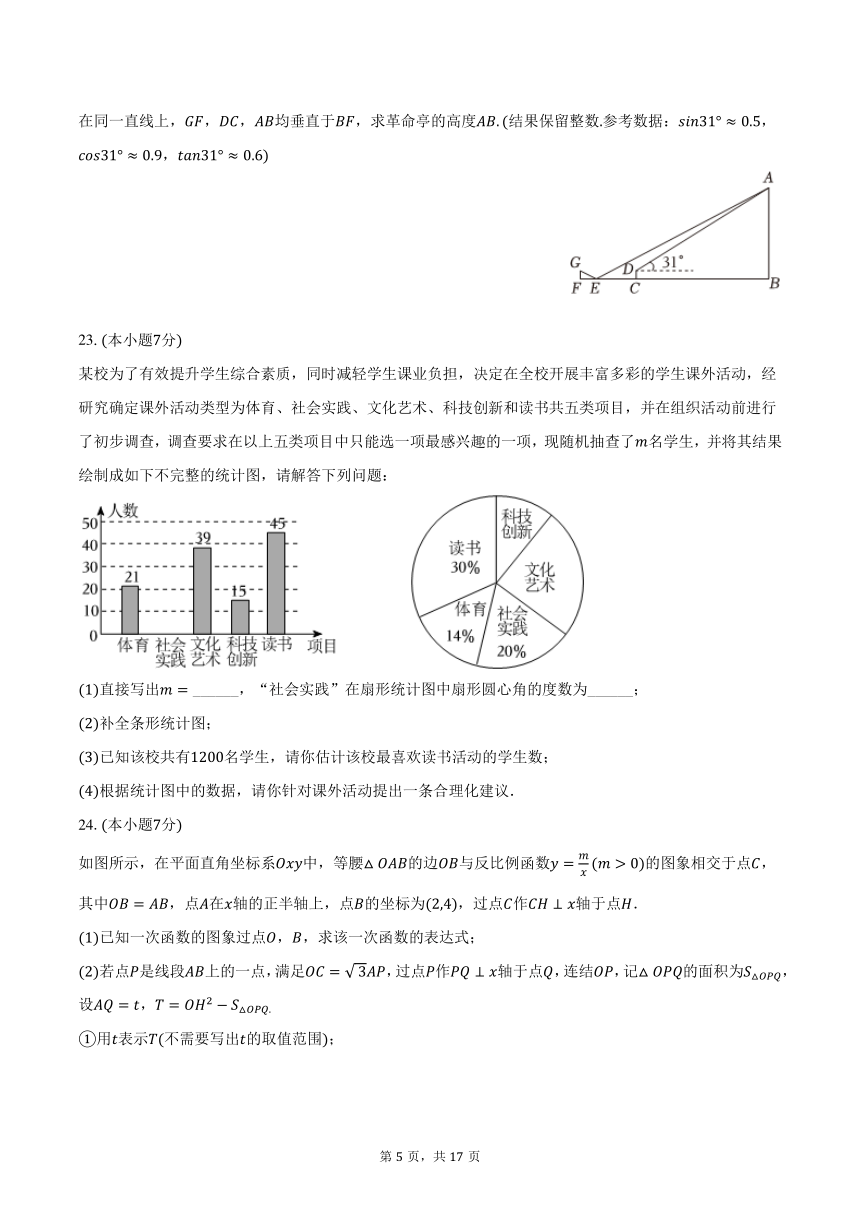
革命亭为西安革命公园标志性建筑,年革命亭被列为西安市市级重点文物保护单位为测量革命亭的高度,小明和小华作出了如下测量方案:如图,小明在点处利用测角仪测得革命亭顶部的仰角为,小华在距小明的点处水平放置了一块平面镜,当小华向后退至距平面镜的点处时,从平面镜中恰好可以看到革命亭顶部,已知小华的眼睛距地面的高度,测角仪的高度均为,点,,,在同一直线上,,,均垂直于,求革命亭的高度结果保留整数参考数据:,,
23.本小题分
某校为了有效提升学生综合素质,同时减轻学生课业负担,决定在全校开展丰富多彩的学生课外活动,经研究确定课外活动类型为体育、社会实践、文化艺术、科技创新和读书共五类项目,并在组织活动前进行了初步调查,调查要求在以上五类项目中只能选一项最感兴趣的一项,现随机抽查了名学生,并将其结果绘制成如下不完整的统计图,请解答下列问题:
直接写出 ______,“社会实践”在扇形统计图中扇形圆心角的度数为______;
补全条形统计图;
已知该校共有名学生,请你估计该校最喜欢读书活动的学生数;
根据统计图中的数据,请你针对课外活动提出一条合理化建议.
24.本小题分
如图所示,在平面直角坐标系中,等腰的边与反比例函数的图象相交于点,其中,点在轴的正半轴上,点的坐标为,过点作轴于点.
已知一次函数的图象过点,,求该一次函数的表达式;
若点是线段上的一点,满足,过点作轴于点,连结,记的面积为,设,
用表示不需要写出的取值范围;
当取最小值时,求的值.
25.本小题分
如图,在平面直角坐标系内,已知点,,,,记线段为,线段为,点是坐标系内一点.给出如下定义:若存在过点的直线与,都有公共点,则称点是联络点.例如,点是联络点.
以下各点中,______是联络点填出所有正确的序号;
;;.
直接在图中画出所有联络点所组成的区域,用阴影部分表示;
已知点在轴上,以为圆心,为半径画圆,上只有一个点为联络点,
若,求点的纵坐标;
求的取值范围.
26.本小题分
【探究发现】
如图,在四边形中,对角线,垂足是,求证:.
【拓展迁移】
如图,以三角形的边、为边向外作正方形和正方形,求证:.
如图,在小题条件不变的情况下,连接,若,,,求.
27.本小题分
定义:如果一条抛物线与轴有两个交点,且以该抛物线的顶点和这两个交点为顶点的三角形是等边三角形,那么称这条抛物线为“和谐抛物线”.
“和谐抛物线”中一定是______填“大于”、“小于”或“等于”零.
若抛物线是“和谐抛物线”,请求出、满足的关系式.
如图,抛物线是“和谐抛物线”,是否存在以原点为对称中心的矩形?若存在,求出、两点的坐标;若不存在,请说明理由.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】或
15.【答案】
16.【答案】
17.解:原式
;
原式
.
18.解:,
解不等式得:,
,
,
,
解不等式得:,
,
,
,
不等式组的解集为:.
19.解:,
,
即,
,
;
,
,
,
,
,
.
20.证明:,是的三等分点,
所以,
是的直径,
,
是的切线,
,
;
解:如图,连接,
,
,
,
,
又,
≌,
,
设,则.
,
.
.
在中,由勾股定理得:,
,
解得:负值舍去,
;
解:,,
.
,
,
设,则,.
在和中,由勾股定理得:,
,
解得:.
.
.
,
,.
,
∽,
,
,
,
,
∽,
与的周长比为.
21.解:甲选择“趣挖番薯”小组的概率是,
故答案为:;
画树状图如下:
共有种等可能的结果,其中甲、乙两人选择同一个小组的结果有种,
甲、乙两人选择同一个小组的概率为.
22.解:如图:过点作于点,
由条件可知,
,均垂直于,
四边形为矩形,
,,
,,
,
,
∽,
,即,
解得:,
.
革命亭的高度约为.
23.解:,
,
故答案为:,;
选择“社会实践”的学生人数为人,
补全条形统计图如下:
人,
答:估计该校最喜欢读书活动的学生数有人;
由图表可知,参加科技创新的人数较少,我认为学校要加强科技创新的宣传,并提供相应条件,促进科技创新活动的开展.建议有积极意义即可.
24.解:将点、的坐标代入一次函数表达式:得:,
解得:,
故一次函数表达式为:,
过点作,
则,
则,,
,则,则点,
设:,则,
在中,,
同理,
则,,
则点,
,
,有最小值,当时,
取得最小值,
此时点,
故:.
25.解:,是的联络点,
故答案为:;
所有的联络点所组成的区域为图中阴影部分含边界,如图所示:;
点在轴上,上只有一个点为的联络点,阴影部分关于轴对称,
和直线相切于,或与直线相切于,如图所示,
又的半径,
点的坐标为或,
经检验:此时与直线,无交点,上只有一个点为联络点,符合题意.
点的坐标为或,
点的纵坐标为或;
阴影部分关于直线对称,故不妨设点位于阴影部分下方.
点在轴上,上只有一个点为联络点,
阴影部分关于轴对称,
与直线相切于,且与直线相离.
作于,设与的交点为,
,,
在中,,,,
,,
在中,,,,
.
,
又,
.
26.证明:如图,于点,
,
,,,,
,,
.
证明:如图,交于点,交于点,
四边形和四边形都是正方形,
,,,
,
在和中,
,
≌,
,
,
,
,
.
解:如图,连接、,
由得,
,
,,,
,,
,,
,
,,
,
,
.
27.解:抛物线与轴有两个交点,
关于的一元二次方程有两个不相等的实数根,
.
故答案为:大于.
如图,设抛物线的顶点为,与轴交于、两点,
作于点,则,
抛物线是“和谐抛物线”,
是等边三角形,
,,
;
当时,则,
,
,
,
,
,
,
,
存在.
如图,由图象得,抛物线经过原点,且顶点为,与轴的另一个交点为,
作于点,
抛物线是“和谐抛物线”,
是等边三角形,
由得,;
当时,由得,,,
,
,
;
,
,
,
,
解得,不符合题意,舍去,
,;
四边形是以原点为对称中心的矩形,
点、分别与点、关于原点成中心对称,
,.
第8页,共17页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.杰伦最近几次英语测验的成绩如下:第一次考了分,第二次比第一次高分,第三次比第二次高分,那么杰伦第三次英语成绩是( )
A. 分 B. 分 C. 分 D. 分
2.二十大报告中,一组组亮眼的数字,吸引无数目光,折射出新时代十年的非凡成就.其中,国内生产总值从万亿元增长到万亿元.请你把万亿元用科学记数法表示为( )
A. 元 B. 元 C. 元 D. 元
3.下列运算中,正确的是( )
A. B.
C. D.
4.如图,在中,,将绕点逆时针旋转到的位置,使得,则的度数是( )
A.
B.
C.
D.
5.若关于的一元二次方程有两个不相等的实数根,则的值可以是( )
A. B. C. D.
6.石墨烯在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景它的分子结构如图所示,所有多边形都是正六边形一个正六边形的内角和为( )
A.
B.
C.
D.
7.半圆的直径在直尺上所对的刻度如图所示,点在半圆上,且,连接,取的中点,连接,则图中阴影部分的面积为( )
A. B. C. D.
8.李老师布置了道练习题,图是全班做对题数的条形统计图,则该班做对题数的中位数是( )
A. B. C. D.
9.如图所示的抛物线形构件为某工业园区的新厂房骨架,为了牢固起见,构件需要每隔加设一根不锈钢的支柱,构件的最高点距底部,则该抛物线形构件所需不锈钢支柱的总长度为( )
A. B. C. D.
10.“深究而悉讨,慎思而明辨”,育才学子爱钻研:如图,将直角三角板竖直立于水平桌面上,动点从点出发沿路径在三角板边缘匀速运动,到达点处停止.已知,,记点到点的距离平方为,运动时间为,则能准确反映与之间函数关系的图象为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.分解因式: .
12.当 ______时,关于的方程的解是.
13.若反比例函数的图象上有两点,,若,则,的大小关系是______.
14.矩形纸片,,,在矩形边上有一点,且将矩形纸片折叠,使点与点重合,折痕所在直线交矩形两边于点,,则______.
15.我们假设把两边平方和等于第三边平方的两倍的三角形叫做奇异三角形.如果是奇异三角形,在中,,,,,且,其中,,那么 .
16.如图,在正六边形中,,将一个含的直角三角板的直角放入正六边形内,保证点,同时在三角板的边,上,转动三角板连接,则线段的最小值为______.
三、解答题:本题共11小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:;
化简:
18.本小题分
解不式组.
19.本小题分
小芳解答问题“已知,求的值”的过程如下:
,
,即,
.
.
请你根据小芳的解答过程,解决下列问题:
,求的值;
化简.
20.本小题分
如图,在中,是一条不过圆心的弦,,是的三等分点,直径交于点,连接交于点,连接,过点的切线交的延长线于点.
求证:;
若,求的值;
连接交于点,连接,若的半径为,,求与的周长比.
21.本小题分
学校为了践行“立德树人,实践育人”的目标,开展劳动课程,组织学生走进农业基地,欣赏田园风光,体验劳作的艰辛和乐趣,该劳动课程有以下小组:搭豇豆架、斩草除根趣挖番薯、开垦播种,学校要求每人只能参加一个小组,甲和乙准备随机报名一个小组.
甲选择“趣挖番薯”小组的概率是______;
请利用列表或画树状图的方法,求甲、乙两人选择同一个小组的概率.
22.本小题分
革命亭为西安革命公园标志性建筑,年革命亭被列为西安市市级重点文物保护单位为测量革命亭的高度,小明和小华作出了如下测量方案:如图,小明在点处利用测角仪测得革命亭顶部的仰角为,小华在距小明的点处水平放置了一块平面镜,当小华向后退至距平面镜的点处时,从平面镜中恰好可以看到革命亭顶部,已知小华的眼睛距地面的高度,测角仪的高度均为,点,,,在同一直线上,,,均垂直于,求革命亭的高度结果保留整数参考数据:,,
23.本小题分
某校为了有效提升学生综合素质,同时减轻学生课业负担,决定在全校开展丰富多彩的学生课外活动,经研究确定课外活动类型为体育、社会实践、文化艺术、科技创新和读书共五类项目,并在组织活动前进行了初步调查,调查要求在以上五类项目中只能选一项最感兴趣的一项,现随机抽查了名学生,并将其结果绘制成如下不完整的统计图,请解答下列问题:
直接写出 ______,“社会实践”在扇形统计图中扇形圆心角的度数为______;
补全条形统计图;
已知该校共有名学生,请你估计该校最喜欢读书活动的学生数;
根据统计图中的数据,请你针对课外活动提出一条合理化建议.
24.本小题分
如图所示,在平面直角坐标系中,等腰的边与反比例函数的图象相交于点,其中,点在轴的正半轴上,点的坐标为,过点作轴于点.
已知一次函数的图象过点,,求该一次函数的表达式;
若点是线段上的一点,满足,过点作轴于点,连结,记的面积为,设,
用表示不需要写出的取值范围;
当取最小值时,求的值.
25.本小题分
如图,在平面直角坐标系内,已知点,,,,记线段为,线段为,点是坐标系内一点.给出如下定义:若存在过点的直线与,都有公共点,则称点是联络点.例如,点是联络点.
以下各点中,______是联络点填出所有正确的序号;
;;.
直接在图中画出所有联络点所组成的区域,用阴影部分表示;
已知点在轴上,以为圆心,为半径画圆,上只有一个点为联络点,
若,求点的纵坐标;
求的取值范围.
26.本小题分
【探究发现】
如图,在四边形中,对角线,垂足是,求证:.
【拓展迁移】
如图,以三角形的边、为边向外作正方形和正方形,求证:.
如图,在小题条件不变的情况下,连接,若,,,求.
27.本小题分
定义:如果一条抛物线与轴有两个交点,且以该抛物线的顶点和这两个交点为顶点的三角形是等边三角形,那么称这条抛物线为“和谐抛物线”.
“和谐抛物线”中一定是______填“大于”、“小于”或“等于”零.
若抛物线是“和谐抛物线”,请求出、满足的关系式.
如图,抛物线是“和谐抛物线”,是否存在以原点为对称中心的矩形?若存在,求出、两点的坐标;若不存在,请说明理由.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】或
15.【答案】
16.【答案】
17.解:原式
;
原式
.
18.解:,
解不等式得:,
,
,
,
解不等式得:,
,
,
,
不等式组的解集为:.
19.解:,
,
即,
,
;
,
,
,
,
,
.
20.证明:,是的三等分点,
所以,
是的直径,
,
是的切线,
,
;
解:如图,连接,
,
,
,
,
又,
≌,
,
设,则.
,
.
.
在中,由勾股定理得:,
,
解得:负值舍去,
;
解:,,
.
,
,
设,则,.
在和中,由勾股定理得:,
,
解得:.
.
.
,
,.
,
∽,
,
,
,
,
∽,
与的周长比为.
21.解:甲选择“趣挖番薯”小组的概率是,
故答案为:;
画树状图如下:
共有种等可能的结果,其中甲、乙两人选择同一个小组的结果有种,
甲、乙两人选择同一个小组的概率为.
22.解:如图:过点作于点,
由条件可知,
,均垂直于,
四边形为矩形,
,,
,,
,
,
∽,
,即,
解得:,
.
革命亭的高度约为.
23.解:,
,
故答案为:,;
选择“社会实践”的学生人数为人,
补全条形统计图如下:
人,
答:估计该校最喜欢读书活动的学生数有人;
由图表可知,参加科技创新的人数较少,我认为学校要加强科技创新的宣传,并提供相应条件,促进科技创新活动的开展.建议有积极意义即可.
24.解:将点、的坐标代入一次函数表达式:得:,
解得:,
故一次函数表达式为:,
过点作,
则,
则,,
,则,则点,
设:,则,
在中,,
同理,
则,,
则点,
,
,有最小值,当时,
取得最小值,
此时点,
故:.
25.解:,是的联络点,
故答案为:;
所有的联络点所组成的区域为图中阴影部分含边界,如图所示:;
点在轴上,上只有一个点为的联络点,阴影部分关于轴对称,
和直线相切于,或与直线相切于,如图所示,
又的半径,
点的坐标为或,
经检验:此时与直线,无交点,上只有一个点为联络点,符合题意.
点的坐标为或,
点的纵坐标为或;
阴影部分关于直线对称,故不妨设点位于阴影部分下方.
点在轴上,上只有一个点为联络点,
阴影部分关于轴对称,
与直线相切于,且与直线相离.
作于,设与的交点为,
,,
在中,,,,
,,
在中,,,,
.
,
又,
.
26.证明:如图,于点,
,
,,,,
,,
.
证明:如图,交于点,交于点,
四边形和四边形都是正方形,
,,,
,
在和中,
,
≌,
,
,
,
,
.
解:如图,连接、,
由得,
,
,,,
,,
,,
,
,,
,
,
.
27.解:抛物线与轴有两个交点,
关于的一元二次方程有两个不相等的实数根,
.
故答案为:大于.
如图,设抛物线的顶点为,与轴交于、两点,
作于点,则,
抛物线是“和谐抛物线”,
是等边三角形,
,,
;
当时,则,
,
,
,
,
,
,
,
存在.
如图,由图象得,抛物线经过原点,且顶点为,与轴的另一个交点为,
作于点,
抛物线是“和谐抛物线”,
是等边三角形,
由得,;
当时,由得,,,
,
,
;
,
,
,
,
解得,不符合题意,舍去,
,;
四边形是以原点为对称中心的矩形,
点、分别与点、关于原点成中心对称,
,.
第8页,共17页
同课章节目录
